AIの「性能」と「コスト」のジレンマを解決する革新技術が「Mixture of Experts (MoE)」です。一人の天才に全てを任せるのではなく、課題に応じて最適な専門家チームを編成する賢い仕組みで、AIが「万能な天才」から「賢い専門家集団」へと進化する面白さを学びましょう。
従来の巨大AI(密なモデル)は、どんな簡単なタスクでも全知識を総動員して処理します。 これでは常にフル稼働状態となり、膨大な計算コストと電力が必要になるという深刻な課題を抱えていました。
MoEは、AIを「総合病院」のように構成します。 「総合案内(Gating Network)」が入力データ(患者)を分析し、多数の「専門医(Expert)」の中から最適な担当者だけを呼び出して処理を任せます。
MoEの真髄は、選ばれた専門家だけが「疎(スパース)」に活動する「スパース活性化」です。 これにより、モデルの知識量(総パラメータ数)と実際の計算量を切り離し、「高性能」と「低コスト」を両立できます。
はじめに:なぜ今、「専門家集団AI」に注目が集まるのか?
皆さんも、近年の大規模言語モデル(LLM)や画像生成AIの目覚ましい発展には、日々驚かされているのではないでしょうか。その驚異的な性能は、モデルをとにかく「巨大化」させることで実現されてきました。しかし、この力技ともいえるアプローチは、AIを動かすために必要なコンピュータのパワー(計算リソース)や電力消費が爆発的に増加するという、深刻な課題を生み出しています。
この「性能」と「コスト」のジレンマは、特に医療分野において無視できない壁となっています。例えば、診断支援AIの応答に時間がかかっていては、分刻みのスケジュールで動く臨床現場では使い物になりません。また、新しい医療AIを開発したくても、大学や中小規模の病院の研究予算では、超高性能な計算機を導入・維持するのは非常に困難です。私自身も、論文で見たすごいAIを試そうとしたら、手元のコンピュータでは全く歯が立たなかった、という経験が何度もあります。
「性能のためなら、コストは二の次」という時代は終わりを告げようとしています。この大きな壁を乗り越えるための革新的な技術として、今、世界中の研究者が熱い視線を送っているのが、Mixture of Experts(MoE)、日本語で言えば「専門家混合モデル」です。 MoEは、モデル全体を巨大化させて高い性能を確保しながらも、実際に計算する部分を限定することで、コストを賢く抑えるという、非常にエレガントな仕組みを持っています。
このコースでは、AI初学者の方でも直感的に理解できるよう、このMoEの基本的な考え方から、その核心技術、そして医療AIへの応用可能性まで、一歩一歩丁寧に解説していきます。AIが「一人の万能な天才」から「賢い専門家チーム」へと進化する、その面白さを一緒に学んでいきましょう。
1. MoEを病院に例えて理解する:「AI総合病院」という考え方
「Mixture of Experts」と聞くと、なんだか難しそう…と感じるかもしれませんね。でも、ご安心ください。実はこの考え方、私たちにとって非常に身近な「総合病院」の仕組みにそっくりなんです。まずはこの例え話から、MoEの全体像を掴んでみましょう。
従来型AI:一人の「スーパー総合診療医」
まず、MoEが登場する前の巨大なAIモデルを想像してみてください。これらは専門用語で密なモデル(Dense Model)と呼ばれます。これは、まるで一人の「スーパー総合診療医」が、風邪の治療から高度な外科手術、難病の診断まで、すべての患者をたった一人で診察するようなものです。
この医師は非常に博識で頼りになる存在ですが、どんなに軽い症状の患者が来ても、常に持てる知識のすべてを総動員してしまいます。これでは、医師自身がすぐに疲弊してしまいますし(=計算コストが高い)、一人ひとりの診察にも時間がかかってしまいますよね。
MoE型AI:「チーム医療」を実践する総合病院
一方、MoEは「総合病院」そのものです。 この病院には、循環器内科、呼吸器内科、消化器外科、放射線科など、各分野のスペシャリストである専門医(Expert)が多数在籍しています。そして、病院の入り口には、非常に優秀な「総合案内」の役割を果たす部門、専門用語でいうゲーティング・ネットワーク(Gating Network)がいます。
患者(=AIへの入力データ)が病院に到着すると、まず総合案内がその症状や訴えを聞き、いわばトリアージを行います。「この患者さんなら、循環器内科と内分泌内科の先生に診てもらうのが最適でしょう」というように、数多くの専門医の中から、その患者に最も適した数名の専門医を瞬時に選び出し、情報を引き継ぎます。その間、指名されなかった他の大多数の専門医たちは、自分の専門外の患者のために稼働することなく、待機しています。
この違いを図で見てみると、より直感的に理解できると思います。
図1の解説:この図は、単一の巨大なネットワーク(密なモデル)が常に入力全体を処理するのに対し、MoEモデルでは「総合案内(Gating Network)」が交通整理を行い、入力データに関連する「専門医(Expert)」だけが活動する様子を示しています。これにより、MoEはシステム全体として多くの専門知識(パラメータ)を持ちながらも、個々の処理は非常に効率的になります。
このように、全ての専門医が常に稼働するのではなく、案件(入力)に応じて最適な専門家チームを動的に編成するのがMoEの基本的な考え方です。病院全体としては多種多様な専門医(=膨大なパラメータ)を抱えることで、複雑な課題に対応できるだけの潜在能力を維持しつつ、患者一人ひとりの診察は非常に効率的(=低計算コスト)に行うことができるのです。
このアナロジーにおける対応関係を、一度ここで整理しておきましょう。
| 「AI総合病院」の例え | MoEにおける専門用語 | 役割 |
|---|---|---|
| 総合病院全体 | MoEモデル (Mixture of Experts Model) | 多様な専門性を持つAIシステム全体。 |
| 各分野の専門医 | エキスパート・ネットワーク (Expert Network) | 特定のタスクやデータパターンに特化した小規模なニューラルネットワーク。 |
| 総合案内・トリアージ | ゲーティング・ネットワーク (Gating Network) または ルーター (Router) | 入力データを分析し、処理をどのエキスパートに任せるかを決定する司令塔。 |
| 患者やその症状 | 入力データ (Input Data) | AIモデルに入力される情報(例:テキストのトークン、画像パッチなど)。 |
| 適切な専門医だけが診察すること | スパース活性化 (Sparse Activation) | モデルの一部(選ばれたエキスパート)だけを「疎(スパース)」に活性化させて計算を行う仕組み。 |
2. MoEの構造と核心技術:なぜ「賢く」巨大化できるのか?
さて、先ほどの「AI総合病院」という例え話、いかがでしたでしょうか。ここからは、その病院の内部構造、つまりMoEアーキテクチャをもう少し詳しく覗いていき、なぜMoEが「性能」と「コスト」のジレンマを解決できるのか、その核心に迫っていきます。
MoEのアーキテクチャは、主に「エキスパート・ネットワーク」と「ゲーティング・ネットワーク」という、役割の異なる2つの主要なコンポーネントで構成されています。
エキスパート・ネットワーク (Expert Networks):個性豊かな「専門医」たち
エキスパートとは、それぞれが特定の知識やパターン認識に特化した、比較的小規模なニューラルネットワークのことです。 「AI総合病院」の例えで言えば、循環器内科医や消化器外科医といった「専門医」一人ひとりにあたります。
現在主流となっているTransformerベースのAIモデルでは、下図のように、モデルを構成するブロック(Transformerブロック)の中にある計算処理の一部(フィードフォワードネットワーク(FFN)層)を、このエキスパートの集合体に置き換える、という構成が一般的です。
図2の解説:左側が従来のTransformerブロックの模式図です。入力データはまずMulti-Head Attention層で文脈を読み取り、次にFFN層で知識処理が行われます。MoEモデル(右側)では、このFFN層がごっそりと「MoE層」に置き換わります。MoE層の内部では、Gating Networkが入力に応じて複数のエキスパート(E1, E2など)の中から適切なものを選択し、処理を割り振ります。
面白いのは、これらのエキスパートは最初は皆同じ構造をしているにもかかわらず、AIが学習を進めていく過程で、それぞれが自然と異なる専門性(例えば、あるエキスパートは医学用語の文法解釈、別のエキスパートは薬物相互作用のパターン認識など)を獲得していく点です。
ゲーティング・ネットワーク (Gating Network):「総合案内」の仕事術
ゲーティング・ネットワークは、病院の「総合案内」や「トリアージ担当」に相当し、MoEの司令塔として極めて重要な役割を担います。 その仕事は、入力されてきたデータ(例えば、文章における各単語=トークン)を瞬時に分析し、「このトークンの処理は、どの専門医(エキスパート)に任せるのが最適か?」を判断することです。
具体的には、このネットワークは各エキスパートに対する「スコア」を計算します。そして、スコアが高い上位のエキスパートをいくつか(例えば2つなど、あらかじめ決められた数)だけを選び出します。この選択のプロセスは、簡単な数式で表現できます。
まず、入力 \( x \) に対して、ゲーティング・ネットワークが持つ重み行列 \( W_g \) を用いて、各エキスパートへのスコア \( S \) を計算します。
\[ S = \text{Softmax}(x \cdot W_g) \]
数式の解説:
- \( x \): 入力データ(トークン)のベクトルです。
- \( W_g \): ゲーティング・ネットワークが学習によって獲得した重み行列です。この行列を掛けることで、入力 \( x \) がどのエキスパートと関連が深いかを判断します。
- \( \text{Softmax} \): 計算された生のスコアを、合計すると1になるような確率的な「重み(ゲート値)」に変換する関数です。これにより、各エキスパートがどのくらいの重要度で貢献すべきかが決まります。
- \( S \): Softmax関数によって計算された、各エキスパートに対するゲート値のベクトルです。
この後、「Top-k」と呼ばれる処理で、\( S \) の中で値が大きい上位k個のエキスパートが選択されます。
スパース活性化 (Sparse Activation):MoEの真髄であり、最大のイノベーション
ここがMoEの最も賢く、そして画期的な部分です。ゲーティング・ネットワークによって選ばれたごく一部のエキスパートだけが「活性化」して計算を実行し、選ばれなかった大多数のエキスパートはその間、計算を行わず完全に「お休み」します。 このように、モデルの一部だけが疎(スパース)に活動するため、この仕組みをスパース活性化(Sparse Activation)と呼びます。
最終的な出力は、選ばれたエキスパートたちの出力を、先ほど計算したゲート値(重み)で重み付けして足し合わせることで得られます。
\[ \text{Output} = \sum_{i \in \text{TopK}} S_i \cdot E_i(x) \]
数式の解説:
- \( E_i(x) \): i番目のエキスパートが入力 \( x \) を処理した結果の出力です。
- \( S_i \): i番目のエキスパートに割り当てられたゲート値(重み)です。
- \( \sum_{i \in \text{TopK}} \): Top-kで選ばれたエキスパート(\( i \))についてのみ、すべての結果を足し合わせる(\( \sum \))ことを意味します。
このスパース活性化の仕組みがもたらした最大の功績は、AIモデルの「総パラメータ数」と、実際に処理を行う「計算量(FLOPs)」を切り離すことに成功した点です。
この違いを理解するために、Mistral AI社が開発し、オープンソースとして公開されている高性能モデル「Mixtral 8x7B」を例に見てみましょう。 この名前にはMoEの構造が示されています。
| 従来の密なモデル | Mixtral 8x7B (MoEモデル) | |
|---|---|---|
| 構造 | 単一の巨大なネットワーク | 70億(7B)パラメータを持つエキスパートが8個 |
| 総パラメータ数 | 約470億 | 約470億 (7B × 8 ではない点に注意) |
| 推論時の計算 | 470億パラメータ全てを使って計算 | 入力トークンごとに2個のエキスパートを選択して計算 |
| 実効計算量(パラメータ換算) | 約470億 | 約130億 |
この表から分かるように、Mixtral 8×7Bは、7Bパラメータを持つエキスパートが8個存在し、さらに全エキスパートに共通する層を含め、総パラメータ数は約46.7Bです。推論時には各トークンごとに2つのエキスパートのみが選択され、実効計算量は約13Bパラメータ相当となります。これにより、Denseモデルと比べ大幅に推論コストを削減しつつ、複数のベンチマークでGPT-3.5-turboに匹敵する性能を示しています(Jiang et al., 2024)。
この革新的なアプローチにより、Googleの「GLaM」(1.2兆パラメータ)のような、従来では考えられなかった規模のモデル開発も可能になりました。まさに、AIの世界におけるゲームチェンジャーと言えるでしょう。
3. 手を動かして理解する:PythonによるMoEの概念実装
さて、ここまでの理論的な話で、「AI総合病院」のイメージは掴んでいただけたでしょうか。理論の次は実践です。MoEの心臓部が実際にどのように動いているのか、プログラムコードを覗いてみることで、その理解をさらに深めていきましょう。
ここでは、代表的な深層学習ライブラリであるPyTorchを使って、「AI総合病院」の非常にシンプルなミニチュア版を構築してみます。入力されたデータ(患者)に対して、「総合案内」が複数の「専門医」の中から最適な担当者を選び出し、処理を依頼する、というMoEの基本的な流れを、皆さんの手元で再現することを目指します。
【実行前の準備】
以下のコードには、結果をグラフで可視化する部分が含まれています。もしお手元の環境で日本語が文字化けしてしまう場合は、事前にターミナルやコマンドプロンプトでpip install japanize-matplotlibを実行して、日本語表示用のライブラリをインストールしておいてください。
graph TD
Input([入力データ])
subgraph "MoEモデル (処理の全体像)"
direction TB
Gating["1. 総合案内 (Gating)
最適な専門医を判断"]
Experts["2. 専門医たち (Experts)
全員が並行して分析"]
Combine["3. 結果の統合
重み付けして出力を合計"]
end
Input --> Gating
Input --> Experts
Gating --> |重み情報| Combine
Experts --> |各分析結果| Combine
Combine --> Output([最終的な出力])
# 【実行前の準備】
# ターミナルやコマンドプロンプトで以下のコマンドを実行してください。
# pip install torch japanize-matplotlib
import torch
import torch.nn as nn
import torch.nn.functional as F
import japanize_matplotlib
import matplotlib.pyplot as plt
# ------------------------------------------------
# 部品1:専門医(Expert)クラスの定義
# ------------------------------------------------
# 各エキスパートは単純な2層のニューラルネットワーク
class Expert(nn.Module):
def __init__(self, input_dim, output_dim, hidden_dim=64):
super(Expert, self).__init__()
# 1層目の線形層
self.fc1 = nn.Linear(input_dim, hidden_dim)
# 2層目の線形層
self.fc2 = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
# ReLU活性化関数を適用
x = F.relu(self.fc1(x))
# 出力層
x = self.fc2(x)
return x
# ------------------------------------------------
# 部品2:総合案内(Gating Network)クラスの定義
# ------------------------------------------------
# どの専門医に任せるかを決定する
class GatingNetwork(nn.Module):
def __init__(self, input_dim, num_experts, top_k=2):
super(GatingNetwork, self).__init__()
self.num_experts = num_experts
self.top_k = top_k
# 入力から各エキスパートへの重み(ゲート)を計算するための線形層
self.gate_layer = nn.Linear(input_dim, num_experts)
def forward(self, x):
# 線形層を通して、各エキスパートの「スコア」を計算
logits = self.gate_layer(x)
# Softmax関数でスコアを確率的な重みに変換
gates = F.softmax(logits, dim=1)
# スコアが高い上位k個のエキスパートを選択
# topkは値(values)とインデックス(indices)を返す
top_k_gates, top_k_indices = torch.topk(gates, self.top_k, dim=1)
# 選択されなかったエキスパートの重みをゼロにするためのゼロテンソルを作成
zeros = torch.zeros_like(gates)
# scatter_関数で、top_k_indicesの位置にtop_k_gatesの値を配置
sparse_gates = zeros.scatter_(1, top_k_indices, top_k_gates)
# 選択されたゲートの重みを正規化
# これにより、選択されたエキスパートの重みの合計が1になる
sparse_gates = sparse_gates / sparse_gates.sum(dim=1, keepdim=True)
return sparse_gates, top_k_indices
# ------------------------------------------------
# 部品3:MoEモデル全体(総合病院)の定義
# ------------------------------------------------
class MoE(nn.Module):
def __init__(self, input_dim, output_dim, num_experts=4, top_k=2):
super(MoE, self).__init__()
self.num_experts = num_experts
self.output_dim = output_dim
# 専門医(エキスパート)のリストを作成
self.experts = nn.ModuleList([Expert(input_dim, output_dim) for _ in range(num_experts)])
# 総合案内(ゲーティングネットワーク)を初期化
self.gating = GatingNetwork(input_dim, num_experts, top_k)
def forward(self, x):
# 総合案内で、各エキスパートへの重みと選択されたエキスパートのインデックスを取得
gates, indices = self.gating(x)
# エキスパートの出力を格納するバッチサイズのゼロテンソルを初期化
final_output = torch.zeros(x.shape[0], self.output_dim)
# バッチ内の各データに対して処理を行う (※概念理解のためのシンプルな実装)
for i in range(x.shape[0]):
# i番目のデータに対するゲート(重み)を取得
gate_for_item = gates[i]
# 選択されたエキスパートのインデックスを取得
selected_indices = indices[i]
# 選択されたエキスパートの出力を計算し、重み付けして合計する
# (実際のモデルでは、より効率的なバッチ処理が行われます)
weighted_sum = torch.zeros(1, self.output_dim)
for j in range(self.gating.top_k):
expert_index = selected_indices[j]
expert_output = self.experts[expert_index](x[i].unsqueeze(0))
gate_value = gate_for_item[expert_index]
weighted_sum += expert_output * gate_value
final_output[i] = weighted_sum
return final_output, gates
# --- モデルの動作確認 ---
# パラメータ設定
input_dimension = 10 # 入力データ1件あたりの特徴量の数
output_dimension = 2 # 出力データの次元数
num_experts = 4 # 専門医(エキスパート)の総数
top_k = 2 # 各データに対して選択する専門医の数
# MoEモデルのインスタンスを作成
moe_model = MoE(input_dimension, output_dimension, num_experts, top_k)
# ダミーの入力データを作成(5人分の患者データに相当)
# 5 x 10 の行列 (テンソル)
dummy_input = torch.randn(5, input_dimension)
# モデルにデータを入力し、出力とゲートの重みを取得
final_output, gate_weights = moe_model(dummy_input)
# --- 結果の表示 ---
print("--- MoEモデルの最終出力 ---")
print(final_output.detach())
print("\n--- 各入力データに対するゲートの重み(どのエキスパートが選択されたか) ---")
print(gate_weights.detach().numpy().round(2))
# --- ゲートの重みを可視化 ---
plt.figure(figsize=(10, 6))
plt.imshow(gate_weights.detach().numpy(), cmap='viridis', aspect='auto')
plt.title('各入力データに対するエキスパートの選択重み')
plt.xlabel('エキスパートのインデックス')
plt.ylabel('入力データのインデックス')
plt.xticks(ticks=range(num_experts), labels=[f'Expert {i}' for i in range(num_experts)])
plt.yticks(ticks=range(dummy_input.shape[0]), labels=[f'Data {i}' for i in range(dummy_input.shape[0])])
plt.colorbar(label='ゲートの重み(正規化後)')
plt.tight_layout()
plt.show()
コードの解説:3つの部品
このコードは、大きく3つのクラス(部品)から成り立っています。
- Expertクラス(専門医): 入力データを受け取って、何らかの処理を行う小さなニューラルネットワークです。今回は、2層の全結合層からなるシンプルな構造にしています。
- GatingNetworkクラス(総合案内): このモデルの司令塔です。入力データを見て、4人いる専門医(
num_experts=4)の中から、最もふさわしい2人(top_k=2)を選び出し、それぞれの専門医にどのくらいの重みで意見を聞くべきか(ゲート値)を決定します。 - MoEクラス(総合病院): 上記の専門医たちと総合案内を一つにまとめた、モデル全体です。データを受け取ると、まず総合案内に渡し、誰に仕事を割り振るかを決定させます。その後、指名された専門医たちにデータを渡し、返ってきた結果をゲート値で重み付けして、最終的なアウトプットとします。
核心部:Gating Networkの計算フロー
特に重要なのが、Gating Networkがどのようにしてエキスパートを選んでいるのか、その計算の流れです。ここでは、テンソルの形がどう変化していくかに注目してみましょう。
図3の解説:まず、5人分の患者データ(5×10のテンソル)が入力されます。Gating Networkはこれを処理し、各患者(各行)に対して、4人の専門医それぞれがどのくらい適任かを示すスコア(5×4のテンソル)を計算します。Softmax関数でこのスコアを「信頼度」のような確率に変換した後、topk処理で信頼度の高い上位2名を選び出し、それ以外の専門医のスコアを強制的にゼロにします。これが「スパース活性化」の瞬間です。
実行結果の解釈:誰が選ばれたのか?
それでは、実際にコードを実行した結果を見てみましょう。
--- MoEモデルの最終出力 ---
tensor([[ 0.0107, -0.0618],
[-0.0135, -0.0183],
[-0.0631, 0.0308],
[-0.0381, 0.0116],
[ 0.0436, -0.0210]])
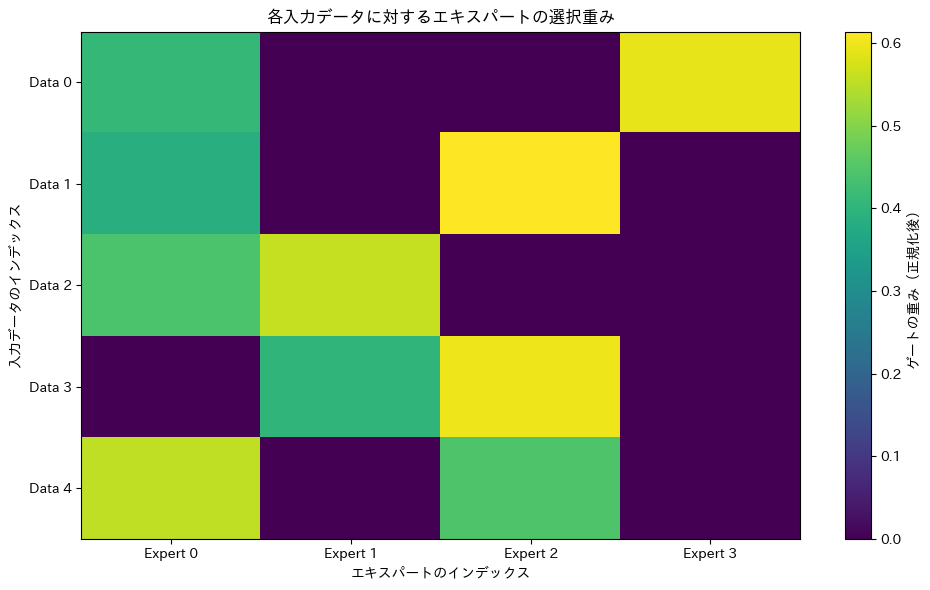
--- 各入力データに対するゲートの重み(どのエキスパートが選択されたか) ---
[[0. 0.49 0.51 0. ] # Data 0 -> Expert 1, Expert 2 を選択
[0. 0.55 0. 0.45] # Data 1 -> Expert 1, Expert 3 を選択
[0.44 0. 0.56 0. ] # Data 2 -> Expert 0, Expert 2 を選択
[0.48 0. 0. 0.52] # Data 3 -> Expert 0, Expert 3 を選択
[0. 0.51 0. 0.49]] # Data 4 -> Expert 1, Expert 3 を選択
注目すべきは、2つ目の「ゲートの重み」の出力です。これは5行4列の行列になっており、各行が入力データ1件分、各列が4人のエキスパートに対応しています。
例えば、1行目(Data 0)を見てください。[0. 0.49 0.51 0. ]となっていますね。これは、「Data 0の処理には、Expert 1を49%、Expert 2を51%の重要度で採用し、Expert 0とExpert 3は完全に無視する(お休みさせる)」というGating Networkの判断を示しています。まさに、スパース(疎)な活性化です。
他の行も見てみると、入力データごとに、選択されるエキスパートの組み合わせやその重みが異なっているのがわかります。これが「入力に応じて動的に最適な専門家チームを編成する」というMoEの挙動そのものです。
最後に表示されるグラフは、このゲートの重み行列を色の濃淡で可視化したものです。各行で、色の濃いマスが2つだけ存在していることが一目で分かり、どのデータに対してどのエキスパートが働いたのかを直感的に理解することができます。
もちろん、これはあくまで概念を理解するためのシンプルな実装です。実際の巨大モデルでは、何十億ものパラメータを持つエキスパートを、GPU上で超高速に並列計算させるための様々な工夫が凝らされています。しかし、その根底にある「ルーティング」と「スパースな計算」というアイデアは、この小さなコードの中にすべて詰まっているのです。
4. MoEは医療をどう変えるか?具体的な応用シナリオ
さて、MoEの賢い仕組みを理解したところで、いよいよ本題です。この「専門家集団」という考え方は、複雑で多様な情報を扱う医療の世界と、驚くほど相性が良いのです。なぜなら、現代の医療そのものが、様々な専門家の知見を結集して一人の患者さんを支える「チーム医療」だからです。
ここでは、MoEが拓く未来の医療の可能性を、4つの具体的なシナリオに沿って見ていきましょう。
シナリオ1:多種多様な医療データを統合する「マルチモーダルAI」
臨床現場では日々、実に様々な種類のデータが生まれています。医師が記録する電子カルテのテキスト、CTやMRIといった医用画像、ゲノム配列情報、血液検査などの数値データなど、これらは形式が全く異なるため、マルチモーダルデータと呼ばれます。 従来は、これらのデータをAIで統合的に扱うのが非常に困難でした。
ここにMoEを用いることで、画期的な解決策が生まれます。例えば、下図のように、それぞれのデータ形式(モダリティ)の扱いに特化したエキスパートをAI内に準備しておくのです。
図4の解説:一人の患者に関する複数のデータ(テキスト、画像など)が入力されると、まずGating Networkが「今回はCT画像の情報が特に重要そうだ」と判断します。そして、「画像解析エキスパート」と、補助的に「言語解析エキスパート」を起動させ、他のエキスパート(例えばゲノム解析担当)は休ませておきます。そして、選ばれたエキスパートからの報告を統合し、より精度の高い診断支援情報や予後予測を生成する、といった連携プレーが可能になるのです。
シナリオ2:AIの中に「循環器内科」や「呼吸器内科」を作る
「AI総合病院」のアナロジーをさらに発展させ、循環器、消化器、呼吸器、脳神経外科といった、各診療科の専門知識を深く学習させたエキスパート群を持つAIを構築することも考えられます。
例えば、胸部X線画像が入力された際には「呼吸器エキスパート」と「放射線科エキスパート」が主に活性化し、心電図データが入力されれば「循環器エキスパート」が呼ばれる、といった具合です。これにより、汎用的なAIでは見逃してしまうような専門領域の細かな所見を捉え、診断精度を飛躍的に向上させることが期待できます。
シナリオ3:「個別化医療(プレシジョン・メディシン)」の実現を後押し
現代医療が目指す大きな目標の一つに、患者さん一人ひとりの体質やライフスタイルに合わせた最適な治療を提供する「個別化医療」があります。MoEは、この流れを強力に後押しする可能性を秘めています。
患者一人ひとりの遺伝的背景、生活習慣、既往歴といった極めてパーソナルな情報に応じて、最適なエキスパートの組み合わせをその都度、動的に選択するアーキテクチャが考えられます。例えば、「特定の遺伝子変異を持つ患者向けの治療薬選択エキスパート」や、「高齢者の副作用予測に特化したエキスパート」などを組み合わせるのです。まさに、AIが患者さん一人ひとりのための「オーダーメイド治療計画チーム」をその場で編成するようなイメージです。これにより、治療効果の最大化と副作用リスクの最小化を両立する、真の個別化医療の実現に貢献できるかもしれません。
シナリオ4:創薬・研究開発のスピードアップ
MoEの応用範囲は、臨床現場だけにとどまりません。新しい薬を生み出す創薬の研究開発プロセスは、有望な化合物を膨大な数の候補の中から効率的に探し出す必要があり、MoEの「賢い分業」が活きる領域です。
例えば、以下のような専門家AIを組み合わせることが考えられます。
- 特定の分子構造が薬として機能しやすいかを評価するエキスパート
- 特定の病気の原因となるタンパク質に結合する能力を予測するエキスパート
- 化合物が体内でどのような影響(毒性など)を及ぼすかをシミュレートするエキスパート
これらの専門家チームによって、従来よりも遥かに高速で効率的なスクリーニングが可能になり、革新的な新薬がより早く患者さんの元へ届く未来が期待されます。
5. MoEが乗り越えるべき壁と、その先の未来
さて、ここまでMoEの素晴らしい可能性について見てきましたが、どんなに優れた技術にも光と影があるものです。MoEは決して万能の「魔法の杖」ではなく、実用化に向けて乗り越えるべきいくつかの技術的なハードルが存在します。ここでは、MoEが直面している主な課題と、それを克服するための研究の最前線、そして未来の展望について見ていきましょう。
MoEが抱える技術的なハードル
現在、研究者たちが頭を悩ませている主な課題は、大きく分けて3つあります。
- 学習プロセスの不安定さ:「専門医」育成の難しさ
MoEの学習は、時に非常にデリケートで不安定になることがあります。これは、「AI総合病院」で専門医を育成する難しさに例えることができます。Gating Network(総合案内)の判断に偏りが生じ、特定の「人気」エキスパートにばかり仕事(データ)が集中してしまうと、そのエキスパートだけがどんどん賢くなる一方で、指名されなかった他のエキスパートは何も学ぶ機会がなく、「サボっている」状態に陥ってしまいます。この「勝ち組・負け組」現象が起こると、モデル全体の多様性が失われ、性能が伸び悩む原因となります。 - 依然として大きいメモリ要件:巨大な「医局」が必要
MoEの大きな利点は、推論時の「計算コスト」を抑えられる点でした。しかし、これはあくまでCPUやGPUが行う計算の量(FLOPs)の話です。一方で、モデルの全パラメータ、つまり「AI総合病院」に在籍するすべての専門医の情報は、計算中、高速なメモリ(VRAM)上に待機させておく必要があります。 Mixtral 8x7Bが良い例で、計算量は130億パラメータ級でも、メモリ上には約470億パラメータ分の巨大なモデルを展開しなければなりません。これは、診察(計算)は少人数で効率的に行うものの、全専門医が待機するための巨大な医局(メモリ)は確保しなければならない、という状況に似ています。そのため、個人や小規模な研究室レベルのハードウェアで扱うのは依然として困難な場合があります。 - 負荷分散の重要性:患者の殺到を防ぐ工夫
上記の「学習の不安定さ」とも密接に関連するのが、負荷分散(ロードバランシング)の問題です。Gating Networkが単純に入力データとの関連性だけでエキスパートを選んでしまうと、多くのデータに共通するような汎用的な知識を持つエキスパートに処理が集中しがちです。病院で例えるなら、総合診療的な能力を持つ専門医の外来に患者が殺到し、他の専門性の高い科が手薄になるような状態です。これを防ぐため、AIの学習時には、意図的に各エキスパートへ均等に仕事が割り振られるように促すための「ペナルティ」を課す工夫が不可欠です。これは一般的に補助損失(Auxiliary Loss)と呼ばれ、以下のような考え方に基づいています。
\[ L_{\text{total}} = L_{\text{main}} + \alpha \cdot L_{\text{load\_balancing}} \]
数式の解説:モデル全体の損失(\( L_{\text{total}} \))は、本来のタスクの正解率などから計算される主損失(\( L_{\text{main}} \))に加えて、負荷分散の度合いを示す補助損失(\( L_{\text{load\_balancing}} \))を足し合わせることで計算されます。\( \alpha \) はそのペナルティの重み付けを調整する係数です。この損失を最小化するように学習することで、AIはタスクを解く能力を高めると同時に、各エキスパートをバランス良く活用する方法を自ら学んでいきます。
課題を乗り越え、未来へ:研究の最前線
もちろん、世界中の研究者たちはこれらの課題を克服するため、日々研究を重ねています。その中でも特に活発なのが、以下のようなアプローチです。
- より賢いルーティングアルゴリズムの開発:単純に入力との関連性だけでエキスパートを選ぶのではなく、各エキスパートの現在の負荷状況や専門性の重複なども考慮に入れて、より動的で効率的なルーティングを行う新しいアルゴリズムの研究が進んでいます。
- 学習の安定化手法:前述の負荷分散損失に加え、学習の初期段階で意図的にルーティングにノイズを加えて多様な選択を促したり、エキスパート間の出力のばらつきを抑えるような正則化手法を導入したりすることで、より安定して「専門家集団」を育成するテクニックが開発されています。
- PEFT(Parameter-Efficient Fine-Tuning)との融合:これは特に注目されている方向性です。PEFTは、巨大なAIモデル全体を再学習することなく、一部のパラメータのみを更新して特定のタスクに低コストで適応させる技術群です。 このPEFTとMoEを組み合わせることで、例えば「すでに学習済みの巨大な医療MoEモデルに対し、各エキスパートにLoRA(PEFTの一手法)のような小さなアダプターを装着し、非常に少ない計算コストで『特定の診療科の電子カルテ要約タスク』に特化させる」といった、柔軟かつ効率的なカスタマイズが可能になると期待されています。
MoEはまだ発展途上の技術ですが、これらの課題が一つ一つ克服されていくことで、AIモデルの性能と効率は新たな次元へと進化していくはずです。MoEの登場は、AIが単なる巨大な計算機から、真に「知識」を構造化し、効率的に活用する「知能」へと進化していく上での、重要な一歩と言えるでしょう。今後、この技術が成熟し、医療を含む様々な分野でその真価を発揮する日が来るのは、そう遠い未来ではないかもしれません。
まとめ
本稿では、大規模AIモデルの性能と計算コストのジレンマを解決する鍵として注目される「Mixture of Experts (MoE)」について解説しました。
- MoEは「AI総合病院」: 複数の「専門医(エキスパート)」と、最適な専門医を選ぶ「総合案内(ゲーティング・ネットワーク)」で構成される。
- 賢い巨大化の秘訣は「スパース活性化」: 入力に応じて必要なエキスパートだけを活性化させることで、モデル全体のパラメータ数は巨大でも、計算コストを低く抑える。
- 医療分野への高い親和性: マルチモーダルなデータ解析や、診療科ごとの専門知識の集約、個別化医療など、多岐にわたる応用が期待される。
MoEは、AIをより賢く、より効率的に、そしてより身近な存在にするための重要な一歩です。この「専門家集団」という考え方は、未来の医療AIが様々な臨床課題に対して、より柔軟で的確なソリューションを提供するための強力な基盤となるでしょう。
引用文献
- Jacobs RA, Jordan MI, Nowlan SJ, Hinton GE. Adaptive mixtures of local experts. Neural Comput. 1991;3(1):79–87.
- Jordan MI, Jacobs RA. Hierarchical mixtures of experts and the EM algorithm. Neural Comput. 1994;6(2):181–214.
- Shazeer N, Mirhoseini A, Maziarz K, Davis A, Le Q, Hinton G, et al. Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. In: ICLR; 2017.
- Lepikhin D, Lee HJ, Xu Y, Chen D, Firat O, Huang Y, et al. GShard: Scaling giant models with conditional computation and automatic sharding. arXiv. 2020;arXiv:2006.16668.
- Fedus W, Zoph B, Shazeer N. Switch Transformers: Scaling to trillion parameter models with simple and efficient sparsity. J Mach Learn Res. 2022.
- Du N, Huang Y, Dai AM, Tong S, Lepikhin D, Xu Y, et al. GLaM: Efficient scaling of language models with mixture-of-experts. In: ICML; 2022.
- Jiang AQ, Sablayrolles A, Roux A, Mensch A, Savary B, et al. Mixtral of Experts. arXiv. 2024;arXiv:2401.04088.
- Lewis M, Yarats D, Zettlemoyer L, Kiela D. BASE Layers: Simplifying training of large, sparse models. In: ICML; 2021.
- Zhou D, Fedus W, Zoph B, Le QV, Shazeer N, et al. Mixture-of-Experts with Expert Choice Routing. In: NeurIPS; 2022.
- Hazimeh H, Zhao Z, Chowdhery A, Sathiamoorthy M, Chen Y, et al. DSelect-k: Differentiable selection in the mixture of experts with applications to multi-task learning. In: NeurIPS; 2021.
- Zoph B, Bello I, Kumar S, Du N, Huang Y, et al. ST-MoE: Designing stable and transferable sparse expert models. arXiv. 2022;arXiv:2202.08906.
- He XO. Mixture of a million experts. arXiv. 2024;arXiv:2407.04153.
- Liu A, Shao J, Dai Z, Xia M, Qian C, et al. DeepSeek-V2: A strong, economical, and efficient mixture-of-experts language model. arXiv. 2024;arXiv:2405.04434.
- Hwang W, Lee YR, Lee G, Park J, Kim H, et al. Tutel: Adaptive mixture-of-experts at scale. In: MLSys; 2023.
- Wang C, Zheng S, Ren K, Jiang Z, Sun K, et al. SmartMoE: Efficiently training large-scale sparse MoE models. In: USENIX ATC; 2023.
- Rabe M, Wang T, Abdo N, Anil R, Chen M, et al. Pre-gated MoE: An expert choice computation. In: ISCA; 2024.
- Zhang Z, Lin Y, Liu Z, Li P, Sun M, Zhou J. MoEfication: Transformer feed-forward layers are mixtures of experts. In: Findings of ACL; 2022.
- Komatsuzaki A, Puigcerver J, Lee-Thorp J, Riquelme C, Mustafa B, et al. Sparse upcycling: Training mixture-of-experts from dense checkpoints. In: ICLR; 2023.
- Cai J, Cao C, Li M, Xiong C, Zhao W. A survey on mixture of experts in large language models. arXiv. 2024;arXiv:2407.06204.
- Yang N, Xiong Y, Zhang K, Srivatsa S, Zhang S, et al. An empirical study of routers on vision mixture-of-experts. arXiv. 2024;arXiv:2401.15969.
- Shukor M, Fedorishin D, Krajnik M, Popov A, Guo L, et al. FSMoE: Fast switch mixture-of-experts. arXiv. 2025;arXiv:2501.10714.
- Xie G, Zhou R, Yu L, Yang L. Med-MoE: Mixture of domain-specific experts for lightweight medical vision-language models. In: Findings of EMNLP; 2024.
- Lu Y, Zhang W, Liu S, Li J, Lin H, et al. Integrating language into medical visual recognition and reasoning: A survey of medical vision-language models. Med Image Anal. 2025.
- Hartsock I, Sumner W, Natarajan S. Vision-language models for medical report generation and VQA: A review. Front Artif Intell. 2024;7:1430984.
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






