系列データ(心電図やカルテなど)の「順序」を理解するために、RNN(再帰型ニューラルネットワーク)は「記憶」の仕組みを持ちます。過去の情報を保持し、それを現在の判断に活かすことで、時間の流れに沿ったデータの文脈を捉えることができます。
内部にループ構造を持ち、前の時刻の「隠れ状態(記憶)」を次の時刻の入力の一部として利用します。これにより、時系列データの時間的なつながりや文脈を捉えることができます。
BPTT(Backpropagation Through Time)を用いて、予測の誤差を時間軸に沿って過去に伝え、モデルの重みを更新します。これにより系列全体の文脈を考慮した学習が可能です。
時系列が長くなると、BPTTで勾配が消失または爆発し、遠い過去の情報を学習するのが困難になります。この課題を解決するために、LSTMやGRUといった改良モデルが生まれました。
はじめに:時をかけるネットワーク、RNNの世界へようこそ!
皆さん、第1章の冒険、本当にお疲れ様でした! あの章では、私たちの日常や医療の現場に潜む「系列データ」――例えば、心臓のリズムを刻む心電図の波形だったり、日々の診療が綴られる電子カルテの文章だったり――そういった「順番」に大切な意味が込められたデータたちと、どうやって向き合っていくか、その第一歩を踏み出しましたよね。PyTorchという道具を使って、それらをコンピュータが理解できる形にする方法も学びました。
ただ、ちょっと思い返してみてください。第1章で登場した基本的なニューラルネットワークの部品だけだと、系列データが持つ一番の魅力、つまり「時間の流れ」や「言葉のつながり」といった、あの独特の「順序」の情報を、心の底から理解してあげるのは、実はずいぶんと骨が折れる作業なんです。まるで、パラパラ漫画を一枚一枚バラバラに見ているような感じで、全体のストーリーがなかなか見えてこない、そんなもどかしさがあるかもしれません。
そこで、この第2章では、いよいよ本命の登場です!系列データを専門的に、そしてもっとエレガントに扱うための代表的なAIモデルの一つ、再帰型ニューラルネット(Recurrent Neural Network、親しみを込めてRNNと呼ばせてください)の世界へと、皆さんをいざないたいと思います。
このRNN、何がそんなにすごいのかと言うと、まるで私たち人間が文章を読むときや、音楽を聴いて感動するときのように、過去の情報を「記憶」しながら、新しい情報を処理していくことができる、という非常に賢くて、なんだか人間っぽい仕組みを持っているんです。単語の意味を文脈の中で理解したり、メロディーの流れを追いかけたり…。この「記憶」という魔法の力こそが、RNNが系列データの扱いで右に出るものが(かつては)いなかった、その秘密なんですね。
この章では、皆さんと一緒に、このRNNという魅力的なモデルの基本的な考え方から、その心臓部とも言える「どうやって記憶しているの?」という動作の仕組み、そしてもちろん、実際にPyTorchを使って「じゃあ、どうやってRNNを組み立てて、動かしてみるの?」という実践的な部分、さらには「RNNにも苦手なことってあるの?」といった課題に至るまで、一歩一歩、手を取り合うように丁寧に解き明かしていきたいと思っています。
医療の現場に目を向ければ、RNNが活躍できる場面は本当にたくさんあります。例えば、患者さんのバイタルサインの時系列データを解析して、何か変化の兆しを捉えたり、山のような診療記録の中から大切な情報を見つけ出したり…。その応用範囲は、皆さんのアイデア次第で無限に広がっていくはずです。
この章でRNNの基礎をしっかりと自分のものにすることができれば、それは間違いなく、これから皆さんがより高度な医療AIモデルを理解し、そしていつの日か自らの手で新しい何かを生み出していくための、力強い翼になるはずです。
さあ、準備はいいですか?一緒に、時をかけるネットワーク、RNNの奥深い世界へ、探検の旅に出かけましょう!ワクワクしますね!
2.1 RNNの基本構造と動作原理:「記憶」を持つネットワーク
さて、第1章では系列データという、時間や順序が大切な意味を持つデータについて学びました。でも、私たちが以前に触れた全結合型ニューラルネットワーク(フィードフォワードネットワークとも呼ばれましたね)を思い出してみてください。あのネットワークは、情報が一方向に流れるシンプルな構造で、例えば一枚の静止画を分類するようなタスクではとてもパワフルでした。しかし、心電図の波形のように刻々と変化するデータや、電子カルテの文章のように言葉が連なって初めて意味をなすデータを扱うには、いくつかの大きな壁があったんです。
具体的には、入力されるデータの長さ(系列の長さ)が変わると扱いにくかったり、そして何よりも、「一つ前のデータが、今のデータにどう影響しているのか?」といった、時間的なつながりや文脈を直接的にモデルに取り込むことが苦手でした。例えるなら、単語単語の意味は分かっても、文全体の意味を掴むのが難しい、といった感じでしょうか。
この、系列データを扱う上での「うーん、どうしたものか…」という課題を解決するために考え出されたのが、今回主役の再帰型ニューラルネット(RNN)です。RNNの最大の発明ポイントは、ネットワークの内部にまるで「帰り道」のような「ループ構造」を持つ点にあります。このループがあるおかげで、RNNは過去の出来事を情報として保持し続け、それを現在の判断材料に加えることができるのです。この素晴らしい性質を、私たちはよく、RNNが過去の情報を「記憶」できる、と表現するんですね。なんだか、AIが短期記憶を持ったみたいで、ワクワクしませんか?
RNNの心臓部:「RNNセル」とその仲間たち
RNNの基本的な仕組みは、「RNNセル」と呼ばれる比較的小さな計算ユニット(部品のようなものですね)が、系列データを一つずつ、順番に処理していく、という形になっています。ちょうど、私たちが文章を単語ごとに目で追っていくのに似ていますね。
このRNNセルには、主に3種類のデータが出入りします。
- 入力 \(x_t\) (エックス・ティー): これは、ある特定の時刻 \(t\) における入力データのことです。「\(t\)」は英語のtimeの頭文字で、時刻を表すのによく使われます。例えば、心電図データなら時刻 \(t\) での電圧値、天気予報なら \(t\) 時の気温や湿度、テキストデータなら \(t\) 番目の単語(これは第1章で学んだ「埋め込みベクトル」という形で数値化されていることが多いです)などが、この \(x_t\) にあたります。
- 隠れ状態 (Hidden State) \(h_t\) (エイチ・ティー): これこそが、RNNの「記憶」の正体であり、このモデルの最も重要な心臓部と言えるでしょう。時刻 \(t\) における隠れ状態 \(h_t\) は、その瞬間の入力 \(x_t\) と、一つ前の時刻(\(t-1\))の隠れ状態 \(h_{t-1}\) の両方から計算されるんです。つまり、\(h_t\) には、時刻 \(t\) までの過去の入力系列の情報が、ぎゅっと要約されて蓄積されている、そんなイメージです。私はよく、この隠れ状態を「文脈ベクトル」とか「記憶カプセル」なんて呼んだりしています。
- 出力 \(y_t\) (ワイ・ティー): これは、時刻 \(t\) におけるRNNからの最終的な出力です。例えば、次の単語を予測するタスクなら \(y_t\) は次に来る単語の確率分布かもしれませんし、各時刻の心電図波形から異常を検出するなら「正常」か「異常か」のラベルかもしれません。タスクによっては、系列全体の処理が終わった後の、最後の隠れ状態 \(h_T\)(\(T\)は系列の最後の時刻)だけを使って最終的な判断をすることもあります。
これらの入力、隠れ状態、出力の関係は、多くの場合、以下のような数式で表されます。ここでは、隠れ状態の計算に\(\tanh\) (ハイパボリックタンジェント) という活性化関数を使う、ごく一般的な例を見てみましょう。
隠れ状態 \(h_t\) の更新ルール:「今の情報」と「過去の記憶」を混ぜ合わせる
\[ h_t = \tanh(W_{xh}x_t + W_{hh}h_{t-1} + b_h) \]
この式が、RNNの魔法の核心です。一つ一つ見ていきましょう。
\(x_t\): 今、この瞬間の入力データですね。
\(h_{t-1}\): 一つ前の瞬間の「記憶カプセル」です。これが過去からの情報を運んできます。
\(W_{xh}\) (ダブリュー・エックスエイチ): 今の入力 \(x_t\) を、隠れ状態の「言葉」に翻訳するための重み(パラメータ)です。行列の形をしています。
\(W_{hh}\) (ダブリュー・エイチエイチ): 過去の記憶 \(h_{t-1}\) を、今の隠れ状態にどれだけ引き継ぐかを決めるための重みです。これも行列です。この \(W_{hh}\) があるからこそ、「再帰的」と呼ばれるんですね。
\(b_h\) (ビー・エイチ): バイアス項と呼ばれるもので、計算結果を微調整する役割があります。
\(W_{xh}x_t\): 「今の入力」に重みをかけたものです。
\(W_{hh}h_{t-1}\): 「過去の記憶」に重みをかけたものです。
これらを足し合わせ(\(+ b_h\) も忘れずに)、最後に \(\tanh\) という関数を通します。この \(\tanh\) は、入力された値をだいたい-1から1の間にぎゅっと押し込める働きをする活性化関数の一種です。これによって、隠れ状態の値が際限なく大きくなったり小さくなったりするのを防ぎ、ネットワークの学習を安定させる効果があると考えられています。また、非線形な変換を加えることで、RNNがより複雑なパターンを学習できるようになる、という大切な役割も担っています。
つまり、この式は「現在の入力情報と、一つ前の時刻までに蓄積された記憶情報を、それぞれ重みを付けて混ぜ合わせ、新しい記憶 \(h_t\) を作る」というプロセスを表しているんです。なんだか、人間が新しい情報に触れたときに、過去の経験と照らし合わせて物事を理解するのに少し似ていると思いませんか?
ここで、行列計算のイメージを少し掴んでおきましょう。仮に、入力 \(x_t\) が input_size 次元のベクトル、隠れ状態 \(h_{t-1}\) および \(h_t\) が hidden_size 次元のベクトルだとします。すると、重み行列のサイズは以下のようになります。
【RNN隠れ状態の計算フロー: h_t = tanh(W_xh*x_t + W_hh*h_{t-1} + b_h)】
1. 入力x_tと重みW_xhの行列積:
x_t (形状: 1 × I) W_xh (形状: I × H)
+-----------------+ +-----------------+
|x_1, x_2,...,x_I | ● | W_11 ... W_1H |
+-----------------+ | ... |
| W_I1 ... W_IH |
+-----------------+
|
▼ 行列積 (x_t @ W_xh)
term1 (形状: 1 × H)
+-----------------+
| r1_1,...,r1_H |
+-----------------+
2. 前の隠れ状態h_{t-1}と重みW_hhの行列積:
h_{t-1} (形状: 1 × H) W_hh (形状: H × H)
+-----------------+ +-----------------+
|h'_1,...,h'_H | ● | W'_11 ... W'_1H |
+-----------------+ | ... |
| W'_H1 ... W'_HH |
+-----------------+
|
▼ 行列積 (h_{t-1} @ W_hh)
term2 (形状: 1 × H)
+-----------------+
| r2_1,...,r2_H |
+-----------------+
3. 要素ごとの和 (term1 + term2 + b_h):
term1 (1 × H) term2 (1 × H) b_h (1 × H)
+---------------+ +---------------+ +---------------+
|r1_1,...,r1_H | |r2_1,...,r2_H | |b_1,...,b_H |
+---------------+ +---------------+ +---------------+
| | |
+--------(+)-------+---------(+)-------+
|
▼ 要素ごとの和
Sum (形状: 1 × H)
+-----------------+
| s_1,...,s_H |
+-----------------+
4. 活性化関数 tanh の適用:
Sum (形状: 1 × H)
+-----------------+
| s_1,...,s_H |
+-----------------+
|
▼ tanh(Sum) (要素ごと)
h_t (形状: 1 × H)
+-----------------+
| out_1,...,out_H |
+-----------------+
-----------------------------------------------------------------------
凡例:
I = input_size (入力特徴の次元数)
H = hidden_size (隠れ状態の次元数)
● = 行列積 (Matrix Multiplication)
(+) = 要素ごとの加算 (Element-wise Addition)
[v_1,...,v_D] は次元Dの行ベクトルを模式的に示す
[W_ij] は行列を模式的に示す
-----------------------------------------------------------------------
注釈:
※ 上記は概念的なサイズ感と演算フローです。
実際のPyTorchなどの実装では、入力x_tや隠れ状態h_tは通常
(バッチサイズ × 系列長 × 特徴数) や (バッチサイズ × 特徴数) といった
多次元テンソルとして扱われ、行列積やバイアス加算時には
適切なブロードキャストや次元操作が伴います。
この図は、RNNの1ステップにおける主要な計算要素と
その際のベクトル/行列の形状変化の基本を示しています。出力 \(y_t\) の計算ルール:「今の記憶」から答えを出す
\[ y_t = W_{hy}h_t + b_y \]
こうして更新された最新の記憶(隠れ状態 \(h_t\))を使って、その時刻 \(t\) での出力 \(y_t\) を計算します。
\(W_{hy}\) (ダブリュー・エイチワイ): 記憶 \(h_t\) を、最終的な出力の形に変換するための重み行列です。
\(b_y\) (ビー・ワイ): 出力側のバイアス項です。
この式自体は、実はシンプルな線形変換ですね。タスクによっては、この \(y_t\) にさらにソフトマックス関数(分類問題で確率を出したい場合など)や、別の活性化関数を通すこともあります。
この一連の計算(隠れ状態の更新と出力の計算)が、系列データの最初の要素(時刻 \(t=1\))から最後の要素(時刻 \(t=T\))まで、一つずつ時刻を進めながら、まるでバトンを渡すように繰り返されていくのです。そして、とっても重要なポイントは、この計算の途中で使われる重み行列(\(W_{xh}, W_{hh}, W_{hy}\))とバイアス項(\(b_h, b_y\))は、すべての時刻で全く同じものが使われるということです。これを「パラメータ共有(parameter sharing)」と呼びます。これにより、RNNは系列のどの部分に対しても同じパターン認識のルールを適用できるようになりますし、学習しなければならないパラメータの数を大幅に抑えることができる、という大きなメリットがあるんですね。
このRNNの処理の流れを、時間軸に沿って展開して描いた図をよく見かけます。それはまるで、同じRNNセルが何度もコピーされて並んでいるように見えるかもしれません。
テキストベース図
時刻: t-1 t t+1
-------------INPUT x_{t-1}-------------INPUT x_t--------------INPUT x_{t+1}------------>
| | |
V V V
h_{t-2} -->[ RNNセル ]--h_{t-1}-->[ RNNセル ]--h_t-->[ RNNセル ]--h_{t+1}--> ...
| (W) | (W) | (W)
V V V
OUTPUT y_{t-1} OUTPUT y_t OUTPUT y_{t+1}
(W) は全時刻で共有される重み (W_xh, W_hh, W_hy) を表す
図11: RNNセルの時間展開図のイメージ
解説: 左から右へ時間が流れていく様子を表しています。各時刻tで、
入力x_tと前の時刻の隠れ状態h_{t-1}がRNNセルに入力され、
新しい隠れ状態h_tと出力y_tが計算されます。
隠れ状態h_tは次の時刻のRNNセルへと伝播し、「記憶」の役割を果たします。
重要なのは、全てのRNNセルで同じ重み(W)が使われる点です。
この図を見ると、情報が時間と共にどう流れていくのか、そして「記憶」である隠れ状態がどう引き継がれていくのかが、より直感的に理解できるのではないでしょうか。
「再帰的」とは、一体どういうこと? ~時間を通じた情報のバトンパス~
「再帰的(Recurrent)」という言葉、なんだか少し難しそうに聞こえるかもしれませんが、その本質は「自分自身を繰り返し参照する」というループ構造にあります。RNNの場合、具体的には、時刻 \(t-1\) で計算された隠れ状態 \(h_{t-1}\) が、次の時刻 \(t\) の隠れ状態 \(h_t\) を計算するための入力の一部として使われ、そしてその \(h_t\) が、さらにその次の時刻 \(t+1\) の隠れ状態 \(h_{t+1}\) の計算に使われる…というように、隠れ状態という名の「情報バトン」が、時間軸に沿って次々と未来の自分自身へと渡されていく様子を指しています。これが「再帰」という言葉の所以(ゆえん)なんですね。
この仕組みがあるからこそ、RNNは例えば、「昨日、ある患者さんが『ひどい頭痛』を訴えていて、さらに今日のバイタルサインを見ると『微熱』もある。これらの情報(頭痛という過去の記憶と、微熱という現在の入力)を総合的に考えると、明日はどうなるだろうか?」といった、過去の文脈を踏まえた上での判断や予測を行う能力を獲得できるわけです。一つ一つの情報をバラバラに見るのではなく、それらの時間的なつながりの中で意味を見出そうとする、とても賢いアプローチだと言えるでしょう。
医療の現場でRNNの「記憶力」はどう活きる?
では、このRNNの「記憶」を持つ構造が、医療の現場でどんな風に役立つのか、もう少し具体的にイメージしてみましょう。
- 時系列バイタルサインの予測や異常検知: 入院中の患者さんの心拍数、血圧、呼吸数、体温といったバイタルサインは、まさに時々刻々と変化する時系列データです。RNNは、これらの過去数時間、あるいは数日間にわたる変動パターンを隠れ状態に「記憶」として蓄積します。そして、その「記憶」と「現在のバイタルサイン」を総合的に評価することで、「この患者さんは数時間後に状態が急変するリスクが高いかもしれない」といった予測を行ったり、普段とは異なる危険なパターン(異常)を検知したりするタスクに応用できると考えられています。早期発見・早期対応に繋がる可能性を秘めているわけですね。
- 電子カルテなどの医療テキストデータの解析: 電子カルテに自由記述形式で書かれた診療録や看護記録は、貴重な情報の宝庫ですが、その量は膨大です。例えば、「患者は3日前から続く咳嗽と昨夜からの38度の発熱を主訴に来院。胸部X線にて右下葉に浸潤影を認める。」といった文章をRNNが単語(あるいは文字)ごとに読み進めていくとしましょう。RNNは、「3日前から」「咳嗽」「昨夜から」「38度」「発熱」「右下葉」「浸潤影」といったキーワードだけでなく、それらがどのような順序で、どのような関連性を持って出現したかという文脈情報を、隠れ状態を通じて保持していきます。この「文脈を記憶する力」があるからこそ、AIは例えば、その文章全体が肺炎を示唆しているのか、あるいは別の疾患の可能性もあるのか、といったより深いレベルでのテキスト理解に近づくことができるのです。診断支援や、膨大な記録からの情報抽出に役立つと期待されています。
このように、RNNが持つ「記憶」の仕組みは、系列データの中に隠された時間的な依存関係や文脈のパターンを捉える上で、非常に強力な武器となるのです。まさに、AIが「流れを読む」ための第一歩と言えるでしょう。
2.2 RNNにおける順伝播と時間を通じた逆伝播(BPTT):AIはどうやって「学ぶ」のか?
さて、RNNがどうやって過去の情報を「記憶」として保持し、それを現在の処理に活かしているのか、その基本的な構造が少しずつ見えてきましたね。あのループ構造と隠れ状態という「記憶カプセル」が鍵なのでした。
では、この賢いRNNは、一体どうやって「学習」していくのでしょうか?つまり、どうやって正しい答えを導き出すための「知識」(ニューラルネットワークの世界では、これは主に「重み」や「パラメータ」と呼ばれる数値の集まりですね)を獲得していくのか、その秘密に迫ってみましょう。
AIの学習プロセスは、多くの場合、大きく分けて2つのメインステップから成り立っています。一つは、情報がネットワークの中を駆け巡り、答えを出すまでの「順伝播」。そしてもう一つが、その答えがどれだけ正しかったかを評価し、間違いを修正していく「逆伝播」です。RNNでは、この逆伝播が時間軸を遡る形で行われるため、ちょっと特別な名前がついています。まずは、情報が流れる「順伝播」から、一緒に見ていきましょう。
順伝播 (Forward Propagation) – 情報が時間を駆け巡るタスキリレー
さて、RNNの学習の旅、最初のステップは「順伝播」です。これは、まるで駅伝の選手たちが、タスキに「これまでの情報」という想いを込めて次へ次へとつないでいくように、入力された系列データがRNNのネットワークの中を時間の流れに沿って駆け抜けていく様子を指します。この情報のリレーを通じて、各地点(つまり各時刻)でRNNは「現在の記憶」を更新し、そして「現時点での答え」を導き出していくんですね。
One More Thing!
RNNの出力:タスクに応じた使い分け
| 利用するRNNの情報 | こんな時に使う(主な目的) | 代表的なタスク例 |
|---|---|---|
| 各時刻の出力 (\(y_1, \dots, y_T\)) | 入力系列の各要素に対して、それぞれ何かを出力したい(逐次的な判断や生成)。 | ・品詞タグ付け (各単語の品詞を判定) ・固有表現認識 (NER) (各単語が固有表現か識別) ・機械翻訳 (デコーダ側で翻訳先の単語を1つずつ生成) |
| 最終隠れ状態 (\(h_T\)) | 入力系列全体の情報(文脈)を一つにまとめて、それに基づいて単一の判断や要約を行いたい。 | ・文章分類/感情分析 (文章全体のカテゴリや感情を判定) ・機械翻訳 (エンコーダ側で入力文全体の意味をベクトル化) ・系列全体の異常検知 (期間全体のデータから異常を判断) |
では、具体的にこのタスキリレーがどのように行われるのか、系列の最初の時刻を \(t=1\) として、一緒にスタートラインから見ていきましょう!
- 旅の始まり:最初のタスキパス (時刻 \(t=0 \rightarrow 1\)) どんな旅にも始まりがあるように、RNNの順伝播も最初の「記憶」、つまり初期隠れ状態 \(h_0\) からスタートします。この旅の始まりの「記憶」は、まだ何も情報がないまっさらな状態なので、普通はすべての要素が0のベクトル(ゼロベクトルって言いますね)で静かにスタートを切ります。ここに、物語の最初のページが開かれるわけです。 そこへ、系列の最初の入力データ \(x_1\) がやってきます。これが、駅伝で言うところの最初の区間のランナーが受け取るタスキの情報のようなものです。この \(x_1\)(今、この瞬間の情報)と \(h_0\)(これまでの文脈、今はまだ空っぽですが)が、RNNセルという名の「中継所」で出会います。そして、2.1節で見たように、それぞれ専用の「翻訳機」とも言える重み行列 \(W_{xh}\) と \(W_{hh}\) によって処理され、バイアス項 \(b_h\) という微調整役の助けも借りて足し合わされます。最後に、その結果が \(\tanh\) という活性化関数によってキュッとまとめられて、最初の新しい記憶、隠れ状態 \(h_1\) が出来上がるのでしたね。数式で書くと、こうでした。 \[ h_1 = \tanh(W_{xh}x_1 + W_{hh}h_0 + b_h) \] そして、この生まれたてのほやほやの記憶 \(h_1\) を使って、RNNは時刻1における最初の「答え」(出力)\(y_1\) を導き出します。これも2.1節で見た通り、重み \(W_{hy}\) とバイアス \(b_y\) を使った計算ですね。 \[ y_1 = W_{hy}h_1 + b_y \] これで、最初の区間のタスキリレーが無事完了した、というわけです!
- タスキをつなぎ、未来へ:次の区間へ (時刻 \(t \rightarrow t+1\)) そして、このRNN駅伝はまだまだ続きます。時刻 \(t=2\) になると、どうなるでしょう?今度は、先ほど時刻1で生まれたばかりの記憶 \(h_1\) が、貴重な情報が詰まったタスキとして、次の時刻(\(t=2\))のRNNセルへと渡されます。そして、そこへ新しい区間の情報である入力 \(x_2\) がやってきます。この二つの情報が出会うことで、時刻1と全く同じ計算プロセス(ただし、入力は \(x_2\) と \(h_1\) に変わります)を経て、新たな記憶 \(h_2\) が作り出され、そしてそれに基づく出力 \(y_2\) が計算される…。 \[ h_2 = \tanh(W_{xh}x_2 + W_{hh}h_1 + b_h) \] \[ y_2 = W_{hy}h_2 + b_y \] もうお分かりですね!この「現在の入力と過去の記憶から新しい記憶を作り、それを使って答えを出し、そして新しい記憶を次の時刻へ渡す」という一連のプロセスが、系列データの最後の要素(最後の時刻を \(T\) としましょう)に到達するまで、ひたすら、まるで決意を固めたランナーのように繰り返されていくわけです。この時、各区間(各時刻)で使われる計算ルール(つまり重み \(W_{xh}, W_{hh}, W_{hy}\) やバイアス \(b_h, b_y\))は、前回お話ししたように、すべて同じものが共有されているのでしたね。これがRNNの賢さの一つです。
こうして、各時刻 \(t=1, 2, …, T\) で得られた出力 \(y_1, y_2, …, y_T\) たちですが、その使い道は、RNNにどんなお仕事をさせたいか(つまり、どんなタスクを解かせたいか)によって、実に様々なんです。
例えば、私たちが今読んでいるような文章をAIに読ませて、次にどんな単語が来るかを予測させるようなお仕事(これを言語モデルと呼んだりします)では、各時刻 \(t\) での出力 \(y_t\) が、まさに「\(t+1\) 番目の単語は、これかな?」という予測結果そのものに対応することが多いです。なんだか、AIが一緒に文章を読み進めながら、次に続く言葉を考えてくれているみたいですよね。
一方で、例えば患者さんのある期間のバイタルサインのデータ全体を読んで「この期間中に、何か危険な状態に陥った瞬間はあっただろうか?」と判断するようなお仕事(これは系列分類の一種ですね)の場合は、各時刻の出力すべてを使うというよりは、系列全体の情報をぎゅっと凝縮したと考えられる最後の隠れ状態 \(h_T\) や、あるいは全ての時刻の隠れ状態 \(h_1, …, h_T\) をうまく平均したり、一番重要そうなものを選び出したりしたものを使って、最終的な「はい」か「いいえ」の判断を下すことが多いんですよ。この出力の使い分けができる柔軟性が、RNNを色々な問題に応用できる秘密の一つでもあるんですね。
このように、順伝播では、情報が時間の流れに沿ってRNNの内部を伝わり、各時刻で「記憶」が更新され、「答え」が生み出されていくのです。なんだか、生き物の思考プロセスにも少し似ているような気がしませんか?
RNNのセルは、基本的には全て同じものです。
これはRNNの非常に重要な特徴であり、「重み共有(Weight Sharing)」と呼ばれます。
具体的には:
- 同じ構造: 各時刻 (t-1, t, t+1…) で使われるRNNセルは、内部の計算ロジック(入力に対する処理、隠れ状態の更新、出力の生成など)が全く同じです。
- 同じ重み: そして、これらのセルは全て同じ重みパラメータ(Wxh, Whh, Why など)を共有しています。
なぜ重みを共有するのか?
- パラメータ数の削減: 各時刻ごとに異なる重みを持つと、非常に長い系列データ(例:長い文章)を扱う場合にパラメータ数が膨大になり、学習が非効率になったり、過学習のリスクが高まったりします。重みを共有することで、限られたパラメータ数で長期的な依存関係を学習できます。
- 時系列データの特性への対応: 自然言語や音声のような時系列データでは、ある時点でのパターン認識のルール(例えば、「動詞の次には名詞が来やすい」など)は、他の時点でも同じように適用できることが多いです。重みを共有することで、モデルは時間的な位置によらず、これらのパターンを一般化して学習することができます。
- 汎化能力の向上: 同じ重みを使うことで、モデルは特定の時刻に特化した学習ではなく、時間軸全体にわたる一般的なパターンを学習するようになり、未知のデータに対する汎化能力が向上します。
したがって、RNNは、異なる時刻に同じセルが「再利用」され、同じルール(重み)が適用されることで、効率的に時系列データを処理している、と理解することができます。
損失関数 (Loss Function) – AIの「反省ノート」の採点基準
さて、RNNが順伝播というプロセスで、入力された系列データに対して一通りの「答え」(つまり予測値ですね)を出し終えました。でも、その答えが果たして「素晴らしい!」と褒められるべきものだったのか、それとも「うーん、これはちょっと残念…」な結果だったのか、AI自身がそれを知ることができなければ、どうやって自分を改善していけばいいのか、途方に暮れてしまいますよね。
そこで登場するのが、AIが成長し、賢くなっていくために絶対に欠かせない「自己評価ツール」、それが「損失関数 (Loss Function)」です。これはまるで、テストの答案を自分で採点して、「あぁ、ここが間違ってた!次はこうしよう」と反省点を見つけるための「採点基準」や、日々の頑張りを記録する「反省ノート」のようなものだと考えてみてください。この損失関数が「間違いの大きさ」を具体的な数値で教えてくれるからこそ、AIは「どうすればもっと良くなるか」を学習できるのです。
RNNが扱うのは、時間の流れや順序が大切な系列データでした。ですから、多くの場合、損失も単純に最後の結果だけで判断するのではなく、系列全体を通して「どれだけ上手くタスクをこなせたか」を評価します。例えば、10個の単語からなる文章を要約するタスクなら、要約文全体としての質が問われる、といった具合です。
具体的に見ていきましょう。例えば、ある特定の時刻 \(t\) におけるAIの出力(予測した値)を \(y_t\) とし、私たちが「これが正解だよ」と知っている「本当の答え」(専門用語ではターゲット (target) とか教師ラベル (ground truth label) なんて言ったりします)を \(target_t\) だったとします。損失関数は、このAIが出した \(y_t\) と、お手本となる \(target_t\) を、数学的な手法を使って比較し、「うーん、今回はこれだけズレちゃったね」という「ズレの大きさ」を一つの数値 \(L_t\) として計算してくれるんです。
この「ズレの測り方」にも、実は色々な種類があります。どんなタスクに取り組んでいるかによって、使い分けられることが多いですね。
- 平均二乗誤差 (MSE: Mean Squared Error): もしAIが予測するのが連続的な数値、例えば「明日の患者さんの体温は36.8度」といったものなら、「平均二乗誤差(MSE)」というものがよく使われます。これは、予測値 (\(y_t\)) と正解値 (\(target_t\)) の差を計算し、その差を二乗して(マイナスをなくして、大きなズレをより重視するためですね)、その平均を取る、というものです。予測がピタリと当たればズレは0、大きく外れればこのMSEの値も大きくなります。
- クロスエントロピー誤差 (Cross-Entropy Error): もしAIが予測するのがカテゴリー、例えば「この心電図波形は正常?不整脈A?不整脈B?」といったもの(分類問題と言います)なら、「クロスエントロピー誤差」というものがよく顔を出します。これは、AIが出した「各カテゴリーである確率」の予測(例:正常である確率70%、不整脈Aである確率20%、不整脈Bである確率10%)と、実際の正解カテゴリー(例:実は不整脈Aだったので、不整脈Aである確率100%、他は0%)が、情報量という観点からどれだけ「似ているか」(あるいは「食い違っているか」)を測るものさしです。これも、AIの予測が正解のカテゴリーを高い確率で言い当てていればいるほど、小さな値になります。
これらの損失関数の詳しい数学的な中身や、他にもどんな種類があるのかは、また別の機会に譲るとして、ここではまず「損失関数とは、AIの予測と“あるべき姿”との間のギャップを、具体的な数値として定量化してくれるものなんだな」というイメージを持っていただければ十分です。この数値が、AIの「成長の伸びしろ」を示してくれるわけですね。
そして、系列全体の「反省点の総まとめ」とも言える総損失 \(L\) は、こうして計算された各時刻 \(t\) での小さな反省点(個別の損失 \(L_t\))を、系列の最初から最後まで全部足し合わせることで求められることが多いです。数式で書くと、こうなります。
\[ L = \sum_{t=1}^{T} L_t \]
この \(\sum\) (シグマ) という記号は「全部足し合わせる」という意味で、\(t=1\) から \(T\) (系列の最後の時刻) までの全ての \(L_t\) を合計することを示しています。
あるいは、系列の長さ \(T\) がデータごとに異なる場合などには、単純に合計するのではなく、系列の長さ \(T\) で割って、いわば「1時刻あたりの平均的な間違いの大きさ」を総損失とすることもあります。
\[ L = \frac{1}{T} \sum_{t=1}^{T} L_t \]
AIの学習の最終目標は、この総損失 \(L\) を、できるだけゼロに近づけること。つまり、「反省ノート」の点数を限りなく満点に近づけることです。そして、そのためにAIは何をするかというと、自分が持っているたくさんの「知識の部品」である重み(2.1節で登場した \(W_{xh}\) や \(W_{hh}\), \(W_{hy}\) といった、AIの判断基準やパターンの捉え方を形作る、たくさんの数値の集まり=パラメータですね)を、この損失 \(L\) という「道しるべ」が小さくなる方向へと、ほんの少しずつ、しかし根気強く調整していくわけです。この地道な「重みの調整作業」こそが、AIがデータから経験を学び、賢くなっていく「学習」の正体なんですね。
損失関数が示す「間違いの方向と大きさ」を手がかりに、AIは自らをより良い方向へと導いていく。なんだか、人間が試行錯誤しながら成長していく姿にも重なるように思えませんか?
この損失関数と、それを最小化するための学習の仕組み(次にお話しするBPTTがそれにあたります)が、AIモデルを鍛え上げるための両輪となるのです。
以下に、損失計算の概念的な流れを図で示します。
時刻 t における処理:
+-----------------+ +---------------------+
| RNNからの出力 | --> | | --> 時刻tの損失 (L_t)
| (予測値 y_t) | | 損失関数 | (例: (y_t - target_t)^2 )
+-----------------+ | (間違いを数値化) |
| |
+-----------------+ --> | |
| 正解データ | +---------------------+
| (ターゲット target_t) |
+-----------------+
系列全体での総損失:
[L_1] --┐
[L_2] --┼-- (合計 または 平均) --> [総損失 L] ----┐
[...] --┘ |
[L_T] --┘ |
▼
この L を最小化するよう
AIモデルの重みを調整 (学習)
図 (損失計算の概念フロー)
解説: 各時刻tでRNNの出力(y_t)と正解(target_t)を損失関数に入力し、
時刻tの損失(L_t)を計算します。次に、系列全体の各時刻の損失
(L_1からL_Tまで)を集計(合計や平均)して総損失(L)を求めます。
AIの学習とは、この総損失Lが小さくなるようにモデル内部の
パラメータ(重み)を調整していくプロセスです。
時間を通じた逆伝播 (BPTT) – 過去の自分に「こうすれば良かったね」と教える旅
さて、AIの「反省ノート」(損失関数ですね!)に、今回のパフォーマンスに対する「点数」(つまり損失 \(L\))が付きました。もし点数が満点じゃなかったら、次はどうすればもっと良い点数が取れるようになるでしょう?ここで登場するのが、RNNが過去の経験から学ぶための、まさに時間旅行のようなアルゴリズム、時間を通じた逆伝播(BPTT: Backpropagation Through Time)です。名前はちょっと仰々しいですが、その考え方はとってもエレガントで、そして面白いんですよ。
皆さんは、以前に全結合型ニューラルネットワークなどで使われる「逆伝播(バックプロパゲーション)」という手法について聞いたことがあるかもしれません。あれは、ネットワークの出力側で生じた「間違い」(損失)を、まるで伝言ゲームを逆再生するように、ネットワークの層を一つずつ入力側へと遡って伝え、「各層の重みが、最終的な間違いにどれだけ責任があったのかな?」(これを専門用語で勾配 (gradient) と言います)を計算し、それを基に重みを少しずつ「こっちの方向に修正した方が良さそうだぞ」と調整していく、という学習のテクニックでしたよね。
BPTTは、この逆伝播の基本的な考え方を、RNNが特別に持っている「時間」という軸にも拡張したものなんです。思い出してください、2.1節で見たように(図11が頭に浮かびますか?)、RNNは時間を展開していくと、同じ計算ルール(つまり同じ重みセット)を持つRNNセルがたくさん、たくさん時間軸に沿って並んだ、まるで長ーいフィードフォワードネットワークのように見える、というお話をしました。BPTTは、この時間軸に沿って展開された、いわば「時間という名の深さ」を持つネットワーク全体に対して、通常の逆伝播を適用する、とイメージすると、スッキリと理解しやすいかもしれません。
このBPTTの概念を、もう少し具体的に、簡単な図で見てみましょう。ここでは、情報がどう流れて、どう「反省」が伝わるかに注目してください。
時刻: t-1 t t+1 ... T (最終時刻)
損失Lへの影響の流れ(勾配)
<--------------------------------------------- L (総損失)
↖︎ ↖︎ ↖︎ ↖︎
勾配の伝播: δ_t-1 <----- δ_t <----- δ_t+1 <---- ... <---- δ_T (時刻Tの誤差情報)
| | | |
V V V V
RNN展開図: ...-[RNNセル]-h_{t-1}-[RNNセル]- h_t -[RNNセル]-h_{t+1}-...-[RNNセル]-h_T
(重みW) | | (重みW) | | (重みW) |
v v v v
y_{t-1} y_t y_{t+1} ... y_T (各時刻の出力)
| | | |
v v v v
L_{t-1} L_t L_{t+1} ... L_T (各時刻の損失)
図12: BPTTにおける誤差逆伝播の概念図
解説: この図は、RNNが時間展開された状態での誤差の伝播を示しています。
まず、系列全体(あるいは最終時刻T)での総損失Lから、時刻Tにおける
出力y_Tや隠れ状態h_Tに対する誤差情報δ_Tが計算されます。
このδ_Tが、時間を遡る形で前の時刻の隠れ状態h_{T-1}や、
その計算に関わった重み(W)へと伝播していきます。
同様に、各時刻tでも損失L_tが生じていれば、その誤差も合流し、
さらに過去へと流れます。この「時間を通じた」誤差情報の
流れがBPTTの核心であり、これにより、系列全体の文脈を考慮した
重みの更新が可能になるのです。δ(デルタ)は、ここでは誤差や
勾配の情報を象徴的に表しています。
具体的には、BPTTはこんな風に「反省の旅」を進めていきます。想像してみてください。駅伝のアンカー(これが最終時刻 \(T\) ですね)がゴールテープを切ったとき、もし目標タイムに届かなかったとしたら(これが損失 \(L\) が大きい状態です)、その「遅れ」の原因を辿っていく作業が始まります。
- ゴール地点での反省 (時刻 \(T\)): まず、一番最後の時刻 \(T\) での「結果」(出力 \(y_T\))が、最終的な「目標」(総損失 \(L\) のうち、時刻 \(T\) の処理が関わった部分、あるいは時刻 \(T\) での個別損失 \(L_T\))に対してどれくらいズレていたか、その「責任」を計算します。これは、\(y_T\) や隠れ状態 \(h_T\) の計算に使われた重み(例えば \(W_{hy}\) や \(W_{hh}\))を、この瞬間のズレを減らすためには、それぞれどれだけ、どちらの方向に修正すれば良かったのか、その手がかり(勾配)を調べることに相当します。ここまでは、通常の逆伝播と似たような感覚ですね。
- 一つ前の区間へ、未来からの伝言を手に (時刻 \(T-1\)): 次に、時間を一つ巻き戻して、時刻 \(T-1\) に注目します。ここがBPTTの面白いところであり、巧妙なところ! 時刻 \(T-1\) での処理が直接生み出した間違い(つまり \(L_{T-1}\) から来る勾配)への責任はもちろんのこと、実は、未来である時刻 \(T\) の損失からも「ちょっと待った!君のあの時の判断が、未来の私(時刻 \(T\) の結果)にも影響してるんだよ!」という形で、影響が伝わってくるんです。なぜなら、思い出してください、時刻 \(T\) の記憶である隠れ状態 \(h_T\) は、時刻 \(T-1\) の記憶である隠れ状態 \(h_{T-1}\) を使って作られているからですね(\(h_T = \tanh(W_{xh}x_T + W_{hh}h_{T-1} + b_h)\) のように)。つまり、\(h_{T-1}\) の値がほんの少し違っていたら、それによって \(h_T\) の値も変わり、それが巡り巡って最終的な損失 \(L\) にも響いてくる…という、まさに「風が吹けば桶屋が儲かる」的な(ちょっと違いますが)連鎖的な影響があるわけです。BPTTでは、これらの時刻 \(T-1\) で直接生じた影響と、未来(時刻 \(T\))から間接的に伝わってきた影響を全てひっくるめて、時刻 \(T-1\) における重みや、さらにその前の記憶 \(h_{T-2}\) をどれだけ修正すべきだったのか、その手がかりを計算します。
- 過去へ、過去へと、反省のバトンをつなぐ (時刻 \(T-2, …, 1\)): このようにして、誤差の情報が、まるで時間を遡るタイムマシンのように、系列の最初の時刻 \(t=1\) まで一つずつ、一つずつ丁寧に伝播していくのです。各時刻の「記憶カプセル」(隠れ状態ですね)が、未来の自分からの「あの時こうすれば良かったんだよ」という貴重な反省のメッセージ(勾配)を受け取り、それをさらに過去の自分へと伝えていく…。なんだか、私たちが過去の経験から教訓を学んでいくプロセスにも、少し似ているように思えませんか?
そして、もう一つ大切なことを思い出してください。RNNでは、全ての時刻で全く同じ重みセット(\(W_{xh}, W_{hh}, W_{hy}\)など)が、まるで同じスタンプのように使い回されているのでした。BPTTでは、この「みんなで共有している重み」に対して、「結局のところ、トータルでどれくらいの責任があったのだろうか?」ということを計算します。これは、時間を遡る中で各時刻から計算された「この重みを、この方向に、これくらい変えれば良かった」という修正案(つまり、各時刻で計算された勾配ですね)を、全部丁寧に足し合わせる(あるいは平均を取ることもあります)ことで求められます。これにより、系列全体の経験、つまり最初から最後までの全ての情報処理の過程を総合的に考慮した上で、共有されているパラメータが一斉に、そしてより賢明な方向へと更新されるわけです。これこそが、RNNが系列全体を通じた複雑なパターンや文脈を学習できる大きな秘訣なんですね。
このBPTTという巧妙な仕組みがあるからこそ、RNNは「系列のずっと前の出来事が、最終的な結果(例えば、長い文章全体の意味の理解や、数日間にわたる時系列データのトレンド予測)にどんな風に影響を与えたのか」という、時間的に遠く離れた場所にある情報同士の関連性(これを専門用語で長期依存性 (long-term dependency) と言います)を捉え、それを学習に反映させることができるようになる、と考えられているのです。
ただ、このBPTT、本当に素晴らしいアルゴリズムなんですが、万能というわけでもありません。特に、系列がものすごーく長くなった場合(例えば、何千もの単語からなる非常に長い文章を読ませたり、何時間にもわたるセンサーデータを扱ったりするような場合ですね)、誤差の情報をたくさんのステップを遡って伝えなければならなくなります。これは、単純に計算に時間がかかるというだけでなく、もっと困ったことに、後で詳しくお話しする「長期依存性の問題」(具体的には、勾配が途中で消えてしまったり(勾配消失)、逆に大きくなりすぎたり(勾配爆発)する現象です)という、RNNの学習をとても難しくしてしまう、ちょっと厄介な性質を引き起こしやすくなるんです。この興味深くも悩ましい問題については、次の2.4節でじっくりと、その原因と、先人たちが編み出してきた対策について考えていきましょうね。
Deep Dive! 徹底解説!BPTTの中身
時間軸で展開するRNNの計算グラフ 〜まるで紙芝居のように〜
BPTTを理解するためには、まずRNNがどのように時間軸で計算を進めているのかを、計算グラフという形で見てみるのが一番です。RNNは、厳密には時間軸で「同じレイヤーが繰り返し適用されている」と考えることができます。これを、あたかも異なるレイヤーであるかのように時間軸に沿って展開して描くのが、BPTTを理解するための第一歩です。
まるで紙芝居を一枚一枚めくるように、RNNの計算を時間軸に沿って展開してみましょう。
時刻t-1 時刻t 時刻t+1
-------- -------- --------
xt-1 -> [RNN_Cell] -> ht-1 -> [RNN_Cell] -> ht -> [RNN_Cell] -> ht+1
| | |
v v v
W_xh W_xh W_xh
| | |
ht-1 -> [W_hh] -------/ /
| ht -> [W_hh] ----/
v |
yt-1 yt
W_xh: 入力xから隠れ状態hへの重み
W_hh: 前の隠れ状態hから現在の隠れ状態hへの重み
RNN_Cell: RNNの基本的な計算を行うユニット(例: 隠れ状態の更新、出力の生成)
xt: 時刻tの入力
ht: 時刻tの隠れ状態(内部状態)
yt: 時刻tの出力この図は、RNNの計算が時間軸に沿って展開されている様子を表しています。まるで同じ細胞が時間とともに分裂・増殖しているかのようですね。
- 入力
xt: 各時刻でRNNに入力されるデータです。 - 隠れ状態
ht: RNNの「記憶」にあたる部分です。前の時刻の隠れ状態ht-1と、現在の入力xtを元に計算されます。このhtが、次の時刻へと情報を受け渡していきます。 - 出力
yt: 各時刻でRNNが出力するデータです。隠れ状態htを元に計算されます。
重要なのは、この展開された計算グラフにおいて、時刻 t の隠れ状態 ht が、時刻 t-1 の隠れ状態 ht-1 に強く依存している点です。そして、この依存関係を辿っていくことで、現在の時刻で生じた誤差が、過去の時刻にまで伝わっていくのです。これこそがBPTTの神髄です。
誤差の逆流 〜鎖のように繋がる微分の連鎖〜
それでは、いよいよ誤差がどのように逆流していくのか、その核心に迫っていきましょう。BPTTの基本は、これまで学んできた誤差逆伝播法と同じく、連鎖律(Chain Rule)です。
最終的な損失(誤差)を \(L\) とすると、各時刻における重み \(W\) や、隠れ状態 \(h\) に関する勾配を計算したいわけです。例えば、時刻 \(T\) の出力に対する損失 \(L_T\) があったとしましょう。この損失が、時刻 \(t\) における重み \(W\) にどのように影響を与えるかを考えます。
\[ \frac{\partial L}{\partial W} = \sum_{t=1}^{T} \frac{\partial L_t}{\partial W} \]
これは、各時刻 \(t\) での損失が重み \(W\) に与える影響を合計するという意味です。そして、各時刻 \(t\) での \( \frac{\partial L_t}{\partial W} \) は、連鎖律を使って次のように計算できます。
\[ \frac{\partial L_t}{\partial W} = \frac{\partial L_t}{\partial y_t} \frac{\partial y_t}{\partial h_t} \frac{\partial h_t}{\partial W} \]
ここまでは通常の誤差逆伝播と同じように見えます。しかし、RNNの場合、時刻 \(t\) の隠れ状態 \(h_t\) は、その前の時刻の隠れ状態 \(h_{t-1}\) に依存しています。つまり、
\[ h_t = \text{tanh}(W_{xh}x_t + W_{hh}h_{t-1} + b) \]
のような計算が行われているとすると(RNNの内部計算は活性化関数 \(\text{tanh}\) を含むことが多いです)、\( \frac{\partial h_t}{\partial W} \) の中には、過去の隠れ状態を経由したパスが含まれることになります。
例えば、隠れ状態に関する勾配 \( \frac{\partial L}{\partial h_t} \) を考えてみましょう。時刻 \(t\) の損失からだけでなく、時刻 \(t+1\) の隠れ状態 \(h_{t+1}\) を経由して伝わってくる勾配も考慮する必要があります。
\[ \frac{\partial L}{\partial h_t} = \frac{\partial L}{\partial y_t} \frac{\partial y_t}{\partial h_t} + \frac{\partial L}{\partial h_{t+1}} \frac{\partial h_{t+1}}{\partial h_t} \]
この式が、まさに「時を超えて誤差が逆流する」ことを表しています。現在の時刻 \(t\) における \(h_t\) への勾配は、現在の時刻での損失からの影響だけでなく、未来の時刻 \(t+1\) での隠れ状態 \(h_{t+1}\) を経由して伝わってくる勾配も足し合わせることで計算されるのです。
これをさらに展開していくと、時刻 \(t\) の隠れ状態 \(h_t\) への勾配は、最終的な時刻 \(T\) までのすべての損失からの影響を連鎖的に受け取ることになります。
\[ \frac{\partial L}{\partial h_t} = \frac{\partial L}{\partial y_t} \frac{\partial y_t}{\partial h_t} + \frac{\partial L}{\partial y_{t+1}} \frac{\partial y_{t+1}}{\partial h_{t+1}} \frac{\partial h_{t+1}}{\partial h_t} + \dots + \frac{\partial L}{\partial y_T} \left( \frac{\partial y_T}{\partial h_T} \prod_{k=t}^{T-1} \frac{\partial h_{k+1}}{\partial h_k} \right) \]
ちょっと複雑に見えますが、要するに、各時刻における隠れ状態への勾配は、その時刻での損失と、それ以降のすべての時刻の隠れ状態を通じて伝わってくる勾配の合計で計算される、ということを意味しています。まるでリレーのように、後ろのランナーが前のランナーにバトンを渡していくように、誤差が時間を遡って伝わっていくイメージです。
そして、この \( \frac{\partial h_{k+1}}{\partial h_k} \) という部分は、RNNの重み \(W_{hh}\) や活性化関数の微分が含まれています。
\[ \frac{\partial h_{k+1}}{\partial h_k} = W_{hh}^T \cdot \text{diag}(\text{tanh}'(W_{xh}x_{k+1} + W_{hh}h_k + b)) \]
ここで、\( \text{diag}(\cdot) \) は対角行列を意味し、\( \text{tanh}'(\cdot) \) は \( \text{tanh} \) 関数の微分です。この部分が何度も連鎖的に掛け合わされることで、勾配が非常に大きくなったり(勾配爆発)、非常に小さくなったり(勾配消失)する問題を引き起こすことがあります。これについては後ほど少し触れましょう。
行列計算で見るBPTTの舞台裏 〜テンソルの形を追いかけよう〜
ここまで抽象的な話が続いたので、今度はもう少し具体的な計算のイメージを、行列計算とテンソルの形状を意識しながら見ていきましょう。ディープラーニングでは、ほとんどの計算が行列やテンソルで行われます。それぞれのデータがどんな「形」をしているのかを意識すると、グッと理解が深まりますよ。
RNNのフォワードパス(順伝播)の計算は、ざっくりと次のように表せます。
\[ h_t = \text{tanh}(X_t W_{xh} + H_{prev} W_{hh} + B_h) \]
\[ y_t = H_t W_{hy} + B_y \]
ここで、それぞれの行列やテンソルの形状をブロックで表現してみましょう。
RNN_Cell (時刻tの計算)
入力 X_t (バッチサイズ x 入力次元)
H_prev (バッチサイズ x 隠れ状態次元)
W_xh (入力次元 x 隠れ状態次元)
W_hh (隠れ状態次元 x 隠れ状態次元)
B_h (隠れ状態次元)
W_hy (隠れ状態次元 x 出力次元)
B_y (出力次元)
(1) 隠れ状態の更新: X_t W_xh
[B x I] x [I x H] = [B x H]
(2) 隠れ状態の更新: H_prev W_hh
[B x H] x [H x H] = [B x H]
(3) 隠れ状態の更新: tanh( (X_t W_xh) + (H_prev W_hh) + B_h ) = H_t
[B x H]
(4) 出力の生成: H_t W_hy
[B x H] x [H x O] = [B x O]
(5) 出力の生成: (H_t W_hy) + B_y = Y_t
[B x O]このように、それぞれの行列がどのような「形」をしていて、それらが結合することでどのような「形」になるのかをイメージすると、計算がクリアに見えてきます。
そして、BPTTでは、これらの計算の逆を辿って勾配を伝播させていきます。例えば、出力 \(Y_t\) から隠れ状態 \(H_t\) への勾配 \( \frac{\partial L}{\partial H_t} \) を計算するときは、
\[ \frac{\partial L}{\partial H_t} = \frac{\partial L}{\partial Y_t} \cdot W_{hy}^T \]
という計算が行われます。ここで、\( W_{hy}^T \) は \( W_{hy} \) の転置行列です。
勾配の逆伝播: dY_t -> dH_t
dY_t (バッチサイズ x 出力次元)
W_hy (隠れ状態次元 x 出力次元)
(1) dH_t の計算: dY_t dot W_hy.T
[B x O] x [O x H] = [B x H]このように、順伝播で掛け算だった部分が、逆伝播では転置行列との掛け算になったり、足し算だった部分がそのまま勾配の足し算になったりします。それぞれの計算が、元の計算の「逆」を表現していることを意識すると、理解が深まるでしょう。
特に重要なのは、隠れ状態の勾配 \( \frac{\partial L}{\partial H_t} \) が、次の時刻 \(t+1\) から伝わってくる勾配 \( \frac{\partial L}{\partial H_{t+1}} \) の影響も受けるという点です。これは、各時刻の隠れ状態が、未来の隠れ状態の計算にも使われているため、未来の損失が現在の隠れ状態に影響を与えるということを意味します。
勾配消失と勾配爆発 〜長距離依存性との戦い〜
BPTTは、RNNの学習において非常に有効な手法ですが、一つ大きな課題を抱えています。それが「勾配消失(Vanishing Gradient)」と「勾配爆発(Exploding Gradient)」です。
先ほどの数式で、\( \prod_{k=t}^{T-1} \frac{\partial h_{k+1}}{\partial h_k} \) という部分がありましたね。この部分は、複数の行列が連鎖的に掛け合わされることを意味します。もし、この行列の各要素が1より小さい値ばかりだと、何度も掛け算するうちに値はどんどん小さくなり、やがて0に限りなく近づいてしまいます。これが勾配消失です。勾配が消失してしまうと、初期の時刻の重みはほとんど更新されなくなり、RNNは長い時系列データにおける「長距離依存性(Long-term Dependencies)」、つまり遠い過去の情報を現在の予測に反映させることが難しくなってしまいます。
想像してみてください。大切な情報が、時間の流れの中でどんどん薄れていって、やがて何も残らなくなってしまうようなものです。
逆に、行列の要素が1より大きい値ばかりだと、何度も掛け算するうちに値は指数関数的に大きくなり、とんでもない数値になってしまいます。これが勾配爆発です。勾配が爆発すると、重みが極端に大きな値に更新されてしまい、学習が不安定になったり、発散してしまったりします。
まるで、時間の流れの中で情報が増幅されすぎて、制御不能になってしまうようなものです。
これらの問題に対処するために、様々な工夫が凝らされてきました。例えば、勾配爆発に対しては「勾配クリッピング(Gradient Clipping)」という、勾配が一定のしきい値を超えたら強制的に値を丸める手法が有効です。また、勾配消失に対しては、LSTM(Long Short-Term Memory)やGRU(Gated Recurrent Unit)といった、ゲート機構を持つ特別なRNNが開発され、長距離の依存関係を捉えやすくすることで、この問題を大幅に改善しています。
BPTTのまとめと、その先の展望
BPTTは、RNNが時系列データを学習するための非常に重要な技術であり、その根幹には、時間軸に沿った計算グラフの展開と、連鎖律を用いた誤差の逆伝播があります。
最後に、BPTTの重要なポイントを表でまとめてみましょう。
| 項目 | 説明 |
|---|---|
| 定義 | RNNにおける誤差逆伝播法。時間軸に沿って展開されたRNNの計算グラフに対して、通常の誤差逆伝播法を適用する。 |
| 目的 | RNNの重みを学習し、時系列データにおけるパターンや依存関係を捉えること。 |
| 基本原理 | 連鎖律。出力の誤差が、時間を遡って各時刻の隠れ状態や重みに伝播していく。 |
| 特徴 | – 時間軸での展開: 同じRNNセルが、あたかも異なるレイヤーであるかのように各時刻で並ぶと考える。 – 誤差の逆流: 未来の時刻の勾配が、現在の時刻の勾配に影響を与える。 |
| 課題 | – 勾配消失: 長い時系列データで、過去の時刻の勾配が非常に小さくなり、学習が進まなくなる。 – 勾配爆発: 勾配が非常に大きくなり、学習が不安定になる。 |
| 対策 | – 勾配クリッピング: 勾配爆発の対策。 – LSTM/GRU: 勾配消失の対策として、特別なゲート機構を持つRNNが開発された。 |
BPTTは、私たちがディープラーニングで時系列データを扱う上で欠かせない基礎技術です。LSTMやGRUといったより洗練されたRNNも、その根底にはBPTTの考え方があります。
この技術があるからこそ、私たちは機械翻訳や音声認識、株価予測など、時間の流れの中に隠された複雑なパターンを、機械に学習させることができるのです。まるで、時空を超えて、過去と未来をつなぐ情報の橋渡しをしているかのようですね。
今回の解説が、BPTTという少し複雑なテーマを、皆さんの心に温かく、そして深く刻み込む一助となれば幸いです。ディープラーニングの旅はまだまだ続きますが、一歩一歩、その奥深さを一緒に探求していきましょう!
Deep Dive! Truncated BPTT (TBPTT) 〜 長い道のりも、分割すれば怖くない!〜
1. はじめに:BPTTの課題からTBPTTへ
さて、先ほどはBPTT(Backpropagation Through Time)が、RNNの時間を遡ってどのように丁寧に誤差を伝播させ、重みを学習していくのか、その詳細な仕組みと、時系列データを扱う上での強力さ、そしてその数学的な背景を一緒に見てきましたね。まるでリレーのバトンのように、未来の誤差が過去へと連鎖していく様子は、なかなか興味深かったのではないでしょうか。
しかし、あの丁寧すぎるほどの誤差の逆流は、特に扱う系列データがとーっても長くなってくると、いくつかの悩ましい問題も抱えているんでした。覚えていますか? 先ほどの解説の最後の方でも触れましたが、主なものとしては、
- 計算量がどんどん増えちゃう問題: 系列が長ければ長いほど、遡るステップも増えるので、コンピュータの計算時間がものすごくかかってしまう。
- メモリがいくらあっても足りない問題: 過去の情報をたくさん記憶しておかないといけないので、メモリを大量に消費してしまう。
- 勾配が迷子になっちゃう問題(勾配消失・爆発): あまりにも長い道のりを遡っているうちに、大切な学習信号である勾配が小さくなりすぎて見えなくなったり(勾配消失)、逆に大きくなりすぎて暴走したり(勾配爆発)することがありましたね。
「うーん、BPTTは理論的には美しいけれど、長い系列データにはちょっと使いにくい部分もあるんだな…」と感じられたかもしれません。
そこで、「何とかしてこの課題を乗り越えつつ、RNNの学習をうまく進められないだろうか?」という現実的なニーズから生まれた、より実践的で賢い工夫が、今回一緒に見ていく Truncated BPTT (TBPTT)、日本語では「打ち切りBPTT」と呼ばれる手法なんです。このTBPTTのおかげで、私たちは非常に長い系列データや、終わりがないようなデータストリーム(例えば、センサーから延々と送られてくるデータなど)も、RNNで扱えるようになってきたんですよ。
2. Truncated BPTT (TBPTT) の核心アイデア 〜「ちょっとここで一区切り!」〜
TBPTTの基本的な考え方は、名前の「Truncated(打ち切り)」が示す通り、実はとってもシンプルです。
BPTTが、まるでマラソンランナーがスタートからゴールまで一気に走り切るように、系列の「最初から最後まで」律儀に誤差を遡って伝えようとするのに対して、TBPTTは、「よし、まずはここまで! ちょっとここで一区切りして、次に行こう!」という感じで、誤差を遡る道のりを、ある一定の決まった長さ(例えば \(k\) ステップ)でバッサリと打ち切ってしまうんです。
BPTT vs TBPTT のイメージ
BPTT:
時刻: 1 2 3 ... t ... T-1 T
誤差L -> ... -> 誤差(t) -> ... -> 誤差(2) -> 誤差(1) (Tステップ全て遡る)
TBPTT (打ち切り長 k):
時刻: ... t-k t-k+1 ... t-1 t
誤差L_t -> ... -> 誤差(t-k+1) (最大kステップだけ遡る)
↑
(ここから先へは、このL_tに関する誤差は伝播させない)
つまり、影響が大きそうな直近の過去 \(k\) ステップの範囲にはしっかり目を配って学習のヒント(勾配)を得るけれど、あまりにも遠い過去までは追いかけすぎないようにする、というバランス感覚の良いアプローチ、と言えるかもしれませんね。これにより、計算量やメモリの問題を大幅に軽減しようというわけです。
3. TBPTTは実際にどう動くの? 〜チャンク処理と勾配の伝播制御〜
では、この「打ち切り」は、具体的にどのように行われるのでしょうか。TBPTTの一般的な動作は、長い系列データをいくつかの短いチャンク(かたまり、セグメントとも言います)に分割して、そのチャンクごとに学習を進めていく、と考えると分かりやすいです。
- 順伝播 (Forward Pass) はいつも通り、でもちょっとした工夫も: 入力される系列データ \(x_1, x_2, \dots, x_T\) は、RNNの各時刻のセルを順番に通っていき、隠れ状態 \(h_t\) と出力 \(y_t\) が計算されていきます。ここまでは通常のRNNと同じです。
重要なのは、各時刻の隠れ状態 \(h_t\) は、その計算において \(h_{t-1}\) からの情報をしっかり引き継いでいるという点です。つまり、たとえ後で勾配の伝播を打ち切るとしても、順伝播の際には、過去からの情報(文脈)は隠れ状態を通じてきちんと未来へと伝えられていきます。TBPTTが打ち切るのは、あくまで「学習のための勾配の流れ」であって、RNNが情報を記憶・伝達する「順方向の流れ」ではないんですね。これがTBPTTがうまく機能するための大切なポイントです。 - 逆伝播 (Backward Pass) とパラメータ更新 〜ここが「打ち切り」の本領発揮!〜:
- まず、非常に長い入力系列を、例えば長さ \(k\) のチャンクに区切ります。
(例: チャンク1: \(x_1, \dots, x_k\)、チャンク2: \(x_{k+1}, \dots, x_{2k}\)、など) - そして、各チャンクごとに、そのチャンク内で生じた損失(例えば、そのチャンク内の各時刻の損失の合計)を計算します。
- 次に、そのチャンクの損失に基づいて、そのチャンクの範囲内でのみ BPTTを実行します。つまり、勾配の逆伝播は、最大でもチャンクの長さである \(k\) ステップしか遡りません。
- ここが肝心な点で、あるチャンクの勾配を計算する際、そのチャンクの開始点よりも過去の隠れ状態へは、勾配を伝播させません。あたかも、そのチャンクはその開始時の隠れ状態から始まったかのようにして勾配を計算するわけです。(実際には、その開始時の隠れ状態の値自体は、それ以前のすべての履歴をちゃんと反映しています。)
- こうして計算された勾配を使って、RNNの重み \(W\) を更新します。
- そして、次のチャンクの処理に移ります。次のチャンクの順伝播は、現在のチャンクの最後の隠れ状態を引き継いで開始します。
.detach()というメソッドを呼び出すことで実現されることが多いです。これを呼び出すと、そのテンソルは計算グラフから切り離され、それより過去への勾配の流れがそこでストップする、という仕組みになっています。 - まず、非常に長い入力系列を、例えば長さ \(k\) のチャンクに区切ります。
TBPTTのチャンク処理のイメージ図
<pre><code>
系列全体: X_1, X_2, ..., X_k, X_{k+1}, ..., X_{2k}, X_{2k+1}, ...
|<--- チャンク1 (長さk) --->|<---- チャンク2 (長さk) ---->| ...
【チャンク1の処理】
h_0 (初期状態) → X_1 → h_1 → ... → X_k → h_k (順伝播)
↓
L_k (損失計算: L_1~L_kの合計など)
↓ (逆伝播: h_kからh_1の範囲のみ)
勾配計算 (∂L/∂W)
↓
W を更新
【チャンク2の処理】
h_k (チャンク1の最終状態、勾配は伝播させない=detach)
↓
h'_0 (チャンク2の初期状態として使用) → X_{k+1} → h'_1 → ... → X_{2k} → h'_k (順伝播)
↓
L'_k (損失計算)
↓ (逆伝播: h'_kからh'_1の範囲のみ)
勾配計算 (∂L/∂W)
↓
W を更新
... (以下、同様に繰り返す) ...
解説:
- 各チャンクの順伝播では、前のチャンクの最後の隠れ状態が、次のチャンクの最初の隠れ状態として
利用されます(図中のh_kがh'_0になる部分)。これにより、情報はチャンクをまたいで伝わります。
- しかし、逆伝播(勾配計算)は、各チャンク内で閉じて行われます。
チャンク2の損失から計算される勾配が、チャンク1の隠れ状態や計算に影響を与えることはありません。
これが「打ち切り」の意味するところです。
</code></pre>4. 計算グラフで見るTBPTT (BPTTとの比較)
先ほどのBPTTの解説では、誤差が時間を遡ってどこまでも伝播していく可能性が示されていました。TBPTTでは、この「どこまでも」という部分に制限を設けます。
以下の図は、あるチャンク(ここでは簡単のため、打ち切り長を \(k\) とし、時刻 \(t-k+1\) から \(t\) までの \(k\) ステップの区間とします)におけるTBPTTのイメージです。
TBPTT: チャンク内の勾配伝播
<pre><code>
時刻: ... t-k-1 | t-k (前のチャンク) | t-k+1 ... t-1 t | t+1 ... (次のチャンク)
-----------------------|--------------------|-------------------------|--------------------
隠れ状態h: h_{prev} ----> h_{t-k+1} → ... → h_{t-1} → h_t ----> h_{next}
↑ (順伝播では影響) ↑ ↑
入力x: x_{t-k+1} ... x_{t-1} x_t
(このチャンクの入力)
出力y: y_{t-k+1} ... y_{t-1} y_t
損失L: L_{t-k+1} ... L_{t-1} L_t
--------------------------------------------------------------------
勾配の逆伝播 (このチャンクの損失 ΣL_i に基づく):
X <----------------------------------+
(h_{prev}へは勾配を伝播しない。ここで打ち切り)
解説:
- 図の中央部分が、現在処理している1つのチャンク(時刻 t-k+1 から t まで)です。
- このチャンクの最初の隠れ状態 h_{t-k+1} は、前のチャンクの最後の隠れ状態 h_{prev} (図ではh_{t-k}に相当)
と、入力 x_{t-k+1} から計算されます。順伝播では、h_{prev} の情報は h_{t-k+1} にしっかり伝わります。
- このチャンク内で計算された損失(例えば L_{t-k+1} から L_t までの合計)に基づいて、
重みWや、このチャンク内の隠れ状態 h_t, h_{t-1}, ..., h_{t-k+1} に対する勾配が計算されます。
- しかし、この勾配は、このチャンクの開始点である h_{t-k+1} を計算する際に使われた
h_{prev} へは遡って伝播しません(図の左側の大きなX印の箇所)。
ここで勾配の流れが「打ち切られる」わけです。
</code></pre>このように、各チャンクが独立したミニBPTTの単位として扱われることで、計算全体が現実的なものになります。
5. 数式で少しだけ補足 (概念的に)
先ほどのBPTTの解説で、時刻 \(t\) の損失 \(L_t\) が重み \(W\) に与える影響 \(\frac{\partial L_t}{\partial W}\) は、
\[ \frac{\partial L_t}{\partial W} = \sum_{j=1}^{t} \frac{\partial L_t}{\partial y_t} \frac{\partial y_t}{\partial h_t} \frac{\partial h_t}{\partial h_j} \frac{\partial h_j}{\partial W} \]
と書けることを見ましたね。この \(\sum_{j=1}^{t}\) の部分が、時刻 \(t\) から過去の全ての時刻 \(j\) まで遡って影響を考慮することを意味していました。
TBPTT(打ち切り長 \(k\))では、この和の範囲を、現在処理しているチャンクの範囲内、あるいは最大でも直近の \(k\) ステップに限定します。
もし、チャンク単位で処理する場合(チャンクの長さも \(k\) とすると)、あるチャンク内の時刻 \(t\) (チャンクの先頭から数えて \(i\) 番目、つまり \(t = \text{チャンク開始時刻} + i – 1\))における \(L_t\) からの勾配は、概念的には
\[ \left(\frac{\partial L_t}{\partial W}\right)_{\text{TBPTT}} = \sum_{j=\text{チャンク開始時刻}}^{t} \frac{\partial L_t}{\partial y_t} \frac{\partial y_t}{\partial h_t} \frac{\partial h_t}{\partial h_j} \frac{\partial h_j}{\partial W} \]
というように、そのチャンクの開始時刻 \(j=\text{チャンク開始時刻}\) までしか遡らない、と考えることができます。これにより、\(\frac{\partial h_t}{\partial h_j}\) の時間を通じた連鎖律の展開が、高々 \(k-1\) ステップに抑えられます。
6. RNNの1ステップの計算について (BPTTの解説からの参照)
個々のRNNセル内で行われる具体的な計算、つまり入力 \(x_t\) と前の隠れ状態 \(h_{t-1}\) から新しい隠れ状態 \(h_t\) や出力 \(y_t\) を計算する際の行列積や活性化関数といった詳細については、先ほどのBPTTの解説セクション「行列計算で見るBPTTの舞台裏 〜テンソルの形を追いかけよう〜」で詳しく見ましたね。そこでは、各行列(テンソル)がどんな「形」をしていて、どのように計算が進むのかを追いかけました。
TBPTTは、これらのRNNセル内部の計算式そのものを変えるわけではありません。変えるのは、これらの計算の連鎖を、損失の勾配を計算するために時間軸に沿ってどれだけ長く遡るか、その「範囲」なのです。ですから、1ステップごとの計算の仕組みは、BPTTの時と全く同じものを思い浮かべてくださいね。
7. TBPTTのメリット・デメリット
ここで、TBPTTの嬉しい点(メリット)と、少し気をつけないといけない点(デメリット)を整理しておきましょう。
嬉しい点(メリット):
- 計算が速くなる!: 各パラメータ更新時に遡る時間ステップが限られるので、勾配計算にかかる時間が大幅に短縮されます。
- メモリに優しい!: 順伝播の情報を記憶しておく必要があるのは、打ち切り長 \(k\) ステップ分だけで済むようになります。これにより、メモリの消費量が格段に減り、非常に長い系列データ(原理的には無限長のデータストリームも!)を扱う道が開けます。
- オンライン学習と相性が良い: データが次から次へとやってくるような状況(オンライン学習)でも、系列全体を一度に見ることなく、チャンクごとに区切って学習を進めていけるので、とても実用的です。
- 勾配消失・爆発問題が少し和らぐことも: 勾配を伝播させる経路が物理的に短くなるため、BPTTで深刻だった勾配消失や勾配爆発の問題が、ある程度緩和される効果が期待できます。完全に解決するわけではありませんが、学習が少し安定しやすくなるんですね。
気をつけないといけない点(デメリット):
- 勾配はあくまで「近似値」: TBPTTで得られる勾配は、系列全体の情報を考慮した「真の」勾配(フルBPTTで得られる勾配)の近似に過ぎません。そのため、学習の収束の仕方や、最終的に到達できるモデルの性能に、多少の影響を与える可能性があります。
- あまりにも長い「記憶」の学習は苦手かも: 打ち切り長 \(k\) を超えるような、非常に長期にわたる依存関係(例えば、文章のはるか昔に出てきた情報が、現在の単語を予測するのにとても重要である、といったケース)は、勾配を通じて直接的に学習することが難しくなります。もちろん、順伝播の隠れ状態 \(h_t\) は過去の情報を保持し続けているのですが、その情報を形作った「遠い過去の重み」に対する学習の信号(勾配)が、打ち切りによって届きにくくなってしまう、というイメージです。
- 打ち切り長 \(k\) のさじ加減が大切: 打ち切り長 \(k\)(またはチャンクの長さ)をどのくらいにするか、というのは重要な調整ポイント(ハイパーパラメータと言います)になります。\(k\) が小さすぎると、十分な過去の文脈を捉えられずに学習がうまくいかないかもしれませんし、逆に \(k\) が大きすぎると、TBPTTのメリットである計算効率やメモリ効率の良さが薄れてしまいます。この \(k\) の値は、解きたいタスクやデータの性質によって、試行錯誤しながら適切な値を見つけていく必要があります。
8. TBPTTのまとめと、BPTTとの賢い使い分け
さて、Truncated BPTT (TBPTT) について、その考え方から動作の仕組み、そしてメリット・デメリットまで見てきました。TBPTTは、長い系列データをRNNで学習させる際の計算コスト、メモリ使用量、そして厄介な勾配の問題を軽減するための、非常に実用的で広く使われているテクニックだということが、お分かりいただけたのではないでしょうか。
誤差の逆伝播を一定の長さに「打ち切る」ことで、完全なBPTTの計算を近似的に行いますが、多くの現実的な問題において、その効果は絶大です。
ここで改めて強調しておきたいのは、TBPTTが打ち切るのはあくまで「勾配の流れ」であり、順伝播における「情報の流れ」ではないということです。RNNの隠れ状態は、過去の情報をきちんと未来へと伝えていきます。ただ、その情報を形作った「ずっと昔の出来事」に対する「学習のきっかけ」となる勾配が、打ち切りによって少し届きにくくなるかもしれない、という点を心に留めておくと、TBPTTの挙動をより深く理解できると思います。
実際のところ、どのくらいの長さの系列までならフルBPTTが現実的で、どこからTBPTTを検討すべきか、という明確な境界線があるわけではありません。それは、利用できる計算資源(CPU、GPU、メモリ)や、求められるモデルの精度、そしてデータの特性などによって変わってきます。短い系列で、かつ長期の依存関係が非常に重要だと分かっている場合には、可能であればフルBPTTを試みる価値があるかもしれません。しかし、現代の多くの応用、特に非常に長いテキストや音声、センサーデータなどを扱う場合には、TBPTT(あるいはこの後学ぶLSTMやGRUといったより洗練されたRNNユニットと組み合わせたTBPTT)が、現実的かつ効果的な選択肢となるでしょう。
このTBPTTの概念をしっかりと押さえておくことは、この先、LSTMやGRUといった、勾配問題をより巧みに回避するために考案された特別なRNNユニットの仕組みを学ぶ上でも、きっと役立つはずです。
医療応用でのイメージ ~AIドクターの「経験からの学び」と「過去の症例分析」~
BPTTが医療の現場でどんな風に役立つか、もう少しイメージを膨らませてみましょう。例えば、RNNを使ってある患者さんの1週間後の血糖値を予測するAIドクターを育成しているとします。もし、ある日の予測が実際の血糖値と大きくズレてしまった場合(つまり、損失関数が大きな値を示した場合ですね)、BPTTはその「なぜ予測がこんなにズレてしまったんだろう?」という原因を、ただ直前の食事内容だけでなく、3日前、5日前、あるいは1週間前のインスリン投与の記録、運動量、睡眠時間といった、より過去の様々な入力データ、そしてそれらの情報を処理したときのRNNの「記憶」(隠れ状態)の計算の仕方にまで遡って、「うーん、どうやらあの時のインスリン量の判断が、今のこの大きなズレに繋がってしまったんじゃないか?」とか「この生活パターンの変化を見落としていたかもしれない。このパラメータをこういう風に調整すれば、きっと次はもっと患者さんの状態を正確に予測できるはずだ」といった手がかり(勾配ですね)を、まるでベテラン医師が過去の症例を詳細に分析するように見つけ出し、モデル自身を賢く成長させていく、そんなプロセスをイメージできるかもしれません。
BPTTの仕組みを(たとえ一つ一つの数式や微分計算を完璧に追いかけるのが最初は難しかったとしても)概念的にでも理解しておくことは、RNNがどうやって複雑な系列データからパターンを学習し、まるで経験を積んでいくように賢くなっていくのか、その魔法のタネの一つを垣間見る上で、とても大切だと思いますよ。
2.3 PyTorch nn.RNN モジュールの使い方
理論的な背景を学んだところで、いよいよPyTorchを使ってRNNを実際に動かしてみましょう。PyTorchには、RNNを簡単に実装するための便利なモジュール torch.nn.RNN が用意されています。これを使うことで、先ほど説明したRNNの複雑な計算(隠れ状態の更新やBPTTなど)の詳細を自分で一から書かなくても、手軽にRNNモデルを構築し、利用することができます。
torch.nn.RNN クラスをインスタンス化(実体化)する際に、いくつか重要なパラメータを指定する必要があります。
input_size: 入力特徴量の数(次元数)です。例えば、各時刻の入力が5つの異なるセンサー値からなるベクトルであれば、input_size=5となります。hidden_size: 隠れ状態の次元数です。これはRNNの「記憶容量」の大きさに相当し、私たちが自由に設定できるハイパーパラメータの一つです。この値が大きいほど、より複雑なパターンを記憶できる可能性がありますが、計算コストも増加し、過学習のリスクも高まります。num_layers: RNN層を何層重ねるか、という数です。デフォルトは1ですが、2層、3層と重ねることで、より深い特徴表現を獲得しようとする試みも行われます(スタックドRNNと呼ばれます)。batch_first: これをTrueにすると、入力テンソルや出力テンソルの形状の最初の次元がバッチサイズになります(バッチサイズ, 系列長, 特徴数)。デフォルトはFalseで、その場合は(系列長, バッチサイズ, 特徴数)となります。どちらの形式を主に使うかによって設定します。最近はbatch_first=Trueが好まれる傾向にあるかもしれません。- 他にも、
nonlinearity(活性化関数の種類、デフォルトはtanh)、bias(バイアス項を使うか、デフォルトはTrue)、dropout(ドロップアウト率)、bidirectional(双方向RNNにするか、デフォルトはFalse)といったパラメータがあります。
入力、隠れ状態、出力の次元設定
nn.RNN モジュールに入出力するテンソルの形状(次元の並びと各次元のサイズ)を正しく理解することは、PyTorchでRNNを扱う上で非常に重要です。混乱しやすいポイントでもあるので、丁寧に見ていきましょう。
ここでは、batch_first=False(デフォルト)の場合を基本に説明し、batch_first=True の場合も併記します。
- 入力テンソル (input):
- 形状:
(系列長, バッチサイズ, input_size) batch_first=Trueの場合:(バッチサイズ, 系列長, input_size)- これは、モデルに入力する系列データそのものです。
系列長は系列の長さ、バッチサイズは一度に処理する系列の数、input_sizeは各時刻における入力の特徴の次元数です。
- 形状:
- 初期隠れ状態テンソル (h_0):
- 形状:
(層数 * 方向数, バッチサイズ, hidden_size) 層数 (num_layers)はnn.RNNのnum_layersパラメータで指定した値です。方向数は、通常のRNN(一方向)なら1、双方向RNN(bidirectional=True)なら2になります。- このテンソルは、RNNの計算を開始する際の最初の隠れ状態を指定するために使います。もし指定しなければ、PyTorchは自動的に全ての要素が0のテンソルを初期隠れ状態として使ってくれます。
- 形状:
- 出力テンソル (output):
- 形状:
(系列長, バッチサイズ, 方向数 * hidden_size) batch_first=Trueの場合:(バッチサイズ, 系列長, 方向数 * hidden_size)- これは、RNNの各時刻における隠れ状態(通常は最終層の隠れ状態)をまとめたものです。
方向数 * hidden_sizeとなっているのは、双方向RNNの場合、順方向と逆方向の隠れ状態が連結されて出力されるためです。
- 形状:
- 最終隠れ状態テンソル (h_n):
- 形状:
(層数 * 方向数, バッチサイズ, hidden_size) - これは、系列全体の処理が終わった後の、最後の時刻における隠れ状態です(多層RNNの場合は各層の最終隠れ状態)。初期隠れ状態と同じ形状ですね。系列全体の情報を要約したベクトルとして、分類タスクなどに使われることがあります。
- 形状:
これらの形状をしっかり意識してデータを用意し、モデルからの出力を解釈することが大切です。
隠れ状態の初期化と伝播
RNNの計算を始めるにあたって、最初の時刻 \(t=0\) における隠れ状態 \(h_0\) が必要です。これは通常、私たちが明示的に指定することもできますし、指定しなければ全ての要素がゼロのベクトル(ゼロベクトル)で自動的に初期化されます。
nn.RNN モジュールを呼び出す際、この初期隠れ状態 h_0 をオプションとして与えることができます。もし与えればそれが使われ、与えなければゼロベクトルが使われます。そして、入力系列がRNNセルを一つずつ通過していく中で、隠れ状態は \(h_0 \rightarrow h_1 \rightarrow h_2 \rightarrow \dots \rightarrow h_T\) と、時刻ごとに更新され、次の時刻へと情報が伝播していきます。この伝播の計算は、nn.RNN モジュールが内部でよしなに行ってくれます。
Pythonコード例:nn.RNN を使ってみる 〜テンソルの形に注目!〜
さて、理論的なお話も大切ですが、「百聞は一見にしかず」とも言いますよね。実際にPyTorchの nn.RNN を使って、ごく簡単なデータでその動きを体験してみましょう。ここで目指すのは、AIに何か複雑なタスクを解かせることではなく、まずは「どんな形のデータ (テンソル) を nn.RNN に入力すると、どんな形のデータが返ってくるのか」という、いわばRNNとの最初の挨拶のようなものです。この「形」をしっかり掴むことが、後々もっと複雑なモデルを扱う上での大切な一歩になりますよ。
早速ですが、必要な道具(ライブラリ)を準備して、小さなRNNモデルを作り、ダミーのデータを流し込んでみましょう!
# まずは、PyTorchの基本機能を使うためのおまじないです。
import torch
# 次に、ニューラルネットワークの部品(層や活性化関数など)がたくさん詰まっている
# torch.nn モジュールを nn という別名でインポートします。こちらもお決まりの書き方ですね。
import torch.nn as nn
# --- 1. RNNモデルのパラメータを設定しましょう ---
# ここでは、RNNモデルを作るときに必要な「設計図」の数値をいくつか決めます。
# input_size: 各時刻でRNNに入力されるデータ1つ1つが持つ特徴の数(次元数)です。
# 例えば、株価予測なら1(その日の株価)、もし株価と出来高を使うなら2、といった具合です。
# 今回は、仮に各時刻の入力が3つの数値で構成されるとしましょう。
input_size = 3
# hidden_size: RNNの「隠れ状態」の次元数です。これは、RNNが過去の情報をどれだけ
# 「豊かに」記憶できるかの容量のようなもの、と考えてみてください。
# 大きくすれば表現力は増しますが、計算も大変になります。ここでは小さめの5にしてみます。
hidden_size = 5
# num_layers: RNNの層を何層重ねるか、という数です。
# 1層でもRNNとして機能しますが、層を深くする(スタックする)ことで、
# より複雑なパターンを捉えられるようになることもあります。
# まずは一番シンプルな1層で試してみましょう。
num_layers = 1
# batch_first: 入力や出力のテンソルの次元の順番を指定する、ちょっとした設定です。
# Trueにすると、テンソルの最初の次元が「バッチサイズ」になります。(バッチサイズ, 系列長, 特徴数)という形ですね。
# False (デフォルト) だと、(系列長, バッチサイズ, 特徴数) になります。
# どちらでも良いのですが、最近は True を指定するコードをよく見かける気がしますので、こちらに合わせましょう。
batch_first = True
print(f"--- RNNのパラメータ設定 ---")
print(f"入力特徴の次元数 (input_size): {input_size}")
print(f"隠れ状態の次元数 (hidden_size): {hidden_size}")
print(f"RNNの層の数 (num_layers): {num_layers}")
print(f"バッチサイズを最初の次元にする (batch_first): {batch_first}\n")
# --- 2. nn.RNN モデルのインスタンス(実物)を作成 ---
# 設定したパラメータを使って、RNNモデルの実体を作ります。
# これで、rnn_model という名前のRNNが使えるようになりました!
rnn_model = nn.RNN(input_size=input_size,
hidden_size=hidden_size,
num_layers=num_layers,
batch_first=batch_first)
print(f"--- 作成したRNNモデル ---")
print(rnn_model) # モデルの構造を表示してみましょう。
print(f"\n")
# --- 3. ダミーの入力テンソルを作成 ---
# 次に、このRNNモデルに入力するデータを作ります。
# 今回は「ダミーデータ」として、ランダムな数値のテンソルを使いましょう。
# バッチサイズ: 一度に処理する系列データの数。例えば、2つの異なる文章や時系列データを同時に処理するイメージ。
batch_size = 2
# 系列長: 各データが持つ時間の長さ(ステップ数)。例えば、4つの単語からなる文章や、4時点のセンサーデータなど。
seq_len = 4
# 入力テンソルの形状は、batch_first=True なので (バッチサイズ, 系列長, 入力特徴の次元数) になります。
# torch.randn() は、平均0、分散1の正規分布に従うランダムな数値でテンソルを埋めてくれます。
input_tensor = torch.randn(batch_size, seq_len, input_size)
print(f"--- ダミー入力データ ---")
print(f"入力テンソルの形状: {input_tensor.shape}")
# 期待される形状: (2, 4, 3) (batch_size, seq_len, input_size)
print(f"入力テンソルの内容 (最初のバッチの最初の要素だけ表示):\n{input_tensor[0,0,:]}\n")
# --- 4. (オプション) ダミーの初期隠れ状態テンソルを作成 ---
# RNNは過去の情報を隠れ状態に蓄えますが、一番最初の時刻には「過去」がありません。
# そのため、最初の隠れ状態 h_0 を与える必要があります。
# 指定しなければ、PyTorchが自動的に全ての要素がゼロのテンソルで初期化してくれます。
# ここでは、練習のためにあえて作ってみましょう。
# 初期隠れ状態の形状は、(RNNの層の数 * 方向数, バッチサイズ, 隠れ状態の次元数) です。
# 今回は単方向RNNなので方向数は1です。
initial_hidden_state = torch.randn(num_layers * 1, batch_size, hidden_size)
print(f"--- ダミー初期隠れ状態 ---")
print(f"初期隠れ状態テンソルの形状: {initial_hidden_state.shape}")
# 期待される形状: (1, 2, 5) (num_layers * 1, batch_size, hidden_size)
print(f"初期隠れ状態の内容 (最初の層の最初のバッチだけ表示):\n{initial_hidden_state[0,0,:]}\n")
# --- 5. モデルに入力テンソル(と初期隠れ状態)を渡し、順伝播を実行! ---
# これがRNNの計算のメイン部分です。
# rnn_model に入力テンソルと初期隠れ状態を渡すと、2つのものが出力として返ってきます。
# 1つ目 (output_features): 系列の各時刻における、RNNの最後の層の隠れ状態の集まり。
# 2つ目 (final_hidden_state): 系列全体の情報を処理し終えた後の、最後の時刻における「各層の」隠れ状態。
output_features, final_hidden_state = rnn_model(input_tensor, initial_hidden_state)
# もし初期隠れ状態を渡さない場合は、以下のように書けます。
# output_features, final_hidden_state = rnn_model(input_tensor) # この場合、h_0はゼロで初期化されます。
print(f"--- RNNからの出力 ---")
print(f"出力特徴テンソル (output_features) の形状: {output_features.shape}")
# 期待される形状: (2, 4, 5) (batch_size, seq_len, hidden_size)
# なぜなら、batch_first=Trueで、各時刻(seq_len)の隠れ状態(hidden_size)がバッチごとに出てくるからです。
print(f"最終隠れ状態テンソル (final_hidden_state) の形状: {final_hidden_state.shape}")
# 期待される形状: (1, 2, 5) (num_layers * 1, batch_size, hidden_size)
# これは、最後の時刻の隠れ状態が、層ごと・バッチごとに出てくるからです。
# === ここから下が上記のprint文による実際の出力の例 (乱数値なので毎回変わります) ===
# --- RNNのパラメータ設定 ---
# 入力特徴の次元数 (input_size): 3
# 隠れ状態の次元数 (hidden_size): 5
# RNNの層の数 (num_layers): 1
# バッチサイズを最初の次元にする (batch_first): True
#
# --- 作成したRNNモデル ---
# RNN(3, 5, batch_first=True)
#
# --- ダミー入力データ ---
# 入力テンソルの形状: torch.Size([2, 4, 3])
# 入力テンソルの内容 (最初のバッチの最初の要素だけ表示):
# tensor([ 0.1234, -0.5678, 0.9012])
#
# --- ダミー初期隠れ状態 ---
# 初期隠れ状態テンソルの形状: torch.Size([1, 2, 5])
# 初期隠れ状態の内容 (最初の層の最初のバッチだけ表示):
# tensor([ 0.4321, -0.8765, 0.2109, -0.9999, 0.5432])
#
# --- RNNからの出力 ---
# 出力特徴テンソル (output_features) の形状: torch.Size([2, 4, 5])
# 最終隠れ状態テンソル (final_hidden_state) の形状: torch.Size([1, 2, 5])
出力結果の解説 〜テンソルの形は何を語る?〜
さて、コードを実行すると、いくつかのテンソルの「形状 (shape)」が表示されたはずです。この形が、RNNの入出力を理解する上でとっても大切なんですよ。
入力テンソル (input_tensor) の形状: (2, 4, 3)
- 最初の「2」は バッチサイズ です。つまり、2つの異なる系列データを同時に処理している、ということです。
- 次の「4」は 系列長 (シーケンス長) です。各データが4つの時刻ステップ(例えば4つの単語や4時点のデータ)を持っていることを意味します。
- 最後の「3」は 入力特徴の次元数 (
input_size) です。各時刻の入力データが、3つの数値で構成されるベクトルであることを示しています。
初期隠れ状態テンソル (initial_hidden_state) の形状: (1, 2, 5)
- 最初の「1」は (層の数 × 方向数) です。今回は
num_layers=1で、単方向RNNなので方向数は1。なので \(1 \times 1 = 1\) となります。もし2層のRNNならここが2になります。 - 次の「2」は バッチサイズ です。入力テンソルのバッチサイズと一致している必要があります。
- 最後の「5」は 隠れ状態の次元数 (
hidden_size) です。RNNの「記憶」の大きさを表します。
出力特徴テンソル (output_features) の形状: (2, 4, 5)
- 最初の「2」は バッチサイズ。
- 次の「4」は 系列長。
- 最後の「5」は 隠れ状態の次元数 (
hidden_size) です。
おや? output_features の最後の次元が hidden_size になっていますね。これは何を意味するのでしょうか?
実は、PyTorchの nn.RNN が返すこの output_features というのは、系列の各時刻 \(t\) における、RNNの「最後の層の」隠れ状態 \(h_t\) が、ずらっと並んだものなんです。ちょっと紛らわしいのですが、これが nn.RNN の「出力」とされています。もし、このRNNの後にさらに全結合層(線形層)などを繋げて、各時刻 \(t\) での最終的な予測値 \(y_t\) (例えば、次の単語の確率分布とか、株価の予測値とか) を作りたい場合は、この output_features テンソルをその層への入力として使うことになります。
output_features テンソルのイメージ (batch_first=True の場合)
形状: (バッチサイズ, 系列長, 隠れ状態の次元数)
( 2 , 4 , 5 ) <-- 今回の例
例: バッチサイズが2、系列長が4、隠れ状態次元が5 の場合
データサンプル1 (1つ目のバッチ):
時刻1: [h_11, h_12, h_13, h_14, h_15] <-- 時刻1の最後の層の隠れ状態 (5次元ベクトル)
時刻2: [h_21, h_22, h_23, h_24, h_25] <-- 時刻2の最後の層の隠れ状態 (5次元ベクトル)
時刻3: [h_31, h_32, h_33, h_34, h_35] <-- 時刻3の最後の層の隠れ状態 (5次元ベクトル)
時刻4: [h_41, h_42, h_43, h_44, h_45] <-- 時刻4の最後の層の隠れ状態 (5次元ベクトル)
データサンプル2 (2つ目のバッチ):
時刻1: [h'_11, h'_12, h'_13, h'_14, h'_15]
時刻2: [h'_21, h'_22, h'_23, h'_24, h'_25]
時刻3: [h'_31, h'_32, h'_33, h'_34, h'_35]
時刻4: [h'_41, h'_42, h'_43, h'_44, h'_45]
つまり、output_features[i, j, :] が、i番目のバッチの、j番目の時刻における、
RNNの最後の層の隠れ状態ベクトルそのものになっている、というわけですね。
最終隠れ状態テンソル (final_hidden_state) の形状: (1, 2, 5)
- 最初の「1」は (層の数 × 方向数) です。
initial_hidden_stateと同じですね。 - 次の「2」は バッチサイズ。
- 最後の「5」は 隠れ状態の次元数 (
hidden_size)。
こちらは、系列全体の情報(この例では4ステップ分の情報)を処理し終えた後の、「最後の時刻 \(T\) (この例では \(T=4\))」における「各層の」隠れ状態 を集めたものです。もし num_layers が1なら、これがまさに私たちがよく \(h_T\) と書く、系列全体の文脈を要約したベクトルに相当します。文章全体の分類や感情分析など、系列全体の情報に基づいて何かを判断したいタスクでは、この final_hidden_state が特徴量としてよく使われます。 もし num_layers が例えば2だったら、final_hidden_state の形状は (2, batch_size, hidden_size) となり、0番目の要素が1層目の最終隠れ状態、1番目の要素が2層目(最後の層)の最終隠れ状態、というように格納されます。
どうでしょう? こうして実際にテンソルの形を追いかけてみると、nn.RNN モジュールへのデータの渡し方や、返ってくるテンソルが何を意味しているのか、というイメージが、先ほどまでの理論的な説明と具体的につながってきたのではないでしょうか。
最初はちょっと呪文のように見えるかもしれませんが、一つ一つのパラメータの意味やテンソルの各次元が何を表しているのかが分かってくると、だんだんRNNと「会話」できるようになってくると思いますよ。この「形を合わせる」感覚は、ディープラーニングのプログラミングではとても大切なので、ぜひ覚えておいてくださいね。
医療応用での考慮点
- 医療時系列データの入力: 例えば、ICUで1時間ごとに記録される患者さんの複数のバイタルサイン(心拍数、血圧、体温、SpO2など)をRNNに入力する場合を考えてみましょう。もし12時間分のデータを見るなら系列長は12、バイタルサインの種類が4つなら
input_sizeは4になります。これを複数の患者さんについて同時に処理するなら、その患者さんの数がバッチサイズです。これらの数値を基に、適切な形状のテンソルとしてデータを準備する必要があります。 - 隠れ状態の活用: RNNの隠れ状態は、過去の情報を要約した「文脈ベクトル」と見なせます。例えば、患者さんの診療記録(テキスト)を単語ごとにRNNで処理していった場合、各単語を処理した後の隠れ状態は、それまでの文脈を捉えた表現になっていると期待できます。この隠れ状態ベクトルを使って、例えばその診療記録が特定の疾患に関連するかどうかを分類したり、重要な情報を抽出したりするタスクに応用できます。
nn.RNN の使い方に慣れることは、より複雑な系列モデル(LSTMやGRU、Transformerなど)を学ぶ上での基礎となりますので、ぜひ実際にコードを動かして試してみてください。
2.4 RNNの課題:長期依存性の問題(勾配消失・爆発問題)
RNNは過去の情報を記憶し、それを現在の処理に活かせるという素晴らしい特徴を持っています。しかし、その「記憶」が、あまりにも遠い過去の情報にまで及ぶ必要がある場合、つまり系列が非常に長くなった場合に、うまく学習できないという課題を抱えています。これは長期依存性の問題 (Long-Term Dependency Problem) と呼ばれ、RNNを実用化する上での大きなハードルの一つでした。
この問題の主な原因は、RNNの学習アルゴリズムであるBPTT(時間を通じた逆伝播)において、勾配(損失関数を各重みで偏微分したもの、つまり重みをどちらに更新すれば損失が減るかを示す指標)が時間を遡るにつれて、極端に小さくなってしまう(勾配消失)か、逆に極端に大きくなってしまう(勾配爆発)という現象が起こりやすいためです。
勾配消失 (Vanishing Gradient Problem)
勾配消失は、誤差の情報を時間を遡って伝播させていく際に、その情報(勾配)が途中でほとんどゼロに近い非常に小さな値になってしまい、遠い過去の重みにはほとんど更新が伝わらなくなってしまう現象です。
これは、RNNの隠れ状態を計算する際に使われる活性化関数(例えば \(\tanh\) やシグモイド関数)の導関数(微分したものの値)が、多くの場合1以下の値を取ることが一因とされています。BPTTでは、これらの導関数が時間ステップの数だけ繰り返し掛け合わされるため、系列が長くなると、勾配は指数関数的に小さくなりやすいのです。
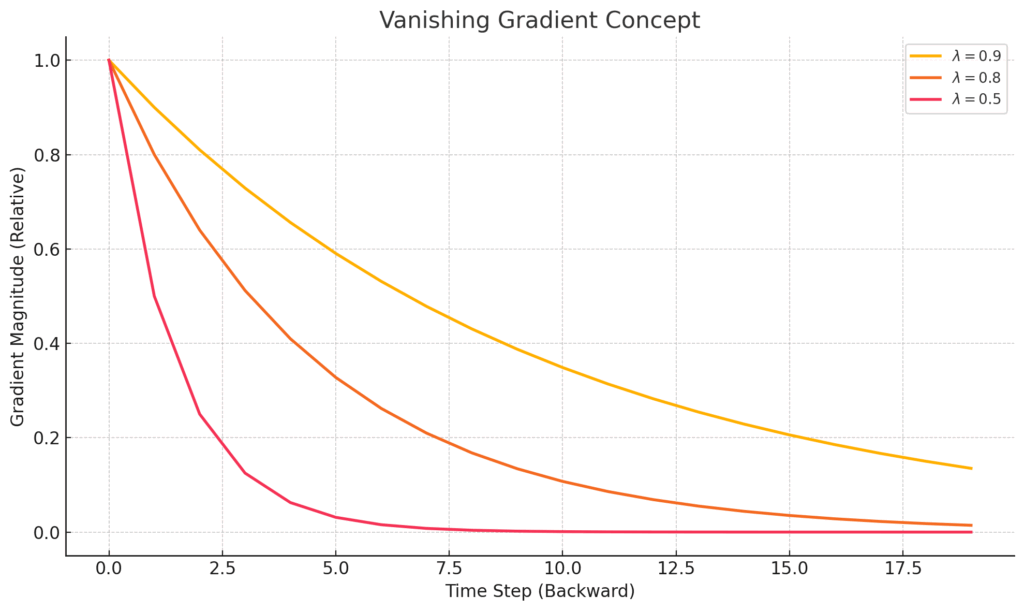
もし勾配が消失してしまうと、AIモデルは「系列のかなり前の入力が、最終的な出力の誤差にどう影響したか」を正しく評価できなくなります。その結果、RNNは目先の短い期間の依存関係しか学習できず、長期にわたるパターンや文脈を捉えることが非常に困難になってしまうのです。
勾配爆発 (Exploding Gradient Problem)
勾配爆発は、勾配消失とは逆に、時間を遡る勾配が指数関数的に増大し、非常に大きな値になってしまう現象です。これは、RNNの重み行列 \(W_{hh}\) の値が大きい場合に起こりやすいとされています。
勾配が爆発すると、重みの更新量が極端に大きくなりすぎてしまい、学習プロセスが非常に不安定になります。最悪の場合、数値がオーバーフローして学習が発散し、全く収束しなくなってしまうこともあります。
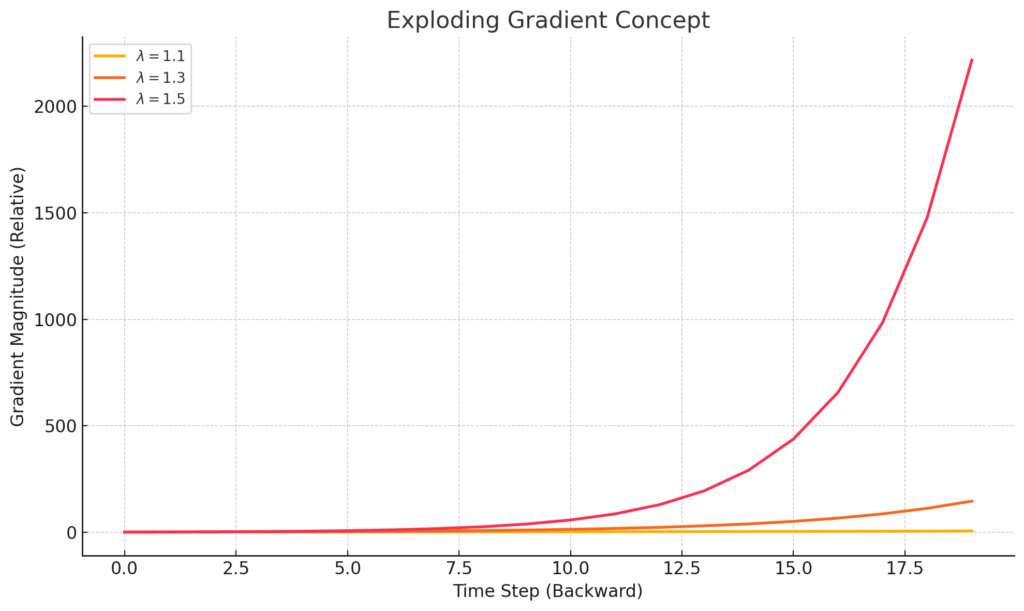
勾配爆発に対しては、勾配の大きさが一定の閾値を超えたら強制的に小さくする「勾配クリッピング (Gradient Clipping)」というテクニックである程度対処できることが知られています。しかし、勾配消失はより根深い問題であり、単純な対処法では解決が難しいとされてきました。
医療応用における長期依存性の影響
- 長期的な患者予後の予測: 例えば、がん患者さんの数年間にわたる治療記録(投薬履歴、検査値の推移、副作用の有無など)を入力として、その後の生存期間や再発リスクを予測するようなタスクを考えてみましょう。この場合、治療初期の重要な情報(例えば、特定の遺伝子変異の有無や初期治療への反応など)が、数年後の予後に大きな影響を与える可能性があります。しかし、RNNが勾配消失の問題を抱えていると、このような遠い過去の重要な情報を現在の予測に十分に活かせないかもしれません。
- 慢性疾患の管理: 糖尿病や高血圧のような慢性疾患の管理では、数ヶ月から数年にわたる患者さんの生活習慣、服薬状況、検査値の微妙な変化といった長期的なトレンドを把握することが重要です。RNNでこれらのデータをモデル化しようとする際も、長期依存性をうまく捉えられないと、個々の患者さんに最適化された介入策の提案などが難しくなる可能性があります。
この長期依存性の問題、特に勾配消失は、RNNがそのポテンシャルを十分に発揮する上での大きな制約となっていました。そして、この課題を克服するために、より洗練された「記憶」の仕組みを持つ新しいタイプのRNNアーキテクチャ、すなわち次章以降で学ぶLSTM(Long Short-Term Memory)やGRU(Gated Recurrent Unit)が考案されることになったのです。RNNの課題を理解することは、これらの改良型モデルがなぜ登場し、どのように機能するのかを理解するための重要な布石となります。
まとめと次のステップ
この第2章では、系列データを扱うための基本的なニューラルネットワークであるRNNについて、その核心的なアイデアからPyTorchを用いた具体的な実装方法、そしてそれが抱える重要な課題までを一緒に見てきました。
RNNが持つ「ループ構造」によって過去の情報を隠れ状態に保持し、それを現在の処理に活かすという「記憶」のメカニズムは、系列データが持つ時間的な順序性や文脈を捉える上で非常に画期的でしたね。そして、その学習が時間を通じた逆伝播(BPTT)というアルゴリズムによって行われることも理解いただけたかと思います。PyTorchの nn.RNN モジュールを使えば、これらの複雑な処理を手軽に実装できることも体験しました。
しかし同時に、RNN、特にシンプルな構造のものは、「長期依存性の問題」、とりわけ勾配消失によって、遠い過去の情報を現在の判断にうまく活かせないという大きな課題も抱えていることも明らかになりました。
このRNNの基礎と限界を理解した上で、次はいよいよ、この長期依存性の問題を克服するために設計された、より強力なRNNの仲間たち、LSTMとGRUの世界へと足を踏み入れていきます。これらのモデルが、どのようにして「忘れるべき情報」と「記憶し続けるべき情報」を賢く取捨選択し、長期的な依存関係を捉えることを可能にしているのか。その驚くべき仕組みを、また一緒に学んでいきましょう。本章で得た知識は、必ずや次章以降の理解を助けてくれるはずです。
参考文献
- Rumelhart DE, Hinton GE, Williams RJ. Learning representations by back-propagating errors. Nature. 1986;323(6088):533-536.
- Goodfellow I, Bengio Y, Courville A. Deep Learning. MIT Press; 2016. (Chapter 10: Sequence Modeling: Recurrent and Recursive Nets)
- Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput. 1997;9(8):1735-1780.
- Bengio Y, Simard P, Frasconi P. Learning long-term dependencies with gradient descent is difficult. IEEE Transactions on Neural Networks. 1994;5(2):157-166.
- Paszke A, Gross S, Massa F, et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. Advances in Neural Information Processing Systems 32 (NeurIPS 2019).
- PyTorch nn.RNN Documentation. (PyTorchの公式ドキュメントへのリンクを想定)
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






