PyTorchでは、AIモデルをクラスとして設計します。まず構造の「部品」(層)を__init__()で定義し、次にデータの「流れ」をforward()で記述します。この2段階の設計が、あらゆるカスタムAIを構築する上での基本となります。
PyTorchの全モデルはnn.Moduleを継承したクラスとして定義します。これにより、パラメータの自動登録、GPU転送(.to())、学習/評価モードの切替(.train()/.eval())といった必須機能が利用可能になります。
__init__()メソッド
モデルの構造を定義する部分です。全結合層(nn.Linear)や活性化関数(nn.ReLU)など、ネットワークを構成する「部品」をここでインスタンス化し、準備します。
forward()メソッド
データがモデル内を通過する「流れ」を記述します。__init__()で定義した部品をどのような順序で適用するかをここで定義し、入力から出力までの順伝播プロセスを完成させます。
この構造を応用し、例えば「年齢、BMI、血圧」などを入力して「疾患リスク」を分類するAIを構築できます。複雑な特徴間の関係性を捉え、医師の診断支援ツールとして機能します。
✅ はじめに:いよいよ「自分のAI」を組み立てる段階へ!
これまでの章では、ニューラルネットワークを支える基礎的な理論と仕組みを学んできました。
- 内積や行列計算といった線形代数
- 微分と勾配降下法による学習の原理
- 誤差逆伝播法(Backpropagation)によるパラメータの更新
- そして、PyTorchを使ったTensor操作や自動微分(
.backward())の実践
これらは、まるで「脳の回路図」のようなニューラルネットワークが どう動くか を理解するための準備運動でした。
🧱 本章からは「構築編」へステップアップ
いよいよ今回は、自分でニューラルネットワークの構造を定義するという実践的ステップに進みます。
この章では、PyTorchが提供する強力な仕組みである nn.Module を使って、
- ニューラルネットの「部品」(全結合層や活性化関数など)をどう組み立てるか
- データがそのネットワークを通ってどう処理されるか(順伝播:
forward())
を、自分の手で書いていけるようになります。
🎯 目指すゴール:
- PyTorchにおけるモデル定義の基本構文を理解する
- クラス構造(
__init__()とforward())を通して、「処理の流れ」を直感的に把握する - 医療や実データに応用できるベースモデルを自作できるようになる
🧠 1. ニューラルネットの構造を振り返ろう
— データはネットワークの中でどう変換されていくのか?
ニューラルネットワークとは、入力されたデータを少しずつ「意味のある表現」へと変換しながら、最終的に分類や予測といった目的に適した出力を得るための仕組みです。
その変換プロセスの基本となるのが「順伝播(forward propagation)」と呼ばれる流れです。

🔄 順伝播の基本ステップ
以下は、典型的なニューラルネットワークの処理の流れです。たとえば「患者の身長・体重・血圧・年齢」などのデータを入力し、「病気のリスク」を分類するといったケースをイメージしてみてください。
- 入力ベクトルの受け取り
データを数値ベクトルとしてネットワークに入力します。
例:\(\mathbf{x} = [170, 65, 130, 45]\)(cm, kg, mmHg, 歳) - 重み行列との線形変換(全結合)
各層では、入力ベクトルに対して重み行列との積とバイアスの加算を行います: \[ \mathbf{z}^{(1)} = \mathbf{x} \mathbf{W}^{(1)} + \mathbf{b}^{(1)} \] - 活性化関数による非線形変換
線形変換だけでは表現力が不足するため、ReLUやSigmoidなどの活性化関数で非線形性を加えます: \[ \mathbf{h}^{(1)} = \text{ReLU}(\mathbf{z}^{(1)}) \] - 中間層を繰り返す(必要に応じて複数回)
活性化後の出力を次の層へ渡し、同様の処理を繰り返します。 - 出力層による最終結果の生成
最終層では分類や回帰などのタスクに応じた出力を得ます。たとえば3クラス分類なら、出力ベクトルの次元は3になります。
🧠 ニューラルネットは「入力 → 意味抽出 → 出力」の変換装置
この一連の流れが、ニューラルネットワークが「入力 → 意味抽出 → 出力」という思考回路のような動作を行う仕組みです。
次のセクションでは、この構造を実際に PyTorch を使ってどのようにコードで定義するかを学んでいきましょう。
🔧 2. PyTorchにおけるモデル定義の基本構文
— ニューラルネットは「Pythonクラス」で設計する
PyTorchでは、ニューラルネットワークを構築する際、モデル全体を「ひとつのPythonクラス」として定義します。これは、複雑な構造を部品ごとに整理し、学習可能なパラメータ(重みやバイアス)を自動で管理するための仕組みです。
🧱 基本構造は nn.Module の継承で決まる
PyTorchのモデルクラスは、必ず torch.nn.Module を継承します。これは「ニューラルネットの基本機能(パラメータ管理、GPU移行、保存など)」をすべて備えた親クラスであり、すべての独自モデルの土台になります。
🔄 モデルクラスの2本柱
モデルクラスを定義するときには、必ず次の2つのメソッドを記述します:
| メソッド名 | 役割 |
|---|---|
__init__() | ネットワークの「構造」(層や関数)を定義する部分 |
forward() | 入力データがその構造をどう通るか、「処理の流れ」を記述する部分 |
これにより、モデルは「どんな部品を持ち」「入力をどう処理するか」を明示的に設計できるのです。
🧪 実装に向けたインポート準備
モデルを定義するには、以下の2つのモジュールを読み込む必要があります:
import torch # PyTorch本体:テンソル操作や自動微分などを含む
import torch.nn as nn # ニューラルネット構築のためのモジュール(nn.Linearなどが含まれる)
次章では、これらを実際に使って「シンプルな3層のニューラルネットワーク」を構築してみましょう。どのように __init__() と forward() を書けばよいのか、コードとともに具体的に解説します。
🏗️ 3. 実装:3層の全結合ニューラルネットを定義してみよう
— nn.Module を継承した「自作モデル」の最小構造
ここでは、入力4次元 → 中間層16 → 中間層8 → 出力3クラスというシンプルなニューラルネットワークを例に、nn.Module を使ったモデルの定義方法を学びます。
この構造は以下のようなタスクに応用できます:
- 入力:患者の基本情報(身長・体重・年齢・血圧など)
- 出力:病気のリスク(低・中・高の3クラス)
🔍 コード全体(日本語コメント付き)
import torch # PyTorch 本体のインポート(Tensor操作など)
import torch.nn as nn # ニューラルネット構築用の nn モジュールをインポート
# 自作ニューラルネットワーククラスを定義(nn.Module を継承)
class SimpleNet(nn.Module):
def __init__(self):
super(SimpleNet, self).__init__() # nn.Module の初期化処理
self.fc1 = nn.Linear(4, 16) # 入力層(4次元) → 第1隠れ層(16ユニット)
self.relu1 = nn.ReLU() # 第1層の活性化関数:ReLU(非線形変換)
self.fc2 = nn.Linear(16, 8) # 第1隠れ層 → 第2隠れ層(8ユニット)
self.relu2 = nn.ReLU() # 第2層の活性化関数:ReLU
self.output = nn.Linear(8, 3) # 第2隠れ層 → 出力層(3クラス分類)
def forward(self, x):
x = self.fc1(x) # 入力を第1層に通す
x = self.relu1(x) # 第1層にReLUを適用
x = self.fc2(x) # 第2層に通す
x = self.relu2(x) # 第2層にReLUを適用
x = self.output(x) # 出力層に通して最終スコアを得る
return x # 出力を返す
╔═══════════════════════════════════════════════════════════════════════════════════╗
║ 🧠 SimpleNet:3層の全結合ニューラルネット構造図(超詳細版・医療データ対応) ║
╚═══════════════════════════════════════════════════════════════════════════════════╝
┌──────────────────────────────────────────────────────────────┐
│ 🔢 入力ベクトル x(形状: [1 × 4]) │
│ - 実データ例:[年齢, BMI, HbA1c, 血圧] │
│ - 特徴量 = 4次元。各値は連続値。 │
│ - 医療の診断補助タスクで使われる基礎データ。 │
└──────────────────────────────────────────────────────────────┘
│
▼
┌──────────────────────────────────────────────────────────────┐
│ 🧱 第1全結合層 fc1 = nn.Linear(4, 16)(線形変換その1) │
│ - 入力:4次元 → 出力:16次元(次元拡張) │
│ - パラメータ:重み W₁ ∈ ℝ¹⁶ˣ⁴、バイアス b₁ ∈ ℝ¹⁶ │
│ - 数式:z₁ = xW₁ᵀ + b₁ │
│ - 目的:特徴量の重み付き和によって「意味のある抽象表現」を学習 │
└──────────────────────────────────────────────────────────────┘
│
▼
┌──────────────────────────────────────────────────────────────┐
│ 🔄 活性化関数 ReLU (relu1) — 非線形性の導入 │
│ - 式:ReLU(z) = max(0, z) │
│ - 負の値は0に、正の値はそのまま通す │
│ - 出力:h₁ = ReLU(z₁) ∈ ℝ¹ˣ¹⁶ │
│ - 目的:線形変換だけでは表現できない非線形パターンを学習する │
└──────────────────────────────────────────────────────────────┘
│
▼
┌──────────────────────────────────────────────────────────────┐
│ 🧱 第2全結合層 fc2 = nn.Linear(16, 8)(線形変換その2) │
│ - 入力:16次元 → 出力:8次元 │
│ - パラメータ:重み W₂ ∈ ℝ⁸ˣ¹⁶、バイアス b₂ ∈ ℝ⁸ │
│ - 数式:z₂ = h₁W₂ᵀ + b₂ │
│ - 目的:より抽象的な「中間特徴」を形成し、最終分類の前段階を構築する │
└──────────────────────────────────────────────────────────────┘
│
▼
┌──────────────────────────────────────────────────────────────┐
│ 🔄 活性化関数 ReLU (relu2) — さらなる非線形性の注入 │
│ - 式:ReLU(z) = max(0, z) │
│ - 出力:h₂ = ReLU(z₂) ∈ ℝ¹ˣ⁸ │
│ - 目的:複雑な条件分岐や領域的表現(閾値を超えたパターンなど)を学習可能にする │
└──────────────────────────────────────────────────────────────┘
│
▼
┌──────────────────────────────────────────────────────────────┐
│ 🎯 出力層 output = nn.Linear(8, 3)(クラススコア生成) │
│ - 入力:8次元 → 出力:3次元(3クラス分類) │
│ - パラメータ:重み W₃ ∈ ℝ³ˣ⁸、バイアス b₃ ∈ ℝ³ │
│ - 数式:y = h₂W₃ᵀ + b₃ │
│ - 出力:logits ∈ ℝ¹ˣ³(クラスごとのスコア) │
└──────────────────────────────────────────────────────────────┘
│
▼
┌──────────────────────────────────────────────────────────────┐
│ 📈 Softmax で確率化:分類結果をわかりやすくする │
│ - 各クラスのスコア y₁, y₂, y₃ に対し: │
│ Pᵢ = e^{yᵢ} / ∑ⱼ e^{yⱼ}(i = 1, 2, 3) │
│ - 出力:P = [0.1, 0.3, 0.6] → 最も高い P₃ を採用 → 「高リスク」 │
└──────────────────────────────────────────────────────────────┘
✅ 全体構造のポイント
このモデルには、ニューラルネットワークの実装と設計を理解するうえで重要な 3つの特徴 があります:
① __init__() メソッドで、全結合層(nn.Linear)と活性化関数(nn.ReLU)を「インスタンスとして」定義
- PyTorchでは、これらの層や関数も
nn.Moduleを継承した「クラス」であり、nn.Linear(4, 16)のようにインスタンス化されます。 - たとえば
self.fc1 = nn.Linear(4, 16)と書くことで、SimpleNetモデル内に「fc1」というサブモジュールが定義されます。 - つまり、モデル(SimpleNet インスタンス)の中に、レイヤー(Linear, ReLUなど)のインスタンスが含まれるという「入れ子構造」になっています。
- この構造により、次のような利点があります:
model.parameters()で全パラメータを自動取得model.to("cuda")やmodel.eval()で全レイヤーに一括適用state_dict()による保存と復元がシンプル
② forward() メソッドで、入力テンソルがどの順序で層を通るかを記述
- このメソッドでは、
__init__()で定義した層に入力テンソルを通して、順伝播の流れを明確に記述します。 - たとえば次のように書かれます:
def forward(self, x):
x = self.fc1(x) # 第1全結合層に入力
x = self.relu1(x) # 活性化関数ReLU
x = self.fc2(x) # 第2全結合層
x = self.relu2(x) # 再度ReLU
x = self.output(x) # 出力層
return x # 出力を返す
- この関数によって、データが「どこを通って」「どう変換されて」「最終出力になるのか」をロジカルに確認できます。
③ 入力から出力までを論理的につなぐ、簡潔かつ柔軟な構造
- モデル全体が
nn.Moduleを継承したクラスとして定義され、すべての処理が一つのオブジェクト内に統合されています。 - この構造により、定義 → 順伝播 → 学習 → 推論 → 保存 の各ステップが首尾一貫して管理されます。
- また、柔軟に層を追加・変更したり、他のモデルと組み合わせることも容易です。
🧠 補足:この構造が意味するもの
このように、「モデルインスタンスの中に、レイヤーインスタンスが入れ子で存在する」という設計は、PyTorchが提供するオブジェクト指向的な深層学習の根幹です。これにより、モデル構造と学習のあらゆる側面が、一貫性と拡張性を持って記述・運用できるのです。
📌 解説まとめ
| 部分 | 内容 | 説明 |
|---|---|---|
__init__() | 構造の定義 | 各層(Linear, ReLU)をインスタンスとして定義 |
forward() | 処理の流れ | 入力データがネットワークをどう通るかを記述 |
nn.Linear(in, out) | 全結合層 | 入力 \(\in \mathbb{R}^{\text{in}}\) を出力 \(\in \mathbb{R}^{\text{out}}\) に変換 |
nn.ReLU() | 活性化関数 | 非線形性によりネットワークの表現力を高める |
🔄 処理のイメージ(数学的表現)
このネットワークの順伝播(forward propagation)は、以下のように数式で表現できます:
まず、入力ベクトル \(\mathbf{x}\) に重み行列 \(\mathbf{W}_1\) を掛け、バイアス \(\mathbf{b}_1\) を加算した後、ReLU関数を適用して中間層の出力 \(\mathbf{h}_1\) を得ます。
同様の操作をもう一度行って \(\mathbf{h}_2\) を得たあと、最後の全結合層で最終出力 \(\mathbf{y}\) を計算します。
数式で書くと、次のようになります:
\[ \begin{aligned} \mathbf{h}_1 &= \text{ReLU}(\mathbf{x} \mathbf{W}_1 + \mathbf{b}_1) \\ \mathbf{h}_2 &= \text{ReLU}(\mathbf{h}_1 \mathbf{W}_2 + \mathbf{b}_2) \\ \mathbf{y} &= \mathbf{h}_2 \mathbf{W}_3 + \mathbf{b}_3 \end{aligned} \]
このように、ニューラルネットワークでは「線形変換+非線形変換」のセットを層として重ねることで、入力から出力までの複雑な関係を表現しています。
🧠 応用への一歩
この構造を理解できれば、より高度なネットワーク(画像認識、自然言語処理など)でも応用可能です。
📌 4. 各パーツの意味と直感的な理解
— コードの背後にある構造と役割を、イメージと数式でつかもう
SimpleNet のコードに出てくる各関数やメソッドには、それぞれ明確な役割があります。ここでは、それらを構造ごとに分解し、何をしているのか/なぜ必要なのかを、数式・直感・図解を交えて整理します。
🧱 ① nn.Linear(4, 16):全結合層(線形変換)
✅ 機能:
入力ベクトル(次元数 4)を、重み付きで変換し、16次元の中間ベクトルを出力します。数式的には以下のように表されます:
\[ \mathbf{z} = \mathbf{x} \mathbf{W} + \mathbf{b} \]
ここで:
- \(\mathbf{x} \in \mathbb{R}^4\):入力ベクトル
- \(\mathbf{W} \in \mathbb{R}^{4 \times 16}\):重み行列
- \(\mathbf{b} \in \mathbb{R}^{16}\):バイアス項
- \(\mathbf{z} \in \mathbb{R}^{16}\):出力ベクトル
🧠 図で見る「全結合層」のイメージ:
╔════════════════════════════════╗ ║ 全結合層(nn.Linear) ║ ╚════════════════════════════════╝ 入力ベクトル(4次元):
[x₁, x₂, x₃, x₄]
│ ▼ 重み付き和を計算(× W + b) │ ▼ 中間ベクトル(16次元)出力:
[z₁, z₂, …, z₁₆]
🧩 解説: この層は、入力の各要素に重みをかけて線形結合する処理です。医学的に言えば、「患者の特徴量(年齢、血圧など)から、リスクファクターを抽出する」イメージに近いです。
🔸 ② nn.ReLU():活性化関数(非線形変換)
✅ 機能: 入力が正ならそのまま、負ならゼロにします:
\[ \text{ReLU}(x) = \max(0, x) \]
🧠 なぜ必要? 線形変換だけでは、複雑なパターン(非線形)を学習できません。ReLUは簡単な関数でありながら、勾配消失を防ぎつつ、非線形性を導入できます。
🔍 図で見る「ReLU関数」の形と直感:
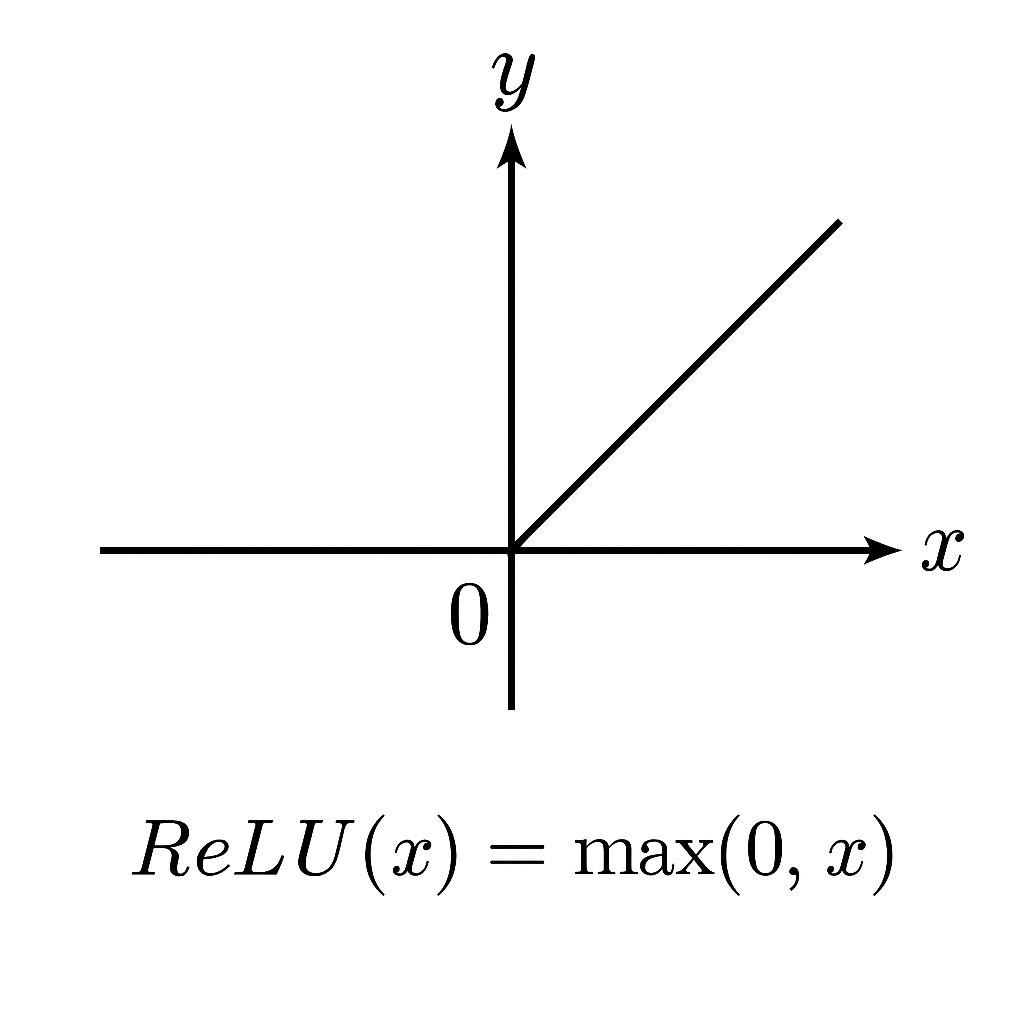
🧩 解説: ReLUは「重要な特徴だけを通し、ノイズや不要な信号は遮断するフィルターのような役割」を果たします。
🔸 ③ forward(x):順伝播の定義
✅ 機能: モデルに入力されたデータ(テンソル)を、層に沿ってどのように処理するかを定義します。
🧠 なぜ必要? __init__() は「部品を定義」する場所、forward() は「その部品をどう使うか(接続・流れ)」を記述する場所です。
🔄 処理の流れ(forwardの中身)を簡略図で表すと:
入力データ(Tensor)
│
▼
fc1(Linear: 4 → 16)
▼
ReLU1
▼
fc2(Linear: 16 → 8)
▼
ReLU2
▼
output(Linear: 8 → 3)
▼
出力ベクトル(logits)
✅ まとめ表:各関数とその役割
| 関数・構文 | 役割 | 解説(直感) |
|---|---|---|
nn.Linear(4,16) | 線形変換(全結合) | 入力の重み付き合計を計算(特徴量抽出) |
nn.ReLU() | 活性化関数(非線形変換) | 必要な信号だけを通すフィルター |
forward(x) | 順伝播の処理フロー定義 | 入力→中間層→出力の「通り道」を作る |
このように、SimpleNet の各部品は「入力→意味抽出→出力」という構造を自然に表現するために設計されています。
次はこのモデルに実際のデータを入れて「出力がどうなるのか」を見ていきましょう。
🔍 5. モデルを「動かしてみる」
— 実際に入力データを通して出力を得てみよう
ここまでで、自作ニューラルネット SimpleNet の構造は完成しました。
では、いよいよこのモデルを 「動かす」=推論(inference) してみましょう。
✅ 推論とは?
- 訓練済みまたは初期状態のモデルに対して、
- ダミーデータや実データを入力し、
- モデルがどんな出力を返すかを確認するプロセスです。
これは、モデルの動作確認や形状のチェックにとても重要なステップです。
✅ コード例:SimpleNet のインスタンス化と推論
# 1. モデルのインスタンス化(=クラスのオブジェクト化)
model = SimpleNet()
# 2. ダミー入力を作成(バッチサイズ1、特徴量4次元)
dummy_input = torch.randn(1, 4)
# 3. 推論(forwardを呼び出す)
output = model(dummy_input)
# 4. 結果を表示(出力ベクトル)
print(output)
🧠 出力結果の形と意味
tensor([[ 0.241, -0.089, 0.510]], grad_fn=<AddmmBackward>)
出力の形状は (1, 3):
1は バッチサイズ(入力データ1件)3は 分類対象のクラス数(3クラス分類)
この出力は logits(ロジット)と呼ばれる「生のスコア」です。
🔬 数式で表すと?
\[ \begin{aligned} \mathbf{h}_1 &= \text{ReLU}(\mathbf{x} \mathbf{W}_1 + \mathbf{b}_1) \\ \mathbf{h}_2 &= \text{ReLU}(\mathbf{h}_1 \mathbf{W}_2 + \mathbf{b}_2) \\ \mathbf{y} &= \mathbf{h}_2 \mathbf{W}_3 + \mathbf{b}_3 \end{aligned} \]
ここで:
- \(\mathbf{x} \in \mathbb{R}^{1 \times 4}\):入力テンソル(バッチ1件・特徴量4)
- \(\mathbf{W}_1 \in \mathbb{R}^{4 \times 16}\):第1層の重み
- \(\mathbf{W}_2 \in \mathbb{R}^{16 \times 8}\):第2層の重み
- \(\mathbf{W}_3 \in \mathbb{R}^{8 \times 3}\):出力層の重み
🔧 推論プロセスのテキスト図(データの流れ)
╔════════════════════════════════════════════════╗
║ 🔍 推論処理の流れ(データの変換) ║
╚════════════════════════════════════════════════╝
[1×4] 入力テンソル(dummy_input)
│
▼
fc1: Linear(4 → 16) → 出力 [1×16]
│
▼
ReLU1 → 非線形変換 [1×16]
│
▼
fc2: Linear(16 → 8) → 出力 [1×8]
│
▼
ReLU2 → 非線形変換 [1×8]
│
▼
output: Linear(8 → 3) → 出力 [1×3]
│
▼
[1×3] 出力テンソル(logits)
🔍 出力はなぜ「logits」なのか?
- Softmax などで正規化される前の「生スコア」なので、logits(線形スコア)と呼ばれます。
- 分類タスクでは、この logits に対して CrossEntropyLoss を使って学習します。
- 実際の「クラス確率」が欲しい場合は Softmax を使います:
import torch.nn.functional as F # Softmaxを使うために必要
probs = F.softmax(output, dim=1) # 各クラスの確率を計算
print(probs) # 確率の出力
✅ まとめ:このステップの目的
| ステップ | 目的 |
|---|---|
| モデルのインスタンス化 | SimpleNet() の構造確認 |
| ダミー入力の作成 | 入力次元が合っているか検証 |
| 推論(forward) | モデルが正しく動作するか確認 |
| 出力結果の表示 | 形状やスコアの意味を理解 |
🧠 6. モデル内部を見てみよう
— 構造とパラメータの「中身」を観察する
ニューラルネットワークを定義しただけでは、その中身はブラックボックスのままです。
そこで、print(model) や model.named_parameters() を使って、モデルの構造や重み行列の形を確認してみましょう。
✅ モデル構造を表示する:print(model)
# モデルの構造を出力(定義された各層の情報が表示される)
print(model)
🔍 出力例:
SimpleNet(
(fc1): Linear(in_features=4, out_features=16, bias=True)
(relu1): ReLU()
(fc2): Linear(in_features=16, out_features=8, bias=True)
(relu2): ReLU()
(output): Linear(in_features=8, out_features=3, bias=True)
)
これは __init__() で定義した層を自動的に読み取って表示したもので、nn.Linear の入力・出力サイズ、バイアスの有無などが明示されます。
✅ 各パラメータの形を表示する:named_parameters()
# 各パラメータ(重み・バイアス)の名前と形状を出力
for name, param in model.named_parameters():
print(name, param.shape)
🔍 出力例:
fc1.weight torch.Size([16, 4])
fc1.bias torch.Size([16])
fc2.weight torch.Size([8, 16])
fc2.bias torch.Size([8])
output.weight torch.Size([3, 8])
output.bias torch.Size([3])
✅ 各パラメータの形状を図で確認
╔══════════════════════════════════════╗
║ SimpleNet のパラメータ構造(形状) ║
╚══════════════════════════════════════╝
fc1: Linear(4 → 16)
├─ 重み: W₁ ∈ ℝ¹⁶ˣ⁴
└─ バイアス: b₁ ∈ ℝ¹⁶
fc2: Linear(16 → 8)
├─ 重み: W₂ ∈ ℝ⁸ˣ¹⁶
└─ バイアス: b₂ ∈ ℝ⁸
output: Linear(8 → 3)
├─ 重み: W₃ ∈ ℝ³ˣ⁸
└─ バイアス: b₃ ∈ ℝ³
🧮 各パラメータが使われる数式
各層の出力は以下のように計算されています:
\[ \begin{aligned} \mathbf{h}_1 &= \text{ReLU}(\mathbf{x} \mathbf{W}_1^\top + \mathbf{b}_1) \\ \mathbf{h}_2 &= \text{ReLU}(\mathbf{h}_1 \mathbf{W}_2^\top + \mathbf{b}_2) \\ \mathbf{y} &= \mathbf{h}_2 \mathbf{W}_3^\top + \mathbf{b}_3 \end{aligned} \]
- \(\mathbf{x} \in \mathbb{R}^{1 \times 4}\):入力ベクトル(1サンプル)
- \(\mathbf{W}_1 \in \mathbb{R}^{4 \times 16}\):第1層の重み(出力 × 入力)
- \(\mathbf{W}_2 \in \mathbb{R}^{16 \times 8}\):第2層の重み
- \(\mathbf{W}_3 \in \mathbb{R}^{8 \times 3}\):出力層の重み
PyTorch では weight は [出力, 入力] の形で格納されるため、行列積では転置されたように動作します。
✅ パラメータ総数の確認
# 全パラメータの数を合計して出力する
total = sum(p.numel() for p in model.parameters())
print(f"パラメータ総数: {total}")
出力例:
パラメータ総数: 299
これらのパラメータはすべて requires_grad=True となっており、誤差逆伝播の際に勾配が計算されて自動的に更新されます。
📌 まとめ:内部構造を見て理解を深めよう
| コマンド | 目的 |
|---|---|
print(model) | モデルの層構成を確認する |
named_parameters() | 各パラメータの名前と形状を確認する |
numel() | 各パラメータの要素数(総数)を取得する |
このようにモデルの中身を可視化することで、形状ミスや意図しない構造を早期に検出でき、より信頼性の高いモデル設計が可能になります。
💡 7. nn.Module を使う利点
— なぜ PyTorch では「クラス定義」でモデルを作るのか?
前章では SimpleNet の構造やパラメータを可視化しました。
ここでは、PyTorchにおいて nn.Module を使うことで得られる主要なメリットを整理します。
✅ 1. パラメータが自動で登録される
__init__() 内で定義した各層(nn.Linearなど)は、自動的にパラメータ管理対象として登録されます。
# モデルの全パラメータ(重み・バイアス)を取得して表示
for param in model.parameters():
print(param.shape)
たとえば以下のように、すべての学習対象パラメータが取得できます:
fc1.weight torch.Size([16, 4])
fc1.bias torch.Size([16])
fc2.weight torch.Size([8, 16])
fc2.bias torch.Size([8])
output.weight torch.Size([3, 8])
output.bias torch.Size([3])
🔍 図:パラメータ自動登録の仕組み
╔═══════════════════════════════╗
║ model = SimpleNet() ║
╠═══════════════════════════════╣
║ self.fc1 = nn.Linear(4, 16) ║ ← モジュール登録
║ self.relu1 = nn.ReLU() ║ ← モジュール登録(パラメータなし)
║ ... ║
╚═══════════════════════════════╝
↓ 内部で自動的に格納される
model.parameters() →[fc1.weight, fc1.bias, fc2.weight, …]
✅ 2. 状態管理やAPIがシンプルになる
モデルの動作状態やデバイス移動を、1行で簡単に制御できます。
# GPUへ転送(デバイス移動)
model = model.to('cuda')
# 推論モードに切り替え(DropoutやBatchNormが推論仕様に)
model.eval()
# 学習モードに戻す
model.train()
.eval() はモデル全体に training=False を伝播させ、Dropout を無効化します。
✅ 3. モデルの保存と読み込みが簡単
# モデルのパラメータ(state_dict)を保存
torch.save(model.state_dict(), "model.pth")
# 同じ構造のモデルにパラメータを読み込む
model.load_state_dict(torch.load("model.pth"))
PyTorchの state_dict() は、モデルのすべてのパラメータ(テンソル)を辞書形式で保存・復元できる仕組みです。
🧠 なぜこれは「クラス構造」だからこそ可能なのか?
SimpleNet(nn.Module)のように継承されたクラスは、オブジェクト指向の構造を持ちます。- モデルの定義・パラメータ保持・学習状態・保存形式などを一貫して管理できます。
✅ まとめ:nn.Module がもたらす「設計の一貫性」
| 機能 | 説明 |
|---|---|
| パラメータ管理 | model.parameters() で自動的に取得可能 |
| デバイス移動 | .to("cuda") や .cpu() によって容易に制御 |
| 状態管理 | .eval() と .train() で推論と学習を切り替え |
| 保存と復元 | state_dict() を通じて再現性と再利用が高い |
| 拡張性 | カスタムモデルの継承やネストが容易 |
このように、nn.Module は単なるコードの「型」ではなく、深層学習モデルを「運用できる形で設計」するための基盤です。
🏥 8. 医療データでの応用イメージ
— AIは医師の診断やリスク評価をどう支援できるのか?
これまで構築してきたシンプルなニューラルネット SimpleNet は、医療データを入力として活用することで、疾患リスクの予測に応用できます。
ここでは「糖尿病リスクの予測」を例に、医療現場での適用イメージを解説します。
✅ 想定される入力と出力
| 入力(特徴量) | 説明 | 単位例 |
|---|---|---|
| 年齢 | 患者の年齢 | 歳 |
| BMI | 体格指数 | kg/m² |
| HbA1c | 糖化ヘモグロビン | % |
| 血圧 | 収縮期血圧 | mmHg |
これらをまとめた4次元ベクトルを入力とし、出力は以下の3クラスを分類します:
| クラス | 意味 |
|---|---|
| 0 | リスク低 |
| 1 | リスク中 |
| 2 | リスク高 |
🔧 構造の流れ(テキスト図)
╔════════════════════════════════════════════════════╗
║ 🧠 医療データ → ニューラルネット → リスク分類 ║
╚════════════════════════════════════════════════════╝
[年齢, BMI, HbA1c, 血圧](4次元ベクトル)
│
▼
Linear(4 → 16) → fc1
▼
ReLU(非線形活性化)
▼
Linear(16 → 8) → fc2
▼
ReLU(非線形活性化)
▼
Linear(8 → 3) → 出力層(クラス数3)
▼
出力:logits(3クラスのスコア)
🔬 数式で見るモデル内部の変換
このニューラルネット内部では、以下のような計算が行われています:
\[ \begin{aligned} \mathbf{x} &= [\text{age}, \text{BMI}, \text{HbA1c}, \text{BP}] \in \mathbb{R}^{1 \times 4} \\ \mathbf{h}_1 &= \text{ReLU}(\mathbf{x} \mathbf{W}_1^\top + \mathbf{b}_1) \quad \text{(16次元)} \\ \mathbf{h}_2 &= \text{ReLU}(\mathbf{h}_1 \mathbf{W}_2^\top + \mathbf{b}_2) \quad \text{(8次元)} \\ \mathbf{y} &= \mathbf{h}_2 \mathbf{W}_3^\top + \mathbf{b}_3 \quad \text{(3次元)} \end{aligned} \]
- \(\mathbf{x}\):患者データの数値ベクトル
- \(\mathbf{W}_i\):各層の重み行列
- \(\mathbf{b}_i\):バイアス項
🎯 Softmaxによる確率化と意思決定
出力ベクトル \(\mathbf{y} = [z_1, z_2, z_3]\) に対して Softmax を適用すると、各クラスの確率が得られます:
\[ P_i = \frac{e^{z_i}}{\sum_{j=1}^{3} e^{z_j}} \quad (i = 1,2,3) \]
たとえば次のように解釈されます:
| クラス | 確率 |
|---|---|
| 低 | 0.10 |
| 中 | 0.30 |
| 高 | 0.60 ← 最も高いので「高リスク」と判断 |
✅ 医療応用の価値とは?
- 複数の指標(年齢、体格、血糖、血圧)を組み合わせて、複雑なリスクパターンを学習
- 医師の判断を補完し、予防医療や早期介入を促進
- 人間では見落としがちな非線形関係をAIが自動で抽出
🧠 今後の発展例
- 電子カルテ情報や画像診断データとの統合
- 治療方針の推薦や個別化医療への拡張
- 患者へのリアルタイムなリスク通知・行動変容支援
🔚 9. まとめ
— ニューラルネット構築と推論の基本を体系化しよう
この章では、PyTorchを用いてシンプルなニューラルネットワークを構築し、医療データに応用できる推論モデルを完成させるまでの一連の流れを学びました。
✅ 学んだ内容を整理しよう
| ステップ | 内容 |
|---|---|
| モデルの定義 | nn.Module を継承して SimpleNet クラスを定義 |
| 構造設計 | __init__() で層(Linear, ReLU)を定義、forward() で処理の流れを明示 |
| インスタンス化 | クラスからモデルを生成し、model(dummy_input) で推論を実行 |
| パラメータ管理 | model.parameters() で全パラメータが自動管理される仕組みを理解 |
| 医療応用のイメージ | 年齢・BMI・HbA1c・血圧を使ったリスク分類モデルの構想 |
🔧 全体の流れを図にすると?
╔════════════════════════════════════════════════════════╗
║ PyTorchによるモデル定義・推論の全体像 ║
╚════════════════════════════════════════════════════════╝
1. モデル定義(nn.Module を継承)
└─ __init__() で各層(Linear, ReLU)を定義
└─ forward() で入力の流れを構築
2. モデルインスタンス化
└─ model = SimpleNet()
3. 入力データ生成(例:torch.randn(1, 4))
4. 推論(順伝播)
└─ output = model(dummy_input)
5. 出力確認(logits、Softmax)
6. 医療応用へ展開(例:糖尿病リスク分類)
🧮 数式で復習する「順伝播」の全体像
\[ \begin{aligned} \mathbf{h}_1 &= \text{ReLU}(\mathbf{x} \mathbf{W}_1^\top + \mathbf{b}_1) \\ \mathbf{h}_2 &= \text{ReLU}(\mathbf{h}_1 \mathbf{W}_2^\top + \mathbf{b}_2) \\ \mathbf{y} &= \mathbf{h}_2 \mathbf{W}_3^\top + \mathbf{b}_3 \\ \mathbf{p} &= \text{Softmax}(\mathbf{y}) \end{aligned} \]
- \(\mathbf{x}\):入力ベクトル(例:年齢・BMIなど)
- \(\mathbf{W}_i, \mathbf{b}_i\):各層の重み行列とバイアス
- \(\mathbf{y}\):クラスごとのスコア(logits)
- \(\mathbf{p}\):Softmax による出力確率分布
🔜 次章予告:「損失関数と最適化」
この「モデル定義 → 推論まで」のステップを理解したら、いよいよ次は モデルを学習させるフェーズへ。
次章では以下の内容を学びます:
- 損失関数(例:
CrossEntropyLoss) - 最適化手法(
SGD,Adamなど) - 学習ループ(ミニバッチ処理、勾配更新)
これにより、モデルは「正しい予測ができるように」学習し、より実用的な医療支援AIへと進化します。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






