AIが現実世界の複雑な問題を解くためには、単純な「直線」ではなく、自在な「曲線」を描く能力が不可欠です。その能力の源泉こそが、ニューロンに組み込まれた「活性化関数」という、驚くほどシンプルなスイッチなのです。
現実の問題は、単純な直線(線形)では分類できない複雑な関係(非線形)で溢れています。例えば、健常群に囲まれた疾患群を一本の線で分離することは不可能です。AIが賢くなるには、この「まっすぐじゃない」境界線を描く能力が必要でした。
AIの神経細胞(ニューロン)には、入力信号を処理する「活性化関数」というスイッチが備わっています。このスイッチが「ある値を超えたらON、それ以外はOFF」といった非線形な判断をすることで、AI全体として複雑な曲線を描く能力を獲得します。
ReLUは「入力がプラスならそのまま、マイナスなら0にする」という驚くほど単純なルールです。このシンプルさで計算が高速化し、学習信号が消えにくい「勾配消失問題」を解決。ディープラーニングの発展を加速させる立役者となりました。
もし、あなたが診断を下すとき、使えるルールが「血圧が高ければ高いほど、リスクもまっすぐ高くなる」という一本の直線しかなかったらどうでしょうか? きっと「いやいや、現実はそんなに単純じゃないよ」と思いますよね。ある数値を超えたら急にリスクが跳ね上がったり、複数の要因が複雑に絡み合ったり…。そう、私たちの世界は「まっすぐ」な関係だけでは到底捉えきれない、「単純じゃない」世界です。
AIもまったく同じ悩みを抱えています。初期のAI研究で使われていた「パーセプトロン」や「線形回帰」といったモデルは、まさにこの「まっすぐな定規」しか持っていませんでした。しかし、レントゲン写真の複雑な陰影から病変を見つけたり、患者さんの膨大なデータから予後を予測したりといった、医療現場で本当に求められる高度な判断は、とてもじゃないですが直線だけでは扱いきれません。
なぜ「まっすぐ」なモデルだけではダメなのか? — 現実世界の複雑な境界線
少し具体的に考えてみましょう。AIの仕事は、データを見て「病気がある(A群)」と「病気がない(B群)」のように、グループ分けの境界線を引くことだとイメージしてください。データがシンプルなら、一本の直線でスパッと分けられますよね。
図の解説:この図では、例えば「特徴量1」を収縮期血圧、「特徴量2」をコレステロール値として、患者さんをプロットしたとします。「O」が健常群、「X」が疾患群です。この場合、右肩上がりの一本の直線を引くだけで、2つのグループをうまく分離できています。これが「線形分離可能」な、AIにとっては簡単な問題です。

しかし、実際の医療データはもっと複雑です。例えば、ある2つの検査値が「両方とも中くらいの範囲」にある場合にだけリスクが高まる、といった状況を考えてみてください。
図の解説:この図では、「O」の疾患群が「X」の健常群にドーナツのように囲まれています。どう頑張っても、一本の直線を引いてこの2つのグループをきれいに分けることは不可能ですよね。このような「まっすぐじゃない」関係性を、専門用語で「非線形(ひせんけい)」な関係と呼びます。
AIが賢くなるためには、このドーナツ形のような複雑な境界線を自由に描けるようにならなければなりません。直線しか引けない定規だけではなく、どんな形にも曲がる「自在な曲線」を描く能力が必要なのです。
では、AIはどうやってこの「自在な曲線」を描く能力を手に入れたのでしょうか? その秘密の鍵を握るのが、AIの神経細胞(ニューロン)の一つ一つに組み込まれた「活性化関数(かっせいかかんすう)」という仕組みです。そして、その中でも特に、現代のAIの発展を支えるスター選手が「ReLU(レル)」という、驚くほどシンプルな仕組みなんです。
活性化関数ってなに? ― AIのニューロンに「ひらめき」を与えるスイッチ
AI、特にディープラーニングの頭脳は、人間の脳の神経細胞(ニューロン)を模した小さな計算ユニットがたくさん集まってできています。この考え方は、まさしく私たちの脳機能からヒントを得ています。生物学的なニューロンは、他の多数のニューロンから電気信号を受け取り、その刺激の合計がある「いき値」を超えたときに、自らも「発火」して次のニューロンに信号を伝えますよね。AIのニューロンも、実はこれとそっくりな仕組みで動いているんです。

データがAIに入力されると、その情報はニューロンからニューロンへとリレーのように次々に伝えられていきます。このとき、各ニューロンはただ情報を右から左へ受け流しているだけではありません。受け取った情報をもとに、「この情報は重要だから次に伝えるべきか?」「それとも無視すべきか?」という判断をしています。もう少し中身を覗いてみましょう。この判断は、大きく2つのステップで行われます。
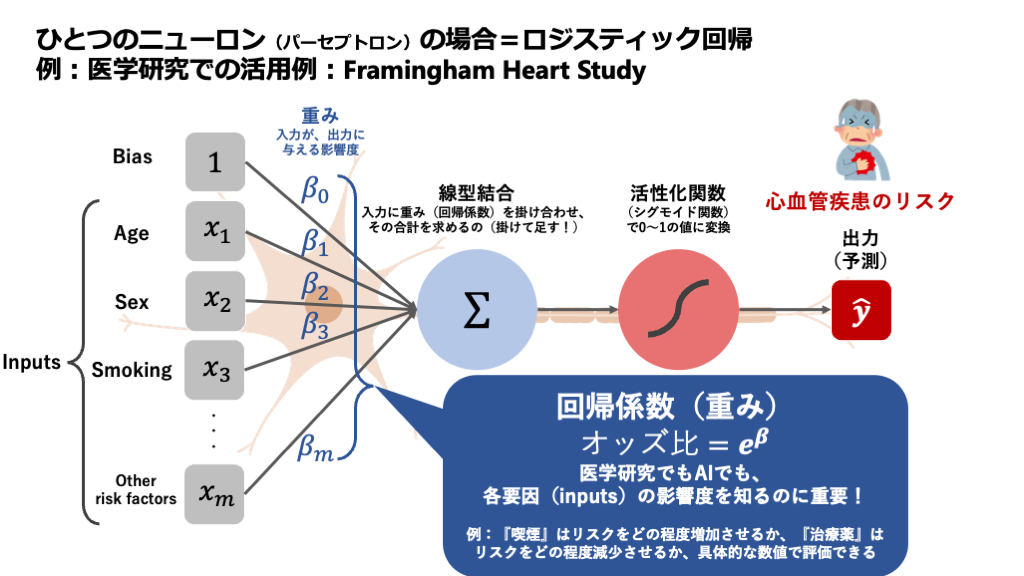
図の解説:これはAIの神経細胞、つまり人工ニューロンの働きを模式的に表したものです。左から複数の入力信号(\(x1, x2, x3, \dots\))が入ってきます。各信号は「重み(\(w1, w2, w3, \dots\))」によってその重要度が調整されます。ニューロン内部では、まずこれらの重み付けされた信号がすべて足し合わされ(Σ)、そこに「バイアス(b)」というゲタが履かされます。そして、その合計値が最後に「活性化関数(f())」というフィルターを通り、最終的な出力信号「y」として外に出ていきます。
ステップ1:情報の重みづけと足し合わせ(線形部分)
まず、ニューロンは複数の前のニューロンから信号(\(x\))を受け取ります。ただし、すべての情報を平等に扱うわけではありません。それぞれの入力信号には、「重み(Weight)」という「重要度」を表す係数が掛け合わされます。
これは、私たちが診断を下すプロセスに似ています。例えば、ある疾患を疑うとき、特異度の高い検査結果(A)には大きな「重み」を置き、一方でよく見られる一般的な症状(B)には比較的小さな「重み」を置きますよね。AIの重みもまさにその役割で、学習を通じて、どの情報が重要なのかを自動で調整していきます。
こうして重み付けされた信号は、すべて足し合わされます。さらに、そこへ「バイアス(Bias)」という固定値が加えられます。バイアスは、ニューロンがどれだけ「発火しやすいか」のベースラインを調整する役割を持ちます。いわば、感度の調整ダイヤルのようなものです。数式で書くと、ここまでの計算は以下のようになります。
\[ u = (w_1 x_1 + w_2 x_2 + w_3 x_3 + \dots) + b \]
この\(u\)が、ニューロン内部で統合された情報の総量です。面白いのは、ここまでの計算(掛け算と足し算)はすべて「まっすぐ」な線形計算だということです。
ステップ2:「発火」の判断と出力(非線形部分)
さて、ステップ1で計算された合計値 \(u\) を、ニューロンはそのまま次のニューロンに流すわけではありません。ここからが本番です。この合計値 \(u\) を、最後の関門である活性化関数(数式では \(f(u)\) と書きます)に通します。
この活性化関数こそが、ニューロンの出口についている「信号のON/OFFスイッチ」の正体です。活性化関数は、受け取った \(u\) の値に応じて、最終的な出力 \(y\) を決めるのです。例えば、「\(u\) が0より大きければ信号をそのまま通し、0以下なら信号を完全にシャットアウトする」といったルールを適用します(これは後で登場するReLUの働きそのものです)。
この「ある値を超えたら反応がガラッと変わる」という性質こそが「非線形性」です。もしこの活性化関数がなく、ステップ1の線形計算だけでニューロンが繋がっていたら、どれだけ層を深く重ねても、AI全体としては結局大きな線形モデルと変わりません。つまり、図1のような単純な境界線しか引けないのです。
AIが図2のドーナツ形のような複雑な判断をできるのは、この活性化関数という「まっすぐじゃない」スイッチが無数に組み合わさることで、結果的に滑らかで複雑な曲線を描く能力を獲得するからなのです。

ヒーローの登場! なぜ「ReLU」は世界を変えたのか?
さて、AIが賢くなるためには「非線形」なスイッチ、つまり活性化関数が必要不可欠だという話をしてきました。では、どんなスイッチでも良いのでしょうか?実は、ここにAIの発展を長年阻んできた、大きな壁がありました。
かつてのスター選手が抱えたジレンマ — 勾配消失問題
ReLUが登場する2010年頃まで、活性化関数の主役は「シグモイド関数」や「tanh関数」でした。これらは滑らかなS字カーブを描く美しい関数で、ニューロンの「発火率」を0から1の間の確率として表現するなど、生物学的にもっともらしい解釈ができました。
しかし、これらのかつてのスター選手たちは、AIの層を深くしようとすると、ある深刻な問題を引き起こしました。それが「勾配消失問題(こうばいしょうしつもんだい)」です。
AIの学習は、出力の「間違い(誤差)」を各ニューロンにフィードバックし、「君の担当の重みは、もう少し大きく(小さく)すべきだったね」と少しずつ調整していくことで進みます。このフィードバック信号が「勾配」です。しかし、シグモイド関数を通ると、この勾配が必ず小さくなってしまう性質があったのです。シグモイド関数の傾き(微分係数)は、最大でも0.25しかありません。AIの層を遡ってフィードバックが伝わるたびに、この0.25以下の数値が繰り返し掛け算されることになります。
\[ \text{勾配} \times (\dots \times 0.25 \times 0.25 \times 0.25) \dots \]
これは、まるで伝言ゲームですよね。メッセージ(勾配)が何人ものニューロンを経由するうちに、どんどん声が小さくなり、曖昧になって、AIの入り口に近い層にいるニューロンには「何を学習すればいいか、もう聞こえません…」という状態になってしまうのです。これでは、AIの層を深くして複雑なことを学ばせようとしても、全く学習が進まないという深刻なジレンマに陥っていました。
常識を覆した、驚くほどシンプルな解決策「ReLU」
この長年の停滞を打ち破ったのが、今回主役のReLU (Rectified Linear Unit、正規化線形ユニット) です。2010年にNairとHintonによって提案され、その有効性が広く示されたこのアイデアは(Nair and Hinton, 2010; Glorot, Bordes and Bengio, 2011)、驚くほどシンプルでした。
\[ f(x) = \max(0, x) \]
数式だけ見ると難しく感じるかもしれませんが、やっていることは本当に単純です。
- 入力された値(\(x\))が0より大きければ(プラスなら)、その値をそのまま出力する。
- 入力された値(\(x\))が0以下なら(マイナスなら)、強制的に0にしてしまう。
たったこれだけです。まるで、ニューロンに届いた信号がポジティブな内容ならそのまま通し、ネガティブな内容ならシャットアウトする、非常に単純明快なゲートキーパーのようです。グラフにすると、そのシンプルさがよくわかります。
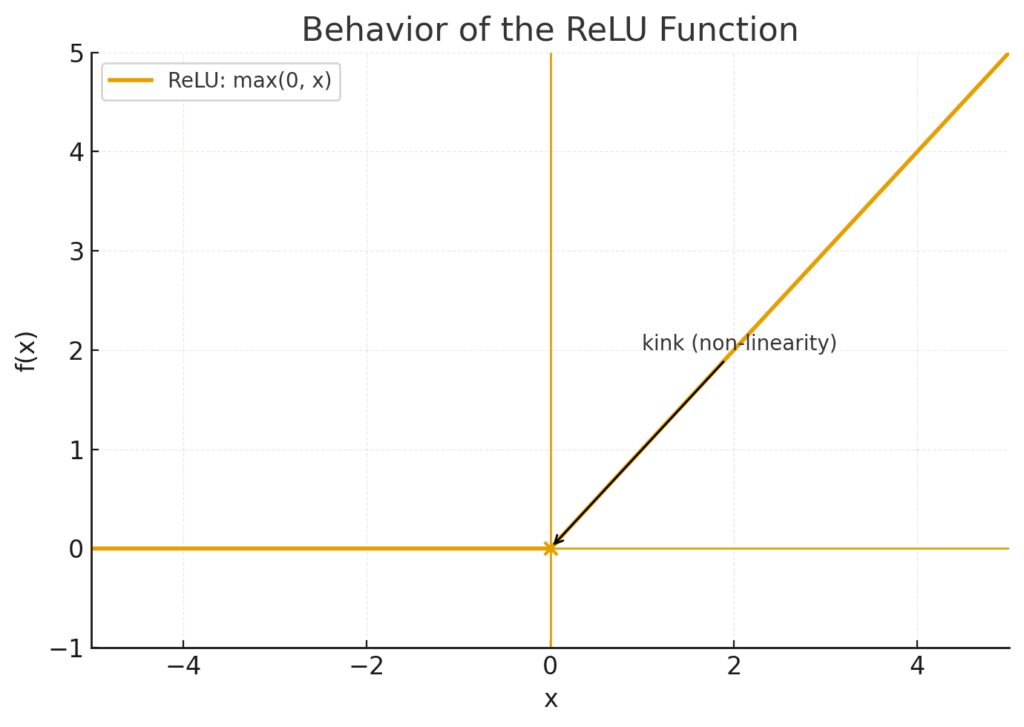
図の解説:この図はReLU関数の振る舞いを視覚的に表したものです。横軸が入力\(x\)、縦軸が出力\(f(x)\)です。入力\(x\)がマイナスの領域では、出力は常に0(横軸にピッタリくっついています)。入力\(x\)が0を超えると、出力は入力とまったく同じ値を取る傾き1の直線(\(y=x\))になります。原点(0,0)でカクっと折れ曲がっているのが特徴で、この「折れ曲がり」こそがAIに非線形性をもたらす源泉なのです。
なぜこのシンプルさが革命的だったのか?
ReLUのすごさは、そのシンプルさにこそ隠されています。
- 計算がとにかく速い!
従来の関数が複雑な指数計算を必要としたのに対し、ReLUは入力がプラスかマイナスかをチェックするだけ。これはコンピュータにとって非常に得意な処理で、AIの学習スピードを劇的に向上させました。 - 勾配消失問題を「緩和」した!
ここが最大のポイントです。入力がプラスの場合、ReLUの「傾き(勾配)」は常に1です。シグモイド関数の最大0.25と比べてみてください。勾配に1を何度掛けても、その値は小さくなりませんよね? \(1 \times 1 \times 1 \times \dots = 1\) です。これにより、学習のフィードバック信号が弱まることなく、AIの深い層までしっかりと届くようになりました。伝言ゲームで言えば、「メッセージをそのまま、まったく変えずに次の人に伝えて!」というルールに変わったようなものです。
もちろん、ReLUだけで全てが解決したわけではありません。その真価は、ReLUに最適化された重みの初期化手法(He初期化)(He et al., 2015)や、学習を安定させるBatch Normalization(Ioffe and Szegedy, 2015)といった他の技術革新と組み合わさることで、最大限に発揮されました。 - より「深い」AIの構築を可能にした
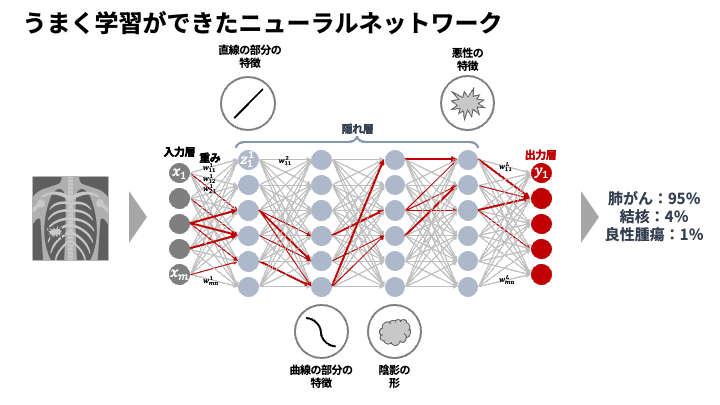
これらの合わせ技によって、研究者たちはついに、何十、何百もの層を持つ「深い」ニューラルネットワーク(ディープラーニング)を安定して学習させられるようになりました。なぜ「深さ」が重要かというと、層が深いほど、AIはより複雑で抽象的な特徴を捉えられるからです。例えば画像認識なら、浅い層が「線や角」を認識し、中間の層がそれらを組み合わせて「目や鼻」を、そして深い層がさらに組み合わせて「顔全体」を認識する、といった階層的な学習が可能になります。この功績が世界に衝撃を与えたのが、2012年の画像認識コンテストで圧勝した深層学習モデル「AlexNet」でした(Krizhevsky, Sutskever and Hinton, 2012)。AlexNetは活性化関数にReLUを採用し、ディープラーニングの時代の幕開けを告げたのです。
完璧じゃない? ReLUの弱点と進化する仲間たち
さて、ReLUがAIの世界に革命をもたらしたわけですが、もちろん完璧なヒーローというわけではありませんでした。しばらく使われるうちに、ReLUにも一つ、厄介な弱点があることがわかってきたのです。
ヒーローの弱点 —「Dying ReLU」問題
その弱点とは、「Dying ReLU(死んだReLU)」と呼ばれる現象です。これは、ニューロンが学習の途中で完全に「沈黙」してしまい、二度と活動しなくなる状態を指します。
なぜこんなことが起きるのでしょうか? ReLUの定義を思い出してください。入力がマイナスの場合、出力は0になり、その部分の傾き(勾配)も0でしたよね。もし、学習の過程で重みが更新された結果、あるニューロンへの入力の合計が常にマイナスになってしまうとどうなるでしょう。そのニューロンの出力は常に0。そして、学習のためのフィードバック信号である勾配も、そこを通過するたびに0になってしまいます。勾配が0ということは、そのニューロンの重みは二度と更新されません。
つまり、スイッチが「OFF」の状態で壊れてしまい、二度とONにならなくなるのです。こうなると、そのニューロンは学習に一切貢献できない「死んだ」状態になってしまいます。これは特に、学習率(一度に重みを更新する幅)が大きすぎるときに起こりやすいとされています(Lu et al., 2019)。
Dying ReLUへの挑戦者たち:ReLUファミリー
この問題を解決するために、ReLUにはたくさんの親戚や改良版、いわば「ヒーローの仲間たち」が生まれました。基本的なアイデアは、「入力がマイナスでも、完全に0にはしないでおこう」というものです。
1. Leaky ReLU (LReLU)
最もシンプルな解決策です。「入力がマイナスなら、完全な0ではなく、ほんのわずかな傾きを持たせよう」という考え方です。例えば、0.01倍のような小さな値を掛けます。
\[ f(x) = \begin{cases} x & \text{if } x \ge 0 \\ 0.01x & \text{if } x < 0 \end{cases} \]
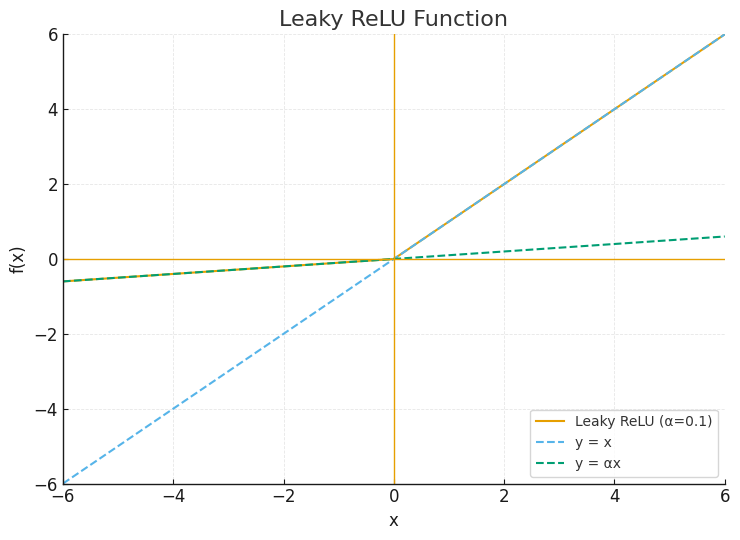
図の解説:Leaky ReLUのグラフです。正の領域はReLUと同じですが、負の領域でわずかにマイナスの傾きを持っているのが分かります。このおかげで、入力がマイナスでも勾配が0にならず、ニューロンが死んでしまうのを防ぎます(Maas, Hannun and Ng, 2013)。
2. Parametric ReLU (PReLU)
Leaky ReLUの「0.01」という数値を、人間が決め打ちするのではなく、「AI自身に学習させよう」というのがPReLUです(He et al., 2015)。
\[ f(x) = \begin{cases} x & \text{if } x \ge 0 \\ \alpha x & \text{if } x < 0 \end{cases} \quad (\alpha\text{は学習パラメータ}) \]
マイナス側の傾き \(\alpha\) を、データに応じて最適な値に自動で調整してくれます。「ドアの開き具合を自動調整してくれる」ような、より賢い仕組みと言えるかもしれません。
3. Exponential Linear Unit (ELU)
ELUは、マイナス側を滑らかな曲線(指数関数)にすることで、さらに学習を安定させようという試みです(Clevert, Unterthiner and Hochreiter, 2015)。
\[ f(x) = \begin{cases} x & \text{if } x \ge 0 \\ \alpha(e^x – 1) & \text{if } x < 0 \end{cases} \]
出力の平均が0に近くなる性質があり、これが学習を高速化する助けになることがあります。「ゆっくり閉まるクッション付きのドア」のように、急激な変化を避けて滑らかに振る舞うのが特徴です。
ReLUを超えて — 現代の活性化関数たち
ReLUファミリーの登場でAIの性能は大きく向上しましたが、研究者たちの探求は終わりませんでした。「もっと滑らかで、もっと効率的に勾配を伝えられる関数はないだろうか?」という探求が、新世代の活性化関数を生み出しました。特に、非常に大規模で複雑なモデルが主流となった現代において、これらの新しい関数が標準的な選択肢となりつつあります。
ここでの共通テーマは、ReLUの「カクっと曲がる」点(微分不可能な点)をなくし、全体的に滑らかな(smooth)曲線にすることで、勾配の流れをよりスムーズにし、AIの学習を安定させる、という狙いです。
GELU: 確率が生み出す滑らかなスイッチ
GELU (Gaussian Error Linear Unit) は、あのGPTシリーズやBERTといった、現代の自然言語処理を支えるTransformerモデルで広く採用されていることで非常に有名な関数です。そのアイデアは少しユニークで、「確率」の考え方を取り入れています。
GELUは、入力値 \(x\) をそのまま通すか、0にする(つまりマスクする)かを確率的に決めます。具体的には、入力値 \(x\) が、標準正規分布からサンプリングされた他の値より大きい確率を計算し、その確率を入力 \(x\) 自身に掛け合わせる、という処理を行います。数式では \(f(x) = x \cdot \Phi(x)\)(\(\Phi(x)\) は正規分布の累積分布関数)と表現されます。
たとえるなら、入力信号の強さに応じて「自信度」を計算し、その自信度に応じて信号の大きさを調整するゲートのようなものです。入力が非常に大きな正の値なら「100%に近い自信で通す」、非常に大きな負の値なら「0%に近い自信で通さない」と判断します。これにより、ReLUに似ていながらも、全体が滑らかな曲線を描くのが特徴です。

図の解説:GELUのグラフの概形です。ReLUのように振る舞いますが、原点付近で急に折れ曲がるのではなく、滑らかな曲線で立ち上がります。負の領域ではわずかにマイナスの値を取ります。
Swish (SiLU): 自身で門を開閉する賢い関数
Swishは、Googleの研究者らが提案した非常に強力な関数で、SiLU (Sigmoid-weighted Linear Unit) とも呼ばれます。その式は \(f(x) = x \cdot \text{sigmoid}(x)\) と、驚くほどシンプルです。
これは、入力 \(x\) に対して、同じ \(x\) をシグモイド関数に通した値(0から1の間の値)を掛け合わせる、という構造をしています。このシグモイド部分が「ゲート(門)」の役割を果たし、入力自身の値に応じて「どれくらい信号を通すか」を動的に調整します。これを「自己ゲート(self-gating)」と呼びます。
ReLUと違う面白い特徴は、「非単調性(non-monotonicity)」です。グラフを見るとわかりますが、入力が少しマイナスの領域で、出力もわずかに負の値に沈み込む「くぼみ」があります。この性質が、一種の正則化のように機能し、性能向上に寄与するのではないかと考えられています(Ramachandran, Zoph and Le, 2017)。
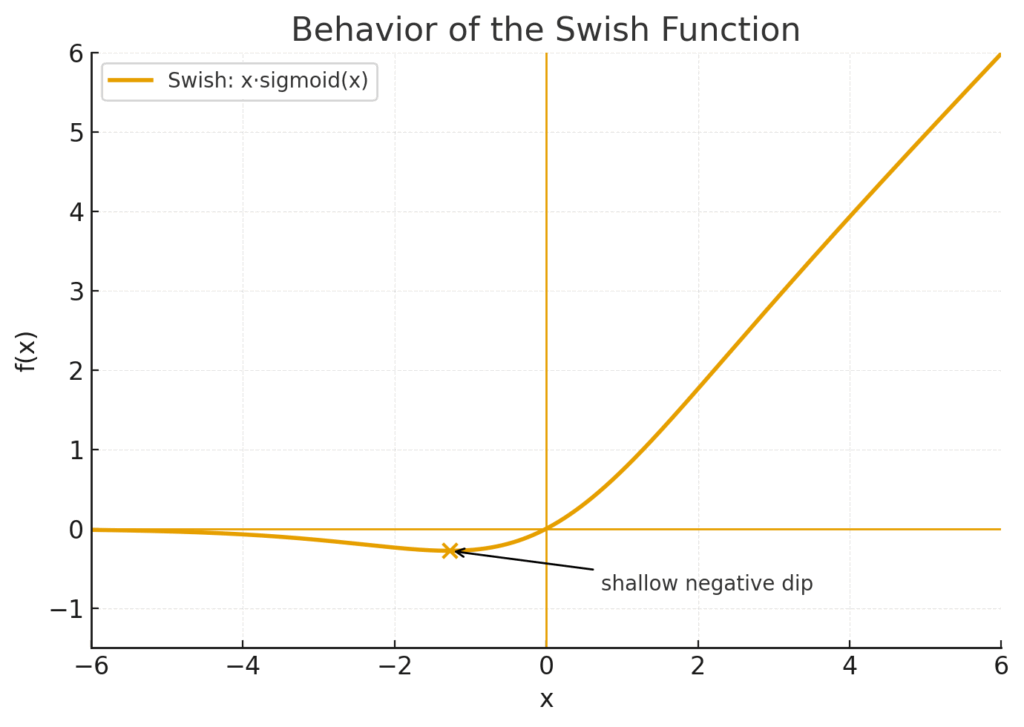
図の解説:Swishのグラフの概形です。GELUと同様に滑らかですが、原点より少し左側で出力がわずかにマイナスになる「くぼみ」を持つのが特徴です。
Mish: Swishの先を目指した滑らかな探求
Mishは、Swishに似た滑らかな形状を持ちつつ、さらに性能を改善したとされる関数です(Misra, 2019)。数式は \(f(x) = x \cdot \tanh(\text{softplus}(x))\) と少し複雑になりますが、基本的な考え方はSwishと同様に、滑らかで非単調な特性を持つことを目指しています。
Mishは、特に非常に深いネットワークにおいても、情報の損失を最小限に抑え、勾配を安定して伝える能力が高いと報告されており、コンピュータビジョンの分野などで高い性能を発揮することがあります。Swishよりもさらに滑らかな曲線を描くのが特徴です。
これらの新世代の活性化関数は、計算コストがReLUよりも少し高いという側面はありますが、それを補って余りある性能向上をもたらすことが多く、AIの性能の限界を押し上げる上で重要な役割を担っています。
結局、どれを使えばいいの? — 実用的な使い分けガイド
これだけ種類があると、一体どれを使えばいいのか迷ってしまいますよね。以下に、それぞれの特徴と使い分けの目安をまとめてみました。
| 活性化関数 | 特徴 | どんな時に考えるか |
|---|---|---|
| ReLU | 基本にして最強。計算が速く、ほとんどの場合でうまく機能する。 | まずはこれから試す。ディープラーニングのデフォルトであり、鉄板の選択肢。 |
| Leaky ReLU / PReLU | Dying ReLUを回避したい場合に有効。 | ReLUで学習がうまくいかない、あるいは学習中に性能が頭打ちになった場合に試す価値あり。 |
| ELU | マイナス側が滑らか。出力の平均が0に近づく。 | PReLUなどと同様、学習の安定化や高速化を期待したい場合に。ただし計算コストは少し上がる。 |
| GELU / Swish / Mish | 現代の標準。滑らかで高性能。特に大規模モデルで効果を発揮。 | Transformerベースのモデルを扱う場合や、とにかく最高の性能を追求したい場合の第一候補。 |
結論として、絶対的な「最強」の活性化関数というものはなく、課題やモデルの構造によって最適なものは変わります。しかし、一般的な指針として「まずはReLUから始め、性能に満足できなければLeaky ReLUや、さらに高性能なSwish/GELUなどを試してみる」というのが、現在のAI開発における一つの定石になっていると言えるでしょう。
まとめ:単純な「カクッ」が、賢いAIを生み出す
今回は、AIが「まっすぐじゃない」複雑な世界を理解するための鍵、非線形関数とReLUについて見てきました。
一見、ただ「マイナスなら0にする」という、あまりにも単純なルールに見えるかもしれません。しかし、このシンプルな「カクっと曲がる」性質を持つスイッチ(ニューロン)が、何百万、何千万と集まって組み合わさることで、AIはとてつもなく複雑で滑らかな判断の境界線を描くことができるようになります。
それはまるで、直線的なレゴブロックだけを使って、巨大で美しい曲線を持つ宇宙船を組み立てるようなものです。一つ一つの部品は単純でも、その組み合わせが知性を生み出す。ReLUは、その根源的な力を見事に体現しているのです。
医療AIがCT画像から微小な病変を発見できるのも、この無数の「ReLUスイッチ」が、ピクセルの一つ一つの情報を「これは重要」「これはノイズ」と判断し、その組み合わせから複雑なパターンを学習しているからに他なりません。AIの「ひらめき」や「直感」のように見えるものの裏側では、こんなにもシンプルで、しかし強力な数学が働いていると思うと、少しワクワクしてきませんか?
参考文献
- Glorot, X., Bordes, A. and Bengio, Y. (2011) ‘Deep sparse rectifier neural networks’, in Proceedings of the fourteenth international conference on artificial intelligence and statistics, pp. 315–323.
- Krizhevsky, A., Sutskever, I. and Hinton, G.E. (2012) ‘ImageNet classification with deep convolutional neural networks’, Communications of the ACM, 60(6), pp. 84–90.
- Nair, V. and Hinton, G.E. (2010) ‘Rectified linear units improve restricted boltzmann machines’, in Proceedings of the 27th international conference on machine learning, pp. 807–814.
- Sharma, S., Sharma, S. and Sharma, A. (2020) ‘Activation Functions in Neural Networks: A Comprehensive Survey and Comparative Analysis’, Journal of Physics: Conference Series, 1634(1), p. 012017.
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






