TL; DR (要約)
AIは、どうやって複雑な地形(損失関数)の中から「最も急な坂」を見つけるのか?
その答えが偏微分です。「一度に一つのことだけ考える」という、シンプルで強力な戦略の要点です。
① 偏微分
(一つの軸でスライス)
多次元の複雑な問題を、一つの変数だけ動かし、他は固定して考える。3Dの山を2Dの坂道にスライスして、その傾きを求めるイメージです。
② 勾配ベクトル
(最強の矢印)
各変数の偏微分(各軸方向の傾き)を全て集めてベクトルにしたもの。この矢印が「最も急な上り坂」の方向と険しさを表します。
③ AIの学習
(勾配降下法)
AIは、この勾配ベクトルと正反対の方向(最も急な下り坂)に一歩ずつ進むことで、損失を最小化し、賢くなっていきます。
この章の学習目標と前提知識
前回の旅では、私たちは霧深い山の中で、勾配(Gradient)という名の、進むべき方向を指し示してくれる魔法のコンパスを手に入れましたね。このコンパス(勾配ベクトル)は、「最も急な上り坂」の方向を一本の矢印で教えてくれる、とても頼もしい存在でした。AIは、その矢印と正反対の方向(最も急な下り坂)へ一歩ずつ進むことで、着実に山の谷底(損失が最小の地点)へと近づいていくのでした。
でも、ここで一つの素朴な疑問が湧いてきませんか?
このコンパスは、一体どうやって「最も急な坂の方向」を計算しているのでしょうか?
AIモデルの現在地(損失)は、何百万というパラメータ(変数)が互いに影響し合って決まる、超多次元の地形の上にあります。そんな複雑な場所で「最も急な坂」を見つけるために、AIは、実はとても地道で賢い戦略をとります。
それは、「一度に一つのことだけ考える」という戦略です。
つまり、「もし、パラメータAだけを少し動かしたら、損失はどう変わる?」「では、パラメータBだけを動かしたら?」というように、膨大な数のパラメータを一つずつ順番に、個別に評価していくのです。この、「他の変数はすべて止まっている(定数だ)」と仮定して、たった一つの変数に対する傾きだけを計算する、という操作こそが、今回のテーマである偏微分 (Partial Differentiation) なのです。
一見すると遠回りに思えるかもしれませんが、この地道な「偏微分」の積み重ねこそが、最終的にあの強力な羅針盤である「勾配ベクトル」を作り上げます。今回の講座では、この偏微分というシンプルで強力な考え方の本質に、一緒に迫っていきましょう。
1. 偏微分とは? — 複雑な世界を「一つの軸」で切り取って見る技術
AIが向き合う損失関数という「山」は、何百万ものパラメータ(変数)が絡み合った、超高次元の複雑な地形をしています。その全体の傾き(勾配)を一度に理解するのは、不可能に思えますよね。
そこで、科学者が昔から使ってきた、複雑な問題を解決するための強力なアプローチが役立ちます。それは「問題を単純化して、一つずつ考える」という方法です。
多変数関数という3Dの地形を、特定の軸に沿って「スライス」して、2Dのただの断面図(カーブ)として見てみる、というイメージ。これこそが偏微分 (Partial Differentiation) の本質です。
3Dの山を「スライス」して、2Dの坂道を見る
百聞は一見に如かず、ですね。2つの変数 \(x\) と \(y\) によって高さが決まる関数 \(f(x, y)\) という「山」を例に、この「スライス」のイメージを具体的に見ていきましょう。まずは、私たちの現在地と、そこから広がる地形を確認します。
【図1】2つの変数で決まる関数 f(x, y) という「山」
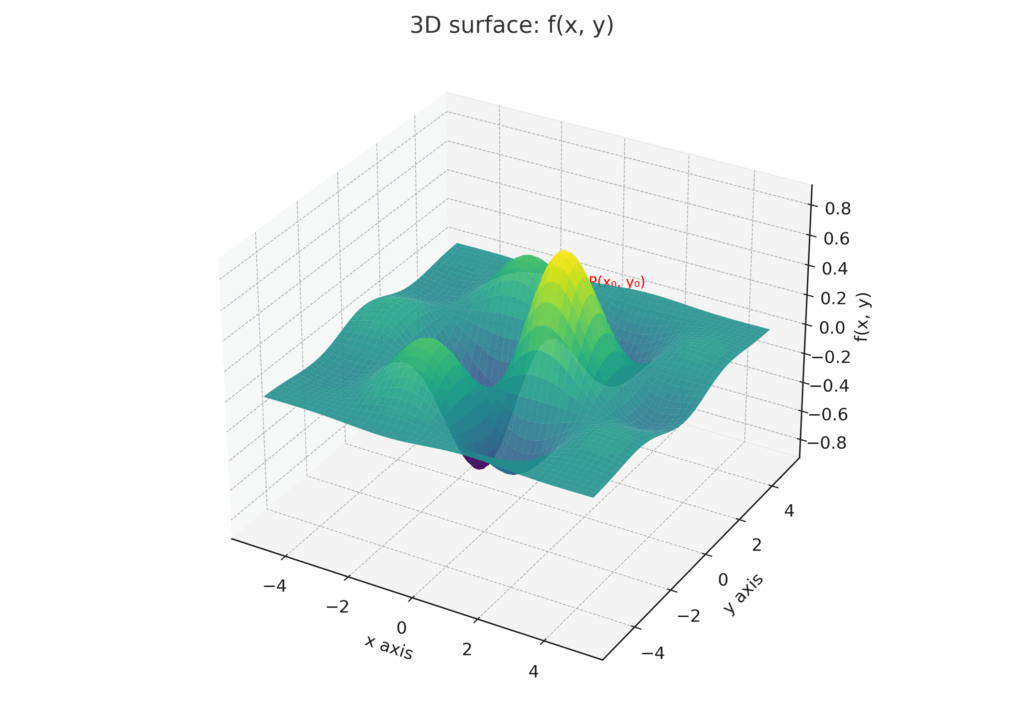
この図は、\(x\) と \(y\) という2つの変数で高さが決まる、なだらかな山(曲面)を表しています。私たちは今、点P \((x₀, y₀)\) に立っているとします。この地点での全体の「傾き」を知りたいのですが、360度あらゆる方向があって、どこから手をつけていいか分かりませんよね。
そこで、偏微分では問題を分割して考えます。
まずは「y軸方向」だけの傾きを知る(xを固定)
最初に、「もし、y軸方向(この図で言うと奥行き方向)にしか動けないとしたら、この坂はどれくらい急だろう?」と考えてみます。これは、\(x = x_0\) という透明な壁で、この山をスパッと垂直に断ち切るイメージです。その壁に沿ってできた断面は、どうなっているでしょうか。
【図A】山を x = x₀ でスライスした断面
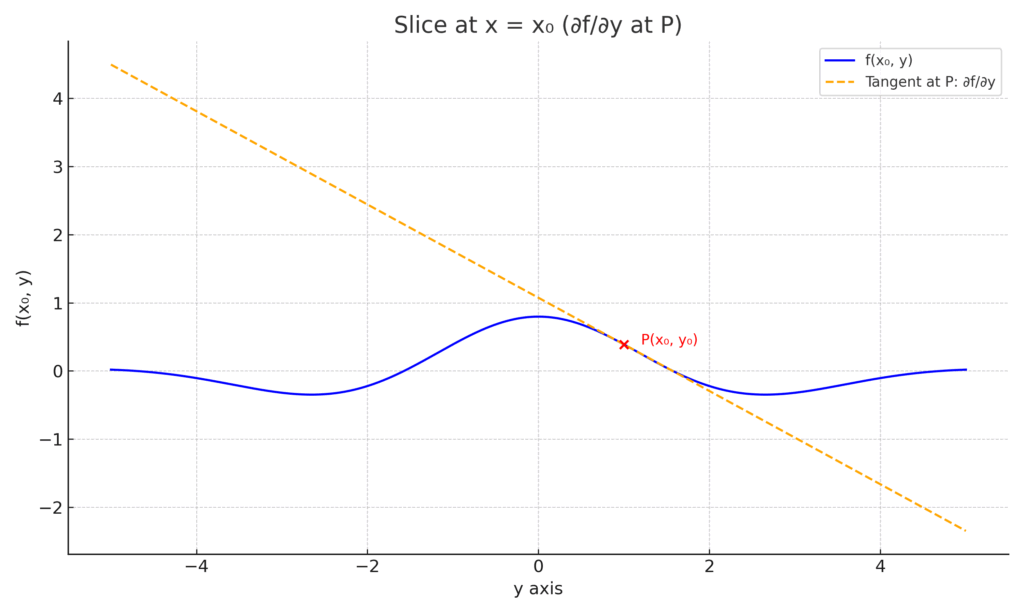
すると、その断面には、私たちがよく知るただの2Dのカーブ(坂道)が現れます。この坂道の、点Pにおける接線の傾きを求めること。これこそが、「\(y\)に関する偏微分 \(\frac{\partial f}{\partial y}\)」の正体です。\(x\)は\(x_0\)というただの数字(定数)として扱っているので、これはもう私たちが知っている1変数の微分と全く同じように考えられます。
次に「x軸方向」だけの傾きを知る(yを固定)
同様に、今度は「もし、x軸方向(左右)にしか動けないとしたら…?」と考えます。今度は、山を \(y = y_0\) という壁で、奥から手前に向かって断ち切ります。
【図B】山を y = y₀ でスライスした断面
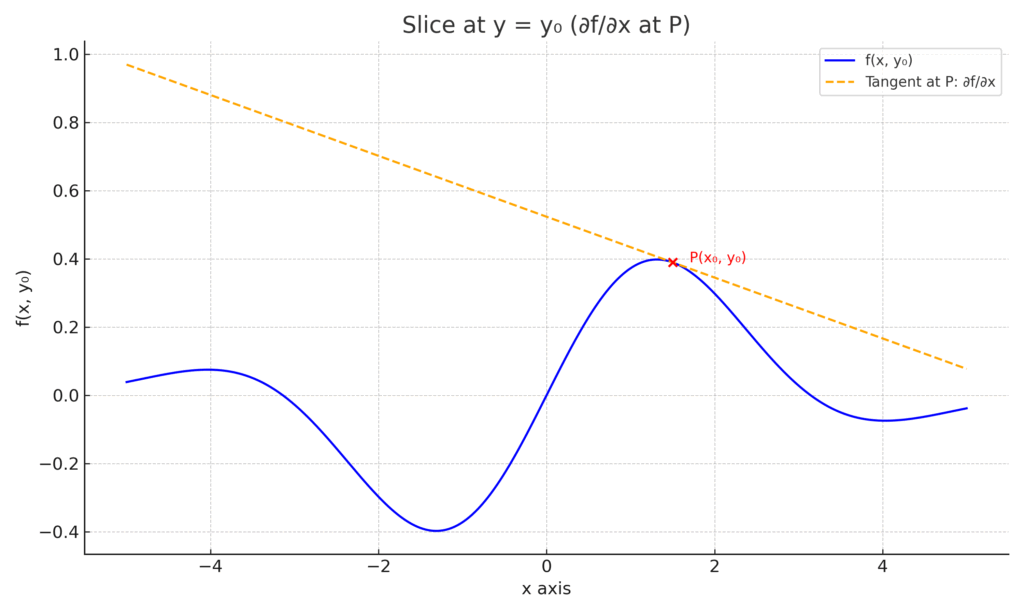
すると、そこにもまた2Dのカーブが現れます。この坂道の、点Pにおける接線の傾きが「\(x\)に関する偏微分 \(\frac{\partial f}{\partial x}\)」です。このとき、\(y\)は\(y_0\)という定数として扱われています。
医療の例で考える偏微分
この考え方を、より身近な「リスクスコア = f(年齢, BMI)」という関数に当てはめてみましょう。
- \(\frac{\partial f}{\partial \text{年齢}}\) とは、「BMIをある特定の値(例えば22)に固定した集団だけを見たときに、年齢が1歳上がるとリスクがどれだけ変化するか」という傾きを示します。他の要因(BMI)の影響を排除して、年齢という一つの要因だけの純粋な影響を見ているわけです。
- \(\frac{\partial f}{\partial \text{BMI}}\) も同様に、「年齢をある特定の値(例えば50歳)に固定した集団だけを見たときに、BMIが1上がるとリスクがどれくらい変化するか」という傾きです。
偏微分の表記法
この「一つの変数だけに注目して微分しましたよ」ということを明確にするために、数学では通常の微分で使う d の代わりに、∂ (デル、パーシャル、ラウンドディーなどと呼ばれます) という記号を使います。関数 \(f(x_0, x_1)\) を変数 \(x_0\) で偏微分することは、以下のように表記します。
\[\frac{\partial f}{\partial x_0}\]
これは、「\(x_1\) は一旦ただの数字と見なして、\(x_0\) だけを変数として微分しましたよ」という、読み手に対する親切な宣言なのです。
2. なぜ「偏」微分なのか? — 勾配という「最強の矢印」を組み立てる
前のセクションで、私たちは複雑な3Dの山を、x軸方向とy軸方向という、2つの単純な2Dの坂道に「スライス」して、それぞれの傾き(偏微分)を求めましたね。
でも、これらはあくまで「特定の方向に限定した傾き」です。私たちが本当に知りたいのは、360度全方向の中で「最も急な上り坂」を指し示す、最強の一本の矢印でした。
実は、この最強の矢印、すなわち勾配(Gradient)は、先ほど求めた2つのスライスの傾きを、ただ組み合わせるだけで作れてしまうんです。
各軸の傾きを「合成」して、本当の傾きを知る
この考え方を、簡単な図で見てみましょう。点Pにおける、各軸方向の傾き(偏微分)が、それぞれ短い矢印として計算できたとします。
【図の解説】
- まず、\(x\)軸方向の傾き(\(\frac{\partial f}{\partial x}\))を、x軸に沿った短い矢印(ベクトル)として描きます。
- 次に、\(y\)軸方向の傾き(\(\frac{\partial f}{\partial y}\))を、y軸に沿った矢印(ベクトル)として描きます。
- そして、この2つのベクトルを合成(ベクトルとして足し算)すると、斜め上を指す新しい一本のベクトルが生まれます。
この合成されたベクトルこそが、勾配ベクトル \(\nabla f\) の正体です。
この合成された矢印の向きが「最も急な上り坂の方向」を、そして矢印の長さが「その坂の険しさ」を、一度に教えてくれるのです。驚くほどシンプルだと思いませんか?
この直感的なイメージを、数式で書くと次のようになります。2変数関数 \(f(x_0, x_1)\) の場合、勾配 \(\nabla f\) (ナブラfと読みます) は、各方向の偏微分を成分として持つベクトルとして定義されます。
\[\nabla f(x_0, x_1) = \left( \frac{\partial f}{\partial x_0}, \frac{\partial f}{\partial x_1} \right)\]
AIの学習における勾配
この考え方は、AIの学習にそのまま応用されます。
AIの損失関数は、何百万ものパラメータ \(w_1, w_2, \dots, w_N\) を持つ超多次元関数 \(L(w_1, w_2, \dots, w_N)\) です。
AIが勾配を計算するとは、この何百万個あるパラメータの一つ一つについて、地道に偏微分 \(\frac{\partial L}{\partial w_1}, \frac{\partial L}{\partial w_2}, \dots, \frac{\partial L}{\partial w_N}\) を計算し、それらを成分とする巨大な勾配ベクトル \(\nabla L\) を作り上げることなのです。
そして、そのベクトルが指し示す逆方向(負の勾配)に向かって、全パラメータをほんの少しだけ更新する。これこそが、AIの学習(勾配降下法)の、たったワンステップで行われていることの全てです。
3. Pythonで勾配を計算する — 「地図」と「コンパス」を可視化する
理論はなんとなく分かったところで、今度は「百聞は一見に如かず」の精神で、多次元の勾配計算もPythonで実装してみましょう。これを通じて、勾配が「ベクトル(矢印)」として計算される感覚と、それが本当に「最も急な坂」を指しているのかを、自分の目で確かめていきます。
ここでは、最もシンプルな2変数関数 \( f(x_0, x_1) = x_0^2 + x_1^2 \) の勾配を計算してみます。この関数は、地図で描くと原点 \((0, 0)\) が一番低い「すり鉢(お椀)」のような形で、勾配降下法の動きを見るのにうってつけの題材です。
a) 勾配を計算する「道具」の準備
まず、勾配を計算するための「道具」となる関数を準備します。この関数は、前のセクションで見た数値微分の考え方を、各変数に対して順番に適用してくれるものです。
# 必要なライブラリをインポートします
import numpy as np
# 勾配を計算したい2変数関数を定義
def function_2d(x):
"""
お椀型の関数 f(x0, x1) = x0^2 + x1^2 を定義します。
Args:
x (np.ndarray): [x0, x1] というNumPy配列を想定
"""
return np.sum(x**2)
# 勾配(各変数の偏微分のベクトル)を計算する関数
def numerical_gradient(f, x):
"""
多変数関数の勾配を数値的に計算します。
"""
h = 1e-4 # 0.0001 という微小な値
grad = np.zeros_like(x) # xと同じ形状の配列を生成(勾配ベクトルを格納するため)
# 各変数 (x0, x1, ...) について、偏微分を計算
# enumerate(x) を使うと、インデックス(idx)と要素(val)を同時に取り出せる
for idx in range(x.size):
tmp_val = x[idx] # 元の値を一時的に保存
# f(x+h) の計算(注目している変数だけを少し動かす)
x[idx] = float(tmp_val) + h
fxh1 = f(x)
# f(x-h) の計算
x[idx] = float(tmp_val) - h
fxh2 = f(x)
# 中心差分 (f(x+h) - f(x-h)) / 2h で偏微分を計算
grad[idx] = (fxh1 - fxh2) / (2 * h)
x[idx] = tmp_val # 値を元に戻す(重要!)
return grad
ちなみに、このコードでは、より精度の高い近似を得るために、微分の計算に中心差分という少し賢い方法を使っています。
【計算方法のちょっとした工夫:中心差分】
シンプルな前方差分:
(f(x+h) - f(x)) / h
x と x+h の2点から傾きを計算。x地点での真の傾きとは、少しズレが生じやすい。
より高精度な中心差分 (今回使用):
(f(x+h) - f(x-h)) / (2*h)
x-h と x+h の2点から傾きを計算。xをちょうど中心に挟んでいるため、誤差が少なく、より精度の高い近似になる。
b) 勾配の計算と可視化
それでは、この関数を使って、いくつかの点における勾配を実際に計算し、可視化してみましょう。
【実行前の準備】
以下のコードで日本語のグラフを表示させるには、あらかじめターミナルやコマンドプロンプトで pip install japanize-matplotlib を実行してライブラリをインストールしてください。
import matplotlib.pyplot as plt
import japanize_matplotlib
# --- 勾配をいくつかの点で計算し、可視化 ---
# 関数の等高線プロットを作成
x0 = np.arange(-10, 10.1, 1.0)
x1 = np.arange(-10, 10.1, 1.0)
X0, X1 = np.meshgrid(x0, x1)
Z = X0**2 + X1**2
plt.figure(figsize=(8, 8))
# contourは等高線を描画する関数
plt.contour(X0, X1, Z, levels=np.arange(0, 201, 20), colors='gray')
# 勾配を描画したい点
points = [np.array([-8.0, 6.0]), np.array([5.0, -5.0]), np.array([-2.0, -8.0]), np.array([7.0, 7.0])]
for p in points:
# 各点での勾配を計算
grad = numerical_gradient(function_2d, p.copy()) # 元の配列を変更しないようコピーを渡す
# 勾配ベクトルを描画 (quiverプロット)
# p[0], p[1]が矢印の始点
# -grad[0], -grad[1]が矢印の方向と大きさのベクトル
# マイナスをつけて「最も急な下り坂」の方向を描画
plt.quiver(p[0], p[1], -grad[0], -grad[1], angles="xy", color="red", scale_units='xy', scale=15)
plt.plot(p[0], p[1], 'bo') # 点をプロット
plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.xlabel("x0")
plt.ylabel("x1")
plt.title('関数の等高線と負の勾配ベクトル')
plt.gca().set_aspect('equal', adjustable='box') # グラフのアスペクト比を1:1に
plt.grid(True)
plt.show()
# --- 点(3, 4)での具体的な計算値も確認 ---
point_specific = np.array([3.0, 4.0])
gradient_specific = numerical_gradient(function_2d, point_specific.copy())
print(f"--- 関数 f(x0, x1) = x0^2 + x1^2 ---")
print(f"点 {point_specific} における勾配ベクトル: {gradient_specific}")
print(f"理論値 [2*x0, 2*x1] = [6.0, 8.0] とほぼ一致している。")
(注:上記コードを実行すると、関数の等高線と勾配ベクトルが描画されます。また、コンソールには以下の計算結果が出力されます。)
▼コンソールへの出力結果
--- 関数 f(x0, x1) = x0^2 + x1^2 ---
点 [3. 4.] における勾配ベクトル: [6. 8.]
理論値 [2*x0, 2*x1] = [6.0, 8.0] とほぼ一致している。
c) コードと結果のウォークスルー
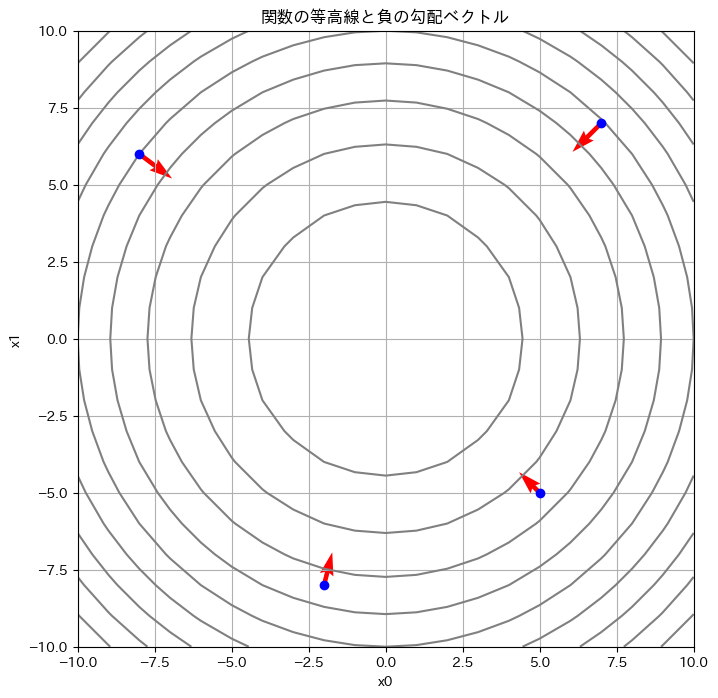
このコードを実行すると、まずお椀型をした関数の「地図(等高線図)」が表示されます。灰色の線が同じ高さの地点を結んだ線です。そして、青い点がいくつかの現在地、そこから伸びる赤い矢印が、私たちのコードが計算した「負の勾配」、つまり最も急な下り坂の方向を示しています。
この結果から、とても重要なことが分かります。
それは、どの地点から出発しても、赤い矢印(負の勾配)は常にお椀の底、つまりこの関数の唯一の最小値である原点 \((0, 0)\) を指しているということです。
これこそが、AIが学習を進めるべき「正しい方向」に他なりません。
また、コンソールに出力される結果を見ると、点(3, 4)における勾配ベクトルが [6., 8.] となり、理論値である [2*3, 2*4] と見事に一致していることも確認できますね。
こうして、私たちはAIが広大なパラメータの山を駆け下りるための、最も基本的なコンパスを、自分の手で作り上げることができました。
まとめ:多次元世界の傾きとその集合
- 偏微分は、多変数関数において、特定の一つの変数だけに着目してその方向の「傾き」を求める操作です。
- 勾配は、全ての変数に関する偏微分を計算し、それらを成分として一つのベクトルにまとめたものです。このベクトルが、関数の値を最も増加させる方向を示します。
- AIの学習(勾配降下法)は、この勾配の逆方向に進むことで、損失関数の値を効率的に最小化していきます。
偏微分は、複雑な多次元の山を理解するために、まず一つの方向(例えば南北)だけに集中して傾きを調べるような、賢い「分割統治」のアプローチと言えるでしょう。
しかし、パラメータが数百万個もある深層学習モデルで、毎回この計算を行うのは非効率です。この膨大な計算を、驚くほど高速に実行するアルゴリズムが「誤差逆伝播法」であり、その心臓部にあるのが、次回のテーマ「0.3.3: 連鎖律」です。
参考文献
- Strang G. Calculus. Wellesley-Cambridge Press; 2017. Chapter 14.
- Goodfellow I, Bengio Y, Courville A. Deep Learning. MIT Press; 2016. Chapter 6.
- Deisenroth MP, Faisal AA, Ong CS. Mathematics for Machine Learning. Cambridge, UK: Cambridge University Press; 2020. Chapter 6.
- Nielsen MA. Neural Networks and Deep Learning [Internet]. Determination Press; 2015. Chapter 2.
- Khan Academy. Partial derivatives [Internet]. Available from: https://www.khanacademy.org/math/multivariable-calculus/multivariable-derivatives
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






