TL; DR (要約)
AIは、霧深い山中で谷底(最適解)を探す旅人。その旅に不可欠な「下り坂の方向」を教える魔法のコンパスが微分です。
AIの学習の心臓部である「微分」と「勾配」の役割を、直感的なイメージで理解しましょう。
① 微分
(瞬間の傾き)
関数のグラフ上の「ある一点」における接線の傾き。その瞬間の「変化の勢い」を数値で表します。
② 偏微分
(一つの軸でスライス)
多次元の複雑な問題を、一つの変数だけ動かし、他は固定して考える。3Dの山を2Dの坂道にスライスして、その傾きを求めるイメージです。
③ 勾配
(最強のコンパス)
各変数の偏微分をまとめたベクトル。「最も急な上り坂」を指す矢印。AIはこの逆方向に進むことで、賢くなります(勾配降下法)。
この章の学習目標と前提知識
前のセクション(0.2節)では、ベクトルや行列という便利な道具を使って、例えば患者さんのカルテ情報や心電図の波形といった、複雑な医療データをコンピュータが扱える「数値のカタマリ」に変換する方法を見てきましたね。
少しイメージを膨らませてみましょう。一人の患者さんのデータが、下図のように1本のベクトルとして表現されるわけです。
解説: このように、年齢や身長といった数値データはそのまま、性別や喫煙歴のようなカテゴリカルなデータは「男性なら1、女性なら0」のように数値に置き換えます。こうして出来上がった数字のリスト(ベクトル)が、AIにとっての「入力データ」となります。
ただ、データをこのように数値に置き換えただけでは、AIはまだ何もできません。例えるなら、これは料理のレシピに書かれた材料をすべて計量して、まな板の上に並べただけの状態。ここから美味しい料理を完成させるには、実際に調理を進めながら、途中で味見をして「うーん、少し塩が足りないな」「もう少しだけ火を通した方が良さそうだ」といった調整を繰り返していく必要がありますよね。
AIも全く同じです。自分の出した予測が、どれくらい「正解」からズレているか(これを損失や間違いと呼びます)を認識し、そのズレを少しでも小さくするように自分自身を賢く調整していくプロセスが不可欠です。この調整プロセスこそが、AIの「学習」に他なりません。
そして、このAIの「学習」という調整プロセスにおいて、ナビゲーションシステムのように「どちらの方向に、どれくらい調整すれば正解にもっと近づけるか」を指し示してくれる、ものすごく重要な数学的ツールがあります。それが、今回のテーマである微分なのです。AIの学習の、まさに心臓部であり、賢くなるための羅針盤と言っても過言ではないでしょう。
「うっ、微分…」と聞いただけで、ちょっと身構えてしまう方もいるかもしれません。私も学生時代は、ひたすら公式を暗記させられて、一体これが何の役に立つんだろう…なんて思った経験がありました。
でも、どうか安心してください。このコースでは、難しい数式の証明や暗記は一切しません。私たちが目指すのは、「微分がAIの学習という物語の中で、どんな役割を果たし、どうしてそんなに重要なのか?」という本質的な意味を、直感的なイメージと、実際に動かせるPythonコードを通して、体感的に理解することです。数式が持つ「気持ち」を一緒に探るような旅だと思って、リラックスして読み進めていただけると嬉しいです。
微分との出会い:なぜAIに「変化」の計算が必要なのか?
では、どうやってAIは自分の「間違い」を認識し、それを修正して賢くなっていくのでしょうか?このプロセスを理解するために、一つ、とてもしっくりくる例え話をしてみましょう。
AIの学習を、「霧深い山の中で、最も低い谷底を探す旅」だと想像してみてください。
あなたは旅人、つまりAIモデルそのものです。そして、旅の目的は、山の中で最も標高が低い安住の地、すなわち「谷底」を見つけ出すこと。この「谷底」こそが、AIの予測の「間違い(損失)」が最も少なくなる、理想の状態を指します。
さて、あなた(AI)は、自分のいる場所の「標高」だけは知ることができます。これは、現在のAIモデルがどれくらい間違っているか、つまり「損失の大きさ」を計算できることに対応します。
でも、ここが難しいところ。山は霧に包まれていて、谷底がどの方角にあるのか全く見えません。わかるのは、今いる地点の標高だけ。360度、どちらに一歩踏み出せば、谷底に近づけるのでしょうか?闇雲に歩いても、むしろ山を登ってしまうかもしれませんよね。
こんな絶望的な状況で、もしあなたが一つだけ魔法の道具を持てるとしたら、何が欲しいですか?
おそらく、多くの人が「方位磁針」や「地図」と答えるかもしれませんが、もっと直接的で便利なものがあります。それは、足元の地面の傾きを教えてくれる「高性能な傾斜計」です。
この傾斜計は、次の二つのことを正確に教えてくれます。
- 方向:どの向きが「上り坂」で、どの向きが「下り坂」か。
- 険しさ:その坂が、どれくらい急なのか。
この情報さえ手に入れば、霧で周りが見えなくても、「最も急な下り坂」の方向を選んで、そちらに一歩踏み出すことができます。そして、移動した先でまた傾斜計を使い、再び最も急な下り坂へ…。このプロセスを何度も繰り返していけば、いずれ安全に谷底へたどり着けそうな気がしませんか?
このAIの学習の旅路を、簡単な図にしてみると、こんなイメージになります。
この図の要素を、AIの学習と照らし合わせてみましょう。
| 「山下り」の例え話での要素 | AIの学習における対応する要素 | 説明 |
|---|---|---|
| 旅人 | AIモデル(が持つパラメータ) | 学習によって調整されていく主体です。 |
| 山の地形 | 損失関数 | パラメータの値によって「間違いの大きさ」がどう変わるかを示します。 |
| 現在地の標高 | 現在の損失 (Loss) の値 | 今のAIモデルがどれだけ間違っているかを示す数値です。 |
| 谷底 | 損失が最小になる地点 | AIの学習が目指す最終ゴールです。 |
| 足元の傾き(方向と険しさ) | 勾配 (Gradient) | パラメータを動かした時に、損失が最も増える方向とその度合いを示します。 |
| 最も急な下り坂の方向 | 負の勾配 (-Gradient) | まさにAIが進むべき、損失が最も減る方向です。 |
| 谷底へ向かって一歩進むこと | パラメータの更新 | 「負の勾配」の方向に、AIモデルのパラメータを少しだけ調整する操作です。 |
そう、この「ある瞬間の、最も急な坂道の方向と険しさ」を、数学的にピタリと教えてくれる魔法の道具こそが、微分であり、特に私たちが見ている山のような多次元の地形(=たくさんのパラメータを持つ関数)における「傾き情報」を、その名もズバリ勾配(Gradient)と呼びます。
AIは、この勾配という名のコンパスを頼りに、損失という名の山を少しずつ下っていくことで、着実に賢くなっていくのです。
1. 微分とは? ― 「瞬間の変化率」を捉える虫眼鏡
さて、AIの学習の羅針盤となる「微分」や「勾配」ですが、その正体は何なのでしょうか。まずは一番シンプルな、変数が一つだけの「微分」から探っていきましょう。
微分と聞くと、なんだか複雑な数式が並んでいて、見るのも嫌だ…なんて感じる方もいるかもしれませんね。私も最初はそうでした。でも、その本質は驚くほどシンプルで、「ある一点における、ごくわずかな変化の割合」を求めること、ただそれだけなんです。グラフの世界で言えば、それはその点における「接線の傾き」にピッタリ対応します(1)。
言葉だけだとピンとこないかもしれないので、一番身近な二次関数、\(y = x^2\) のグラフを例に、一緒に見ていきましょう。
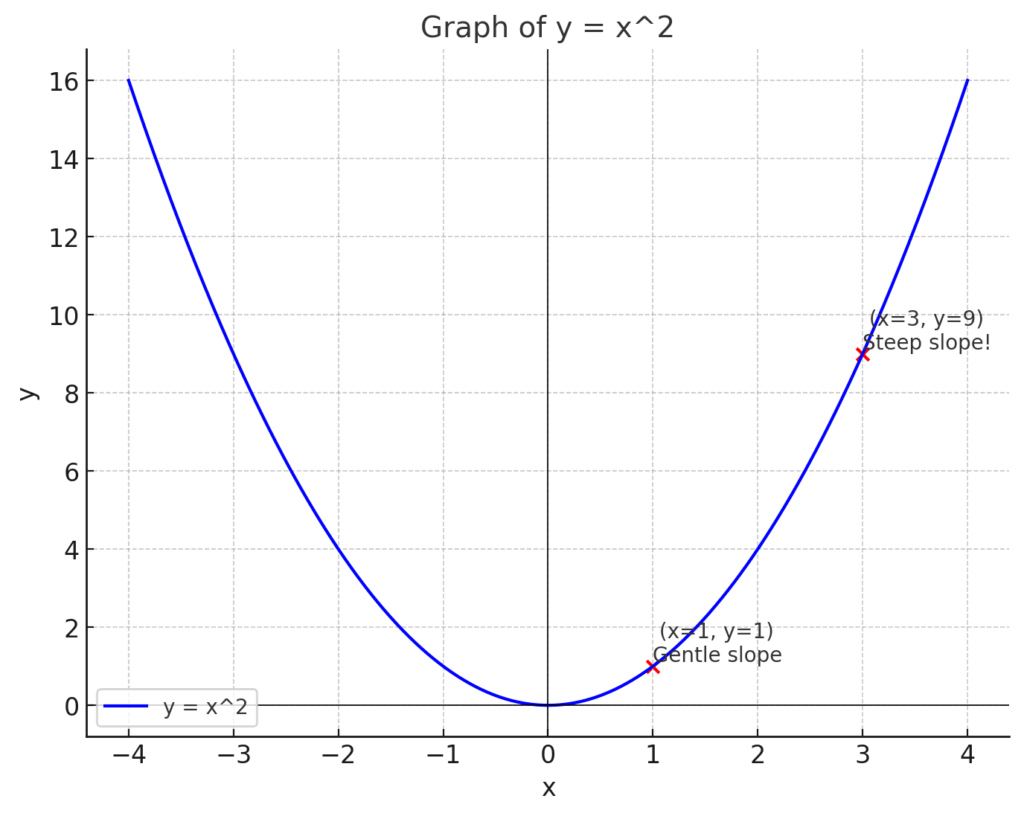
このグラフを、スキーのジャンプ台だと思って見てみてください。
- \(x=1\) の地点:まだ滑り始めで、坂は比較的ゆるやかです。もしこの点に接する直線を引いたら、その傾きは小さいはずです。
- \(x=3\) の地点:かなり滑り降りてきて、坂はとても急になっています。ここに接する直線を引けば、その傾きはきっと大きくなっているでしょう。
このように、同じ一つのカーブでも、場所によって「変化の勢い」は全然違いますよね。微分というのは、この「その瞬間の勢い」を、傾きという一つの数値として、ピタリと正確に捉えるための、まるで虫眼鏡のような道具なのです。
では、数学の世界では、この「瞬間の傾き」をどうやって計算するのでしょうか。ここで登場するのが「極限 (limit)」という、ちょっと賢いアイデアです。
いきなり「瞬間の傾き」を求めるのは難しいので、まずは「2点間の平均的な傾き」から考えてみましょう。これは中学で習った、直線の傾きの計算と同じです。
傾き = (yの変化量) / (xの変化量)
この考え方を使って、点 \(x\) と、そこからほんの少しだけ離れた点 \(x+h\) の2点間の傾きを計算してみます。
| 項目 | 意味 |
|---|---|
| x座標の変化 | (x + h) - x = \(h\) |
| y座標の変化 | f(x + h) - f(x) |
| 2点間の平均の傾き | \( \frac{f(x+h) – f(x)}{h} \) |
この式は、2点を結んだ直線の傾きを示しています。でも、私たちが本当に知りたいのは「1点」での瞬間の傾きです。どうすればいいでしょうか?
答えは、「もう一方の点を、限りなく近づけていけばいい」のです。つまり、2点間の距離 \(h\) を、どんどん小さくしてゼロに近づけていく。この「限りなくゼロに近づける」という操作を、数学では lim (リミット) という記号で表現します。
このアイデアを数式にまとめると、微分の定義式が完成します。
\[ f'(x) = \lim_{h \to 0} \frac{f(x+h) – f(x)}{h} \]
この式、一見すると難しそうですが、パーツに分解すれば、先ほどの話そのものです。
- \(\frac{f(x+h) – f(x)}{h}\):これは、2点間(\(x\) と \(x+h\))を結んだ直線の「平均の傾き」を計算している部分です。
- \(\lim_{h \to 0}\):そしてこれが、「\(h\)(2点間の横の距離)を限りなくゼロに近づけてね!」という魔法の呪文。この呪文を唱えることで、「平均の傾き」が、私たちが知りたかった「\(x\)という一点での瞬間の傾き」へと昇華するわけです。
幸いなことに、AI開発の現場で、私たちがこの極限計算を手で解く必要はほとんどありません。AI向けのライブラリが、この定義に基づいた計算を(近似的にですが)一瞬で実行してくれます。
大切なのは、この式の「気持ち」を理解しておくこと。なぜなら、次に私たちがPythonで実装する数値微分は、この式の考え方をそっくりそのままコードに落とし込んだものだからです。
2. Pythonで微分の計算を体験する(数値微分)
さて、前章で微分の「心」とも言える定義式を見てきました。
\[ f'(x) = \lim_{h \to 0} \frac{f(x+h) – f(x)}{h} \]
この式の意味は「2点間の距離\(h\)を限りなくゼロに近づけて、瞬間の傾きを求める」でしたね。これをコンピュータに実行させるにはどうすれば良いでしょうか?
コンピュータは「限りなくゼロ」という無限の操作は苦手です。しかし、「ゼロに限りなく近い、とても小さな値」を使って近似計算をすることは大得意。このアプローチで微分の値を求める方法を数値微分 (numerical differentiation) と呼びます。
それでは早速、この考え方をPythonコードに落とし込んで、実際に\(y=x^2\)のグラフの傾きを計算してみましょう。コードを動かしながら、理論が現実の計算になっていく様子を体感してみてください。
【実行前の準備】
以下のコードで日本語のグラフを表示させるには、あらかじめターミナルやコマンドプロンプトで pip install japanize-matplotlib を実行してライブラリをインストールしてください。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib # matplotlibの日本語表示を簡単にする
# --- 1. 微分の対象となる関数を定義 ---
def function_f(x):
"""シンプルな二次関数 y = x^2 を定義します。"""
return x**2
# --- 2. 微分の定義式を元に、数値微分を計算する関数を実装 ---
def numerical_diff(f, x):
"""
関数の定義に基づいて数値微分を計算します。
Args:
f (function): 微分したい関数(ここでは function_f)
x (float): 傾きを求めたい点のx座標
Returns:
float: xにおける微分係数(瞬間の傾き)
"""
# hは「限りなくゼロに近い」値の代わり。10の-4乗 = 0.0001
h = 1e-4
# 微分の定義式 (f(x+h) - f(x)) / h をそのまま計算
return (f(x + h) - f(x)) / h
# --- 3. 実際に計算して、結果を可視化 ---
# x=3 のときの傾きを計算してみましょう
x_point = 3.0
slope = numerical_diff(function_f, x_point)
# 計算結果を出力
print(f"関数 y = x^2 の x = {x_point} における傾きは、約 {slope:.4f} です。")
# 実行結果:
# 関数 y = x^2 の x = 3.0 における傾きは、約 6.0001 です。
# --- 4. 結果をグラフで分かりやすく確認 ---
# 元の関数 y = x^2 のグラフデータを作成
x_range = np.arange(-1.0, 5.0, 0.1) # -1.0から4.9まで0.1刻みのx値
y_range = function_f(x_range) # 対応するy値
# x=3 における接線のデータを作成
# 点(x_point, y_point)を通り、傾きがslopeの直線の式: y = slope * (x - x_point) + y_point
y_point = function_f(x_point)
tangent_line = slope * (x_range - x_point) + y_point
# グラフを描画
plt.figure(figsize=(8, 6)) # グラフサイズを少し大きめに設定
plt.plot(x_range, y_range, label='y = x² (元の関数)')
plt.plot(x_range, tangent_line, 'r--', label=f'x={x_point}での接線 (傾き ≈ {slope:.2f})')
plt.scatter(x_point, y_point, color='red', s=100, zorder=5, label=f'計算点 (x={x_point})') # 点をプロット
# グラフの見た目を整える
plt.title('数値微分で求めた接線の描画')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.legend()
plt.show()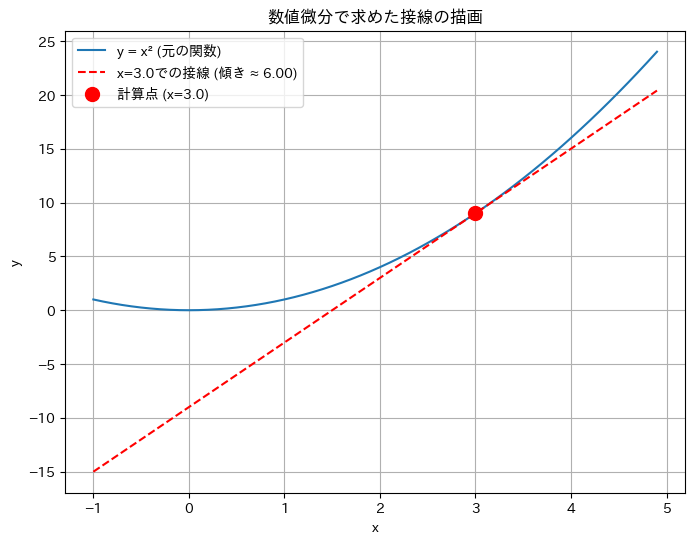
コードと結果のウォークスルー
コードを実行すると、まずコンソールに ...傾きは、約 6.0001 です。 と表示され、続いて計算結果を可視化したグラフが現れます。この結果が何を意味しているのか、一つずつ見ていきましょう。
1. numerical_diff関数の中身
この関数が今回の心臓部です。やっていることは非常にシンプル。
h = 1e-4: 微分の定義式に出てきた、微小な変化量hを0.0001という具体的な数値で設定しています。なぜこの値かというと、あまりに小さすぎるとコンピュータの計算誤差(丸め誤差)が逆に大きくなってしまうため、このくらいの値が実用上よく使われます。return (f(x + h) - f(x)) / h: 見てください、これは前章で学んだ微分の定義式そのものですよね。数学の理論が、たった一行のコードとして表現されているのが面白いところです。
2. 計算結果 6.0001 は正しい?
「本当にこの計算、合ってるの?」と気になりますよね。ここで答え合わせをしてみましょう。高校の数学で習ったかもしれませんが、\(y = x^2\) を微分すると、その導関数(どの点でも傾きを計算できる関数)は \(y’ = 2x\) となります。
- 手計算(解析的な解): 傾きを知りたい点 \(x=3\) をこの式に代入すると、\(y’ = 2 \times 3 = 6\) となります。
- 今回の結果(数値的な解): 私たちのコードが出した答えは
6.0001でした。
どうでしょう? 真の値である 6 と、ほとんど同じ値になっていますね! \(h\) を使った近似計算なので完全にピッタリとはなりませんが、実用上は十分な精度で「瞬間の傾き」が計算できていることが分かります。
3. グラフが教えてくれること
最後にグラフを見てみましょう。青い放物線が \(y=x^2\) のグラフです。そして、私たちのコードが計算した傾き 6.0001 をもとに引いた赤い点線が、点 (3, 9) でグラフに見事に接しているのが一目でわかります。
このように、数式(理論)をコード(実装)に落とし込み、その結果を可視化(検証)するという流れは、AIやデータサイエンスの世界では基本中の基本です。理論の正しさを自分の目で確かめられると、理解がぐっと深まりますよね。
3. 勾配とは? ― 最も急な坂道を探す、多次元世界のコンパス
ここまでは、変数が x 一つだけの、いわば直線上を進むようなシンプルな世界で「傾き」を見てきました。しかし、現実のAIが向き合う世界は、もっとずっと複雑です。
AIの「間違いの大きさ(損失)」を決めるのは、一つの要因だけではありません。モデルが持つ何百万、何千万という膨大な数のパラメータ(重みやバイアス)が、それぞれ少しずつ影響し合って、最終的な損失の値が決まります。これはまるで、山の標高が「緯度」と「経度」だけで決まるのではなく、「標高」「湿度」「風速」「気温」…といった無数の要素で決まる、超多次元の山を歩くようなものです。
このように、変数がたくさんある関数に対して、「すべての変数を考慮した上で、関数値が最も大きくなる方向と、その勢い」を一本の矢印(ベクトル)として示してくれるもの。それが勾配 (Gradient) です(2)。
もう一度、あの「山下りの旅」の例えに戻ってみましょう。
- あなたは、緯度(\(x_0\))と経度(\(x_1\))で表される地点に立っています。山の高さは \(f(x_0, x_1)\) で決まります。
- その地点で勾配を計算すると、それは「最も急な上り坂を指す矢印(ベクトル)」になります。矢印の向きが最も険しい上り坂の方向を、矢印の長さがその坂の急さを示します。
- では、私たちが目指す「谷底」へ向かうには?簡単ですね。勾配が指す方向と真逆の方向へ進めば良いのです。この「最も急な下り坂」の方向こそが、負の勾配(-勾配)です。
AIの学習目標は「損失関数の値を最小にする」ことでした。これは、損失という名の山の「谷底」を探す旅そのものです。だからこそ、AIは各ステップで損失関数の負の勾配を計算し、その矢印が指し示す方向にパラメータをほんの少しだけ更新していくのです。この、AI学習の最も基本的で重要な最適化アルゴリズムを、後のセクションで詳しく学ぶ勾配降下法 (Gradient Descent) と呼びます。
Pythonで勾配の計算を体験する
理屈はなんとなく分かったところで、今度は多次元の勾配計算もPythonで実装してみましょう。これを通じて、勾配が「矢印」として計算される感覚を掴んでいきます。
ここでは、最もシンプルな2変数関数 \( f(x_0, x_1) = x_0^2 + x_1^2 \) の勾配を計算してみます。この関数は、地図で描くと原点 \((0, 0)\) が一番低い「すり鉢(お椀)」のような形で、勾配降下法の動きを見るのにうってつけの題材です。
勾配を計算するための手順は、次の通りです。
- 変数 \(x_0\) についての傾きを計算する(このとき、\(x_1\) はただの数字として無視する)。
- 変数 \(x_1\) についての傾きを計算する(今度は、\(x_0\) を無視する)。
- 1と2の結果を、ベクトルとして
[x0の傾き, x1の傾き]のようにまとめる。
この「ある特定の変数だけに注目して微分する」操作を、数学の言葉で偏微分と呼びます。私たちのコードは、この偏微分を各変数に対して順番に行い、勾配ベクトルを作り上げます。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
# --- 1. 勾配を計算したい2変数関数を定義 ---
def function_2d(x):
"""
お椀型の関数 f(x0, x1) = x0^2 + x1^2 を定義します。
Args:
x (np.ndarray): [x0, x1] というNumPy配列を想定
"""
return x[0]**2 + x[1]**2
# --- 2. 勾配(各変数の偏微分のベクトル)を計算する関数 ---
def numerical_gradient(f, x):
"""
多変数関数の勾配を数値的に計算します。
Args:
f (function): 勾配を計算したい関数
x (np.ndarray): 勾配を求めたい点(例: np.array([3.0, 4.0]))
Returns:
np.ndarray: 各変数での偏微分からなる勾配ベクトル
"""
h = 1e-4 # 微小な変化量
grad = np.zeros_like(x) # xと同じ形状で、要素がすべて0の配列を生成(勾配ベクトルを格納するため)
# 各変数 (x0, x1, ...) について、偏微分を計算
# enumerate(x) を使うと、インデックス(idx)と要素(val)を同時に取り出せる
for idx in range(x.size):
tmp_val = x[idx] # 元の値を一時的に保存
# f(x+h) の計算(注目している変数だけを少し動かす)
x[idx] = tmp_val + h
fxh1 = f(x)
# f(x-h) の計算
x[idx] = tmp_val - h
fxh2 = f(x)
# 中心差分 (f(x+h) - f(x-h)) / 2h で偏微分を計算
grad[idx] = (fxh1 - fxh2) / (2 * h)
x[idx] = tmp_val # 値を元に戻す(重要!)
return grad
# --- 3. 勾配をいくつかの点で計算し、可視化 ---
# 関数の等高線プロットを作成
x0 = np.arange(-10, 10.1, 1.0)
x1 = np.arange(-10, 10.1, 1.0)
X0, X1 = np.meshgrid(x0, x1)
Z = X0**2 + X1**2
plt.figure(figsize=(8, 8))
# contourは等高線を描画する関数
plt.contour(X0, X1, Z, levels=np.arange(0, 201, 20), colors='gray')
# 勾配を描画したい点
points = [np.array([-8.0, 6.0]), np.array([5.0, -5.0]), np.array([-2.0, -8.0]), np.array([7.0, 7.0])]
for p in points:
# 各点での勾配を計算
grad = numerical_gradient(function_2d, p)
# 勾配ベクトルを描画 (quiverプロット)
# p[0], p[1]が矢印の始点
# -grad[0], -grad[1]が矢印の方向と大きさのベクトル
# マイナスをつけて「最も急な下り坂」の方向を描画
plt.quiver(p[0], p[1], -grad[0], -grad[1], angles="xy", color="red", scale_units='xy', scale=15)
plt.plot(p[0], p[1], 'bo') # 点をプロット
plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.xlabel("x0")
plt.ylabel("x1")
plt.title('関数の等高線と負の勾配ベクトル')
plt.gca().set_aspect('equal', adjustable='box') # グラフのアスペクト比を1:1に
plt.grid(True)
plt.show()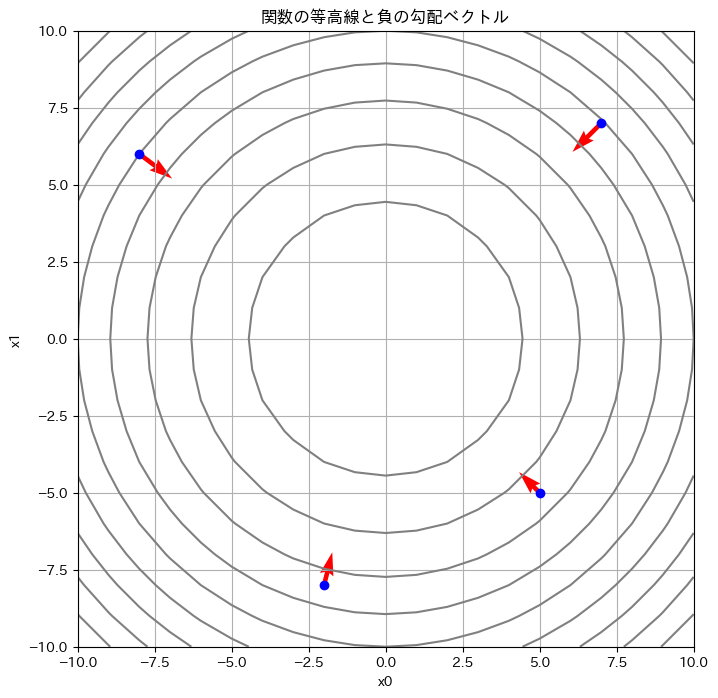
コードと結果の解説
このコードを実行すると、お椀型をした関数の「地図(等高線図)」が表示されます。灰色の線が同じ高さの地点を結んだ線です。そして、青い点がいくつかの現在地、そこから伸びる赤い矢印が、私たちのコードが計算した「負の勾配」、つまり最も急な下り坂の方向を示しています。
この結果から、とても重要なことが分かります。
それは、どの地点から出発しても、赤い矢印(負の勾配)は常にお椀の底、つまりこの関数の唯一の最小値である原点 \((0, 0)\) を指しているということです。
これこそが、AIが学習を進めるべき「正しい方向」に他なりません。
ちなみに、numerical_gradient関数の中で、少しだけ賢い計算方法を使っています。
【計算方法のちょっとした工夫:中心差分】
前のセクションで使った計算方法(前方差分):
(f(x+h) - f(x)) / h
x と x+h の2点から傾きを計算します。
x地点での真の傾きとは、少しズレが生じやすいです。
今回使った計算方法(中心差分):
(f(x+h) - f(x-h)) / (2*h)
x-h と x+h の2点から傾きを計算します。
xをちょうど中心に挟んでいるため、誤差が少なく、より精度の高い近似になります。numerical_gradient関数は、入力されたベクトル x の各要素(x0, x1, …)に対して、この精度の高い中心差分を使って偏微分を一つずつ計算し、その結果を grad という一つのベクトルにまとめて返してくれます。この grad こそが、多次元空間における「傾き情報」の正体、勾配なのです。
まとめと次のステップ
今回は、AIの学習の根幹をなす「微分」と「勾配」の世界に足を踏み入れました。
- 微分とは、関数の「ある一点での瞬間の傾き」を求める操作である。
- 勾配とは、多変数関数において「関数値が最も増加する方向を示すベクトル」である。
- AIの学習は、損失関数の「負の勾配」を道しるべに、パラメータを少しずつ更新していくことで行われる。
私たちは、AIが膨大なパラメータの山を駆け下りるための、最も基本的なコンパスを手に入れたことになります。
しかし、今回の数値微分は、計算コストが非常に高いという欠点があります。パラメータが100万個あれば、1回の勾配計算で100万回以上も関数を計算し直さなければなりません。
そこで次回以降のテーマとなるのが、この計算を劇的に高速化する誤差逆伝播法(バックプロパゲーション)です。その核心には、今回少しだけ顔を出した「偏微分」や、合成関数の微分ルールである「連鎖律(0.3.3)」が関わってきます。まずは、次の「0.3.2: 偏微分」で、多変数関数に対する微分の概念をもう少し深掘りしていきましょう。
参考文献
- Strang G. Introduction to Linear Algebra. 5th ed. Wellesley-Cambridge Press; 2016.
- Goodfellow I, Bengio Y, Courville A. Deep Learning. MIT Press; 2016. Chapter 4, Numerical Computation.
- Nielsen MA. Neural Networks and Deep Learning [Internet]. Determination Press; 2015. Available from: http://neuralnetworksanddeeplearning.com/
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






