AIの解説でよく見る記号「e」と「ln」。これらは「連続的な成長」とその「逆の操作」を象徴し、確率計算を安定させるAIの必須ツールです。その本質的な意味と役割を直感的に理解しましょう。
約2.718という特別な定数。「100%の成長」を無限に細かく分割して複利計算したときの限界値です。自然界の増殖や減衰など、変化率がその時点の量に比例する現象を表す「ものさし」となります。
「e を何乗すればある数xになるか?」という問いに答える操作です。指数関数的な急激な成長を、穏やかなスケールに変換します。グラフ上では y=eˣ と y=x の直線に対して鏡写しの関係(逆関数)にあります。
AIでは無数の確率(小数)を掛け合わせます。lnは「掛け算を足し算」に変え、計算エラーを防ぎます。eで確率を出力し(ソフトマックス)、lnでその誤差を評価する(交差エントロピー)など、AIの学習の根幹を支えます。
AIや機械学習の解説で、当然のように登場する記号「\(e\)」や「\(\ln\)」。これらは一体何者で、なぜAIの世界でこれほど重要なのでしょうか。今回は、AIの根幹を支えるこれらの概念を、直感的に理解することを目指します。
ネイピア数 \(e\) とは?—「連続的な成長」の物語
AIの数式で頻繁に見かける、謎めいた定数 \(e\)。これは一体何者なのでしょうか。その正体は、実は「成長」という現象の奥深くに隠されています。円周率 \(\pi\) が全ての円に共通する普遍的な比率であるように、ネイピア数 \(e\) は、あらゆる「連続的な成長」のプロセスに現れる、これまた普遍的な定数なのです。
その値は、およそ 2.71828… と続く、割り切れない無理数です。
銀行の利息でイメージする「成長の限界」
この \(e\) の本質を掴むために、少し非現実的ですが「年利100%」という、とても景気の良い銀行預金を例に考えてみましょう。元本は100万円とします。
もし、利息の計算が年に1回なら…
1年後、元本100万円に100%の利息がついて、資産は倍になります。
\[ 100万円 \times (1 + 1) = 200万円 \]
では、計算を「半年に1回」に分割したら…?
年利100%を分割し、「半年ごとに50%」の利息がつく契約です。
半年後:\(100万円 \times (1 + 0.5) = 150万円\)
1年後:\(150万円 \times (1 + 0.5) = 225万円\)
年に1回よりも、もらえる金額が増えました。これは、前半の利息(50万円)に、さらに後半の利息がかかる「複利」の効果ですね。
計算回数をどんどん増やしていくとどうなる?
この調子で、利息の計算回数をどんどん細かくしていくと、資産は無限に増えていくのでしょうか?下の表で、その結果を追ってみましょう。
| 利息の計算回数 (n) | 計算式(元本100万円の場合) | 1年後の金額 | 元本の何倍か |
|---|---|---|---|
| 年に1回 | \(100 \times (1 + 1/1)^1\) | 200.000 万円 | 2.00000 倍 |
| 半年ごと (年2回) | \(100 \times (1 + 1/2)^2\) | 225.000 万円 | 2.25000 倍 |
| 四半期ごと (年4回) | \(100 \times (1 + 1/4)^4\) | 244.141 万円 | 2.44141 倍 |
| 毎月 (年12回) | \(100 \times (1 + 1/12)^{12}\) | 261.304 万円 | 2.61304 倍 |
| 毎日 (年365回) | \(100 \times (1 + 1/365)^{365}\) | 271.457 万円 | 2.71457 倍 |
| 連続的 (n→∞) | 極限値 | 約 271.828 万円 | 約 2.71828… 倍 |
面白いことに、計算回数を増やせば増やすほど、受取額は増えるものの、その伸び幅はどんどん小さくなっていきます。そして最終的には、ある特定の数字に限りなく近づいていく(収束する)のです。
この「元本の何倍か」という値がたどり着く極限値、それこそがネイピア数 \(e\) なのです。数式で表現すると、分割回数 \(n\) を無限に大きくしたときの、この式の値が \(e\) になります。
\[ e = \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n \approx 2.71828\dots \]
なぜこの話がAIに重要なのか?
この「連続的な成長」という考え方は、私たちの世界に満ち溢れています。
- 薬剤の血中濃度: 投与後の薬の量は、時間と共に連続的に減少(負の成長)していきます。
- 細胞の増殖: 理想的な環境下での細胞数は、連続的に増加していきます。
- 放射性同位体の崩壊: 残存量は時間と共に連続的に減衰します。
これらの現象はすべて、その変化の度合いが「その時点での量」に比例するという共通の性質を持っています。そして、このような現象を数学的に記述する際に、最も自然で、最も扱いやすい「ものさし」となるのが、このネイピア数 \(e\) なのです。
AIの世界でも、ニューラルネットワークで確率を扱うソフトマックス関数や、モデルの性能を評価する交差エントロピー誤差といった、根幹をなす数々の理論が \(e\) を土台として構築されています。\(e\) は、AIが連続的で複雑な現象を捉えるための、欠くことのできない数学的な基盤と言えるでしょう。
自然対数 \(\ln\) とは? — 成長の物語を「巻き戻す」魔法
前回、私たちはネイピア数 \(e\) が「連続的な成長」の物語を語る特別な数字であることを見ました。では、もし「ある値まで成長した結果」が分かっているとき、そこに至るまでに「どれだけの時間(あるいは強さ)で成長したのか」を知りたくなったらどうでしょう?
この「成長の時間を巻き戻す」という問いに答えてくれるのが、自然対数 (natural logarithm, \(\ln\)) なのです。
一般に、対数 \(\log_a(x)\) は「底(てい)と呼ばれる数 \(a\) を、何乗したら \(x\) になりますか?」という問いを意味します。自然対数 \(\ln(x)\) は、この底がネイピア数 \(e\) に限定された、いわば「連続成長専用」の対数です。つまり、
\(\ln(x)\) とは、「\(e\) を何乗すれば \(x\) になりますか?」という問いそのものです。
- \(e^1 \approx 2.718\) なので、\(\ln(2.718)\) はおよそ 1 です。
- \(e^2 \approx 7.389\) なので、\(\ln(7.389)\) はおよそ 2 です。
- どんな数も0乗すれば1になるので、\(e^0=1\)、つまり \(\ln(1)\) は 0 となります。
\(e^x\) が凄まじい勢いで成長していく関数だとすれば、\(\ln(x)\) はその勢いをぐっと抑え、穏やかに成長する関数です。グラフで見てみると、その「逆再生」の関係性が一目瞭然です。
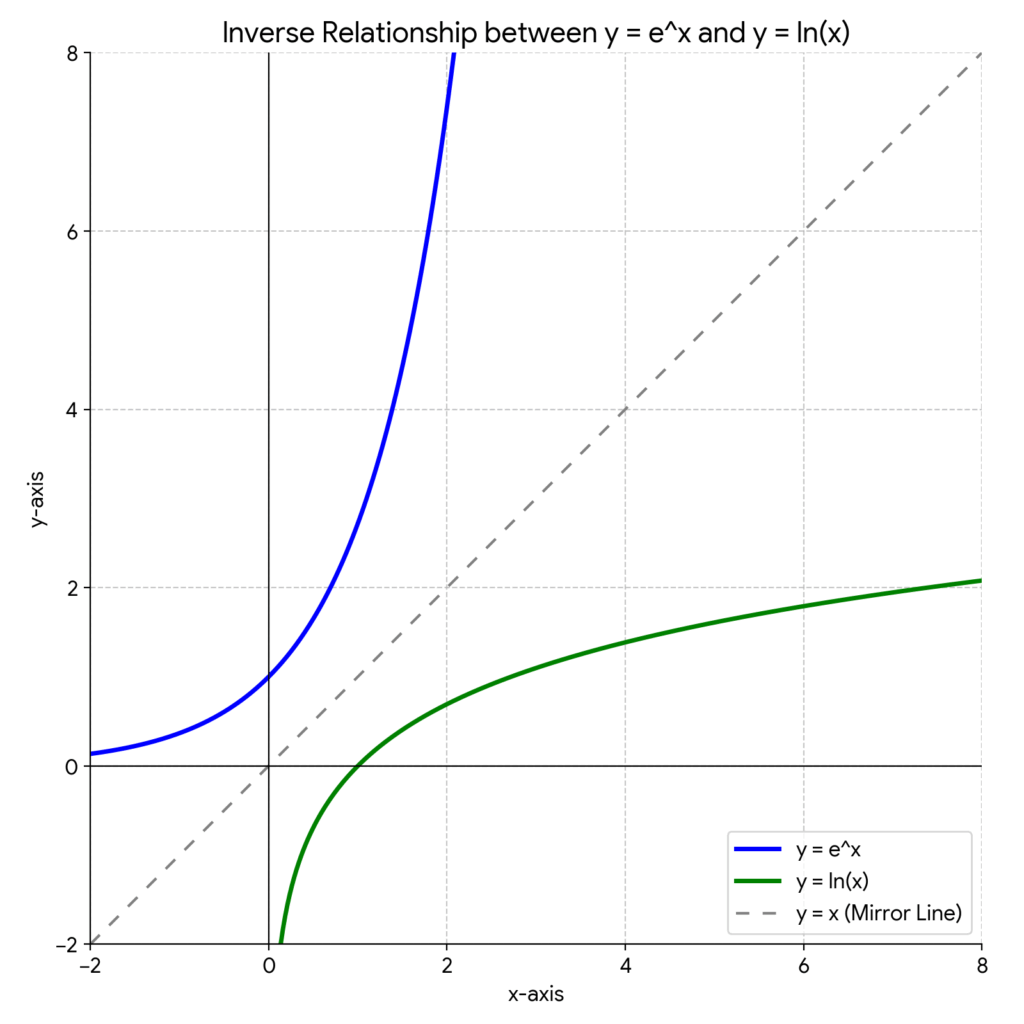
この図のように、\(y=e^x\) と \(y=\ln(x)\) のグラフは、直線 \(y=x\) を軸として、まるで鏡に映したように完全な対称形をしています。これは、一方が他方の「逆関数」である、つまり互いに「逆の操作」であることを美しく示しています。
なぜ \(e\) と \(\ln\) は、AIにおける「最強のペア」なのか?
この「成長」と「巻き戻し」という関係性が、AI、特に確率を扱うモデルにおいて、驚くほど重要な役割を果たします。その理由は大きく2つあります。
1. コンピュータを「桁落ち」の悪夢から救う
AIが分類問題に取り組む際、「この画像が猫である確率は0.9、犬である確率は0.05、…」といったように、多数の確率を計算します。そして、モデル全体の「確からしさ(尤度)」を評価するには、これらの小さな確率(0から1の間の小数)を、何千、何万と掛け合わせる必要があります。
しかし、コンピュータは極端に小さい小数を何度も掛け合わせると、計算結果がゼロになってしまう「アンダーフロー(桁落ち)」という問題を起こしやすい、という弱点があります。
ここで対数が魔法の力を発揮します。対数には、「掛け算を足し算に変える」という非常に便利な性質(\(\ln(a \times b) = \ln(a) + \ln(b)\))があるからです。
【対数が「掛け算」を「足し算」に変える力】
通常の確率計算(尤度):
P = p1 * p2 * p3 * ...
= 0.01 * 0.02 * 0.005 * ... ==> コンピュータ上ではほぼ 0 に? (桁落ちの危険)
対数確率の計算(対数尤度):
ln(P) = ln(p1) + ln(p2) + ln(p3) + ...
= (-4.6) + (-3.9) + (-5.3) + ... ==> 扱いやすい負の数の足し算に! (安定)
このように、各確率の対数を取る(対数尤度を計算する)と、不安定な「掛け算の連鎖」が、安定した「足し算の連続」に変わります。\(\ln(P) = \ln(p_1) + \ln(p_2) + \dots\)。0に近い確率の自然対数は、扱いやすい大きさの負の数になるため、いくら足し合わせても桁落ちの心配がありません。この「対数尤度」という考え方は、AIモデルの学習における、極めて標準的で重要なテクニックです。
2. AIの「出力」と「評価」を担う
このペアは、ニューラルネットワークの核心部分でも活躍しています。
- 出力: AIが予測確率を出力する際によく使われるソフトマックス関数では、\(e\) が使われ、各選択肢の「起こりやすさ」を自然な形で表現します。
- 評価: その予測がどれだけ正解に近かったか、という「間違いの度合い(損失)」を測る交差エントロピー誤差関数では、ソフトマックスが出力した確率の \(\ln\) を取って計算します。
このように、\(e\) で確率を表現し、\(\ln\) でその誤差を測る。この美しいペアによって、AIの学習は支えられているのです。
まとめ
- ネイピア数 \(e\) は「連続的な成長」を象徴する、約2.718という特別な定数。
- 自然対数 \(\ln\) は、\(e\) の指数的な変化を元に戻す「逆の操作」。
- このペアは、AIにおける確率計算を安定かつシンプルにし、重要な関数の土台となっている。
\(e\) と \(\ln\) は、AIが複雑なデータから学習し、確率的な予測を行うための、目立たないながらも極めて重要な数学的ツールなのです。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






