はじめに:データの「設計図」としての確率分布
前回の講座で私たちは、ベイズの定理という強力なツールを手にし、新しい「証拠」に基づいて確率的な「信念」を更新する方法を学びました。これは、個々の患者さんを前にしたときのミクロな推論プロセスでしたね。
しかし、優れた臨床判断や、AIによる高精度な予測のためには、もう一つ、マクロな視点が必要になります。
例えば、ある患者さんの血糖値が「130 mg/dL」だったとします。この数字一つだけを見て、私たちは何を判断できるでしょうか?「正常高値かな?」「糖尿病の境界型?」…この数字の意味合いは、比較対象となる「基準」があって初めて、その輪郭を現します。
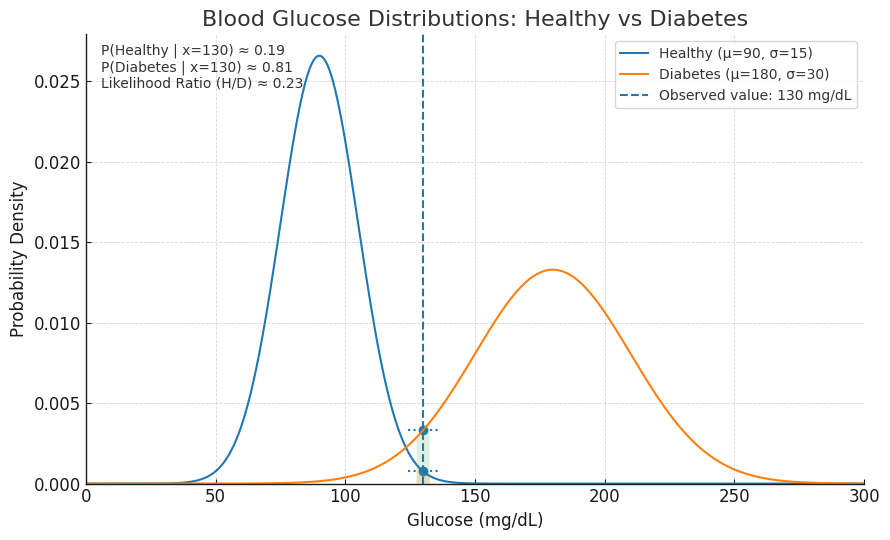
上の図のように、もし私たちが「健常者の血糖値は、平均90mg/dLを中心になだらかな山を描く」という分布(A)と、「糖尿病患者の血糖値は、平均180mg/dLを中心とする、より広がった山を描く」という分布(B)を知っていれば、「130」という値の解釈は大きく変わります。健常者集団から見れば少し外れ値ですが、糖尿病患者集団から見ればむしろ低い値です。
このように、個々のデータを評価するための背景地図、あるいは「取扱説明書」の役割を果たすのが、確率分布 (Probability Distribution) なのです。
数学の言葉で言えば、確率分布とは、ある確率変数がとりうる全ての値と、それぞれの値をとる確率(あるいは確率の密度)の関係性を、一つの関数やグラフとして体系的に示したものです。
この「設計図」をAIに与える、あるいはデータからAI自身にこの設計図を「学習」させることで、AIは初めて、新しいデータが「ありふれた値」なのか「稀な異常値」なのかを統計的に判断し、より高度な予測を行うことができるようになります。
今回の講座では、この確率分布という広大なテーマの中から、特に医療とAIの世界で頻繁に登場し、基本となる2つの分布ファミリー、正規分布とベルヌーイ分布に焦点を当て、その性質と役割を探っていきます。
1. 確率分布の2つの顔:離散型と連続型
前回の講座で、私たちは「確率変数」という、現実の出来事を数値に変換する便利な道具を手に入れました。この確率変数がとる値の性質によって、その「設計図」である確率分布は、大きく2つの顔を使い分けます。それが離散型と連続型です。
a) 離散確率分布 — カチッと決まる確率
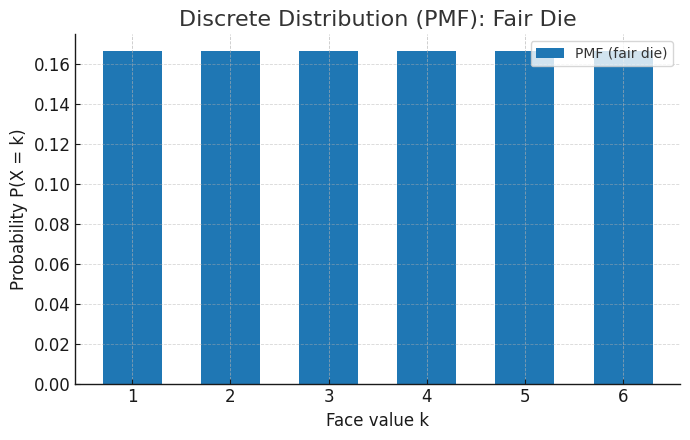
サイコロの目や治療への反応(奏効/非奏効)のように、確率変数がとびとびの値(1, 2, 3… や 0, 1)しかとらない場合、その分布を離散確率分布と呼びます。
この場合、私たちは「サイコロの目がちょうど3である確率」のように、特定の値そのものに対する確率を直接定義できます。これを確率質量関数 (Probability Mass Function, PMF) といいます。「質量(Mass)」という言葉が使われているように、各値の上に、その確率の重さ分の「おもり」が乗っているようなイメージですね。図Aのように、全ての棒の高さを足し合わせると、当然ながら合計は1になります。
b) 連続確率分布 — 「密度」で考える確率
一方、患者さんの身長や血圧、検査値のように、確率変数が連続的な値をとる場合は、少し考え方を変える必要があります。
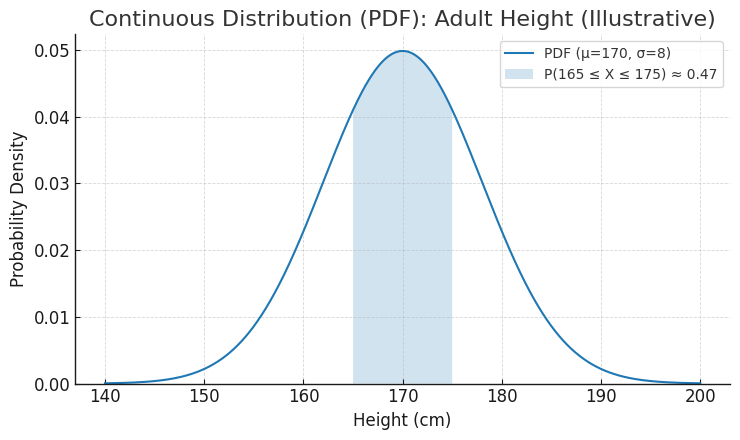
「身長が、小数点以下無限桁まで含めて、寸分違わず170.000…cmである確率」を考えてみてください。無数の可能性がある中でのピンポイント一点なので、その確率は限りなくゼロに近い、と考えるのが自然ですよね。
そこで、連続型の場合は、「身長が170cmから171cmの間である確率」のように、ある「範囲」に対する確率を考えます。これを表現するのが確率密度関数 (Probability Density Function, PDF) です。図Bの曲線がそれにあたり、この曲線の下の面積が、その範囲の確率に対応します。曲線が高い場所は、その周辺の値が「起こりやすい(密度が高い)」ことを示しています。そして、もちろん、曲線の下の全面積を合計すると1になります。
この「離散」と「連続」という区別は、AIモデルを設計する上でとても大切です。例えば、患者さんの退院の有無(0 or 1)を予測する分類モデルを作るなら、その出力は離散確率分布(ベルヌーイ分布)の考え方に基づきますし、明日の血糖値を予測する回帰モデルを作るなら、その誤差は連続確率分布(正規分布)に従う、と仮定することが多いです。扱うデータの性質に合わせて、適切な「設計図」を選ぶ。これが、優れたAIモデルを作るための第一歩なのです。
2. 連続データの王様「正規分布」— 多くの自然現象に潜む美しい”釣鐘”
もし、あなたが確率分布の世界で、たった一つだけ名前を覚えるとしたら、それは間違いなく正規分布 (Normal Distribution) でしょう。その釣鐘(ベル)のような美しい形から「ベルカーブ」とも呼ばれ、自然界から社会現象、そしてもちろん医療データに至るまで、驚くほど多くの場面で顔を出す、まさに分布の「王様」です。
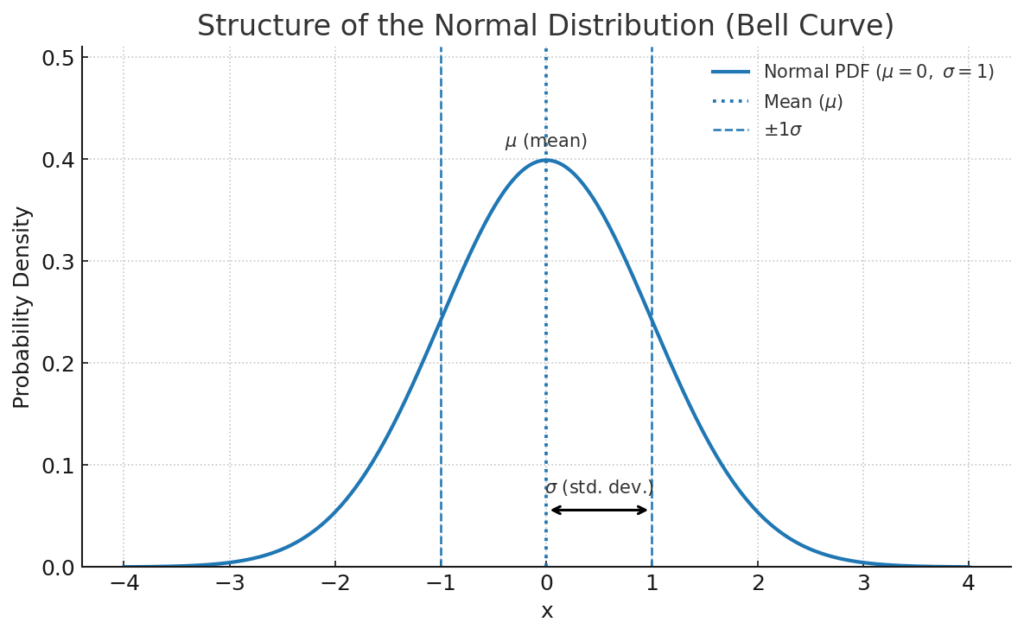
このおなじみの釣鐘の形は、実はたった2つの「設計図」、すなわちパラメータで決まります。
- 平均 (\(\mu\)): 分布の「中心」、つまり釣鐘が最も高くなる場所を決めます。これは、データの最も代表的な値と考えることができます。
- 標準偏差 (\(\sigma\)): 分布の「広がり具合」を決めます。(\(\sigma\))が小さいほど、データは平均(\(\mu\))の周りにギュッと集まり、鋭く尖った釣鐘になります。逆に大きいほど、データは広範囲に散らばり、なだらかな丘のような形になります。
なぜ正規分布はこれほど普遍的なのか?
では、なぜこのベルカーブは、これほどまでに普遍的に現れるのでしょうか?その背景には、「中心極限定理 (Central Limit Theorem)」という、統計学における最も重要で美しい定理の一つがあります。
この定理をものすごく簡単に言うと、「互いに独立な、たくさんの小さな要因が足し合わさってできたものは、元の要因がどんな形であれ、最終的には正規分布に近づいていく」というものです。
患者さんの身長や血圧といった指標が、なぜ正規分布に近くなるのかを考えてみましょう。これらは、単一の要因で決まるのではなく、無数の遺伝的要因、生活習慣、環境要因といった、たくさんの小さな「偶然」が足し合わさった結果です。統計学の大家であるDeGrootとSchervishの著名な教科書でも論じられているように、中心極限定理によれば、こうしたプロセスから生まれる結果が、正規分布に従うのは、むしろ自然なことなのです(DeGroot and Schervish, 2012)。
ハーバード大学の公衆衛生学の教科書でも述べられているように、身長、体重、血圧といった多くの人体計測値は、健常者集団において正規分布に近い分布を示すことが知られています(Rosner, 2011)。この性質を利用することで、AIはデータの「正常範囲」を統計的に学習することができます。例えば、ある患者さんの検査値が、健常者集団の正規分布から見て、平均から標準偏差3つ分(3σ)も離れていたら、それは「統計的に極めて稀な、異常である可能性が高いイベント」としてフラグを立てることができるのです。これは、多くの異常検知AIの基本的な考え方になっています。
3. 0か1かの世界「ベルヌーイ分布と二項分布」— 二値的イベントをモデル化する
正規分布が連続的な計測値を扱ったのに対し、医療の世界では「Yes/No」「陽性/陰性」「奏効/非奏効」といった、二値的(バイナリ)な結果が極めて重要です。このような「0か1か」の世界を数学的に記述するための、シンプルで強力な分布が、ベルヌーイ分布と二項分布のペアです。
a) ベルヌーイ分布 (Bernoulli Distribution) — 「たった一度」のコイントス
ベルヌーイ分布は、「たった一度のコイントス」の結果をモデル化します。コインの表が出る確率を\(p\)とすれば、裏が出る確率は自動的に\(1-p\)に決まります。これだけです。非常にシンプルですよね。
この単純なモデルが、AIにとっては非常に重要です。例えば、AIがある画像を見て「悪性である確率 = 0.95」と出力したとします。これは、結果を1(悪性)と0(良性)に割り当てる確率変数\(X\)が従うベルヌーイ分布のパラメータ\(p\)を、AIが0.95だと予測した、ということに他なりません。
b) 二項分布 (Binomial Distribution) — 「何度も」繰り返されるコイントス
では、この「一度きりのコイントス(ベルヌーイ試行)」を、独立に何回も繰り返したらどうなるでしょうか。例えば、10人の患者さんに同じ治療を行う、というような状況です。
この「成功確率pのベルヌーイ試行をn回繰り返したときに、成功がk回起こる確率」を教えてくれるのが、二項分布です。
この確率は、以下の二項分布の確率質量関数で計算できます。
\[ P(X=k) = \binom{n}{k} p^k (1-p)^{n-k} \]
この式を分解してみましょう。
- \(\binom{n}{k}\) (コンビネーション): これは「n回中、どのk回で成功が起こるか」の組み合わせの数です。「n個の中からk個を選ぶ組み合わせ」ですね。
- \(p^k\): k回成功する確率です。(例:p × p × … をk回)
- \((1-p)^{n-k}\): 残りの (n-k)回が失敗する確率です。
つまり、この式は「(特定の成功パターンの確率)×(そのようなパターンが何通りあるか)」を計算しているわけです。
この分布は、臨床研究において極めて重要です。例えば、新薬の奏効率がプラセボの奏効率と比べて統計的に有意に高いかどうかを評価する際の「p値」の計算などに、二項分布の考え方が用いられます (Swinscow and Campbell, 2002)。
まとめ:データが従う「パターン」を数式で表現する
確率分布は、データがどのような値を、どのくらいの頻度でとりうるかを示す「設計図」です。
- 正規分布は、多くの生物学的指標が従う釣鐘型の分布で、平均と標準偏差で特徴づけられます。
- ベルヌーイ分布は単一の二値的結果を、二項分布はその繰り返し試行における成功回数をモデル化します。
AIは、これらの確率分布を「仮定」として用いることで、データの背後にある構造を学習します。例えば、生成モデルの一種である変分オートエンコーダ(VAE)は、データの本質的な特徴が正規分布に従うと仮定することで、新しいデータを生成することを可能にしています (Kingma and Welling, 2013)。
次回は、これらの分布を特徴づける、より具体的な統計量である「M0.4.4: 期待値、分散、共分散」について、その意味と計算方法を探求していきます。
参考文献
- (1) DeGroot, M.H. and Schervish, M.J. (2012) Probability and Statistics. 4th ed. Pearson.
- (2) Rosner, B. (2011) Fundamentals of Biostatistics. 7th ed. Cengage Learning.
- (3) Swinscow, T.D.V. and Campbell, M.J. (2002) Statistics at Square One. 10th ed. BMJ Books.
- (4) Kingma, D.P. and Welling, M. (2013) ‘Auto-Encoding Variational Bayes’, arXiv preprint arXiv:1312.6114.
- (5) Bishop, C.M. (2006) Pattern Recognition and Machine Learning. Springer.
- (6) Hastie, T., Tibshirani, R. and Friedman, J. (2009) The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd ed. Springer.
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






