TL; DR (要約)
AIは「似ている」をどう判断する? その答えは「距離」より「角度」にあり、それを測るのが内積です。
このシンプルな計算が、AIに「意味」を教えるEmbedding技術の核心です。
① 内積
(「角度」を測る道具)
2つのベクトルがどれだけ「同じ方向を向いているか」を測る計算。データの大きさ(強弱)ではなく、パターンの類似性を捉えます。
② コサイン類似度
(類似性のスコア化)
内積から計算される「角度」の指標。スコアが1に近いほど「似ている」、0なら「無関係」、-1なら「正反対」と評価できます。
③ Embedding
(意味の地図作り)
単語や患者を「意味」を表すベクトルに変換。意味が近いほどコサイン類似度が高くなるよう、AIが自動で配置します。
前回の探検で、私たちは患者さん一人ひとりや、医療で使われる一つ一つの単語を、高次元空間に浮かぶユニークな「星(ベクトル)」としてプロットする方法を学びましたね。これで、AIの「目」には、無数の星々が輝く広大な宇宙が見えている状態です。
では、ここからが本題です。この星空を眺めながら、AIは一体どうやって「あの星とこの星は、同じような輝きを持つ”兄弟星”だ」とか、「この星の集団は”特定の疾患を持つ星団”を形成している」といった、星々の関係性を見抜いているのでしょうか?
人間の目にはただの点の集まりにしか見えないかもしれないこの空間で、「似ている」という、曖昧で人間的な感覚をどうやって数値化しているのか。気になりませんか?
今回の旅では、この「似ている」という概念を、内積(Inner Product)という、一見地味ながらも非常にパワフルな計算を通じて、具体的な「類似度スコア」として捉える方法を探求します。この内積という道具が、星と星の間の「角度」を測るための、驚くほど便利な分度器として機能する様子を見ていきます。
さらに、この考え方が、現代AIの根幹をなすEmbedding(エンベディング)という、「意味」の宇宙を設計する壮大な技術にどう繋がっているのか、その世界の扉を一緒に開けていきましょう。
1. 「似ている」をどう測るか? — 単純な「距離」から、本質的な「角度」へ
高次元空間に浮かぶ、たくさんの「星(ベクトル)」たち。これらのうち、どれとどれが「似ている」のかを、コンピュータにどうやって教えればいいのでしょうか。
最も素朴で、誰もが最初に思いつく方法は、おそらく2つの星の間の「物理的な近さ」、つまりユークリッド距離を測ることでしょう。確かに、空間上で近くにいる星同士は、似ている可能性が高そうですよね。これは多くの場合で有効な、とても直感的なアプローチです。
しかし、この「距離」という“ものさし”だけでは、時としてデータの本質を見誤ってしまうことがあります。
「距離」だけでは見抜けない、隠れた関係性
例えば、2つの薬剤(AとB)に対する、ある遺伝子群の発現パターンの変化をベクトルで表現したとします。薬剤Aは低用量、薬剤Bは高用量で投与したとしましょう。
【図の解説】
上の図を見てみてください。
- 薬剤Aと薬剤B: どちらも遺伝子1と遺伝子2を同じような比率で増加させています。作用の「プロファイル」はそっくりです。ただ、高用量である薬剤Bの方が、その効果の大きさ(ベクトルの長さ)が大きくなっています。
- 薬剤C: 全く違う作用プロファイルを示しています。
この状況を、2つの異なる“ものさし”で測ってみると、どうなるでしょう。
- ケース1:「距離」で測る
薬剤Aから見ると、物理的な距離は薬剤Cの方が薬剤Bよりも「近い」ですね。もし「距離が近いほど似ている」と判断するなら、「薬剤AとCは似ている」という、私たちの医学的な直感とはズレた結論が出てしまいかねません。 - ケース2:「角度」で測る
ここで、ベクトルの長さ(この例では薬剤の効果の大きさ)を一旦無視して、純粋に作用の方向性だけに着目するのです。すると、薬剤AとBの間の角度は非常に小さい(ほぼ0度)ことがわかります。一方で、薬剤AとCの間の角度は大きく、90度に近い。この“ものさし”なら、「薬剤AとBは、作用のメカニズムが非常に似ている」という本質を、見事に捉えることができます。
「角度」という、新しい“ものさし”
このように、ベクトルの「角度」を測ることは、大きさ(magnitude)の影響を排除し、データの持つパターンや傾向、つまり「プロファイル」そのものの類似性を評価するのに、非常に強力な方法なのです。
AIの世界では、「レコメンドエンジン」がこの考え方をよく使います。例えば、映画をたくさん見ているヘビーユーザー(長いベクトル)と、数本しか見ていないライトユーザー(短いベクトル)がいたとします。二人の距離は遠いかもしれませんが、見ている映画の「好み(ジャンルの方向性)」が似ていれば、角度は小さくなります。AIはこれを見て、「この二人は好みが似ているから、ヘビーユーザーが見た別の映画を、ライトユーザーにも推薦しよう」と考えるわけです。
では、この重要な「角度」を、どうやって計算すれば良いのでしょうか。その鍵となるのが、次にお話しする内積です。
2. 内積 (Inner Product) — 2つのベクトルの「対話」から角度を求める
前のセクションで、ベクトルの「角度」こそが、データの大きさの影響を受けない、本質的な類似度を測るための優れた“ものさし”だという話になりましたね。では、いよいよその「角度」を計算するための、シンプルで美しい道具、内積(Inner Product)の登場です。
内積は、しばしば「ドット積(dot product)」とも呼ばれ、2つのベクトルがどれだけ「同じ方向を向いているか」を数値化する、いわばベクトル同士の「対話」のようなものです。
内積の計算方法:驚くほどシンプル
まず、内積の計算ルールを見てみましょう。これは拍子抜けするほど簡単です。
2つのベクトル \(\vec{a} = (a_1, a_2, \dots)\) と \(\vec{b} = (b_1, b_2, \dots)\) があるとき、その内積 \(\vec{a} \cdot \vec{b}\) は、対応する要素同士をそれぞれ掛け算して、その結果を最後に全て足し合わせるだけです。
数式で一般的に書くと、こうなります。
\[\vec{a} \cdot \vec{b} = a_1b_1 + a_2b_2 + \dots + a_nb_n = \sum_{i=1}^{n} a_i b_i\]
内積の幾何学的な意味:「影」と「長さ」の掛け算
さて、この「掛けて足す」だけの地味な計算結果。これだけ見ても、正直なところ何のことだかさっぱり分かりませんよね。しかし、この内積には、実は深い幾何学的な意味が隠されています。これこそが、内積の最も美しい側面です。
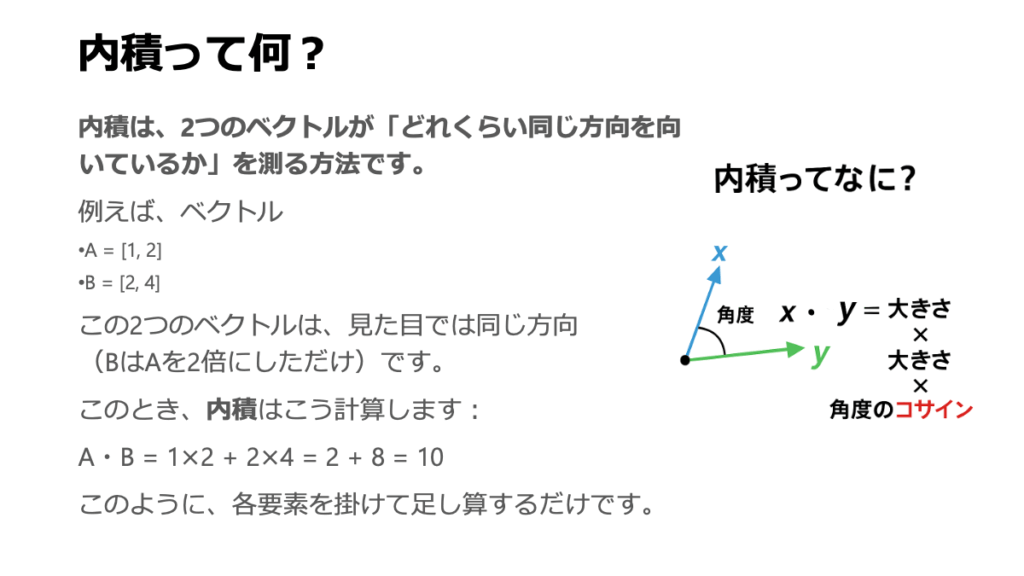
内積が何を計算しているかというと、実は「片方のベクトルを、もう片方のベクトルに投影したときの『影』の長さ」と、「投影された側のベクトルの長さ」を掛け合わせたものなのです。
図で言うと、ベクトル\(\vec{a}\)の先端からベクトル\(\vec{b}\)の方向へ垂線を下ろし、その「影」の長さを測ります。この影の長さは、三角関数を使うと \(\|\vec{a}\| \cos(\theta)\) と表せます。そして、この「影の長さ」に、影が落ちている地面であるベクトル\(\vec{b}\)の長さ \(\|\vec{b}\|\) を掛け合わせる。
この \( (\|\vec{a}\| \cos(\theta)) \times \|\vec{b}\| \) という計算結果が、不思議なことに、先ほどの地味な代数計算 \(a_1b_1 + a_2b_2 + \dots\) の結果と、常にピッタリ一致するのです。数式で書くと、以下のようになります。
\[\vec{a} \cdot \vec{b} = \|\vec{a}\| \|\vec{b}\| \cos(\theta)\]
角度を求める「コサイン類似度」の導出
これで、2つの異なる側面から内積を眺めることができました。一つは「代数的な計算」、もう一つは「幾何学的な意味」。そして、この2つの定義は、当然ながら等しくなります。この等式こそが、私たちが欲しかった「角度」への扉を開けてくれます。
上の式を、\(\cos(\theta)\) について解くように、少しだけ並べ替えてみましょう。
\[\cos(\theta) = \frac{\vec{a} \cdot \vec{b}}{\|\vec{a}\| \|\vec{b}\|}\]
見てください。左辺は私たちが知りたかった「角度の情報(コサイン)」。右辺は、私たちが簡単に計算できるものばかりです。分子の「内積」は対応する要素を掛けて足すだけ。分母の「ベクトルの長さ」も三平方の定理で計算できます。
こうして、私たちは2つのベクトルさえあれば、その間の角度(のコサイン)、すなわちコサイン類似度 (Cosine Similarity) をいつでも計算できるようになったのです。
- \(\cos(\theta) = 1\) (\(\theta=0^\circ\)): 2つのベクトルは全く同じ方向を向いており、最も似ている。
- \(\cos(\theta) = 0\) (\(\theta=90^\circ\)): 2つのベクトルは直交しており、関連性がない。
- \(\cos(\theta) = -1\) (\(\theta=180^\circ\)): 2つのベクトルは正反対の方向を向いており、最も似ていない。
内積は、シンプルな代数計算と、データの「意味」を解釈する上で重要な幾何学的性質とを結びつける、非常に強力な「橋渡し」の役割を果たしているのです。
3. Embedding — 「意味」の空間に、データをマッピングする技術
さて、内積とコサイン類似度という、ベクトル同士の「角度」を測る強力な道具が手に入りました。ここからが、いよいよ現代AIの最もエキサイティングな領域、Embedding(エンベディング、埋め込み)の世界です。これは、これまで学んできたベクトルや類似度の考え方を総動員して、AIに「意味」そのものを学習させる、という壮大な試みだと言えるかもしれません。
Embeddingとは何か?
Embeddingとは、一言でいえば、本来はただの記号やIDでしかないモノ(例えば「心筋梗塞」という単語や、「患者ID-007」など)を、そのモノが持つ豊かな意味を表現する、高次元空間の「一点(ベクトル)」に変換する技術、あるいはそのベクトルそのものを指します。
重要なのは、このベクトル(座標)は、人間が手作業で決めるのではない、という点です。
この技術の核心は、AIモデル(ニューラルネットワーク)を訓練して、元の世界で「意味的に似ている」オブジェクト同士が、ベクトル空間内でも「近くに(=コサイン類似度が高く)配置される」ように、ベクトルの値を自動で調整させる点にあります。
どうやって「意味」を学習するのか?
この「意味の地図作り」のプロセスを、医療言語モデルを例に考えてみましょう。
- スタート地点(無秩序な宇宙):
最初は、全ての医療用語(「高血圧」「心不全」「インスリン」…)は、ベクトル空間の中にランダムに、無秩序にばら撒かれています。この時点では、「高血圧」の隣に「骨折」があるような、意味のない状態です。 - 文脈からの学習:
ここからAIの学習が始まります。AIは、何百万もの医療論文や電子カルテといった膨大なテキストデータを読み込み、「”心筋梗塞”という単語の近くには、”虚血”や”冠動脈”という単語がよく現れるな」という文脈上の共起関係をひたすら学習していきます。 - ベクトルの座標調整:
そして、「文脈が似ている単語は、意味も似ているはずだ」という仮説のもと、文脈が似ている単語のベクトル同士が、意味の地図の上で互いに引き寄せ合うように、ベクトルの座標を少しずつ、何億回となく調整していくのです。
この果てしない調整作業の末に、意味の地図は再編成され、関連する概念が自然と集まる「意味の空間」が出来上がります。
学習後の「意味の空間」を覗いてみると、上図のように、関連する概念が近くに集まっているのがわかります。AIは、もはや単語を単なる記号としてではなく、この空間内の座標、つまり「意味」として扱えるようになったのです。そして、私たちは2つの単語ベクトルのコサイン類似度を計算するだけで、その「意味の近さ」を定量的に評価できます。
イメージ
医療におけるEmbeddingの応用
- 医療言語モデルへの応用:
この技術によって、AIは電子カルテの自由記述欄から「この患者は心不全のリスクが高い」といった臨床的な洞察を得たり、膨大な医療文献から特定の治療法に関する論文を意味的に検索したりすることが可能になります。「”高血圧” AND “新規治療薬”」といったキーワード検索ではなく、「”ACE阻害薬に不応だった高齢高血圧患者向けの、次の選択肢”に関連する論文」といった、意味に基づいた検索が実現するのです。 - 患者の層別化への応用:
同じように、患者さん一人ひとりも、その検査値、治療歴、処方薬といった膨大な情報から、一意の「患者Embeddingベクトル」として表現できます。すると、似たようなベクトルを持つ患者(つまり、似たような臨床的プロファイルを持つ患者)は、未知の疾患の早期発見や、新薬の臨床試験における最適な被験者グループの選定(患者層別化)など、個別化医療を加速させるための強力なツールとなるのです。
4. Pythonで類似度を計算する — ベクトルの「角度」を測ってみる
理論を学んだところで、いよいよ手を動かしてみましょう。架空の医療概念のベクトルを作り、それらの間のコサイン類似度を実際に計算してみます。数式で見た内積やベクトルの長さが、コード上ではどのように表現され、そして最終的に「類似度」という一つの数値に結実するのか、そのプロセスを一緒に体験していきましょう。
Step 1: 道具の準備(コサイン類似度を計算する関数)
まず、どんなベクトルがきてもコサイン類似度を計算してくれる、便利な「道具」としての関数をPythonで準備します。この関数は、前のセクションで学んだコサイン類似度の定義式を、そのままコードに翻訳したものです。
再掲:コサイン類似度の定義式
\[\cos(\theta) = \frac{\vec{a} \cdot \vec{b}}{\|\vec{a}\| \|\vec{b}\|}\]
# 数値計算ライブラリNumPyをインポートします
import numpy as np
def cosine_similarity(v1, v2):
"""
2つのベクトル間のコサイン類似度を計算します。
cos(theta) = (v1・v2) / (||v1|| * ||v2||)
"""
# (A) 分子:v1とv2の内積を計算
dot_product = np.dot(v1, v2)
# (B) 分母:各ベクトルの大きさ(L2ノルム)を計算
norm_v1 = np.linalg.norm(v1)
norm_v2 = np.linalg.norm(v2)
# (C) 定義式に従って割り算を実行
similarity = dot_product / (norm_v1 * norm_v2)
return similarity
【関数の中身を覗いてみよう】
この関数の中では、3つのステップが実行されています。
- (A)
np.dot(v1, v2): これが、分子の内積 \(\vec{a} \cdot \vec{b}\) を計算している部分です。NumPyのdot関数は、まさしくこの計算を行ってくれます。 - (B)
np.linalg.norm(v): これは、分母のベクトルの長さ \(\|\vec{v}\|\) を計算しています。linalgは線形代数(Linear Algebra)の略で、normはベクトルの大きさ(ノルム)を求める、という意味です。 - (C)
dot_product / (norm_v1 * norm_v2): 最後に、定義式通りに内積を長さの積で割り算して、最終的なコサイン類似度を返します。
Step 2: ベクトルの定義と類似度の計算
次に、この関数を使って、いくつかの医療概念の類似度を測ってみましょう。ここでは、簡単のために3次元のベクトルを考え、「循環器系の度合い」「骨格系の度合い」「症状の緊急性」という3つの軸で、各概念を無理やり表現してみます。本来、こうしたベクトルはAIが大量のデータから学習して獲得するものですが、今回はその気持ちを味わうための、手作りのベクトルです。
# 3つの医療概念を表す、仮のベクトルを定義
# [循環器系, 骨格系, 緊急性] という3次元で表現
heart_attack = np.array([0.9, 0.1, 0.9]) # 心筋梗塞
cardiac_arrest = np.array([0.8, 0.1, 1.0]) # 心停止
broken_bone = np.array([0.1, 0.9, 0.5]) # 骨折
# --- 類似度の計算 ---
# 「心筋梗塞」と「心停止」の類似度
sim_1_2 = cosine_similarity(heart_attack, cardiac_arrest)
print(f"「心筋梗塞」と「心停止」のコサイン類似度: {sim_1_2:.4f}")
# 「心筋梗塞」と「骨折」の類似度
sim_1_3 = cosine_similarity(heart_attack, broken_bone)
print(f"「心筋梗塞」と「骨折」のコサイン類似度: {sim_1_3:.4f}")
Step 3: 結果の考察と可視化
【計算結果】
「心筋梗塞」と「心停止」のコサイン類似度: 0.9852
「心筋梗塞」と「骨折」のコサイン類似度: 0.4495
【考察】
計算結果を見ると、私たちの直感通り、「心筋梗塞」と「心停止」の類似度は非常に高く(1に近い)、一方で「心筋梗塞」と「骨折」の類似度は低い値になっていることが確認できます。これは、ベクトルが持つ方向性が、概念の類似性をうまく捉えられていることを示しています。
数字だけだと、いまいちピンとこないかもしれませんね。そこで、これらのベクトルが3次元空間の中で、実際にどのような位置関係にあるのか、グラフで可視化してみましょう。そうすれば、コサイン類似度の値が「角度」を反映していることが一目でわかるはずです。
【実行前の準備】
以下のコードで日本語のグラフを表示させるには、あらかじめターミナルやコマンドプロンプトで pip install japanize-matplotlib を実行してライブラリをインストールしてください。
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import japanize_matplotlib
# 前のコードブロックのベクトル定義を再度記述
heart_attack = np.array([0.9, 0.1, 0.9])
cardiac_arrest = np.array([0.8, 0.1, 1.0])
broken_bone = np.array([0.1, 0.9, 0.5])
# --- 3Dグラフでベクトルを可視化 ---
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# ベクトルを描画 (quiver)
# quiver(始点x,y,z, 方向x,y,z, ...)
ax.quiver(0, 0, 0, heart_attack[0], heart_attack[1], heart_attack[2],
color='red', arrow_length_ratio=0.1, label='心筋梗塞')
ax.quiver(0, 0, 0, cardiac_arrest[0], cardiac_arrest[1], cardiac_arrest[2],
color='magenta', arrow_length_ratio=0.1, label='心停止')
ax.quiver(0, 0, 0, broken_bone[0], broken_bone[1], broken_bone[2],
color='blue', arrow_length_ratio=0.1, label='骨折')
# グラフの見た目を設定
ax.set_xlim([0, 1])
ax.set_ylim([0, 1])
ax.set_zlim([0, 1])
ax.set_xlabel('循環器系の度合い')
ax.set_ylabel('骨格系の度合い')
ax.set_zlabel('症状の緊急性')
ax.set_title('医療概念ベクトルの3D空間における可視化')
ax.legend()
ax.view_init(elev=20, azim=30) # 見やすい角度に調整
plt.show()
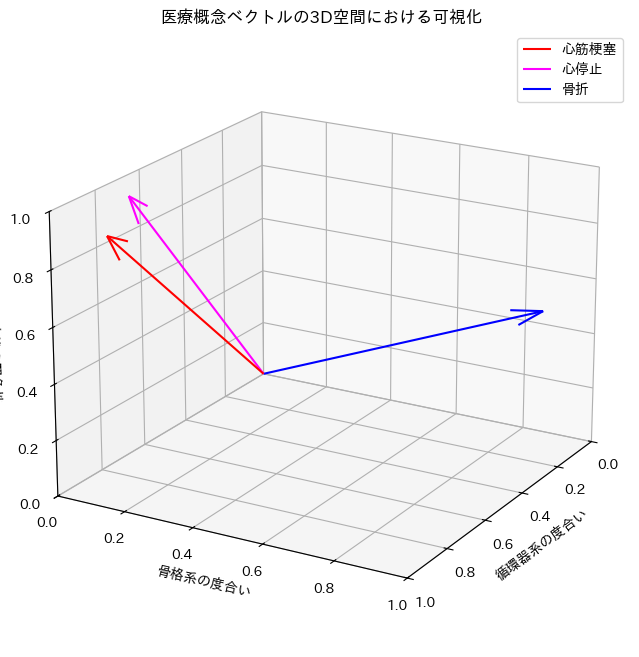
この3Dグラフを見ると、「心筋梗塞」と「心停止」のベクトルは、非常によく似た方向を向いており、なす角度が小さいことが分かります。一方で、「骨折」のベクトルは全く違う方向を向いているため、他の2つのベクトルとの角度は大きく、コサイン類似度も低い値になっているのです。
このように、理論をコードで実装し、その結果を可視化して確かめる、というサイクルは、AIやデータサイエンスの理解を深める上で非常に有効なアプローチだと思います。
まとめ:「意味」を測る、数学の“ものさし”
- 内積は、ベクトルの角度に関する情報を含んでおり、2つのベクトルの関係性を測るための重要な計算です。
- コサイン類似度は、内積を用いて計算され、ベクトルの大きさに関わらず、純粋なパターンの類似性を-1から1の間の数値で示します。
- Embeddingは、単語や患者といったオブジェクトを、意味的な類似性がベクトル間のコサイン類似度として反映されるようなベクトルに変換するAI技術です。
内積というシンプルな計算が、AIに「意味」を理解させるための強力な“ものさし”を与えているのです。この考え方は、類似症例の検索、医療文献の分類、個別化治療の推奨など、医療AIの様々な応用の中核をなしています。
さて、これまではデータをどう表現し(ベクトル)、どう比較するか(内積)を見てきました。次回、第4回「『微分』と『勾配』って何がすごいの? — 学習のエネルギー源」からは、いよいよAIが自ら賢くなるための「学習」のメカニズム、その原動力である微分と勾配の世界に足を踏み入れます。
参考文献
- Mikolov T, Sutskever I, Chen K, Corrado GS, Dean J. Distributed representations of words and phrases and their compositionality. In: Proceedings of the 26th International Conference on Neural Information Processing Systems. 2013; p. 3111–3119.
- Strang G. Introduction to Linear Algebra. 5th ed. Wellesley, MA: Wellesley-Cambridge Press; 2016. Chapter 1.
- Jurafsky D, Martin JH. Speech and Language Processing. 3rd ed. draft. 2023. Chapter 6, Vector Semantics and Embeddings.
- Choi E, Bahadori MT, Searles E, Coffey C, Thompson M, Bostjancic J, et al. Multi-layer representation learning for medical concepts. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2016; p. 1495–1504.
- Goldberg Y, Levy O. word2vec Explained: deriving Mikolov et al.’s negative-sampling word-embedding method. arXiv preprint arXiv:1402.3722. 2014.
- Deisenroth MP, Faisal AA, Ong CS. Mathematics for Machine Learning. Cambridge, UK: Cambridge University Press; 2020. Chapter 3.
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






