この記事では、AIがデータをどのように「見て」いるかを解説します。数値の羅列である「ベクトル」がデータに意味のある住所を与え、「行列」がそのデータを有益な情報へと変換する、この2つの強力なツールの役割と、実際の応用例を掴みましょう。
患者データのような数値の集まりを、空間内の「点」として捉えます。点同士の「距離」を計算することで、AIはデータの類似性やグループ(例:高リスク群)を直感的に判断します。
行列は、データの「器」であると同時に、入力ベクトルを別のベクトルに変換する「変換器」です。AIは、この変換ルール(重み)を学習し、リスクスコア計算や画像の特徴抽出などを行います。
PythonのNumPyライブラリでベクトルや行列を効率的に操作できます。この技術は、電子カルテ解析、医用画像診断(テンソル)、単語の意味を捉える自然言語処理の基盤となります。
前回は、AIの思考を支える「3種の神器」として、大きな数学の地図を広げてみましたね。その冒険の始まりとして、今回は最初の神器である「線形代数」の世界に、一歩深く足を踏み入れてみたいと思います。
線形代数と聞くと、もしかしたら少し身構えてしまう方もいるかもしれません。ですが、その主役であるベクトルと行列は、AIがこの世界を「見る」ための「目」そのものなんです。私たちが患者さんを診るとき、その表情や検査データ、言葉の端々から全体像を掴もうとするように、AIはこのベクトルと行列という「目」を通して、無機質な数字の羅列から意味を読み取ろうとします。
この記事では、そんなAIの「視点」を、皆さんと一緒に体験していきたいと思っています。単なる“数のカタマリ”が、どうやって一人の患者さんの物語になり、一枚の医療画像になり、さらには言葉のニュアンスさえも表現できるようになるのか。その仕組みを解き明かしながら、最後にはPythonを使って、ご自身の手でこのパワフルなツールを動かしてみましょう。きっと、AIがぐっと身近な存在に感じられるはずです。
ベクトル:高次元空間に浮かぶ「点」としての患者
前回、患者さんのデータを整理して「デジタルカルテ」である行列にまとめる、というお話をしました。そのカルテの「一行一行」にあたるのが、今回主役となるベクトルです。
まずはシンプルに、ある患者さんのデータが4つの検査項目で構成されていると考えてみましょう。
- 年齢:58歳
- BMI:22.5
- 収縮期血圧:130 mmHg
- HbA1c:6.5 %
AIにとってこの情報は、[58, 22.5, 130, 6.5]という、ただの数字が並んだリストに見えます。これが「ベクトル」の正体です。しかし、この見方だけでは、少しもったいない。AIの可能性を広げるには、もう一歩進んだイメージを持つことが大切です。
そのイメージとは、このベクトルを「高次元空間に浮かぶ、たった一つの『点』」として捉えることです。
言葉だけだとピンと来ないかもしれませんね。もちろん、4次元や50次元の空間を私たちが紙に描くことはできません。でも、大丈夫。本質的な考え方は、私たちがよく知っている2次元のグラフと全く同じなのです。試しに、先ほどのデータから「BMI」と「収縮期血圧」の2つだけを取り出して、グラフにプロットしてみましょう。
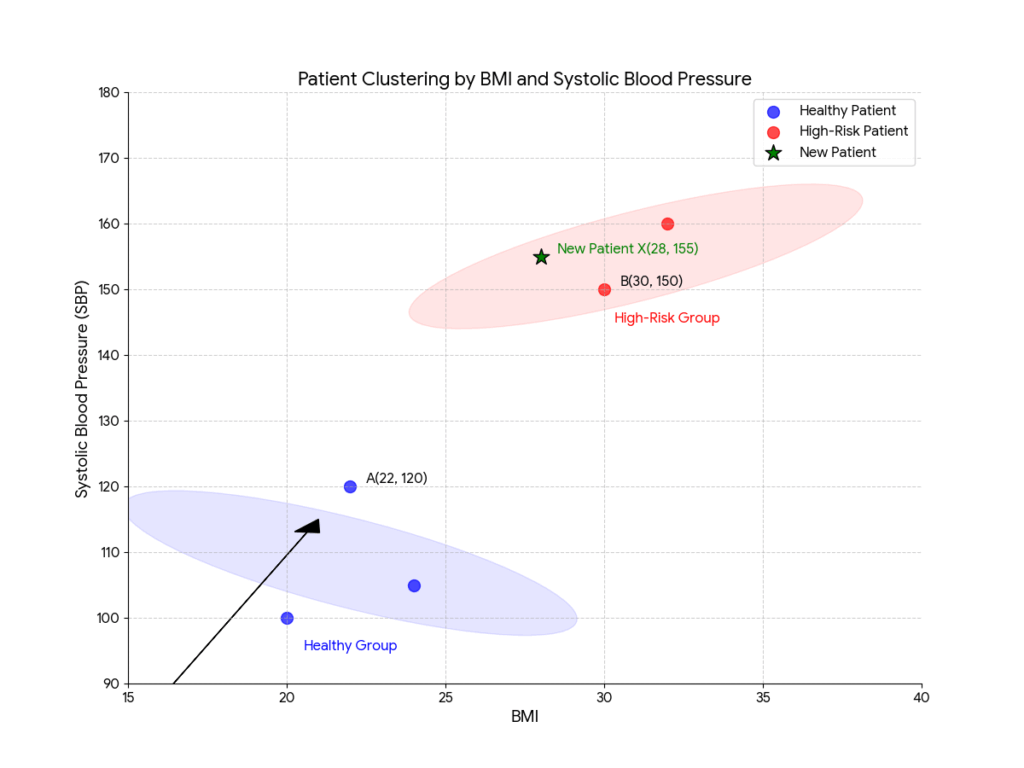
この図を見ると、いろんなことが想像できませんか?
- 患者Aさん(BMI 22, SBP 120)と、その近くにいる患者さんたちは、なんとなく「健常群」を形成しているように見えます。
- 一方、患者Bさん(BMI 30, SBP 150)の周りには「高リスク群」がいそうです。
- このグラフの原点(0, 0)から患者Aさんに向かって伸びる矢印、これこそがベクトル
[22, 120]の幾何学的なイメージです。ベクトルの正体は、空間内の一点の「位置」を示す矢印、あるいはその「点の座標」そのものなのです。
では、ここに新しい患者Xさん(BMI 28, SBP 155)が来院したとします。その点をプロットすると、目で見ただけで「この方は高リスク群に近いな」と直感的に判断できますよね。AIが行っているのも、本質的にはこれと同じことです。
この「近さ」を、AIはユークリッド距離という、私たちにも馴染み深い計算で数値化します。名前は少し難しそうですが、中身は中学校で習った三平方の定理の応用です。2点A(\(x_A, y_A\))とX(\(x_X, y_X\))の間の距離 \(d\) は、以下の式で計算できます。
\[ d(A, X) = \sqrt{(x_X – x_A)^2 + (y_X – y_A)^2} \]
この式が何をしているか、一つずつ見てみましょう。
- \( (x_X – x_A) \): 2点間の「横方向の距離」(BMIの差)
- \( (y_X – y_A) \): 2点間の「縦方向の距離」(血圧の差)
- \( (\dots)^2 \): それぞれを2乗して、距離がマイナスにならないようにし、大きな差をより重視する効果も生みます。
- \( \sqrt{\dots} \): 最後に平方根を取ることで、単位を元のスケール(BMIや血圧のスケール)に戻しています。
驚くべきことに、このシンプルな式は、データが50項目(50次元)になっても全く同じように拡張できます。2乗の項を50個足し算して、最後に平方根を取るだけです。人間には想像もつかない高次元空間でも、コンピューターは瞬時に2点間の「距離」を計算し、「どちらのグループにより近いか」を判断できるのです。
このように、ベクトルとは単なる数字の入れ物ではなく、高次元空間におけるデータの「意味のある住所」を定義してくれる、非常にパワフルな概念なのです。この「距離」という考え方が、後の回で学ぶ様々なAIアルゴリズムの基礎になっていきます。
行列:データの集合体、そして万能な「変換器」
先ほど、一人の患者さんを「ベクトル」という空間上の一点として捉えましたね。では、その患者さんたちが100人集まったらどうなるでしょう?答えはシンプルで、100人分のベクトルをただ積み重ねるだけ。そうして出来上がった、まさしく「デジタルなカルテの束」こそが行列です。これが、行列が持つ一つ目の顔、データを格納する「器」としての役割です。
でも、行列の本当の面白さは、ここから始まります。単なるデータの入れ物という静的な役割だけでなく、行列には、入力されたデータを別のデータに「変換」する、動的な役割があるんです。
これが、行列の二つ目の顔、万能な「変換器」(Transformer / Operator)としての姿です。
入力されたベクトルに行列を掛けると、そのベクトルは拡大されたり、縮小されたり、回転したり、時には全く別の次元のベクトルに姿を変えたりします。この「変換」の仕組みを、簡単な例で覗いてみましょう。
患者さんの特徴を2つだけ(例えば、LDLコレステロール値と、拡張期血圧)に絞ったベクトルがあるとします。このベクトルを行列に掛けて、「心疾患リスクスコア」と「脳血管疾患リスクスコア」という、2つの新しい特徴を持つベクトルに変換する場面を想像してください。
この図が、行列による「変換」の心臓部です。
- 出力の1行目(心疾患スコア)の計算:
変換行列の1行目[a, b]が、心疾患スコアを計算するための「レシピ」になります。これは「入力ベクトルの1つ目(LDL値)をa倍して、2つ目(eDBP値)をb倍したものを足し合わせなさい」という命令です。結果は \(ax + by\) となります。 - 出力の2行目(脳血管スコア)の計算:
同様に、変換行列の2行目[c, d]が脳血管スコアのレシピです。「LDL値をc倍、eDBP値をd倍して足し合わせなさい」となり、結果は \(cx + dy\) となります。
数式でまとめると、この変換は次のようになります。
\[ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} ax + by \\ cx + dy \end{pmatrix} \]
そして、AIの「学習」の凄みは、この a, b, c, d という変換レシピの数字(重みやパラメータと呼ばれます)を、大量のデータから自動で見つけ出してくれる点にあります。最も精度の高い予測ができる、魔法のような「変換行列」を自力で作り上げてしまうのです。
この「変換」という考え方は、医療画像の世界では特にパワフルです。CT画像はピクセル輝度値の巨大な行列ですよね。この画像行列に対して、「輪郭抽出」のレシピが書き込まれた小さな行列(カーネルやフィルタと呼ばれます)を作用させると、変換後の画像では輪郭だけがくっきりと浮かび上がります。
AIは、このカーネルの中の数字を学習することで、「腫瘍の境界」や「微小な骨折線」といった、診断に重要な特定の特徴を抽出する専門の「目」を獲得していくのです。
このように、行列は単なるデータの入れ物ではなく、データに特定の操作を加えて、より有益な情報へと姿を変えさせる、ダイナミックな「変換器」なのです。この二面性を理解することが、現代AIの仕組みを掴む上で、とても大切な鍵となります。
Python (NumPy)でベクトルと行列を操る
さて、ここまではベクトルや行列が持つ「意味」や「役割」といった、少し概念的な話が中心でした。ここからは、いよいよ実際に手と頭を動かして、AIの「視点」をコードで実装してみましょう。理論と実践が結びつくと、理解は一気に深まるはずです。
PythonでAIやデータサイエンスを扱う際、ほぼ必ずと言っていいほど登場するのが、NumPy(ナンパイ)というライブラリです。これは、ベクトルや行列といった「数字のカタマリ」を、驚くほど高速かつ直感的に扱うために作られた、まさに縁の下の力持ちのような存在です。
なぜ標準のPythonリストではなくNumPyを使うのか、というと、理由は大きく2つあります。一つは圧倒的な計算速度。NumPyの内部はC言語のような高速な言語で書かれているため、大量の数値計算を非常に速くこなせます。もう一つは、計算の記述がシンプルになる利便性です。これから見ていくように、forループで一つずつ処理するような計算を、たった一行で、しかも人間が数式を眺めるのに近い感覚で書けてしまいます。
準備:
もしご自身の環境にNumPyがインストールされていない場合は、一度だけ、ターミナルやコマンドプロンプトで以下のコマンドを実行してください。pip install numpy
例1:ベクトルと行列を作ってみる
まずは、理論編で登場した「患者さんのデータ」を、NumPyを使ってベクトルと行列の形で表現してみましょう。
# NumPyライブラリをインポートし、慣例として「np」という短い別名を付けます
import numpy as np
# 患者1人(年齢, BMI, 収縮期血圧)のデータからベクトルを作成します
# Pythonのリスト [58, 22.5, 130] を np.array() に渡すだけです
patient_vector = np.array([58, 22.5, 130])
print("--- 1人の患者さんのベクトル ---")
print(patient_vector)
# .shape は配列の「形状」を、.ndim は「次元数」を教えてくれます
print(f"形状: {patient_vector.shape}, 次元数: {patient_vector.ndim}次元")
print("\n")
# 3人分の患者データから行列を作成します
# リストの中にリストを入れることで、2次元の配列(行列)になります
patient_matrix = np.array([
[58, 22.5, 130], # 患者1のベクトル
[45, 25.1, 115], # 患者2のベクトル
[72, 21.0, 142] # 患者3のベクトル
])
print("--- 3人分の患者さんの行列 ---")
print(patient_matrix)
print(f"形状: {patient_matrix.shape}, 次元数: {patient_matrix.ndim}次元")
--- 全員のBMIデータだけを抽出 ---
[22.5 25.1 21. ]
平均BMI: 22.87このコードのポイントを少しだけ解説します。np.array() が、Pythonの普通のリストを、計算に強いNumPy配列へと「変身」させる魔法の呪文です。
そして、出力に出てきた .shape は、配列の「設計図」のようなものです。
(3,)は「1次元方向に要素が3つ並んでいる」という意味で、まさにベクトルですね。(3, 3)は「最初の次元(行)に3つ、次の次元(列)に3つ要素が並んでいる」という意味で、3行3列の行列であることを示しています。
例2:データの一部を切り出す(スライシング)
行列の中から、欲しい部分だけを的確に取り出す操作は非常に重要です。例えば、「全員のBMIのデータだけが欲しい」という場合、NumPyなら驚くほど簡単です。
# patient_matrixは、例1で作成したものをそのまま使います
import numpy as np
patient_matrix = np.array([
[58, 22.5, 130],
[45, 25.1, 115],
[72, 21.0, 142]
])
# 行列から「全行(:)の、インデックス1の列(2列目)」を切り出します
# これが3人全員のBMIデータ(ベクトル)になります
bmi_vector = patient_matrix[:, 1]
print("--- 全員のBMIデータだけを抽出 ---")
print(bmi_vector)
# 切り出したデータを使って、一気に平均値を計算します
average_bmi = np.mean(bmi_vector)
print(f"\n平均BMI: {average_bmi:.2f}")
この patient_matrix[:, 1] という書き方が、NumPyの強力さを象徴しています。これは「スライシング」と呼ばれ、次のような意味を持っています。
patient_matrix [ 行の指定 , 列の指定 ]
↓ ↓
[:] [1]
↓ ↓
「全ての行」 「インデックス1(2番目)の列」
[ 年齢, BMI, 血圧 ]
┌─────────────────────┐
│ 58, [22.5], 130 │
│ 45, [25.1], 115 │
│ 72, [21.0], 142 │
└─────────────────────┘
↓
[22.5, 25.1, 21.0] <- このベクトルが取り出される
もしこれが普通のPythonリストなら、forループを回して一行ずつ、2番目の要素を取り出して…という少し面倒な処理が必要です。NumPyなら、このようにたった一行で、やりたいことを直感的に表現できる。この感覚、なかなか気持ち良いと思いませんか?
例3:行列を「変換器」として使ってみる(内積)
最後に、理論編で学んだ「行列を変換器として使う」アイデアを、コードで実践してみましょう。各検査項目に「重要度(重み)」を掛けて、一人ひとりの「総合リスクスコア」を計算する、あの処理です。
# 例1で作成した3人分の患者行列
import numpy as np
patient_matrix = np.array([
[58, 22.5, 130],
[45, 25.1, 115],
[72, 21.0, 142]
])
# 各項目(年齢, BMI, 血圧)に対する「重要度(重み)」をベクトルで定義します
# この重みの値は、本来はAIが学習して見つけ出します
weights = np.array([0.2, 0.5, 0.3]) # 年齢の重み0.2, BMIの重み0.5, ...
# 行列とベクトルの「内積」を計算します
# これで3人分のスコアが一気に計算されます
# @ はNumPy 1.10以降で使える内積の演算子で、np.dot()と同じです
risk_scores = patient_matrix @ weights
print("--- 各患者の総合リスクスコア ---")
print(risk_scores)
--- 各患者の総合リスクスコア ---
[61.85 56.05 67.5 ]この patient_matrix @ weights という一行が、まさに「変換」の瞬間です。@ 演算子は内積(dot product)を計算せよ、という命令で、裏側では次のような計算が3人分、一気に行われています。
3人分の患者データ(3×3行列)が、重みベクトル(3要素ベクトル)によって変換され、3人分のリスクスコア(3要素ベクトル)という、全く新しい意味を持つデータに生まれ変わりました。
このように、NumPyを使えば、複雑に見える行列計算も、数式のようにシンプルに記述し、効率的に実行できます。この「ベクトルや行列をカタマリとして一気に操作する」という考え方は、この先のAIプログラミングのあらゆる場面で登場する、基本かつ最も重要な作法なのです。
医療応用:カルテから言語、そして画像へ
さて、ここまで学んできたベクトルや行列という、少し抽象的にも思える道具が、実際の医療現場でどのように息づき、未来を変えようとしているのか。その最前線を、3つの領域に分けて少し覗いてみることにしましょう。
1. 電子カルテ・ゲノム解析:数万人の「デジタル症例集団」を読み解く
研究や臨床の現場で、「この治療法は、どんな患者さんに最も効果的なのだろう?」あるいは「この疾患を持つ患者さんに共通する背景因子は何か?」といった問いに日々向き合っている方も多いと思います。こうした問いに答えるには、何千、何万人という膨大な患者データを横断的に解析する必要がありますよね。
これこそ、まさに行列の独壇場です。
一人ひとりの患者さんが持つ数百の検査項目や遺伝子情報が一本の「ベクトル」となり、それが数万人分集まることで、10000人 × 500項目 といった巨大な「行列」が完成します。これは、いわば数万人規模の「デジタル症例集団(デジタルコホート)」です。
人間がこの巨大な表を眺めても、意味のあるパターンを見つけ出すのはほぼ不可能です。しかしAIは、この行列全体を一個のデータとして数学的に分析することで、人間では到底気づけないような、変数間の微細な相関や、疾患と特定の遺伝子パターンの間の隠れた関係性を浮かび上がらせることができます。
2. 医用画像診断:3次元の「テンソル」で人体をスキャンする
ベクトルや行列の考え方は、医用画像の世界で、より直感的かつパワフルにその真価を発揮します。
2次元のレントゲンや病理標本のデジタル画像が、ピクセルの輝度値を並べた「行列」であることは、もう簡単に想像がつくかと思います。では、多数のスライスから成る3DのCTやMRI画像は、どう表現されるのでしょうか?
ここで登場するのがテンソル(Tensor)という概念です。テンソルと聞くと難しそうですが、心配は要りません。これは単に「ベクトルや行列を、さらに高次元に一般化したもの」です。言わば、ベクトルが1階建て(1次元)、行列が2階建て(2次元)なら、テンソルは3階建て以上の高層ビルのようなものです。
【3D医療画像(CT/MRI)とテンソル表現】
Slice 1 Slice 2 Slice 3
(2D行列) (2D行列) (2D行列)
┌──────┐
/ 10, 25,.../│ ┌──────┐
/ 12, 28,.../ │ / 11, 26,.../│
┌──────┐ │ ┌──────┐ │
深さ / 10, 25,.../高│/ 11, 26,.../高│
(D) │ 12, 28,...│さ││ 13, 29,...│さ│ ...
│ ... │ ││ ... │ │
└──────┘ │└──────┘ │
(幅 W) │ (幅 W) │
│ │
└──────────┘
全体として、(幅 Width × 高さ Height × 深さ Depth) の「3Dテンソル」を形成
このように、3Dの医用画像は、一枚一枚の断層画像(行列)を積み重ねた「3Dテンソル」として表現されます。このテンソル構造をそのまま扱えるAI(特に畳み込みニューラルネットワーク、CNN)は、画像が持つ奥行きや立体的な構造といった重要な情報を失うことなく解析できるため、2Dの画像解析を遥かに超える精度で、病変の検出やセグメンテーション(領域分割)を行うことが可能になるのです。
3. 医療NLP:単語の「意味」をベクトルで捉える
最後に、生成系AIの心臓部とも言える、最もエキサイティングな応用例に触れておきましょう。それは「言葉」の世界です。「急性増悪」や「寛解」といった単語が持つ繊繊な意味を、AIはどうやって数字で表現しているのでしょうか。
その答えが、単語埋め込み(Word Embedding)という革新的なアイデアです。これは、それぞれの単語に、高次元空間内のユニークな「住所」を与える、という考え方に基づきます。つまり、全ての単語を一本の「ベクトル」として表現するのです。
この「意味空間」では、似た意味を持つ単語は、空間内でご近所さんになります。例えば、「医師」と「看護師」のベクトルは近い位置に、「アセトアミノフェン」と「イブプロフェン」のベクトルもまた、近い位置にプロットされるでしょう。
さらに驚くべきは、この空間では「意味の足し算・引き算」が成り立つことです。一般によく知られる例として、次のようなベクトル演算があります。
この図が示すように、「vec('王様') - vec('男性') + vec('女性')」を計算すると、その結果は「vec('女王様')」が位置する座標に、驚くほど近くなります。これはAIが、単語そのものではなく、単語と単語の間に存在する「関係性」や「概念」をベクトルとして学習していることを意味します。
この技術があるからこそ、AIは「Hb低下、貧血に合致」といった文章の意味を理解し、大量の診療録や医療論文を要約したり、専門的な質問に答えたりすることができるのです。ベクトルと行列は、もはや単なる数字のカタマリではなく、AIが人間のように思考するための、意味豊かな表現基盤そのものと言えるでしょう。
まとめ
今回は、AIの「目」となり、世界の情報を数値データとして捉えるための基本ツールであるベクトルと行列について深掘りしました。
- ベクトルは、一人の患者や一つの単語などを、高次元空間における「一点」として表現する。その「位置」や「距離」が意味を持つ。
- 行列は、データの集まりを格納する「器」であると同時に、ベクトルに作用して別のベクトルへと変換する「変換器」としての強力な役割を持つ。
NumPyライブラリを使うことで、これらのベクトルや行列をPythonで効率的に扱うことができる。
データをベクトルや行列という「カタマリ」で表現し、操作する感覚は掴めたでしょうか。さて、データが意味を持つ「点」として空間に表現できるなら、次なる疑問は「2つの点がどれくらい似ているか、あるいは関連しているか」をどうやって数値化するか、です。
次回、第3回「内積で測る「似ている」とは? — Embeddingと類似度の世界」では、この「似ている」という曖昧な概念を、内積というシンプルな計算で定量化する手法に迫ります。これは、類似症例検索やレコメンデーションシステムの核心となる、非常にエキサイティングなテーマです。
参考文献
- Goodfellow I, Bengio Y, Courville A. Deep Learning. Cambridge, MA: MIT Press; 2016.
- Strang G. Introduction to Linear Algebra. 5th ed. Wellesley, MA: Wellesley-Cambridge Press; 2016.
- Harris CR, Millman KJ, van der Walt SJ, Gommers R, Virtanen P, Cournapeau D, et al. Array programming with NumPy. Nature. 2020;585(7825):357-362.
- Mikolov T, Sutskever I, Chen K, Corrado GS, Dean J. Distributed representations of words and phrases and their compositionality. In: Proceedings of the 26th International Conference on Neural Information Processing Systems. 2013; p. 3111–3119.
- LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521(7553):436-444.
- Gillies RJ, Kinahan PE, Hricak H. Radiomics: Images Are More than Pictures, They Are Data. Radiology. 2016;278(2):563-77.
- Rajkomar A, Dean J, Kohane I. Machine Learning in Medicine. N Engl J Med. 2019;380(14):1347-1358.
- Deisenroth MP, Faisal AA, Ong CS. Mathematics for Machine Learning. Cambridge, UK: Cambridge University Press; 2020.
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






