理想的な実験(RCT)が難しい観察データから真実を探るには、「交絡」という見えないバイアスを乗り越える必要があります。ここでは、データに隠された「偶然」を利用する2つの強力な分析アプローチ、「操作変数法」と「回帰不連続デザイン」の要点を解説します。
治療の選択が患者の重症度など「見えない要因」と結びつき、真の因果関係が見えなくなる問題。相関関係が必ずしも因果関係を意味しない根本原因です。
治療にのみ影響を与える「外からの偶然の力」(例: 医師の好み、遺伝子)を利用し、交絡の影響を切り離して因果効果を推定する探偵のようなアプローチです。
明確なルール(例: 診断基準値)による「境界線」のすぐ両側を比較。「偶然」で運命が分かれた人々を比べることで、局所的な因果効果を強力に推定します。
臨床の現場にいると、私たちは日々「この治療法、この薬剤は、本当に患者さんのためになっているのだろうか?」という根源的な問いと向き合っています。科学的な答えを求めるなら、その最も信頼性の高い方法はランダム化比較試験(RCT)であることは、誰もが知るところです。しかし、理想と現実は違います。倫理的な制約、莫大なコスト、あるいは単純に時間の問題で、知りたいこと全てをRCTで検証するのはほとんど不可能です。教科書通りの研究が、目の前の臨床現場で常に実施できるわけではない…そんなもどかしさを感じることも少なくないはずです。
そこで、我々が頼りにするのが、日々の診療で蓄積されるリアルワールドデータ、すなわち「観察データ」です。しかし、この観察データには「交絡」という、非常に厄介な落とし穴が潜んでいます。例えば、「新しい手術手技を受けた患者群は、従来の手技を受けた群よりも予後が悪かった」というデータが得られたとしましょう。これは、新しい手技が劣っている証拠なのでしょうか?おそらく、そう単純な話ではありません。もしかしたら、その新しい手技は非常に高度で、他に選択肢のない末期の、極めて重篤な患者さんにのみ適用されていたのかもしれません。これが「交絡」です。治療の選択そのものが、患者さんの背景因子(重症度など)と強く結びついてしまっている状態ですね。
もちろん、統計モデルを使えば、年齢や性別、検査値といった「測定できている交絡因子」の影響をある程度調整することは可能です。しかし、本当に恐ろしいのは「測定できていない、未知の交絡」の存在です。例えば、患者さん本人の治療に対する意欲、ご家族のサポート体制、データには現れない生活習慣、あるいは遺伝的な背景…。私たちがどれだけ多くの変数をモデルに投入したとしても、こうした”見えない因子”が結果を静かに、しかし確実に歪めている可能性を、完全に否定することはできないのです。
もう、打つ手はないのでしょうか?観察データからは、真の因果関係に迫ることはできないのでしょうか?
…いいえ、科学の探求はここで終わりません。まるで優れた探偵が、現場に残されたわずかな手がかりから事件の真相を解き明かすように、データの中に隠された「自然が作り出した偶然の状況」を利用して、交絡の壁を乗り越えようとするアプローチが存在します。それが、今回ご紹介する「操作変数法(Instrumental Variable: IV)」と「回帰不連続デザイン(Regression Discontinuity: RD)」です。これらは、観察研究から真の因果効果を推定するための、非常に有力かつ独創的なアプローチであり、多くの研究者がその可能性に注目しています。
操作変数(IV)法:「外生的な偶然」を利用する分析術
まずは操作変数法から見ていきましょう。一言でいうと、これは「分析したい要因(処置)とは直接関係ない、外生的に生じた偶然の変動」を利用して、交絡の影響を避けて因果効果を推定する、非常に賢い方法です。
観察研究における最大の敵は、測定できない交絡因子でしたね。どんなに多くの変数を統計モデルで調整しても、「患者さんの治療への意欲」や「食生活」といったデータ化されていない要因が結果を歪めているかもしれません。IV法は、このような未知の交絡が存在する状況でも、因果関係に迫るための強力なツールです。
この考え方は、経済学者のヨシュア・アングリストとアラン・クルーガーが、徴兵制の抽選番号という「偶然」を利用して、兵役経験がその後の収入に与える影響を分析した研究などで広く知られるようになりました(Angrist and Krueger, 1991)。
一体、操作変数って何?
言葉だけだと難しいので、身近な例をじっくり深掘りしてみましょう。
課題:「勉強時間(処置X)が、テストの成績(結果Y)にどれだけ影響するか?」を知りたいとします。
単純に2つの関係を分析すると、おそらく「勉強時間が長い学生ほど成績が良い」という相関が見られるでしょう。しかし、ここには「もともとの学習意欲や能力(未測定の交絡U)」という見えない因子が潜んでいます。意欲や能力が高い学生は、自ずと勉強時間が長くなり、かつ、もともと成績も良い傾向があるでしょう。このため、観測された相関関係が、本当に勉強時間だけの効果なのか、それとも単に元々の能力を反映しているだけなのか、区別がつきません。
ここで、こんな「偶然の出来事」が起きたとします。それは「いくつかの学生の通学路に、自治体が新しく公立図書館を建設した」というイベントです。この「図書館の開設(操作変数Z)」が、今回の主役である操作変数(Instrumental Variable, IV)になり得るのです。
なぜこれが強力な武器になるのか?それは、この偶然の出来事が、学生の勉強時間に対して一種の「自然実験」を作り出してくれるからです。図書館という存在が、一部の学生の背中を「ポン」と押し、勉強時間を増やすきっかけになったと考えられます。この「外からの偶然のひと押し」だけを使って因果効果を測れば、学生本人の元々の能力という交絡の影響を切り離せるのではないか、というのがIV法の核心的なアイデアです。
ただし、どんな変数でも操作変数になれるわけではありません。それには、絶対にクリアしなければならない3つの厳しい条件、いわば「操作変数であるための掟」を満たす必要があります。
操作変数であるための3つの必須条件
ある変数(Z)が、処置(X)から結果(Y)への因果効果を推定するための有効な操作変数であるためには、以下の3つの条件をすべて満たさなければなりません。これらは非常に重要なので、一つずつ丁寧に見ていきましょう。
※この図は、変数間の関係を示しています。実線は直接的な影響、X印のついた矢印は「あってはならない影響」を表します。
条件1:関連性 (Relevance) 🕵️♀️
操作変数(Z)は、分析したい処置(X)と強く関連している必要があります。
これは最も直感的で、かつデータで確認できる唯一の条件です。「図書館の開設」が、学生の「勉強時間」に何らかの影響を与えなければ、話は始まりません。もし新しい図書館ができたのに、誰も利用せず、学生たちの勉強時間が1分も変わらなかったとしたら、この操作変数は何の手がかりももたらしてくれない「無関係な出来事」になってしまいます。
どうやって確認するの?
これは後の「2段階最小二乗法」の第1段階で統計的に検証します。具体的には、操作変数で処置を予測する回帰分析を行い、その関連性の強さをF統計量という指標で評価します。一般的に、このF統計量が10以上であることが、関連性が十分に強いことの一つの目安とされています(Staiger and Stock, 1997)。
条件2:独立性 (Independence / Ignorability) ⚖️
操作変数(Z)は、測定されていない交絡因子(U)と無関係でなければなりません。
これは「操作変数の純粋性」を問う条件です。操作変数を割り振る「偶然」が、他の要因に汚染されていてはいけません。「図書館の開設」という出来事が、学生個人の「元々の能力や意欲」とは全く無関係に起こる必要があります。
もし市が「もともと教育熱心な家庭が多い、成績優秀な地域」を意図的に選んで図書館を建てていたとしたらどうでしょう?その場合、「図書館の開設」と「学生の元々の能力」が関連してしまい、この条件は満たされません。この条件が崩れると、結局は交絡を分離できなくなってしまいます。
重要な注意点
この独立性の条件は、データから統計的に証明することはできません。これは、そもそも交絡因子(U)が「未測定」だからです。そのため、この条件が満たされているかは、研究分野の専門知識(ドメイン知識)に基づいて「理論的に妥当である」と主張する必要があります。
条件3:除外制約 (Exclusion Restriction) 🚪
操作変数(Z)は、処置(X)を経由するルート以外で、結果(Y)に影響を与えてはなりません。
これは最も重要で、かつ解釈が難しい条件です。「影響のルートはただ一つ」という掟だと考えてください。
「図書館の開設」が「テストの成績」に影響を与えるルートは、あくまで「勉強時間」を増やすという一本道だけでなければなりません。もし、その図書館が勉強場所を提供するだけでなく、「超優秀なチューターが無料で学習相談に乗ってくれる」という特別なサービスを提供していたらどうでしょう?その場合、「チューターの助言」という勉強時間以外の別のルート(裏口)を通って、直接テストの成績に影響を与えてしまう可能性があります。これでは、純粋な勉強時間の効果だけを測ることができなくなり、除外制約は破られてしまいます。
この条件も独立性と同様に、データから直接証明することは不可能であり、その妥当性は理論的な考察に依存します。
医療現場での応用例
例1:医師の処方傾向
この「医師の好み」を操作変数として使うアプローチは、特に医薬品の観察研究において、非常に有名かつ強力な分析手法として知られています。その代表的な事例が、ハーバード大学のM. Alan Brookhart氏らが2006年に医学雑誌『American Journal of Epidemiology』で発表した研究です(Brookhart et al., 2006)。この研究は、観察データから医薬品の副作用リスクを評価する際に、いかにして「処方選択の偏り」という大きな壁を乗り越えるか、その見事な一例を示してくれました。
ここで彼らが挑んだ具体的な課題を見てみましょう。
- 課題: 高齢の患者さんにおいて、当時比較的新しかった鎮痛薬「COX-2阻害薬」(処置)は、従来から使われていた「非選択的NSAIDs」と比べて、深刻な副作用である「消化管出血」(結果)のリスクを本当に下げることができるのか?
この問いに答えるのは、実は簡単ではありません。なぜなら、そこには「交絡バイアス」、特に「適応による交絡(confounding by indication)」と呼ばれる厄介な問題が潜んでいるからです。少し想像してみてください。消化管出血のリスクがもともと高い、例えば胃潰瘍の既往があるご高齢の患者さんが来たとします。医師としては、できるだけ安全な薬を使いたいと考え、副作用が少ないと期待される新しいCOX-2阻害薬を積極的に選択するかもしれません。逆に、若くて健康な患者さんには、安価で実績のある従来のNSAIDsを処方するでしょう。
この状況で、もし単純に「COX-2阻害薬を飲んだグループ」と「従来のNSAIDsを飲んだグループ」の消化管出血の発生率を比較したら、どうなるでしょうか? もしかしたら、COX-2阻害薬グループの方が出血率が高い、という直感に反する結果が出てしまうかもしれません。しかし、それは薬のせいではなく、もともと出血リスクの高い患者さんがCOX-2阻害薬グループに集まっていたせいかもしれないのです。これが適応による交絡です。治療の選択そのものが、患者さんの背景(重症度やリスク)と分かちがたく結びついてしまっているのですね。
そこでBrookhart氏らが持ち出した切り札が、「医師個人の処方に対する好み(Physician’s Prescribing Preference)」を操作変数として利用するアイデアでした。これは、「個々の患者さんの状態とは無関係に、その医師が新しい薬を好んで使う傾向があるか、それとも伝統的な薬を好む傾向があるか」という、医師側の特性に着目したものです。患者さんからすれば、たまたま受診した医師が「新薬好き」か「保守的」かはある種の偶然と言えます。この「偶然」を利用して、交絡の鎖を断ち切ろうというわけです。
この「医師の好み」が、操作変数として機能するための3つの条件をクリアしているか、彼らの研究に沿って見てみましょう。
- 関連性 (Relevance) 🕵️♀️: 「医師の好み」は、実際に処方される薬(処置)と本当に関連しているのでしょうか?これは当然、関連しています。新薬を好む医師は、そうでない医師に比べて、実際にCOX-2阻害薬を処方する確率が高いはずです。研究では、これをデータで確認するために、ある医師が「直前の似たような患者さんに何を処方したか」を代理の変数として用いるなどして、この関連性の強さを統計的に証明しています。
- 独立性 (Independence) ⚖️: 「医師の好み」は、測定できていない交絡因子(患者の重症度や出血リスク)と無関係でしょうか? これはおそらく、イエスだと言えます。特定の患者さんが出血リスクが高いからといって、わざわざ「新薬好きの先生」を探して受診するということは、通常考えにくいでしょう。どの医師に当たるかは、患者さんの重症度とは無関係な、ある種の偶然の割り当て(as-if random assignment)と見なせる、というのがこの仮定の根拠です。
- 除外制約 (Exclusion Restriction) 🚪: 「医師の好み」は、処方する薬(処置)を通じて以外に、消化管出血(結果)に影響を与えないでしょうか? これも、おそらく満たされていると考えられます。医師が「新薬好き」であるという事実そのものが、患者さんの胃の粘膜を直接的に強くしたり弱くしたりするわけではありません。その影響は、あくまで「どの薬を処方したか」というルート一本道を通るはずです。もちろん、「新薬を好む医師は、他の医療行為も先進的で、結果的に予後が良くなる」といった可能性もゼロではありませんが、消化管出血という具体的なアウトカムに対して、処方薬以外に直接的な影響を与える経路は考えにくいと主張できるわけです。
このように、3つの厳しい条件をクリアすることで、「医師の処方傾向」は強力な操作変数となり得ます。このアプローチを用いることで、研究チームは患者背景の違いという交絡の影響を巧みに分離し、COX-2阻害薬が消化管出血リスクに与える真の因果効果の推定に成功したのです。これは、臨床現場に溢れる「偶然」の中に、いかにして科学的な真実を見出すかを示す、独創的で美しい研究事例だと思います。
例2:専門病院までの距離
地理的な要因が、あたかもランダムな割り付けのように機能することがあります。この「距離」を操作変数として利用するアプローチは、医療アクセスや治療効果の研究で古くから用いられてきた、非常に古典的かつ強力な手法です。その礎を築いた研究の一つとして、ハーバード大学のMark McClellan氏、Barbara J. McNeil氏、Joseph P. Newhouse氏らが1994年に権威ある医学雑誌『JAMA』で発表した論文が挙げられます (McClellan, McNeil and Newhouse, 1994)。
彼らが取り組んだのは、以下のような臨床上のきわめて重要な問いでした。
- 課題: 急性心筋梗塞(AMI)で入院した高齢者に対して、心臓カテーテル検査のような侵襲的で高度な治療(処置)を行うことは、本当に生存率(結果)を改善するのか?
この問いもまた、「誰がその治療を受けるか」という選択の偏り、すなわちセレクションバイアスの問題を抱えています。心臓カテーテル検査は患者さんへの負担も大きいため、一般的には、比較的若くて、合併症が少なく、全身状態が良い(つまり、もともと予後が良いと期待される)患者さんが選択されやすい傾向があります。もし、単純にカテーテル治療を受けた患者群と受けなかった患者群の死亡率を比べると、治療群のほうが圧倒的に生存率が高いという結果が出るでしょう。しかし、それは治療そのものの効果なのか、それとも単に「もともと助かる見込みの高かった患者さんを選んで治療した」結果なのか、区別がつきません。
そこで研究チームが利用したのが、「患者の自宅から、心臓カテーテル検査が可能な専門病院までの距離」という操作変数です。このアイデアの根幹にあるのは、「心筋梗塞という緊急事態において、患者は最も近い病院に搬送されることが多い。その最寄りの病院がたまたまカテーテル治療のできる施設か、そうでないかによって、高度治療を受ける確率が偶然左右されるのではないか」という考え方です。つまり、患者さんの重症度ではなく、「住んでいる場所」という地理的な偶然が、治療選択の背中をポンと押す「外からの力」として機能すると考えたのです。
この「病院までの距離」が、操作変数の3つの条件を満たしているか、この研究の文脈で検証してみましょう。
- 関連性 (Relevance) 🕵️♀️: 専門病院までの距離は、実際にカテーテル治療を受ける確率と関連しているでしょうか? 答えはイエスです。McClellanらの分析によると、カテーテル治療が可能な病院の近くに住んでいる患者さんは、遠くに住んでいる患者さんと比べて、実際にその治療を受ける確率が有意に高いことがデータで示されました。これは非常に直感的で、かつ統計的に検証可能な条件です。
- 独立性 (Independence) ⚖️: 患者さんの住んでいる場所(=病院までの距離)は、測定できていない交絡因子(例えば、データには現れない本人の基礎体力や健康意識など)と無関係でしょうか? これも、概ね妥当な仮定だと考えられます。人がどこに住むかは様々な要因で決まりますが、「将来心筋梗塞になった時の重症度」を予測して住居を決める人はいません。したがって、患者の住居の場所は、心筋梗塞発作時点での未測定の健康状態とは無関係、つまりランダムであると考えることができます。
- 除外制約 (Exclusion Restriction) 🚪: 病院までの距離は、カテーテル治療を受けるかどうか(処置)という経路以外を通って、1年後の死亡率(結果)に影響を与えないでしょうか? これは最も慎重な検討を要する、この分析の核心部分です。例えば、「カテーテルができる病院は、そもそも他の一般治療の質も高く、そのせいで死亡率が低い」という可能性はないでしょうか?もしそうであれば、距離が近いことのメリットは、カテーテル治療以外の「質の高いケア」という別の経路(裏口)を通って死亡率に影響を与えてしまい、この仮定は成り立ちません。研究者たちはこの点を深く考察し、病院の特性などを分析することで、この除外制約が(完全ではないにせよ)ある程度は妥当であると主張しています。
これらの仮定のもとで分析を行った結果、非常に興味深い結論が導き出されました。単純比較ではカテーテル治療によって死亡率が劇的に下がるように見えたのに対し、操作変数法による分析では、その効果ははるかに小さく、統計的に有意な差ではない可能性が示唆されたのです。これは、これまで治療効果と信じられていたものの多くが、実は治療そのものの力というよりは「良い予後が見込める患者さんを選んでいただけ」というセレクションバイアスの影響だったことを意味します。この研究は、観察データから安易に因果関係を結論づけることの危険性と、それを乗り越えるための洗練された統計手法の重要性を見事に示した、歴史的な事例と言えるでしょう。
例3:メンデルランダム化 (Mendelian Randomization)
最後にご紹介するのは、遺伝情報という究極の「生まれ持った偶然」を利用する、メンデルランダム化(Mendelian Randomization: MR)という、近年非常に注目されている強力な手法です。この名前の由来は、もちろん遺伝学の父であるグレゴール・メンデルから来ています。彼が発見した、親から子へ遺伝子がランダムに受け継がれる仕組み(メンデルの法則)を、あたかも神様が実施してくれた壮大な「ランダム化比較試験(RCT)」と見なす、という画期的なアイデアに基づいています。
このアプローチの重要性や独創性については、因果推論の大家であるGeorge Davey Smith氏とShah Ebrahim氏が2003年に『International Journal of Epidemiology』で発表した総説で、その概念的枠組みと可能性が見事に示されています (Davey Smith and Ebrahim, 2003)。
MRが解決しようとする、医学研究における根源的な課題を見てみましょう。
- 課題: 血中の特定のバイオマーカー(例えば、LDLコレステロール)が高いこと(処置/暴露)は、心筋梗塞(結果)の真の原因なのだろうか?
長年にわたり、LDLコレステロール値が高い人ほど心筋梗塞になりやすい、という観察研究の結果が数多く報告されてきました。しかし、ここでも「本当にコレステロールだけが悪者なのか?」という疑問がつきまといます。なぜなら、交絡と逆の因果という2つの大きな壁があるからです。
- 交絡: LDLコレステロールが高い人は、食生活の乱れ、運動不足、喫煙といった他の不健康な生活習慣を併せ持っていることが多いかもしれません。これらの生活習慣もまた、心筋梗塞の強力なリスク因子です。そのため、観察された関連が、LDLコレステロール自体の影響なのか、背後にある不健康なライフスタイル全般の影響なのかを区別するのは非常に困難です。
- 逆の因果 (Reverse Causation): 何らかの病的な状態が、結果としてLDLコレステロール値を変動させている可能性も、理論的には否定できません。
ここで登場するのがメンデルランダム化です。その基本的な考え方は、「生涯にわたるLDLコレステロール値に影響を与えることが分かっている特定の遺伝子多型(SNPなど)を、操作変数として利用する」というものです。人は親から遺伝子を受け継ぐ際、どの遺伝子を受け取るかは偶然(ランダム)に決まります。このランダムな割り当ては、その人が生まれてからどのような生活習慣を送るか、といった後天的な要因からは完全に独立しています。つまり、生まれつきLDLコレステロールが高くなりやすい遺伝子を持つ人と、そうでない人が、あたかもRCTの介入群と対照群のようにランダムに割り付けられている、と考えるわけです。
このアプローチが、操作変数の3つの条件をどのように満たすのかを見ていきましょう。
- 関連性 (Relevance) 🕵️♀️: 操作変数(特定の遺伝子多型)は、処置(LDLコレステロール値)と強く関連している必要があります。これは、現代のゲノムワイド関連解析(GWAS)によって、非常に多くの遺伝子多型と疾患・量的形質との関連が明らかにされており、検証可能です。例えば、PCSK9遺伝子のある種の多型がLDLコレステEロール値に強い影響を与えることは、広く知られています。
- 独立性 (Independence) ⚖️: 操作変数(遺伝子多型)は、交絡因子(食生活や運動習慣など)と無関係でなければなりません。これがMRの最も強力な点です。どのような遺伝子を持って生まれるかは、その後の本人の努力や選択とは無関係な、生まれつきのものです。したがって、遺伝子は後天的なライフスタイル要因とは独立している、という極めて妥当性の高い仮定を置くことができます(※ただし、集団の遺伝的背景が異なる場合に生じる「集団成層化」など、この仮定を脅かす要因には注意が必要です)。
- 除外制約 (Exclusion Restriction) 🚪: 操作変数(遺伝子多型)は、処置(LDLコレステロール値)の経路以外を通って、結果(心筋梗塞)に影響してはなりません。これはMRにおける最大の関門であり、「多面発現(Pleiotropy)」がない、という仮定に相当します。多面発現とは、一つの遺伝子が複数の、一見無関係な形質に影響を与える現象のことです。もし、ある遺伝子がLDLコレステロール値を上げるだけでなく、全く別のメカニズムで血圧も上げてしまうとしたらどうでしょう?その場合、その遺伝子と心筋梗塞との関連が、LDLコレステロールを介したものなのか、血圧を介したものなのか、区別がつかなくなってしまいます。この多面発現の問題は、MRを解釈する上で最も慎重な検討が必要な点であり、その影響を評価するための様々な統計手法(例: MR-Egger回帰)が開発されています。
これらの仮定が満たされる限り、もし「生まれつきLDLコレステロールが高くなる遺伝子を持つ集団」で心筋梗塞の発生率が有意に高ければ、それはLDLコレステロールが心筋梗塞の真の原因であることの強力な証拠となります。実際に、MRを用いた数多くの研究がLDLコレステロールの因果的役割を証明し、スタチンやPCSK9阻害薬といった脂質低下療法の開発・評価の理論的根拠を強固なものにしてきました。このようにMRは、観察データから因果関係を推論するための、非常にエレガントで強力なツールなのです。
このように、様々な「外生的な偶然」を見つけ出すことで、交絡を乗り越えて因果効果に迫ることができるわけです。
推定できるのは「動かされた人」だけの効果:LATE
一つ、非常に重要な注意点があります。操作変数法で推定できるのは、集団全体の平均的な効果(ATE: Average Treatment Effect)ではありません。推定できるのは、LATE (Local Average Treatment Effect)、日本語で言うと「局所的平均処置効果」です。
これは、「操作変数によって行動を変化させられた人たち(Compliers)における処置効果」を意味します(Angrist, Imbens, and Rubin, 1996)。
図書館の例に戻りましょう。学生は、図書館ができたという出来事に対して、4つのタイプに分かれると考えられます。
IV法が推定しているのは、このCompliers、つまり「図書館ができたことで背中を押され、行動を変えた人たち」だけの勉強時間の効果なのです。もともと意識の高い層(Always-takers)や、全く興味のない層(Never-takers)の効果は含まれていません。
このLATEが意味を持つためには、「モノトニシティ(Monotonicity)」という仮定が不可欠です。これは、操作変数が処置を一方向にしか動かさない、つまり「Defiers(へそ曲がり)」は存在しない、という仮定です。図書館ができたせいで、逆に勉強時間が「減ってしまう」ような学生はいない、という前提ですね。この仮定があって初めて、Compliersの効果をきれいに特定できるのです。
どうやって計算するの?:2段階最小二乗法 (2SLS)
では、操作変数(IV)のロジックを使って、具体的にどうやって因果効果を計算するのでしょうか。その最も標準的な手法が、2段階最小二乗法(Two-Stage Least Squares: 2SLS)です。名前の通り、2回のステップ(回帰分析)を経て、交絡の呪縛を解き放つプロセスをイメージしてもらえると分かりやすいかもしれません。
全体の目的は、交絡因子(\(U\): 未測定の能力など)と相関してしまっているせいで「汚染されている」処置変数(\(X\): 勉強時間)を、そのまま使わずに、一度「浄化」することです。汚染された水から不純物を取り除き、純水だけを使って本来の性質を調べるようなものですね。さあ、その2つの段階を一緒に見ていきましょう。
第1段階:処置変数から「聖域」を取り出す(The Purification Stage)
最初のステップの目的は、処置変数(\(X\): 勉強時間)を、交絡の影響を受けている「汚れた部分」と、受けていない「クリーンな部分」に分解することです。IV法のロジックを思い出してください。処置(勉強時間)の変動には2種類あると考えます。
- 汚染された変動: 学生自身の意欲や能力といった、未測定の交絡因子(\(U\))に由来する部分。
- クリーンな変動: 操作変数(\(Z\): 図書館の開設)という、外部からの「偶然のひと押し」によってのみ生み出された部分。
このうち、私たちが因果効果の推定に使いたいのは、後者の「クリーンな変動」だけです。そこで、このクリーンな部分だけを抽出するために、まず処置(\(X\))を操作変数(\(Z\))を使って説明する、1回目の回帰分析を行います。
\[ \text{処置}(X) = \beta_0 + \beta_1 \cdot \text{操作変数}(Z) + \epsilon \]
この数式は、一体何をしているのでしょうか? これは「学生たちの勉強時間(\(X\))が人によってバラバラなのはなぜか?」という問いに対して、「そのうち、新しくできた図書館(\(Z\))のせいで説明できる部分はどれくらいだろう?」と尋ねているのと同じです。この回帰分析によって、勉強時間(\(X\))は2つの成分に分解されます。
- 予測値 (\(\hat{X}\))(エックスハット): この回帰式から得られる予測部分です(\(\hat{X} = \hat{\beta}_0 + \hat{\beta}_1 \cdot Z\))。これは、操作変数(\(Z\))の情報だけから作られた、いわば勉強時間の「似姿」です。操作変数の条件(独立性)により、\(Z\)は交絡因子(\(U\))とは無関係でしたね。したがって、\(Z\)のみから作られたこの\(\hat{X}\)もまた、交絡因子(\(U\))の影響から切り離された「浄化された処置変数」と考えることができます。これこそが私たちが探し求めていた「聖域」、つまりクリーンな変動部分なのです。
- 誤差(残差)(\(\epsilon\)): 一方、この\(\epsilon\)は、操作変数(\(Z\))を使っても説明しきれなかった、\(X\)の残りの変動部分です。ここには、学生本人のやる気や能力、家庭環境といった、まさに私たちが取り除きたかった交絡因子(\(U\))の影響が、ゴミのようにすべて溜まっています。したがって、この\(\epsilon\)の部分は、分析にとって有害なので、思い切って捨ててしまいます。
この第1段階は、処置変数\(X\)から、信頼できるクリーンな変動部分\(\hat{X}\)だけを抽出するための「フィルタリング」のプロセスなのです。
第2段階:「聖域」だけを使って真の効果を推定する(The Causal Estimation Stage)
第1段階で、交絡から浄化された処置変数\(\hat{X}\)を手に入れることができました。いよいよ本丸です。最終目的である、処置が結果に与える因果効果を推定します。そのために、2回目の回帰分析を行います。
ここでのポイントは、説明変数として、元の「汚染された」処置変数\(X\)を使うのではなく、先ほど作り出した**「浄化された」処置変数\(\hat{X}\)を用いる**ことです。
\[ \text{結果}(Y) = \gamma_0 + \gamma_1 \cdot \text{予測された処置}(\hat{X}) + \nu \]
この式で推定された係数\(\gamma_1\)(ガンマ・ワン)こそが、私たちが求めていた、交絡バイアスの影響を限りなく取り除いた因果効果(より正確にはLATE)の推定値となります。
なぜ、これがより真実に近いと言えるのでしょうか? 通常の回帰分析(\(Y\)を\(X\)で回帰)では、説明変数である\(X\)が、誤差項に含まれる未測定の交絡因子\(U\)と相関してしまうため、係数が偏って(バイアスを持って)しまいます。しかし、今回の回帰では、説明変数として使っている\(\hat{X}\)は、\(U\)とのつながりを断ち切られたクリーンな変数です。そのため、\(U\)によるバイアスが生じず、\(\gamma_1\)は処置(勉強時間)が結果(テストの成績)に与える純粋な影響を捉えることができるのです。
この巧妙な2段階のプロセスを図解すると、以下のようになります。
⚠️ 最重要チェックポイント:「弱い操作変数」の問題
ただし、この2SLSを正しく使うためには、一つだけ絶対に確認しなければならないことがあります。それは、第1段階で用いる操作変数\(Z\)が、処置\(X\)と本当に強い関連を持っているか、という点です。もしこの関連が弱い場合、これを「弱い操作変数の問題(Weak Instrument Problem)」と呼び、分析結果が信頼できなくなってしまいます。
先ほどの浄水器の例で言えば、フィルターの性能が悪く、ほんの数滴しか純水(\(\hat{X}\))を抽出できないような状況です。わずかなデータで無理に分析しようとすると、結果は非常に不安定になり、少しの仮定違反(例えば、操作変数\(Z\)と交絡\(U\)の間にほんのわずかな相関があった場合)の影響が極端に増幅され、とんでもなく偏った推定値が出てしまうことが知られています。
この「弱さ」を診断するために、研究者は第1段階の回帰分析における\(F\)統計量を確認します。ハーバード大学のJames Stock氏らが提唱した経験則として、この\(F\)統計量の値が10を十分に超えていることが、操作変数が十分に強力であることの一つの目安とされています (Staiger and Stock, 1997; Stock and Yogo, 2005)。これは、2SLSを行う上での、いわば「お作法」のようなものだと考えてください。
回帰不連続デザイン(RD):「境界線」に隠された偶然を利用する
さて、次にご紹介する有力なアプローチが、回帰不連続デザイン(Regression Discontinuity Design: RD)です。もし操作変数法が「偶然の代理人」を探す探偵術だとすれば、RDは「ルールによって引かれた一本の境界線に隠された、まるで神様が用意したかのような偶然」を利用する、非常にエレガントな手法です。RCTが「人為的に」介入群と対照群を作るのに対し、RDは社会や自然界に存在する「ルール」によって生まれる群分けを利用する点で、まさに「自然実験」の真骨頂と言えるかもしれません。
RDの基本的な考え方:運命を分ける一本の線
また例え話から始めましょう。これがRDの考え方を理解する一番の近道だと思います。「ある大学が、成績優秀者を対象とした特別な奨学金制度(処置)を設けており、これがその後の学生の学業成績(結果)に良い影響を与えるか」を調べたいとします。
この奨学金は、入学試験の成績が「80点以上」の学生にのみ給付される、という明確なルールがあったとします。この「80点」という線引き、すなわちカットオフ値が、RDのすべての鍵を握ります。
想像してみてください。合格発表の日、自分の番号を見つけた学生たち。一人は、試験の点数が80.1点で、奨学金給付の通知に歓声を上げます。もう一人は、79.9点で、わずかに届かず肩を落とします。さて、この二人の学生の学力に、本質的な差はあるでしょうか?おそらく、ほとんどないはずです。彼らの点数の差は、その日の体調や、たまたまヤマが当たったか外れたか、といったまさに「誤差」や「偶然」の産物と言えるでしょう。
しかし、このほんのわずかな偶然の差によって、一方は奨学金を受け取り、もう一方は受け取れないという、全く異なる経験をすることになります。ここに、擬似的なランダム化比較試験(Pseudo-RCT)と見なせる状況が生まれているのです!カットオフ値をまたぐという「偶然」が、あたかも研究者がコインを投げて「あなたは奨学金グループ」「あなたは非奨学金グループ」とランダムに割り付けたかのような状況を作り出してくれているわけです。RDは、このカットオフ値のごく近傍にいる人々を比較することで、処置の純粋な効果を推定する、極めて強力な手法なのです(Imbens and Lemieux, 2008)。
医療現場での応用例:その「閾値」は自然の実験室
例1:診療ガイドラインの閾値
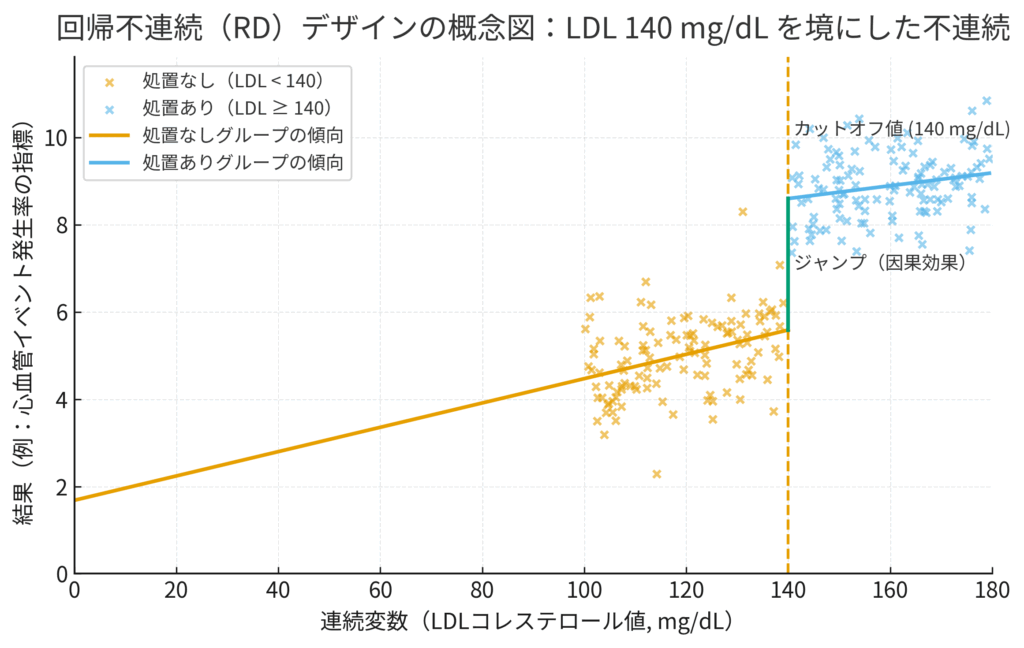
例えば、(あくまで説明のための例示ですが)「LDLコレステロール値が140mg/dL以上の患者にスタチン製剤を処方する」というような診療ガイドラインが存在したと仮定しましょう。(※実際の基準値は、日本動脈硬化学会の「動脈硬化性疾患予防ガイドライン」など、最新の公式文書をご確認ください)。
ここに、非常に似通った二人の患者さんがいるとします。LDL値が139mg/dLのAさんと、141mg/dLのBさんです。二人の年齢、生活習慣、遺伝的背景はほとんど同じかもしれません。しかし、ガイドラインという一本の線によって、Bさんだけがスタチン治療という新しい旅路を歩み始める可能性が高いのです。この二人のような、境界線のすぐ両側にいる患者さんたちの、その後の心血管イベントの発生率を比較すれば、スタチンの真の効果に迫ることができる、というわけです。
下の図は、このRDのコンセプトを視覚化したものです。横軸が連続的に変化する変数(Running Variable、この場合はLDL値)、縦軸が結果(アウトカム)です。もし処置(スタチン投与)に効果があれば、カットオフ値(140mg/dL)を境にして、結果の平均値に不連続な「ジャンプ(ギャップ)」が生じるはずです。RD分析の目的は、このジャンプの大きさを正確に推定することにあります。
例2:医療政策の評価
RDは、医療政策の効果を評価する上でも極めて有用です。
- 高齢者の医療費負担: 例えば「70歳の誕生日を迎えると、医療費の自己負担割合が3割から2割に軽減される」という制度があったとします。この「70歳」という年齢をカットオフとして、負担軽減(処置)が受診行動や健康アウトカムに与える影響を分析できます。
- 低出生体重児への介入: 「出生体重が1500g未満」の新生児に対して、特別な医療介入や発達フォローアッププログラムが適用される場合があります。この「1500g」という境界線を利用して、そのプログラムの有効性を検証することが可能です。
RDの信頼性を支える2つの重要な仮定
この強力なRDですが、そのロジックが成立するためには、絶対に守らなければならない重要な仮定が2つあります。
仮定1:連続性の仮定 (Continuity Assumption)
これは、「もし処置が行われなかったとしたら、結果(アウトカム)はカットオフ値の周辺で連続的に(スムーズに)変化するはずだ」という仮定です。
つまり、アウトカムに見られるジャンプが、処置の効果以外の理由で起こっている可能性を排除するための仮定です。例えば、LDL値が140mg/dLを境に、スタチンとは全く無関係な別の要因(例:食事指導の厳しさなど)が急に変化するようなことがあってはなりません。カットオフ値のすぐ近くでは、人々は非常に似通っているため、処置以外の要因はスムーズに変化しているだろう、と考えるのがこの仮定の根拠です。
仮定2:カットオフ値の操作がないこと (No Manipulation)
これは、「人々が処置を受ける(あるいは避ける)ために、カットオフ値を超えるように意図的に値を操作していない」という仮定です。これが崩れると、RDの根幹である「ランダム性」が失われてしまいます。
例えば、もし医師が「この患者さんを助けたいから、基準に届くように数値を少しだけ甘く記録しよう」と考えて、LDL値138mg/dLを140mg/dLとして申告したとします。このようなことが多発すると、カットオフ値のすぐ上側には「医師が特に気にかけている、本来なら基準値未満の患者」が集まってしまい、もはやランダムとは言えなくなります。逆に、患者側が「薬は飲みたくないから」と検査前に食事制限をして、意図的に値を下げるケースも考えられます。
これをチェックする有名な方法として、経済学者のJustin McCraryが提案したMcCrary検定があります。これは、カットオフ値の周辺で、連続変数(LDL値など)の分布(ヒストグラム)を調べるものです。もし意図的な操作があれば、カットオフ値のすぐ片側に不自然な人数の「崖」や「山」ができるはずです。McCrary検定は、そうした不自然な分布のジャンプがないかを確認します(McCrary, 2008)。
Sharp RDとFuzzy RD:ルールの厳格さによる違い
回帰不連続デザイン(RD)は、「境界線」をまたぐことで処置の有無が決まる状況を利用する手法でしたね。しかし、現実の世界では、その「ルール」の厳格さには少しバリエーションがあります。この厳格さの違いによって、RDは大きく2つのタイプに分けられます。この区別は、分析方法そのものに関わる非常に重要なポイントです。
Sharp RD (シャープRD):運命の分かれ道が明確なケース
まず、ルールが絶対的なケース、これがSharp RDです。「シャープ」という言葉通り、カットオフ値を境に処置の割り当てがナイフで切り分けたように100%決まる状況を指します。
- 例:「試験の点数が80点以上なら、例外なく『全員が』奨学金をもらえる。79.9点なら『誰も』もらえない」
この場合、処置を受けるかどうかが、カットオフ値を超えるか否かだけで完全に決まります。言い換えれば、「処置を受けたかどうか」と「カットオフ値を超えたかどうか」は全く同じ情報になります。下の図のように、処置の割り当て確率が、カットオフ値で0%から100%へと垂直にジャンプするわけです。
分析は非常にシンプルです。カットオフ値のすぐ両隣の人々(例:79.9点の人と80.1点の人)は、処置(奨学金)の有無以外はほぼ同じはずです。したがって、彼らの間で観察される結果(アウトカム)の平均値の差、つまりグラフ上の「ジャンプの大きさ」を測ることで、処置の因果効果を直接推定することができるのです。
Fuzzy RD (ファジーRD):「推奨」のようにルールが絶対でないケース
一方、現実世界のルールの多くは、もう少し「あいまい」です。これがFuzzy RDです。「ファジー(曖昧)」という名の通り、カットオフ値を超えることで処置を受ける確率が不連続にジャンプはするものの、0%から100%になるわけではない状況を指します。「ルールはあくまで強い推奨であり、最終決定には他の要素も絡む」というケースですね。
- 例:「LDLコレステロール値が140mg/dL以上でスタチン投与が『強く推奨』される」
このシナリオでは、カットオフ値(140mg/dL)が処方判断の強力な後押しになることは間違いありません。しかし、絶対ではありません。
- 基準を超えても(例: 141mg/dL)、医師や患者さんの判断で「まずは食事療法で様子を見ましょう」と、スタチンが処方されないケースは十分にあり得ます。
- 逆に、基準未満でも(例: 139mg/dL)、糖尿病や高血圧など他のリスク因子を多く持つ患者さんには、予防的にスタチンが処方されることもあります。
その結果、下の図のように、処置を受ける確率がカットオフ値で明確にジャンプはするものの、そのジャンプは例えば30%から70%へ、といった具合に、0%から100%にはなりません。
この「あいまいさ」が分析を難しくします。カットオフのすぐ上にいる人々は「処置を受けた人」と「受けなかった人」が混在しており、すぐ下にいる人々も同様です。これでは、Sharp RDのように単純に両側の平均値を比較しても、処置の真の効果は分かりません。得られるのは、様々な人が混ざった集団での効果であり、薄まってしまった推定値になってしまいます。
Fuzzy RDを解き明かす鍵:操作変数法(IV)の応用
では、どうすれば良いのでしょうか? ここで、前の章で学んだ操作変数(IV)法、特にその計算エンジンである2段階最小二乗法(2SLS)が、見事な解決策を与えてくれます。Fuzzy RDは、実はIV法を応用した分析手法なのです。
考え方はこうです。
- 操作変数 (\(Z\)): 「カットオフ値を超えたかどうか」という事実。これはルールによって決まる、クリーンで客観的な変数です(例:LDL値が140以上なら \(Z=1\), 140未満なら \(Z=0\))。
- 処置 (\(X\)): 「実際にスタチンを処方されたかどうか」という事実。これには医師や患者の裁量が入り込むため、「汚染」されている可能性があります(例:処方されたら \(X=1\), されなかったら \(X=0\))。
- 結果 (\(Y\)): 心血管イベントの発生など、私たちが知りたいアウトカムです。
この設定は、まさに操作変数法の3つの条件を満たしています。
- 関連性: カットオフ値を超えること(\(Z\))は、実際にスタチンを処方される確率(\(X\))を間違いなく高めます。
- 独立性: カットオフ値をわずかに超えるか超えないかは、患者さんの未測定の健康状態(交絡因子\(U\))とは無関係な「偶然」と見なせます。
- 除外制約: カットオフ値(140mg/dL)という事実そのものが、直接心筋梗塞を減らすわけではありません。その影響は、あくまでスタチンが処方される(\(X\))という経路を通じてのみ結果(\(Y\))に伝わるはずです。
この関係性が見えたら、あとは2SLSの出番です。
- 第1段階: まず、処置(\(X\))が操作変数(\(Z\))によってどれだけ動かされるかを推定します。これは上の図の「確率のジャンプの大きさ」を測っていることに相当します。「カットオフを超えるというルールは、スタチンの服用確率を一体何%押し上げる効果があったのか?」を計算するわけです。
- 第2段階: 次に、結果(\(Y\))のカットオフ前後でのジャンプの大きさを、第1段階で求めた「確率のジャンプの大きさ」で割り算します。
直感的に言うと、Fuzzy RDの因果効果は以下の式で推定されます(これはIV法におけるWald推定量と呼ばれるものと同じです)。
\[ \text{Fuzzy RDの因果効果} = \frac{\text{結果Yのジャンプの大きさ}}{\text{処置確率Xのジャンプの大きさ}} \]
例えば、カットオフを境に心血管イベントの発生率が5%低下し(\(Y\)のジャンプ)、処方確率が40%上昇した(\(X\)のジャンプ)とします。この場合、因果効果は 5% / 40% = 12.5% となります。これは、「もしルールによって100%の人が処置を受けたとすれば、イベント発生率は12.5%低下したはずだ」と解釈できます。処置を実際に受けた人たちへの効果を正しく推定するために、行動の変化分(確率のジャンプ)で補正(割り算)してあげているのですね。
このように、一見すると厄介な「あいまいさ(Fuzzy)」も、操作変数法という強力なレンズを通すことで、その奥にある因果関係を鮮やかに浮かび上がらせることができます。異なる手法が根底で深く結びついていることを知ると、因果推論の世界がより一層、面白く感じられるのではないでしょうか。
まとめ:観察研究の限界を突破するために
今回は、ランダム化比較試験(RCT)が実施できない状況で、観察データに潜む「未測定の交絡」という大きな壁に立ち向かうための2つの有力なアプローチ、操作変数法(IV)と回帰不連続デザイン(RD)について詳しく解説しました。
これらの手法の根底に流れる思想は、どちらも私たちの周りの世界に隠れている「自然実験(Natural Experiment)」や「擬似的なランダム化」の状況を見つけ出し、それを巧みに利用するという点で共通しています。研究者が介入しなくても、社会のルールや自然の成り行きが、あたかも実験であるかのような状況を稀に作り出してくれるのです。IVとRDは、その貴重な瞬間を捉えるための洗練されたレンズと言えるでしょう。
ここで、両者のアプローチの違いと特徴を改めて整理してみましょう。
| 特徴 | 操作変数法 (IV) | 回帰不連続デザイン (RD) |
|---|---|---|
| 利用する「偶然」 | 処置の選択に影響を与える「外生的なひと押し」(例:医師の好み、遺伝子) | 処置の割り当てを決定する「明確な境界線(ルール)」(例:診断基準値、年齢) |
| 主な課題 | 3つの条件(特に独立性と除外制約)を満たす、妥当で強力な操作変数を見つけること。 | カットオフ値周辺での「as-if random」を正当化し、値の意図的な操作がないことを確認すること。 |
| 推定される効果 | LATE:操作変数によって行動を変化させられた集団(Compliers)における局所的な効果。 | カットオフ値のすぐ近傍における局所的な効果。 |
もちろん、これらの手法は決して万能の魔法ではありません。統計学に「フリーランチ(ただ飯)はない」という言葉があるように、IVとRDは、「未測定の交絡を調整できる」という大きな利益を得る代わりに、「強力かつ検証が困難な仮定を受け入れる」という代償を支払う必要があります。強力な操作変数を見つけるのは非常に困難ですし、RDが綺麗に適用できる状況も限られます。そして何より、その背後にある仮定(IVの除外制約やRDの連続性の仮定など)が満たされているかを、専門知識を総動員して慎重に吟味し、その妥当性を説得力をもって論じることが、研究の信頼性を担保する上で不可欠です。
しかし、こうした限界を理解した上で使いこなせば、RCTの実施が難しい医療リアルワールドデータから、より信頼性の高い因果関係を探求していく上で、これ以上ないほど強力な武器となります。これらの手法を学ぶことは、単に分析の選択肢を増やすだけではありません。それは、論文を批判的に吟味する際の「新しい視点」を手に入れることであり、日々の臨床や研究計画の中で「この状況、ひょっとしたら自然実験として捉えられないだろうか?」と考える「因果推論の思考様式」を身につけることでもあります。
ぜひ、この視点を日々の臨床や研究に取り入れてみてください。皆さんの周りにも、まだ誰も気づいていない「偶然の実験室」が隠されているかもしれません。
参考文献
- Angrist, J. D. and Krueger, A. B. (1991). ‘Does Compulsory School Attendance Affect Schooling and Earnings?’, The Quarterly Journal of Economics, 106(4), pp. 979–1014.
- Angrist, J. D., Imbens, G. W. and Rubin, D. B. (1996). ‘Identification of causal effects using instrumental variables’, Journal of the American Statistical Association, 91(434), pp. 444–455.
- Brookhart, M. A., Wang, P. S., Solomon, D. H. and Schneeweiss, S. (2006). ‘Instrumental variable analysis for observational comparative effectiveness research’, American Journal of Epidemiology, 163(12), pp. 1159-1168.
- Carpenter, C. and Dobkin, C. (2009). ‘The Effect of Alcohol Consumption on Mortality: Regression Discontinuity Evidence from the Minimum Drinking Age’, American Economic Journal: Applied Economics, 1(1), pp. 164–82.
- Davey Smith, G. and Ebrahim, S. (2003). ‘‘Mendelian randomization’: can genetic epidemiology contribute to understanding environmental determinants of disease?’, International Journal of Epidemiology, 32(1), pp. 1–22.
- Imbens, G. W. and Lemieux, T. (2008). ‘Regression discontinuity designs: A guide to practice’, Journal of Econometrics, 142(2), pp. 615–635.
- Lee, D. S. and Lemieux, T. (2010). ‘Regression Discontinuity Designs in Economics’, Journal of Economic Literature, 48(2), pp. 281–355.
- McClellan, M., McNeil, B.J. and Newhouse, J.P. (1994). ‘Does more intensive treatment of acute myocardial infarction in the elderly reduce mortality? Analysis using instrumental variables’, JAMA, 272(11), pp. 859–866.
- McCrary, J. (2008). ‘Manipulation of the running variable in the regression discontinuity design: A density test’, Journal of Econometrics, 142(2), pp. 698-714.
- Staiger, D. and Stock, J. H. (1997). ‘Instrumental Variables Regression with Weak Instruments’, Econometrica, 65(3), pp. 557-586.
- Stock, J. H. and Yogo, M. (2005). ‘Testing for weak instruments in linear IV regression’, in Andrews, D. W. K. and Stock, J. H. (eds.) Identification and Inference for Econometric Models: Essays in Honor of Thomas Rothenberg. Cambridge: Cambridge University Press, pp. 80-108.
- 日本動脈硬化学会 (最新年). 動脈硬化性疾患予防ガイドライン.
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






