RCT(ランダム化比較試験)ができない状況でも、観察データから「真の効果」を探ることは可能です。ここでは、そのための強力な分析手法である「差分の差分法 (DiD)」と「合成コントロール法 (SCM)」の基本コンセプトを解説します。
RCTが理想ですが、現実には実施困難な場合が多いです。単純な前後比較やグループ比較では、景気変動や元々の地域差といった「交絡」の影響を取り除けず、介入の真の効果を正しく評価できません。
介入があったグループと無かったグループ、双方の「時間による変化(1つ目の差)」を計算します。次に、その変化量の「差(2つ目の差)」を取ることで、両グループに共通する影響を相殺し、介入の純粋な効果を抽出します。
国や県など、比較対象が1つしかない場合に有効です。介入されなかった複数の候補を重み付けして組み合わせ、介入前の動向がそっくりな「もしも」の対象(合成コントロール)を創出。その後の軌跡の差から効果を推定します。
「新しい診療ガイドラインが導入された」「地域で新たな健康増進キャンペーンが始まった」「診療報酬が改定された」。
私たちの周りでは、患者さんのアウトカムを改善するための様々な「介入」が日々行われています。そのたびに、頭をよぎる素朴な、しかし根源的な問いがあります。
「この変化は、本当に効果があったのだろうか?」
この問いに最も力強く答えられるのが、科学的証拠の頂点に立つランダム化比較試験(RCT)であることは、皆さんもよくご存知だと思います。しかし、現実の世界は研究室の中とは違います。
例えば、ある都道府県全体で施行された新しい禁煙条例の効果を検証したいとしましょう。RCTを行うには、同じような都道府県をたくさん用意して、くじ引きで条例を施行するグループとしないグループに分ける必要があります。これは倫理的にも、政治的にも、そして費用的にも不可能ですよね。過去に遡って介入をランダムに割り付けることは、神様でもない限りできません。このような観察データからの因果推論の難しさは、Hernán & Robins (2020) のような専門書でも中心的なテーマとして議論されています。
では、私たちは手元にある「観察データ」—日々の診療記録やレセプトデータ—を眺めて、ため息をつくしかないのでしょうか?
「介入があった地域の入院率が下がったから、効果ありだ!」と単純に結論づけるのは、あまりに危険です。もしかしたら、その地域では全く別の要因(例えば、経済状況の改善や、有力な病院が新設されたなど)が、入院率の低下を引き起こしたのかもしれません。これが、因果推論における永遠の課題、「交絡」です。
諦めるのはまだ早い。ここに、観察データという制約の中で「もしも介入がなかったらどうなっていたか?」という世界を科学的に描き出し、真の効果に迫るための強力な助っ人がいます。
それが、今回ご紹介する「差分の差分法(Difference-in-Differences, DiD)」と「合成コントロール法(Synthetic Control Method, SCM)」です。
これらは経済学、特に政策評価の世界で磨き上げられてきた分析手法で、今や医療データサイエンスにおいても「鉄板」ツールとして欠かせない存在になっています。
この記事では、
- なぜ単純な前後比較やグループ比較ではダメなのか?
- DiDが「差の差」を取ることで、見えない影響をどう打ち消すのか?
- 似た相手がいない時に、SCMがどうやって「オーダーメイドの比較相手」を作り出すのか?
といった核心部分を、具体的な医療現場のシナリオを交えながら、一つひとつ丁寧に解き明かしていきます。
統計学の専門知識に自信がない方でも大丈夫です。この記事を読み終える頃には、ニュースで目にする政策評価の裏側が理解でき、ご自身の臨床や研究における問いに、データを使ってどう答えればよいかの確かな羅針盤を手にしているはずです。さあ、一緒に因果推論の面白い世界へ足を踏み入れてみましょう。
差分の差分法(DiD):時間を味方につける比較の魔法
さて、ここからは観察データから因果効果を探るための強力な武器の一つ、「差分の差分法(Difference-in-Differences, DiD)」の世界に深く飛び込んでいきましょう。「差の差」なんて聞くと、何だか数学的で難しそうに感じるかもしれませんが、安心してください。その根本にあるアイデアは、驚くほど直感的でエレガントです。
なぜ単純比較は危険なのか?2つの罠を徹底解剖
DiDの賢さを理解するために、まずは「やってはいけない」比較方法、つまり単純比較の限界から見ていきましょう。ここには、私たちの判断を大きく誤らせる2つの大きな「罠」が潜んでいます。
先ほどのコーヒーショップの例をもう一度、今度は具体的な数字を交えて考えてみます。
- 介入群: 東京支社(新サンドイッチを導入)
- 対照群: 大阪支社(従来メニューのまま)
- アウトカム: 1店舗あたりの月間平均売上(万円)
| 介入前 (t=0) | 介入後 (t=1) | |
| 東京 | 100万円 | 120万円 |
| 大阪 | 80万円 | 90万円 |
このデータを見て、どう考えますか?
罠1:時間の流れがもたらす「見せかけの効果」(単純な前後比較)
最も安直なのは、東京の店舗だけを見て、「売上が100万円から120万円に、20万円も増えた!新サンドイッチは大成功だ!」と結論づけることです。
\[ \text{東京の変化} = 120 – 100 = 20\text{万円} \]
しかし、この20万円の増加は、すべてが新サンドイッチのおかげでしょうか? もし、この期間に景気が全国的に上向いていたり、コーヒーの新しいブームが来ていたりしたらどうでしょう。その場合、たとえ新商品を導入しなくても、売上は自然と伸びていたかもしれません。この「時間と共に変化する共通の要因(時間トレンド)」を無視してしまうのが、この比較方法の致命的な欠点です。
罠2:もともとの違いがもたらす「誤った結論」(単純な介入後比較)
では、介入後のデータだけを見て、東京と大阪を比べるのはどうでしょう。「介入後、東京の売上は120万円、大阪は90万円。その差は30万円だ!」
\[ \text{介入後の群間差} = 120 – 90 = 30\text{万円} \]
これもまた危険な結論です。そもそも、東京と大阪では市場の規模や顧客層、物価などが全く違います。介入前から、東京の売上は大阪より20万円高かった(100万円 vs 80万円)ですよね。この「時間によらず存在する、グループ間の固定的な違い」が、介入後の差にも影響を与えてしまっています。
DiDの登場:2つの「差」で真実に迫る
DiDは、これら2つの罠を同時に、そして見事に回避します。その名の通り、2段階の「差」を取ることで、邪魔な要因を打ち消し合い、純粋な介入効果だけを浮かび上がらせるのです。
ステップ1:それぞれの「時間変化」を計算する(1つ目の差)
まず、介入群と対照群、それぞれで「時間による変化量」を計算します。
- 東京(介入群)の時間変化:
\(120\text{万円} – 100\text{万円} = +20\text{万円}\)
この中には、「新サンドイッチの効果」と「時間トレンド」の両方が含まれているはずです。 - 大阪(対照群)の時間変化:
\(90\text{万円} – 80\text{万円} = +10\text{万円}\)
大阪では新商品は導入していないので、この変化は純粋に「時間トレンド」だけを反映していると考えられます。
ステップ2:「時間変化の差」から介入効果を抽出する(2つ目の差)
次に、ステップ1で計算した2つの変化量の「差」を取ります。
\[ \begin{aligned} \text{DiD推定量} &= (\text{東京の時間変化}) – (\text{大阪の時間変化}) \\ &= (20\text{万円}) – (10\text{万円}) \\ &= 10\text{万円} \end{aligned} \]
この計算が何をしているか、分かりますか?
東京の変化量(効果+トレンド)から、大阪の変化量(トレンドのみ)を差し引いています。これにより、共通の時間トレンドが相殺され、私たちが本当に知りたかった「新サンドイッチの純粋な効果」だけが残るのです。
DiDのロジックを図で理解する
この考え方をグラフで見てみると、さらに直感的に理解できます。
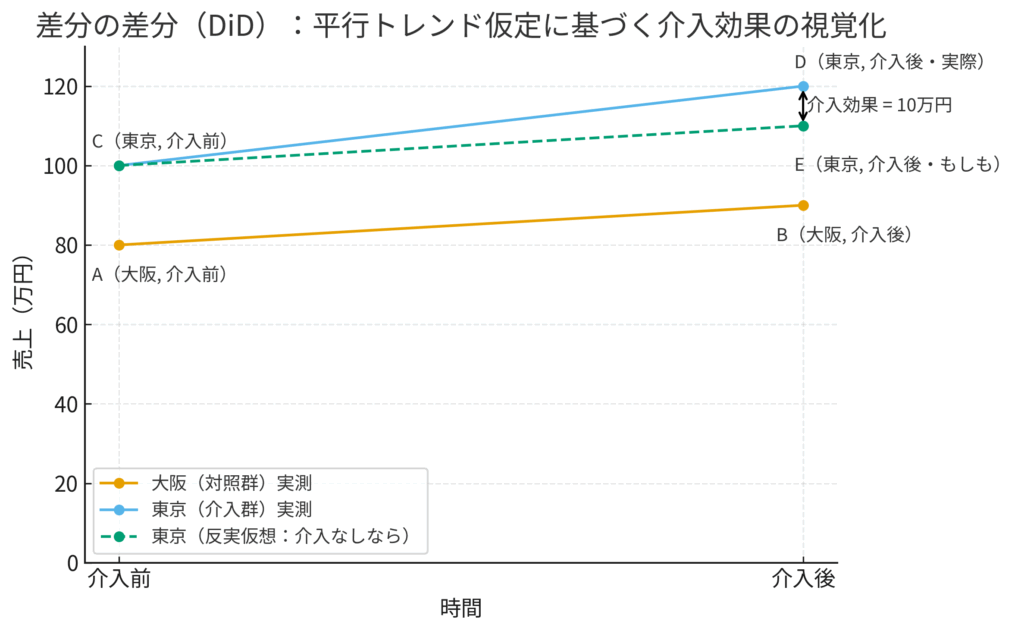
上の図で、
A -> Bの線は、大阪(対照群)で実際に観測された売上の変化、つまり「時間トレンド」を表しています(+10万円)。C -> Dの線は、東京(介入群)で実際に観測された売上の変化です(+20万円)。- 点線の
C -> Eは、DiDの根幹をなす「もしも東京で新商品を導入しなかったら(反実仮想)」という世界線です。DiDでは、この「もしも」の世界の変化は、対照群の変化と同じ(平行)であると仮定します。つまり、C点からB点と同じ傾きで伸びるはずだと考えるのです。 - その結果、
Eの売上は \(100 + 10 = 110\) 万円になったはずだと推定できます。 - 実際に観測された東京の売上
D(120万円)と、この「もしも」の世界E(110万円)の差こそが、介入の純粋な効果(10万円)となるわけです。
DiDの心臓部:「平行トレンド仮定」という絶対的なお約束
DiDのロジックが、上の図の点線、つまり「もし介入がなかったら、介入群と対照群のトレンドは平行だっただろう」という仮定の上に成り立っていることにお気づきでしょうか。これが、DiDの分析全体の妥当性を支える、最も重要で、そして最も議論を呼ぶ「平行トレンド仮定(Parallel Trends Assumption)」です。
もし仮定が崩れたら…?
この仮定がもし成り立っていなかったら、何が起こるでしょうか。例えば、東京の店舗周辺だけで大規模な再開発があり、新商品を導入しなくても売上が急上昇する運命にあったとします。
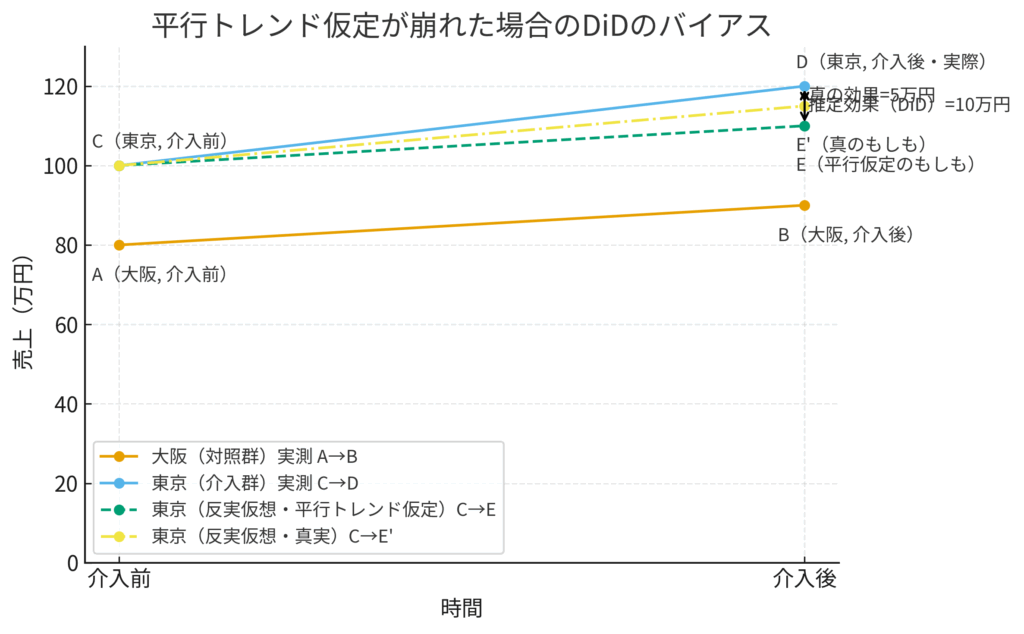
この場合、「真のもしも」のトレンド(C -> E')は、大阪のトレンド(A -> B)よりも急になります。DiDはそれを知らずに、あくまで大阪のトレンドを基準に「もしも」の値を計算してしまうため、介入効果を D - E'(真の効果 = 5万円)ではなく、それよりも大きく(10万円)推定してしまいます。これは、本来は再開発による効果の一部を、新商品の効果だと勘違いしてしまっている状態です。
仮定のもっともらしさをどう確認するか?
この仮定は「もしも」の話なので、介入後のデータを使って直接証明することはできません。しかし、私たちはこの仮定が「もっともらしい」かどうかを、ある程度検証することができます。
最も一般的な方法は、介入が行われる前の、複数時点のデータを使ってグラフを描いてみることです。もし介入前の数年間、介入群と対照群のトレンドが実際に平行に推移しているのであれば、「介入後も、もし介入がなければ平行だっただろう」という主張の説得力は増しますよね。これは、分析の信頼性を担保するために、論文などでは必ずと言っていいほど示される、非常に重要なステップです。
数式で見るDiDの世界:回帰モデルでエレガントに表現する
これまで図や言葉で説明してきたDiDのロジックは、一本の回帰式でエレガントに表現することができます。これが、DiDが統計学的に強力なツールである理由の一つです。
\[ Y_{it} = \beta_0 + \beta_1 \text{Post}_t + \beta_2 \text{Treat}_i + \delta (\text{Post}_t \times \text{Treat}_i) + \epsilon_{it} \]
この数式が、先ほどのコーヒーショップの例とどう対応しているのか、各パーツを解剖してみましょう。
- \( Y_{it} \): 個人や施設
iの時点tにおけるアウトカム。まさに、表の中の売上(100, 120, 80, 90)そのものです。 - \( \text{Treat}_i \): グループを表す変数です。東京(介入群)なら1、大阪(対照群)なら0が入ります。
- \( \text{Post}_t \): 時間を表す変数です。介入後(t=1)なら1、介入前(t=0)なら0が入ります。
- \( \epsilon_{it} \): モデルでは説明しきれない誤差です。
そして、係数(βやδ)が、それぞれの「差」に対応します。
- \( \beta_0 \): 切片。基準となるグループ(対照群・介入前、つまり大阪の介入前)の平均売上です。この例では80万円に相当します。
- \( \beta_1 \): 時間の効果。介入の有無にかかわらず、時間が経過することで生じる売上の変化(時間トレンド)です。大阪の売上変化(+10万円)に相当します。
- \( \beta_2 \): グループの効果。時間によらない、グループ間の固定的な差です。介入前における東京と大阪の売上差(100-80=20万円)に相当します。
- \( \delta \): 交互作用項の係数。これこそがDiDの推定量です。
TreatとPostの両方が1のとき、つまり「介入群」で「介入後」の場合にのみ、上乗せされる効果を意味します。
なぜ交互作用項 \( \delta \) が「答え」になるのか?
4つのグループそれぞれの平均売上が、この式でどう表現されるか見てみましょう。
- 大阪・介入前 (Treat=0, Post=0):
\( E[Y] = \beta_0 \) - 大阪・介入後 (Treat=0, Post=1):
\( E[Y] = \beta_0 + \beta_1 \) - 東京・介入前 (Treat=1, Post=0):
\( E[Y] = \beta_0 + \beta_2 \) - 東京・介入後 (Treat=1, Post=1):
\( E[Y] = \beta_0 + \beta_1 + \beta_2 + \delta \)
この式を使って、先ほどのDiDの計算 (D-C) - (B-A) を行ってみると…
D - C= (東京・後) – (東京・前) = \((\beta_0 + \beta_1 + \beta_2 + \delta) – (\beta_0 + \beta_2) = \beta_1 + \delta\)B - A= (大阪・後) – (大阪・前) = \((\beta_0 + \beta_1) – (\beta_0) = \beta_1\)
そして、これらの差を取ると、
\((D – C) – (B – A) = (\beta_1 + \delta) – (\beta_1) = \delta \)
見事に、交互作用項の係数 \( \delta \) だけが残りました。つまり、この回帰モデルをデータに当てはめて \( \delta \) の値を推定することは、私たちが手計算で行った「差の差」を計算することと全く同じなのです。回帰モデルを使うことで、標準誤差やp値も同時に計算でき、統計的な推論が可能になります。
医療現場での応用例:診療報酬改定の効果を測る
この強力なDiDを、医療データ分析の現場で使ってみましょう。
- シナリオ: 2020年度の診療報酬改定(厚生労働省, 2020)を参考に、ある特定の心疾患治療に対する新しいチーム医療加算が、A県でのみ先行導入されたと仮定します。この政策が、患者の平均在院日数を短縮させたかどうかを検証したい。
- 介入群: A県の対象病院群
- 対照群: 人口構成や医療資源レベルが似ているが、新加算が導入されなかったB県の病院群
- データ: 政策導入の前後数年間にわたる、各病院の心疾患患者のレセプトデータから得られる平均在院日数
- 分析: 上記のDiD回帰モデルを用いて、県(A県=1, B県=0)と改定時期(改定後=1, 改定前=0)の交互作用項 \( \delta \) を推定します。この \( \delta \) が、新加算導入による在院日数の純粋な短縮効果(ATT)の推定値となります。
分析の最後の、そして最大の落とし穴:「クラスター化」されたデータへの配慮
さて、DiD回帰モデルという強力なエンジンを手に入れ、介入効果 \( \delta \) を推定する準備が整いました。しかし、ここでアクセルを踏み込む前に、絶対に確認しなければならない安全装置の話があります。これを怠ると、どんなに精巧な分析も一瞬で信頼性を失いかねません。それは、医療データが持つ特有の性質、「クラスター構造」への配慮です。
これは、統計に慣れていない人が最も見落としがちで、しかし結果を根本から覆しかねない、非常に重要なポイントです。
クラスター構造とは何か?:データは「個人」で完結していない
これまでの例で、私たちは「病院」のデータを見てきました。病院の中には、たくさんの患者さんがいますよね。ここで質問です。同じ病院に入院している患者さんAと患者さんBのデータは、全く無関係(統計学の言葉で「独立」)と言えるでしょうか?
答えは、おそらく「ノー」です。
なぜなら、彼らは同じ病院という「クラスター(集団)」に所属しているからです。
- 同じ治療方針のプロトコルが適用されているかもしれない。
- 同じ医師団や看護チームが担当しているかもしれない。
- 同じ医療設備や院内環境を共有している。
こうした共通の要因によって、同じ病院内の患者さんのアウトカム(この例では在院日数)は、赤の他人である別の病院の患者さんと比べて、多かれ少なかれ似通った傾向を持つはずです。言わば、彼らは「同じ釜の飯を食った仲間」のようなもので、そのデータには目に見えない相関が潜んでいるのです。
このような構造は、病院単位に限りません。
- 担当医: 同じ医師が診た患者さんたちは、その医師のスキルや治療スタイルという共通要因に影響されます。
- 地域: 同じ市町村に住む住民は、地域の医療資源や健康意識、環境要因などを共有しています。
- 家族: 家族内のメンバーは、遺伝的要因や生活習慣を共有しています。
このように、多くの医療データは個人単位で完結しておらず、何らかのグループ(クラスター)にまとめられる構造を持っているのです。
なぜクラスター構造が問題なのか?:「情報の水増し」という罠
「なるほど、データに相関があるのは分かった。でも、それが分析にどう影響するの?」と思うかもしれません。これが、致命的な問題を引き起こすのです。
一言で言うと、クラスター構造を無視することは、手元にある情報の量を不当に「水増し」してしまうことにつながります。
たとえ話で考えてみましょう。全国の高校生の意識調査をしたいとして、無作為に40人の高校生を全国から選んできました。この40人の意見は、非常に多様で価値のある「40人分の情報」と言えるでしょう。
一方で、ある学校のあるクラスから、そこにいた40人全員にアンケートを取ったとします。これも40人のデータですが、果たして先ほどと同じ「40人分の情報」と言えるでしょうか? クラスメイトたちは、同じ先生に教わり、同じ環境で過ごしているため、その意見は似通っている可能性が高いですよね。実質的な情報の量は、「1クラス分の情報」に近く、全国から集めた40人分の情報量には到底及びません。
統計モデルでクラスター構造を無視するということは、この「クラスの40人」を、あたかも「全国から無作為に集めた40人」であるかのように扱ってしまうことと同じなのです。
この「情報の水増し」は、統計的な推定、特に「標準誤差」の計算に深刻な影響を与えます。
- 標準誤差の過小評価: 標準誤差とは、推定された係数(例えば介入効果 \( \delta \))が「どれくらい不確実か、ばらつくか」を示す指標です。情報量が多ければ多いほど、私たちはその推定値に自信を持てるので、不確実性は小さく(標準誤差は小さく)なります。クラスターを無視して情報量を水増しすると、モデルは「こんなにたくさんの独立したデータがあるなら、この推定値はかなり正確なはずだ!」と勘違いし、標準誤差を不当に小さく計算してしまうのです。
- p値への影響と誤った結論: 標準誤差が不当に小さくなると、何が起こるか。統計的有意性を示すp値も、不当に小さくなります。その結果、本来は偶然の範囲内のわずかな差であったとしても、「統計的に有意な差がある(p < 0.05)」という誤った結論を導き出すリスクが劇的に増加します。これは、「本当は効果がないのに、効果があったと叫んでしまう」という、科学における最も避けるべき過ち(第1種の過誤)です。
Bertrandらの衝撃的な研究:DiD分析の常識を変えた警鐘
この問題の深刻さを、実証的に示したのが、経済学の分野におけるBertrand、Duflo、Mullainathanによる、2004年の非常に影響力のある研究です。彼らは、過去のDiD分析でよく使われていたデータを用いてシミュレーションを行い、クラスター構造(この場合は州ごとの相関)を無視した場合に何が起こるかを検証しました。
その結果は、研究者たちを震撼させました。本来、統計的に有意と判断する誤りの確率(有意水準)は5%にコントロールされているはずです。しかし、クラスター構造を無視したDiD分析では、この誤審率が実際には40%以上にまで跳ね上がってしまうケースがあることを示したのです。これは、20回に1回間違えるはずの判断を、2回に1回近く間違えてしまうということであり、分析の信頼性が根底から覆ることを意味します。
解決策:「クラスターロバスト標準誤差」という現代の標準作法
では、どうすればこの深刻な罠を回避できるのでしょうか。そのための現代的な標準作法が、「クラスターロバスト標準誤差(Cluster-Robust Standard Errors)」を用いることです。
これは、難しい数式に立ち入る必要はありませんが、そのコンセプトは「同じクラスター内のデータは独立ではないという現実を認めた上で、標準誤差をより堅牢に(ロバストに)計算し直す方法」と理解してください。「サンドイッチ推定量」とも呼ばれるこの手法は、クラスター内の相関を考慮して、不当に小さくなった標準誤差を、より現実的な大きさに補正してくれます。
現在では、Stata、R、Pythonといった主要な統計ソフトを使えば、オプションを一つ指定するだけで、このクラスターロバスト標準誤差を簡単に計算することができます。
結論として、DiD分析、特に複数の個人が複数の施設に所属するような医療データ(パネルデータ)を扱う際には、クラスターを指定してクラスターロバスト標準誤差を計算することは、もはや「推奨」ではなく「必須」のお作法です。それは、分析の信頼性を守り、科学者としての誠実さを示すための、最後の、しかし最も重要な仕上げなのです。
合成コントロール法(SCM):オーダーメイドの「もしも」を創り出す
差分の差分法(DiD)は、比較可能な対照群が複数存在するときに絶大な威力を発揮します。しかし、もし私たちが評価したい介入が、たった一つの対象にしか行われなかったとしたらどうでしょう?
例えば、
- ある国が、国民皆保険制度を抜本的に改革した。
- ある都道府県が、独自の高度医療センターを設立した。
- ある大学の附属病院が、電子カルテとAI診断支援システムを統合した新システムを導入した。
これらのケースでは、DiDの前提となる「似たような対照群」を複数見つけるのは極めて困難です。国や都道府県、あるいは特定のブランド力を持つ病院は、それぞれが唯一無二の存在であり、全く同じ歴史や特性を持つ「双子」は存在しません。このような「比較対象は一つ(N=1)のケーススタディ」は、因果推論における長年の難問でした。
DiDの限界とSCMの登場:「なければ、作ればいい」という革命
この難問に対する、非常に独創的でパワフルな答えが「合成コントロール法(Synthetic Control Method, SCM)」です。
SCMのアイデアを一言で言うなら、「本物そっくりの『もしも』の世界を、データからオーダーメイドで作り上げる」というものです。一つのはっきりとした対照群を探すのではなく、複数の対照群「候補」を材料として、それらを巧みに混ぜ合わせることで、介入を受けた群の「もし介入がなかった場合の姿(反実仮想)」、いわば架空の双子のクローンをコンピューター上で合成するのです。
SCMの仕組みを徹底解剖:架空の双子を作る3つのステップ
この魔法のようなプロセスを、具体的な医療シナリオで見ていきましょう。
- シナリオ: A県が、AIを活用した画期的ながん検診受診率向上プログラムを2015年から開始した。このプログラムの真の効果を測定したい。
- 課題: A県と全く同じ人口動態、医療インフラ、そして県民性を持つ「双子」のB県は、日本のどこにも存在しない。
ここでSCMが登場します。
ステップ1:ドナープール(材料候補のリスト)を作成する
まず、介入を受けていない他の46都道府県を「比較対象の候補」としてリストアップします。これが「ドナープール」と呼ばれます。彼らが、これから作る「合成A’県」の材料となります。
ステップ2:最適なレシピ(重み)を探求し、「合成A’県」を生成する
次に、この46の材料を、どのような割合で混ぜ合わせれば、最もA県にそっくりな「合成A’県」が作れるかを探ります。この「混ぜ合わせる割合」が「重み(weight)」です。
では、何をもって「そっくり」と判断するのでしょうか? SCMでは、プログラムが導入される前の期間(例:2005年〜2014年)において、以下の2点が実際のA県と合成A’県で可能な限りピッタリ一致するように、コンピューターが最適な重みを自動的に計算します。
- アウトカムの軌跡: 過去の「がん検診受診率」の年々の推移が、瓜二つになるようにします。
- 重要な共変量: 受診率に影響を与えそうな他の要因(例:高齢者人口比率、一人あたり所得、医師数など)の平均値も、ほぼ同じになるように調整します。
その結果、例えば以下のような「レシピ」が決定されます。
\[ \text{合成A’県} = (0.4 \times \text{B県}) + (0.2 \times \text{C県}) + (0.15 \times \text{D県}) + \dots \]
これは、「合成A’県」が、B県のデータを40%、C県のデータを20%、D県のデータを15%…といった割合で混ぜ合わせたものであることを意味します。この重みは、研究者の主観ではなく、データに基づいて客観的に決定されるのが最大のポイントです。
ステップ3:「現実」と「もしも」を比較して効果を推定する
介入前の期間で、実際のA県にそっくりな「合成A’県」という完璧な双子を作り出すことに成功したら、いよいよ効果の推定です。
プログラムが導入された2015年以降、実際に観測されたA県の受診率と、合成A’県が示す「もしもプログラムがなかった場合のA県の受診率」の差を計算します。この差こそが、プログラムがもたらした純粋な効果(受診率の押し上げ効果)の推定値となります。
このプロセスをグラフで可視化すると、SCMの説得力が一目瞭然となります。
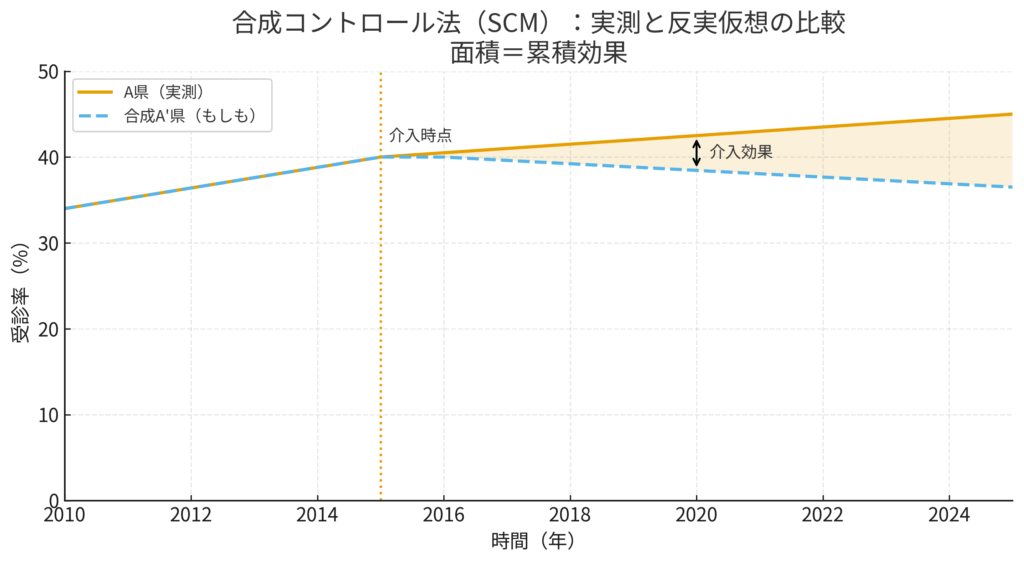
このグラフでは、2015年の介入時点まで、実線のA県と点線の合成A’県がぴったりと重なって推移しています(これが「良いフィット」です)。しかし、介入後は、実際のA県の受診率が「もしも」の軌跡から上方に乖離していく様子がはっきりと見て取れます。この2本の線の間の面積が、プログラムがもたらした累積的な効果と解釈できます。
SCMの強みと注意点:使いこなすための勘所
SCMは非常に強力なツールですが、その力を正しく引き出すためには、いくつかの重要なポイントを理解しておく必要があります。
SCMの3つの強み
- 客観性: 研究者が「この県が似ているだろう」と恣意的に対照群を選ぶ「チェリーピッキング」のリスクを排除します。重みはデータによって決定されるため、分析の透明性と再現性が高まります。
- 透明性: どの都道府県がどれくらいの重みで「合成A’県」の作成に貢献したかが明確にわかります。もし、全く無関係と思われた県に大きな重みが割り当てられた場合、その理由を考察することで、新たな発見につながる可能性もあります。
- 自己診断能: SCMの最大の美点の一つは、分析の信頼性を自分自身で診断できることです。もし介入前の期間に、実際のA県と合成A’県の軌跡がうまく一致しない(フィットが悪い)場合、それは「信頼できる双子を作れなかった」ことを意味し、この分析結果を信じるべきではない、という明確な警告サインになります。
SCMの3つの注意点
- 十分な介入前データが必要: 信頼できる「双子」を作るためには、その特徴を学習するための十分な長さの介入前期間のデータが不可欠です。数年程度のデータでは、偶然トレンドが一致しただけかもしれず、信頼性の高い合成はできません。
- ドナープールの質: ドナープール(材料候補)の中に、介入群とあまりにもかけ離れた特徴を持つものばかりだと、いくら組み合わせても良い「双子」は作れません。これは、材料がないのに美味しい料理は作れないのと同じです。
- 統計的推論の複雑さ: 「観測された差は、本当に統計的に有意なのか?」を評価する手続きが、DiDより少し複雑です。SCMでは「Permutation Test(偽薬検定)」という手法がよく用いられます。これは、「もし介入が、効果がゼロであるはずの他の都道府県で行われたとしたら?」というシミュレーションを何度も繰り返し、実際にA県で観測されたほどの大きな差が、偶然でも生じる確率がどれくらいかを評価する方法です。
医療分野での金字塔:カリフォルニアのタバコ規制研究
SCMの有用性を世界に知らしめた金字塔的な研究が、政治経済学者のAbadieらによる、カリフォルニア州のタバコ規制プログラム(プロポジション99)の効果検証です(Abadie et al., 2010)。
1988年、カリフォルニア州はタバコ税を大幅に引き上げ、その税収を包括的なタバコ規制策に充てるという、当時としては画期的な法律を施行しました。これが一人当たりのタバコ消費量に与えた影響を評価するため、研究チームは他の38州をドナープールとして、「もし規制がなかった場合のカリフォルニア(合成カリフォルニア)」を作成しました。
分析の結果は衝撃的でした。合成カリフォルニアのタバコ消費量がほぼ横ばいであったのに対し、実際のカリフォルニアの消費量は法律施行後に劇的に低下していました。これにより、プロポジション99がタバコ消費量を大幅に減少させたという強力な証拠が、誰の目にも明らかなグラフとして示されたのです。この研究は、N=1のケーススタディにおける政策評価のあり方を一変させ、その後の多くの医療・公衆衛生研究に絶大な影響を与えました。
DiDとSCM、どう使い分ける?:あなたの研究に最適なツールを選ぶ羅針盤
さて、私たちは「差分の差分法(DiD)」と「合成コントロール法(SCM)」という、2つの非常に強力な武器を手に入れました。どちらも、ランダム化比較試験(RCT)が使えない状況で、観察データから介入の因果効果を探るための頼もしい相棒です。
しかし、いざ自分の研究テーマを前にしたとき、多くの人がこう思うはずです。「私のこのケースでは、一体どちらを使えばいいのだろう?」と。
この2つの手法は似ているようで、その哲学と得意なシチュエーションが異なります。完璧なルールブックはありませんが、どちらを選ぶべきか判断するための、いくつかの重要な指針があります。ここでは、その使い分けの核心に迫っていきましょう。
核心的な違いは「比較対象」の作り方
両者の最も根本的な違いは、「もしも介入がなかったら」という反実仮想を、どのようにして作り出すかというアプローチにあります。
- 差分の差分法(DiD)のアプローチ:
DiDは、「介入群と似たような『平均的な』振る舞いをする対照群」を探し出し、そのグループの時間的変化を「もしも」の世界の基準として借用します。多数の施設や個人を含む対照群全体のトレンドを見ることで、個々のばらつきをならし、安定した「共通のトレンド」を推定することを目指します。 - 合成コントロール法(SCM)のアプローチ:
SCMは、似たような単一の対照群が存在しないことを前提とします。その代わり、「複数の対照群候補を材料として、介入群にそっくりな『オーダーメイドのクローン』を合成する」というアプローチを取ります。平均的なグループではなく、介入群そのものの過去の軌跡を再現することに特化しています。
この違いから、それぞれが得意とする「問いの種類」も見えてきます。
- DiDは「介入の『平均的な』効果は何か?」(ATT: Average Treatment effect on the Treated) を問うのに適しています。
- SCMは「『この特定の』ケース(国、地域、病院)で何が起こったか?」という問いに答えるのに適しています。
実践的なシナリオで考える使い分け
この違いを、具体的な医療現場のシナリオに当てはめてみましょう。
DiDが輝くシナリオ:
- 状況: 全国の数千のクリニックを対象に、ある生活習慣病の新薬に関する診療ガイドラインが改訂された。このガイドライン遵守率が高い病院グループと、低い病院グループで、患者の検査値改善に差があるかを見たい。
- なぜDiDか?:
- 多数の比較対象: 介入群(遵守率が高い群)と比較可能な対照群(遵守率が低い群)が多数存在します。
- 平均的な効果の関心: 私たちが知りたいのは、個々のクリニックの特殊な事情ではなく、「ガイドラインを遵守するという介入が、平均してどれくらいの効果を持つか」です。
- 仮定の検証: 介入前のデータが豊富にあれば、多数のクリニックの平均的なトレンドを比較することで、平行トレンド仮定がもっともらしいかを検証しやすいです。
SCMが輝くシナリオ:
- 状況: 日本の特定の都道府県(例:A県)だけが、海外の先進事例を参考に、AIとゲノム情報を活用した最先端のがんプレシジョン・メディシン拠点を設立した。5年後、この政策がA県の県民のがん死亡率にどのような影響を与えたかを評価したい。
- なぜSCMか?:
- 唯一無二の介入対象: A県という特定の行政単位が対象であり、これと全く同じ条件の「双子」の都道府県は存在しません。
- 特定のケースへの関心: 私たちが知りたいのは、他の地域にも適用できるような平均的な効果ではなく、「A県で実施された、この大規模プロジェクトが、A県民に何をもたらしたか」という、まさにそのケース自体です。
- クローンの作成: 他の46都道府県のデータを材料に、「もし拠点病院が設立されなかった場合のA県」という合成コントロールを作り出すことで、説得力のある比較が可能になります。
比較表で見るDiDとSCMのまとめ
これまでの議論を、以下の比較表にまとめました。あなたの研究計画と照らし合わせながら、どちらのツールがよりフィットするかを考えてみてください。
| 特徴 | 差分の差分法 (DiD) | 合成コントロール法 (SCM) |
|---|---|---|
| 主な問い | 介入の平均的な効果 (ATT) は何か? | この特定のケースで何が起こったか? |
| 介入対象 | 多群・多数のデータ(例:多くの病院、個人) | 単一または少数の介入群(例:特定の国、都道府県) |
| 対照群の作り方 | 似た振る舞いをする実在の対照群を利用 | 複数の対照群候補から架空のクローンを合成 |
| 中心的な仮定 | 平行トレンド仮定 | 介入前の期間における良好なフィット |
| データの要求 | 介入前後、複数群のデータ。介入前が複数時点あると望ましい | 長期間の介入前データが不可欠 |
| 統計的推論 | 回帰モデルの係数と(クラスターロバスト)標準誤差 | Permutation Test(偽薬検定)などが一般的 |
進化し続けるツールたち:最新の研究動向
DiDとSCMの世界は、統計学者や経済学者たちの活発な研究によって、今もなお進化し続けています。
例えば、現実のデータでは、介入のタイミングが施設や地域によってバラバラなケースがよくあります。このような「Staggered Adoption」と呼ばれる状況では、従来の単純なDiDモデルが誤った結果を導く可能性があることが指摘され、Callaway & Sant’Anna (2021)やSun & Abraham (2021)といった研究者たちから、より頑健な新しい推定方法が次々と提案されています。
またSCMにも、回帰分析の利点を取り入れて予測精度を高めようとする拡張版(Augmented SCMなど)が登場しており (Ben-Michael, Feller & Rothstein, 2021)、その応用範囲はさらに広がりを見せています。
これらの発展は、私たちが観察データという制約の中で、より真実に近い因果効果を探求するための強力な追い風となっています。
最終的に、どちらの手法を選ぶかは、あなたの「研究の問い」と手元にある「データの構造」に深く依存します。完璧な手法は存在しません。それぞれの長所と限界を深く理解し、自分の問いに最も誠実に答えられるツールを選択し、その分析の妥当性を注意深く検証する。そのプロセスこそが、信頼性の高いエビデンスを生み出すための鍵となるのです。
まとめ:政策評価の羅針盤を手に、エビデンスの海へ
さて、私たちは差分の差分法(DiD)と合成コントロール法(SCM)という、政策評価や因果推論の広大な海を航海するための、2つの強力な「羅針盤」を手に入れました。ここまで長い旅でしたが、いかがでしたでしょうか。
これらの手法は、単なる複雑な統計モデルではありません。それは、私たちが日々直面する「あの介入は本当に意味があったのか?」という根源的な問いに対して、ランダム化比較試験(RCT)という理想の船が使えない状況でも、手元にある観察データという海図を頼りに、科学的な根拠を持って答えを探しにいくための知恵であり、技術です。
核心は「質の高い『もしも』の世界」を科学すること
振り返ってみれば、DiDとSCM、アプローチは違えど、その思想の根幹は共通していました。それは、「介入がなかった場合の『もしも』の世界(反実仮想)を、データからいかに説得力を持って構築するか」という一点に尽きます。
- DiDは、介入を受けなかった対照群の「平均的な時間の流れ」を借りてきて、「もしも」のトレンドを描き出しました。
- SCMは、介入を受けなかった複数の候補たちを巧みに組み合わせることで、「もしも」の瓜二つのクローンをオーダーメイドで創り出しました。
どちらの手法も、交絡という霧が立ち込める観察データの海の中で、介入の真の効果という目的地を指し示すために、「もしも」という名の北極星をデータから見つけ出す試み、と言えるのかもしれません。
羅針盤を使いこなすための最も大切な「心構え」
しかし、どんなに精巧な羅針盤も、それを使う航海士が空や海の様子を読めなければ、宝の持ち腐れになってしまいます。DiDやSCMを使いこなす上で最も重要なのは、モデルをただ実行することではなく、その結果を批判的に吟味する視点を常に持ち続けることです。
- 「平行トレンド仮定は、本当に信じられるだろうか?」(DiD)
- 「介入前のフィットは、本当に良好と言えるだろうか?」(SCM)
これらの問いかけは、分析の妥当性を担保するための単なるチェックリストではありません。それは、データと誠実に向き合い、私たちの分析が導き出す結論の限界を正直に認めるための、科学者としての誠実さが問われるプロセスです。このステップを怠れば、どんな高度な手法も、誤った結論を導き出す危険な道具になりかねません。
次のステップへ:データから因果を見抜く「眼」を養う
これらの分析手法を理解し、その長所と限界を把握することは、あなたの武器庫に新しい統計ツールを加える以上の意味を持ちます。それは、医療ビッグデータという膨大な情報の海を見る「解像度」を上げ、単なる相関関係に惑わされずに、その背後に隠された因果関係を見抜く「眼」を養うことに他なりません。
この「眼」を養うことで、私たちは臨床現場での日々の意思決定をより確かなものにし、医療政策の立案に質の高いエビデンスを提供し、そして最終的には、真にエビデンスに基づいた医療の実現に貢献することができるはずです。
今回の講座が、その大きな一歩となることを心から願っています。
参考文献
- Abadie, A., Diamond, A., & Hainmueller, J. (2010). Synthetic control methods for comparative case studies: Estimating the effect of California’s tobacco control program. Journal of the American Statistical Association, 105(490), 493-505.
- Angrist, J. D., & Pischke, J. S. (2009). Mostly harmless econometrics: An empiricist’s companion. Princeton University Press.
- Ben-Michael, E., Feller, A., & Rothstein, J. (2021). The Augmented Synthetic Control Method. Journal of the American Statistical Association, 116(536), 1789–1803.
- Bertrand, M., Duflo, E., & Mullainathan, S. (2004). How much should we trust differences-in-differences estimates?. The Quarterly Journal of Economics, 119(1), 249-275.
- Callaway, B., & Sant’Anna, P. H. (2021). Difference-in-differences with multiple time periods. Journal of Econometrics, 225(2), 200-230.
- Card, D., & Krueger, A. B. (1994). Minimum wages and employment: a case study of the fast-food industry in New Jersey and Pennsylvania. American Economic Review, 84(4), 772-793.
- Hernán, M. A., & Robins, J. M. (2020). Causal inference: What if. Chapman & Hall/CRC.
- Sun, L., & Abraham, S. (2021). Estimating dynamic treatment effects in event studies with non-staggered adoption. Journal of Econometrics, 225(2), 175-199.
- 厚生労働省 (2020). 令和2年度診療報酬改定について. (参照した具体的な資料名やURLを記載することが望ましい)
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






