GLMは、線形回帰の「縛り」を解き放つ強力な分析の道具箱です。データの性質に合わせて「確率分布」と「リンク関数」という部品を交換することで、YES/NOの確率やイベントの発生回数など、多様な医療データを統一的な視点で分析できます。
血圧のような連続値には強力ですが、臨床で頻出する「YES/NO」や「回数」データには不向きです。予測値が100%を超えたりマイナスになる原因は、①正規分布、②直線性、③線形結合という3つの暗黙の前提(縛り)にあります。
GLMはこの縛りを3つの構成要素で解決します。
1. 確率分布: データの性質(二値、回数など)に適合させます。
2. リンク関数: 予測値を適切な範囲(例: 0-1の確率)に変換します。
3. 線形予測子: 全モデル共通の不変の計算コアです。
ロジスティック回帰やポアソン回帰などを個別に学ぶ必要はありません。GLMという統一された視点を使えば、データの種類に応じて「確率分布」と「リンク関数」という部品を交換するだけで、様々な分析に一貫して対応できます。
はじめに:なぜ「線形回帰」だけでは不十分なのか?
この記事は、医療データ分析の強力なツールである一般化線形モデル(Generalized Linear Model, GLM)について、その本質的な考え方から実践的な応用までを解説します。
この記事を読み終える頃には、皆さんは次の点を理解できるようになるはずです。
- なぜ臨床研究や医療データサイエンスにおいて、基本的な線形回帰だけでは対応できない場面が多いのか。
- 多種多様に見える回帰モデル(ロジスティック回帰、ポアソン回帰など)が、「GLM」という一つの統一された視点で理解できること。
- GLMが、私たちのデータ分析の引き出しをどれほど豊かにし、より現実に即した問いに答える力を与えてくれるのか。
それでは、さっそく本題に入っていきましょう。
臨床現場にあふれる「線形」では捉えきれないデータ
「患者さんの血圧を予測したい」——こんなとき、多くの人がまず線形回帰モデルを思い浮かべるかもしれません。確かに、血圧のように数値が連続的に変化する値を予測する場合、線形回帰は非常に有効なツールです。
しかし、私たちが日常の臨床や研究で向き合う現実は、もっと複雑で多様な顔を持っていますよね。例えば、以下のような問いに答えたいと思ったことはないでしょうか?
- ある新しい治療法によって、がんが寛解する「か」、しない「か」(結果は0か1の二択)
- 特定のケア介入によって、患者さんの1ヶ月あたりの転倒「回数」は減少するか(0回以上の整数)
- 疾患の重症度は、ICUへの入院「日数」とどう関連しているか(マイナスにはならない正の連続値)
これらの問いに、単純な線形回帰を無理やり当てはめようとすると、途端に不都合な事態に直面します。例えば、「寛解する確率が120%になる」「転倒回数がマイナス0.5回になる」といった、現実にはありえない予測値が計算されてしまうのです。Dobson & Barnett (2018) のような標準的な教科書でも、こうした線形モデルの限界は明確に指摘されています。
分析手法の「断片化」という壁と、統一理論「GLM」への招待状
「なるほど、じゃあ問題の種類ごとにロジスティック回帰、ポアソン回帰…と、それぞれの使い方を個別に、全部バラバラに覚えなければいけないのか…」
そう感じてしまうのは、ごく自然なことだと思います。まるで、症状ごとに全く別の薬を処方し、その薬理作用や副作用をゼロから一つひとつ学び直していくような、少し途方に暮れる感覚に近いかもしれません。
でも、もし、これら一見すると全く別物に見える回帰モデルたちが、実はある共通の「設計思想」を持つ“親戚”のようなもので、たった一つの美しく、統一された理論で理解できるとしたら、どうでしょう?
その魔法のようなフレームワークこそが、今回ご紹介する一般化線形モデル(Generalized Linear Model, GLM)なんです。GLMは、いわば線形回帰を拡張した「多様な状況に対応できる道具箱」のような存在、とたとえることができます。それは、ネジの種類(つまり、データの性質)に合わせてドライバーの先端(分析手法のパーツ)を柔軟に付け替えるような、非常に合理的で強力なアプローチを提供してくれます。
このGLMという視点を手に入れることで、分析手法の「断片的な知識」が有機的に結びつき、あなたのデータ分析の引き出しは一気に増え、より現実に即した問いに自信を持って答えられるようになるはずです。
1. 線形回帰が持つ「3つの暗黙のルール」という名の“縛り”
一般化線形モデル(GLM)の本当のすごさを理解するためには、まず、その土台となっている線形回帰モデルが、実はどのような「暗黙のルール」の上で成り立っているのかを知るのが近道です。
普段、何気なく使っているかもしれない線形回帰ですが、その裏には、モデルが正しく機能するための3つの重要な前提条件、いわば“縛り”が存在します。これらを一つずつ見ていきましょう。
縛り①:データのばらつき方は「正規分布」であるべし!
一つ目の縛りは、予測したい値(専門用語で「応答変数」)のばらつき方が、きれいな釣鐘型を描く「正規分布」に従う、という仮定です。
しかし、臨床現場のデータが全て正規分布するとは限りません。「手術が成功したか/失敗したか」の2択データや、「1ヶ月の喘息発作の回数」のように0回が最も多く、回数が増えるほど急激に減っていくデータには、この正規分布という“縛り”はフィットしないのです。
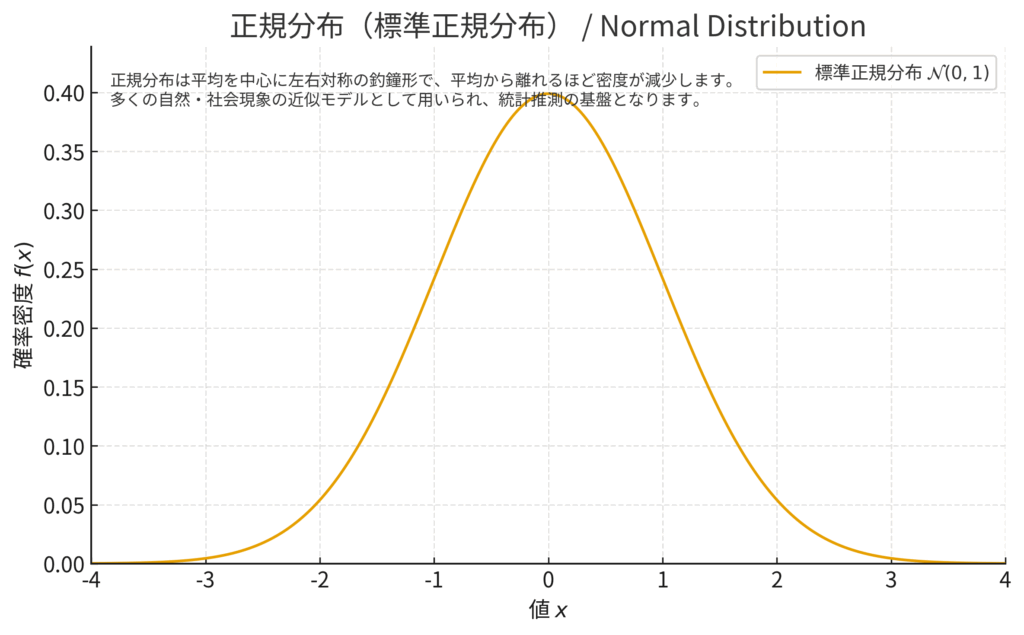
図の解説:
正規分布は、平均値を中心に左右対称な釣鐘の形をしています。多くの自然現象や社会現象がこの分布に近似することが知られており、古典的な統計モデルの多くがこの分布を前提としています (Montgomery, Peck, & Vining, 2021)。
縛り②:予測値はどこまでも「直線的」に変化すべし!
二つ目の縛りは、予測値の変化の仕方が、どこまでもまっすぐな「直線」であるという仮定です。
これは、どんな距離でも測れる一本の硬い定規を持っているようなものです。「年齢が1歳上がると、収縮期血圧は常に0.5mmHg上がる」といったように、説明変数が1増えたときに応答変数が常に一定量だけ変化する関係性を表すには、この定規はとても便利です。
しかし、この定規はマイナス方向にも無限に目盛りが続いています。そのため、「薬の投与量を増やすと、がんが寛解する確率が上がる」という関係を予測しようとすると、投与量を増やしすぎた場合に確率が100%を突き抜けて120%になったり、逆にマイナスになったりする、というありえない数値をはじき出してしまいます。0から100%の間でしなやかに曲がる巻尺が必要な場面で、硬い定規を無理やり使おうとしているようなものですね。
縛り③:説明変数と応答変数の関係は「線形」であるべし!
最後の縛りは、②とも関連しますが、モデルの根幹をなす計算が「線形」、つまり単純な足し算で表現されるという点です。
モデルの予測式は \( \text{応答変数} = \text{切片} + \text{係数} \times \text{説明変数} \) というシンプルな構造をしています。この単純さこそが線形回帰の魅力であり、結果の解釈を容易にしています。
しかし、この3つの縛りがあるからこそ、線形回帰はシンプルで強力なのですが、同時に、この縛りが「確率」や「回数」といった、正規分布に従わない、かつ特定の範囲(0以上、0~1など)に限定されるデータを扱う上での根本的な限界を生んでいたわけです。
そこで登場したGLMは、これらの縛りを柔軟に解き放つための「3つの秘密道具」を我々に与えてくれるのです。次の章で、その魅力的な道具たちを見ていきましょう。
2. GLMを解き明かす3つの鍵(コンポーネント)
さて、線形回帰が持つ「3つの縛り」を見てきましたが、GLMはそれらをどのようにして乗り越えるのでしょうか。その秘密は、これから紹介する「3つの鍵(主要な構成要素)」に隠されています。
GLMを、どんな食材(データ)でも最高の料理に仕上げる「万能調理器具」だと想像してみてください。3つの鍵は、その性能を最大限に引き出すための交換式アタッチメントのようなものです。一つずつ、その役割を解き明かしていきましょう。
鍵①:確率分布 ~データの「生まれつきの性質」に合わせる~
最初の鍵は、分析したいデータの「生まれつきの性質」や「値の取り方のパターン」に合わせて、準拠する確率分布を柔軟に選べる点にあります。
線形回帰では、「正規分布」という一つの調理法(データのばらつき方の仮定)しか選べませんでした。しかしGLMでは、まるで食材に最適な調理法を選ぶように、データの個性に合わせて確率分布を“着せ替える”ことができます。
- 二項分布: 結果が「成功か/失敗か」「あり/なし」の2種類しかないデータに使います。例えば、コインを10回投げて表が何回出るか、という状況をモデル化するのに使われます。臨床研究では、治療による寛解の有無や、副作用の発現の有無などがこれに該当します。
- ポアソン分布: 「単位時間あたりに、平均して\( \lambda \)回起こるような稀なイベントが、実際に何回観測されるか」をモデル化します。例えば、「1時間に病院の救急外来を訪れる患者の数」や「1000人・年あたりの特定の合併症の発生件数」など、カウントデータを扱うのに適しています。
各データタイプに応じた確率分布と、後ほど説明するリンク関数の代表的な組み合わせを表にまとめました。これを見ると、GLMがいかに体系的なフレームワークであるかが直感的に理解できると思います。
| データの種類 | 具体例(医療分野) | 対応する確率分布 | 代表的なリンク関数 |
|---|---|---|---|
| 連続値 | 血圧、BMI、検査値 | 正規分布 | Identity(恒等) |
| 二値(0/1) | 疾患の有無、30日以内の再入院 | 二項分布 | ロジット |
| カウント(0以上の整数) | 救急搬送件数、合併症の発生数 | ポアソン分布 | 対数(Log) |
| 正の連続値(歪みあり) | 入院日数、医療費 | ガンマ分布 | 逆数(Inverse) |
このように、データの性質に合わせて適切な確率分布を選ぶことで、より現実に即した、信頼性の高いモデリングが可能になるのです。
鍵②:リンク関数 ~予測値の“暴走”を防ぐ賢い翻訳機~
確率分布を選んだだけでは、まだ予測値がマイナスになったり1を超えたりする問題は解決しません。そこで登場するのが2つ目の鍵、リンク関数です。これは、非常に賢い「数学的な翻訳機」だと考えてください。
線形回帰の予測部分 \( \beta_0 + \beta_1 x_1 + \dots \) は、どんな実数値でも取りうる、いわば“標準語”のようなものです。この部分を線形予測子(\( \eta \) イータ)と呼びます。この\( \eta \) は \(-\infty\) から \(+\infty\) まで自由に行き来できる、いわば“暴れん坊”でしたね。
リンク関数は、この暴れん坊な \( \eta \) を、私たちが本当に知りたい値の範囲(例えば、確率なら0~1、カウントなら0以上)へと、ルールに従って正確に“翻訳”してくれる役割を担います。
ロジスティック回帰(二項分布)の場合:ロジットリンク関数
予測したいのは、0から1の範囲に収まるべき確率 \( p \) です。ここで使われるのがロジットリンク関数です。
\[ \eta = \log\left(\dfrac{p}{1-p}\right) \]
この数式、少し複雑に見えますが、やっていることは段階的な翻訳です。
- まず、\( p \) を \( \dfrac{p}{1-p} \) という形に変換します。これはオッズと呼ばれ、「成功確率が失敗確率の何倍か」を示す指標です。\( p \) が0から1に動くとき、オッズは0から無限大(\(+\infty\))の範囲を動きます。
- 次に、そのオッズの対数(log)を取ります。すると、値はマイナス無限大(\(-\infty\))からプラス無限大(\(+\infty\))の範囲を取れるようになります。
つまり、ロジットリンク関数は、0~1の範囲に住む確率 \(p\) を、\(-\infty\)~\(+\infty\) の世界に住む線形予測子 \( \eta \) へと見事に橋渡ししてくれる翻訳機なのです。
ポアソン回帰(ポアソン分布)の場合:対数リンク関数
予測したいのは、0以上でなければならない平均発生回数 \( \lambda \) (ラムダ)です。ここで使われるのが対数(log)リンク関数です。
\[ \eta = \log(\lambda) \]
これはシンプルですね。\( \eta \) がどんな負の値を取ったとしても、それを元に戻す計算(\( \lambda = e^\eta \))をすれば、\( \lambda \) は必ず正の値になります。これで、予測される発生回数がマイナスになる心配は完全になくなります。
鍵③:線形予測子 ~すべてのモデルに共通する「不変の設計図」~
そして、GLMの最も美しく、強力な点がここにあります。どんな確率分布を選び、どんなリンク関数を使っても、その中核にある計算の構造は、私たちが見慣れたあの線形回帰の式と全く同じなのです。
\[ \eta = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots \]
- \( \eta \): 線形予測子(リンク関数によって変換される前の予測値)
- \( \beta_0 \): 切片(すべての説明変数が0のときの \( \eta \) の値)
- \( \beta_1, \beta_2, \dots \): 各説明変数の係数(変数が1単位増加したときの \( \eta \) の変化量)
- \( x_1, x_2, \dots \): 説明変数(年齢、体重、投薬の有無など)
これが、GLMが「一般化された線形モデル」と呼ばれる理由です。どんなに外観(確率分布)や内装(リンク関数)が違う家を建てるとしても、その基礎となる「設計図」は不変だということです。根っこの部分は同じ線形の足し算。その計算結果を、どの世界(確率分布)に、どの翻訳機(リンク関数)を使って着地させるかを変えているだけなのです。まさに「統一理論」だと思いませんか?
この仕組みを、もう一度整理した図で見てみましょう。
図の解説:
この図はGLMの3つの鍵がどう連携するかを示しています。まずステップ1で、年齢や検査値といった説明変数(X)が、不変の設計図である線形予測子によって計算され、\( \eta \) が求められます。次にステップ2で、この \( \eta \) がデータの種類に応じたリンク関数という翻訳機にかけられ、適切な範囲の値を持つ期待値 \( \mu \)(ミュー)に変換されます。最後にステップ3で、この \( \mu \) を平均に持つ確率分布から、私たちが実際に観測する応答変数(Y)が生成される、と考えるのがGLMの全体像です。
3. 実践編:ポアソン回帰を使いこなすための3つの処方箋
GLMの理論的な枠組みがわかってきたところで、もう少し具体的に、医療データ分析で頻繁に登場するポアソン回帰を例にとって、実践的な側面と、初心者が陥りがちな「落とし穴」への対処法を見ていきましょう。ここでは、ポアソン回帰を正しく、そしてより深く使いこなすための「3つの処方箋」をご紹介します。
同じく、医療データ分析で最もよく使われるもののひとつであるロジスティック回帰については、こちら。

処方箋①:観察期間がバラバラなら「オフセット項」で率を揃える
臨床研究では、「一定期間におけるイベントの発生件数」を扱う場面が非常に多いですよね。例えば、ある病棟での術後感染症の発生件数を分析したいとします。
ここで注意したいのが、患者さんごとに入院日数、つまり観察期間がバラバラであるケースです。単純に「Aさんは2件、Bさんは1件」と発生「件数」だけを比較するのは、果たしてフェアでしょうか? もしAさんの入院期間が100日、Bさんが10日だとしたら、1日あたりの発生「率」で考えれば、むしろBさんの方がリスクが高いと解釈できます。
このように、患者ごとに観察期間や曝露量が異なる場合、その影響を公平に補正するために使うのがオフセット項というテクニックです。
なぜ「log(観察期間)」をモデルに加えるのか?
ポアソン回帰では、リンク関数として対数(log)リンクを使うのが一般的でした。つまり、モデルが予測するのは発生件数\( \lambda \)そのものではなく、\( \log(\lambda) \) です。
\[ \log(\text{予測される件数}) = \beta_0 + \beta_1 x_1 + \dots \]
この式の両辺の「単位」を揃えるために、オフセット項として加える観察期間にも対数をとった \( \log(\text{観察期間}) \) を用います。そして、この項を「係数1で固定」してモデルに投入します。
\[ \log(\text{予測される件数}) = \beta_0 + \beta_1 x_1 + \dots + 1 \times \log(\text{観察期間}) \]
この式を、中学校で習った対数の性質を使って変形してみましょう。\( \log(A) – \log(B) = \log(A/B) \) を思い出してください。
\[ \begin{aligned} \log(\text{予測される件数}) – \log(\text{観察期間}) &= \beta_0 + \beta_1 x_1 + \dots \\ \log\left(\dfrac{\text{予測される件数}}{\text{観察期間}}\right) &= \beta_0 + \beta_1 x_1 + \dots \end{aligned} \]
いかがでしょう。式の左辺が「件数」から「件数 ÷ 期間」、つまり「発生率」に変わりました。オフセット項を加えるという一工夫で、私たちのモデルは発生「件数」ではなく、単位時間あたりの発生「率」を予測してくれる賢いモデルに変身するのです。これは臨床研究において極めて重要な考え方です。
処方箋②:データが想定より“暴れる”なら「過分散」を疑う
ポアソン分布には、実は「平均と分散が等しい」という、やや強い仮定があります。しかし、実際の医療データでは、このお約束が破られることが頻繁に起こります。イベントが特定の人に集中するなどして、データのばらつき(分散)が平均よりもずっと大きくなってしまうのです。この現象を過分散(Overdispersion)と呼びます。
例えば、クラスのテストの平均点が70点でも、みんなが65~75点にぎゅっと固まっている(分散が小さい)のと、0点と100点を取る生徒が多くて平均70点になっている(分散が大きい)のとでは、全く状況が違いますよね。過分散はまさに後者の状態で、患者さんごとのリスクの異質性(heterogeneity)が大きい場合や、あるイベントが次のイベントを誘発するような場合(例:感染症)によく見られます。
この過分散を無視してポアソン回帰を強行すると、係数の標準誤差を不当に小さく見積もってしまい、本当は統計的に意味のない差を「有意差あり!」と誤って判断してしまう危険性が高まることが知られています (Hilbe, 2011; Zuur et al., 2009)。
この問題に対する主な対処法(処方箋)は2つです。
- 準尤度(Quasi-likelihood)推定: これは、推定された標準誤差を「分散が平均の何倍か」という推定値(分散パラメータ)を使って“後から補正”する、いわば現実的な応急処置です。
- 負の二項回帰: こちらはより根本的な解決策です。ポアソン分布よりも柔軟で、平均と分散が異なることを許容できる負の二項分布を確率分布として採用します。いわば、モデルの前提そのものを、より現実に合ったものに取り替えるアプローチです。実務では過分散が疑われる場合に、第一の選択肢としてしばしば用いられます。
処方箋③:「ゼロ」が多すぎるデータには専用モデルを
「過去1年間の転倒回数」や「1ヶ月の禁煙失敗回数」などを分析しようとすると、データに「0」が異常に多くなることがあります。多くの人は一度も転倒・失敗しないからです。このような「ゼロばっかり」のデータに通常のポアソン回帰や負の二項回帰を当てはめても、データ構造をうまく捉えきれないことがあります。
そこで考え出されたのが、この「ゼロの多さ」を積極的にモデリングに取り入れる専門のモデルです。
ゼロ過剰モデル (Zero-Inflated Model; ZIM)
このモデルは、データの中の「0」には2種類ある、とユニークな仮定をします。
- 構造的ゼロ (Structural Zeros): 「絶対にイベントが起こりえない」グループから来る0。例えば、「男性における子宮頸がん検診の受診回数」を分析する場合、男性は構造的に受診しえないため、そのデータはすべて0になります。
- 偶然のゼロ (Sampling Zeros): 「イベントが起こりうる」グループに属するが、調査期間中“たまたま”0回だった場合の0。
ゼロ過剰モデルは、①まず、対象者がどちらのグループに属するのかを予測するロジスティック回帰を行い、②次に、「イベントが起こりうる」グループの中で何回イベントが起こるかをポアソン回帰や負の二項回帰で予測する、という2段階の合わせ技を使います。この独創的なアプローチはLambert (1992)によって提案されました。
ハードルモデル (Hurdle Model)
こちらは少し考え方が違い、「イベントが1回でも起こるかどうか」という最初の“ハードル”と、「ハードルを越えた場合に何回起こるか」という2つのプロセスに明確に分けます。
- ハードル部分: まず、イベント発生回数が0か、1以上かをロジスティック回帰で予測します。(ハードルを越えるか否か)
- カウント部分: 次に、1以上だった人たち(ハードルを越えた人)だけを対象に、その回数をゼロ切断(Zero-truncated)ポアソン/負の二項モデルで予測します。ゼロ切断モデルとは、1以上の値しか取らないという条件付きのカウントモデルです。
「ある薬の副作用としての頭痛の発生回数」を分析する際、「そもそも頭痛が起こる体質かどうか」と「起こる人の中で何回起こるか」を分けて考えたい場合などに自然な選択肢となります。
どちらのモデルを使うかは、データの「0」がどのようなメカニズムで生まれているかを考察して判断します。これらのモデルは、より複雑な医療データを現実に即して分析するための強力なツールと言えるでしょう。
4. まとめ:GLMという「統一言語」を手に入れることの価値
今回は、一見すると複雑な回帰モデルの世界を、一般化線形モデル(GLM)という一つの統一された視点から探検してきました。
最初は少し難しく感じられたかもしれませんが、最も重要なポイントは、線形回帰、ロジスティック回帰、ポアソン回帰などをバラバラの知識として暗記するのではなく、すべてが一つの共通した設計思想から成り立っていると理解することです。それは、中心にある不変の「線形予測子」という設計図に対して、「確率分布」と「リンク関数」という2つのアタッチメントを、データの性質に応じて付け替えているだけ、という考え方でした。
GLMの3つの鍵:もう一度振り返る
GLMという強力な道具箱を使いこなすための鍵は、以下の3つのコンポーネントを理解することに集約されます。
| コンポーネント | 役割 | 選択のポイント |
|---|---|---|
| ① 確率分布 | データの「生まれつきの性質」を表現する | 応答変数が連続値か、二値か、カウントか? |
| ② リンク関数 | 予測値の範囲を適切に“翻訳”する | 予測したい値が取りうる範囲はどこからどこまでか? |
| ③ 線形予測子 | 説明変数から予測の核を計算する「不変の設計図」 | (これは全てのGLMで共通) |
このGLMという「統一言語」を身につけることで、私たちは新しいデータや研究課題に直面したとき、闇雲に手法を探すのではなく、次のように体系的に思考を整理できるようになります。
「この応答変数の性質は何か?(→ 確率分布はどれにしよう?)」
「予測したい値の範囲はどうあるべきか?(→ リンク関数はどれが適切か?)」
たったこれだけの問いかけで、無数にあるように見えた分析アプローチの中から、最も合理的で適切な候補を自信を持って選べるようになるのです。これは、医療データサイエンスという広大な海を航海するための、非常に強力で信頼性の高い分析の指針を手に入れることに他なりません。
ぜひ、このパワフルな視点を、あなたの日々の研究や臨床での疑問解決に役立ててみてください。最初は完璧でなくても、この2つの問いを意識するだけで、分析モデルの選択ミスは劇的に減るはずです。
さらに深い理論や応用に興味が湧いた方は、GLMの基礎を築いたNelderとWedderburnによる独創的な原論文(1972)に目を通したり、Dobson and Barnett (2018) やMcCullagh and Nelder (1989) のような優れた教科書を手に取ってみることをお勧めします。それらは、あなたの知的好奇心を満たす、素晴らしい道標となるでしょう。
参考文献
- Dobson, A. J. & Barnett, A. G. (2018). An Introduction to Generalized Linear Models (4th ed.). CRC Press.
- Hilbe, J. M. (2011). Negative Binomial Regression (2nd ed.). Cambridge University Press.
- Lambert, D. (1992). Zero-Inflated Poisson Regression, with an Application to Defects in Manufacturing. Technometrics, 34(1), 1–14.
- McCullagh, P. & Nelder, J. A. (1989). Generalized Linear Models (2nd ed.). Chapman and Hall/CRC.
- Nelder, J. A. & Wedderburn, R. W. M. (1972). Generalized Linear Models. Journal of the Royal Statistical Society. Series A (General), 135(3), 370–384.
- Zuur, A. F., Ieno, E. N., Walker, N. J., Saveliev, A. A., & Smith, G. M. (2009). Mixed Effects Models and Extensions in Ecology with R. Springer.
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.





