生存時間分析でよく見るKaplan-Meier曲線は、複数のイベントが起こりうる状況(競合リスク)では結果を誤解させる危険があります。ここでは、その問題点と、より現実に即した分析手法の要点を解説します。
目的のイベント(例:心不全死)を妨げる別のイベント(例:脳卒中死)を「打ち切り」と誤って扱います。これにより、本来のイベント発生率を過大評価し、結果を歪める危険があります。
競合イベントの存在を考慮し、現実世界でのイベント発生確率を正直に計算します。「結局、このイベントは時間tまでにどれくらい起こるのか?」という臨床的な問いに正確に答えます。
なぜ?(メカニズム解明):
原因別ハザードモデル (Cox)
どうなる?(予後予測):
部分分布ハザードモデル (Fine-Gray)
リサーチクエスチョンがモデルを決めます。
カンファレンス室でよく見る「あの曲線」に潜む罠
臨床カンファレンスや論文抄読会で、新しい治療法の効果を示す生存曲線が提示される場面を想像してみてください。治療群の線がプラセボ群よりも明らかに上方にあり、誰もが「この治療は有効だ」と納得する…そんなお馴染みの光景ですよね。このとき、私たちの目に映っているのは、ほとんどの場合Kaplan-Meier(カプランマイヤー)曲線です。これはイベント(例:死亡)が起こるまでの時間を可視化する、非常に強力でポピュラーなツールです。
しかし、もし、その美しい曲線が臨床の現実を少しだけ「楽観的」に描き出しているとしたら…どう思われますか?
ここで、具体的なシナリオを考えてみましょう。対象は、高齢の心不全患者さん。私たちが本当に知りたいのは、「新しい心不全治療薬Aが、心不全が原因の死亡をどれだけ減らせるか」だとします。
研究期間中、患者Aさんは心不全の増悪で亡くなりました。これは、私たちが注目している「イベント」です。一方で、患者Bさんはとても元気でしたが、ある日突然、重度の脳卒中を発症して亡くなりました。
さあ、この患者Bさんのデータをどう扱えばよいでしょう?
Kaplan-Meier法では、この「脳卒中による死亡」を「打ち切り(censoring)」として処理します。打ち切りとは、本来「引っ越しで追跡不能になった」というようなケースを想定したものです。つまり、「その時点では生存が確認されているが、その後のことは分からない。でも、もし追跡できていれば、他の患者さんと同じように心不全死のリスクを抱え続けていたはずだ」と仮定するのです。
でも、この仮定、本当におかしいと思いませんか? なぜなら、脳卒中という別の原因で亡くなってしまった患者Bさんは、もはや絶対に「心不全で死亡する」ことはないからです。
このように、本来知りたかったイベント(心不全死)の発生確率が、別のイベント(脳卒中死)が先に起こることによって影響を受けてしまう状況。これが、今回の大テーマである「競合リスク(competing risks)」です。
この競合リスクを無視して、何でもかんでも「打ち切り」として扱ってしまうと、本来のイベント発生率を過大評価してしまう、つまり治療効果を実態以上によく見せてしまう危険性があります。この問題は多くの専門家によって指摘されており、例えば米国の循環器内科医Peter C. Austinらが医学雑誌『Circulation』で発表した解説論文でも、競合リスクの不適切な取り扱いが臨床的な結論を歪めるリスクについて警鐘を鳴らしています (Austin, Lee, and Fine 2016)。
そこで登場するのが、より現実に即した分析を可能にする「競合リスク分析」と、さらに視野を広げて患者さんのたどる多様な道のりを描く「多状態モデル(multi-state models)」です。この記事では、Kaplan-Meier法の限界から一歩踏み出し、臨床現場のリアルをより忠実に捉えるための不可欠な手法について、一緒に探検していきましょう!
Kaplan-Meier法の「死角」:競合リスクという名の隠れた罠
さて、ここからは競合リスクというコンセプトの核心に迫っていきましょう。なぜ、あれほど万能に見えるKaplan-Meier法が、特定の状況では問題を引き起こすのでしょうか。そのメカニズムを、一緒にじっくりと解き明かしていきます。
なぜ「打ち切り」ではダメなのか?その本質的な理由
Kaplan-Meier(カプランマイヤー)法は、生存時間分析の主役ともいえる非常に優れたツールです。しかし、この手法がその真価を発揮するには、絶対に守らなければならない「黄金律」があります。それは、「打ち切り(分析の中断)は、その後のイベント発生とは全く無関係に起こる」という大前提です。これを専門用語でノン・インフォマティブ・センサリング(non-informative censoring / 無情報な打ち切り)と呼びます。
「無情報な打ち切り」とは? (The Golden Rule ✅)
これは、「打ち切り」という事実に、患者さんの将来の運命に関する情報が一切含まれていない状態を指します。
一番わかりやすい例が、研究に参加していた患者さんが遠方に引っ越してしまい、追跡できなくなるケースです。「引っ越した」という事実は、その方の心不全が他の人より悪化しやすい、あるいは改善しやすいといった情報とは無関係ですよね。私たちは、その方の未来は分からないけれど、もし追跡できていれば、他の参加者と同じような経過をたどっただろう、と仮定することができます。これがルール通りの「無情報な打ち切り」です。
「情報を持つ打ち切り」の罠 (The Rule-Breaker ❌)
ところが、今回のテーマである競合リスクは、この黄金律を根本から破ってしまいます。
心不全の研究で、目的のイベントが「心不全による死亡」だとしましょう。ここで、ある患者さんが「脳卒中」で亡くなられたとします。もしこれをKaplan-Meier法で単純な「打ち切り」として扱ってしまうと、統計モデルはこう解釈してしまいます。
「この方は5年目で追跡できなくなった(打ち切り)。でも、もし脳卒中で亡くなっていなければ、きっとその後も心不全で亡くなる可能性を秘めたままだったはずだ…。」
でも、これは明らかにおかしいですよね? 🧠 考えてみてください。脳卒中で亡くなった方は、その瞬間、未来永劫「心不全で死亡する」可能性は完全にゼロになります。つまり、「脳卒中死」という出来事は、「この人はもう心不全死のリスク人口から永久に脱落した」という決定的で重要な情報を持っているのです。これがインフォマティブ・センサリング(informative censoring / 情報を持つ打ち切り)です。
マラソンに例えると、違いは一目瞭然です。
- 無情報な打ち切り: 家族の急用で、レースを途中棄権した選手。棄権しなければ完走できたかもしれないし、できなかったかもしれない。その後の結果は「不明」です。
- 情報を持つ打ち切り (競合リスク): ルール違反で「失格」になった選手。その選手がそのレースで「完走」する可能性は、未来永劫ゼロです。結果は「不明」ではなく、「完走しない」と確定しています。
なぜ結果が歪むのか?
競合イベントを「無情報な打ち切り」として扱うと、モデルは「失格になった選手も、まだレースを続けている可能性がある」と勘違いしたまま計算を続けます。本来なら目的のイベント(完走)が起こり得ない人が、いつまでも「起こり得る」候補者として扱われてしまうのです。
その結果、目的のイベント(この場合は心不全死)の累積発生確率は、系統的に過大評価されてしまいます。これは単なる統計上の細かい話ではありません。
- 臨床試験では: 新薬の効果を過大評価してしまうかもしれません。例えば、がんを抑制するが心臓への毒性が強い薬があった場合、がん死だけを見ると薬が非常に有効に見える(心臓死は打ち切り扱いのため)という誤った結論を導く可能性があります。
- 患者さんへの説明では: 「この治療を受けると、5年後に〇〇が原因で亡くなる確率は10%です」と、本来よりも楽観的な(過大評価された)数字を伝えてしまうことになりかねません。
このような理由から、複数の専門家は、競合リスクが存在する研究ではKaplan-Meier法を慎重に使い、それを補うための適切な分析手法(累積発生関数など)を用いることが不可欠であると指摘しています (Andersen et al. 2012; Austin, Lee, and Fine 2016; Putter, Fiocco, and Geskus 2007)。
ヒーローの登場:現実を直視する「累積発生関数(CIF)」
はい、承知いたしました。「累積発生関数(CIF)」のコンセプトについて、その役割、計算の考え方、そして解釈を、たとえ話を使いながらさらに分かりやすく解説します。
Kaplan-Meier法が描く「もしも」の世界の問題を解決するために登場したのが、今回のヒーロー、累積発生関数(Cumulative Incidence Function, CIF)です。
もしKaplan-Meier法が「競合リスクがなければ…」と夢を語る理想主義者だとしたら、CIFは「いや、現実はこうだ」と事実を告げる現実主義者です。
CIFは、競合イベントの存在を真正面から受け入れます。その上で、「で、結局、私たちの知りたいイベントは、この厳しい現実世界の中で、ある時点までにどれくらいの確率で起こるのか?」という、最も臨床家が知りたい問いに、正直に答えてくれるのです。
CIFが計算するのは、現実世界におけるイベントの「絶対的な発生確率」です。これは、論文を読んだり、患者さんに説明したりする上で、極めて重要なポイントになります。
CIFの考え方:正直なスコアキーパーはどうやって確率を計算するか? 📝
「数式は苦手…」という方も、ご安心ください。CIFの考え方は、非常にフェアで直感的です。
先ほどの「ゴールが複数あるマラソン」の例えに戻りましょう。CIFは、このレースの正直なスコアキーパーの役割を果たします。スコアキーパーの仕事は、「心不全ゴール」に到達した選手の割合を、時間経過と共に記録していくことです。
このスコアキーパーは、レースの瞬間、瞬間に、常に2つのことを確認しています。
- 今、コース上にいる選手が「心不全ゴール」に向かう勢い(瞬間的なリスク)はどれくらいか?
これが、数式に出てくるハザード \(\lambda_k(u)\) の正体です。心不全ゴールに引き寄せられる「引力」のようなものだと考えてください。 - そもそも、その引力を感じる対象となる選手が、コース上に何%残っているか?
これが全生存関数 \(S(u)\) です。レースが進むにつれて、「心不全ゴール」や「脳卒中ゴール」に到達する選手が増え、コース上の選手は減っていきます。この「現実の残存率」を正直に反映します。
そして、ある一瞬で「心不全ゴール」に到達する選手の割合は、単純にこの2つを掛け合わせることで計算されます。
(その瞬間に心不全ゴールする確率) = (心不全ゴールへの引力) × (コースに残っている選手の割合)
CIFとは、この「瞬間の確率」を、レース開始(時間ゼロ)から私たちが知りたい時間 \(t\) まで、パラパラ漫画のように時間を進めながら、すべて足し合わせたもの(累積したもの)なのです。
この一連のフェアな計算プロセスを、数学者がエレガントな数式で表現したのが、こちらです。
\[ \text{CIF}_k(t) = \int_0^t \lambda_k(u)S(u)\,du \]
数式記号は難しそうに見えますが、やっていることは先ほどのスコアキーパーの仕事そのものです。
確率の「パイ」を正しく切り分ける 🥧
CIFのもう一つの素晴らしい点は、全体の確率を各イベントにきれいに分配してくれることです。
下の図を見てください。一番上の線(1-KM)は、原因を問わず「とにかく何らかのイベント(死亡)が起こった」確率の全体像です。これを確率の大きな「パイ」だと考えてください。
Kaplan-Meier法では、このパイ全体を無理やり「心不全死」の確率だと見なそうとして、過大評価が起きていました。
しかしCIFは、このパイを「原因A(心不全死)が取った分」と「原因B(脳卒中死)が取った分」に、きっちり切り分けてくれます。
図の解説: 点線で示された「原因Aの取り分(CIF)」と、網掛けで示された「原因Bの取り分(CIF)」を足し合わせると、パイ全体(1-KM)の大きさとぴったり一致します。
このように、CIFは競合リスクが存在する複雑な現実の中で、私たちが知りたいイベントがどれくらいの割合を占めるのかを、偏りなく正直に描き出してくれる、極めて強力なヒーローなのです。
「なぜ」と「どうなる」に答える2つのアプローチ
さて、競合リスクの存在を認識した上で、それを分析するにはどうすればよいのでしょうか。ここが統計モデリングの面白いところで、「何を知りたいか?」というリサーチクエスチョンによって、使うべき道具(モデル)が変わってきます。競合リスク分析には、主に2つの強力なモデリング戦略があります。それぞれ見ていきましょう。
① 原因別ハザードモデル:「病気のメカニズム」を探る旅(Etiology)
競合リスクを分析するための最初のアプローチが、原因別ハザード(Cause-Specific Hazard, CSH)をモデル化する方法です。名前の通り、これは「原因ごと」にハザード、つまり瞬間的なイベント発生リスクを評価していきます。
CSHが答えてくれる問いは、非常に純粋で科学的です。「あるイベントがまだ起きていない人たちの中で、次の瞬間に、この特定の原因のイベントが起こるリスクはどれくらいか?」という点に、徹底的に焦点を当てます。
このアプローチの最大のルールは、分析したい特定のイベント(例:心不全死)以外のイベント(例:脳卒中死)は、すべて「打ち切り」として扱うことです。これにより、他のイベントによる影響を一旦脇に置き、知りたいイベントそのものの発生メカニズムを分離して考えることができます。
たとえ話で考えてみよう ⚽
サッカーの試合で、「ストライカーA選手がゴールを決める直接的な要因は何か?(どんなパスを受けるとシュートしやすいか、など)」を分析するのを想像してください。この分析では、味方のB選手がゴールを決めた場合や、試合が終了した場合は、A選手にとっての「イベント(ゴール)」ではないため、すべて「打ち切り」として扱います。つまり、純粋に「A選手がピッチにいて、ゴールを狙える状態にある限り、何が彼のゴール確率を高めるのか」という、個人のパフォーマンスに直結するメカニズム(病因論、etiology)の解明に特化するわけです。
臨床現場での使い方と結果の解釈 🩺
このCSHアプローチの素晴らしい点は、私たちが日頃から使い慣れているCox比例ハザードモデルをそのまま利用できることです。実際には、イベントの原因ごとに個別のCoxモデルを構築します。
例えば、「心不全死」と「それ以外の死」という2つの競合リスクがある場合、
- 「心不全死」をイベント、「それ以外の死」を打ち切りとしたCoxモデルを一つ作る。
- 「それ以外の死」をイベント、「心不全死」を打ち切りとしたCoxモデルをもう一つ作る。
というように、分析を完全に分けて行います。
ここから得られる原因別ハザード比(Cause-Specific Hazard Ratio, CSHR)の解釈は、通常のCoxモデルのハザード比と同じです。例えば、新薬Aの「心不全死」に対するCSHRが0.7だった場合、それは次のように解釈します。
「ある任意の時点において、まだ生存している患者さんの間で比べると、新薬Aを服用している患者さんは、服用していない患者さんに比べて、『心不全で死亡する』というイベントの瞬間的なリスク(ハザード)が30%低い。」
このように、CSHモデルは「特定のバイオマーカーの上昇は、心不全による死亡の生物学的なリスクを直接高めるか?」といった、イベント発生の純粋なメカニズムや、リスク因子の直接的な影響を探る研究に非常に適しています。
② 部分分布ハザードモデル:「患者の未来」を予測する旅(Prediction)
もう一つのアプローチが、部分分布ハザード(Subdistribution Hazard, SDH)をモデル化する方法です。このアプローチの最終目的は非常に明確で、私たちが知りたい累積発生関数(CIF)そのものを直接モデル化し、予測することにあります。
このモデルの代表格が、提唱者の名前にちなんでFine-Grayモデルとして広く知られています (Fine and Gray 1999)。このモデルは非常に賢いのですが、その仕組みは少し風変わりです。
Fine-Grayモデルの「賢いトリック」とは? 🎩
Fine-Grayモデルの核心は、リスク計算の分母、すなわちリスクセット(Risk Set)の定義にあります。
通常のCoxモデル(原因別ハザード)では、何らかのイベント(心不全死であれ脳卒中死であれ)が起きた人は、その時点からリスクセットから除外されます。これは直感的で分かりやすいですよね。
しかしFine-Grayモデルは、目的のイベント(例:心不全死)を予測するために、一見奇妙なことをします。競合イベント(例:脳卒中死)が起こった人を、リスクセットから除外せず、数学的に分母に含め続けるのです。もちろん、脳卒中で亡くなった方が心不全で死亡するリスクはゼロですが、計算上は「まだいる」かのように扱います。
なぜこんなトリックを使うのでしょうか? これは、ハザード(瞬間リスク)ではなく、累積した結果(CIF)に焦点を合わせるための、巧みな数学的工夫なのです。この「特殊なリスクセット」を用いることで、モデルから得られるハザード比(部分分布ハザード比)が、最終的なCIF曲線を直接上下させる効果を持つようになります。つまり、予測という目的に特化した設計になっているのです。
たとえ話で考えてみよう 🏟️
今度は、「A選手がいることで、チーム全体の最終的な勝利確率がどれだけ上がるか?」を予測したいとしましょう。この場合、A選手自身のゴール(目的イベント)だけでなく、彼がレッドカードで退場してしまう(競合イベント)ことも、チームの勝利確率に直接影響します。A選手が退場すれば、チームは不利になり、勝利という最終アウトカムの確率は下がりますよね。
SDHモデルは、このような「目的イベント」と「競合イベント」が最終的なアウトカムに与える影響をすべてひっくるめて、「A選手の存在は、チームの勝利確率を最終的に上げるのか、下げるのか」という問いに答えるのに役立ちます。
臨床現場での使い方と結果の解釈【最重要注意点】 ⚠️
このモデルは、「ある治療法Bは、競合イベントによる死亡も考慮した上で、最終的に心不全で死亡する患者の割合を5年後までにどれだけ減らすことができるか?」といった問いに答えるのに最適です。つまり、個々の患者の予後予測モデルを作成したり、治療介入が累積発生確率に与える全体的な影響を評価したりする研究で真価を発揮します。
ここから得られる部分分布ハザード比(Subdistribution Hazard Ratio, SHR)の解釈には、細心の注意が必要です。これはCoxモデルのハザード比(CSHR)とは全くの別物です。
【警告】SHRを瞬間リスク比として解釈してはいけません。
SHRが0.7だったからといって、「瞬間的なリスクが30%低い」と解釈するのは誤りです。【正しい解釈】
SHRは、累積発生関数(CIF)への影響として解釈します。SHRが1より小さい(例:0.7)ということは、その因子(例:治療薬)を持つ群では、持たない群に比べて、イベントの累積発生確率(CIF)が時間を通じて低く推移することを意味します。
患者さんから「結局、この治療を受けたら、5年後に心臓が原因で亡くなる可能性はどれくらい下がるの?」と聞かれた時、その問いに最も近い答えを与えてくれるのが、このFine-Grayモデルから得られる予測なのです。
で、結局どっちを使えばいいの?:リサーチクエスチョンがすべてを決める
さて、ここまで原因別ハザード(CSH)モデルと部分分布ハザード(SDH)モデル、2つのアプローチを見てきました。「結局、自分の研究ではどちらを使えばいいのか?」という疑問は、この分野で最もよく聞かれる質問の一つです。
結論から言うと、「どちらが優れている」という話ではなく、「知りたいこと(リサーチクエスチョン)が違う」のです。あなたの目的がどちらに近いかで、使うべきツールは自ずと決まります。
これを車の「自動車整備士」と「交通情報アナリスト」の仕事に例えてみましょう。
- 自動車整備士(=原因別ハザードモデル) 🧑🔧
整備士の仕事は、「なぜこのエンジン部品は故障するのか?」というメカニズムを解明することです。部品そのものの耐久性や、オイルの種類が故障率にどう影響するかを調べます。その時、ガレージまでの道が渋滞しているか(=他のリスク)は、部品の故障メカニズムとは無関係です。純粋な科学的因果関係を探求するのが整備士の役割です。 - 交通情報アナリスト(=部分分布ハザードモデル) 🗺️
アナリストの仕事は、「この車が目的地に時間通りに到着する確率はどれくらいか?」という未来を予測することです。車の最高速度だけでなく、渋滞、事故、天候(=競合リスク)など、現実に起こりうるあらゆる要因を考慮に入れます。最終的なアウトカムを現実的に予測するのがアナリストの役割です。
あなたの研究は、どちらの仕事に近いでしょうか?
- 「なぜ、そのイベントが起こるのか?」(Etiology) を知りたい場合:
→ あなたは「整備士」です。原因別ハザードモデル (Coxモデル) を選びましょう。病気の生物学的なメカニズムや、リスク因子の直接的な影響を評価したい場合に最適です。 - 「結局、そのイベントはどれくらい起こるのか?」(Prediction) を知りたい場合:
→ あなたは「アナリスト」です。部分分布ハザードモデル (Fine-Grayモデル) を選びましょう。患者さん個人への予後説明や、治療方針の決定、公衆衛生的なインパクトの評価など、最終的なイベント発生確率の予測が重要な場合に最適です。
結果が食い違って見えるときこそ、物語が深まる
時に、CSHモデルとSDHモデルは一見すると矛盾した結果を示すことがあります。しかし、それこそが競合リスク分析の醍醐味であり、深い洞察を与えてくれる瞬間です。
ケーススタディ:高齢者のがんに対する強力な化学療法
- 原因別ハザード(CSH)モデルの結果:
この化学療法は、「がんによる死亡」のハザードを劇的に下げる(CSHR << 1.0)。つまり、この薬はがん細胞を叩く力が非常に強いことが分かります。 - 部分分布ハザード(SDH)モデルの結果:
しかし、「がんによる死亡」の累積発生確率(CIF)への影響はほとんどない(SHR ≈ 1.0)。つまり、この治療を受けても、最終的にがんで亡くなる患者の割合は、受けなかった場合とあまり変わらないという結果です。
なぜこんなことが起こるのでしょうか? それは、この治療法が非常に強力なあまり、毒性も強く、「治療関連死」という競合リスクのハザードを上げてしまうからです。多くの患者さんが、がんが治る前に治療の副作用で亡くなってしまうため、がんを抑制する強力な「メカニズム」がありながら、最終的な「予測」には結びつかないのです。
このように、両方のアプローチを併用することで、「この治療はメカニズムは正しいが、実臨床で使うには毒性が強すぎる」という、極めて重要で多角的な結論を導くことができます。実際の一流の研究論文で両方の結果が併記されているのは、このような深い考察のためなのです。
2つのアプローチのまとめ
以下の表に、2つのアプローチの主な違いを改めてまとめます。
| 特徴 | 原因別ハザード (CSH) モデル | 部分分布ハザード (SDH) モデル |
|---|---|---|
| 視点 | 自動車整備士(メカニズム解明) | 交通情報アナリスト(未来予測) |
| 主なモデル | Cox比例ハザードモデル | Fine-Grayモデル |
| リサーチクエスチョン | Why?(なぜ起こる?) | What will happen?(どうなる?) |
| 結果の解釈 | 瞬間リスク(ハザード)への直接効果 | 累積発生確率(CIF)への最終的な影響 |
| 主な用途 | 病因論、リスク因子の探索 | 予後予測、臨床的な意思決定 |
共変量調整なしで群間比較するなら:Gray検定
最後に、もしあなたの目的が「治療群AとBで、イベントの累積発生率に差はあるか?」という単純な群間比較だけで、他の因子(年齢や性別など)で調整する必要がない場合(例:ランダム化比較試験の主要評価)、モデルを使わずに直接CIF曲線を比較するノンパラメトリックな検定手法があります。それがGray検定です (Gray 1988)。
これは、Kaplan-Meier曲線同士を比較するログランク検定の、競合リスク版だと考えてください。CIF曲線が2つのグループで統計的に有意に異なるかどうかを直接検定するための、シンプルかつ強力なツールです。
人生は一本道じゃない:多状態モデルへの招待
競合リスク分析は、「心不全で亡くなるか、それとも他の原因で亡くなるか」といった、いわば人生の最終的な「終着点」に焦点を当てていました。しかし、臨床現場で私たちが向き合う患者さんの経過は、もっと動的で複雑ですよね。それはまるで、様々な地点を経由しながら進む「旅」のようです。
例えば、がん患者さんなら、「治療開始」→「寛解(がんが縮小・消失)」→「再発」→「再治療」→「死亡」といった複数の状態(state)を、時間をかけて遷移(transition)していきます。腎臓病の患者さんであれば、慢性腎臓病(CKD)のステージ間を進行していくかもしれません。
このように、患者さんがたどる複雑な健康状態の旅路を、地図のように丸ごとモデル化してしまうのが、今回ご紹介する多状態モデル(Multi-state Models)です。このアプローチは、臨床経過の全体像を生き生きと動的に捉えることができるため、疫学や生物統計学の分野で非常に広く活用されています (Putter, Fiocco, and Geskus 2007; Andersen et al. 2012)。
患者さんの「健康地図」を描く
多状態モデルの基本は、患者さんが取りうる健康状態を「箱(state)」で、状態から状態への移動を「矢印(transition)」で表現することです。これはまさに、患者さんのたどる道のりを描いた「健康地図」と言えるでしょう。
実は、先ほどまで議論していた競合リスクモデルも、下図のように3つの状態(生存、イベントA、イベントB)を持つ、最もシンプルな多状態モデルの一つと見なすことができます。
図の解説:「生存」という初期状態から、「目的のイベント(例:がん死)」または「競合イベント(例:その他の原因による死)」のどちらかに遷移します。どちらの死亡イベントも、一度入ると二度と他の状態には移れないため、「吸収状態(absorbing state)」と呼ばれます。
この考え方を応用すれば、もっとずっと複雑で、臨床的に豊かなモデルを構築できます。その代表例が、臨床研究で頻繁に用いられる「Illness-Deathモデル」です。
Illness-Deathモデルの模式図。「健康」「病気」「死亡」の3つの状態と、それらの間の遷移を示しています。
図の解説:このモデルでは、「健康」状態から「病気」状態への遷移(Transition 2)、そしてそれぞれの状態から「死亡」への遷移(Transition 3, 4)を同時にモデル化できます。さらに、「病気」状態から「健康」状態へ戻る(寛解など)矢印(Transition 1)を追加することも可能です。これにより、「病気になる確率」「病気になってから死亡する確率」「病気が治る確率」などを一度に評価できるのです。
モデルのエンジンルーム:各「矢印」を個別にモデル化する
多状態モデルの真に強力な点は、この地図上のそれぞれの「矢印(遷移)」ごとに、独立したハザードモデル(例えばCoxモデル)を当てはめることができる点です。
これは何を意味するのでしょうか? 例えば、新しい治療薬の効果を評価する際に、単に「生存期間が延びたか」だけでなく、「どのプロセスに、どのように効いたのか」を明らかにできるのです。
- その薬は、病気になるリスク(Healthy → Illnessのハザード)を下げたのか?
- それとも、病気になってからの死亡リスク(Illness → Deadのハザード)を下げたのか?
- はたまた、寛解に至る確率(Illness → Healthyのハザード)を上げたのか?
- もしかすると、病気からの死亡リスクは下げるが、健康な状態からの(副作用による)死亡リスク(Healthy → Deadのハザード)は上げてしまう、といった想定外の効果はないか?
このように、各遷移を分解して評価することで、治療効果や予後因子に関する、より深く、解像度の高い洞察を得ることが可能になります。
旅のGPS:Aalen-Johansen推定量
さて、こんなに複雑な地図を描いた後で、私たちが最も知りたいのは「ある時刻 \( t \) に、患者さんがそれぞれの状態にいる確率は、結局どれくらいなのか?」ということでしょう。この推移確率(Transition Probability)を計算してくれるのが、Aalen-Johansen(アーラン・ヨハンセン)推定量です。
これは、Kaplan-Meier法を多状態モデルの世界に一般化したもの、と考えると分かりやすいでしょう。各状態にいる確率を、時間経過とともに積み上げグラフのように示してくれます。
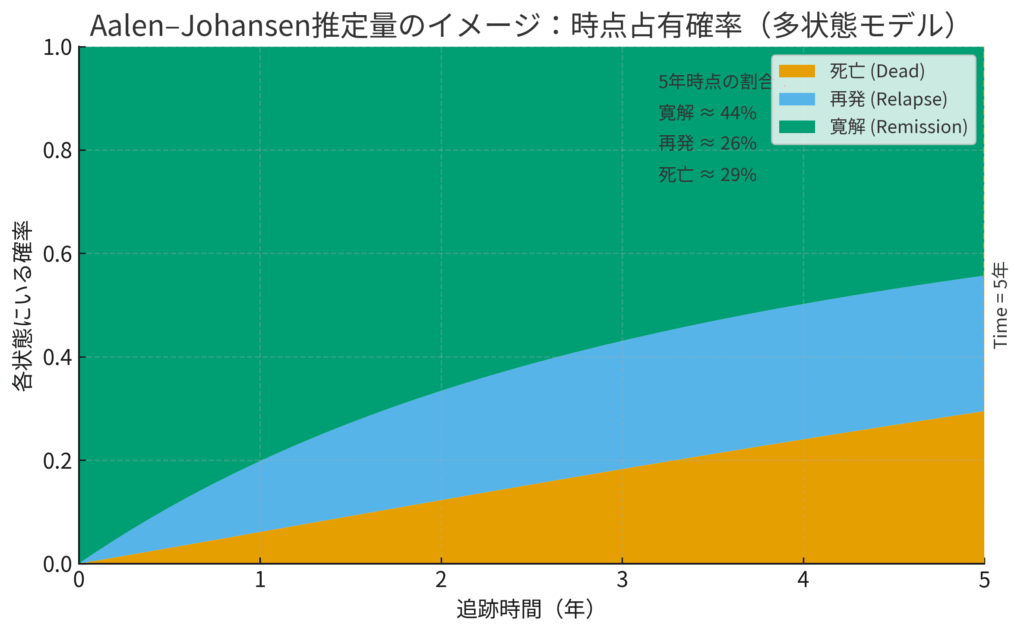
Aalen-Johansen推定量の出力を示す積み上げ棒グラフのイメージ。ある時点で各状態にいる患者の割合を示しています。
例えば、「治療開始から5年後に、患者が『寛解』状態にいる確率は60%、『再発』状態にいる確率は25%、『死亡』している確率は15%」といった、臨床的に極めて有益な情報を提供してくれます。これは、臨床医が患者さんに予後を説明したり、治療方針を決定したりする上で、非常に重要な根拠となります。
時間の測り方とモデルの「記憶」
最後に、多状態モデルを扱う上での、少し専門的ながら重要な2つの注意点に触れておきます。
- 時間の測り方:Clock-Forward vs. Clock-Reset
時間の起点をどこに置くか、という問題です。Clock-Forwardは研究開始時点(例:診断日)を0とする最も一般的な方法で、「診断から5年後の状態は?」という問いに答えます。一方、Clock-Resetは新しい状態に入るたびに時計を0にリセットする方法で、「寛解状態に入ってから、再発するまでの時間は?(いわゆるギャップタイム)」といった問いに答えるのに役立ちます。 - 過去は関係ある?:マルコフ vs. セミマルコフ
モデルが過去の情報をどれだけ「記憶」するかの仮定です。マルコフ(Markov)モデルは「未来の確率は、現在の状態のみに依存する」という「記憶喪失」の仮定を置きます。計算は簡単ですが、非現実的な場合もあります。対してセミマルコフ(Semi-Markov)モデルは、「未来の確率は、現在の状態と、その状態に滞在している期間に依存する」と考えます。「寛解状態に長くいればいるほど、再発のリスクは減る」といった、より臨床感覚に合った状況をモデル化できます。
どのモデルや設定を使うかは、分析の目的と、データがどの仮定を支持するかに基づいて慎重に選ぶ必要があります (Putter, Fiocco, and Geskus 2007)。
より具体的にイメージする:臨床研究での応用例
さて、ここまでの少し理論的な話が、実際の臨床研究でどのように見えるのか、具体的なシナリオで考えてみましょう。概念を視覚的に捉えることで、「なるほど、そういうことか!」と腑に落ちる瞬間が訪れるはずです。
ここでも、高齢の心不全患者さんの予後を追跡する研究を例に取ります。私たちが評価したいアウトカムを、「心不全による死亡」と「心不全以外の原因による死亡」の2つに分けました。
もし、研究者が競合リスクの存在に気づかず、単純に「心不全死」をイベント、「心不全以外の死亡」を打ち切りとしてKaplan-Meier解析を行ってしまった場合と、競合リスクを適切に考慮してCIFを算出した場合とでは、下図のように全く異なる景色が見えてきます。
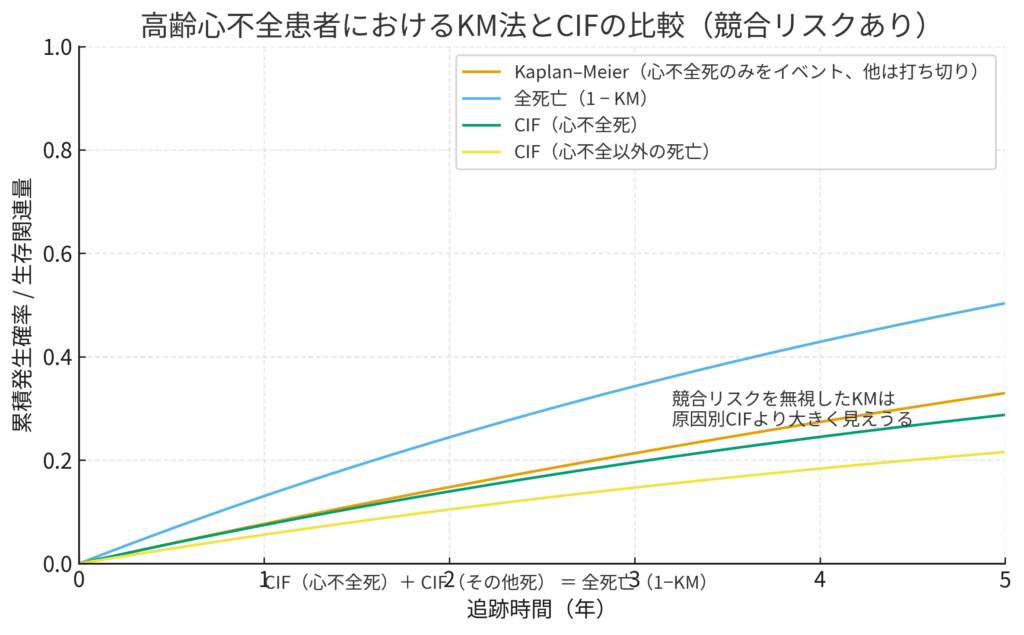
高齢心不全患者におけるKaplan-Meier法とCIFの比較図。競合リスクを無視したKaplan-Meier法がCIF(心不全死)よりも高い発生確率を示すこと、そして各原因のCIFの和が全死亡確率と一致することを示しています。
この図から何を読み取るべきか?
このグラフを正しく読み解く鍵は、4本の線の関係性、特にオレンジ、緑、そして水色の線が何を表しているかを理解することです。
オレンジ色の線 (Kaplan-Meier):誤解を招く「もしも」の確率 🟠
これは、競合リスク(心不全以外の死亡)を「無かったこと(=単なる打ち切り)」として計算した、見かけ上のKaplan-Meier曲線です。「もし誰も心不全以外で死ななかったとしたら、心不全死の確率はこれくらいだろう」という非現実的な仮定の下での確率であり、グラフの注釈にもある通り、過大評価された「心不全死」の確率を示しています。
緑色の線 (CIF 心不全死):現実世界での「心不全死」の確率 🟢
こちらが、競合リスクを適切に考慮したCIF(心不全死)です。現実の臨床現場で、ある患者さんが特定の時間までに「心不全で亡くなる」累積確率を示しており、これこそが私たちが本当に知りたい現実的な確率です。オレンジ色の線とこの緑色の線の間の「ギャップ」こそが、競合リスクを無視することによって生じるバイアスの大きさを視覚的に表しています。
水色の線 (全死亡 1-KM):全体の死亡確率 🔵
これは原因を問わない全死亡の確率です。そして最も重要なことは、グラフ下部の数式 CIF(心不全死) + CIF(その他死) = 全死亡(1-KM) が示す通り、2つの現実的な確率、つまり緑色の線(心不全死のCIF)と黄色の線(心不全以外の死亡のCIF)を足し合わせると、この水色の線(全死亡確率)とぴったり一致するということです。
臨床的洞察がどう変わるか?
このようにCIFを用いて分析を分解することで、治療効果の評価がより深く、本質的になります。
例えば、新薬Aの臨床試験で、全死亡率には群間差がなかったとします。Kaplan-Meier法しか見ていないと、「この薬は効果なし」と結論付けてしまうかもしれません。しかし、競合リスク分析を行ったところ、「新薬Aは心不全死のCIFを劇的に下げるが、感染症による死亡のCIFをわずかに上げており、結果として全死亡が変わらなかった」という発見があるかもしれません。
これは「効果なし」とは全く異なる、非常に重要な知見です。薬の主要な作用機序は正しく機能していること、そして今後は感染症という副作用をいかに管理するかが課題である、という次の研究開発につながる具体的な洞察を与えてくれます。
論文を読むときのチェックポイント
ここまで学んだあなたは、もう生存時間分析を含む論文を、より批判的に読めるようになっているはずです。特に高齢者やがん患者など、競合イベントが起こりやすい集団を対象とした研究を読む際は、ぜひ以下の点を確認してみてください。
- そもそも、著者らは競合リスクの存在を認識し、言及しているか?
- 結果として、主要なイベントの累積発生関数(CIF)が図や表で示されているか?
- 多変量解析を行っている場合、その目的(メカニズム解明か、予測か)に応じて、原因別ハザードモデルか部分分布ハザードモデルかを適切に使い分けているか?
これらの視点を持つことで、研究の結論の妥当性を、より深く評価することができるようになります。
まとめ:臨床の現実を「ありのまま」に捉えるために
今回は、日常的に目にする標準的な生存時間分析から一歩踏み込んで、競合リスクと多状態モデルという、より現実に即した分析の世界を探検しました。一見すると複雑に感じられたかもしれませんが、その根底にある思想は驚くほどシンプルです。それは、「臨床現場で実際に起きていることを、私たちのデータ解析も、もっと忠実に、もっと正直に表現するべきだ」という願いに他なりません。
この講座の重要ポイント(Key Takeaways)
今回の講座で、ぜひ皆さんの「知的ツールキット」に加えていただきたい最重要ポイントを4つにまとめました。
- ポイント1:Kaplan-Meier法の「限界」を知る
目的のイベントが、別のイベント(競合リスク)によって妨げられる可能性がある状況では、標準的なKaplan-Meier法はイベント発生率を過大評価し、臨床的判断を誤らせる危険性があります。 - ポイント2:CIFで「現実の確率」を語る
競合リスクが存在する状況では、累積発生関数(CIF)を用いることで、現実世界でのイベントの「絶対的な発生確率」を正しく推定できます。 - ポイント3:「なぜ?」と「どうなる?」でモデルを使い分ける
イベント発生のメカニズム(なぜ?)を探りたいなら原因別ハザードモデル(Coxモデル)を、最終的な発生確率の予測(どうなる?)がしたいなら部分分布ハザードモデル(Fine-Grayモデル)を選びます。リサーチクエスチョンがすべてを決めます。 - ポイント4:「点」ではなく「旅」で患者を捉える
患者さんの臨床経過は、単一のイベントで終わる「点」ではなく、様々な健康状態を行き来する「旅」です。多状態モデルは、この複雑な旅路全体を地図のように描き出し、治療効果や予後をよりダイナミックかつ多角的に評価することを可能にします。
明日からの臨床と研究に向けて
これらの高度な手法を学ぶことは、単に新しい統計知識を増やすこと以上の意味を持ちます。それは、私たちの手元にあるデータを、より深く、より敬意をもって見つめるための「新しいレンズ」を手に入れることに他なりません。
このレンズを通して見れば、これまで一つの曲線で語られていた物語が、実は様々な原因が絡み合う、もっと豊かで示唆に富んだ物語であったことに気づくはずです。その気づきは、より精度の高い予後予測、より本質的な治療効果の評価、そして最終的には、目の前の患者さん一人ひとりに対する、より個別化された医療へと繋がっていきます。
医療がますますデータ駆動型になる現代において、臨床の複雑性をありのままに受け入れ、それを表現できる分析手法を理解することは、もはや一部の専門家だけのものではありません。エビデンスに基づいた最善の医療を目指す、すべての臨床家・研究者にとって不可欠なスキルとなりつつあるのです。
今日学んだこの視点が、皆さんの明日からの臨床、そして研究の世界を、よりクリアに、より深く照らす一助となることを願っています。
参考文献
- Andersen, P.K., Geskus, R.B., de Witte, T. and Putter, H. (2012) ‘Competing risks in epidemiology: possibilities and pitfalls’, International Journal of Epidemiology, 41(3), pp. 861–870.
- Austin, P.C., Lee, D.S. and Fine, J.P. (2016) ‘Introduction to the analysis of survival data in the presence of competing risks’, Circulation, 133(6), pp. 601–609.
- Fine, J.P. and Gray, R.J. (1999) ‘A proportional hazards model for the subdistribution of a competing risk’, Journal of the American Statistical Association, 94(446), pp. 496–509.
- Gray, R.J. (1988) ‘A class of K-sample tests for comparing the cumulative incidence of a competing risk’, The Annals of Statistics, 16(3), pp. 1141–1154.
- Putter, H., Fiocco, M. and Geskus, R.B. (2007) ‘Tutorial in biostatistics: competing risks and multi-state models’, Statistics in Medicine, 26(11), pp. 2389–2430.
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






