生存時間分析は、病気の再発や生存期間など「イベントが発生するまでの時間」を分析する統計手法です。研究途中で情報が途切れてしまう「打ち切り」データを適切に扱うことで、より正確な治療評価を可能にします。
単にイベントの有無だけでなく「いつ起きたか」という時間情報を分析に組み込みます。最大の課題は、観察期間の終了などでデータが不完全になる「打ち切り」をどう扱うか、という点にあります。
時間経過とともにイベントを免れている集団の割合を、階段状の曲線で可視化します。「打ち切り」データを賢く計算に含めることで、手元の情報から生存の軌跡を正確に描き出すことができます。
ある瞬間のイベント発生リスク(ハザード)を2群間で比較する指標です。HRが1未満ならリスクが低く、1より大きければリスクが高いことを示し、治療効果を定量的に評価する際に広く用いられます。
なぜ「時間」を分析する必要があるのか?
臨床の現場では、私たちは日々「時間」との闘いの中にいます。例えば、新しい抗がん剤が登場したとき、私たちの頭に浮かぶのはこんな疑問ではないでしょうか。
- 「この薬は、従来の治療と比べて再発までの期間をどれくらい延ばせるのだろう?」
- 「治療を開始してから5年後、どれくらいの患者さんが元気に過ごしているだろうか?」
また、心不全の新しい治療薬について考えるときも同様です。
- 「この薬を服用することで、次に入院するまでの期間はどれだけ長くなるんだろう?」
これらの問いに共通するのは、単に「再発したか、しなかったか」「入院したか、しなかったか」という結果(イベント)だけを見ているのではない、という点です。私たちが本当に知りたいのは、そのイベントが発生するまでの「時間」です。この「時間」という貴重な情報を統計モデルに組み込むことで、治療法の評価をより深く、正確に行うことができるようになります。
なぜロジスティック回帰では不十分なのか?
「イベントの有無なら、ロジスティック回帰でも分析できるのでは?」
そう考えるのは自然なことです。しかし、その手法には致命的な欠点があります
2人の患者の「同じ結果」
新薬を服用した2人の患者さんが、どちらも「再発」したとします。
- 患者A: 服用開始から 10日後に再発
- 患者B: 10年間、元気に過ごした後に再発
ロジスティック回帰のモデルでは、この2人は「再発=1」という全く同じ結果として扱われ、「10日」と「10年」という天と地ほどの差がある時間情報が完全に失われてしまいます。
臨床研究における避けられない壁:「打ち切り」
しかし、この「時間」データを分析するのは、実は一筋縄ではいきません。なぜなら、臨床研究には特有の難しさがあるからです。
想像してみてください。5年間の追跡調査を行う大規模な臨床試験を計画したとします。しかし、現実は計画通りには進みません。
- 研究期間の終了: 5年間の研究期間が終わった時点で、まだイベント(例:再発)が起きていない参加者が大勢います。彼らは「5年間は無事だった」という重要な情報を持っています。
- 追跡不能(ロスト・トゥ・フォローアップ): 参加者の中には、途中で引っ越してしまったり、連絡が取れなくなったりする方もいるでしょう。
- 他の理由による死亡: 研究の目的であるイベントとは異なる理由(例:交通事故)で亡くなる方もいるかもしれません。
こうした「最後までイベントの発生を観察できなかったデータ」を、統計学の世界では「打ち切り(Censoring)」と呼びます。もし、これらのデータを単純に「イベントが起きなかった」として扱ったり、分析から除外してしまったりすると、結果は大きく歪んでしまいます。実際に、米国食品医薬品局(FDA)が公表しているガイドラインにおいても、この打ち切りデータの適切な取り扱いは、医薬品の有効性を評価する上で極めて重要であると強調されています (FDA, 2021)。
この「打ち切り」という壁を乗り越え、手元にある不完全な情報から最大限、真実に近い答えを導き出すための強力な武器。それが、これから私たちが学んでいく生存時間分析 (Survival Analysis) なのです。
生存時間分析は、どんな時に使うか?
生存時間分析は「死」だけに限らず、イベントが起こるまでの時間を扱いたいあらゆる場面で使われます。臨床研究や医療システム研究の多くで応用が可能です。
- がん領域: 死亡までの時間(全生存期間: OS)、再発までの時間、病勢進行までの時間(無増悪生存期間: PFS)
- 循環器疾患: 心筋梗塞の発症までの時間、心不全での再入院までの時間
- 感染症: 治癒までの時間、再感染までの時間
- 医療システム研究: 退院までの時間、医療機器やデバイスが故障するまでの時間
つまり、生存時間分析は「生きる/死ぬ」という二分法を超え、時間情報と打ち切り(途中で観察が途絶えるケース)を適切に扱える点に強みがあります。これにより、単純なロジスティック回帰や割合比較では得られない、より豊かな洞察を与えてくれるのです。
このセクションで学ぶこと
この入門セクションでは、生存時間分析の世界を探検するための「地図」と「コンパス」を手に入れます。具体的には、以下のキーワードを一つひとつ、身近な例え話を交えながら解き明かしていきます。
- 生存時間データと打ち切り: 分析の主役となるデータの構造を理解します。
- 生存関数とKaplan-Meier曲線: 時間の経過とともにイベントを免れている割合を可視化する方法を学びます。
- ハザード関数とハザード比: 「ある瞬間のリスク」を捉え、グループ間で比較するための指標を学びます。
統計学的な手法に馴染みがない方でも、直感的に「なるほど!」と思っていただけるように解説を進めていきますので、どうぞリラックスして読み進めてください。さあ、一緒に時間データを読み解く冒険に出発しましょう!
生存時間分析は「マラソン大会」のようなもの
生存時間分析の考え方を直感的に理解するために、一つたとえ話をさせてください。この分析は、まるで「マラソン大会」の記録を分析するようなものなんです。ただし、普通の大会とは少し違う、特別なルールがあります。
マラソン大会の登場人物たち
この特別なマラソン大会の参加者とルールを見ていきましょう。
- イベント (Event): これは私たちが最も注目している出来事、つまり「ゴール」です。臨床研究では、このゴールは研究目的によって様々です。例えば、病気の再発、特定の合併症の発生、死亡、あるいは逆に症状が改善して「回復」することかもしれません。
- 生存時間 (Survival Time): 文字通り、「スタート」から「ゴール(イベント発生)」までにかかった時間です。「Time-to-Event(イベントまでの時間)」とも呼ばれるのはこのためですね。
- 打ち切り (Censoring): これが生存時間分析を特徴づける、最も重要なコンセプトです。マラソンの途中で、選手の正確なゴールタイムが分からなくなってしまう状況を指します。
なぜ「打ち切り」がそんなに重要なのか?
「打ち切り」は、いわばレースのリタイアや、時間切れのようなものですが、その理由が分析の鍵を握ります。もし、ゴールタイムが不明な選手を単純にデータから除外してしまうと、「ゴールできなかった選手(イベントが起きなかった良い結果の選手)」がごっそり抜け落ちてしまい、全体の成績(生存率など)を不当に悪く見積もってしまう可能性があります (Klein and Moeschberger, 2003)。
生存時間分析では、こうした選手が持っている「途中までの記録」という貴重な情報を、決して無駄にしないのです。打ち切りにはいくつかの種類がありますが、臨床研究で最も頻繁に遭遇するのが右側打ち切り (Right Censoring)です。
- マラソンの例:
- 大会の制限時間(例:6時間)が来た時点で、まだ元気に走っている選手。この選手は「少なくとも6時間は走り続けられた」ことが分かります。
- コースの途中で「家族の応援に来たので、ここでレースを降ります」と言ってコースアウトした選手。この選手も「コースアウトした時点まではゴールしていなかった」という事実が記録されます。
- 臨床研究の例:
- 研究の観察期間(例:5年間)が終了した時点で、イベントが発生していない患者さん。
- 患者さんが遠方に引っ越してしまい、その後の状況が追えなくなった(追跡不能)。
あまり頻繁ではありませんが、他にも以下のような打ち切りが存在します。
- 左側打ち切り (Left Censoring): いつスタートしたか正確には分からない状態です。マラソンで言えば「気づいたらコースを走っていたけれど、スタートゲートを通過した正確な時刻が不明な選手」のようなイメージです。
- 区間打ち切り (Interval Censoring): イベントが「ある期間内」に起こったことは分かるけれど、正確な時点は不明な状態です。「3ヶ月目の診察では異常がなかったのに、6ヶ月目の診察で再発が確認された」といったケースがこれにあたります。
これらの登場人物を、下の表にまとめてみました。
| 用語 | マラソンのたとえ | 臨床研究での例 |
|---|---|---|
| 生存時間 | スタートからゴールまでの走行時間 | 治療開始から再発・死亡までの期間 |
| イベント | ゴールテープを切ること | 病気の再発、死亡、特定の症状の出現 |
| 右側打ち切り | 制限時間まで走り続けている、途中で追跡不能になる | 研究終了時点で生存、転居による追跡不能 |
このように、生存時間分析のキモは、「打ち切り」は単なる欠損データではなく、「途中経過」という価値ある情報なのだと捉え、それを統計モデルにうまく組み込む点にあるのです。
生存の軌跡を描く:生存関数とKaplan-Meier曲線
さて、マラソン大会に参加した個々の選手の記録(ゴールタイムやリタイアした時間)が集まりました。次に知りたくなるのは、「この大会全体として、時間とともにどれくらいの選手が走り続けているんだろう?」ということですよね。この集団全体のパフォーマンスの軌跡を、打ち切りという不完全なデータを含んだまま美しく描き出してくれるのが、生存関数 (Survival Function) と、それを推定するためのカプラン・マイヤー法 (Kaplan-Meier method)です。
生存関数 S(t) とは? — 集団のスタミナを測る物差し
生存関数は、ある時間 \(t\) を超えて生存している(まだイベントが起きていない)確率を表します。マラソンの例で言えば、「レース開始から \(t\) 時間が経過した時点で、まだコース上に残って走っている選手の割合」と考えると、とても分かりやすいと思います。数式で書くと少し難しそうに見えますが、意味はシンプルです。
\[ S(t) = P(T > t) \]
- \( T \): イベントが発生するまでの時間(ある人のゴールタイム)を表す確率変数です。
- \( t \): 私たちが関心を持っている特定の時点(マラソン開始からの経過時間)です。
- \( P(T > t) \): ある人のゴールタイム \(T\) が、ある時点 \(t\) よりも後である確率。つまり、時点 \(t\) でまだゴールしていない(生存している)確率のことです。
この生存関数をグラフにすると、特徴的な形になります。スタート時点(\(t=0\))では、全員がまだ走り始めているので生存確率は1.0(100%)です。そして、誰かがイベントを迎える(ゴールする)たびに、その確率はカクンと階段状に下がっていきます。選手がコースからいなくなることはあっても、戻ってくることはないので、この曲線が上がることはありません。
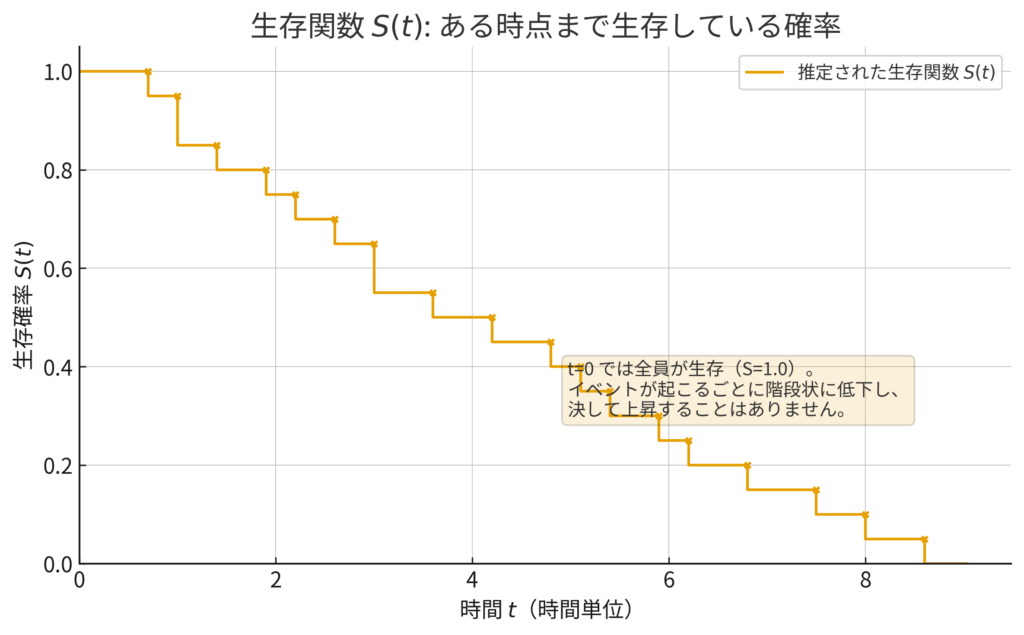
打ち切りデータを賢く扱う:Kaplan-Meier推定量
ここで再び問題になるのが、「打ち切り」の存在です。もし打ち切られた人(途中でリタイアした選手)を単純にデータから除外してしまうと、生存率を系統的に過小評価してしまう可能性があることは、すでに指摘されています (Klein and Moeschberger, 2003)。では、どうすれば彼らの持つ「途中までの情報」を活かせるのでしょうか?
この問いに対する見事な解答を提示したのが、統計学者のエドワード・カプラン氏とポール・マイヤー氏が1958年に発表した、今や生存時間分析の代名詞とも言えるカプラン・マイヤー法です (Kaplan and Meier, 1958)。
この方法の賢い点は、「イベントが起きた各時点」で、その瞬間を乗り越える確率(条件付き生存確率)を計算し、それを掛け合わせていくというアプローチにあります。これを「積率法」と呼びます。
少し具体的に見てみましょう。
- まず、イベントが発生した全ての時点を時間順に並べます。
- 各イベント時点の直前で、「何人がリスクに晒されているか(まだ走っているか)」を数えます。
- その時点でイベントが発生した人数を使って、「その瞬間を生き延びる確率」を計算します。(例:10人中1人がイベント発生 → 生存確率は 9/10 = 0.9)
- そして、全体の生存確率 \(S(t)\) を、それまでに計算した区間ごとの生存確率を次々と掛け合わせることで更新していくのです。
では、「打ち切り」の人はどうなるのでしょう?彼らは、打ち切りが発生した時点まではリスクに晒されている人数(分母)に含まれ、生存に貢献します。そして、その次のイベント時点からは、分母から静かに除外されます。こうすることで、「その時点までは生存していた」という情報を余すところなく活用できるわけです。
Kaplan-Meier曲線から読み取れること
こうして描かれたカプラン・マイヤー曲線を見れば、いくつかの重要な指標を直感的に読み取れます。
- 中央生存期間 (Median Survival Time): 生存率がちょうど50%(\(S(t)=0.5\))に低下する時間点です。グラフの縦軸0.5のところから水平に線を引き、曲線とぶつかった点の横軸を読み取ります。一部の極端に長生きした人の影響を受けにくいため、平均生存時間よりも頑健(ロバスト)な指標として広く用いられます (Altman and Bland, 1998)。
- 時点生存率 (Time-point Survival Rate): 例えば「1年生存率」や「5年生存率」といった、特定の時点での生存確率です。これもグラフから簡単に読み取れます。
- 信頼区間: カプラン・マイヤー曲線はあくまでサンプルから得られた「推定値」です。そのため、通常は曲線の周りに信頼区間(Confidence Interval)も一緒に描画され、推定の不確実性(ばらつき)がどれくらいあるかを示します。一般的に、時間が経過して対象となる人数が減るほど、この区間の幅は広がっていきます。
下の図は、カプラン・マイヤー曲線の典型的な例です。イベント発生(|--)で生存率が階段状に下がり、打ち切り(+)では印が付くだけで曲線は下がりません。
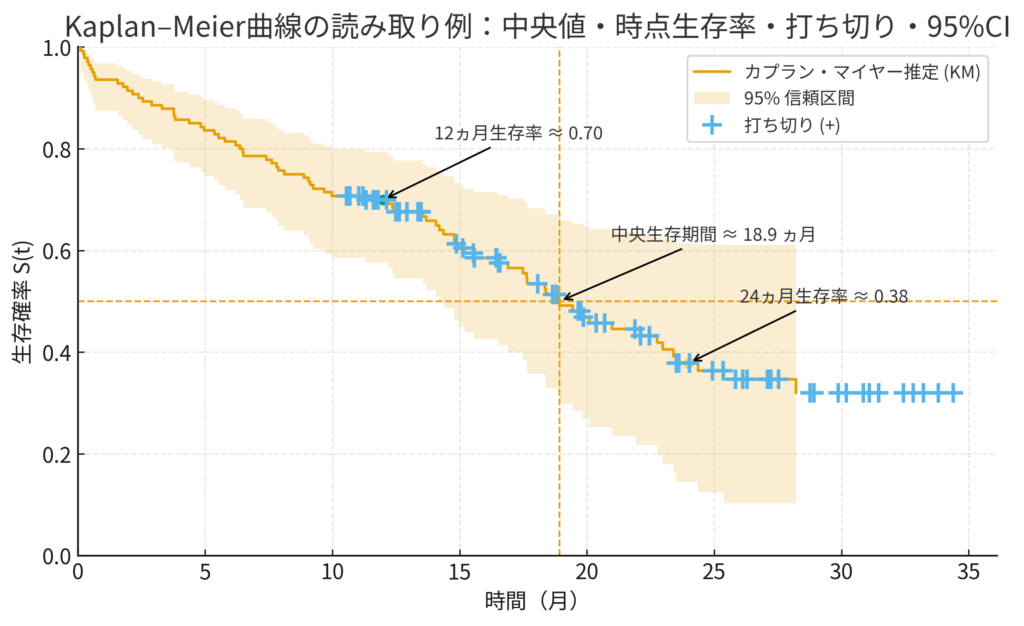
このように、カプラン・マイヤー法は、複雑な時間データからでも、生存の軌跡を豊かに描き出すことができる、非常に強力でエレガントなツールなのです。
「瞬間のリスク」を測る物差し:ハザード関数とハザード比
カプラン・マイヤー曲線は、グループ全体の生存の軌跡を視覚的に見せてくれる、非常に優れた「記述的」なツールです。しかし、そこから一歩進んで、「ある治療法が、もう一方に比べてどれくらいリスクを低減させるのか」を定量的に評価し、統計的に比較したくなるのが自然な流れですよね。
そのために必要になるのが、もっとミクロな視点、つまり「ある一瞬におけるイベントの起こりやすさ」です。この「瞬間のリスク」という概念を捉えるのがハザード関数 (Hazard Function)、そしてそれをグループ間で比較するための強力な指標がハザード比 (Hazard Ratio, HR)です。
ハザード関数 h(t) とは? — リスクの「スピードメーター」
ハザード関数は、よく車のスピードメーターに例えられます。この例えをもう少し深掘りしてみましょう。
- 生存関数 S(t): 車が出発してから、ある時間 \(t\) までに「まだ事故を起こさずに走り続けている確率」です。これは車の耐久性や安全性能の全体像を示します。
- ハザード関数 h(t): 「今、この瞬間」の運転の危険度を示すスピードメーターの針です。たとえ安全な車でも、危険な山道でスピードを出せば、その瞬間の事故リスク(ハザード)は高まります。逆に、高性能なスポーツカーでも、安全な高速道路をゆっくり走っていれば、その瞬間のリスクは低いでしょう。
重要なのは、ハザードは「確率」そのものではなく、「単位時間あたりのイベント発生率」つまり速度や率 (rate)であるという点です。だからこそ、確率と違って1を超えることもあり得ます。
この「瞬間のリスク率」を数式で表現すると、以下のようになります。
\[ h(t) = \lim_{\Delta t \to 0} \dfrac{P(t \le T < t + \Delta t \mid T \ge t)}{\Delta t} \]
この式を分解してみましょう。
- \( T \ge t \): 「時点 \(t\) までイベントを起こさずに生き延びてきた」という条件を表します。(「今まで無事故で運転してきた」という前提です。)
- \( P(t \le T < t + \Delta t \mid \dots) \): その前提のもとで、「次のごくごく短い時間(\(\Delta t\))の間にイベントが起こる条件付き確率」です。(「次の瞬間に事故が起こる確率は?」)
- \( \dfrac{\dots}{\Delta t} \): この確率を、その非常に短い時間で割ることで、「率」に変換しています。これにより、「瞬間の勢い」や「イベント発生の速度」が計算できるのです。
ハザード比 (HR) — 2台の車のスピードメーターを比べる
さて、いよいよ臨床研究で最もよく目にする指標の一つ、ハザード比 (Hazard Ratio, HR) の登場です。これは、2つのグループ(例えば、新薬を投与したグループとプラセボを投与したグループ)のハザード関数、つまり2台の車のスピードメーターを直接比べるための指標です (Cox, 1972)。
\[ HR = \dfrac{h_1(t)}{h_0(t)} \]
ここで、\(h_1(t)\) は新薬グループのハザード関数(新薬カーの速度)、\(h_0(t)\) はプラセボグループのハザード関数(プラセボカーの速度)です。
この指標の解釈は非常に直感的です。
- HR = 2.0 の場合: 新薬カーのスピードメーターは、常にプラセボカーの2倍を指している、ということです。つまり、「新薬グループは、プラセボグループに比べて、どの瞬間においても2倍イベントが起こりやすい」と解釈できます。
- HR = 0.5 の場合: 新薬カーの速度が、常にプラセボカーの半分であることを意味します。つまり、「新薬グループは、どの瞬間においてもイベント発生リスクが半分になる」と解釈できます。これは治療が有効であることを強く示唆します。
まとめると、ハザード比の解釈は以下のようになります。
- HR > 1: 比較しているグループ(例:新薬群)の方が、基準となるグループ(例:プラセボ群)よりリスクが高い。
- HR < 1: 比較しているグループの方が、リスクが低い。(治療が有効であることを示唆します)
- HR = 1: 両グループのリスクは同じ。
ただし、この便利なハザード比を正しく解釈するためには、「2つのグループのハザードの”比”が、時間を通じて一定である」という比例ハザード性の仮定が満たされている必要があります。この非常に重要な前提については、次のセクションで詳しく見ていきましょう。
ハザード比を解釈する上での「黄金律」:比例ハザード性
ハザード比は、2つのグループのリスクをたった一つの数値で比較できる、非常にパワフルで便利な指標です。しかし、その便利さには一つだけ、とても大切な「お約束」が付いてきます。これを破ってしまうと、ハザード比の解釈そのものが意味をなさなくなってしまうため、それが、「比例ハザード性の仮定 (Proportional Hazards Assumption)」です。
この「お約束」の本当の意味とは?
この仮定の提唱者であるD. R. Coxの独創的な論文(Cox, 1972)に端を発するこの考え方は、「2つのグループのハザードの”比”が、観測期間を通じて一定である」というものです。先ほどの車のスピードメーターの例えに戻ってみましょう。
- 比例ハザード性が成り立つ場合: A車(治療群)の速度が常に時速50kmで、B車(対照群)の速度が常に時速100kmだとします。この場合、いつどの瞬間に見ても、A車の速度はB車の半分です。ハザード比は常に0.5で一定。これが比例ハザード性が満たされている状態です。
- 比例ハザード性が成り立たない場合: A車(治療群)が、手術直後のような短期的なリスクを伴う治療だとします。これはスタート直後に猛烈な加速をするドラッグレーサーのようなものです。一方、B車(対照群)は、リスクはそこそこでも、それが長く続くような状態で、一定のペースで走り続けるマラソンランナーだとします。
- レース序盤: A車(治療群)の速度はB車(対照群)よりずっと速い(ハザードが高い)。
- レース終盤: A車はすぐに燃料を使い果たしてゆっくり走る一方、B車は変わらぬペースで走り続けています。この時点では、B車の方がA車よりずっと速い(ハザードが高い)。
このドラッグレーサーとマラソンランナーのレース全体を、たった一つの「速度比(ハザード比)」で要約しようとしても、無茶だと思いませんか?レースの序盤と終盤で全く状況が違うのですから、平均的な比率を計算しても、それは現実を正しく反映しません。これが、比例ハザード性の仮定が重要である理由です。
仮定が破れているサイン:交差する生存曲線
では、この「お約束」が守られていないとき、データはどんなサインを見せてくれるのでしょうか?最も分かりやすい視覚的なサインが、カプラン・マイヤー曲線の交差です。
先ほどのドラッグレーサー(治療群)の例で考えてみましょう。序盤のリスクが非常に高いため、治療群の生存曲線はスタート直後に急降下します。しかし、その初期リスクを乗り越えた後はリスクが低くなるため、曲線はなだらかになります。一方、マラソンランナー(対照群)の曲線は、一定のペースで下がり続けます。すると、どこかの時点で、一度は下にあった治療群の生存曲線が、対照群の曲線を追い抜いて交差する、という現象が起こり得ます。
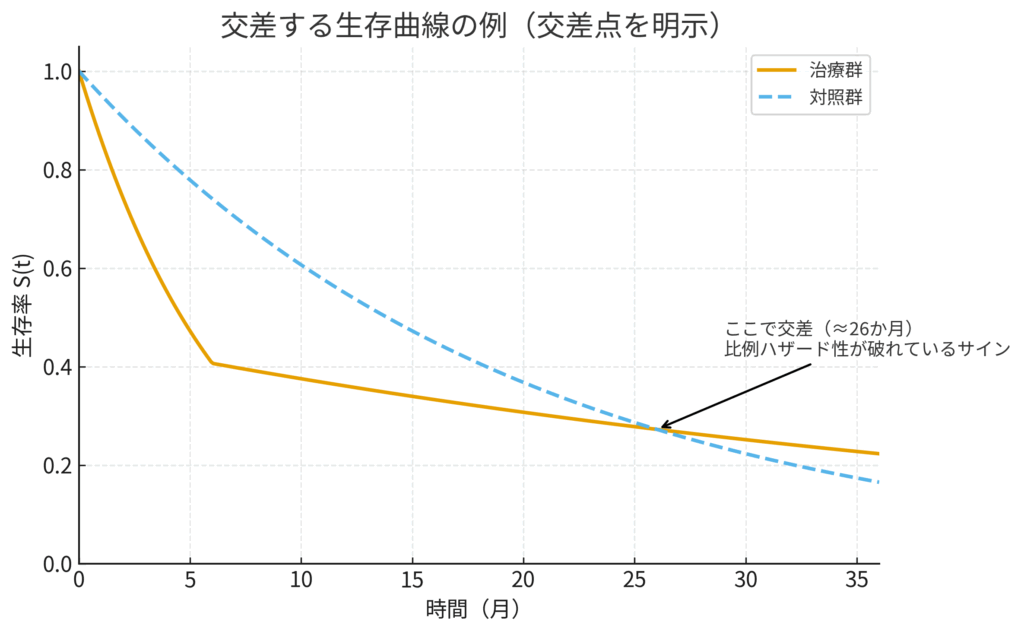
このように生存曲線が交差している場合、比例ハザード性の仮定は明らかに満たされていないと言えます (Parmar et al., 1998)。このような状況で無理やりハザード比を一つだけ計算しても、それは研究期間中の複雑なリスクの変化を平均化してしまい、重要な情報を見えなくしてしまいます。
もし仮定が満たされなかったら?
ハザード比という便利な指標が、「比例ハザード性」という黄金律の上に成り立っていることはご理解いただけたかと思います。では、もし自分のデータでこのお約束が守られていなかったら、どうすればよいのでしょうか?分析を諦めるしかないのでしょうか?
ご安心ください。そんなことはありません。それは単に「ハザード比という単一の物差しでは、この現象をうまく表現できない」というサインに過ぎず、探偵が別の捜査ツールを取り出すように、私たちも別のアプローチに切り替えれば良いのです。
ステップ1:仮定が守られているかチェックする
まず、ハザード比を報告する前に、この仮定が満たされているかをチェックするのが作法です。主なチェック方法には、グラフで確認する方法と、統計的に検定する方法があります。
- グラフで視覚的に確認する
- 生存曲線の確認: 最も直感的な方法です。上述のように、2つのカプラン・マイヤー曲線が交差していたり、時間とともに間隔が極端に開いたり閉じたりしている場合、仮定が満たされていない可能性を疑います。
- Log-logプロット: 生存関数の値を2回対数変換(log-log変換)したものをプロットする方法です。もし比例ハザード性が成り立っていれば、2つのグループの線がおおむね「平行」になります。線が交差したり、大きく離れたりしている場合は、仮定違反のサインです。
- 統計的に検定する
- シェーンフェルド残差検定 (Schoenfeld residuals test): これは、モデルの残差(予測と実際のズレ)が、時間ととも変化していないかを数学的に検証する方法です。検定結果として算出されるp値が有意水準(通常0.05)より小さい場合、「ハザード比が時間とともに変化している」と判断し、比例ハザード性の仮定は満たされない、と結論付けます。
ステップ2:仮定違反だった場合の代替アプローチ
これらのチェックの結果、仮定が満たされていないと判断された場合、以下のような代替アプローチを検討します。
- アプローチ1:時間を区切って分析する(時間依存性Cox回帰) ドラッグレーサー(治療群)とマラソンランナー(対照群)の例を思い出してください。レース序盤と終盤で、リスクの比(ハザード比)は全く異なりました。であれば、分析期間を臨床的に意味のある期間で区切り、それぞれのハザード比を報告するという手があります。例えば、「術後30日間」と「30日以降」でハザード比を別々に計算するのです。これは時間依存性共変量を用いたCox回帰モデルで実現できます。
- アプローチ2:別の物差しを使う(RMST) ハザード比という「瞬間の速度比」を比べる物差しが使えないなら、別の物差しを使えば良いのです。近年、その強力な代替案として注目されているのが、制限付き平均生存時間(Restricted Mean Survival Time, RMST)です。これは、ある特定の時点(例えば5年)までにおける、「生存している期間の平均値」そのものを比較する方法です。カプラン・マイヤー曲線の下の部分の面積を計算している、とイメージすると分かりやすいかもしれません。RMSTは、比例ハザード性の仮定を必要とせず、「治療群は対照群に比べて、5年間で平均〇ヶ月長く生存した」のように、結果の解釈が非常に直感的で臨床家にとって分かりやすい、という大きなメリットがあります。
大切なのは、まずこの「黄金律」の存在を常に意識し、自分のデータがそれを満たしているかどうかを批判的に吟味する姿勢です。そして、もし満たされていなくても、慌てずに適切な分析ツールを選択することが、より真実に近い結論を導く鍵となるのです。
まとめ:今回の冒険の振り返りと次へのステップ
今回は、生存時間分析という広大な世界の入口に立ち、基本的な考え方と、その主役となる用語たちをご紹介しました。一見すると複雑に見えるかもしれませんが、ここまでの内容をマスターすれば、臨床論文で目にする生存曲線やハザード比が、以前とは全く違って見えてくるはずです。
今回の重要ポイント
今回の冒険で手に入れた「3つの神器」と「1つの黄金律」を、最後にもう一度確認しておきましょう。
| コンセプト | 一言でいうと? | 答えてくれる問い |
|---|---|---|
| 生存時間データと打ち切り | 「いつ何が起きたか」という時間付きの情報 | 分析の材料は何か? |
| Kaplan-Meier曲線 | 生存の軌跡を可視化する「物語の絵本」 | 集団の生存パターンは時間とともにどう変化するか? |
| ハザード比 (HR) | 瞬間のリスクを比較する「定量的な物差し」 | 2つのグループのリスクはどれくらい違うのか? |
| 比例ハザード性 | ハザード比を解釈するための「黄金律」 | その物差しは、いつでも信頼できるか? |
途中でデータが追えなくなる「打ち切り」という、一見すると扱いにくい問題に対して、これほど洗練された分析手法があることに、統計学のエレガントさと面白さを感じていただけたなら、とても嬉しく思います。
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸E念やご相談は、必ず専門の医療機関にご相談ください。
参考文献
- Altman, D. G. & Bland, J. M. (1998). ‘Time to event (survival) data’. BMJ, 317(7156), pp.468-469.
- Collett, D. (2015). Modelling Survival Data in Medical Research. 3rd ed. Boca Raton, FL: CRC Press.
- Cox, D. R. (1972). ‘Regression Models and Life-Tables’. Journal of the Royal Statistical Society: Series B (Methodological), 34(2), pp.187-220.
- FDA (2021). Guidance for Industry: Considerations for the Use of Real-World Data and Real-World Evidence to Support Regulatory Decision-Making for Drugs and Biologics. U.S. Department of Health and Human Services, Food and Drug Administration.
- Hosmer, D. W., Lemeshow, S. & May, S. (2008). Applied Survival Analysis: Regression Modeling of Time-to-Event Data. 2nd ed. Hoboken, NJ: John Wiley & Sons.
- Kaplan, E. L. & Meier, P. (1958). ‘Nonparametric Estimation from Incomplete Observations’. Journal of the American Statistical Association, 53(282), pp.457-481.
- Klein, J. P. & Moeschberger, M. L. (2003). Survival Analysis: Techniques for Censored and Truncated Data. 2nd ed. New York: Springer.
- Parmar, M. K. B., Machin, D. & Stewart, L. (1998). ‘Proportional hazards assumption’. Statistics in Medicine, 17(22), pp.2651–2671.
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






