開発したAIドクターが本当に信頼できるかを確認するには、客観的な「成績表」が必要です。その性能は、主に「正しく見分ける能力」と「予測確率の信頼性」という2つの重要な柱で評価されます。
病気の人と健康な人を、どれだけうまく区別できるかという能力。モデルの総合的な実力を測るために、ROC曲線やAUCといった指標で評価します。AIの「視力」の良さに例えられます。
AIが提示する「リスク30%」という確率が、実際の発生頻度と一致しているか。キャリブレーションプロットで視覚的に評価し、AIの「自己評価の的確さ」を測ります。
特定の運用ルール(閾値)を決めた際、「見逃し」や「誤診」が何件発生するかを混同行列で評価します。感度や適合率など、臨床現場での具体的な影響を把握するために不可欠です。
さて、前回までの冒険で、私たちは「ロジスティック回帰」という、病気の発症予測などに使われる強力なツールを手に入れました。これはまるで、未来を予測してくれるAIドクターを育てたようなもので、なんだかワクワクしますよね。
でも、ここで一度立ち止まって、とても大切な問いを立てる必要があります。
「このAIドクター、本当に信頼できるのでしょうか?」
たとえば、AIが「この患者さんは疾患のリスクが高い」と予測したとします。その言葉を鵜呑みにして、侵襲的な検査や治療に進むべきでしょうか? もしAIの予測が外れていたら、患者さんは不必要な負担を強いられることになります。逆に、「リスクは低い」という予測を信じた結果、重大な疾患を見逃してしまったら、取り返しのつかない事態になりかねません。
これは、高性能なエンジンを開発しただけでは、優れた車が完成しないのと同じ話です。どれだけスピードが出ても(予測能力が高くても)、ブレーキの効きやハンドリングの安定性(予測の信頼性や安全性)が検証されていなければ、安心して公道を走ることはできません。
医療における予測モデルの報告に関するガイドラインであるTRIPOD声明でも、モデルの性能評価(Performance)は非常に重要な項目として挙げられています (Collins et al., 2015)。予測モデルを「ブラックボックス」のままにせず、その性能を客観的な指標で評価し、その長所と限界を深く理解すること。これこそが、AIを医療現場で責任を持って活用するための第一歩なのです。
このセクションでは、私たちが育てたAIドクターに客観的な「成績表」をつけるための旅に出ます。この旅を終える頃には、あなたは以下のことができるようになっているはずです。
- モデルの「判別能(Discrimination)」と「適合度(Calibration)」という2つの重要な性能指標の違いを説明できる。
- ROC曲線やAUCといった指標を用いて、モデルがどれだけ正確に患者を分類できるかを評価できる。
- キャリブレーションプロットを見て、モデルが提示する「予測確率」そのものが信頼できるかを判断できる。
- 論文などで新しい予測モデルが提案された際に、その評価パートを批判的に吟味し、臨床的有用性を見抜くための視点を持つことができる。
今回の旅では、このAIドクターの「成績表」の付け方を、一緒に見ていくことにしましょう。具体的には、モデルの予測がどれだけ当たっているか(判別能)、そして予測確率そのものがどれだけ信頼できるか(キャリブレーション)という、2つの大きな視点から評価する方法を学んでいきます。さあ、AIドクターの健康診断を始めましょう。
オッズ比の信頼性:95%信頼区間で「確からしさ」を読む
さて、AIドクターが下す判断の根拠、「オッズ比」から見ていきましょう。
オッズ比は、「ある要因(例えば喫煙)があると、病気になる確率が何倍になるか」を示す、とても便利な指標でしたね。しかし、私たちがどんなに素晴らしい研究を行っても、見ているデータはあくまで母集団(例えば、世界中の全喫煙者)から抽出された一部(標本、つまり研究参加者)にすぎません。
これはまるで、湖にいる「真のオッズ比」という名のたった一匹の魚を、一度だけ網を投げて捕まえようとするようなものです。網に入った魚の位置(計算されたオッズ比)は、本当の魚の位置と少しズレているかもしれませんよね。この避けられない「ズレ」や「誤差」の大きさを考慮に入れるために登場するのが、95%信頼区間(95% Confidence Interval, CI)です。
信頼区間とは、いったい何?
95%信頼区間は、一言でいうと「推定の確からしさの範囲」です。先ほどの魚釣りの例えを続けるなら、「もし同じ性能の網を100回投げたとしたら、そのうち95回は、この網の範囲内に本当の魚が入るだろう」という、網の”信頼性”を示すもの、と考えると分かりやすいかもしれません。
重要なのは、信頼区間の「幅」です。
- 幅が狭い:網の目が細かく、精度が高い推定ができたことを示します。結果の信頼性は高いと考えられます。
- 幅が広い:網の目が粗く、推定の不確実性が大きいことを示します。結果の解釈には慎重さが必要になります。
この「幅」が結果の不確実性、つまりは推定の精度を反映している、という点は統計学者であるBland氏とAltman氏もその重要性を指摘しています (Bland and Altman, 2000)。
信頼区間をビジュアルで理解する
言葉だけだと少し難しいので、数直線を使って視覚的に見てみましょう。オッズ比では、「1」という値が「リスクに全く差がない」ことを示す基準点になります。
ケース1:統計的に有意な結果
例えば、ある治療法の効果を検証し、「オッズ比:2.5(95% CI: 1.5–4.1)」という結果が出たとします。
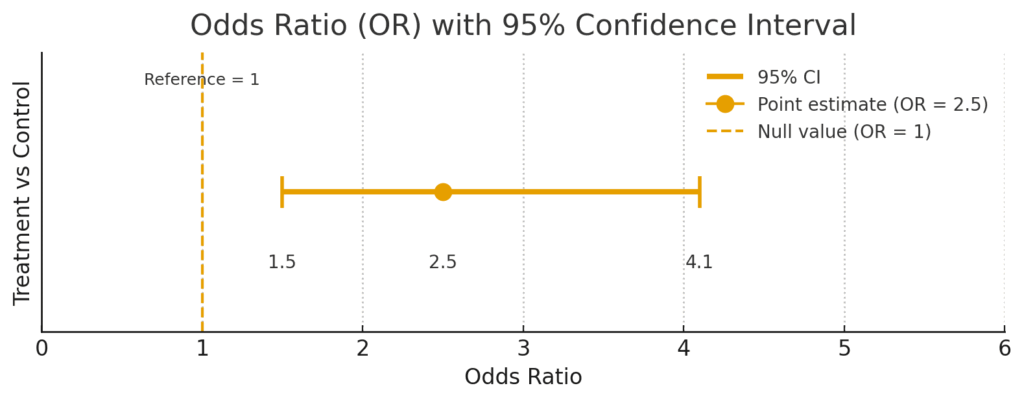
この図を見ると、信頼区間の範囲 [1.5 – 4.1] は、基準となる「1」を全く含んでいません(1より大きい側にあります)。これは、「この治療法は、統計的に意味のあるレベルで、アウトカムのリスクを上げる(または下げる)効果がある」と解釈できます。信頼区間が比較的狭く、この結果は統計的に一定の安定性を示唆していると言えるでしょう。
ケース2:統計的に有意ではない結果
次に、「オッズ比:2.5(95% CI: 0.8–5.2)」という結果だったとします。
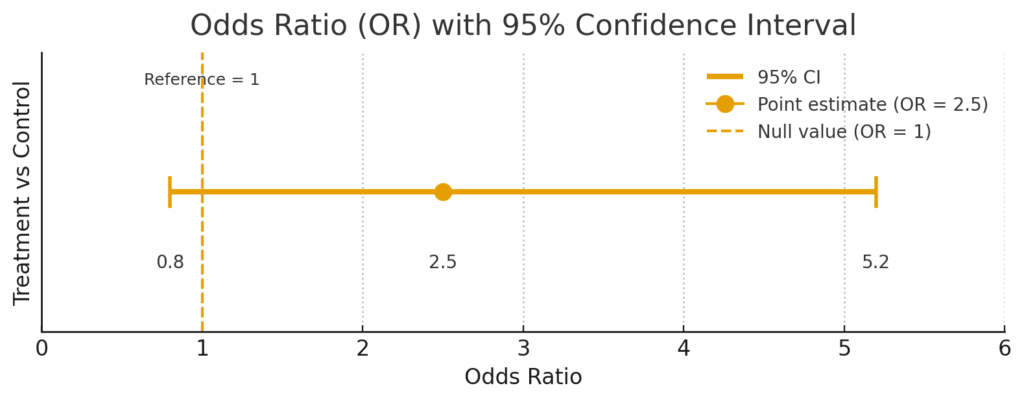
この場合、信頼区間の範囲 [0.8 – 5.2] は、基準の「1」をまたいでしまっています。これは、「真の効果はリスクを下げる側(0.8)にあるかもしれないし、逆に大きく上げる側(5.2)にあるかもしれない。結局のところ、効果があるともないとも断定できない」ということを意味します。このような結果は、「統計学的に有意な差は認められなかった」と結論付けられます。
【一歩進んだ解釈】統計的有意性と臨床的意義は違う
ここで一つ、非常に重要な注意点があります。それは、「統計学的に有意であること」と「臨床的に意味があること」は必ずしもイコールではない、という点です。
例えば、非常に大規模な研究で「オッズ比 1.05 (95% CI: 1.01–1.09)」という結果が出たとします。これは信頼区間が1をまたいでいないので、「統計的に有意」です。しかし、リスクの増加がわずか5%であることが、臨床現場で治療方針を変えるほどのインパクトを持つでしょうか? おそらく、その意義は小さいと判断されることが多いでしょう。
逆に、小規模な研究で「オッズ比 3.0 (95% CI: 0.9–10.1)」という結果が出たとします。これは信頼区間が1をまたいでいるため「統計的に有意ではない」のですが、もしかしたら本当は3倍もの強い効果が隠れている可能性も示唆しています。これは単に研究のサンプルサイズが足りなかった(検出力不足)だけで、もし同じ傾向でより大規模な研究が行われれば、有意な結果が得られるかもしれません。
このように、オッズ比を解釈する際は、点推定の値だけでなく、信頼区間の「幅」と「位置」をしっかり見て、その結果が持つ臨床的な意味合いまで考える癖をつけることが、データを正しく読み解くための鍵となるのです。

AIドクターの判別力チェック①:混同行列で「間違い方のクセ」を分析する
さて、ここからはAIドクターの性能評価の核心に迫っていきます。まずは、AIが下した「陽性(病気です)」「陰性(健康です)」という診断が、どれくらい現実と一致しているのかを見ていきましょう。
この性能評価の基本中の基本となるのが混同行列(Confusion Matrix)です。なんだか物々しい名前ですが、怖がる必要はありません。要は「AIの予測結果」と「実際の正解」を突き合わせた、シンプルな成績表のことです。
混同行列を覗いてみよう
料理にたとえるなら、AIドクターは「これはリンゴ」「これはオレンジ」と仕分ける機械だと考えてみてください。その仕分け結果がどうだったかを、以下の表にまとめたものが混同行列です。
| AIの予測 | |||
|---|---|---|---|
| 陽性 (病気) | 陰性 (健康) | ||
| 実際 | 陽性 (病気) | A (真陽性/TP) | B (偽陰性/FN) |
| 陰性 (健康) | C (偽陽性/FP) | D (真陰性/TN) | |
- A (真陽性, True Positive; TP): 実際に病気の人を、正しく「病気」と予測できた。 (お見事、正解!)
- D (真陰性, True Negative; TN): 実際に健康な人を、正しく「健康」と予測できた。 (これも、お見事!)
- C (偽陽性, False Positive; FP): 健康な人を、間違って「病気」と予測してしまった。 (空振り、第1種の過誤)
- B (偽陰性, False Negative; FN): 病気の人を、間違って「健康」と見逃してしまった。 (見逃し、第2種の過誤)
臨床現場で特に避けたいのは、偽陽性による不要な医療介入と、偽陰性による手遅れですよね。このA, B, C, Dの人数を数えることで、AIドクターの「間違い方のクセ」を定量的に評価できるのです。
具体例で計算してみよう!
概念だけではピンとこないと思うので、具体的な数字を入れてみましょう。ある疾患について、1000人を対象にAIが予測を行ったとします。
- 全体の人数: 1000人
- 実際に病気だった人: 100人
- 実際は健康だった人: 900人
この集団に対するAIの予測結果が、以下のようになったとします。
- A (TP): 病気の人100人のうち、90人を正しく「病気」と予測した。
- B (FN): 病気の人100人のうち、10人を「健康」と見逃してしまった。
- C (FP): 健康な人900人のうち、50人を「病気」と誤診してしまった。
- D (TN): 健康な人900人のうち、850人を正しく「健康」と予測した。
この結果から、様々な評価指標を計算していきます。
① 正解率 (Accuracy):全体の正答率
最も直感的で分かりやすい指標です。全ての予測のうち、どれだけ正解できたかの割合を示します。
\[ \text{Accuracy} = \dfrac{TP+TN}{TP+FN+FP+TN} = \dfrac{A+D}{A+B+C+D} \]
計算例: \( \dfrac{90+850}{90+10+50+850} = \dfrac{940}{1000} = 0.94 \) (94%)
一見すると94%という高い数字で、非常に優秀なモデルに見えます。しかし、正解率には大きな落とし穴があります。例えば、今回の例のように有病率が低い(健康な人が大多数を占める)場合、AIが全員を「健康」と予測するだけでも90%の正解率が出てしまいます (Altman and Bland, 1994)。これでは病気の人を見つけるという目的を果たせません。そこで、もっと多角的な指標が必要になるのです。
② 感度 (Sensitivity) / 再現率 (Recall):病気の見逃しにくさ
実際に病気だった人たちのうち、AIがどれだけ正しく「病気(陽性)」と見つけ出せたかの割合です。
\[ \text{Sensitivity (Recall)} = \dfrac{TP}{TP+FN} = \dfrac{A}{A+B} \]
計算例: \( \dfrac{90}{90+10} = \dfrac{90}{100} = 0.90 \) (90%)
たとえ話: これは「犯人の検挙率」のようなものです。感度が高いほど、病気の見逃しが少ないことを意味します。がん検診のような、一人も見逃したくないスクリーニング検査では、この感度が極めて重要になります。
③ 特異度 (Specificity):健康な人を正しく見抜く力
感度とペアで語られることが多い指標です。実際に健康だった人たちのうち、AIがどれだけ正しく「健康(陰性)」と判定できたかの割合を示します。
\[ \text{Specificity} = \dfrac{TN}{TN+FP} = \dfrac{D}{D+C} \]
計算例: \( \dfrac{850}{850+50} = \dfrac{850}{900} \approx 0.944 \) (94.4%)
たとえ話: これは「冤罪の起こしにくさ」と言えるかもしれません。特異度が高いほど、健康な人を間違って「病気」と診断してしまうことが少ないことを意味し、不要な精密検査や患者の心理的負担を減らすことに繋がります。
④ 適合率 (Precision) / 陽性的中率 (PPV):「陽性」の信頼性
AIが「病気(陽性)」と予測した人たちのうち、本当に病気だった人の割合です。
\[ \text{Precision (PPV)} = \dfrac{TP}{TP+FP} = \dfrac{A}{A+C} \]
計算例: \( \dfrac{90}{90+50} = \dfrac{90}{140} \approx 0.643 \) (64.3%)
たとえ話: 「オオカミが来た!」と叫んだとき、本当にオオカミが来ていた確率です。この値が低いと、AIの「陽性」判定が”空振り”だらけであることを意味します。適合率が高い診断は、その後の侵襲的な検査や治療に進む際の強い根拠となります。
⑤ F1スコア:感度と適合率の絶妙なバランサー
さて、私たちは「感度(見逃しを減らしたい)」と「適合率(空振りを減らしたい)」という、2つの重要な指標を学びました。しかし、この2つは多くの場合、シーソーのようなトレードオフの関係にあります。
たとえ話: テストで高得点を狙う学生を想像してください。
- 感度を優先する戦略: とにかく多くの問題を解こうと、スピードを上げてどんどん回答します。これにより、多くの正解を拾えるかもしれませんが(感度UP)、ケアレスミスが増えて不正解も多くなります(適合率DOWN)。
- 適合率を優先する戦略: 一問一問をじっくり時間をかけて、絶対に間違えないように解きます。回答した問題の正答率は非常に高いでしょうが(適合率UP)、時間が足りずに多くの問題を解き残してしまいます(感度DOWN)。
どちらの戦略も、高得点という最終目標からは遠ざかってしまいますよね。AIの性能評価もこれと同じで、感度と適合率のどちらか一方だけが良くても、総合的に優れたモデルとは言えません。
そこで登場するのが、この2つの指標のバランスをうまくとるための評価指標、F1スコアです。
なぜただの平均ではない?「調和平均」のうまい仕組み
F1スコアは、感度と適合率の調和平均という、少し特殊な平均を使って計算されます。なぜ、単純な算術平均( (A+B)/2 )ではいけないのでしょうか?
それは、調和平均には「両方の値が揃っていないと、スコアが著しく低くなる」という性質があるからです。つまり、どちらか一方の指標だけが極端に悪い場合に、厳しいペナルティを課してくれるのです。
例えば、あるモデルの性能が以下だったとします。
- 適合率 = 0.9 (90%)
- 感度 = 0.1 (10%)
もしこれを単純な算術平均で評価すると、(0.9 + 0.1) / 2 = 0.5 となり、まあまあな性能に見えてしまいます。しかし、F1スコアで計算すると…
\[ \text{F1 Score} = 2 \times \dfrac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} \]
計算例: \( 2 \times \dfrac{0.9 \times 0.1}{0.9 + 0.1} = 2 \times \dfrac{0.09}{1.0} = 0.18 \)
このように、F1スコアは0.18という非常に低い値を示します。これは、感度が著しく低いというモデルの欠点を、算術平均よりも遥かに正直に反映してくれています。この性質のおかげで、F1スコアはバランスの取れたモデルを評価するのに非常に適しているのです。
私たちが前のセクションで用いた例では、適合率が約0.643、感度が0.90でした。
計算例: \( 2 \times \dfrac{0.643 \times 0.90}{0.643 + 0.90} \approx 0.75 \)
これは、2つの指標がある程度バランスが取れていることを示唆しています。
【発展】Fベータスコア:バランスの比重を変える
ちなみに、F1スコアは感度と適合率を平等に重視する場合の指標ですが、もし「感度の方を2倍重視したい」といった要望がある場合は、Fベータスコア (F-beta Score) という一般化された指標を使うこともできます。
- F2スコア (β=2): 感度を適合率より重視する。見逃しをとにかく減らしたい場合に使う。
- F0.5スコア (β=0.5): 適合率を感度より重視する。陽性判定のコストが高い場合に使う。
F1スコアは、このFベータスコアでβ=1とした、最も標準的なケースというわけですね。
このように、F1スコアは、感度と適合率というトレードオフの関係にある2つの指標を、一つの数値に賢く集約してくれる、非常に便利なバランサーなのです。
AIドクターの判別力チェック②:ROC曲線とAUCで「総合的な実力」を評価する
先ほど、感度や特異度といった指標を学びました。これらは非常に重要ですが、実は大きな弱点を抱えています。それは、AIの「陽性」と「陰性」を分ける閾値(いきち)をどこに置くかによって、コロコロと値が変わってしまう点です。
例えば、AIが「疾患の可能性80%」と予測した場合、これを陽性と判断するかもしれません。では、「50%」なら?「30%」ならどうでしょう?この閾値のさじ加減一つで、感度や特異度の数値は大きく変動します。これでは、モデルが持つ本来の実力を公平に評価できません。
そこで登場するのが、ROC曲線(Receiver Operating Characteristic curve)と、その性能を一つの数値に要約したAUC(Area Under the Curve)です。これらは、閾値のとり方に依存しない、モデルの「総合的な判別能力」を評価するための、いわばゴールドスタンダードとも言える手法です。
ROC曲線は、どうやって描かれるのか?
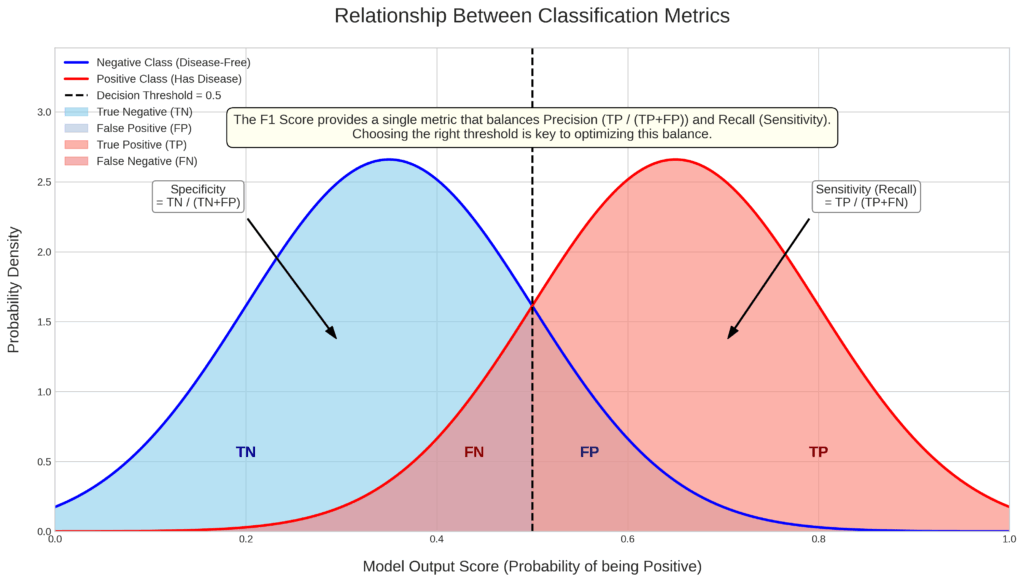
ROC曲線は、AIドクターの「診断の厳しさ(閾値)」を様々に変えていったときに、診断性能がどう変化するかをプロットしたグラフです。具体的には、以下の2つの指標の関係性を可視化します。
- 縦軸:感度(真陽性率)
- 病気の人を、どれだけ正しく「病気」と見つけられるか。1に近いほど良い。
- 横軸:1 – 特異度(偽陽性率)
- 健康な人を、どれだけ間違って「病気」と診断してしまうか。0に近いほど良い。
この曲線を描くプロセスを簡単に説明すると、以下のようになります。
- まず、AIは各患者さんに対して「病気である確率」を0から1の間で計算します。
- 次に、考えうるすべての確率(例えば0.01, 0.02…0.99)を閾値の候補として設定します。
- それぞれの閾値ごとに、「これより確率が高ければ陽性、低ければ陰性」と判断し、その際の感度と偽陽性率を計算して、グラフ上に点を打ちます。
- こうして打たれた無数の点を滑らかにつないだものが、ROC曲線となるのです。
ROC曲線の見方:左上を目指せ!
このグラフ空間には、いくつか重要な意味を持つ場所があります。

- 左上の角 (点A, 座標(0,1)): 偽陽性率が0で感度が1.0。これは、健康な人を一人も間違えず、かつ病気の人を全員見つけ出すという、理論上の完璧なモデルを意味します。
- 対角線 (点線の部分): 感度と偽陽性率が同じになる線です。これは、AIの予測が当てずっぽう(コイン投げ)と同じレベルであることを示します。AUCにすると0.5になります。
したがって、優れたモデルのROC曲線は、この対角線から大きく離れ、左上の角に向かって弓なりに張り出す形になります。
この関係を、お馴染みの「税関の検査官」の例えで考えてみましょう。
- すごく厳しい検査官(閾値が低い): 多くの密輸品を見つける(感度が高い)が、多くの無実の旅行者も足止めする(偽陽性率が高い)。グラフでは右上の点に対応します。
- すごく緩い検査官(閾値が高い): 無実の旅行者を間違えない(偽陽性率が低い)が、多くの密輸品を見逃す(感度が低い)。グラフでは左下の点に対応します。
ROC曲線は、この検査官が厳しさを様々に変えながら取ることができる、全てのパフォーマンスの軌跡を描いたものなのです。
AUC:「判別能力」を一つの数字で表す究極の指標
ROC曲線はモデルの性能を視覚的に示してくれますが、複数のモデルの性能を客観的に比較したい場合、「どちらの曲線がより左上にあるか」を判断するのは難しいことがあります。
そこで、このROC曲線と横軸で囲まれた部分の面積を計算したものがAUC (Area Under the Curve)です。AUCは0から1の値をとり、1に近いほどモデルの判別能力が高いことを示します。
- AUC = 1.0: 完璧なモデル。
- AUC = 0.5: 当てずっぽうと同じレベル。
- AUC < 0.5: 当てずっぽうより悪い(予測のラベルを逆にすれば性能が上がる)。
AUCの解釈には、もう一つ非常に直感的でパワフルな方法があります。それは、「ランダムに選んだ病気の人1人と、ランダムに選んだ健康な人1人がいたときに、AIが病気の人の方により高いリスクスコア(確率)を割り当てる確率」と解釈する方法です。
例えばAUCが0.85だった場合、これは「病気の人と健康な人のペアの85%に対して、AIは正しく『病気の人の方がリスクが高い』とランク付けできる」ということを意味します。これは非常に分かりやすいですよね。
二値分類モデルの場合、AUCはC-statistic (Concordance statistic) とも呼ばれ、同じ値を指します。
AUCの目安は?
以下は予測モデルの性能を評価する際の一般的な目安ですが、米国胸部疾患学会のCook (2007)や統計学の権威であるHosmerら(2013)が指摘するように、これが絶対的な基準ではないことに強く注意する必要があります。求められる精度は領域によって全く異なり、臨床的な有用性は常に文脈の中で判断されるべきです。
- AUC > 0.8: 一般に良好な判別能とみなされることが多い
- AUC 0.7–0.8: まあまあ良い判別能
- AUC 0.6–0.7: やや不十分な判別能
ROC曲線とAUCを理解することで、私たちは閾値という厄介な問題から解放され、モデルが持つ真の「物事を見分ける力」を公平に評価することができるようになるのです。
AIドクターの判別力チェック③:「混同行列の指標」と「ROC/AUC」の賢い使い分け
さて、私たちはAIドクターの判別力を評価するための2つの強力なツールセット、「混同行列から導かれる指標群(感度、適合率など)」と「ROC曲線とAUC」を学びました。ここで、多くの方が疑問に思うかもしれません。
「結局、どちらを使えばいいの?」
この問いへの答えは、「どちらも重要だが、役割が違う」です。両者は対立するものではなく、互いに補完し合うパートナーのような関係にあります。その違いを、車の性能評価に例えてみましょう。
- 混同行列の指標(感度・適合率など):
これは、「時速60kmで走行中に、ブレーキを踏んでから何メートルで停止できるか?」という、特定の条件下での性能テストに似ています。臨床現場での「予測確率が15%を超えたら精密検査を行う」といった具体的な運用ルール(閾値)が決まっている場合に、そのルール下でどれだけの見逃しや空振りが生じるかをピンポイントで評価できます。具体的で、非常に実践的な指標です。 - ROC曲線とAUC:
これは、エンジンの性能を示す馬力・トルク曲線のようなものです。特定の速度やギア(閾値)に依存せず、「そのエンジンが持つポテンシャル全体」を評価します。異なるモデル(エンジン)のどちらが、あらゆる状況を考慮した上で、総合的によりパワフルかを比較するのに適しています。
このイメージを元に、それぞれのツールが特に輝く場面を整理してみましょう。
混同行列の指標(感度・適合率など)が輝く場面 ✨
- 臨床的な運用ルール(閾値)が明確な場合
特定のガイドラインや院内ルールで「このスコアがX点以上なら介入」と決まっている場合、その閾値での感度、特異度、適合率こそが、現場が最も知りたい情報になります。 - 見逃し(偽陰性)と空振り(偽陽性)のコストが大きく異なる場合
「見逃しのコストが極めて高いがん検診」や「偽陽性のコスト(侵襲的検査)が高い疾患」など、臨床的な文脈がはっきりしている場合、その文脈に合わせた感度や適合率を最大化する閾値を探ることが重要になります。 - 具体的な人数で結果を説明したい場合
「このAIを導入すると、1000人あたり約10人の見逃しを防げますが、新たに追加で50人の精密検査が必要になります」といったように、具体的な人数を用いて関係者に説明する際には、混同行列から得られる情報が非常に役立ちます。
ROC曲線とAUCが活躍する場面 🚀
- 異なるモデルの純粋な判別性能を比較したい場合
研究開発の段階で、モデルA、B、Cのどれが最も優れているかを評価したい時、特定の閾値に左右されないAUCで比較するのが最も公平で標準的なアプローチです。 - 最適な運用ルール(閾値)がまだ決まっていない場合
モデルを開発したものの、どのくらいの予測確率で陽性と判断するのがベストか、まだ定まっていない段階では、ROC曲線を描くことで、感度と偽陽性率のトレードオフを視覚的に把握し、最適な閾値を探る手がかりを得ることができます。 - 論文などで性能を客観的に報告する場合
研究成果を学術的に報告する際には、AUCはモデルの性能を単一の数値で要約してくれる、国際的に広く受け入れられた指標です。
まとめ:最高のパートナーシップ
| 観点 | 混同行列の指標(感度・適合率など) | ROC曲線とAUC |
|---|---|---|
| 評価の視点 | 特定の「閾値」における性能のスナップショット | 全ての「閾値」を横断した総合的な性能 |
| キーとなる問い | 「この運用ルールで使うと、どうなる?」 | 「そもそも、このモデルの地力はどれくらい?」 |
| 主な用途 | 実装後の性能モニタリング、具体的な運用ルールの評価 | モデル開発段階での性能比較、学術的な報告 |
| 強み | 臨床的な文脈に即した、具体的で実践的な評価 | 公平で客観的なモデル間の性能比較 |
| 弱み | 閾値の選び方次第で結果が大きく変わる | 臨床的な有用性に直接結びつかないことがある |
理想的な評価のプロセスは、まずAUCで最も性能の良いモデルを選び出し、次にそのモデルのROC曲線や混同行列を使って、臨床目的に最も合った最適な閾値を探り、その閾値での具体的な性能(感度や適合率)を評価・報告する、という流れになります。
このように、両者の特性を理解し、賢く使い分けることが、AIドクターの性能を正しく評価し、その価値を最大限に引き出すための鍵となるのです。
その予測確率は信頼できるか?:キャリブレーションの評価
さて、私たちのAIドクターが、病気の人と健康な人をうまく見分ける能力(判別能、AUCで評価)を持っていることは分かりました。これは素晴らしい第一歩です。しかし、もう一つ、それと同じくらい重要な視点があります。
それは、AIドクターが提示する「確率」そのものが、現実の頻度と一致しているか?という問題です。
これをキャリブレーション(Calibration、較正)と呼びます。判別能が「白か黒かを見分ける力」だとしたら、キャリブレーションは「『たぶん70%くらい黒だと思う』という予測の、”70%”という数字自体の信頼性」を問うものです。
この考え方は、天気予報の評価と非常によく似ています。
天気予報士が「明日の降水確率は30%です」と予報した日を100日集めてきたとしましょう。もし、その100日のうち、実際に雨が降った日が約30日であったなら、この予報士の確率は「よくキャリブレートされている(信頼できる)」と言えます。
AIドクターも全く同じです。「この患者さんが3年以内に心筋梗塞を起こす確率は20%です」と予測した場合、同じように20%と予測された患者さんたちをたくさん集めてくると、その集団では、実際に心筋梗塞を発症する人の割合が、予測値である約20%と一致することが理想です。この一致度が高ければ、私たちはその「20%」という数字を信じて、患者さんへの説明や治療計画の立案に役立てることができますよね。
視覚的な評価:キャリブレーションプロット
この予測確率と実際の確率の一致度を、視覚的に評価するための最も強力なツールがキャリブレーションプロットです。
これは、患者を予測確率ごとにグループ分けし、「グループの平均予測確率(横軸)」と「そのグループでの実際のイベント発生率(縦軸)」をプロットしたグラフです。

- 理想的な線(対角線 A): 予測確率と実際の発生率が完全に一致している状態です。全ての点がこの線上にあれば、モデルは完璧にキャリブレートされています。
- 曲線が対角線より上にある(曲線 B): モデルが過小評価していることを意味します。例えば、AIが「リスクは30%」と予測したグループで、実際には50%の人がイベントを起こしているような状態です。AIが楽観的すぎると言えます。
- 曲線が対角線より下にある(曲線 C): モデルが過大評価していることを意味します。AIが「リスクは70%」と予測したのに、実際には50%しかイベントが起きていないような状態です。AIが悲観的すぎると言えます。
このように、プロットを見ることで、自分のモデルがどのリスク領域で、どのようなズレの傾向を持つのかを一目で把握できます。
統計的な評価:Hosmer-Lemeshow検定
キャリブレーションを統計的に検定する手法として、Hosmer-Lemeshow(H-L)検定が広く知られています。この検定は、予測確率で患者を10グループ(十分位数)に分け、「予測されたイベント数と、実際に観測されたイベント数に統計的な差はない」という帰無仮説を検定します。
この検定の面白いところは、普段とは逆にp値が大きいこと(有意差がないこと)を期待する点です。
- p > 0.05: 予測と実際の間に有意な差は認められない。→ キャリブレーションは良好(Goodness-of-fitが良い)。
- p < 0.05: 予測と実際の間に有意な差がある。→ モデルのキャリブレーションが悪い。
ただし、H-L検定には注意点もあります。Hosmer and Lemeshow (1980)によって提案されたこの方法は便利ですが、後の研究で、特にサンプルサイズに結果が大きく左右されることが指摘されています (Hosmer et al., 2013)。
- サンプルサイズが非常に大きい場合: 臨床的には無視できるようなわずかなズレでも「統計的に有意(p < 0.05)」と判定されてしまい、過敏に反応しすぎる傾向があります。
- サンプルサイズが小さい場合: 本当は大きなズレがあるのに、それを検知できず「問題なし(p > 0.05)」と判断してしまう可能性があります。
そのため、H-L検定の結果だけで判断するのではなく、必ずキャリブレーションプロットと合わせて、視覚的・統計的な両面から総合的に評価することが現代の予測モデル研究では推奨されています。
優れたAIドクターは、ただ白黒を見分けるだけでなく、その確信度(確率)もまた、信頼に足るものでなければならないのです。
【発展】新旧モデル対決! NRIとIDIで改善度を測る
最後に、少し発展的な内容に触れておきましょう。臨床研究の世界では、常に新しい予測モデルが開発されています。例えば、既存の心血管リスクモデルに、新しいバイオマーカーの測定値を加えた「新モデル」を開発したとします。この新モデルは、本当に旧モデルよりも優れているのでしょうか?
この問いに答えるため、旧モデルと新モデルのAUCを比較することがよくあります。しかし、AUCは判別能の変化に対してやや鈍感で、新しいマーカーを追加してもAUCの増加はごくわずか(例えば0.85→0.86)ということが少なくありません。これでは、その改善が臨床的にどれほどのインパクトを持つのか、今ひとつ分かりにくいですよね。
そこで、モデルの改善度をより臨床的な観点から評価するために、ハーバード大学のPencina教授らによって2008年に提案された、NRI(Net Reclassification Improvement)やIDI(Integrated Discrimination Improvement)という指標が注目されるようになりました (Pencina et al., 2008)。
NRI:患者のリスク分類は、より正しくなったか?
NRIは、新モデルが患者をより適切なリスクカテゴリーに再分類できたかを評価する指標です。
たとえ話: 新しい信用スコアのモデルを開発した場面を想像してください。旧モデルでは「中リスク」とされていた人が、新モデルで「高リスク」に再分類され、その後実際に債務不履行になったとします。これは「正しい上方修正」です。逆に、旧モデルで「中リスク」だった優良顧客が、新モデルで「低リスク」に再分類されたなら、それは「正しい下方修正」です。
NRIは、まさにこの「再分類の正しさ」を定量化します。具体的には、以下の2つのパートから成り立っています。
- イベント発生群での改善 (NRI_events): 実際に病気になった人たちのうち、「リスクがより高いカテゴリーに正しく移動した人の割合」から「リスクがより低いカテゴリーに誤って移動した人の割合」を引いたもの。
- イベント非発生群での改善 (NRI_nonevents): 健康だった人たちのうち、「リスクがより低いカテゴリーに正しく移動した人の割合」から「リスクがより高いカテゴリーに誤って移動した人の割合」を引いたもの。
最終的なNRIは、この2つを足し合わせて計算されます (NRI = NRI_events + NRI_nonevents)。NRIがプラスの大きな値であれば、新モデルは旧モデルよりも臨床的に有用な再分類を行っていると解釈できます。
IDI:予測確率は、より正解に近づいたか?
IDIは、カテゴリー分類に注目するNRIとは異なり、個々の患者の予測確率そのものが、どれだけ正解の方向に動いたかを評価します。
具体的には、
- 病気になった人たちにおいて、新モデルの予測確率が旧モデルからどれだけ平均的に上昇したか
- 健康だった人たちにおいて、新モデルの予測確率が旧モデルからどれだけ平均的に減少したか
この2つの改善度を合計したものがIDIです。IDIは、モデルが全体として、より確信をもって正しい予測を行えるようになったかを示します。
【重要】解釈上の注意点と近年の動向
NRIとIDIは、AUCの変化だけでは見えにくいモデルの改善を捉えるための強力なツールです。しかし、これらの指標にも限界があり、近年ではその解釈について活発な議論が行われています。
最も重要な注意点は、NRIは研究者が設定するリスクカテゴリーの閾値に結果が大きく依存するという点です。例えば、「低リスク(<5%)」「中リスク(5-20%)」「高リスク(>20%)」という閾値と、「低リスク(<10%)」「高リスク(>10%)」という閾値では、NRIの値は全く異なる可能性があります (Steyerberg et al., 2010)。
また、一部の統計家からは、NRIやIDIが新しいマーカーの価値を過大評価する傾向がある、という批判もなされています。
こうした背景から、近年では決定曲線分析(Decision Curve Analysis; DCA)という別の手法が注目を集めています。DCAは、モデルの予測を用いて治療介入などの臨床判断を行った場合の「純便益(Net Benefit)」を評価する手法で、「その予測モデルは、臨床的な意思決定において、何もしない場合や全員を治療する場合と比べて、どれだけ有用か」を直接的に評価することができます (Vickers and Elkin, 2006)。
まとめると、NRIやIDIはモデル比較の際に豊かな情報を提供してくれますが、その限界を理解し、DCAのような他の評価手法と組み合わせて多角的に判断することが、より洗練されたモデル評価に繋がると言えるでしょう。
まとめ:AIドクターの成績表・早わかりチートシート
さて、今回の旅で登場した様々な評価指標は、それぞれ異なる側面からAIドクターの性能を照らし出してくれます。最後に、それぞれの指標が持つ意味と役割を一覧できる「チートシート」として整理しておきましょう。どの指標を重視すべきかは、あなたがそのAIドクターに何を最も期待するかによって変わってきます。
| 指標 (Metric) | 何を見ているか? (What it Measures) | キーとなる問い (Key Question) | 特に重要な場面 (Especially Important When…) |
|---|---|---|---|
| オッズ比 (95% CI) | 個々の予測因子の影響度とその推定精度 | 「その因子はリスクと関連しているか?その推定はどれくらい確かか?」 | モデルの解釈や、新しい予測因子の有用性を評価する時。 |
| 正解率 (Accuracy) | 全体に対する正解の割合 | 「全体として、どれくらいの割合で予測が当たったか?」 | データセットの陽性・陰性のバランスが良い場合の、大まかな性能把握。 |
| 感度 (Recall) | 病気の人を見つけ出す能力 | 「病気の人たちのうち、何%を『陽性』と判定できたか?」 | がん検診など、疾患の見逃しが許されないスクリーニング検査。 |
| 特異度 (Specificity) | 健康な人を正しく除外する能力 | 「健康な人たちのうち、何%を『陰性』と判定できたか?」 | 侵襲的な確定診断を避けるため、健康な人を確実に除外したい場合。 |
| 適合率 (Precision) | 「陽性」という予測の信頼性 | 「『陽性』と判定された人のうち、本当に病気だったのは何%か?」 | 陽性判定が侵襲的な検査や治療に繋がるため、”空振り”を減らしたい場合。 |
| F1スコア | 感度と適合率のバランス(調和平均) | 「見逃しも空振りも、バランス良く減らせているか?」 | 感度と適合率のどちらか一方だけを優先できない場合の総合評価。 |
| AUC (C-statistic) | モデルの総合的な判別能力 | 「病気の人と健康な人、うまくランク付けできているか?」 | 閾値に依存せず、異なるモデル間の純粋な判別性能を比較したい時。 |
| キャリブレーション | 予測確率の信頼性 | 「『30%のリスク』という予測は、本当に30%の頻度で起こるか?」 | 予測確率そのものを患者説明や治療介入の意思決定に直接用いる時。 |
この表を見ても分かるように、「最高の指標」というものは存在しません。完璧な予測モデルを目指す旅は、これらの多様な指標をコンパスとして、目的に応じて使い分け、モデルの長所と短所を深く理解することから始まります。高いAUC(優れた判別能)と良好なキャリブレーション(信頼できる確率)を両立させること、それが私たちが目指す、真に臨床で役立つAIドクターの姿なのです。
まとめ:信頼できるAIドクターを育てるために
今回の旅では、私たちが育てたAIドクター(ロジスティック回帰モデル)に、客観的で厳格な「健康診断」を行い、その性能を評価するための「成績表」の見方を学んできました。
ただモデルを作って「予測精度95%でした!」と喜ぶだけでは、真に責任ある医療AIの開発とは言えません。なぜなら、その数字の裏には、見逃された患者さんや、不要な不安を与えられた健康な人がいるかもしれないからです。今回の学びは、そうした数字の裏側を深く、そして多角的に読み解くための「レンズ」を手に入れるプロセスでした。
最後に、今回の旅で得た最も重要な知見を振り返っておきましょう。優れた予測モデルには、必ず2つの柱が必要です。
- 優れた「判別能」 (Discrimination) これは、AIが病気の人と健康な人をどれだけうまく見分けられるかという能力です。私たちは、ROC曲線を描き、その面積であるAUCという強力な指標で、この総合的な実力を評価する方法を学びました。AUCが高いモデルは、いわば「目が良い」AIドクターと言えます。
- 良好な「キャリブレーション」 (Calibration) これは、AIが示す「80%の確率で病気です」といった、確率そのものの信頼性を指します。私たちは、キャリブレーションプロットを用いて、AIの自信が現実の頻度と一致しているかを確認しました。キャリブレーションが良好なモデルは、「自己評価が的確な」AIドクターと言えるでしょう。
この2つは、どちらか一方だけでは不十分です。判別能は高いけれどキャリブレーションが悪いモデルは、まるで「勘は鋭いが、自信過剰で言うことが当てにならない名探偵」のようなもの。臨床現場で安心して頼ることはできません。
今回手に入れた評価のツールキットは、あなた自身がモデルを開発する際はもちろん、新しいAIに関する論文や報告に触れた際に、その結果を批判的に吟味するための強力な武器となります。
モデルの構築は、この「評価」というプロセスとセットになって、初めて意味を成します。そしてこの評価の旅は、モデルが本当に患者の利益に貢献できるかを見極める、外部データを用いた「妥当性検証(Validation)」という、次なる冒険へと続いていくのです。
参考文献
- Altman, D.G. and Bland, J.M. (1994). Diagnostic tests 1: sensitivity and specificity. BMJ, 308(6943), p.1552.
- Bland, J.M. and Altman, D.G. (2000). The odds ratio. BMJ, 320(7247), p.1468.
- Collins, G.S., Reitsma, J.B., Altman, D.G. and Moons, K.G.M. (2015). Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis (TRIPOD): The TRIPOD Statement. Annals of Internal Medicine, 162(1), pp.55–63.
- Cook, N.R. (2007). Use and Misuse of the Receiver Operating Characteristic Curve in Risk Prediction. Circulation, 115(7), pp.928–935.
- Fawcett, T. (2006). An introduction to ROC analysis. Pattern Recognition Letters, 27(8), pp.861-874.
- Fletcher, R.H. and Fletcher, S.W. (2014). Clinical epidemiology: the essentials. 5th ed. Philadelphia: Wolters Kluwer Health/Lippincott Williams & Wilkins.
- Gordis, L. (2014). Epidemiology. 5th ed. Philadelphia, PA: Elsevier Saunders.
- Hosmer, D.W. and Lemeshow, S. (1980). A goodness-of-fit test for the multiple logistic regression model. Communications in Statistics – Theory and Methods, 9(10), pp.1043–1069.
- Hosmer, D.W., Lemeshow, S. and Sturdivant, R.X. (2013). Applied Logistic Regression. 3rd ed. Hoboken, NJ: Wiley.
- Pencina, M.J., D’Agostino, R.B., D’Agostino, R.B. and Vasan, R.S. (2008). Evaluating the added predictive ability of a new marker: From area under the ROC curve to reclassification and beyond. Statistics in Medicine, 27(2), pp.157–172.
- Steyerberg, E.W. (2019). Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating. 2nd ed. Springer.
- Steyerberg, E.W., Vickers, A.J., Cook, N.R., Gerds, T., Gonen, M., Obuchowski, N., Pencina, M.J. and Kattan, M.W. (2010). Assessing the Performance of Prediction Models: A Framework for Traditional and Novel Measures. Epidemiology, 21(1), pp.128–138.
- Vickers, A.J. and Elkin, E.B. (2006). Decision Curve Analysis: A Novel Method for Evaluating Prediction Models. Medical Decision Making, 26(6), pp.565–574.
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.





