この記事では、複数の要因から一つの結果を予測する「重回帰分析」の基本から注意点までを、オーケストラや料理の例えで分かりやすく解説します。
1つの結果(音楽)に対し、多くの要因(楽器)が影響します。重回帰分析は、他の楽器の音量を固定し、特定の楽器が持つ純粋な影響度を聴き分ける指揮者のような手法です。これにより交絡(見せかけの関係)を排除できます。
結果(Y) = ベース(β₀) + 影響(β₁) × 要因(X₁) + … + 誤差(ε) という数式で表現します。予測と実際のズレが最小になる最適な「さじ加減(β)」を、最小二乗法(OLS)という方法で見つけ出します。
決定係数(R²): モデルが結果のばらつきを何%説明できたかを示す「説明力」。
F検定: モデル全体が偶然でなく、統計的に意味があるか(p < 0.05)を判断する「実力テスト」。
要因同士が似すぎる「多重共線性」や、相乗効果を生む「交互作用」に注意が必要です。最も重要なのは、分析結果は「関連性」であり、「因果関係」を直接証明するものではない、という点です。
日々の臨床や研究で、目の前のデータと向き合いながら、「この患者さんの血糖値がなかなか下がらないのは、本当に年齢だけのせいだろうか?」「もしかしたら、BMIや腎機能、日々の運動量、食事の傾向まで、色々なことが複雑に関係しているのかもしれない…」と、ふと考え込むことはありませんか?
多くの臨床的な事象は、決して単一の原因で説明できるものではありません。それはまるで、壮大なオーケストラのハーモニーのようなものです。血糖値という一つの音楽(結果)は、年齢、体重、食事、運動、遺伝といった様々な楽器(要因)が、それぞれ異なる音色と音量で同時に奏でられることで形作られています。
ここで、一つの楽器の音だけ、例えば「年齢」というバイオリンの音色だけを取り出して聴いてみても(これを単回帰分析と呼びます)、全体のハーモニーを理解したことにはなりませんよね。もしかしたら、そのバイオリンの音が大きく聴こえるのは、隣で力強く演奏されている「運動不足」というチェロの音と共鳴しているだけかもしれません。統計学では、このような現象を交絡(Confounding)と呼び、見せかけの関連に騙されてしまう原因となります。
そこで今回の主役となるのが、重回帰分析(Multiple Regression Analysis)です。この手法は、まるでオーケストラの熟練の指揮者のように振る舞います。指揮者は、全ての楽器が同時に演奏される中で、特定の楽器、例えばバイオリンがハーモニー全体に与える「純粋な貢献度」を聴き分けます。他の楽器(BMIや食事など)の音量を統計的に一定に保った状態で、バイオリンの音色だけを評価するのです。
この記事では、この重回帰分析という強力な分析ツールについて、その基本的な仕組みから、結果の解釈、そして臨床研究で活用する上での注意点まで、具体的なたとえ話を交えながら、一歩ずつ一緒に探検していきましょう。
※はじめに: この記事で紹介する重回帰分析は、あくまで要因間の関連性(Association)の強さや方向性を評価するための強力な手法です。分析結果が、そのまま因果関係(Causation)を証明するものではない、という点は非常に重要です。この「関連と因果の壁」については、統計学の大家であるHernánとRobinsがその著書『Causal Inference: What If』の中でも繰り返し強調している通り、常に念頭に置いて読み進めてください (Hernán and Robins, 2020)。
重回帰分析とは?~最高の料理レシピを探す旅~
重回帰分析とは、一言で言うと「複数の説明変数(要因)を使って、一つの目的変数(結果)を予測・説明するための統計手法」です。これは統計モデリングの基本形であり、多くの著名な教科書でその基礎が解説されています (Draper and Smith, 1998; Kutner et al., 2005)。
いきなり専門用語が出てきましたが、怯む必要はありません。これを「最高の料理レシピ作り」という、親しみやすい活動に例えてみましょう。
あなたが「究極のカレー」のレシピを開発していると想像してください。カレーの最終的な「美味しさ(\(Y\))」という結果は、当然ながら、様々な材料の「量(\(X\))」や調理法によって決まりますよね。例えば、
- タマネギを炒める時間(\(X_1\))
- 入れるスパイスのグラム数(\(X_2\))
- お肉の煮込み時間(\(X_3\))
など、たくさんの要因が考えられます。重回帰分析は、これらの材料(説明変数)をどのように組み合わせれば、美味しさ(目的変数)を最も上手に説明できるのか、その「黄金のレシピ」を数式という形で表現しようとする試みなんです。
この関係性を図でイメージすると、以下のようになります。
この図が示すのは、複数の入力要因(説明変数)が、「重回帰モデル」という一つの計算プロセス(レシピ)を経て、単一の出力(目的変数)を予測する、という基本的な流れです。
重回帰モデルの正体:レシピの構造を数式で見る
その「黄金のレシピ」は、数学の世界ではこんな数式で表現されます。
\[ \text{美味しさ}(Y) = \beta_0 + \beta_1 \times \text{炒め時間}(X_1) + \beta_2 \times \text{スパイス量}(X_2) + \beta_3 \times \text{煮込み時間}(X_3) + \varepsilon \]
この数式、一見すると少し難しそうですが、一つ一つのパーツに分解すれば、実はとてもシンプルです。
- \(Y\): 目的変数 (Outcome)
私たちが最も知りたい、予測したい「結果」です。臨床研究なら、患者の血圧、入院日数、特定の治療への反応などがこれにあたります。 - \(X_1, X_2, \dots\): 説明変数 (Explanatory Variables)
結果を説明するための「要因」たちです。患者の年齢、BMI、喫煙歴、服用している薬剤の種類など、結果に影響を与えそうなものを並べます。 - \(\beta_1, \beta_2, \dots\): 偏回帰係数 (Partial Regression Coefficients)
これがレシピの「さじ加減」を決める、最も重要な部分です。それぞれの材料(説明変数)が、最終的な美味しさ(目的変数)にどれだけ、そしてどのように(プラスに?マイナスに?)影響を与えるかを示す数値です。 - \(\beta_0\): 切片 (Intercept)
すべての材料をゼロにした(つまり、何も入れなかった)ときの、ベースとなる味です。料理で言えば「水だけの味」のようなもので、分析の出発点となる基準値と考えることができます。 - \(\varepsilon\): 誤差 (Error)
どんなに完璧なレシピを作っても、実際に料理すれば毎回、微妙な味のブレが生じますよね?その日の気温や湿度、材料の個体差、あるいはレシピには書かれていない隠れた要因(例:作り手の気分!)などによる影響です。このモデルでは説明しきれない部分を、誤差項 `\(\varepsilon\)` が引き受けてくれます。

最適な「さじ加減」の見つけ方:最小二乗法(OLS)
さて、モデルの形は分かりましたが、肝心の「さじ加減(\(\beta\)たち)」は、どうやって決めればよいのでしょうか?ここで登場するのが、最小二乗法 (Ordinary Least Squares, OLS) という、回帰分析の根幹をなす考え方です (Freedman, 2009)。
OLSの仕事は、一言でいえば「実際の値と、モデルによる予測値とのズレ(残差)が、全体として最も小さくなるように係数\(\beta\)を決める」ことです。
もう少し具体的に見てみましょう。
あなたが実際に10人の被験者(データ)でカレーを作り、それぞれの「美味しさ」を測定したとします。一方で、あなたのモデル(レシピの数式)も、それぞれの材料の量から「美味しさ」を予測します。当然、実際の味と予測された味には、少しズレ(残差)が生まれます。
このズレを視覚的にイメージすると、以下のようになります。各点(.)が実際のデータで、直線がモデルの予測線です。点から直線に下ろした縦の線(|)が残差の大きさを表します。
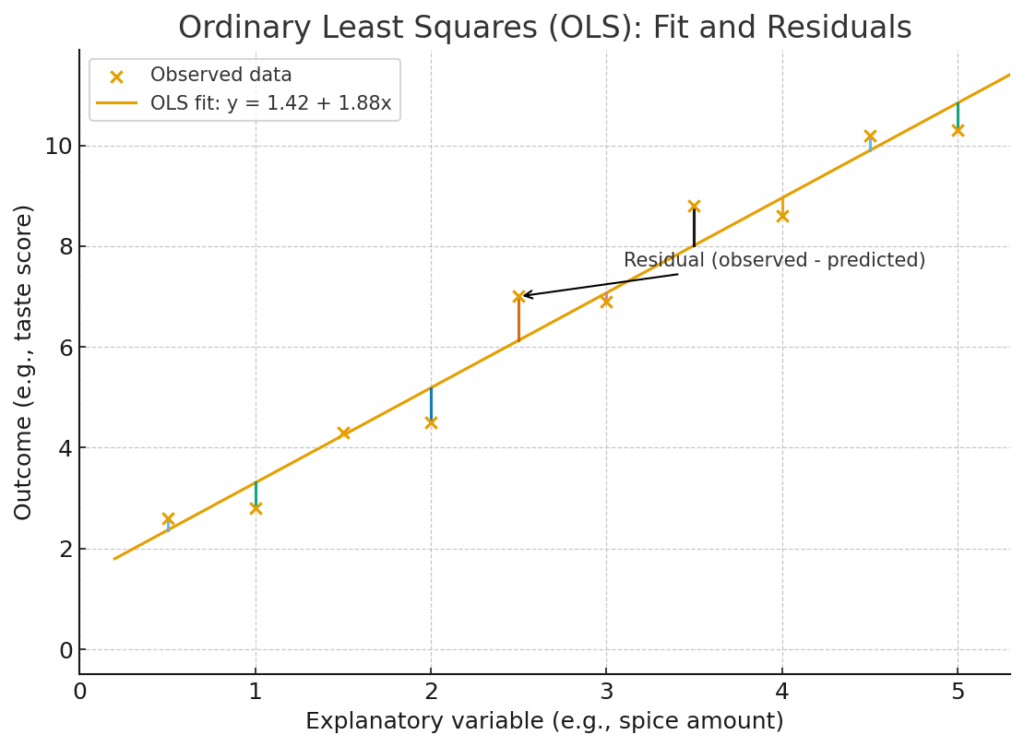
OLSは、この「残差(ズレ)」に注目します。ただし、単に残差を足し合わせるだけだと、予測が大きすぎた場合(マイナスのズレ)と小さすぎた場合(プラスのズレ)が互いに打ち消し合ってしまい、ズレの総量を正しく評価できません。
そこで、それぞれの残差を2乗して、すべてをプラスの値にしてから合計します。この合計値を残差平方和 (Sum of Squared Residuals, SSR) と呼びます。なぜ2乗するかというと、これにはもう一つ重要な意味があります。それは、予測が大きく外れたデータ(大きなズレ)に対して、より大きなペナルティを与える効果です。例えば、ズレが2の点は\(2^2=4\)、ズレが3の点は\(3^2=9\)として勘定されるため、大きな外れ値を出すモデルを避けることができるのです。
そして、OLSの最終目標は、この「残差平方和」が数学的に最小になるような、唯一無二の\(\beta\)の組み合わせを見つけ出すこと。幸いなことに、これは勘で探す必要はありません。微分という数学の力を借りることで、この値を最小化する\(\beta\)を計算式一発で求めることができるのです。こうして、手元のデータに対して最も当てはまりの良い、客観的に「最高」と言えるモデルの係数が決まります。
【発展】コンピュータはどうやって最適な`β`を計算しているのか?
では、コンピュータは具体的にどのような計算式で最適な係数 \(\beta\) を一瞬で見つけ出すのでしょうか。その秘密は行列計算にあります。統計ソフトが内部で行っている計算は、以下の有名なOLSの公式に基づいています。
\[ \hat{\beta} = (X’X)^{-1}X’Y \]
この式は、一見すると複雑な暗号に見えるかもしれませんが、パーツごとに分解すれば、何をしているのかイメージできます。これは、私たちが中学校で習った一次方程式 \(y = ax\) を \(a\) について解くために \(a = y/x = x^{-1}y\) と変形するのと、本質的には同じことを行列の世界で行っているだけなのです。
- \(X\) と \(Y\): これらは、以前のセクションで見た、あなたの手元にある全データ(要因データ\(X\)と結果\(Y\))が詰まった箱(行列)です。
- \(X’\) (転置行列): これは、行列\(X\)の行と列を入れ替えたものです。「’」は転置(Transpose)を意味します。データの見方を変える、準備体操のようなものです。
- \((X’X)\): 転置した\(X’\)と元の\(X\)を掛け合わせます。この計算によって、説明変数同士の関係性(共分散)がギュッと凝縮された、新しい正方形の行列が生まれます。この行列は、モデルの土台となる非常に重要な情報を持っています。
- \((X’X)^{-1}\) (逆行列): これが計算の「鍵」となる部分です。ある行列の「逆行列」とは、「掛け合わせると打ち消し合って1(単位行列)になる」ような、相棒のような行列です。数値の世界で \(5 \times (1/5) = 1\) となる\(1/5\)(\(5^{-1}\))と同じ役割を果たします。\((X’X)\)の逆行列を求めることで、方程式を解き、\(\beta\)を単独で取り出す準備が整います。
- \(\hat{\beta}\): 最後に、この「鍵」\((X’X)^{-1}\)を \((X’Y)\)(要因と結果の関連性をまとめたもの)に掛け合わせることで、最終的に求めたい係数\(\beta\)が計算されます。「
^」(ハット)の記号は、これがデータから計算された推定値であることを示しています。
この一連の計算により、コンピュータはトライ&エラーを一切行うことなく、残差平方和を最小化する\(\hat{\beta}\)の値をたった一回の計算で導き出すことができるのです。
係数の意味を読み解く~オーケストラのパート別音量調整~
さて、統計ソフトウェアが最適なモデル(レシピ)を計算してくれたら、私たちの仕事は終わりではありません。むしろ、ここからが最も面白い部分、つまりモデルの中身を解釈していく作業の始まりです。特に重要なのが、各説明変数の「偏回帰係数(\(\beta\))」を正しく読み解くことです。
偏回帰係数:他の要因の影響を「統計的に固定」して見る
偏回帰係数の「偏」という漢字には、「一方にかたよる」という意味がありますが、ここでは「他の要因から切り離された、一部分」というニュアンスで捉えると分かりやすいかもしれません。つまり、偏回帰係数とは、「他のすべての説明変数の値が一定であると仮定した上で、ある一つの説明変数だけを1単位変化させたときに、目的変数が平均してどれだけ変化するか」を示した数値です。
この「他の変数を一定に保つ」という考え方が、交絡因子(Confounder)の影響を取り除く上で非常に重要になります。
オーケストラの例えに戻ってみましょう。全体のハーモニー(目的変数)に対するトランペット(説明変数の一つ)の真の貢献度を知りたいとします。このとき、レコーディングスタジオのサウンドエンジニアが何をするか想像してみてください。彼らはミキシングボードを使って、バイオリンやピアノなど、他の楽器のトラックの音量を一時的に固定しますよね。その状態で、トランペットのトラックのフェーダーだけを少し上げて、全体のサウンドがどう変わるかを確認します。
重回帰分析が行っているのは、まさにこの作業です。他の変数の影響を統計的に「ミュート」し、一つの変数が持つ純粋な関連性を浮かび上がらせるのです。
例えば、血圧を目的変数とし、年齢とBMIを説明変数とするモデルを考えましょう。分析の結果、BMIの偏回帰係数が \(\beta_{BMI} = 0.8\) だったとします。これは、「年齢という要因の影響を調整した後で、BMIが1 (\(kg/m^2\))増加すると、血圧は平均して0.8 (mmHg)上昇する」と解釈できます。これにより、単に「太っている人は血圧が高い」という観察だけでなく、「年齢に関わらず、BMIが増えること自体が血圧の上昇と関連している」という、より深い洞察が得られるわけです。
標準化偏回帰係数:単位が違う要因たちの「影響力」を比べる
ここで、次のような新たな疑問が生まれます。「血圧に対して、年齢とBMIでは、どちらがより『強く』影響しているんだろう?」
この問いに答えるのは、実は少し厄介です。なぜなら、年齢の単位は「歳」、BMIの単位は「\(kg/m^2\)」であり、土俵が全く違うからです。仮に年齢の係数が`0.5`、BMIの係数が`0.8`だったとしても、「0.8は0.5より大きいからBMIの方が影響力が強い」と結論づけることはできません。
そこで登場するのが、標準化偏回帰係数 (Standardized Partial Regression Coefficient) です。これは、全ての変数(目的変数も説明変数も)を、平均が0、標準偏差が1になるように規格化(標準化)してから、改めて回帰分析を行って得られる係数です。
これは、異なる科目のテストの点数を比べるために「偏差値」を使うのと同じ考え方です。数学の80点と英語の60点では、どちらが「すごい」か一概には言えませんよね。平均点や点数のばらつきが違えば、60点の方が価値ある結果かもしれません。偏差値に変換することで、初めて同じ土俵で成績を比較できるわけです。
標準化偏回帰係数を使えば、変数の元の単位に悩まされることなく、目的変数への「相対的な影響力の強さ」を比較できます。例えば、標準化後の係数が、年齢で`0.25`、BMIで`0.40`だったとします。この場合、「このモデルにおいては、BMIの方が年齢よりも血圧に対して強い関連性を持っている」と評価することが可能になります。
両者の違いをまとめると、以下のようになります。
| 比較項目 | 偏回帰係数(非標準化) | 標準化偏回帰係数 |
|---|---|---|
| 主な目的 | 具体的な予測値の変化を量る | 説明変数間の相対的な影響力を比較する |
| 解釈の例 | 「BMIが1上がると、血圧は0.8mmHg上がる」 | 「BMIが1標準偏差上がると、血圧は0.4標準偏差上がる」 |
| 単位 | あり(目的変数の単位 / 説明変数の単位) | なし(無次元) |
| 主な用途 | 臨床的なインパクトの推定、予測モデルの構築 | どの要因が最も重要かを特定する探索的分析 |
どちらの係数も重要であり、分析の目的に応じて使い分けることが大切です。
モデルは本当に「良いモデル」か?~レシピの通信簿~
さて、最小二乗法という賢い方法で、私たちのモデルに最適な係数(レシピのさじ加減)が見つかりました。しかし、ここで満足してはいけません。「できた!」と思ったそのレシピが、本当に美味しいカレーを作る実力を持っているのか、客観的な成績表で評価してあげる必要があります。
そのための代表的な「通信簿」が、決定係数(\(R^2\))とF検定です。これらは、モデルのパフォーマンスを異なる角度から評価してくれます。
決定係数 (R²): モデルが説明できた「割合」を測る
決定係数(\(R^2\)、アール・スクエア)は、あなたのモデルが、目的変数が持つ「全体のばらつき」のうち、どれくらいの割合をうまく説明できているかを示す指標です。0から1の間の値をとり、1に近いほど、モデルがデータのばらつきをよく説明できている、つまり「当てはまりの良いモデル」とされます (Kutner et al., 2005)。
パイチャートで考えてみましょう。患者さん一人ひとりの血圧が異なる、その「ばらつきの全体像」を一つの大きな円いパイだと想像してください。
もし分析の結果、\(R^2 = 0.7\) だったとすれば、それは「患者さんの血圧の個人差というパイ全体のうち、70%のスライスは、私たちがモデルに投入した変数(年齢、BMIなど)の組み合わせで説明できますよ」という意味になります。残りの30%は、モデルでは説明しきれなかった「謎」の部分、つまり誤差(\(\varepsilon\))の仕業ということになります。
自由度調整済み決定係数 (Adjusted R²): 「無駄な材料」にペナルティを
ここで一つ、決定係数には少し困ったクセがあります。それは、説明変数を追加すればするほど、\(R^2\)の値は下がることがなく、機械的に増加してしまうという性質です。
料理のレシピに例えると分かりやすいでしょう。カレーの味に関係があろうがなかろうが、「隠し味」と称してコショウ、ソース、醤油、パセリ…と材料を10も20も追加していけば、その場で作った一皿(あなたの手元にあるデータ)の味は完璧に再現できるかもしれません。しかし、それはもはや他の誰も作れない、汎用性のない複雑なレシピになってしまいますよね。このような状態を過学習(Overfitting)と呼びます。
そこで、モデルの「見かけの良さ」だけでなく「シンプルさ」も考慮してくれる、より賢い指標が自由度調整済み決定係数 (Adjusted R-squared) です (Harrell, 2015)。
この指標は、モデルに新しい説明変数が追加されるたびに、「その変数は、モデルを複雑にするデメリットに見合うだけの、十分なメリット(説明力の向上)をもたらしたか?」を評価し、一種のペナルティを課します。もし、あまり意味のない変数を加えてしまった場合、\(R^2\)はわずかに上昇するかもしれませんが、自由度調整済み\(R^2\)は逆に低下することがあります。
ですから、異なるモデル(例えば、変数Aだけを入れたモデルと、変数AとBを入れたモデル)を比較する際には、単純な\(R^2\)ではなく、この自由度調整済み\(R^2\)が高くなる方を採用するのが、より堅実なアプローチと言えます。
F検定: そもそも、このレシピは意味があるのか?
決定係数(\(R^2\))がモデルの「説明力の高さ」を評価する指標だとすれば、F検定は、そもそも「この回帰モデル全体が、統計的に意味のあるものと言えるのか?」という、より根本的な問いに答えるための健康診断です。個別の器官(各変数)を詳しく見る前に、まずはモデル全体のバイタルサイン(生命兆候)をチェックするのです。
F検定では、まず非常に悲観的な仮説(帰無仮説)を立てることから始めます。
帰無仮説(\(H_0\)): 「このモデルに含まれる全ての偏回帰係数(\(\beta_1, \beta_2, \dots\))は、本当は全部ゼロである。つまり、どの説明変数も、目的変数の予測に全く役立っていない。」
これは、あなたの作ったカレーのレシピが「ただのデタラメで、何の参考にもならない」と主張しているようなものです。これに対し、F検定はデータから「この帰無仮説がどれくらい成り立ちそうにないか」を客観的な数値(F値とp値)で示してくれます。
F検定の理論:2つの「ばらつき」の綱引き
F検定の核心は、データ全体の「ばらつき(変動)」を2つのパーツに分解し、その大きさを比較する、というアイデアにあります。
まず、「変動」とは何か?
変動とは、シンプルに言えば「データのばらつき具合」のことです。例えば、クラスの生徒の身長データがあったとして、全員の身長が同じということはありませんよね。背が高い子、低い子、平均的な子がいる、この散らばりこそが「変動」です。統計分析の目的は、この「なぜ身長は人によって違うのか?(なぜ変動があるのか?)」という疑問に答えることです。
回帰モデルは、この全体の変動を、次の2つの部品に分解します。
- モデルによって説明された変動(分子側) これは、あなたのモデルが説明できた変動、つまり「功績」の部分です。例えば、「学年」を説明変数に加えたら、6年生の身長は1年生より平均して高いことが分かりました。この「学年が違うことによって生まれる身長の差」が、モデルによって説明された変動です。良いモデルほど、この功績は大きくなります。
- ポイント: 「モデルの予測値がばらついている」とは、モデルが「1年生だから身長はこれくらい」「6年生だからこれくらい」と、入力情報に応じてメリハリのある異なる予測を出せている状態を指します。これはモデルがデータの特徴を捉えられている証拠であり、この予測値のばらつきこそが「説明された変動」の実体です。
- モデルで説明できなかった変動(分母側) これは、モデルを使っても説明しきれなかった、「誤差」の部分です。同じ6年生の中でも、身長には個人差がありますよね。モデルが知らない他の要因(遺伝、栄養など)によるばらつきがこれにあたります。これは予測と実際のデータの間に残るズレ(残差)であり、良いモデルほど小さくなります。
F値は、この2つの変動の大きさ(専門的には平均平方と呼びます)を比べたものです。
\[ F値 = \dfrac{\text{モデルの功績(説明された変動)}}{\text{モデルの誤差(説明できなかった変動)}} \]
モデルが全くの無意味(帰無仮説が正しい)なら、功績も誤差も偶然の産物なので、F値は1に近くなります。逆に、モデルが非常に優れていれば、功績が誤差を大きく上回り、F値は非常に大きな値になります。
F分布の理論:偶然が生み出す世界のルールブック
では、そのF値が「偶然にしては大きすぎる」と判断するための基準であるF分布は、どのような理論から導かれるのでしょうか。
F分布は、一言でいえば「帰無仮説(=変数の間には何の関係もない)が真実である世界で、偶然だけでF値がどのような値を取るかを定めたルールブック」です。
その理論的背景には、カイ二乗(\(\chi^2\))分布というものが関わっています。
- ばらつきの正体: 実は、「説明された変動(SSR)」も「説明できなかった変動(SSE)」も、数学的にはそれぞれが(ある定数で割ると)カイ二乗分布という確率分布に従うことが知られています。これは、どちらの変動も「ズレの2乗」を足し合わせたものであり、「正規分布に従う確率変数の2乗和」がカイ二乗分布に従う、という数学的な性質に基づいています。
- F分布の誕生: そして、「2つの独立なカイ二乗分布の比」が従う確率分布こそが、F分布なのです。
つまり、F値は `(説明された変動)/(説明できなかった変動)` という比の形をしているため、もし帰無仮説が正しく、両者の間に何の関係もなければ、そのF値は必然的にF分布というルールブックに従う、というわけです。
このルールブック(F分布)には、モデルの複雑さ(説明変数の数 \(k\) とサンプルサイズ \(n\))に応じた「章立て(自由度)」があり、私たちの計算したF値が、その章の中でどれくらい珍しい(確率的に起こりにくい)出来事なのかを正確に教えてくれます。その確率こそがp値です。
分析の実践フロー:火災報知器と個別探知機
F検定と、各変数を個別に見るt検定の関係は、分析を進める上で非常に重要です。これは、建物全体の火災報知器(F検定)と、各部屋の煙探知機(t検定)の関係に例えると完璧に理解できます。
Step 1: まずは建物全体の火災報知器(F検定)を確認する
分析結果を見たら、まず最初に確認するのが、分散分析表(ANOVA Table)にあるモデル全体のF検定のp値です。
- 警報作動! (p < 0.05 の場合) 「ピーッ!この建物のどこかで火災が発生しています!」というサインです。これは、モデルに含まれる変数のうち、少なくとも一つは目的変数の予測に役立っていることを示します。モデル全体として統計的に意味があることが確認できたので、次のステップに進むGOサインが出たことになります。
- 警報鳴らず (p ≧ 0.05 の場合) 「この建物は安全です」というサインです。モデル全体として、意味のある変動を捉えられていないことを示します。この時点で、分析は実質的にここで終了です。建物全体で火災が起きていないのに、各部屋の煙探-知機を見て回る意味があまりないのと同じで、たとえ個別の変数(t検定)でたまたまp値が小さいものがあったとしても、それは偶然である可能性が高く、その結果を真に受けるのは危険です。
Step 2: 警報が鳴ったら、各部屋の煙探知機(t検定)を確認する
F検定という火災報知器が鳴った場合に限り、私たちは次に係数の一覧表に移動し、各変数に付けられた個別のt検定のp値を見ていきます。
- 火元を特定する: F検定は「どこかで火事が起きている」としか教えてくれませんでした。どの変数がその「火元」なのかを特定するのが、このt検定の役割です。
- t検定のp値が小さい変数: これが、煙探知機が作動している部屋です。つまり、他の変数の影響を調整した後でも、なお単独で目的変数と有意な関連を持つ、重要な変数であると判断できます。
このように、「F検定でモデル全体の門をくぐり、t検定で個別の貢献者を特定する」という2段階のプロセスを踏むことで、私たちは統計モデルを正しく、かつ慎重に評価することができるのです。
重回帰分析の落とし穴と応用テクニック
重回帰分析は、適切に使えば非常に強力な分析ツールですが、決して万能ではありません。その結果を正しく解釈し、誤った結論を導かないためには、いくつかの典型的な「落とし穴」と、それを乗り越えるための応用テクニックを知っておくことが不可欠です。
注意点1:多重共線性(Multicollinearity)
これは、モデルに投入した説明変数同士の相関が非常に高い状態を指します。臨床の現場では「マルチコ」と略して呼ばれることもありますね。
たとえ話:塩と醤油のジレンマ
カレーのレシピを開発するのに、「塩の量」と「醤油の量」を両方とも説明変数としてモデルに入れたとします。この二つは、どちらも料理に「塩味」を加えるという点で、非常に似た役割を持っていますよね。
この状態で分析を実行すると、コンピュータは混乱してしまいます。「最終的な塩味が強くなったのは、塩を増やしたからなのか?それとも醤油を増やしたからなのか?」その貢献度を綺麗に切り分けることができなくなるのです。
この多重共線性が存在すると、以下のような問題が発生します。
- 係数の推定が不安定になる: 本来プラスの効果を持つはずの変数の係数がマイナスになったり、データが少し変わるだけで係数の値が乱高下したりします。
- 標準誤差が大きくなる: 係数の信頼区間が非常に広くなり、本当は関係があるはずの変数が「統計的に有意ではない(p値が大きい)」という誤った結論に至りやすくなります。
診断と対策
この問題は、VIF (Variance Inflation Factor; 分散拡大要因) という指標で診断するのが一般的です。VIFは、各説明変数が他の説明変数によってどれだけ説明できてしまうかを示す指標で、明確な基準はありませんが、実務上はVIFが10を超えると多重共線性の懸念が高いと判断されることが多いです (Kutner et al., 2005)。
もし高いVIFが検出された場合は、
1. 相関の高い変数の一方をモデルから削除する(例:「塩」か「醤油」のどちらか一方を選ぶ)。
2. 相関の高い変数たちを統合して、一つの新しい指標を作成する(例:ナトリウム摂取量としてまとめる)。
といった対策を検討します。
注意点2:交互作用(Interaction)
これは、「ある説明変数が目的変数に与える影響が、別の説明変数の水準によって変化する」という、より複雑な関係性を指します。単純な足し算では説明できない、「相乗効果」や「打ち消し合う効果」をイメージしてください。
たとえ話:薬とアルコールの相乗効果
ある降圧薬の効果を考えてみましょう。この薬を服用すると血圧が平均10mmHg下がるとします。しかし、それはアルコールを摂取しない人の話かもしれません。もし、アルコールを摂取する習慣のある人がこの薬を飲むと、効果が倍増して20mmHgも下がってしまうとしたらどうでしょう。
これが交互作用です。「降圧薬の効果」は、単独で決まるのではなく、「アルコール摂取の有無」という別の要因とセットになって初めてその真価を発揮するわけです。モデルに交互作用を組み込まないと、このような重要な関連性を見逃してしまいます。
分析では、\(薬の服用量 \times アルコール摂取の有無\) のような、変数同士を掛け合わせた交互作用項をモデルに追加することで、この効果を検証できます。臨床研究では、治療効果が患者の特定の属性(性別、遺伝子型など)によって異なるケース(効果の異質性)を分析する際に、極めて重要な考え方になります (Harrell, 2015)。
応用テクニック:ダミー変数(Dummy Variable)
重回帰分析は、その計算の仕組み上、基本的に数値をインプットとして扱います。しかし、私たちが扱いたいデータには、「性別(男性/女性)」や「血液型(A/B/O/AB)」のような、数値ではないカテゴリカル変数もたくさんありますよね。
このような変数を回帰モデルに投入するためのテクニックが、ダミー変数です。これは、カテゴリを「0」か「1」の数字に変換することで、コンピュータにカテゴリの違いを認識させる手法です。
2つのカテゴリの場合
例えば「性別」なら、「男性」を0、「女性」を1とコーディングします。このとき、「0」とされた男性が基準(リファレンス)となります。分析の結果、女性ダミー変数の係数が`+5`だった場合、それは「他の変数が全て同じ条件なら、女性は男性(基準)に比べて、目的変数の値が平均して5大きい」と解釈します。
3つ以上のカテゴリの場合
「血液型」のようにカテゴリが3つ以上ある場合は少し注意が必要です。この場合、カテゴリの数マイナス1個(k-1個)のダミー変数を作成します。
| 元の変数(血液型) | B型ダミー | O型ダミー | AB型ダミー |
|---|---|---|---|
| A型(基準) | 0 | 0 | 0 |
| B型 | 1 | 0 | 0 |
| O型 | 0 | 1 | 0 |
| AB型 | 0 | 0 | 1 |
このように、一つのカテゴリ(この場合はA型)を基準とし、他のカテゴリのダミー変数を投入します。B型ダミーの係数は「A型に比べてB型はどうか」、O型ダミーの係数は「A型に比べてO型はどうか」というように、全て基準カテゴリとの比較として解釈されることになります。
まとめ:現実をより深く理解するための標準的なレンズ
今回は、複数の要因が複雑に絡み合う現象を解き明かすための、統計学における標準的な分析手法、重回帰分析の世界を探検してきました。非常に多くの情報がありましたが、重要なエッセンスをここで振り返っておきましょう。
- モデル構築は「最高のレシピ探し」
複数の要因(説明変数)が、ある結果(目的変数)にどのように影響を与えるかを一つの数式で表現しました。 - 係数の解釈は「各楽器の音量調整」
他の要因の影響を統計的に固定することで、一つの要因が持つ純粋な関連の大きさを読み解きました。単位を揃えて影響力を比較する「標準化係数」の便利さも確認しましたね。 - モデル評価は「レシピの通信簿」
決定係数(\(R^2\))でモデル全体の説明力を、F検定でその統計的な意味を評価し、モデルが信頼に足るものかを確認しました。 - 実践的な注意点を忘れない
変数同士が影響し合う「多重共線性」や、相乗効果を生む「交互作用」、そしてカテゴリを扱う「ダミー変数」など、現実に即した分析のための重要なポイントも学びました。
重回帰分析は、適切に使いこなせば、臨床研究や疫学研究において非常に豊かで、示唆に富んだ洞察を与えてくれます。しかし、最後に最も重要なことを、もう一度だけ繰り返させてください。
統計学の大家たちが繰り返し警告するように、「相関関係は、因果関係を意味しない」のです (Hernán and Robins, 2020; Freedman, 2009)。
この分析で、「ビタミンDの血中濃度が低いこと」と「特定の疾患の罹患率が高いこと」の間に強い関連が見られたとしても、それだけで「ビタミンDの不足が、その疾患の原因である」と結論づけることはできません。もしかしたら、「屋外での活動量が少ない」という測定されていない交絡因子が、ビタミンD濃度を低下させ、かつ疾患リスクを上昇させているのかもしれないからです。
重回帰分析の結果は、検証可能な「科学的仮説」を生み出すための、力強い第一歩です。決して最終結論ではありません。この標準的なレンズを使いこなし、皆さんの臨床現場における「なぜ?」という素朴な疑問を、よりシャープで、次の研究へと繋がる「仮説」へと磨き上げていってください。
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
参考文献
- Draper, N.R. and Smith, H. (1998). Applied Regression Analysis. 3rd ed. New York: John Wiley & Sons.
- Freedman, D.A. (2009). Statistical Models: Theory and Practice. Cambridge: Cambridge University Press.
- Harrell, Jr., F.E. (2015). Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis. 2nd ed. Cham: Springer.
- Hernán, M.A. and Robins, J.M. (2020). Causal Inference: What If. Boca Raton: Chapman & Hall/CRC.
- Kutner, M.H., Nachtsheim, C.J., Neter, J. and Li, W. (2005). Applied Linear Statistical Models. 5th ed. Boston: McGraw-Hill/Irwin.
- Wooldridge, J.M. (2019). Introductory Econometrics: A Modern Approach. 7th ed. Boston, MA: Cengage Learning.
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






