情報の洪水の中から信頼できる結論を導き出す「システマティックレビュー」と「メタアナリシス」。その基本原則と流れを、3つのステップで視覚的に理解しましょう。
「信頼できる研究だけを、すべて集める」ための体系的な手法です。PICOで疑問を定式化し、網羅的な文献検索を実施。PRISMA声明などの国際ルールに従い、透明性の高いプロセスで論文を厳選します。
「集めた研究を、統計学で統合する」技術です。大規模で精度の高い研究ほど最終結果への影響が大きくなるよう「重み付け」を行うのが特徴。これにより、より信頼性の高い一つの結論を導き出します。
フォレストプロットで結果を視覚的に理解します。ただし、出版バイアス(良い結果だけが出版される偏り)や、元の研究の質が低い(Garbage In, Garbage Out)可能性を常に念頭に置く必要があります。
はじめに:情報の洪水の中で、確かな「羅針盤」を手に入れる
皆さんも、こんな場面に遭遇したことはありませんか?
「期待の新薬〇〇に関する論文が出たぞ。A先生は『これはゲームチェンジャーだ』と絶賛しているけど、B先生は『うちの患者層には合わないかも』と少し懐疑的…。」
「△△という新しい治療法について、ある研究では素晴らしい結果が出ているのに、別の研究では『従来法と大差なし』と報告されている。一体、どちらが本当なんだろう?」
新しい情報が次々と現れる現代、私たちの周りはまさに情報の洪水です。一つの治療法に対して、時に矛盾するような結果を示す研究論文が数多く存在します。個々の研究(木々)を一つ一つ眺めていても、その治療法の真の価値という森全体の姿を捉えるのは、至難の業ですよね。小規模な研究では偶然の結果が出やすかったり、研究ごとに患者さんの背景が異なったりと、一つの研究だけを見て結論を出すことには、どうしても限界があります。
この混沌とした状況に、一本の確かな筋道を示してくれるのが、エビデンスに基づく医療(EBM) の考え方です。そして、そのEBMの世界で「最も信頼性の高いエビデンス」の一つとしてピラミッドの頂点に君臨するのが、今回ご紹介するシステマティックレビューとメタアナリシスです。
これは、単なる文献レビューとは全く異なります。まるで優秀な探偵が、散らばった無数の証言(=個々の研究)の中から、信頼できるものだけを厳選し、客観的なルールに従ってそれらを統合し、事件の核心(=真の効果)に迫るようなプロセスです。
この講座を読み終える頃には、あなたもこの「探偵術」の基本を身につけ、情報の洪水に惑わされることなく、目の前の患者さんにとって最善の選択をするための、強力な羅針盤を手にしているはずです。さあ、一緒にその扉を開けてみましょう。
システマティックレビュー:「最高のカレーレシピ」を探す旅
臨床の疑問を「検索可能な問い」に変える技術:PICO
想像してみてください。あなたは「世界で一番おいしいチキンカレーのレシピ」を探す旅に出たとします。…と言っても、この問いは少し曖昧すぎますよね。「おいしい」の基準は人それぞれですし、「誰が」「何と比べて」おいしいのかが分かりません。
そこで、まず問いを具体的にします。
- P (Patient / Population): どんな人のための? → 「辛いものが好きな大人」
- I (Intervention): どんなレシピ? → 「市販のカレールーを使った」
- C (Comparison): 何と比べて? → 「スパイスから作る本格カレー」
- O (Outcome): 何をもって「最高」とする? → 「30分以内に作れて、満足度が高い」
このようにPICOというフレームワークを使って問いを明確に定式化すること。これが、システマティックレビューの出発点です。臨床現場の疑問、例えば「成人のがん患者さん(P)に、薬A(I)を投与することは、薬B(C)と比べて、生存期間を延ばす(O)か?」という形に整理するわけです。
網羅的な文献調査:全てのレシピをテーブルに乗せる
問いが明確になったら、次はいよいよレシピ探しです。Google検索はもちろん、あらゆる料理本、専門雑誌、個人のブログまで、関連しそうな情報をすべて探し出します。
システマティックレビューも同様に、PubMedやCochrane Libraryといった医学文献データベースを駆使し、設定した問いに関連する研究論文を網羅的に検索します。このとき、「”Chicken Curry” AND “Spicy” NOT “Sweet”」のように検索キーワードを組み合わせる「検索式」を立てますが、これは再現性が保証されるよう、非常に緻密に設計されます。個人的な好みでレシピを選ぶのではなく、客観的で網羅的なルールに基づいて、全ての候補をテーブルの上に乗せる作業。それがシステマティックレビューの探偵術の第一歩です。
適格基準とPRISMA声明:信頼できるレシピだけを選ぶ「地図」
集めた膨大なレシピ(研究論文)の中には、残念ながら質の低いものや、今回の問いとは関係ないものも混じっています。「材料の分量が書いていない」「手順が曖昧」なレシピは、いくら評価が高くても採用できませんよね。
そこで、「鶏肉を使っていること」「調理時間が明記されていること」「ランダム化比較試験(RCT)であること」といった適格基準(選択基準・除外基準)をあらかじめ設定し、それに従って論文をフィルタリングしていきます。
この一連の旅のプロセス、つまり「何件の論文が見つかり、どの基準で何件が除外され、最終的に何件がレビューの対象となったか」を一枚の地図のように示したものがPRISMAフローダイアグラムです。
【解説】PRISMAフローダイアグラムの模式図。文献検索から最終的な選択までの流れを可視化します。
この全体のプロセスを透明化し、誰がやっても同じ結論にたどり着けるようにするための国際的なルールブックが、PRISMA声明(Preferred Reporting Items for Systematic Reviews and Meta-Analyses)です。Cochrane共同計画が発行するハンドブック(Higgins et al. 2019)などにもその詳細な手法が記載されていますが、PRISMA声明は、システマティックレビューという「研究」の質と透明性を担保するための、世界共通の約束事なのです(Page et al. 2021)。
メタアナリシス:個々の評価を統合し、一つの結論を出す統計マジック
さて、システマティックレビューという探偵術によって、信頼できるカレーレシピ候補(研究論文)がいくつか集まりましたね。しかし、それぞれの評価は「星4.5」「星3.8」「星5.0」…とバラバラです。これらをどうやって統合し、「結局のところ、この治療法はどれくらい有効なのか?」という一つの結論を導けばいいでしょうか?
ここで登場するのが、統計学という強力な武器を持った相棒、メタアナリシスです。これは単なる結果の寄せ集めではなく、個々の研究の信頼度を吟味し、それらを公正に統合するための洗練された技術体系です。
なぜ単純平均ではダメ?「重み付け」という考え方
まず、一番シンプルな方法として、すべての研究結果の平均を取ることを考えがちです。しかし、それでは大きな問題があります。例えば、1000人を対象とした信頼性の高い大規模な臨床試験と、わずか20人で行われた小規模なパイロット研究を、同じ「一票」として扱ってしまってよいのでしょうか?
直感的にも、それは公平ではないと感じますよね。参加者が多い研究ほど、偶然の影響を受けにくく、より安定した信頼できる結果が得られるはずです。メタアナリシスでは、この直感を統計的に正当化します。つまり、個々の研究の「信頼性」に応じて重み付け(weighting)を行い、より信頼できる研究の結果が最終的な結論に強く反映されるように調整するのです。この考え方こそ、メタアナリシスの心臓部と言えるでしょう。
信頼性を数値化する「逆分散法」
では、その「信頼性」とは、具体的にどうやって数値で表せばいいのでしょうか?統計学の世界では、結果のばらつきが小さいことを「信頼性が高い」と考えます。結果のばらつき、つまりブレの大きさを表す指標が分散(variance)です。したがって、分散が小さい研究ほど、推定された効果の精度が高く、信頼できるということになります。
信頼性が高いほど重みを大きくしたいのであれば、話は単純です。「分散の逆数」を重みとして使えば、この要求を満たせそうですよね。この非常に合理的でエレガントな考え方を逆分散法(Inverse Variance Method)と呼び、メタアナリシスの最も基本的な原理となっています。この手法の理論的背景や詳細については、Borensteinらが2009年に出版した教科書『Introduction to Meta-Analysis』に詳しくまとめられています。
少し数式を使って、この仕組みを覗いてみましょう。全く難しくありませんので、安心してください。
ある研究 \(i\) が報告した効果量(例えば、リスク比の対数など)を \(Y_i\)、その効果量の分散を \(v_i\) とします。このとき、逆分散法では、研究 \(i\) に与えられる重み \(w_i\) を、分散 \(v_i\) の逆数として、以下のように定義します。
\[ w_i = \dfrac{1}{v_i} \]
この式が意味するのは、「分散(\(v_i\))が小さいほど、重み(\(w_i\))は大きくなる」ということです。非常にシンプルですね。
そして、レビュー対象となる全研究(\(k\)個あるとします)を統合した最終的な効果量 \( \hat{\theta} \) は、それぞれの効果量 \(Y_i\) を先ほどの重み \(w_i\) で重み付けした平均(加重平均)を取ることで求められます。
\[ \hat{\theta} = \dfrac{\sum_{i=1}^{k} w_i Y_i}{\sum_{i=1}^{k} w_i} = \dfrac{\sum_{i=1}^{k} (Y_i / v_i)}{\sum_{i=1}^{k} (1 / v_i)} \]
この数式がやっていることを言葉で説明すると、以下のようになります。
- 分子 \( (\sum w_i Y_i) \):各研究の効果量(\(Y_i\))に、それぞれの重み(\(w_i\))を掛け算してから、全部足し合わせる。
- 分母 \( (\sum w_i) \):すべての研究の重みを、単純に全部足し合わせる。
- 全体:分子を分母で割ることで、重みを考慮した平均値を算出する。
要するに、「分散が小さい(=信頼できる)研究ほど、最終結果への発言権が大きくなる」という、非常に合理的で公平な計算をしているわけです。これにより、小規模で結果が不安定な研究に結論が振り回されるのを防ぎ、より頑健な統合結果を得ることができるのです。
どちらの立場で統合する?:固定効果モデルと変量効果モデル
さて、この重み付け計算には、実は二つの異なる立場(モデル)が存在します。これが固定効果モデルと変量効果モデルで、メタアナリシスを理解する上で避けては通れない重要な概念です。
固定効果モデル:「真の効果は、世界にただ一つ」
- 考え方: 私たちが知りたい「真の効果」はただ一つだけ存在すると仮定します。各研究の結果がばらついているのは、単に偶然による誤差(サンプリング誤差)のせいだと考えます。
- カレーの比喩: 「究極のチキンカレーのレシピは、世界にただ一つだけ存在する」という立場です。集められたレシピの味が少しずつ違うのは、料理人の腕前や材料の微妙な違い(=サンプリング誤差)によるもので、元となっているレシピは同じだと考えます。
- 計算方法: 上で説明した逆分散法をそのまま使います。
変量効果モデル:「真の効果は、研究ごとに少しずつ違う」
- 考え方: 「真の効果」は研究ごとに異なり、ある分布に従っていると仮定します。結果のばらつきは、サンプリング誤差に加えて、研究ごとの「真の効果」そのものの違い(研究間のばらつき=異質性)も原因だと考えます。
- カレーの比喩: 「おいしいチキンカレーのレシピは一つではない」という立場です。レシピの味が違うのは、サンプリング誤差だけでなく、対象とする集団(例:関西の研究では薄味、東北の研究では濃い味など)の違いによって、最適な「真のレシピ」自体が少しずつ異なっているからだと考えます。
- 計算方法: 重みを計算する際、研究内の分散 \(v_i\) に、この研究間の分散を表す \( \tau^2 \) (タウ二乗) という項を加えます。 \[ w_i^* = \dfrac{1}{v_i + \tau^2} \] この \( \tau^2 \) が加わることで、全体の重みの差が少しマイルドになります。結果として、固定効果モデルに比べて、小規模な研究の結果も少しだけ重視される傾向があります。
どっちのモデルを選ぶ?「異質性」の評価が鍵
では、どちらのモデルを使えばいいのでしょうか?その鍵を握るのが異質性 (Heterogeneity)、つまり研究間の結果のばらつきが偶然にしては大きすぎないか、という点です。
異質性は、フォレストプロットを目で見て確認する(各研究の信頼区間がほとんど重なっていない)ほか、以下の統計量で評価します。
- コクランのQ検定: 帰無仮説を「異質性は存在しない」として検定します。p値が小さい(例:p < 0.1)場合、統計学的に有意な異質性があると判断します。
- I² (I-squared) 統計量: 結果のばらつき全体のうち、何%が真の異質性によるものかを示します。Higginsら(2003)によれば、25%, 50%, 75%がそれぞれ低い、中程度、高い異質性の目安とされています。
一般的に、異質性が高い(例:I² > 50%)と判断された場合は、変量効果モデルを選択するのが定石です。異質性が高いということは、そもそも研究結果を一つに統合することの妥当性を慎重に検討する必要がある、というサインでもあります。
結果が一目瞭然!フォレストプロットの読み解き方(深掘り編)
これらの統計的な背景を理解すると、フォレストプロットがさらに味わい深く見えてきます。
【解説】統計情報を加えたフォレストプロットの概念図。
この図から読み取れることを、先ほどより詳しく見てみましょう。
- 個々の研究 (木々):
- 四角 (■)の大きさ: 各研究の重み(\(w_i\) または \(w_i^*\)) を反映しています。大きいほど、信頼性が高く、統合結果への影響力が大きい研究です。
- 横線の長さ: 95%信頼区間。これは分散(\(v_i\))と関連しており、線が短いほど分散が小さく、重みが大きくなります。
- 異質性の評価:
- 図の下部には、異質性の指標(例:I² = 65%, p = 0.02)が記載されることが一般的です。この場合、異質性は中程度から高程度であり、変量効果モデルの選択が妥当であったことが示唆されます。
- 統合結果 (森全体):
- ひし形 (◆): すべての研究を重み付けして統合した結果(統合効果量 \(\hat{\theta}\))とその95%信頼区間です。このひし形の位置と幅は、選択されたモデル(この場合は変量効果モデル)に基づいて計算されています。
- 結論の解釈: ひし形全体が無効線(リスク比 1.0)をまたいでいないため、「複数の研究を統合した結果、この治療法は統計学的に有意な効果を持つことが示唆される」と結論づけることができます。
このように、メタアナリシスは単に平均を取るだけでなく、各研究の信頼性を評価し、それらを統合するための洗練された統計モデルに基づいています。フォレストプロットは、その複雑な計算結果を私たちに直感的に伝えてくれる、強力なコミュニケーションツールなのです。
知っておくべき落とし穴:「出版バイアス」という名の見えざる手
システマティックレビューとメタアナリシスは、客観的なルールに従って証拠を統合する非常に強力なツールです。しかし、その大元となる「証拠」自体が、もし意図的に偏って集められていたとしたらどうでしょうか?ここに、最大の落とし穴の一つである出版バイアス (Publication Bias) が潜んでいます。
なぜ「成功談」ばかりが世に出るのか?
出版バイアスとは、平たく言うと、統計的に有意な差が出た(ポジティブな)研究結果の方が、差が出なかった(ネガティブな)研究や、あるいは有害な結果が出た研究よりも、論文として出版されやすいという、学術界の厄介な傾向のことです。
たとえるなら、「株で大儲けした!」という景気の良い成功談は多くのメディアで取り上げられますが、「投資に失敗して全財産を失った…」という話は、なかなか表に出てきませんよね。もし私たちが成功談ばかりを聞いて投資を始めたら、リスクを完全に見誤ってしまうでしょう。医療の世界でも同じことが起こり得ます。
このバイアスは、様々な要因から生まれます。
- 研究者の心理: やはり「効果があった!」という華々しい結果の方が、有名学術誌に掲載されやすく、キャリアアップにも繋がります。そのため、うまくいかなかった研究結果は、引き出しの奥にしまわれてしまうことがあります(ファイルドロワー問題)。
- 学術誌の編集方針: 読者の関心を引くような「新しい発見」を優先したいというインセンティブが働くことがあります。
- 資金提供者の意図: 製薬企業などがスポンサーの研究で、自社製品に不利な結果が出た場合、その公表に消極的になるケースも指摘されています。
この結果、メタアナリシスで参照できる論文が「成功例」に偏ってしまい、治療効果を過大評価してしまう危険性があるのです。
バイアスを可視化する探偵道具:ファンネルプロット
では、この「見えざる手」によって歪められた証拠の偏りを、どうやって見抜けばいいのでしょうか?ここで登場するのが、ファンネルプロット (Funnel Plot) という探偵道具です。
ファンネルプロットは、縦軸に研究の精度(一般的に標準誤差(SE)の逆数、つまり上にいくほど大規模で精度の高い研究)、横軸に効果量(リスク比やオッズ比など)をとって、各研究をプロットしたグラフです。
もし出版バイアスがなければ、プロットはどのような形になるでしょうか?統計学の理論上、サンプルサイズの小さい研究(プロットの下の方)は偶然による結果のばらつきが大きいため、左右に広く散らばります。一方で、サンプルサイズの大きい研究(プロットの上の方)は、より真の効果に近い値に収束していくため、ばらつきは小さくなります。結果として、プロット全体は左右対称の逆三角形(じょうご=Funnel)のような形になるはずです。
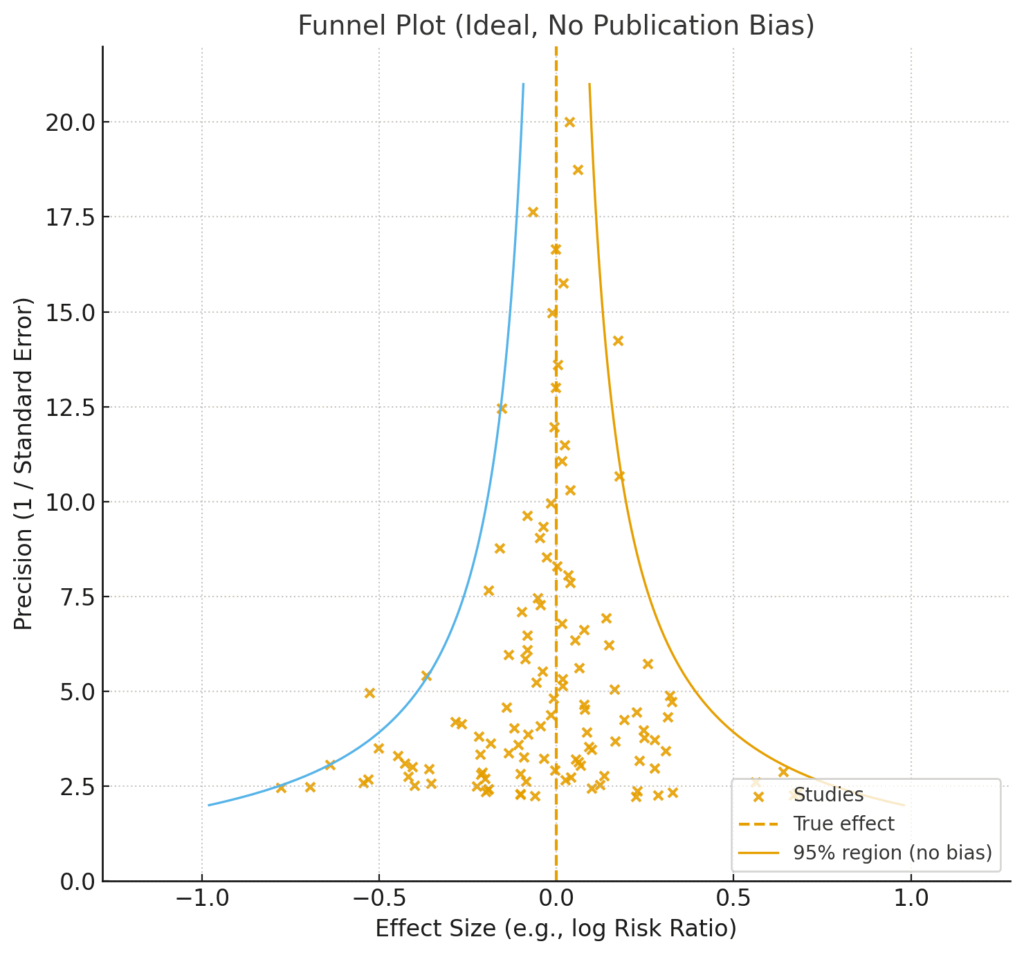
本来であれば、上図のように、プロットされた各研究(オレンジの×印)は、中央の破線(True effect / 真の効果)を中心に、左右対称の「じょうご(ファンネル)」型に分布するはずです。しかし、この図をよく見ると、明らかにファンネルの左下部分の領域がごっそりと抜け落ちています。
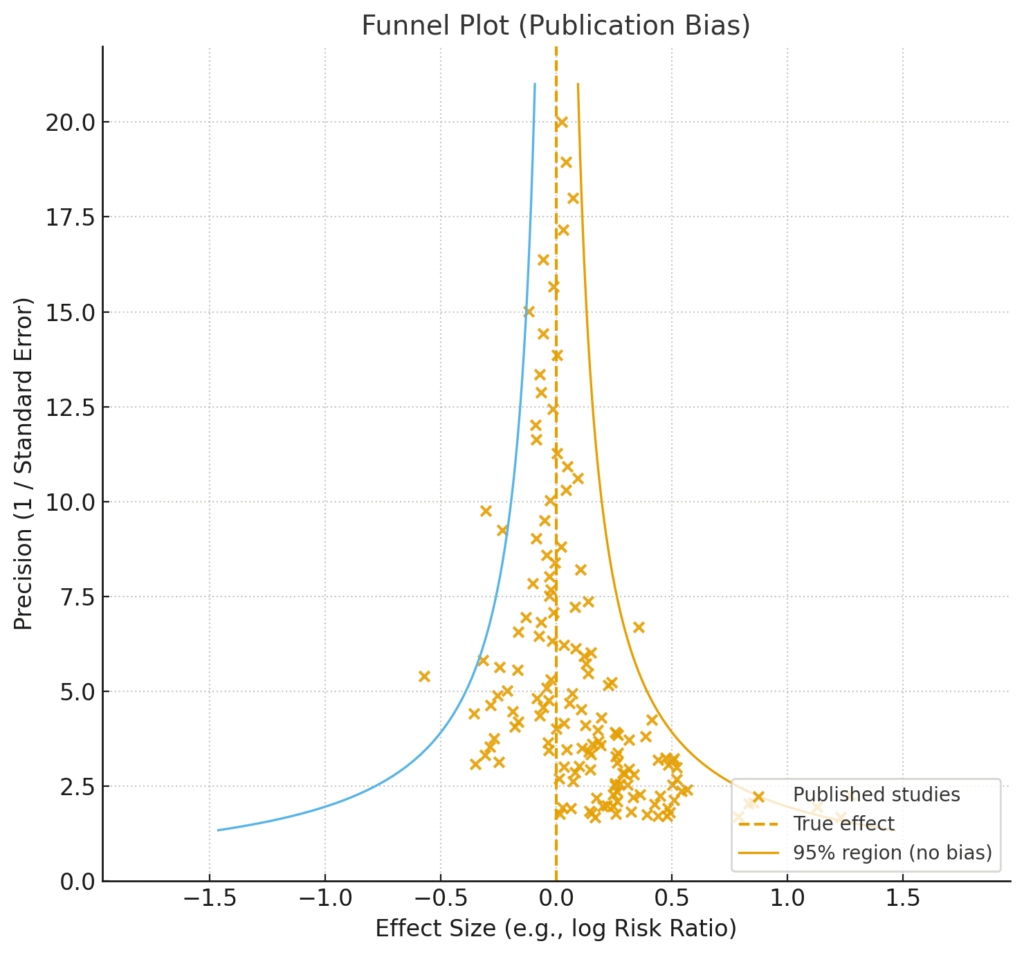
これは一体何を意味するのでしょうか。Y軸の下方は研究の精度が低い(=サンプルサイズが小さい)ことを、X軸の左方は効果が負の方向(=介入の効果がなかった、あるいは有害であった可能性)に出たことを示します。つまり、この欠落は「サンプルサイズが小さく、かつ期待外れの結果が出た研究が、論文として公表されていない」という状況を強く示唆しているのです。これがまさに「出版バイアス」であり、都合の良い結果が出た研究ばかりが世に出てしまう「ファイルドロワー問題」の可視化です。
その結果、私たちが目にすることができる公表済みの論文だけを集めて統合すると、治療効果を実際よりも過大に(この図の場合はより右側、つまり正の効果があるかのように)評価してしまう危険性があるわけです。
このように、ファンネルプロットの形の歪みを視覚的に評価することで、集めたエビデンス全体が偏っている可能性を疑うことができます。この視覚的評価は、バイアスの存在を統計的に検定するEggerの回帰検定のような客観的な手法と併用されます。これらのアプローチは、英国の疫学者であるEggerらが1997年の論文で提唱して以来、メタアナリシスの妥当性を評価する上で広く用いられています (Egger et al. 1997; Sterne et al. 2001)。
出版バイアスへの対抗策
幸いなことに、研究コミュニティもこの問題に手をこまねいているわけではありません。最も重要な対策が、臨床試験登録制度(日本のUMIN-CTRや米国のClinicalTrials.govなど)です。これは、研究を開始する前に「私たちは、こういう計画で、こういう研究を始めます」と事前に公開データベースに登録する制度です。これにより、たとえ結果がネガティブであっても、その研究が存在したという事実が公になり、「ファイルドロワー問題」を減らす効果が期待されています。
システマティックレビューを行う際も、出版された論文だけでなく、こういった登録情報や学会発表、未発表の報告書(灰色文献)まで丹念に探す努力が求められます。
出版バイアスは、エビデンスを歪めかねない深刻な問題です。しかし、ファンネルプロットのようなツールでその存在を評価し、臨床試験登録のような仕組みで対抗することで、私たちはより真実に近い結論を目指すことができるのです。
メタアナリシスの応用編:もっと複雑な問いに答える
標準的なメタアナリシスは、二つの治療法(AとB)を比較した研究を統合するのに非常に強力です。しかし、臨床現場の疑問はもっと複雑ですよね。「AとBとC、結局どれが一番いいの?」「この新しい診断検査、本当に信頼できるの?」こうした、より高度な問いに答えるための応用手法を見ていきましょう。
ネットワークメタアナリシス (NMA):最強の治療法決定戦
臨床現場では、こんなジレンマがよくあります。
「A薬とプラセボ」「B薬とプラセボ」を比較した質の高い研究はたくさんある。でも、本当に知りたい「A薬 vs B薬」の直接対決(head-to-head)の研究が存在しない…。
こんな時、諦めるしかないのでしょうか?いいえ、ここで登場するのがネットワークメタアナリシス (Network Meta-analysis, NMA) です。NMAは、直接比較がない治療法同士を、共通の比較対象(この場合はプラセボ)を介して間接的に比較することを可能にする、画期的な手法です。
「ネットワーク」で全治療法の関係性を可視化する
NMAでは、まず全ての治療法(ノード)と、それらを直接比較した研究(エッジ)の関係性を図に描きます。これをネットワーク図と呼びます。
【解説】ネットワークメタアナリシスの概念図。A, B, C, Pはそれぞれ異なる治療法を示します。実線は直接比較した研究が存在すること、点線は間接的な比較が可能であることを意味します。
NMAは、このネットワーク全体の情報を統計学的に統合することで、A対Cの直接比較がなくても、(A対Pの結果)と(C対Pの結果)から、AとCの優劣を推定できるのです。
治療法ランキングとSUCRA
NMAの最大の魅力は、多数の治療選択肢をランキング付けできる点です。その際に用いられる指標がSUCRA (Surface Under the Cumulative Ranking curve) です。SUCRAは0%から100%までの値をとり、「その治療法が最も優れた治療法である確率」を示唆します。例えば、SUCRAが95%の薬は、ネットワーク内で最も効果が高い可能性が極めて高い、と解釈できます。これにより、臨床家は複数の選択肢の中から最適な治療法を選ぶための、非常に有益な情報を得ることができます。世界中の多くの抗うつ薬の効果を網羅的に比較したCiprianiらの研究(2018)は、このNMAの威力を示す代表例です。
ただし、この強力な手法には「一貫性 (consistency)」という大前提が必要です。これは、「A対Cの直接比較の結果」と「(A対Bの結果)+(B対Cの結果)から推定した間接比較の結果」が、矛盾しないことを意味します。この一貫性が崩れている場合、ネットワークの構造自体に問題がある可能性があり、結果の解釈には注意が必要です。
診断精度メタアナリシス (DTA):その診断、信じていいですか?
新しい診断マーカーや画像検査が登場するたびに、私たちは「この検査、どれくらい正確なんだろう?」という問いに直面します。この問いに答えるのが、診断精度メタアナリシス (Diagnostic Test Accuracy Meta-analysis, DTAメタアナリシス) です。
なぜ単純な平均ではダメなのか?
個々の研究で報告される診断精度(感度:疾患のある人を正しく陽性と見抜く確率、特異度:疾患のない人を正しく陰性と見抜く確率)は、対象となる患者集団の重症度などによって変動しがちです。また、感度と特異度は「あちらを立てればこちらが立たず」のトレードオフの関係にあるため、単純に平均するだけでは検査の真の性能を見誤ってしまいます。
要約ROC曲線(SROC)で総合力を評価する
そこでDTAメタアナリシスでは、個々の研究の(感度, 特異度)のペアをROC空間にプロットし、それらを統計的に統合した一本の要約ROC曲線 (Summary ROC curve, SROC曲線) を描きます。
【解説】要約ROC曲線(SROC)の模式図。個々の研究結果(*)を統合し、検査の総合的な診断能を示す一本の曲線を描き出します。曲線が左上(感度100%, 特異度100%の理想点)に張り出すほど、優れた検査であることを意味します。
このSROC曲線が、グラフの左上の角に近づくほど、その検査の総合的な診断能力が高いことを示します。DTAメタアナリシスでは、感度と特異度の間の相関を考慮した二変量モデルや階層モデルといった専門的な統計手法が用いられ、単なる平均化ではない、より頑健な統合推定を行います。Cochrane共同計画でも、このDTAレビューのための詳細なハンドブックが公開されており、その重要性がうかがえます (Deeks et al. 2010)。
よくある誤解と注意点
メタアナリシスは強力なツールですが、その結果は万能薬ではありません。賢明な解釈と健全な批判的吟味が必要です。単に最終的なp値やフォレストプロットのひし形の見た目だけで判断するのは危険です。ここでは、よくある落とし穴を避けるための重要な注意点をお伝えします。
統計的有意差 ≠ 臨床的な重要性
これは、エビデンスに基づく医療(EBM)の全てにおいて最も重要な区別かもしれません。メタアナリシスは多くの研究データを統合することで、非常に高い統計的検出力を持ちます。そのため、非常に小さな差であっても「統計学的に有意」(例:p < 0.05)だと検出できてしまいます。しかし、統計的に有意な結果が、臨床現場で意味のある重要な差であるとは限りません。
例えば、新しいダイエット薬に関するメタアナリシスで、「プラセボに比べて1年間で平均500g多く体重を減らす」という結果が、p=0.001で統計的に有意だったとします。この結果が偶然である可能性は非常に低いでしょう。しかし、患者さんや臨床家にとって、1年かけてわずか500gの体重減少は、薬のコストや副作用を考慮すると、果たして価値のある治療でしょうか?おそらく、そうとは言えません。
ここで重要になるのが、効果量 (Effect size) と 臨床的に意味のある最小差 (MCID: Minimal Clinically Important Difference) という概念です。
- 効果量: 結果の「大きさ」そのものです(この例では500gの差)。常に自問すべきは、「この効果量は、実臨床で変化をもたらすほど大きいか?」という点です。
- MCID: 患者自身が「状態が改善した」と実感できる最小の変化量のことです。メタアナリシスの結果を読む際は、その効果量の95%信頼区間が、「効果なし」のラインを越えているかだけでなく、このMCIDを十分に超えているかどうかが重要になります。
覚えておくべき教訓: 「差はあるか?」と問うだけでなく、「その差はどれくらい大きく、患者にとって意味のある差なのか?」と常に問う姿勢が重要です。
「Garbage In, Garbage Out (ゴミを入れたら、ゴミしか出てこない)」:元の研究の質がすべて
メタアナリシスは、あくまで既存の研究を定量的に要約する手法です。質の低い一次研究から、質の高いエビデンスを生み出す魔法ではありません。もしメタアナリシスに含まれる研究の質が悪ければ、例えば、バイアスを誘発するような重大な計画上の欠陥があれば、その統合結果もまたバイアスから逃れられず、信頼できないものになります。これが「Garbage in, garbage out」という鉄則です (Ioannidis 2016)。
質の高いシステマティックレビューでは、個々の研究の質を評価するために、必ずバイアス・リスク評価を系統的に行います。例えば、ランダム化比較試験に対してはCochraneのRisk of Biasツール(RoB 2)などを用いて、ランダム化の方法、盲検化、欠測データの扱いなどを厳密にチェックします。
| 含まれる研究の質(バイアス・リスク) | メタアナリシスの結論の信頼性 |
|---|---|
| 高い(バイアス・リスクが低い) | 高い |
| 混合、または中程度 | 限定的(注意深い解釈が必要) |
| 低い(バイアス・リスクが高い) | 低い / 信頼できない |
優れたレビューでは、結論の頑健性を確認するために感度分析 (sensitivity analysis) を行います。これは、例えばバイアス・リスクが高い研究を除外して再度メタアナリシスを行い、それでも結論が変わらないかを確認する手法です。もし結論が同じであれば、その結果はより信頼できると言えます。逆に、結論が大きく変わってしまうなら、それは質の低い研究に結果が左右されている危険な兆候です。
異質性は単なる統計値ではなく、重要な「臨床的な手がかり」である
メタアナリシスの結果で高い異質性(例: I² > 60%)が示された場合、それは単に報告して変量効果モデルに切り替えれば終わり、というわけではありません。高い異質性は、「なぜ研究間でこんなに結果が違うのだろう?」という問いを探求すべき、非常に重要な臨床的な手がかりです。
この「なぜ」を探るのが、サブグループ解析やメタ回帰です。
- 特定の患者集団(例:高齢者と若年者)で効果は違うのか?
- 治療介入の用量や期間によって効果は変わるのか?
- バイアス・リスクが高い研究ほど、大きな効果を示していないか?
異質性の原因を探ることで、「平均するとこの治療は有効である」という漠然とした結論から、「この治療は50歳以下の女性には特に有効だが、高齢男性における有益性は不明確である」といった、より詳細で臨床の意思決定に役立つ知見を得られる可能性があるのです。
まとめ:賢明な臨床判断のために
システマティックレビューとメタアナリシスは、溢れる情報の中から、より信頼性の高いエビデンスを拾い上げ、統合してくれる現代の「知の錬金術」です。
- システマティックレビューが、明確なルールで信頼できる研究を網羅的に集め、
- メタアナリシスが、それらを統計学的に統合して一つの結論を導き出す。
これらの手法と考え方を理解することは、EBM(根拠に基づく医療)を実践する上で不可欠です (Glasziou et al. 2001)。目の前の論文の結果を鵜呑みにするのではなく、「この結果は、より大きなエビデンスの森の中でどういう位置づけなのだろう?」と一歩引いて考える視点を持つこと。そのために、この探偵コンビは、あなたの最も頼りになるパートナーになってくれるはずです。
参考文献
- Borenstein, M., Hedges, L.V., Higgins, J.P.T. and Rothstein, H.R. (2009). Introduction to Meta-Analysis. Wiley.
- Cipriani, A., Furukawa, T.A., Salanti, G., Chaimani, A., Atkinson, L.Z., Ogawa, Y., Leucht, S., Ruhe, H.G., Turner, E.H., Higgins, J.P.T., Egger, M., Takeshima, N., Hayasaka, Y., Imai, H., Shinohara, K., Sugiyama, N., Ioannidis, J.P.A. and Geddes, J.R. (2018). ‘Comparative efficacy and acceptability of 21 antidepressant drugs for the acute treatment of adults with major depressive disorder: a systematic review and network meta-analysis’. The Lancet, 391(10128), pp.1357-1366.
- Deeks, J.J., Bossuyt, P.M., Leeflang, M.M.G., Gatsonis, C. and the Cochrane Diagnostic Test Accuracy Working Group. (2010). Cochrane Handbook for Systematic Reviews of Diagnostic Test Accuracy. The Cochrane Collaboration.
- Egger, M., Smith, G.D., Schneider, M. and Minder, C. (1997). ‘Bias in meta-analysis detected by a simple, graphical test’. BMJ, 315(7109), pp.629-634.
- Glasziou, P. (2001). Systematic reviews in health care: a practical guide. Cambridge University Press.
- Higgins, J.P.T., Thomas, J., Chandler, J., Cumpston, M., Li, T., Page, M.J. and Welch, V.A. (eds) (2019). Cochrane Handbook for Systematic Reviews of Interventions version 6.0. Cochrane. Available from: www.training.cochrane.org/handbook
- Ioannidis, J.P.A. (2016). ‘Why most clinical research is not useful’. PLoS Medicine, 13(6), e1002049.
- Mulrow, C.D. (1994). ‘Rationale for systematic reviews’. BMJ, 309(6954), pp.597-599.
- Page, M.J., McKenzie, J.E., Bossuyt, P.M., Boutron, I., Hoffmann, T.C., Mulrow, C.D., et al. (2021). ‘The PRISMA 2020 statement: an updated guideline for reporting systematic reviews’. BMJ, 372, n71.
- Sterne, J.A.C. and Egger, M. (2001). ‘Funnel plots for detecting bias in meta-analysis: Guidelines on choice of axis’. Journal of Clinical Epidemiology, 54(10), pp.1046-1055.
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






