検査の「陽性」は、必ずしも「疾患あり」を意味しません。このガイドは、検査結果の裏に隠された真の意味を正しく評価するための、感度・特異度から尤度比といった必須ツールを、名探偵のように使いこなすための要点を提供します。
検査が持つ固有の能力。「感度」は病気を見つける力(見逃しを防ぐ網)、「特異度」は健康な人を正しく判断する力(冤罪を防ぐ慎重さ)を指します。
「陽性」が本当に病気である確率(陽性的中率)は、集団の「有病率」(病気のありふれ度)に大きく左右されます。有病率が低いと、的中率は驚くほど低くなります。
「尤度比」は個々の患者の検査前確率を更新する強力な武器です。「AUC」は検査の総合的な識別能力を一つのスコアで示し、性能比較に役立ちます。
目の前の患者さんが気になる症状を訴え、あなたは新しく導入された検査をオーダーしました。数日後、結果は「陽性」。
その一言が持つ重みを、私たちは日々感じています。患者さんやご家族の表情がこわばり、診察室の空気が一変する。その瞬間から、私たちの頭の中では「追加の検査は?」「治療方針は?」といった次の一手を巡る思考が高速で回転し始めます。
しかし、一歩立ち止まって考えてみてほしいのです。その「陽性」という結果は、本当に「疾患がある」という事実とイコールなのでしょうか?
実は、検査結果と「本当に病気かどうか」という真実の間には、時として大きな隔たりが存在します。特にAIによる画像診断支援など、新しいテクノロジーが次々と臨床現場に導入される現代において、この結果を鵜呑みにするリスクはかつてないほど高まっている、と私は感じています。偽陽性(本当は健康なのに陽性と判定されること)は患者さんに不要な不安と侵襲的な精密検査をもたらしかねませんし、偽陰性(本当は病気なのに陰性と判定されること)は、貴重な治療のタイミングを逃す原因にもなり得ます。
ここで、検査を万能な予言者としてではなく、一人の「目撃者」として捉え直してみませんか? ある目撃者は、少しでも怪しい人を見つけるとすぐに報告してくる「心配性」タイプかもしれません(冤罪も多いですが、見逃しは少ない)。また別の目撃者は、動かぬ証拠がない限り口を開かない非常に「慎重派」かもしれません(証言の信頼度は高いですが、目撃をためらうこともある)。
私たちの仕事は、こうした個性豊かな目撃者たちからの証言(=検査結果)のクセを見抜き、その信頼性を冷静に評価し、他の情報と統合して真実に迫る「名探偵」になることです。
この記事では、そのための「探偵道具」を一式お渡しします。感度や特異度、陽性的中率といった、少しとっつきにくく見える統計の言葉たち。これらを、数学が苦手な方でもパズルのピースをはめるように直感的に理解できるよう、誰にでもわかる言葉とたとえ話で一つひとつ解説していきます。
これを読み終える頃には、あなたはただ検査結果を右から左へ解釈するだけでなく、
- 患者さんやご家族へ、検査結果が持つ本当の意味を、自信を持って説明できるようになる。
- 新しい診断技術に関する論文や学会発表を、その長所も限界も見抜いて批判的に吟味できるようになる。
そんな、より深く、より確かな臨床判断のスキルを手にしているはずです。さあ、一緒にワクワクするような知の探偵旅行に出かけましょう。
事件現場の見取り図:すべての基本「2×2分割表」
さあ、最初の探偵道具を手に取りましょう。それは、あらゆる情報を整理し、事件の全体像を浮かび上がらせるための「見取り図」、すなわち2×2分割表(2-by-2 contingency table)です。どんなに複雑に見える診断精度の問題も、実はすべてこのシンプルな表から出発します。分析の信頼性を担保する上で極めて重要なツールであり、多くの臨床疫学研究で基本とされています (Fletcher et al., 2014)。
これは、検査が下した「陽性か陰性か」という証言と、神のみぞ知る「本当に疾患があるかないか」という真実の関係を、4つの部屋にきれいに分類してくれる魔法の箱だと考えてください。
例えば、ある疾患を診断する新しい検査を1000人の集団に実施したとしましょう。この集団のうち、真の患者は100人で、健康な人は900人だったとします。検査の結果、以下のようなデータが得られました。
この具体的な数字が入った見取り図を見ながら、4つの部屋の意味をもう一度確認しましょう。
- 真陽性 (True Positive, TP): 80人
まさに名探偵のファインプレー!です。本当に病気である100人のうち、80人を正しく「陽性」と見つけ出しました。これが診断の根幹をなします。 - 偽陽性 (False Positive, FP): 90人
これが最も厄介な「冤罪事件」です。本当は健康な900人のうち、90人を間違って「陽性」と判定してしまいました。この結果は、患者さんに不要な精神的負担を強いるだけでなく、追加の精密検査(場合によっては侵襲的なものも)へとつながる可能性があります。 - 真陰性 (True Negative, TN): 810人
これも素晴らしい仕事です。健康な900人のうち、810人を正しく「陰性」と判断し、「あなたは大丈夫ですよ」という安心を届けることができました。 - 偽陰性 (False Negative, FN): 20人
臨床上、絶対に見逃したくない「取り逃し事件」です。本当に病気である100人のうち、20人を見逃し、「陰性」という誤った安心を与えてしまいました。これにより、本来必要な治療の開始が遅れる危険性があります。
どうでしょうか?このように数字を入れてみると、それぞれの部屋の意味がよりリアルに感じられると思います。
これからの解説はすべて、このTP, FP, TN, FNという4人の登場人物(数字)が織りなす物語です。この見取り図の描き方さえマスターすれば、もう診断精度の世界で迷子になることはありません。
検査の「性格」を知る:感度と特異度という二つの個性
見取り図が描けたら、次はその検査がどんな「性格」の持ち主かを知る番です。検査の性能は、その固有の性格、すなわち感度 (Sensitivity) と 特異度 (Specificity) という二つの指標で語られます。これらは検査がもともと持っている能力であり、有病率など周りの状況には影響されません。
さっそく、先ほどの1000人の例を使って、この二つの性格を数値化してみましょう。
感度 (Sensitivity):「病気を見つける嗅覚」の鋭さ 👃
感度とは、「本当に病気の人たち(TP + FN)を、どれだけ正しく『陽性』だ(TP)と見抜けるか」という能力です。言い換えれば、「病気の人を見逃さない力」ですね。
数式で見てみましょう。これは見取り図の「疾患あり」の列(タテ)に注目する計算です。
\[ \text{感度 (Sensitivity)} = \dfrac{\text{真陽性 (TP)}}{\text{真陽性 (TP)} + \text{偽陰性 (FN)}} \]
先ほどの例の数字を当てはめてみると、
\[ \text{感度} = \dfrac{80}{80 + 20} = \dfrac{80}{100} = 0.80 \]
つまり、この検査の感度は80%です。100人の患者さんのうち80人を見つけ出せる、ということですね。
この感度という性格をたとえるなら、「病気キャッチャーの巨大な網」です。感度が高い検査は、網目が非常に細かく、どんなに小さな魚(初期の病変など)も見逃しません。そのため、見逃しが致命的になりうるがんのスクリーニングや、感染症の初期診断など、「とにかく見逃しを避けたい」場面で絶大な力を発揮します。
もし、この非常に目の細かい網をすり抜けて「陰性」という結果が出たなら、「まあ、この網にかからないなら、まず病気はいないだろう」とかなり安心して、その病気を除外(Rule Out)できます。これは「SnNout (a Sensitive test, when Negative, helps to rule out the disease)」というEBM(科学的根拠に基づく医療)の世界の経験則として、非常に有名です (Sackett et al., 1991; Straus et al., 2018)。
特異度 (Specificity) = 非常に慎重な宝石鑑定士 💎
特異度は、「本当に健康な人たち(TN + FP)を、どれだけ正しく『陰性』だ(TN)と判定できるか」という能力です。「健康な人を、むやみに病気だと疑わない誠実さ」とも言えるでしょう。
数式では、見取り図の「疾患なし」の列(タテ)に注目します。
\[ \text{特異度 (Specificity)} = \dfrac{\text{真陰性 (TN)}}{\text{真陰性 (TN)} + \text{偽陽性 (FP)}} \]
例の数字で計算すると、特異度は90%です(810 / (810 + 90) = 0.9)。900人の健康な人のうち、810人を正しく「陰性」と判定できる能力を示します。
高特異度な検査は、「偽物を本物と認める誤りを、極限まで減らす」ことを重視する、非常に慎重な宝石鑑定士のようなものです。
- 行動: この鑑定士は、鑑定基準を厳格に適用し、少しでも疑わしい点があれば「本物のダイヤモンド」と認定することに極めて慎重です。
- 結果: そのため、偽物の石を「本物」と間違えてしまう可能性は極めて低くなります(偽陽性が少ない)。その代わり、本物でも品質がわずかに基準に満たない石は「鑑定不能(陰性)」と判定されるかもしれません(偽陰性が増え、感度は低い傾向になります)。
- 臨床での意味 (SpPin): この慎重な鑑定士が「本物です(陽性)」と判定したのであれば、それが本物(病気)であるという確信度が高まり、診断を強く支持する根拠となります。これも「SpPin (a Specific test, when Positive, helps to rule in the disease)」として知られる重要な経験則です (Sackett et al., 1991; Straus et al., 2018)。
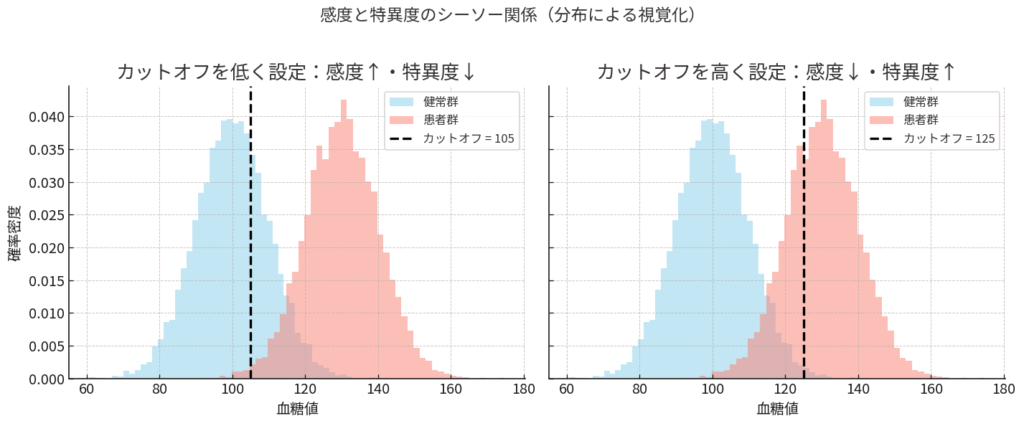
感度と特異度のシーソーゲーム
ここで重要なのは、この二つの性格は、車のアクセルとブレーキのように、しばしばトレードオフ(シーソーのような関係)にあるということです。
例えば、ある血糖値の検査で、「どこからを陽性とするか」というカットオフ値を考えてみましょう。
- カットオフ値を低く(甘く)設定すれば:少しでも血糖値が高い人を拾い上げるので、見逃しは減ります(感度↑)。しかし、健康な人まで「陽性」と判定してしまい、冤罪が増えます(特異度↓)。
- カットオフ値を高く(厳しく)設定すれば:本当に血糖値が高い人だけを陽性にするので、冤罪は減ります(特異度↑)。しかし、境界域の人たちを見逃してしまうかもしれません(感度↓)。
このように、感度を上げれば特異度が下がり、特異度を上げれば感度が下がる。このシーソーゲームのバランスを、検査の目的(スクリーニングなのか、確定診断なのか)に応じてどう取るかが、検査を賢く使いこなす上での最初の関門なのです。
「あなたの患者さん」にとっての意味:陽性的中率(PPV)と陰性的中率(NPV)
感度と特異度は、いわば検査の「取扱説明書」に書かれている性能スペックです。しかし、私たちが臨床現場で直面するのは、「このスペックを持つ検査で陽性と出た、目の前の患者さん」という、より個人的で切実な問題です。
私たちが本当に知りたい問い、それは「この陽性という結果を受け取った患者さんが、本当に病気である確率は何パーセントか?」というものでしょう。この、臨床医と患者さんが最も共有したい問いに答えるのが、陽性的中率 (Positive Predictive Value, PPV) と 陰性的中率 (Negative Predictive Value, NPV) です。
そして、この話をする上で絶対に欠かせない、隠れた主役が登場します。それが有病率 (Prevalence) です。
隠れた影響者:有病率 (Prevalence) 🌐
感度80%、特異度90%という先ほどの検査。この性能は不変ですが、この検査をどこで使うかによって、結果の「意味」は全く変わってしまいます。
たとえるなら、「砂漠で金(ゴールド)を探す探知機」を想像してください。この探知機は非常に優秀で、金があれば80%の確率で鳴り(感度)、金以外の金属(ただの鉄くずなど)には90%の確率で鳴らない(特異度)とします。
- 金鉱山の近く(有病率が高い状況)で使えば:探知機が鳴れば「お、金かな?」と期待が高まりますよね。
- 普通の公園の砂場(有病率が低い状況)で使えば:探知機が鳴っても、「どうせ釘か空き缶だろうな…」と思うのが自然ではないでしょうか?
この「金がありそうな度合い」、それこそが有病率です。検査を行う集団の中に、どれくらいの割合でその疾患を持つ人がいるかを示す数字であり、PPVとNPVを裏で操る最も重要な因子なのです。
先ほどの1000人の例では、100人が患者だったので、有病率は 100 / 1000 = 10% でした。この数字を覚えておいてください。
陽性的中率 (PPV):「陽性」の本当の価値
PPVは、「検査で陽性だった人たち(TP + FP)の中で、本当に病気だった人(TP)の割合」、つまり「陽性が的中している確率」を示します。
計算式は、見取り図の「陽性 (T+)」の行(ヨコ)に注目します。
\[ \text{PPV (陽性的中率)} = \dfrac{\text{真陽性 (TP)}}{\text{真陽性 (TP)} + \text{偽陽性 (FP)}} \]
さあ、有病率10%だった我々の例で計算してみましょう。
\[ \text{PPV} = \dfrac{80}{80 + 90} = \dfrac{80}{170} \approx 0.47 \]
驚きませんか?感度80%, 特異度90%という、かなり優秀に見えた検査でも、いざ陽性と出たときに、その人が本当に病気である確率は47%しかないのです。半分以上は「冤罪」だった、ということになります。
これが有病率の低い疾患をスクリーニングする際の大きな落とし穴です。どんなに優れた検査でも、母集団に占める患者の割合が少ないと、偽陽性の数が真陽性の数を圧倒してしまうのです。この事実を知らずに「陽性です」とだけ伝えれば、患者さんに計り知れない不安を与えかねません。
陰性的中率 (NPV):「陰性」がもたらす安心の度合い
逆にNPVは、「検査で陰性だった人たち(TN + FN)の中で、本当に健康だった人(TN)の割合」、つまり「陰性という結果の信頼度」を示します。
今度は、見取り図の「陰性 (T-)」の行(ヨコ)に注目です。
\[ \text{NPV (陰性的中率)} = \dfrac{\text{真陰性 (TN)}}{\text{真陰性 (TN)} + \text{偽陰性 (FN)}} \]
これも、我々の例で計算してみましょう。
\[ \text{NPV} = \dfrac{810}{810 + 20} = \dfrac{810}{830} \approx 0.976 \]
こちらは非常に高い数値が出ました。97.6%です。つまり、この検査で「陰性」と出た場合、その人が本当に健康である確率はかなり高いと言え、私たちも患者さんも、大きな安心材料とすることができます。
まとめ:二つの視点を使い分ける
ここで、指標の視点を整理しておきましょう。
| 指標の種類 | 視点 | 主な問い |
|---|---|---|
| 感度・特異度 | 検査中心 | 「この検査は、病気の人/健康な人を、どれだけ正しく識別できるか?」 |
| PPV・NPV | 患者中心 | 「この検査結果が出た私の体は、実際にどういう状態なのか?」 |
感度・特異度が検査の「取扱説明書」だとすれば、PPV・NPVは、その説明書を読み解き、有病率という現場の状況を加味した上で、「目の前の患者さん」という個別のケースに適用する、まさに臨床応用そのものです。
この二つの視点を自在に行き来できることこそ、探偵から名探偵へのステップアップの鍵なのです。
性能を丸ごと可視化する:ROC曲線とAUC
さて、探偵道具もだいぶ揃ってきましたね。最後の仕上げに、検査の「総合的な実力」を一枚の絵で評価できる、極めて強力なツール、ROC曲線 (Receiver Operating Characteristic curve) と AUC (Area Under the Curve) をご紹介します。
思い出してください、感度と特異度はカットオフ値(陽性と判断する基準値)によって変動する「シーソーゲーム」の関係にある、という話をしました。例えば、心不全のマーカーであるBNP値を考えてみましょう。「100 pg/mL以上を陽性」とするのか、「150 pg/mL以上を陽性」とするのかで、感度と特異度はガラリと変わります。
では、どのカットオフ値がベストなのでしょうか?そもそも、この検査は心不全を見分ける上でどれくらい「使える」のでしょうか?この問いに、最高の答えを与えてくれるのがROC曲線です。
ROC曲線:検査の「実力カタログ」📈
ROC曲線は、たとえるなら、あるアスリートの「総合能力チャート」です。パワー、スピード、持久力など、様々な能力のバランスを一枚の絵で示す、あのレーダーチャートを想像してください。ROC曲線は、カットオフ値を連続的に変化させたときの、あらゆる感度と特異度の組み合わせをプロットし、検査の総合的な識別能力を可視化します。
具体的には、縦軸に感度(真陽性率)、横軸に 1 – 特異度(偽陽性率) を取ります。
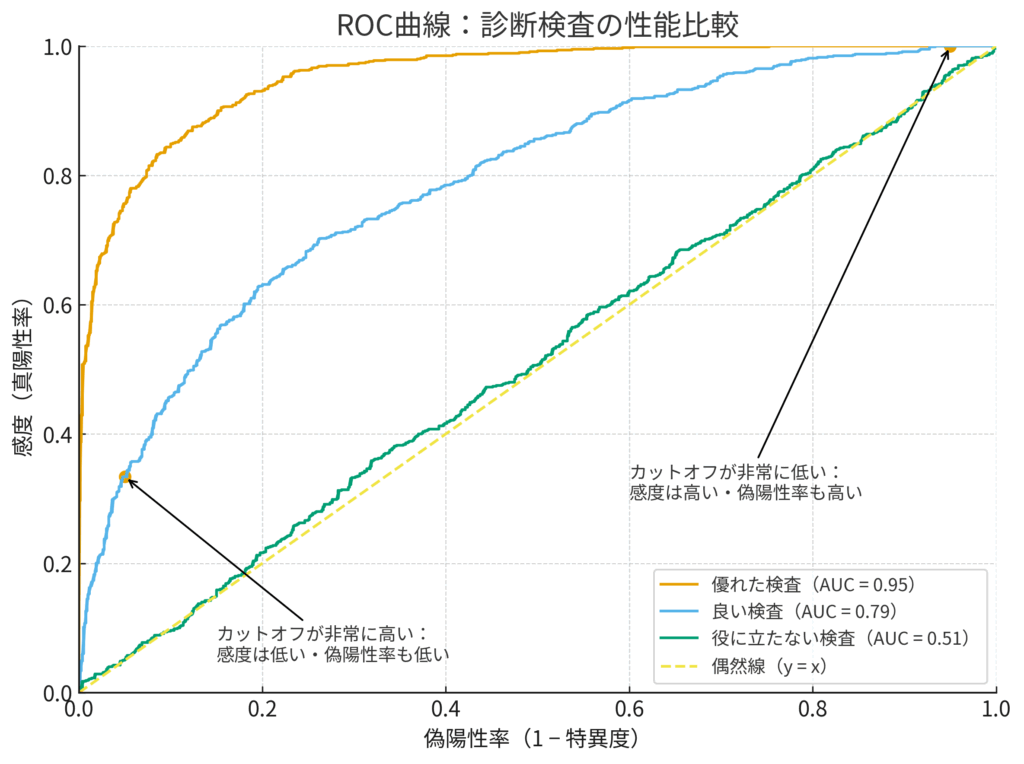
- 縦軸(感度): どれだけ正しく患者を見つけられるか(値が高いほど良い)。
- 横軸(1 – 特異度): どれだけ健康な人を間違って「陽性」としてしまうか(値が低いほど良い)。
この座標の上で、カットオフ値を動かすと何が起こるか見てみましょう。
- カットオフ値を非常に低く設定(例: BNP > 10):
ほとんど全員が陽性になります。患者は全員見つけられますが(感度≈100%)、健康な人もほぼ全員陽性になってしまいます(偽陽性率≈100%)。これはグラフの右上の点に対応します。 - カットオフ値を徐々に上げていく:
感度は少しずつ下がり始めますが、それ以上に偽陽性率がぐっと下がり始めます。つまり、曲線は左上に向かって弓なりに描かれます。 - カットオフ値を非常に高く設定(例: BNP > 1000):
ほとんど全員が陰性になります。陽性になるのは本当に重症な患者さんだけです。冤罪はほぼゼロになりますが(偽陽性率≈0%)、多くの患者を見逃してしまいます(感度≈0%)。これはグラフの左下の原点に対応します。
この曲線の形が、検査の性能そのものを表しています。
- 理想的な検査: 曲線はグラフの左上の角(感度100%, 偽陽性率0%)に張り付く形になります。
- 全く役に立たない検査: 曲線は45度の対角線(偶然線、line of chance)と一致します。これはコインを投げて診断するのと同じレベルです。
ROC曲線を見れば、「感度を80%確保したいなら、偽陽性率は20%まで許容する必要があるな」といった具体的なトレードオフの関係が一目でわかり、目的に応じた最適なカットオフ値を選ぶための強力な手助けとなるのです。
AUC (C-statistic):実力を示す「総合スコア」🏆
ROC曲線という「総合能力チャート」全体を、たった一つの数字で要約したものがAUC (Area Under the Curve)、つまり曲線の下の面積です。C-statistic(Concordance statistic)とも呼ばれます。
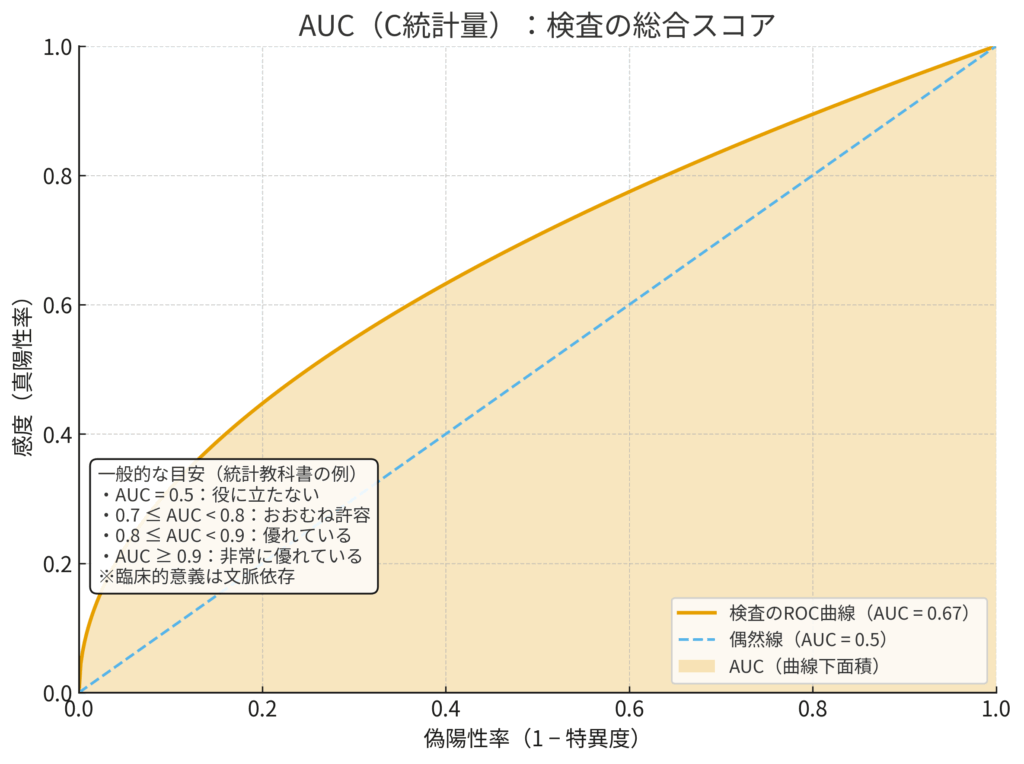
たとえるなら、アスリートの能力チャートの「面積の大きさ」です。面積が大きければ大きいほど、そのアスリートは総合的に優れていると言えますよね。同様に、AUCが大きければ大きいほど、その検査は優れた識別能力を持つと評価できます。
AUCの値は0.5(無価値)から1.0(完璧)の範囲をとり、その解釈には一般的な目安があります。ただし、これはあくまで統計学的な教科書に基づくものであり、臨床的な意義は疾患の重篤度などによって常に考慮されるべきです (Hosmer & Lemeshow, 2000)。
- AUC = 0.5: 役に立たない検査(コイン投げ)
- 0.7 ≤ AUC < 0.8: まあまあ許容できる識別能
- 0.8 ≤ AUC < 0.9: 優れた識別能
- AUC ≥ 0.9: 非常に優れた識別能
AUCには、もう一つ非常に直感的で美しい解釈があります。それは、「ランダムに選んだ一人の患者と、一人の健康な人がいたとして、この検査値が患者の方でより高く(あるいは低く)出る確率は何パーセントか」を示す、というものです。例えばAUCが0.85なら、85%の確率で正しく患者と健康な人を見分けられる、という意味になります。Fawcett (2006) が指摘するように、この理解は、異なる検査の性能を比較する際に非常に有用です。
このように、AUCはカットオフ値という特定の基準に依存しない、検査の「地力」ともいえる総合的な識別能力を示す、極めてパワフルな指標なのです。
診断の確信度を更新する:尤度比(LR)という武器
PPVとNPVは非常に強力ですが、一つの大きな弱点があります。それは、計算の土台となる「有病率」が、ある特定の集団の平均値に固定されてしまう点です。
しかし、私たちの目の前にいる患者さんは、平均的な集団とは異なります。例えば、「80歳、喫煙者、特徴的な胸痛あり」という患者さんの心筋梗塞の検査前確率(Pre-test probability)は、外来に来た全患者の平均的な有病率よりも明らかに高いはずです。
このように、個々の患者さんに応じて私たちが抱く「臨床的な疑いの度合い(探偵の勘)」を、検査結果という新しい証拠によって、どれだけ更新できるか?この、より個別化された問いに答えるための洗練された道具が、尤度比 (Likelihood Ratio, LR) です。
たとえるなら、「証拠の価値を測る倍率」です。尤度比は、ある検査結果が、病気のない人よりも、病気のある人から得られる可能性が何倍高いか(あるいは低いか)を示し、私たちの「疑いの度合い」を客観的にアップデートしてくれます。
陽性尤度比 (LR+):疑いを深める証拠の力
陽性尤度比(Positive Likelihood Ratio, LR+)は、「陽性」という結果が出たときに、私たちの疑いをどれだけ強めて良いかを示す倍率です。
計算式は、感度と特異度から導かれます。
\[ \text{陽性尤度比 (LR+)} = \dfrac{\text{感度}}{1 – \text{特異度}} = \dfrac{\text{真陽性率}}{\text{偽陽性率}} \]
分母の「1 – 特異度」は偽陽性率、つまり「健康な人が間違って陽性になる確率」です。分子の感度は「病気の人が正しく陽性になる確率」。つまりLR+は、「陽性という結果が、健康冤罪者からよりも真犯人から出てくる確率は何倍か」を示しているわけです。
我々の例(感度0.8, 特異度0.9)で計算してみましょう。
\[ \text{LR+} = \dfrac{0.8}{1 – 0.9} = \dfrac{0.8}{0.1} = 8 \]
LR+は8となりました。これは、「この検査で陽性と出た」という事実は、この患者さんが健康である場合よりも、病気である場合に8倍起こりやすい、ということを意味します。DeeksとAltman (2004) の報告によれば、LR+が5を超えると中程度の、10を超えると大きな診断的価値を持つ強力な証拠とされています。
陰性尤度比 (LR-):疑いを晴らす証拠の力
陰性尤度比(Negative Likelihood Ratio, LR-)は、「陰性」という結果が出たときに、私たちの疑いをどれだけ弱めて良いかを示す倍率です。
\[ \text{陰性尤度比 (LR-)} = \dfrac{1 – \text{感度}}{\text{特異度}} = \dfrac{\text{偽陰性率}}{\text{真陰性率}} \]
これは「陰性という結果が、健康な人からよりも、取り逃がした真犯人から出てくる確率はどれくらいか」を示します。値が1より小さく、0に近づくほど「陰性」の信頼性が増します。
我々の例では、
\[ \text{LR-} = \dfrac{1 – 0.8}{0.9} = \dfrac{0.2}{0.9} \approx 0.22 \]
LR-は約0.22。これは、検査後の疾患の可能性が、検査前の約1/5になることを意味します。DeeksとAltman (2004) によれば、LR-が0.2を下回ると中程度の、0.1を下回ると大きな除外診断的価値を持つとされています。
尤度比の使い方:ベイズの定理を臨床現場で
尤度比の使い方は非常にエレガントです。確率を「オッズ」という概念に変換して計算します。
オッズ = 確率 / (1 – 確率)
使い方の3ステップは以下の通りです。
- 検査前確率 → 検査前オッズ: あなたの臨床経験から、目の前の患者さんの検査前確率を推定します(例:30% = 0.3)。これをオッズに変換します
0.3 / (1 - 0.3) ≈ 0.43。 - オッズの更新: 検査結果に応じて、検査前オッズに尤度比を掛け算します。
- 陽性なら:
検査前オッズ × LR+→0.43 × 8 = 3.44(これが検査後オッズ)
- 陽性なら:
- 検査後オッズ → 検査後確率: 最後に、検査後オッズを私たちに馴染み深い確率に戻します。
確率 = オッズ / (1 + オッズ)3.44 / (1 + 3.44) ≈ 0.77
計算の結果、検査前確率が30%だった患者さんは、陽性結果を受けて検査後確率が77%にまで上昇しました。一般的なPPV(47%)よりもずっと高い、この患者さん個人に特化した確率が得られたのです。
このように、尤度比は私たちの臨床的直感を、客観的な数値へと変換し、診断の確信度を柔軟に更新してくれる、まさに「探偵の名パートナー」なのです。
医療統計や論文で頻繁に登場する「オッズ (Odds)」。私たちは「確率 (Probability)」には馴染みがありますが、「オッズ」と言われると、少し戸惑ってしまうかもしれません。なぜ、わざわざオッズという考え方を使うのでしょうか?
実は、オッズは確率を少し違った視点から見たものであり、特に尤度比を使った計算やロジスティック回帰分析など、医療統計の世界では非常に便利な「言葉」なのです。
■ 確率 vs オッズ:リンゴの例
ここにリンゴが5つ入ったカゴがあるとします。そのうち、赤いリンゴが1つ、青いリンゴが4つです。
- 確率 (Probability) とは、「全体のうち、それが起こる割合はいくつか」を示す考え方です。
- このカゴから1つ取って赤いリンゴである確率は、5つのうちの1つなので 1/5 = 0.2 (20%) です。
- オッズ (Odds) とは、「それが起こる回数と、起こらない回数の比」を示す考え方です。
- 赤いリンゴが出るオッズは、「赤が出る回数:赤以外が出る回数」なので 1 : 4 となり、数値としては 1/4 = 0.25 となります。
このように、確率は「全体」を分母にするのに対し、オッズは「それ以外」を分母にするのが大きな違いです。
■ 確率とオッズの変換式
この関係は、数式で簡単に表現できます。ある事象が起こる確率を \( p \) とすると、
確率 → オッズ
\[ \text{オッズ} = \dfrac{p}{1-p} \]
( \( p \) は「起こる確率」、 \( 1-p \) は「起こらない確率」です。まさに定義通りですね。)
オッズ → 確率
\[ p = \dfrac{\text{オッズ}}{1+\text{オッズ}} \]
(オッズが「1対4」なら、全体は `1+4=5` なので、確率は `1/5` に戻ります。)
■ なぜわざわざオッズを使うのか?
オッズが便利な最大の理由は、尤度比との相性の良さにあります。尤度比の説明で出てきたように、
検査前オッズ × 尤度比 = 検査後オッズ
という非常にシンプルな掛け算で、検査によって私たちの確信度がどう変化したかを計算できます。これを確率のまま計算しようとすると、ベイズの定理の複雑な分数式を毎回使わなければなりません。オッズは、このベイジアン的な思考を、臨床現場で実践しやすくしてくれるエレガントなツールなのです。
| 比較項目 | 確率 (Probability) | オッズ (Odds) |
|---|---|---|
| 考え方 | 全体に対する割合 | 起こる回数 vs 起こらない回数の比 |
| 値の範囲 | 0 〜 1 | 0 〜 無限大 |
| 主な用途 | 直感的な理解、割合の提示 | 統計モデル、尤度比との計算 |
オッズは一見とっつきにくいですが、「確率の親戚」であり、特に尤度比を使いこなすための「名パートナー」だと理解すれば、あなたの探偵道具箱の頼れるツールの一つになるはずです。
論文の信頼性を見抜く:STARD声明という羅針盤
さて、私たちの探偵道具箱も、これで最後の道具になります。それは、他のすべての道具の信頼性を保証するための、いわば「品質保証書」ともいえるツールです。
私たちは日々、新しい診断技術に関する論文の洪水にさらされています。AIを用いた画像診断、新規バイオマーカー…。しかし、その研究報告がずさんであったり、重要な情報が隠されていたりしたらどうでしょう?感度99%という華々しい数字も、信頼性の低い土台の上に建てられた砂上の楼閣に過ぎません。
そこで、論文という「証拠」そのものの信頼性を見抜くために開発されたのが、STARD声明 (Standards for Reporting of Diagnostic Accuracy Studies) です。これは、診断精度研究の論文が、科学的に評価されるために「何を」「どのように」報告すべきかを定めた、国際的なガイドラインです。
たとえるなら、中古車を購入するときの「第三者機関による査定書」です。この査定書があれば、見た目がピカピカな車でも、「修復歴あり」「メーター改ざんの可能性」といった重要な欠陥を見抜くことができますよね。STARD声明は、まさに診断精度研究における査定書の役割を果たします。
Cohenらによる2015年の改訂版 (Cohen et al., 2015) では、研究の透明性を高めるための30項目のチェックリストが示されています。例えば、このチェックリストは私たちに以下のような鋭い問いを投げかけるよう促します。
- (項目6 & 7) そもそも、どんな患者さんを対象にした研究なのか?: 患者さんの選択基準が曖昧だと、非常に診断しやすい軽症例ばかりを集めて、見かけ上の性能を良く見せているかもしれません。
- (項目10) 比較対象の「ゴールドスタンダード(最も信頼性の高い診断法)」は適切か?: 例えば、新しい迅速検査の性能を、不正確な従来法と比較していては意味がありません。
- (項目13b) 検査結果は「盲検化」されていたか?: 検査の判定者が、ゴールドスタンダードの結果を事前に知っていたらどうでしょう?無意識のバイアスがかかり、結果が都合よく解釈されてしまう危険性があります。
これらはほんの一例ですが、STARD声明が単なるお題目ではなく、論文の”弱点”を暴くための、極めて実践的なツールであることがお分かりいただけると思います。
次に新しい検査に関する論文を読むとき、あるいは院内の勉強会(ジャーナルクラブ)で論文を抄読するときは、ぜひ「この研究はSTARDの基準を満たしているか?」という視点を持ってみてください。STARDの公式サイトにはチェックリストも公開されています。その論文の著者たちが、自分たちの研究デザインや限界について、どれだけ誠実に報告しているか。その姿勢を見ることこそが、情報の質を見抜く最も確実な方法であり、私たちの患者さんを質の低いエビデンスから守るための防波堤となるのです。
まとめ:名探偵への第一歩
今回の知の探偵旅行も、いよいよ終着点です。お疲れ様でした。私たちは、一つの検査結果の裏に隠された、かくも豊かで奥深い世界を一緒に旅してきましたね。
最後に、今日手に入れた強力な「探偵道具一式」を、もう一度確認しておきましょう。これらは、あなたが明日から出会うであろう、あらゆる「陽性」や「陰性」の謎を解き明かすための武器となります。
| 探偵道具 | この道具で解ける謎(問い) | 主な活躍の場面 |
|---|---|---|
| 2×2分割表 | 「証言と真実の関係性は、どうなっている?」 | すべての分析の出発点となる見取り図 |
| 感度・特異度 | 「この検査(目撃者)は、どんな性格を持っている?」 | 検査固有の性能を理解する |
| PPV・NPV | 「この陽性/陰性は、目の前の患者さんにとって何を意味する?」 | 検査結果を個別の患者さんに説明する |
| ROC・AUC | 「この検査の総合的な識別能力はどれくらいか?」 | 複数の検査性能の比較、最適なカットオフ値の選択 |
| 尤度比 (LR) | 「私の臨床的疑いを、この証拠でどれだけ更新できる?」 | 個別性の高い患者さんの診断確率を精密に計算する |
| STARD声明 | 「この研究論文(証拠)は、そもそも信頼できるのか?」 | 新しいエビデンスを批判的に吟味する |
どうでしょう。一つひとつはシンプルな道具ですが、これらを自在に組み合わせることで、私たちは初めて、検査結果という一つの「証言」に多角的な光を当て、その本当の価値を評価することができるのです。
検査結果は、私たちの思考の「終わり」ではなく、患者さんと共に歩む、より深い対話と探求の「始まり」です。
数字の魔力に振り回されることなく、その裏にある意味を深く理解し、患者さんの価値観と文脈の中で使いこなす。それこそが、情報が氾濫する現代の医療において、私たちが目指すべき「名探偵」の姿ではないでしょうか。
今日手に入れたこれらの思考の道具が、あなたの明日からの臨床を、より確信に満ちた、そして何より、患者さんにとってより良いものにするための一助となることを、心から願っています。
参考文献
- Altman, D.G. and Bland, J.M. (1994a). Diagnostic tests 1: sensitivity and specificity. BMJ, 308(6943), p.1552.
- Altman, D.G. and Bland, J.M. (1994b). Diagnostic tests 2: predictive values. BMJ, 309(6947), p.102.
- Cohen, J.F., Korevaar, D.A., Altman, D.G., Bruns, D.E., Gatsonis, C.A., Hooft, L., Irwig, L., Levine, D., Reitsma, J.B., de Vet, H.C.W. and Bossuyt, P.M.M. (2015). STARD 2015 guidelines for reporting diagnostic accuracy studies: explanation and elaboration. BMJ Open, 5(11), e009551.
- Deeks, J.J. and Altman, D.G. (2004). Diagnostic tests 4: likelihood ratios. BMJ, 329(7458), pp.168–169.
- Fawcett, T. (2006). An introduction to ROC analysis. Pattern Recognition Letters, 27(8), pp.861–874.
- Fletcher, R.H., Fletcher, S.W. and Fletcher, G.S. (2014). Clinical epidemiology: the essentials. 5th ed. Philadelphia: Lippincott Williams & Wilkins.
- Hosmer, D.W. and Lemeshow, S. (2000). Applied logistic regression. 2nd ed. New York: Wiley.
- Sackett, D.L., Haynes, R.B., Guyatt, G.H. and Tugwell, P. (1991). Clinical epidemiology: a basic science for clinical medicine. 2nd ed. Boston: Little, Brown.
- Straus, S.E., Glasziou, P., Richardson, W.S. and Haynes, R.B. (2018). Evidence-based medicine: how to practice and teach EBM. 5th ed. Edinburgh: Elsevier.
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






