平均値という「点」の情報だけでは不十分です。95%信頼区間は、結果の不確かさを「ゾーン」で示すことで、研究データがどれだけ信頼できるかを教えてくれる強力なツールです。
「真の値が95%の確率で入る」は誤り。正しくは「同じ研究を100回繰り返せば、そのうち95回は真の値を捉える優秀な計算手法」という意味です。
- 中心: 最も確からしい値 (標本平均)
- 幅: 推定の不確かさ (標準誤差)
- 信頼度: 95%を保証する係数 (1.96)
- 幅で精度を読む:狭いほど高精度。
- ゼロまたぎで有意性を見る:またがなければ有意差あり。
- 臨床的な意味を考える:統計的な差が実用的な差か吟味する。
はじめに:なぜ「平均10mmHg低下」だけでは不十分なのか?
ある新薬の臨床試験で、「収縮期血圧が平均で10mmHg低下した」という素晴らしい結果が報告されたとします。私たちは、この「10mmHg」という数字を、どれくらい確かなものとして受け止めればよいのでしょうか?
少し想像してみてください。もし、この臨床試験をもう一度、全く同じ条件で、別の患者さんたちを対象に行ったとしたら。果たして、結果はピッタリ「平均10mmHg低下」になるでしょうか?
おそらく、なりませんよね。次は9.5mmHgかもしれませんし、あるいは10.8mmHgかもしれません。私たちが論文や学会で目にする「平均値」という結果は、あくまでその研究に参加した限られた人たち(標本)から得られた、たった一つの点推定値に過ぎないのです。
それは、私たちが本当に知りたい「世界中のすべての患者さんに対する真の効果」(母数)を推測するための、いわば「たった一枚のスナップ写真」のようなもの。もちろん非常に貴重な情報ですが、その一枚だけで全てを判断するには、なんだか少し心もとないと感じませんか?
そこで登場するのが、今回の主役である95%信頼区間(95% Confidence Interval, 95% CI)です。これは、ただ一点のスナップ写真を見せるのではなく、「真の効果は、おそらくこの範囲にありますよ」と、幅を持たせた「ゾーン」で示すための、非常に強力で誠実なツールなのです。この概念を理解することで、データの背後にある物語を、より深く、そして正確に読み解くことができるようになります。
95%信頼区間とは?「魚釣り」のたとえ話、完全マスター版
「95%信頼区間の意味は?」と尋ねると、おそらく多くの方が「真の値が95%の確率でその区間に入る」と答えるのではないでしょうか。実はこれ、統計学の世界で最も広まっている誤解の一つなんです。なぜかこの誤解は非常に根強く、経験豊富な研究者でさえ、つい口にしてしまうことがあります。でも、ご安心ください。この概念の「本当の意味」を理解すれば、論文のデータがまったく違って見えてきます。
この誤解を解きほぐすために、一つ、物語仕立てのたとえ話をさせてください。
物語の始まり:広大な湖と「真実の魚」
想像してみてください。目の前に、どこまでも広がる静かな湖があります。この広大な湖のどこか一点に、たった一匹だけ、ピカピカに光る「真実の魚」が静かに潜んでいます。この魚が、私たちが本当に知りたいけれど、直接見ることはできない母数(parameter)です。例えば、「ある新薬の、全人類に対する真の血圧低下効果」といったものですね。この魚は湖のどこかにいますが、動きません。その位置は不変の真実です。
さて、私たちの仕事は、この魚を捕まえることです。しかし、湖の水をすべて汲み上げる(全人類に薬を投与する)ことは不可能です。私たちができるのは、船の上から一度だけ「網」を投げることだけ。この一度きりの網投げが、私たちが実施する一度の臨床試験や研究にあたります。そして、集めた患者さんのデータ(標本、サンプル)から計算された結果、例えば「平均10mmHg低下、95%信頼区間 [8, 12]」というのが、私たちが投げた「網」そのものなのです。
95%の意味:確率の「主語」は誰?
ここからが本題です。「95%信頼区間」とは、一体何を意味するのか。この考え方の生みの親である20世紀の偉大な統計学者、ジャージー・ネイマンの考え方に沿って説明しましょう (Neyman, 1937)。
ネイマンが提唱した頻度論的統計学の考え方では、確率は「何度も繰り返すことができる事象」に対して使われる、とされています。これを魚釣りのたとえに戻すと、こういうことになります。
「あなたが使っている『網の投げ方(=信頼区間を計算する統計的手法)』は、非常に優秀だ。もし、あなたが場所や時間を変えて100回、同じ投げ方で網を投げたとしたら、そのうち95回は、網の中にちゃんと『真実の魚』が入っているだろう」
どうでしょう? 確率の「主語」が見えてきましたか?
95%という確率は、私たちが今、手元に持っている「たった一つの網(今回の研究結果)」について語っているのではありません。そうではなく、その網を生み出した**「計算プロセスそのもの」の長期的な成功率**を語っているのです。「Confidence Interval(信頼区間)」という名前も、この「計算手法への信頼度」から来ていると考えると、しっくりくるかもしれませんね。
以下の図は、このシミュレーションのイメージです。20回研究(網投げ)を繰り返した様子だと考えてください。網の中心(点推定値)は毎回少しずつズレますし、網の幅(推定の精度)も微妙に変わります。ほとんどの網(青線)は真実の魚(縦の点線)を捉えていますが、時には運悪く外れてしまう網(赤線)も出てきます。95%信頼区間とは、このような「空振り」が100回に5回くらいの頻度で起こりうる手法ですよ、ということを教えてくれているのです。
私たちが論文で目にする信頼区間は、この無数の試行の可能性のうち、たった一本の線に過ぎません。その一本の線(私たちの手元の網)に魚が入っているか、入っていないか。本当のところは誰にも分かりません。でも、「この方法は95%の確率で成功するくらい信頼できるやり方なんだ」と、その背景にある品質を保証してくれている。それが信頼区間の本質なんです。
なぜ「95%の確率で真の値が入る」は間違いなのか?
ここまで読んで、「でも、やっぱり95%の確率で入るって言った方が分かりやすいじゃないか」と感じる方もいるかもしれません。なぜ、この言い方が厳密には間違いとされるのか。最後に、コイントスの例でダメ押しさせてください。
あなたは、これからコインを投げます。投げる前であれば、「表が出る確率は50%だ」と言えますね。これは正しいです。
では、コインを投げて、テーブルの上に「表」が出たとします。この結果が出た後で、私があなたに「このコインが表である確率は何%ですか?」と尋ねたら、あなたは何と答えますか?
「100%です。だって、もう表が出ているのだから」と答えますよね。そうなんです。一度結果が出てしまった事象に対して、もはや「確率」は存在しません。結果は「起こった」か「起こらなかった」かの二択、All or Nothing なのです。
信頼区間もこれと全く同じです。一度、私たちの手元のデータから [8mmHg, 12mmHg] という区間が計算されてしまったら、その瞬間に確率的な揺らぎは消え去ります。真の母数(魚)は、この区間の中に「入っている」か「入っていない」かのどちらか。その事実に95%というような中途半端な確率が入り込む余地はないのです。
近年の統計学の専門家たちも、この誤解が実践に与える影響を懸念しており、正しい解釈の重要性を繰り返し強調しています (Greenland et al., 2016; Morey et al., 2016)。
このたとえ話から持ち帰っていただきたいのは、信頼区間が示すのは「結果の不確かさ」ではなく、「推定プロセスの信頼性」であるという視点です。この違いが分かると、統計的な結果をより深く、そしてより誠実に解釈できるようになるはずです。
信頼区間の計算方法:魔法の数字「1.96」の謎に迫る
さて、「魚を捕まえる網」である信頼区間ですが、その中心の位置や幅は、一体どうやって決まるのでしょうか?ここからは、少しだけ数式を使って、その設計図を覗いてみることにしましょう。数式と聞くと身構えてしまうかもしれませんが、一つ一つの部品の意味が分かれば、決して難しいものではありません。ご安心くださいね。
最も基本的な95%信頼区間の計算式は、このようになっています。
\[ \text{95%信頼区間} = \text{標本平均} \pm 1.96 \times \text{標準誤差} \]
この式は、「標本平均(網の中心)から、左右に『1.96 × 標準誤差』ぶんだけ腕を伸ばして範囲を作る」と読めます。では、それぞれの部品を詳しく見ていきましょう。
網の中心を決める「標本平均」
標本平均 (Sample Mean) は、私たちが集めたデータ(標本)から計算した、文字通りの平均値です。例えば、「臨床試験に参加した100人の血圧が、平均で10mmHg下がった」という場合、この「10mmHg」が標本平均になります。
これは、私たちが「真実の魚(母数)」がどこにいるかを推測する上で、最も頼りになる情報です。そのため、信頼区間という網の中心は、この標本平均に設定されます。いわば、「魚がいそうな、一番もっともらしい場所」として、網を投げる中心点になるわけですね。
網の幅を左右する「標準誤差」
次に、網の幅に直接関わるのが標準誤差 (Standard Error, SE) です。この言葉、少し分かりにくいかもしれませんが、「推定の不確かさ(ぐらつき)」を示す、とても重要な指標です。
もし、同じ規模の臨床試験を何度も何度も繰り返したと想像してください。毎回、標本平均はぴったり同じ値にはならず、少しずつズレますよね。この「標本平均たちのばらつき具合」を推定したものが、標準誤差です。
標準誤差は、主に2つの要素で決まります。
- データのばらつき(標準偏差): 患者さんごとの血圧低下量に個人差が大きく、ばらつきが大きいほど、推定の不確かさは増し、標準誤差は大きくなります。
- サンプルサイズ(n): 参加者が多い(サンプルサイズが大きい)ほど、偶然による影響が減り、より安定した平均値が得られます。そのため、サンプルサイズが大きいほど、標準誤差は小さくなります。
具体的には、標準誤差は「標準偏差をサンプルサイズの平方根で割る」ことで計算されます(\( SE = \dfrac{\sigma}{\sqrt{n}} \))。この式からも、サンプルサイズnが大きくなるほど、分母が大きくなり、標準誤差SEが小さくなることが直感的に分かりますね。
信頼度を決める係数「1.96」
最後に、この「1.96」という、どこからともなく現れたような数字の正体です。ここで読者の皆さんは、「そもそも、なぜ正規分布の性質が使えるの?患者さんのデータがきれいな正規分布をしているとは限らないじゃないか」と疑問に思うかもしれません。
そこで登場するのが、統計学における最も重要で美しい法則の一つ、中心極限定理(Central Limit Theorem)です。
中心極限定理のポイント 🎲
たとえ元の集団のデータ(母集団)がどんな形に分布していても、そこからある程度の大きさの標本(サンプル)を取ってきて「平均値」を計算する、という作業を何度も繰り返すと、その平均値たちが作る分布は、きれいな正規分布(左右対称の釣鐘型)に近づいていく。
これはサイコロを振る例で考えると直感的です。サイコロを1回振ったときに出る目(1〜6)の分布は平坦ですが、サイコロを30個振ってその「平均値」を記録する、という作業を繰り返すと、平均値の分布は3.5を中心としたきれいな釣鐘型になります。
↓より詳しくはこちら!

この強力な定理のおかげで、私たちは「標本平均の分布」を正規分布とみなすことができます。 そして、正規分布には「平均値から±1.96標準偏差の範囲に、全体のデータの95%が含まれる」という、とても都合の良い性質があるのです。
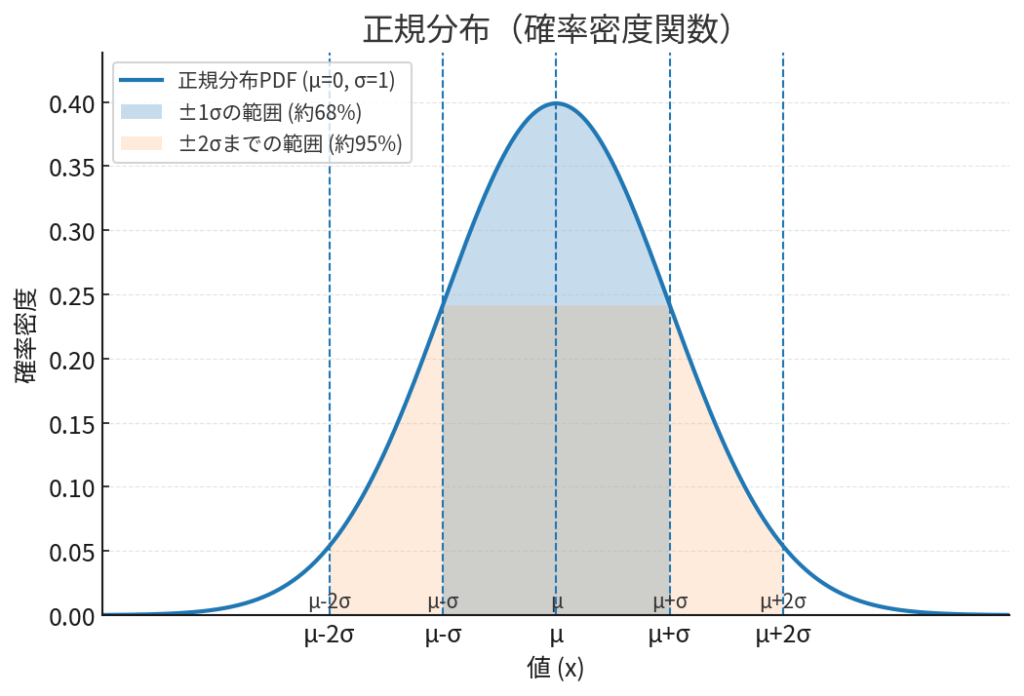
これを今の話に当てはめてみましょう。
標本平均の分布におけるばらつき(標準偏差)は、標準誤差(SE)でした。
ということは、もし研究を何度も繰り返してたくさんの標本平均を集めたら、その標本平均たちの95%は「真の平均値 ± 1.96 × SE」という範囲に収まる、と期待できます。
ここからが巧妙な点で、この関係性を利用して「網」を設計するのです。1回の研究で得た標本平均を中心に「標本平均 ± 1.96 × SE」という幅の網を作る、という計算手法は、もし何度も繰り返せば、100回中95回は真の平均値(魚)を捉えるだけの成功率を持つ手法なのだ、と保証してくれるのです。
この「1.96」は、いわば「95%という手法の成功率を保証するための魔法の数字(信頼係数)」なんですね。 もし、もっと確実性を高めて「99%信頼区間」を作りたい場合はどうなるでしょう?その場合、正規分布で99%のデータが含まれる範囲(約±2.58)を使うため、係数は「2.58」に変わります。
\[ \text{99%信頼区間} = \text{標本平均} \pm 2.58 \times \text{標準誤差} \]
係数が大きくなるので、当然、区間の幅は広くなります。魚釣りのたとえで言えば、「魚を絶対に逃したくない(信頼度を99%に上げたい)なら、もっと大きな網(広い区間)を投げる必要がある」というわけです。これは非常に直感的ですよね。
合理的な設計図
こうして見てみると、信頼区間の計算式は、非常に合理的な設計図に基づいて作られていることが分かります。
- 最も確からしい場所(標本平均)を中心に据え、
- データの不確かさ(標準誤差)に応じて腕の長さを調整し、
- 私たちが求める信頼度(95%なら1.96)で最終的な幅を決定する。
要するに信頼区間とは、「データから得られた推定値を中心に、その推定がどれくらい不確かなのかを考慮し、私たちが納得できる信頼レベルで設定した『真の値が入っていそうな、もっともらしい範囲』」なのです。この計算の背景を知ることで、論文に書かれた数字の重みを、より深く感じ取れるようになるはずです。
臨床でどう活かす?明日から使える信頼区間の「3つの着眼点」
信頼区間の概念がわかると、臨床研究の論文を読む「解像度」が劇的に上がります。これまで何となく眺めていたp値の横にある[ ]で囲まれた数字が、突然、雄弁に語りかけてくるように感じるはずです。ここでは、日々の診療や論文抄読会で明日からすぐに使える、信頼区間の賢い読み方を3つの着眼点に絞って解説します。
着眼点1:「区間の幅」から推定の”精度”を読む 🎯
信頼区間の「幅」は、その研究結果がどれくらい“シャープ”な推定に基づいているか、つまり「推定の精度」を教えてくれます。幅が狭ければシャープ(高精度)、広ければボヤっとしている(低精度)とイメージしてください。
例えば、2つの新しい降圧薬AとBの臨床試験結果が、それぞれ以下のように報告されたとします。
| 薬剤 | 平均血圧低下量(点推定値) | 95%信頼区間(95% CI) | 区間の幅 |
|---|---|---|---|
| 薬剤A | 10 mmHg | [ 8 mmHg, 12 mmHg ] | 4 mmHg |
| 薬剤B | 9 mmHg | [ 2 mmHg, 16 mmHg ] | 14 mmHg |
点推定値(平均値)だけを比べると、薬剤A(10mmHg低下)が薬剤B(9mmHg低下)より、わずかに効果が高そうに見えます。しかし、信頼区間に注目すると、その印象は大きく変わります。
- 薬剤Aの区間の幅は4mmHgと非常に狭いです。これは、研究の精度が高く、「真の効果」はかなり高い確率で8〜12mmHgという狭い範囲に収まっていることを示唆します。結果の再現性が高く、信頼できるデータと言えるでしょう。
- 一方、薬剤Bの区間の幅は14mmHgと非常に広いです。これは、研究のサンプルサイズが小さかったか、効果の個人差が非常に大きかったことを意味します。「真の効果」は2mmHg程度という僅かなものかもしれないし、逆に16mmHgという絶大なものかもしれません。つまり、推定の不確実性が非常に大きく、この研究結果だけを鵜呑みにするのは危険だ、というシグナルになります。
このように、点推定値だけでは見えない「結果の信頼性」を教えてくれるのが、信頼区間の幅なのです。
着眼点2:「ゼロをまたぐか」で”統計的有意性”を見る 👀
信頼区間は、統計的仮説検定におけるp値の代わりとしても機能します。特に「2つの群に差があるか」や「ある介入に効果があるか」を見たいときに、非常に直感的な判断基準を提供してくれます。
ポイントは、「信頼区間が、効果がない状態(=ゼロ)をまたいでいるかどうか」です。
- 例1:薬剤 vs プラセボ
ある薬剤のプラセボに対する血圧低下効果の差を調べたところ、「差の平均は5mmHg、95% CI [2mmHg, 8mmHg]」だったとします。この区間は「2」から「8」までで、「0」を含んでいません。これは、最もあり得そうな真の効果の範囲から「差がない(0)」という可能性が除外されていることを意味し、「統計的に有意な差がある(p < 0.05)」と結論できます。 - 例2:別の薬剤 vs プラセボ
別の研究で、「差の平均は3mmHg、95% CI [-1mmHg, 7mmHg]」だったとします。今度の区間は「-1」から「7」までで、途中で「0」をまたいでいます。これは、真の効果がマイナス(プラセボより悪い)である可能性から、7mmHgの低下効果がある可能性まで、幅広くあり得ることを示します。「差がゼロ」という可能性を否定できないため、「統計的に有意な差があるとは言えない(p ≧ 0.05)」と判断します。
p値が「有意かどうか」という二元的な情報しか与えないのに対し、信頼区間は効果の大きさと推定精度まで同時に示してくれます。この情報量の多さから、英国医師会雑誌(BMJ)をはじめとする主要な医学ジャーナルは、単なるp値の報告よりも信頼区間の併記を強く推奨しています (Gardner and Altman, 1986)。
着眼点3:「区間の重なり」から”2群間の差”を考える 🤔
では、先ほどの薬剤Aと薬剤Bのように、2つの有効な治療法を比較する場合はどう考えればよいでしょうか?それぞれの信頼区間が重なっているから、「両者に有意差はない」と結論づけるのは、実はよくある間違いです。
- 薬剤A: 95% CI [8, 12]
- 薬剤B: 95% CI [2, 16]
この2つの区間は、[8, 12]の範囲で重なっています。しかし、これだけで「薬剤AとBの効果に有意差はない」と判断するのは早計です。2群間の差を正しく評価するためには、「2群の差」そのものの信頼区間を計算する必要があります (Schenker and Gentleman, 2001)。
ただ、経験則として、「もし2つの95%信頼区間がほとんど重なっていない、あるいはギリギリ接するくらいなら、その2群間にはおそらく有意な差があるだろう」と推測することはできます。逆に、大きく重なり合っている場合は、有意な差がない可能性が高いと言えます。
重要なのは、信頼区間が私たちに「臨床的に意味のある差(Clinically Meaningful Difference)」を考えさせてくれる点です。たとえ統計的に有意な差があったとしても、信頼区間の全体が「臨床的には取るに足らない差」の範囲に収まっていれば、その新薬に高いコストを払う価値はないかもしれません。逆に、統計的に有意でなくても、信頼区間の中に「臨床的に非常に大きな効果」が含まれているならば、さらなる大規模な研究を検討する価値があるかもしれません。
信頼区間は、単なる統計的なツールにとどまらず、私たちの臨床的意思決定に深みを与えてくれる強力なパートナーなのです。
結論:点からゾーンへ — 不確実性を味方につける思考法
臨床や研究の世界は、不確実性との絶え間ない対話の中にあります。そんな中、私たちはつい「平均値」や「p値」といった、白黒はっきりしたシンプルな答えに飛びつきたくなるものです。しかし、たった一つの「点」で示された推定値(点推定)は、いわば被写体がブレていないかのように見せかけた、たった一枚の静止画にすぎません。
それに対して、信頼区間は「真実の値がこのあたりで動いている可能性が高いですよ」という範囲を示してくれる、短い動画クリップのようなものです。この動画は、情報の豊かさ、つまり結果の「確かさ」と「不確かさ」の両方を、正直に私たちに見せてくれます。
この記事を通じて、私たちはその動画クリップを読み解くための3つの視点を手に入れました。
- 区間の「幅」を見て、推定の”精度”を読む 🎯
- 「ゼロをまたぐか」で、”統計的有意性”を判断する 👀
- 「臨床的に意味のある差」を、”ゾーン”で考える 🤔
95%信頼区間が教えてくれるのは、「100回やれば95回は真の値を捉える、信頼できる方法で計算した範囲」という、手法そのものへの信頼性です。それは、統計の海を航海するための、単なる地図ではなく、信頼できる羅針盤となってくれます。
明日から論文を読むとき、あるいはご自身で研究を行うとき、どうか点推定値やp値だけで思考を止めないでください。そのすぐ横にある、[ ]で囲まれた数字にこそ目を凝らしてみてください。その「幅」と「位置」に、データの持つ本当の物語、つまり、その研究結果がどれだけ私たちの臨床を変える力を持っているのかという、真の価値が隠されているはずです。
不確実性から目を背けるのではなく、それを「ゾーン」として受け入れ、味方につける。その思考のシフトこそが、私たちをより賢明な科学者、そしてより思慮深い臨床家へと導いてくれるのだと、私は信じています。
参考文献
- Fisher, R. A. (1925). Statistical Methods for Research Workers. Edinburgh: Oliver and Boyd.
- Neyman, J. (1937). Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 236(767), pp. 333–380.
- Gardner, M. J. and Altman, D. G. (1986). Confidence intervals rather than P values: estimation rather than hypothesis testing. British Medical Journal (Clinical Research Ed.), 292(6522), pp. 746–750.
- Altman, D. G., Machin, D., Bryant, T. N. and Gardner, M. J. (2000). Statistics with Confidence: Confidence Intervals and Statistical Guidelines (2nd ed.). BMJ Books.
- Bland, J. M. and Altman, D. G. (1995). Calculating confidence intervals. BMJ, 310(6980), pp. 170–170.
- Cumming, G. (2014). The New Statistics: Why and How. Psychological Science, 25(1), pp. 7–29.
- Cumming, G. and Calin-Jageman, R. (2017). Introduction to the New Statistics: Estimation, Open Science, and Beyond. Routledge.
- Greenland, S., Senn, S. J., Rothman, K. J., Carlin, J. B., Poole, C., Goodman, S. N. and Altman, D. G. (2016). Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations. European Journal of Epidemiology, 31(4), pp. 337–350.
- Morey, R. D., Hoekstra, R., Rouder, J. N., Lee, M. D. and Wagenmakers, E. J. (2016). The fallacy of placing confidence in confidence intervals. Psychonomic Bulletin & Review, 23(1), pp. 103–123.
- Goodman, S. N. (2016). Aligning statistical and scientific reasoning. Science, 352(6290), pp. 1180–1181.
- Amrhein, V., Greenland, S. and McShane, B. (2019). Scientists rise up against statistical significance. Nature, 567(7748), pp. 305–307.
- Schenker, N. and Gentleman, J. F. (2001). On judging the significance of differences by examining the overlap between confidence intervals. The American Statistician, 55(3), pp. 182–186.
- Rothman, K. J. (2010). Six persistent research misconceptions. Journal of General Internal Medicine, 25(8), pp. 753–759.
- Altman, D. G. and Bland, J. M. (1995). Absence of evidence is not evidence of absence. BMJ, 311(7003), pp. 485.
- Spiegelhalter, D. J. (2019). Statistical evidence for health: the basics. BMJ, 364, l268.
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.


