毎日、私たちはたくさんのデータに囲まれていますよね。患者さんの身長や体重、血圧、検査値…。一つとして同じ値はなく、必ず「ばらつき」があります。この一見するとバラバラで、カオスにも思えるデータの中に、実はある美しい「法則」が隠れているとしたら、ワクワクしませんか?
今回は、そのデータのばらつきの背後にある“設計図”ともいえる「確率分布」という考え方をご紹介します。特に、医療の世界でも頻繁に登場する3人のヒーロー、正規分布、二項分布、そしてポアソン分布に焦点を当てて、彼らがどんな得意技を持っているのか、一緒に探っていきましょう。これを読めば、目の前のデータがただの数字の羅列ではなく、意味のある物語を語りかけているように見えてくるはずです。
確率分布って、そもそも何? – データ世界の“設計図”をのぞいてみよう
確率分布と聞くと、なんだか難しそう…と感じるかもしれません。でも、本質はとてもシンプルなんです。
一言でいうと、確率分布とは「ある出来事(専門用語で『確率変数』といいます)が、どれくらいの確率で起こるか」をグラフなどで可視化したもの。いわば、これから起こる現象を予測するための“設計図”や“シナリオ集”のようなものだと思ってみてください。
例えば、サイコロを一個振る、というシンプルな例で考えてみましょう。出る目(1, 2, 3, 4, 5, 6)が「確率変数」です。そして、それぞれの目が出る確率は、どれも同じく\(1/6\)ですよね。これをグラフにすると、こんな感じです。
この単純なグラフも、立派な確率分布の一つです。どの目も同じ確率で出るので、平らな形をしていますね。
そして、この確率分布には大きく分けて2つのタイプがあります。これが「離散型」と「連続型」です。
- 離散型確率分布: サイコロの目のように、値が飛び飛びで数えられるもの(1, 2, 3…)。例えば、1日に救急外来に来る患者さんの数や、ある薬を10人に投与したときに副作用が出た人数などがこれにあたります。カレンダーの日付のように、一つひとつが独立しているイメージです。
- 連続型確率分布: 身長や体重、血圧のように、値が連続していてどこまでも細かく測定できるもの。170cmと171cmの間には170.5cmや170.51cm…と無限の値が存在しますよね。温度計の目盛りのように、値が滑らかにつながっているイメージです。
この2つのタイプを頭の片隅に置きながら、いよいよ3人のヒーローたちの登場です!
“普通”の形、正規分布 – 自然界の王道モデル
まず最初に紹介したいのが、確率分布界のスーパースター、正規分布です。おそらく、皆さんも「ベルカーブ」という言葉で一度は耳にしたことがあるのではないでしょうか。
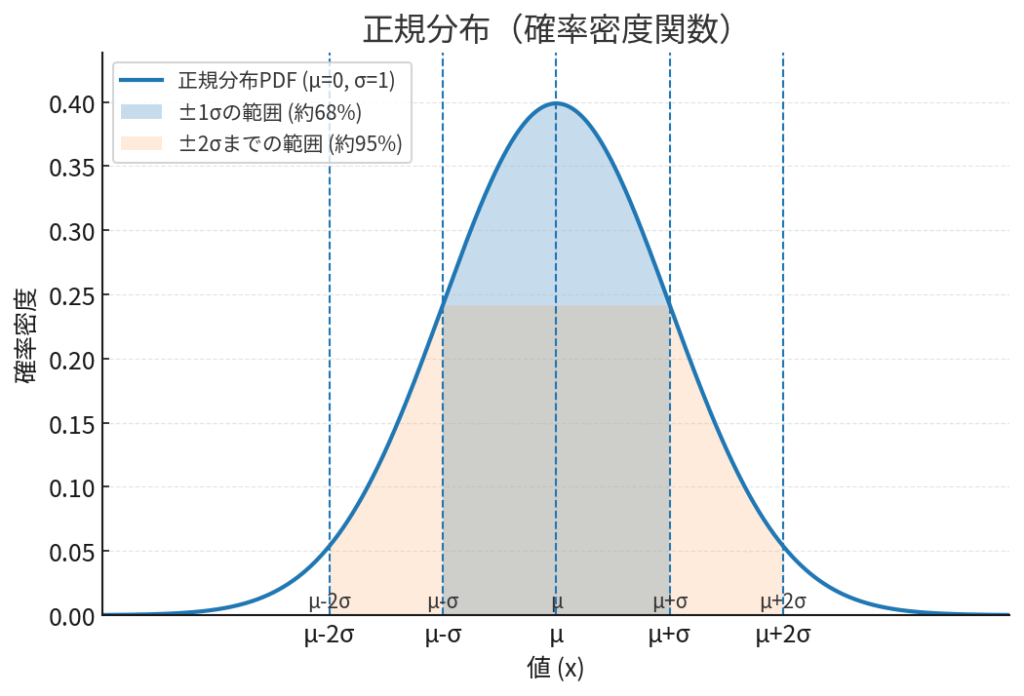
図の解説:これは正規分布の形を模式的に表したものです。左右対称の美しい「釣鐘(つりがね)型」をしているのが特徴です。横軸は身長や検査値などのデータの値(x)を、縦軸はその値が発生する確率の高さ(確率密度)を示します。山の中心が最も確率が高く、これがデータの平均(\(\mu\))にあたります。そして、山のなだらかさ(広がり具合)は、データのばらつきを示す標準偏差(\(\sigma\))によって決まります。
この正規分布、何がすごいかというと、世の中の多くの現象が、なぜかこの美しい左右対称の釣鐘型に従うんです。例えば、たくさんの人の身長を測ってグラフにすると、平均身長のあたりが一番高くなり、平均から離れるにつれてなだらかに低くなっていく、まさにこの形になります。日本人の成人男性の身長データなども、厚生労働省の国民健康・栄養調査で見てみると、きれいな正規分布に近い形をしています(厚生労働省, 2019)。
まるで、自然界が「だいたい平均あたりに集まるのが普通だよね」と決めているかのようです。この「普通」や「平均」をモデル化するのに、正規分布は絶大な力を発揮します。
正規分布の正体を探る:2つのパラメータ
この正規分布の形を決めているのは、たった2つの要素です。
- 平均 (\(\mu\)): グラフの山の中心がどこにあるかを決めます。平均身長が高ければ、山の中心は右にずれます。
- 標準偏差 (\(\sigma\)): データのばらつき具合、つまり山の広がり方を決めます。みんなの身長が似たり寄ったりなら、山は細く尖った形に(標準偏差が小さい)。身長差が大きければ、山はなだらかで幅広の形になります(標準偏差が大きい)。
ちょっとだけ数式をのぞいてみよう
ここで、正規分布の確率密度関数、つまり設計図の本体を見てみましょう。一見すると複雑に見えるかもしれませんが、アレルギーを起こさないでくださいね!
\[ f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]
大丈夫、一つひとつのパーツの意味がわかれば怖くありません。
- \((x-\mu)^2\): これは、あるデータ(x)が平均(\(\mu\))からどれだけ離れているかの「距離」を表しています。中心から離れれば離れるほど、この値は大きくなります。
- \(e^{-\dots}\): これは指数関数というもので、肩に乗っている数字がマイナスで大きくなるほど、値が急激に0に近づく性質があります。つまり、「平均から離れるほど、その値をとる確率は急激に低くなる」という釣鐘の形を作っている張本人です。
- \(\frac{1}{\sqrt{2\pi\sigma^2}}\): 前についているこの部分は、グラフ全体の面積がちょうど「1」になるように調整するための係数です。確率の世界では、すべての可能性を足し合わせると1(=100%)になる、というルールがあるので、その帳尻を合わせるための「おまじない」だと思ってください。
要するにこの数式は、「平均 (\(\mu\)) を中心に、標準偏差 (\(\sigma\)) の幅でばらついている釣鐘型の分布」を数学の言葉で表現したものなんですね。
医療現場での活躍
正規分布は、検査の基準値を設ける際に非常によく使われます。例えば、健康な人のある検査値のデータを集めたとき、その分布が正規分布に従うと仮定できれば、「平均 ± 2標準偏差」の範囲に約95%の人が含まれる、という性質を使えます。この範囲から外れた値が出た場合、「もしかしたら何か異常があるかもしれない」と考える一つのきっかけになるわけです。
“Yes/No”の世界、二項分布 – 成功か失敗かの物語
次に登場するのは、二項分布です。こちらは、結果が2つしかない試行(成功か失敗か、YesかNoか、陽性か陰性か)を、決まった回数だけ繰り返したときに、「成功する回数」がどのくらいの確率で起こるかを示す分布です。
たとえ話で考えてみましょう。ある薬の有効率が80%だとします。この薬を新しく10人の患者さんに投与したとき、「8人に効く」確率はどのくらいでしょうか?あるいは、「全員に効く」確率は?はたまた「5人にしか効かない」確率は…?
こんなシナリオを考えるときに活躍するのが二項分布です。
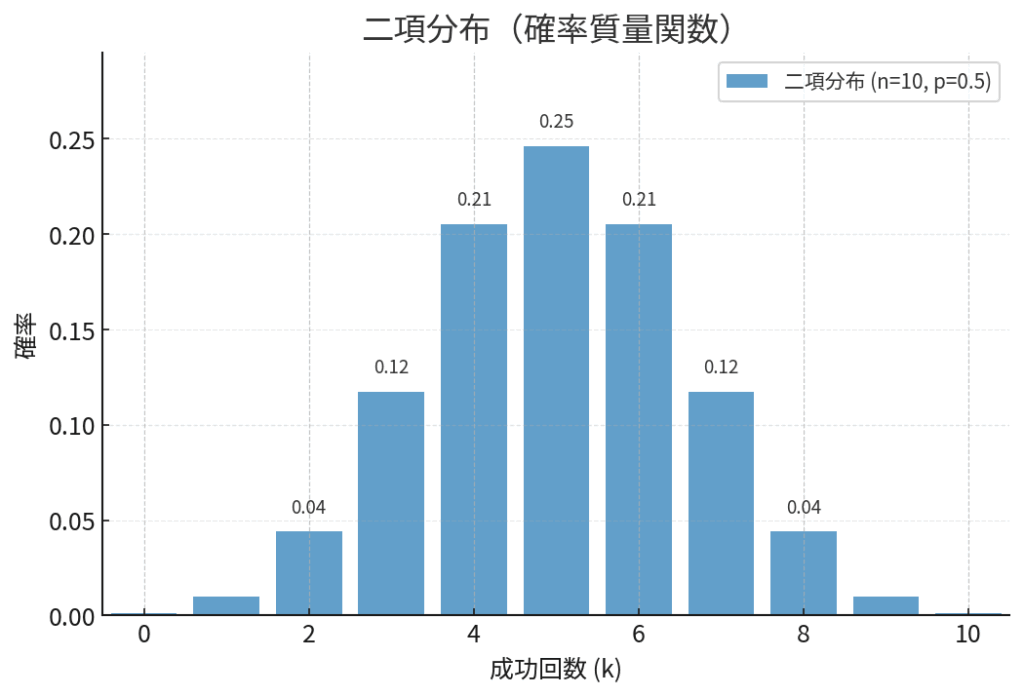
二項分布の正体を探る:2つのパラメータ
二項分布の形は、以下の2つの要素で決まります。
- 試行回数 (\(n\)): 何回その試行を繰り返すか。先ほどの例では、患者さんの数「10人」がこれにあたります。
- 成功確率 (\(p\)): 1回あたりの試行で成功する確率。例では、薬の有効率「80%(0.8)」です。
数式で仕組みを理解しよう
では、10人(\(n=10\))の患者さんに有効率80%(\(p=0.8\))の薬を投与して、8人(\(k=8\))に効果が現れる確率を計算する式を見てみましょう。
\[ P(X=k) = \binom{n}{k} p^k (1-p)^{n-k} \]
これもパーツに分解してみます。
- \(p^k\): これは、\(k\) 回成功する確率です。例では \(0.8^8\) となり、8人に連続で薬が効く確率を表します。
- \((1-p)^{n-k}\): こちらは、残りの \(n-k\) 回が失敗する確率です。\(p\)が成功確率なので、\(1-p\)は失敗確率(例では20%)になります。例では \(0.2^2\) となり、2人に薬が効かなかった確率を指します。
- \(\binom{n}{k}\): これが一番大事なポイントです。「コンビネーション」と呼ばれる記号で、「\(n\) 回中、どの \(k\) 回で成功するか」の組み合わせの数を表します。例えば、「10人のうち8人に効く」と言っても、AさんとBさんに効かないパターン、CさんとDさんに効かないパターン…など、色々な組み合わせがありますよね。その全パターン数を計算しているのがこの部分です。
つまりこの数式は、「特定の成功パターンの確率」×「そのパターンが何通りあるか」を計算しているわけですね。非常に合理的だと思いませんか?
医療現場での活躍
二項分布は、新しい治療法や薬の臨床試験(治験)で非常に重要です。例えば、「新しい薬は、既存の薬よりも有意に有効率が高いか?」を統計的に判断する際に、二項分布の考え方がベースになります。副作用の発生率を比較するときなどにも応用できます。
“まれ”な出来事の専門家、ポアソン分布 – いつ起こるかわからないイベントのモデル
最後のヒーローは、ポアソン分布です。この分布は、「一定の期間や空間の中で、平均して起こる回数はわかっているけれど、いつ起こるかはランダムな、比較的まれな事象」の発生回数をモデル化するのに使われます。
たとえ話をしましょう。ある病院の救急外来には、平均して「1時間に5人」の患者さんが来るとします。では、次の1時間にピッタリ「7人」の患者さんが来る確率はどのくらいでしょうか?あるいは、不運にも「10人」も来てしまう確率は?逆に、平和で「1人も来ない」確率は…?
このような、「いつ鳴るかわからない電話」のようなランダムなイベントの回数を予測するのが、ポアソン分布の得意技です。
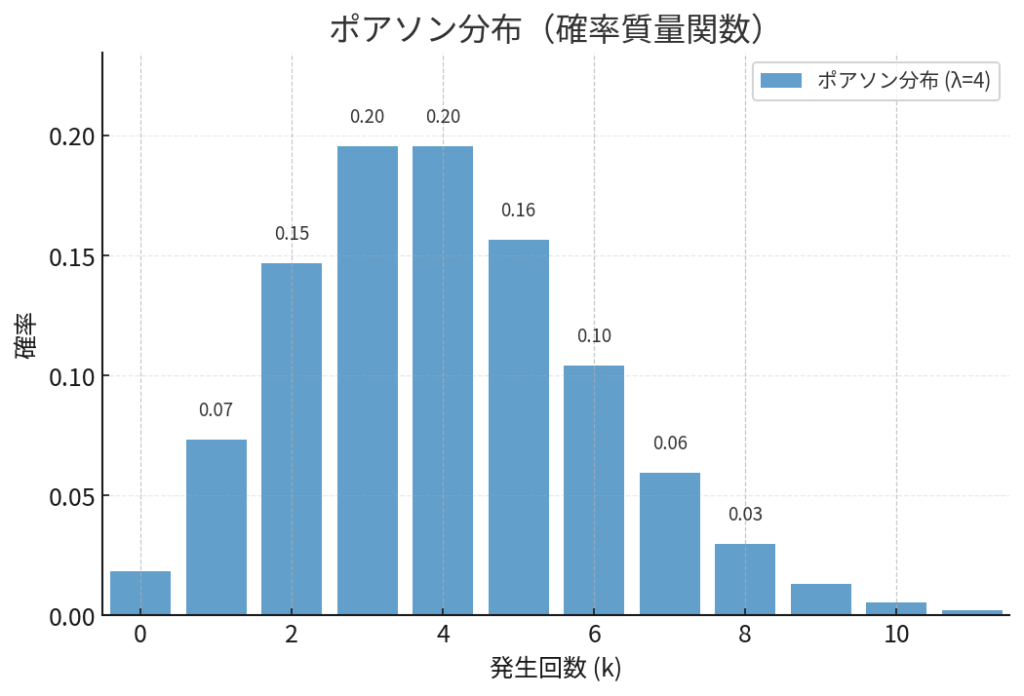
ポアソン分布の正体を探る:たった1つのパラメータ
驚くことに、ポアソン分布の形を決めるのは、たった1つの要素だけです。
- 平均発生回数 (\(\lambda\)): その期間(または空間)あたり、平均して何回その事象が起こるか。先ほどの例では、「1時間あたり5人」の「5」が \(\lambda\) (ラムダ) にあたります。
シンプルな数式に隠された意味
ポアソン分布の数式は、見た目も比較的シンプルです。
\[ P(X=k) = \frac{\lambda^k e^{-\lambda}}{k!} \]
分解してみましょう。
- \(\lambda^k\) と \(k!\): 平均 \(\lambda\) 回起こる場所で、実際に \(k\) 回起こる確率の計算に関わる部分です。
- \(e^{-\lambda}\): これは、その期間にイベントが「1回も起こらない」確率を表しています。実はポアソン分布の計算は、この「ゼロ回」の確率がベースになっている、と考えると少しイメージが湧きやすいかもしれません。
ちなみに、ポアソン分布は二項分布と親戚関係にあります。二項分布で、試行回数 \(n\) がものすごく多くて、成功確率 \(p\) がものすごく小さい(つまり「まれ」な事象)場合、その形はポアソン分布にそっくりになることが知られています。分布同士のつながりが見えると、なんだか面白いですよね。
医療現場での活躍
ポアソン分布は、疫学の分野でよく用いられます。例えば、特定の地域における希少疾患の年間発生患者数や、一定期間内での医療過誤の発生件数などをモデル化するのに適しています。また、放射線技師の方が扱う放射性物質の原子核が一定時間内に崩壊する数なども、ポアソン分布に従う典型的な例です。
まとめ:3つの分布、どう使い分ける?
さて、3人のヒーローたちの特徴を見てきましたが、ここで一度、彼らの得意なことと、医療現場での活躍の場を表にまとめてみましょう。
| 分布名 | どんな現象? | 形を決めるもの | 医療での応用例 |
|---|---|---|---|
| 正規分布 | 連続的な値の「普通のばらつき」 | 平均 (\(\mu\)), 標準偏差 (\(\sigma\)) | 身長、体重、血圧、検査値の基準値設定 |
| 二項分布 | Yes/Noの結果をn回繰り返した成功回数 | 試行回数 (\(n\)), 成功確率 (\(p\)) | 薬の有効性評価、手術の成功率の比較 |
| ポアソン分布 | まれなイベントの一定期間内の発生回数 | 平均発生回数 (\(\lambda\)) | 希少疾患の発生数、医療過誤の件数 |
これらの確率分布という「モデル」を使うことで、私たちは目の前で起きている現象が、単なる偶然の範囲内なのか、それとも何か特別な意味を持つ「異常」なのかを客観的に判断するための強力な武器を手に入れることができます。統計学というと難しく聞こえますが、その本質は、データを通じて現実の世界をより深く理解するための、非常にパワフルで面白いツールなのだと、私は思います。
次回は、これらの分布を使って、実際に「仮説検定」という考え方に入っていきたいと思います。どうぞお楽しみに!
参考文献
- 厚生労働省 (2019) 『令和元年 国民健康・栄養調査報告』. [オンライン] Available at: https://www.mhlw.go.jp/stf/seisakunitsuite/bunya/kenkou_iryou/kenkou/eiyou/r1-houkoku_00002.html (Accessed: 19 August 2025).
- Motulsky, H. (2018) Intuitive Biostatistics: A Nonmathematical Guide to Statistical Thinking. 4th ed. Oxford University Press.
- Zar, J.H. (2010) Biostatistical Analysis. 5th ed. Pearson Prentice-Hall.
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.