[Medical Data Science 100 : S3] 一目で伝わるグラフの魔法：MatplotlibとSeabornでデータを可視化しよう

---

毎日、私たちの周りには膨大なデータが溢れていますよね。特に医療現場では、電子カルテの記録、検査結果、研究データなど、まさに数字の洪水です。目の前にあるExcelシートやデータベースに並んだ数字の羅列を眺めながら、「このデータは、一体私たちに何を語りかけようとしているんだろう…？」と途方に暮れてしまった経験、ありませんか？

数字だけを睨んでいても、なかなかその中に隠された「物語」や「パターン」は見えてきません。それはまるで、びっしりと文字だけで書かれた分厚い医学書を読んでいるようなものかもしれません。もし、そこに図や写真があれば、理解度は格段に上がりますよね。

データの世界でも全く同じです。この数字の羅列を、一目で意味がわかる「絵」に変換する魔法、それが「データの可視化（Data Visualization）」です。そして今回は、Pythonという言語を使ってその魔法を唱えるための、二つの強力な「呪文体系」であるMatplotlibとSeabornというライブラリをご紹介します。この魔法を覚えれば、データは単なる数字の集まりから、示唆に富んだストーリーを語るパートナーに変わるはずです。

---

データ可視化の二大巨頭：MatplotlibとSeaborn

Pythonでグラフを描こうとすると、ほぼ間違いなくこの二つのライブラリの名前を目にすることになります。両者は似ているようで、実は得意なことやキャラクターが少し違います。料理に例えながら、その違いを覗いてみましょう。

Matplotlib：自由自在な“万能包丁”

Matplotlibは、データ可視化界の「万能包丁」のような存在です。野菜を刻む、肉を切る、魚をさばく…どんな要望にも応えてくれる基本の道具。つまり、折れ線グラフ、棒グラフ、散布図といった基本的なグラフはもちろん、非常に細かい部分までカスタマイズできる自由度の高さが魅力です。

• 長所： どんなグラフでも描ける柔軟性と、細かな調整が可能なカスタマイズ性の高さ。
• 少し大変なところ： 自由度が高い分、美しいグラフを仕上げるには、軸のラベル、タイトル、色、線の太さなど、一つひとつ手作業で指定してあげる必要があり、コードが少し長くなることがあります。

ほとんどの可視化ライブラリがMatplotlibを基礎（土台）にして作られていることからも、その重要性がわかると思います（Hunter, 2007）。まさに、Pythonにおけるデータ可視化の父のような存在ですね。

Seaborn：美しい“盛り付けアシスタント”

一方のSeabornは、Matplotlibという万能包丁を使って、誰でも手軽にプロ級の美しい料理を盛り付けられるようにしてくれる「盛り付けアシスタント」です。

Seabornの内部ではMatplotlibが動いているのですが、私たちが使う際には、より少ないコードで見栄えの良い、統計的な意味合いを込めたグラフをサッと作れるように設計されています（Waskom et al., 2021）。

• 長所： 美しいデフォルト設定と、少ないコードで統計的に洗練されたグラフ（例えば、回帰直線入りの散布図など）が描けること。
• 少し大変なところ： Matplotlibほど自由なカスタマイズは得意ではありません。ただ、Seabornで作ったグラフを、後からMatplotlibの機能で微調整することも可能です。

この二つの関係性を図にすると、こんなイメージでしょうか。

【図の解説】この図は、Pythonの可視化ライブラリの階層構造を示しています。土台には、描画の基本的な機能をすべて担うMatplotlibが存在します。その上に、Matplotlibの機能をより使いやすく、より美しく見せるためにSeabornが構築されています。初心者のうちはSeabornから始め、必要に応じてMatplotlibで微調整するという流れが、とてもスムーズでおすすめです。

---

まずはここから！基本のグラフでデータを“解剖”する

それでは、実際にこの魔法のツールを使って、データの中に何が隠れているのかを探ってみましょう。ここでは、全ての基本となる二つのグラフ、「ヒストグラム」と「散布図」を紹介します。

ヒストグラム：データの「分布」を丸裸に

手元に「100人の患者さんの年齢データ」があると想像してください。数字が100個並んでいても、「何歳くらいの人が多いのか？」「若者と高齢者、どちらに偏っているのか？」といった全体像は掴みにくいですよね。

そんな時に役立つのがヒストグラムです。ヒストグラムは、データをいくつかの区間（例えば「20代」「30代」「40代」…）に区切り、それぞれの区間に何人のデータが含まれているかを棒グラフで示したものです。いわば、データの「人口ピラミッド」のようなものですね。

これにより、私たちはデータの分布、つまり「どこにデータが集中していて、どこがスカスカなのか」を一目で把握できます。

【Pythonコード例】

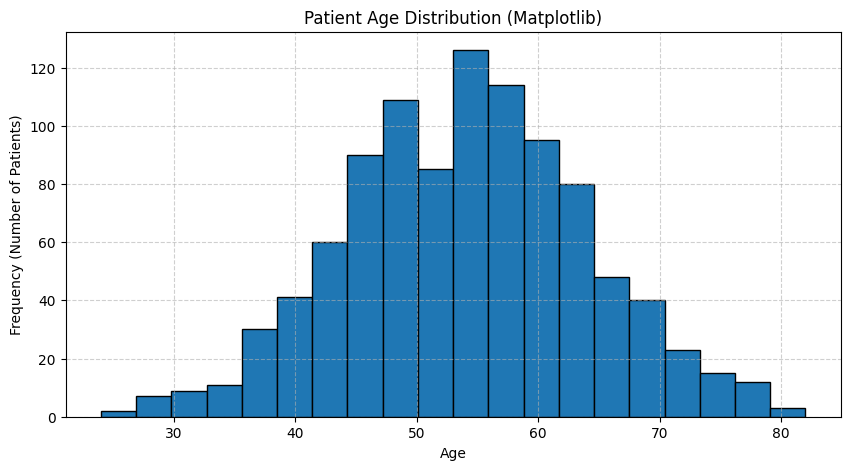
ここでは、平均年齢55歳、標準偏差10歳の正規分布に従う架空の患者1000人の年齢データを作成して、グラフを描いてみましょう。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# 架空の年齢データを生成
# np.random.seed(0) で乱数を固定し、いつでも同じデータが生成されるようにします
np.random.seed(0) 
# 平均(loc)55、標準偏差(scale)10の正規分布に従う乱数を1000個生成します
age_data = np.random.normal(loc=55, scale=10, size=1000)
# 生成されたデータを整数に変換します
age_data = age_data.astype(int) 

# --- Matplotlibで描画 ---
# グラフの描画領域のサイズを横10インチ, 縦5インチに設定します
plt.figure(figsize=(10, 5)) 
# ヒストグラムを描画します。binsは棒の数、edgecolorは棒の枠線の色です
plt.hist(age_data, bins=20, edgecolor='black')
# グラフのタイトルを設定します
plt.title('Patient Age Distribution (Matplotlib)')
# x軸のラベルを設定します
plt.xlabel('Age')
# y軸のラベルを設定します
plt.ylabel('Frequency (Number of Patients)')
# グリッド（補助線）を表示します。点線(--)で、透明度(alpha)を0.6に設定します
plt.grid(True, linestyle='--', alpha=0.6)
# グラフを表示します
plt.show()

# --- Seabornで描画 ---
# 新しい描画領域を準備します
plt.figure(figsize=(10, 5)) 
# Seabornのヒストグラムを描画します。kde=Trueでカーネル密度推定の曲線も同時に描画します
sns.histplot(age_data, bins=20, kde=True) 
# グラフのタイトルを設定します
plt.title('Patient Age Distribution (Seaborn)')
# x軸のラベルを設定します
plt.xlabel('Age')
# y軸のラベルを設定します
plt.ylabel('Frequency (Number of Patients)')
# グリッドを表示します
plt.grid(True, linestyle='--', alpha=0.6)
# グラフを表示します
plt.show()

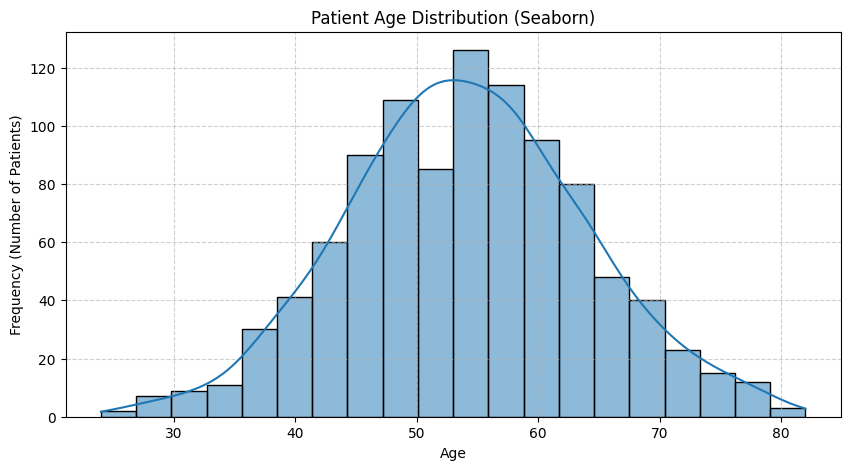
どうでしょうか？どちらのグラフも、55歳あたりをピークにした山なりの形をしているのが一目でわかります。Seabornの方が、デフォルトの色合いが洗練されていて、`kde=True`と一行加えるだけで滑らかな曲線（カーネル密度推定）も描画してくれるので、よりデータの形が掴みやすいかもしれませんね。

散布図：二つのデータの「関係性」を探る

次に、「患者さんの年齢と、収縮期血圧の間には何か関係があるだろうか？」という疑問が湧いたとします。これを調べるのに最適なのが散布図です。

散布図は、横軸と縦軸にそれぞれ異なるデータ（今回は年齢と血圧）を取り、一人ひとりの患者さんを一つの点としてプロットしたグラフです。点が右肩上がりに集まっていれば「正の相関」（年齢が上がると血圧も上がる傾向）、右肩下がりなら「負の相関」、全体にバラバラなら「無相関」といった関係性が見えてきます。

【Pythonコード例】

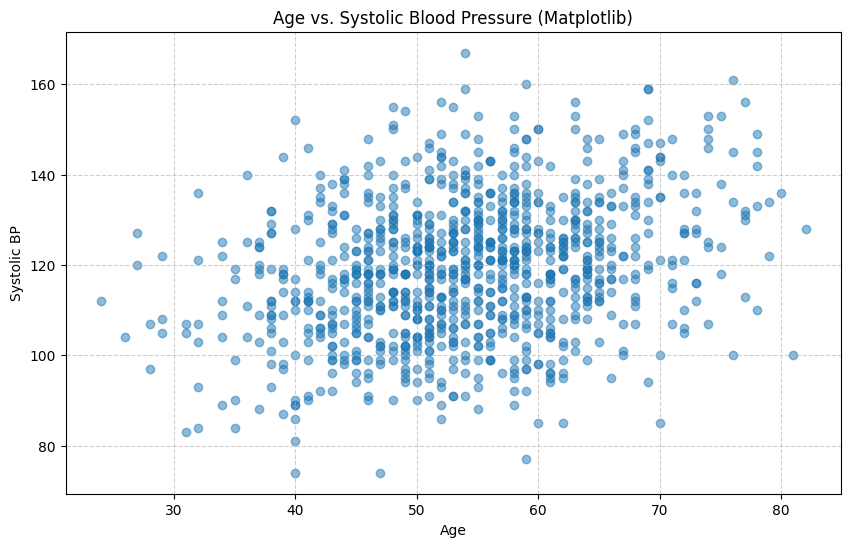
先ほどの年齢データに加えて、架空の血圧データを作成してみましょう。ここでは、年齢が少し高いほど血圧も少し高くなる、という弱い相関を持たせてみます。

import pandas as pd

# 架空の血圧データを生成（年齢と少し相関を持たせる）
# 平均0, 標準偏差15の正規分布に従うノイズを生成します
noise = np.random.normal(0, 15, 1000) 
# 基本血圧120に、年齢に応じた変動(0.5 * (age_data - 55))とノイズを加えます
systolic_bp = 120 + 0.5 * (age_data - 55) + noise
# 血圧データを整数に変換します
systolic_bp = systolic_bp.astype(int)

# データをpandasのDataFrameという表形式にまとめます
df = pd.DataFrame({'age': age_data, 'systolic_bp': systolic_bp})

# --- Matplotlibで描画 ---
# 描画領域のサイズを横10インチ、縦6インチに設定します
plt.figure(figsize=(10, 6))
# 散布図を描画します。x軸に年齢、y軸に血圧をプロットします。alphaは点の透明度です
plt.scatter(df['age'], df['systolic_bp'], alpha=0.5)
# グラフのタイトルを設定します
plt.title('Age vs. Systolic Blood Pressure (Matplotlib)')
# x軸のラベルを設定します
plt.xlabel('Age')
# y軸のラベルを設定します
plt.ylabel('Systolic BP')
# グリッドを表示します
plt.grid(True, linestyle='--', alpha=0.6)
# グラフを表示します
plt.show()

# --- Seabornで描画 ---
# 新しい描画領域を準備します
plt.figure(figsize=(10, 6))
# Seabornの散布図を描画します。x軸, y軸, 使用するデータを指定します
sns.scatterplot(x='age', y='systolic_bp', data=df, alpha=0.5)
# グラフのタイトルを設定します
plt.title('Age vs. Systolic Blood Pressure (Seaborn)')
# グリッドを表示します
plt.grid(True, linestyle='--', alpha=0.6)
# グラフを表示します
plt.show()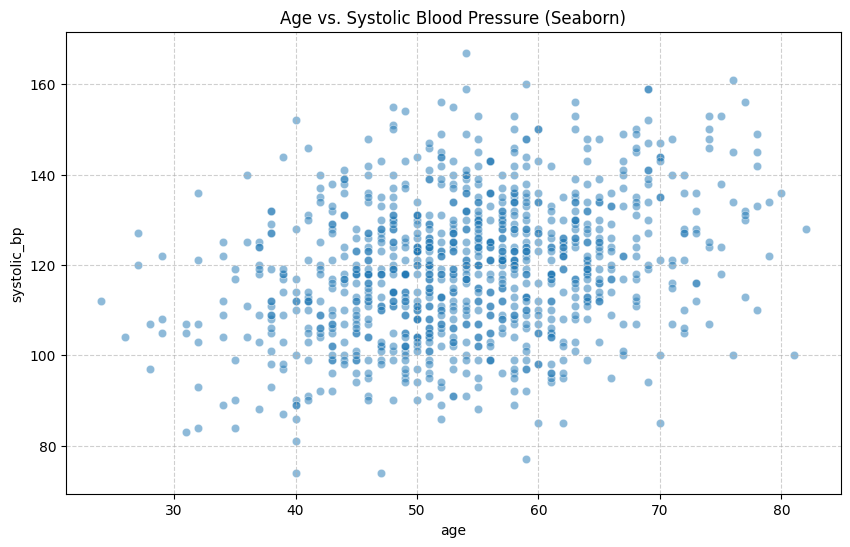

# Seabornなら回帰直線も簡単に追加できる
# 新しい描画領域を準備します
plt.figure(figsize=(10, 6))
# 回帰直線付きの散布図を描画します。scatter_kwsで散布図の点の見た目を調整できます
sns.regplot(x='age', y='systolic_bp', data=df, scatter_kws={'alpha':0.3})
# グラフのタイトルを設定します
plt.title('Age vs. Systolic Blood Pressure with Regression Line (Seaborn)')
# グリッドを表示します
plt.grid(True, linestyle='--', alpha=0.6)
# グラフを表示します
plt.show()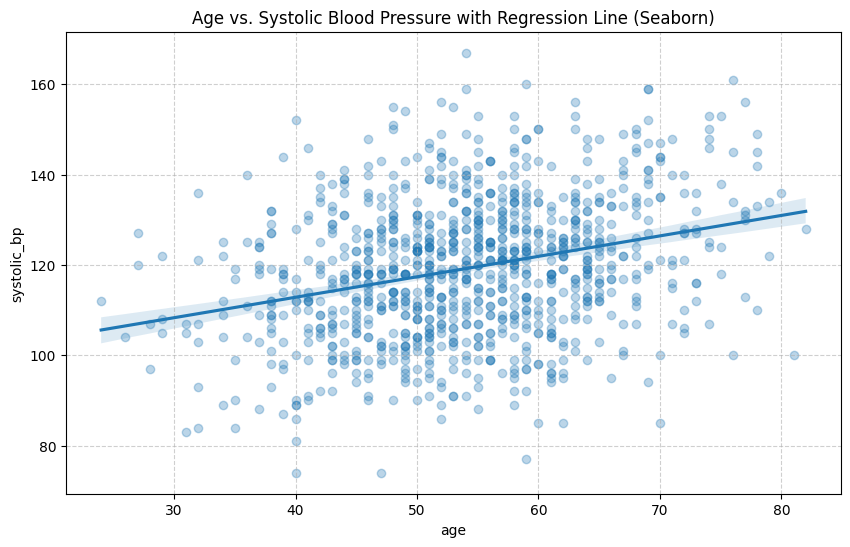

散布図を描くと、なんとなく全体が右肩上がりになっている傾向が見て取れますね。特にSeabornの`regplot`を使うと、この傾向を示す回帰直線と、その信頼区間（薄い色の帯）まで自動で描画してくれます。これは非常に強力で、「二つのデータの間に関係がありそうだ」という仮説を視覚的に裏付けてくれます。

---

探索的データ分析（EDA）：データとの対話を始めよう

さて、ここまでで私たちは、MatplotlibとSeabornという強力な魔法の杖を手に入れました。でも、本当に大切なのはここからです。これらのツールを使って、一体何をすべきなのでしょうか？

分析というと、すぐに難しい統計モデルを組んだり、AIに予測させたりすることをイメージするかもしれません。しかし、熟練の医師が患者さんを診察する時、いきなり高度な検査を指示するのではなく、まずは問診や聴診、触診で全体像を把握しようとしますよね。データ分析も全く同じで、この「初期診察」にあたるステップが、探索的データ分析（Exploratory Data Analysis, EDA）なんです。

今回私たちが行ったように、手元にあるデータに対して様々なグラフを描きながら、「このデータはどんな特徴を持っているんだろう？」「変数同士に面白い関係はないかな？」と、仮説を立てずにデータを多角的に“探検”していくアプローチ。これがEDAの神髄です。

なぜ私たちはデータを“探検”する必要があるのか？

「いきなり分析を始めた方が早いのでは？」と感じるかもしれません。その気持ち、とてもよく分かります。ですが、EDAというステップを飛ばしてしまうと、時にデータが仕掛けた巧妙な「罠」にはまってしまうことがあるんです。

この危険性を示す、統計学の世界では非常に有名な例があります。それが、統計学者フランシス・アンスコムが1973年に提示した「アンスコムのカルテット」です（Anscombe, 1973）。

ここに、4つの異なるデータセットがあります。これらのデータ、実は平均、分散、相関係数といった基本的な統計量は、小数点第2位までほぼピッタリ同じなんです。数字だけを見れば、これらは「そっくりなデータ」に見えるはずです。

ですが、これらを散布図にして可視化してみると…どうでしょう？

驚いたことに、これらは全く異なる物語を持ったデータだったのです。Iは綺麗な右肩上がりの関係、IIは綺麗なカーブ、IIIはほぼ直線ですが一つだけ外れ値が、IVはほとんどが垂直に並んでいますが、一つだけ離れた点が全体の傾向を無理やり引っ張っています。

もし私たちが可視化を怠り、統計量だけを信じて「これらのデータは同じようなものだ」と結論づけていたら、全く見当違いの分析を進めてしまうことになります。EDAは、こうしたデータの“素顔”を見抜き、私たちが正しい道を進むための羅針盤となってくれる、不可欠なステップなのです。

名探偵の捜査手法：EDAの具体的なステップ

では、具体的にEDAでは何をすればよいのでしょうか？これは、名探偵が事件現場で行う捜査によく似ています。一つひとつの証拠を丁寧に観察し、全体の状況を把握していくのです。私が普段データを触るときに意識している、基本的な捜査手順をご紹介します。

捜査ステップ	探偵の行動（たとえ話）	具体的なアクション	主な使用ツール
1. プロフィール確認	関係者のリストを見て、人数や年齢層など、基本的な情報を把握する。	データの行数・列数、各列のデータ型、要約統計量（平均、中央値、標準偏差、最小値、最大値など）を確認する。	.info(), .describe()
2. 欠席者の捜索	聞き込みのリストに、情報が抜けている（欠席している）人がいないかチェックする。	各列に欠損値（データ抜け）がどれくらいあるかを確認し、その原因や対処法を検討する。	.isnull().sum()
3. 不審人物の特定	関係者の中に、極端に怪しい言動をする人物（外れ値）がいないかを探す。	箱ひげ図や散布図を使い、他のデータから大きく外れた値がないかを確認する。入力ミスや測定エラーの可能性も考える。	箱ひげ図 (sns.boxplot)
4. 個々の人物観察	一人ひとりの性格や特徴（分布）を深く知るために、じっくりと観察する。	ヒストグラムや密度プロットを描き、各変数がどのような分布をしているか（正規分布か、偏りがあるかなど）を把握する。	ヒストグラム (sns.histplot)
5. 関係性の調査	人物相関図を作成し、誰と誰が仲が良いか、険悪かといった関係性を探る。	散布図や相関ヒートマップを使い、変数同士の間にどのような関係（正の相関、負の相関など）があるかを探る。	散布図 (sns.scatterplot), ヒートマップ (sns.heatmap)

これらのステップを順番に、あるいは行ったり来たりしながら進めることで、データへの理解は飛躍的に深まります。大切なのは、「答え」を急いで見つけようとしないこと。むしろ、次から次へと湧き上がる「疑問」を楽しむことだと思います。

テューキーの哲学：「グラフは、問いを立てるためにある」

このEDAという概念を提唱した統計学者のジョン・テューキーは、データ分析を大きく二つに分けました。それが「探索的データ分析(EDA)」と「検証的データ分析(CDA)」です（Tukey, 1977）。

【図の解説】この図は、データ分析の2つのフェーズを示しています。左側のEDAは、まるで森の中を探検するように、データの中に何があるかを発見し、面白い「問い」や「仮説」を見つけ出す創造的なプロセスです。ここで得られた仮説を、右側のCDA（私たちがよく知る仮説検定など）のステージに持ち込み、それが統計的に正しいかどうかを厳密にジャッジします。多くの場合、私たちはCDAばかりを学びがちですが、質の高いCDAは、質の高いEDAがあって初めて可能になるのです。

テューキーが伝えたかったのは、「データ分析は、まずグラフを描くことから始まる」という非常にシンプルかつパワフルな思想でした。彼にとってグラフは、綺麗なレポートを作るための「清書」道具ではなく、データと対話し、まだ誰も気づいていないような鋭い「問い」を立てるための「思考」の道具だったのです（Mosteller & Tukey, 1977）。

データ分析も同じで、最初にヒストグラムや散布図でデータをじっくり観察することで、データクリーニングの方針を立てたり、後の高度な分析に繋がる重要なインサイト（洞察）を得たりすることができます。そして、その最強の武器が、今回学んだ「可視化」なのです。

---

まとめ：グラフは、データが語りかける言葉

今回は、データという無口な語り部に口を開かせるための魔法、MatplotlibとSeabornを使ったデータ可視化の基本をご紹介しました。

• 数字の羅列からパターンを見つけるには、可視化が不可欠。
• Matplotlibは自由自在な「万能包丁」、Seabornは手軽で美しい「盛り付けアシスタント」。
• ヒストグラムでデータの「分布」を、散布図で変数間の「関係性」を掴む。
• これらの可視化手法は、探索的データ分析（EDA）という、データと対話するための重要な第一歩。

最初はコードを書くことに少し戸惑うかもしれません。でも、心配はいりません。これらのツールは、私たちがデータをより深く、そして直感的に理解するための強力なサポーターです。ぜひ、ご自身の身の回りにあるデータで、今日学んだグラフを描いてみてください。きっと、今まで見えていなかったデータの「声」が、グラフを通して聞こえてくるはずですよ。

---

参考文献

• Hunter, J. D. (2007). Matplotlib: A 2D graphics environment. Computing in Science & Engineering, 9(3), pp. 90-95.
• McKinney, W. (2017). Python for Data Analysis: Data Wrangling with Pandas, NumPy, and IPython. 2nd ed. O’Reilly Media, Inc.
• Tufte, E. R. (2001). The Visual Display of Quantitative Information. 2nd ed. Graphics Press.
• Tukey, J. W. (1977). Exploratory Data Analysis. Addison-Wesley Publishing Company.
• Waskom, M. L. (2021). Seaborn: statistical data visualization. Journal of Open Source Software, 6(60), 3021.
• Anscombe, F. J. (1973). Graphs in Statistical Analysis. The American Statistician, 27(1), pp. 17-21.
• Mosteller, F. and Tukey, J. W. (1977). Data Analysis and Regression: A Second Course in Statistics. Addison-Wesley Publishing Company.

---

ご利用規約（免責事項）

当サイト（以下「本サイト」といいます）をご利用になる前に、本ご利用規約（以下「本規約」といいます）をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。

第1条（目的と情報の性質）

1. 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
2. 本サイトで提供されるすべてのコンテンツ（文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません）は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為（以下「医行為等」といいます）を提供するものではありません。
3. 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
4. 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。

第2条（法令等の遵守）
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律（薬機法）、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。

第3条（医療行為における責任）

1. 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
2. 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家（医師、歯科医師等）が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
3. 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。

第4条（情報の正確性・完全性・有用性）

1. 本サイトは、掲載する情報（数値、事例、ソースコード、ライブラリのバージョン等）の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
2. 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。

第5条（AI生成コンテンツに関する注意事項）
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション（事実に基づかない情報の生成）やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。

第6条（知的財産権）

1. 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
2. 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。

第7条（プライバシー・倫理）
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。

第8条（利用環境）
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境（OS、ハードウェア、依存パッケージ等）を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。

第9条（免責事項）

1. 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害（直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません）について、その原因の如何を問わず、一切の法的責任を負わないものとします。
2. 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
3. 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
4. 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。

第10条（規約の変更）
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。

第11条（準拠法および合意管轄）
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。

---

For J³, may joy follow you.