医療現場の時系列データ(心電図、バイタルサイン等)の分析に強力なLSTMの基本を解説します。単純なRNNの限界を克服する「ゲート機構」とPyTorchでの実装方法、そして疾患予測など未来の応用までを網羅的に学びます。
単純なAI (RNN) が苦手な「長期記憶」を、「ゲート機構」と「セル状態」で克服。情報の「記憶」「忘却」「出力」を自動で制御し、心電図などの時系列データに潜む重要なパターンを捉えます。
1. データ準備: 時系列データを入力シーケンスとターゲットに変換。
2. モデル構築: `nn.LSTM` と `nn.Linear` 層を組み合わせてモデルを定義。
3. 学習と評価: MSE損失関数とAdamオプティマイザで訓練し、RMSEで精度を評価します。
心不全や敗血症の早期予測、糖尿病患者の血糖値管理、リハビリ支援など応用は多岐にわたります。データの質、プライバシー保護、AIの解釈可能性(XAI)といった課題の克服も重要です。
図を読み込んでいます…
はじめに
この章では、時間の流れと共に記録されるデータ、いわゆる「時系列データ」を扱う上で、現在非常に注目されている「LSTM(Long Short-Term Memory)」という、ちょっと賢いニューラルネットワークの仕組みについて、一緒に学んでいきたいと思います。特に、医療の世界にいらっしゃる皆さんが日々向き合っている、心電図(ECG)や脳波(EEG)の波形、血糖値の変動、あるいは患者さんのバイタルサイン(心拍数、血圧、体温など)といった、刻一刻と変化する貴重なデータたち。これらはまさに、時系列データの宝庫と言えるでしょう。
もし、これらの連続的なデータの中に潜むパターンを巧みに捉え、未来を予測したり、異常の兆候を早期に検知したりできるとしたら…。それは、病気のより早い段階での発見、患者さん一人ひとりに合わせた治療法の最適化、ひいては個別化医療の実現といった、医療の質を大きく飛躍させる夢のような話につながるかもしれません。大げさではなく、LSTMはそのような可能性を秘めた技術の一つだと、私は感じています。
この章を特にお届けしたいのは、日々患者さんと向き合う医師の方々や、新しい治療法や診断技術を追求する医学研究者の方々です。AI、特に深層学習という言葉を耳にする機会が増え、「自分の研究や臨床の現場でも、この新しいツールをPythonを使って活かせないだろうか?」と、そんな風に考えていらっしゃる初学者の方も多いのではないでしょうか。これまでの章で、Pythonの基本的な使い方やニューラルネットワークの考え方、そしてPyTorchという便利な道具(フレームワーク)の初歩には触れてこられたかと思います。この章では、その知識を土台にして、LSTMがどのような理屈で動いているのか、そしてPyTorchを使って実際にどのようにプログラムとして形にしていくのかを、じっくりと解き明かしていきます。最終的には、皆さんがお手元の(あるいは、これから手にするかもしれない)簡単な医療時系列データを使って、ご自身でLSTMモデルを作り、学習させ、その性能を確かめる、そこまでご一緒できれば嬉しいです。
さて、時系列データを扱うニューラルネットワークとして、もしかしたら「RNN(Recurrent Neural Network)」(前の章で解説)という名前をどこかで耳にされたことがあるかもしれませんね。RNNは、過去の情報を記憶することで、時間の流れに沿ったパターンを学習しようとする、基本的な仕組みを持っています。例えば、今日のデータだけでなく、昨日のデータ、一昨日のデータも考慮して何かを予測する、といった具合です。
ただ、このRNN、実はちょっとした弱点があったんです。それは「長期依存性の消失」と呼ばれる問題で、平たく言うと、時間が長く経つにつれて、遠い過去の重要な情報(例えば、数週間前のちょっとした体調の変化が、実は今の状態を理解する上で非常に大切な手がかりだった、といったケース)を、だんだん忘れてしまう傾向があったんですね。まるで、記憶の糸が途中でプツンと切れてしまうようなイメージでしょうか。これでは、長期的な視点での分析や予測が難しくなってしまいます。
そこで脚光を浴びたのが、今回の主役であるLSTMです。LSTMは、このRNNの「忘れっぽい」という性質をうまくカバーするために、いくつかの巧妙な「記憶の仕掛け」を備えた、より洗練されたアーキテクチャとして生まれました。
この章を通じて、LSTMがどのようにして「長期記憶」と「短期記憶」を使い分け、過去の重要な情報をしっかりと保持し続けることができるのか、その秘密に迫ります。そして、その力が医療現場の様々な時系列データ分析にどのような変革をもたらしうるのか、具体的なPythonコードを動かしながら、皆さんと一緒にその可能性を探求していく旅に出かけたいと思います。どうぞ、リラックスして、知的好奇心をエンジンに、最後までお付き合いください。
1. RNNの限界とLSTMの登場
1. RNNの限界とLSTMの登場
さて、いよいよ本題のLSTMに近づいてきましたが、その前に、なぜLSTMのような仕組みが必要になったのか、その背景を少し掘り下げてみましょう。話は、LSTMの先輩にあたる前の章で扱った「RNN(Recurrent Neural Network)」から始まります。

1.1 単純なRNNとその課題:長期依存性の消失
RNN、日本語では再帰型ニューラルネットワークと呼ばれるこのモデルは、時系列データ、つまり時間の流れに沿って変化していくデータを扱うために考案されました。音声や文章、そしてこのコースのテーマである医療の時系列データ(例えば、心電図の波形や日々のバイタルサインなど)のように、一つ前のデータが次のデータに何かしら影響を与えるような連続的な情報のパターンを学習するのが得意なんです。
その秘密は、ネットワークの内部に「ループ構造」を持つ点にあります。ちょっと図でイメージしてみましょうか。
テキストベースの図
時刻 t-1 時刻 t 時刻 t+1
入力: x_{t-1} 入力: x_t 入力: x_{t+1}
↓ ↓ ↓
+---------+ +---------+ +---------+
| RNN | 隠れ状態 | RNN | 隠れ状態 | RNN |
| ユニット | ----------------> | ユニット | ---------------> | ユニット |
| h_{t-1} | | h_t | | h_{t+1} |
+---------+ +---------+ +---------+
↓ ↓ ↓
出力: y_{t-1} 出力: y_t 出力: y_{t+1}
(オプション) (オプション) (オプション)この図は、RNNが各時刻でどのように情報を処理しているかを模式的に表しています。
- \(x_t\) : 時刻 \(t\) での入力データです。医療の例で言えば、ある瞬間の心拍数や血糖値などがこれにあたります。
- \(h_t\) : 時刻 \(t\) での「隠れ状態(hidden state)」と呼ばれるものです。これがRNNの「記憶」の役割を果たします。\(h_t\) は、一つ前の時刻の隠れ状態 \(h_{t-1}\) と、現在の入力 \(x_t\) の両方から影響を受けて計算されます。つまり、過去の情報(\(h_{t-1}\) 経由)と現在の情報(\(x_t\))をミックスして、今の「文脈」を理解しようとするわけですね。
- \(y_t\) : 時刻 \(t\) での出力です。これはタスクによって異なり、例えば次の値を予測したり、現在の状態を分類したりします。必ずしも各時刻で出力が必要なわけではありません。
もう少し具体的に、隠れ状態 \(h_t\) と出力 \(y_t\) がどう計算されるか見てみましょう。数式が出てきますが、何をしているかを掴んでいただければ大丈夫です。
隠れ状態の更新は、だいたいこんな感じです:
\[ h_t = \tanh(W_{hh}h_{t-1} + W_{xh}x_t + b_h) \]
そして、出力はこんなふうに計算されます(出力がある場合):
\[ y_t = W_{hy}h_t + b_y \]
ここで出てくる記号を少し解説しますね。
- \(W_{hh}\), \(W_{xh}\), \(W_{hy}\): これらは「重み行列(Weight matrix)」と呼ばれるもので、ニューラルネットワークが学習するパラメータです。入力や前の隠れ状態が、次の隠れ状態や出力にどれだけ影響を与えるかの「さじ加減」を調整します。
- \(b_h\), \(b_y\): これらは「バイアス項(Bias term)」で、これも学習パラメータです。出力の底上げのような役割をします。
- \(\tanh\): これは「ハイパボリックタンジェント関数」という活性化関数の一つです。入力された値をだいたい-1から1の間にぎゅっと押し込める働きをします。これにより、ネットワークの表現力が増すと考えられています。
行列計算のイメージも少しだけ。例えば、\(W_{xh}x_t\) というのは、入力 \(x_t\)(例えば、ある時刻のバイタルサインのベクトル)に重み行列 \(W_{xh}\) を掛けて、隠れ状態の次元に変換する操作です。
テキストベースの図
入力ベクトル x_t (input_dim × 1)
│
│ 重み行列 W_xh (hidden_dim × input_dim)
│ ┌───┬───┬───┐
▼ │ w │ w │ w │
┌───────┐ ├───┼───┼───┤
│ x_t_1 │ │ w │ w │ w │ ─▶ 行列積の結果
│ x_t_2 │ × ├───┼───┼───┤ (hidden_dim × 1)
│ ... │ │ w │ w │ w │
└───────┘ └───┴───┴───┘
こんな感じで、入力情報が重みによって変換され、前の隠れ状態 \(h_{t-1}\) (これも同様に重み \(W_{hh}\) で変換されます)と足し合わされ、最後に \(\tanh\) 関数を通って新しい隠れ状態 \(h_t\) が出来上がるわけです。この \(h_t\) が次の時刻 \(t+1\) に伝わっていくことで、過去の情報が未来へと流れていきます。
このRNNの仕組み、なかなか良くできていますよね。例えば、医師が患者さんの日々の血糖値を記録し、明日の血糖値を予測するシナリオを考えてみましょう。RNNは今日の血糖値(\(x_t\))だけでなく、昨日までの血糖値の流れ(\(h_{t-1}\) が記憶している過去の情報)も考慮して、明日の血糖値(\(y_t\))を予測しようとします。素晴らしいじゃないですか!
ところが、この単純なRNN君には、ちょっと困ったクセがあったんです。
それが、本章の出発点とも言える「長期依存性の消失問題 (Vanishing Gradient Problem for Long-Term Dependencies)」です。なんだか難しい名前ですが、要は「遠い過去の記憶が、現在までうまく伝わらない」という問題なんです。
時系列が長くなると、つまり、ずっと昔の情報を現在の予測に役立てようとすると、その情報がネットワークの中を遡って学習される際に、だんだん影響力が弱まってしまうんですね。例えるなら、伝言ゲームで情報が歪んだり、薄れたりするのに似ているかもしれません。医療の現場で考えてみましょう。例えば、ある患者さんが数週間前に特定の薬剤Aの服用を開始したという情報が、現在の副作用Bを理解する上で非常に重要だとします。しかし、単純なRNNでは、その「薬剤A服用開始」という重要な情報が、現在(数週間後)まで伝わるうちに、日々の他の多くの情報(食事内容、運動量、他のバイタルサインなど)に埋もれてしまい、その影響がほとんど消え失せてしまうことがあるのです。
技術的な話を少しだけすると、これはニューラルネットワークが学習する際の手がかりとなる「勾配(gradient)」というものが、時間を遡る(これを誤差逆伝播と言います)たびに、何度も何度も小さな値を掛け合わせることになってしまい、最終的にはゼロに限りなく近づいてしまう(勾配が消失する)ために起こることが多いと言われています。勾配が消えてしまうと、ネットワークは「何をどれだけ修正すれば良いか」という学習の手がかりを失ってしまうわけです。結果として、単純なRNNは、比較的短い期間のパターンしか捉えられない、という傾向が出てきてしまうのです。これは、医療のように長期的な視点が求められる分野では、ちょっと困りますよね。
1.2 LSTM(Long Short-Term Memory)とは? 一体何がそんなにスゴイの?
さあ、いよいよ本日の主役であり、時系列データ分析の世界で一世を風靡したと言っても過言ではない、LSTM (Long Short-Term Memory) の登場です! 前のセクションで、単純なRNN君が抱えていた「長期依存性の消失問題」、つまり「昔の大事なことを忘れやすい」というちょっとした弱点についてお話ししましたよね。「あの時のあの情報が、今の判断にすごく重要なのに、途中で薄れちゃって届かない…」そんなRNNの悩みを解決すべく、颯爽と現れたのが、このLSTMなんです。
このLSTMという仕組みは、1997年にSepp HochreiterさんとJürgen Schmidhuberさんという、先見の明のある研究者たちによって提案されました[1]。名前からして、なんだか頼もしい感じがしませんか? 「長い(Long)」「短い(Short)」両方の期間の「記憶(Memory)」を、それはもう巧みに扱えるように設計されている、そんなイメージが湧いてきますね。
では、LSTMは一体どんな魔法を使って、RNNが苦手としていた「長期記憶」の難題を克服したのでしょうか? その核心的なアイデアは、情報の流れをコントロールするための、いくつかの巧妙な「ゲート (Gate)」という名の関所を設けたことにあります。これらのゲートが連携し合うことで、LSTMの内部では、「この情報は長期記憶に残しておこう」「この古い情報はもう必要ないから忘れよう」「そして、今の記憶の中から、この情報を取り出して次の判断に使おう」といったことを、まるで経験豊富な情報管理者のように、データに基づいて学習しながら判断できるようになったのです。情報の取捨選択を自動で行う、非常に賢い仕組みが組み込まれている、と考えてみてください。
LSTMの内部構造は、一見すると単純なRNNよりも部品が多くて、ちょっと複雑に見えるかもしれません。でも大丈夫、一つ一つの部品の役割を理解していけば、全体の動きがきっと見えてきます! 基本的には、「セル状態 (Cell State)」という、情報を長期的に保持するためのメインライン(記憶のハイウェイのようなもの)と、このセル状態を巧みに操作する、主に以下の3種類のゲートから構成されています。
まずは、これらの部品が全体としてどんな風に連携しているのか、大まかなイメージを図で掴んでみましょうか。

テキストベースの図
前の時刻からの情報 現在の時刻の入力
h_{t-1} x_t
| |
▼ ▼
+-------------------------------------------------------------------+
| LSTMユニット内部 |
| |
| +-----------+ * Gate Calculations (f_t,i_t,g_t,o_t) * +-----------+ |
| | |----------------------------------------->| | |
| | C_{t-1} | | C_t | | セル状態 (長期記憶ライン)
| | (前のセル)|-----(× f_t)----⊕----(⊕ i_t・g_t)---------->|(新しいセル)| | 情報のハイウェイ
| | 状態 | | 状態 | |
| +-----------+ +-----------+ |
| ↑ | |
| | ▼ |
| └------------------------( o_t )------------------ h_t | 隠れ状態 (短期記憶/出力)
| | |
+-------------------------------------------------------------------+この図は、LSTMユニットが時刻 \(t-1\) からの情報(前のセル状態 \(C_{t-1}\) と前の隠れ状態 \(h_{t-1}\))と、現在の時刻 \(t\) の入力 \(x_t\) を受け取って、新しいセル状態 \(C_t\) と新しい隠れ状態 \(h_t\) を作り出す流れを、ものすごくシンプルに表したものです。「Gate Calculations」と書かれた部分で、後述する忘却ゲート(\(f_t\))、入力ゲート(\(i_t\))、新しい記憶候補(\(g_t\)、後で\(\tilde{C}_t\)として出てきます)、出力ゲート(\(o_t\))が計算され、それらがセル状態の更新や隠れ状態の出力に影響を与えます。特に注目してほしいのは、上部を横断する \(C_{t-1} \rightarrow C_t\) のラインです。これが「セル状態」で、情報が比較的ストレートに流れやすく、長期的な情報を保持するのに適していると言われています。各ゲートは、この情報の流れを調整する水門のような役割を果たすんですね。
では、各部品の役割を、数式も交えながらもう少し詳しく見ていきましょう。数式が出てくると「うっ…」となるかもしれませんが、それぞれの数式が「何をしていて、どんな意味があるのか」という物語を読み解くつもりで見ていくと、意外と親しみやすく感じられるかもしれませんよ。
セル状態 (Cell State)
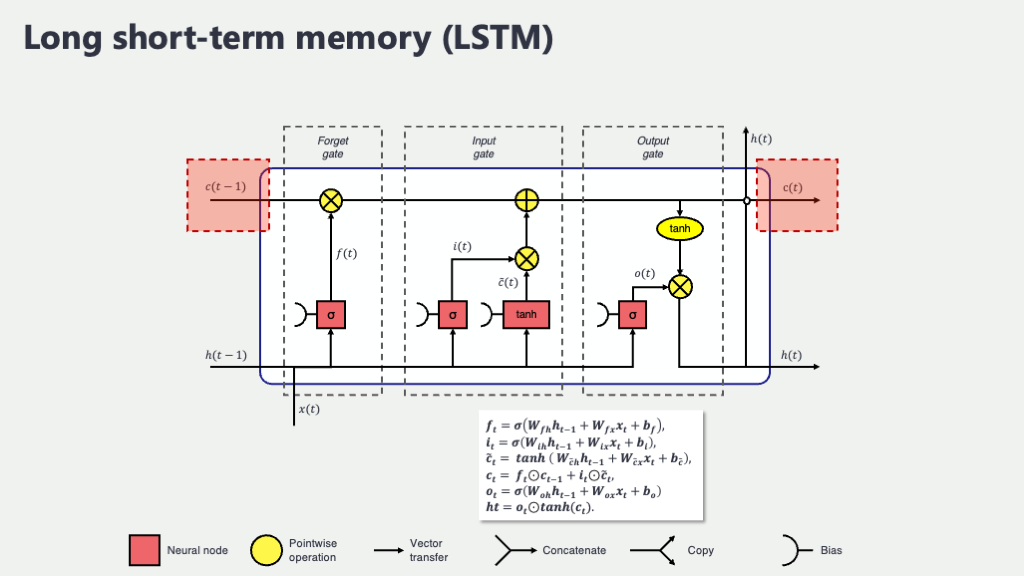
- セル状態 (Cell State), \(C_t\): LSTMの記憶の背骨
これがLSTMの最大の特徴であり、長期記憶を保持するための専用ラインです。先ほどの図でも示したように、情報は基本的にこのセル状態に沿って、過去から未来へと流れていきます。このライン上では、情報が途中で大きく加工されたり薄められたりすることなく、比較的スムーズに伝わっていくように設計されています。まるで、重要な情報を運ぶための専用の高速道路みたいなものですね。単純なRNNでは、隠れ状態が記憶と出力の両方の役割を担っていたため、情報が混線しやすかったのですが、LSTMではこのセル状態という「記憶専用レーン」を設けることで、大切な情報を長期にわたって安定して保持できるようにした、というわけです。
忘却ゲート (Forget Gate)
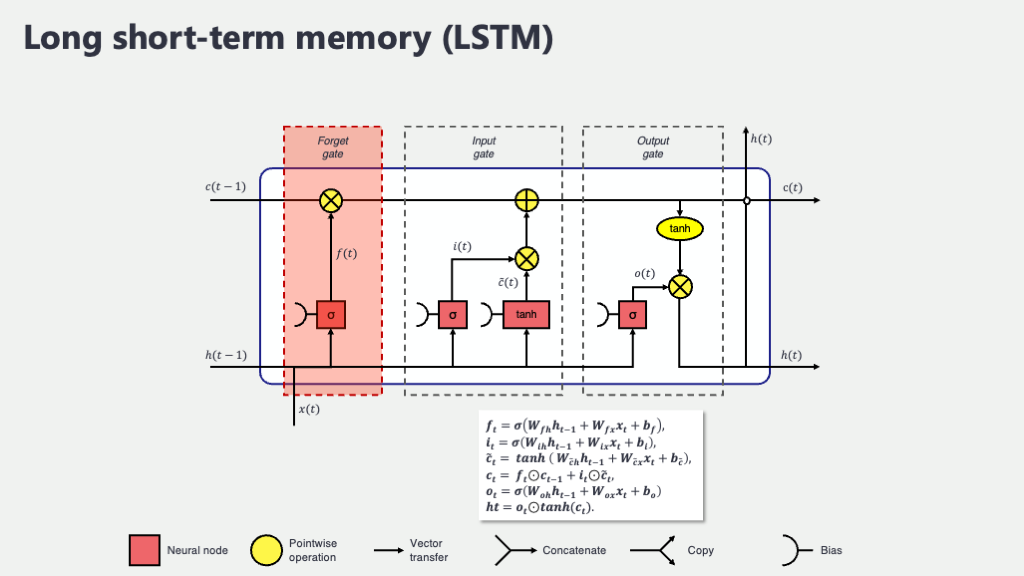
- 忘却ゲート (Forget Gate), \(f_t\): 「何を忘れるか」を決める門番
人間も、新しいことを覚えるためには、時には古い情報を忘れることが必要ですよね。LSTMの忘却ゲートは、まさにその「何を忘れるか」を判断する役割を担います。「過去の長期記憶(前のセル状態 \(C_{t-1}\))のうち、どの情報をどの程度忘れるべきか」を決定するのです。例えば、「数日前の患者さんの体温は、今日の状態を予測するにはもうあまり重要じゃないから、この情報は少し忘れようか」といった判断を、データに基づいて行います。
この忘却ゲート \(f_t\) は、前の時刻の隠れ状態 \(h_{t-1}\)(短期的な記憶や文脈)と、現在の入力 \(x_t\) の両方を見て、「忘れる度合い」を計算します。数式で表すと、以下のようになります。 \[ f_t = \sigma(W_f [h_{t-1}, x_t] + b_f) \] ここで、- \([h_{t-1}, x_t]\) : これは、前の隠れ状態 \(h_{t-1}\) と現在の入力 \(x_t\) を連結(くっつけた)ベクトルです。過去の文脈と現在の情報を両方考慮するための、いわば「判断材料セット」ですね。
- \(W_f\) : 忘却ゲートの「重み行列」です。入力された情報(上記の連結ベクトル)のどの部分をどれだけ重視するかを決定する、学習可能なパラメータです。
- \(b_f\) : 忘却ゲートの「バイアス項」です。これも学習可能なパラメータで、出力の微調整を行います。
- \(\sigma\) (シグマ) : これは「シグモイド関数」という、出力値を必ず0から1の間に収めるS字カーブの関数です。この出力値が、忘却ゲートの「開閉度合い」を表します。値が0に近ければ「ゲートを固く閉じて、情報を完全に忘れる」、1に近ければ「ゲートを全開にして、情報を完全に記憶し続ける(忘れない)」という意味になります。この「0か1か」というスイッチのような性質が、ゲート処理にピッタリなんです。
入力ゲート (Input Gate)
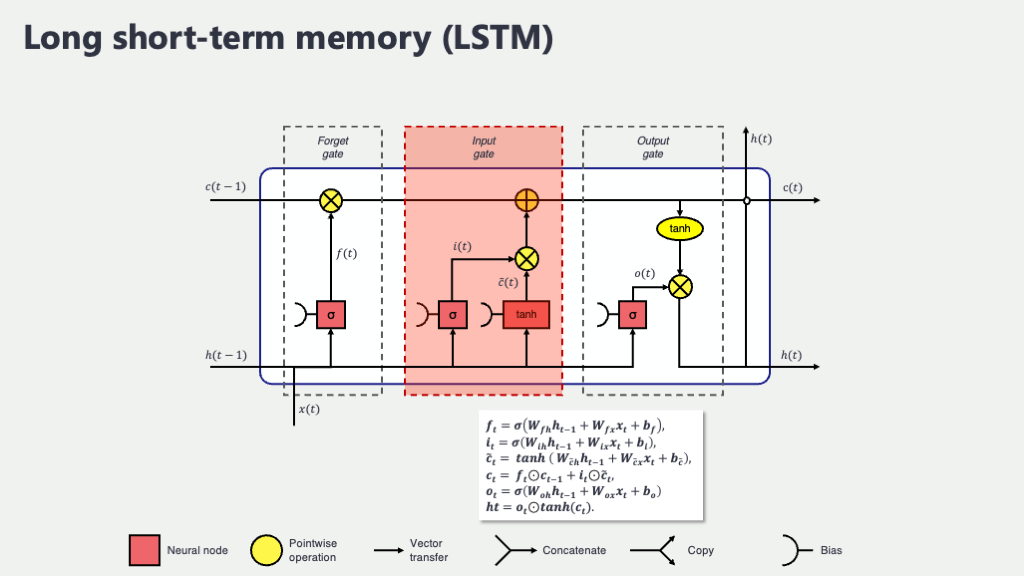
- 入力ゲート (Input Gate), \(i_t\) と 新しい記憶の候補 \(\tilde{C}_t\): 「何を新しく覚えるか」を決める門番たち
古い情報を整理したら、次は新しい情報を記憶に追加する番です。入力ゲートは、「現在の入力 \(x_t\) から得られる新しい情報のうち、どの情報を、どの程度セル状態 \(C_t\) に記憶するか」を決定します。これも、忘却ゲートと同様に、前の隠れ状態 \(h_{t-1}\) と現在の入力 \(x_t\) を材料にして判断します。この処理は、大きく分けて2つのステップで行われます。- どの情報を更新・追加するかの「選択」(入力ゲート \(i_t\)):
まず、「新しい情報のうち、どの部分を実際にセル状態に書き込むか」その「許可度合い」を決めます。これもシグモイド関数 \(\sigma\) を使って、0から1の間の値として出力されます。値が1に近いほど、その新しい情報を強く記憶することを意味します。 \[ i_t = \sigma(W_i [h_{t-1}, x_t] + b_i) \] ここで、\(W_i\) と \(b_i\) は入力ゲート用の重み行列とバイアス項です。 - 記憶に追加する「新しい情報の中身(候補)」の作成 (\(\tilde{C}_t\)):
次に、実際にセル状態に追加される可能性のある「新しい記憶の候補」となる情報ベクトル \(\tilde{C}_t\) (「シーチルダティー」とか「シーティルダティー」と読みます) を作ります。こちらは、活性化関数としてシグモイド関数ではなく「ハイパボリックタンジェント関数 (\(\tanh\))」を使います。\(\tanh\) 関数は、出力値を-1から1の間に収めるS字カーブの関数です。これにより、新しく生成される情報に、プラス方向やマイナス方向の「意味合い」や「強さ」を持たせることができます。 \[ \tilde{C}_t = \tanh(W_C [h_{t-1}, x_t] + b_C) \] ここで、\(W_C\) と \(b_C\) は新しい記憶候補を生成するための重み行列とバイアス項です。「こんな情報を新しく記憶の候補として提案してみるけど、どうかな?」といったニュアンスですね。
- どの情報を更新・追加するかの「選択」(入力ゲート \(i_t\)):
セル状態の更新
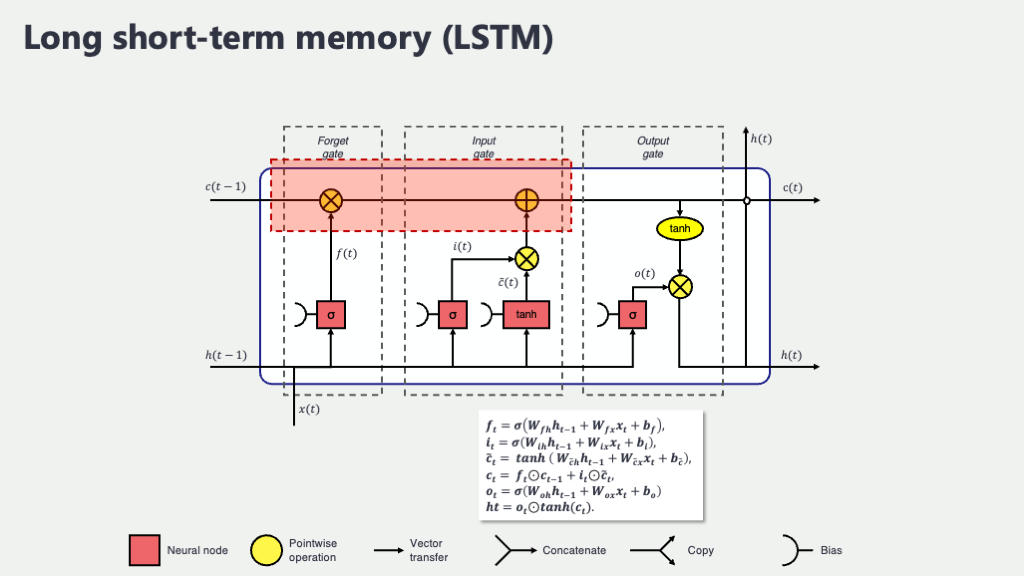
- セル状態の更新: 過去と現在の記憶の融合
さて、忘却ゲート \(f_t\) で「何を忘れるか」が決まり、入力ゲート \(i_t\) と新しい記憶候補 \(\tilde{C}_t\) で「何を新しく覚えるか」とその内容が決まりました。いよいよ、これらを使って、前の時刻のセル状態 \(C_{t-1}\) から現在の時刻の新しいセル状態 \(C_t\) を計算します。この計算式こそ、LSTMの記憶更新メカニズムの心臓部と言えるでしょう! \[ C_t = (f_t \odot C_{t-1}) + (i_t \odot \tilde{C}_t) \] ここで、\(\odot\) (マルの中に点が入った記号) は、「要素ごとの積(アダマール積)」を表します。これは、同じサイズのベクトルや行列の、同じ位置にある要素同士をそれぞれ掛け算するという操作です。行列全体の掛け算(行列積)とは違うので注意してくださいね。 この式が何をやっているか、じっくり見てみましょう。- 最初の項 \((f_t \odot C_{t-1})\) : 前のセル状態 \(C_{t-1}\) の各要素に、忘却ゲート \(f_t\) の出力(0~1の値)を要素ごとに掛け合わせています。これにより、\(f_t\) の値が0に近い要素は情報が弱められ(忘れられ)、1に近い要素は情報がそのまま保持されます。まさに「選択的忘却」ですね。
- 次の項 \((i_t \odot \tilde{C}_t)\) : 新しい記憶の候補 \(\tilde{C}_t\) の各要素に、入力ゲート \(i_t\) の出力(0~1の値)を要素ごとに掛け合わせています。これにより、\(i_t\) の値が1に近い要素の情報が選択的に採用され、0に近い要素の情報は無視されます。これが「選択的記憶」です。
- そして、この2つの結果を「足し合わせる」ことで、新しいセル状態 \(C_t\) が完成します。古い記憶の一部を保持しつつ(忘れるべきは忘れ)、新しい情報を吟味して追加する。なんだか、私たち人間の記憶の仕組みにも少し似ているような気がしませんか?このプロセスのおかげで、重要な情報は長く保持され、不要な情報は流れていく、というダイナミックな記憶の更新が可能になるのです。
出力ゲート (Output Gate)
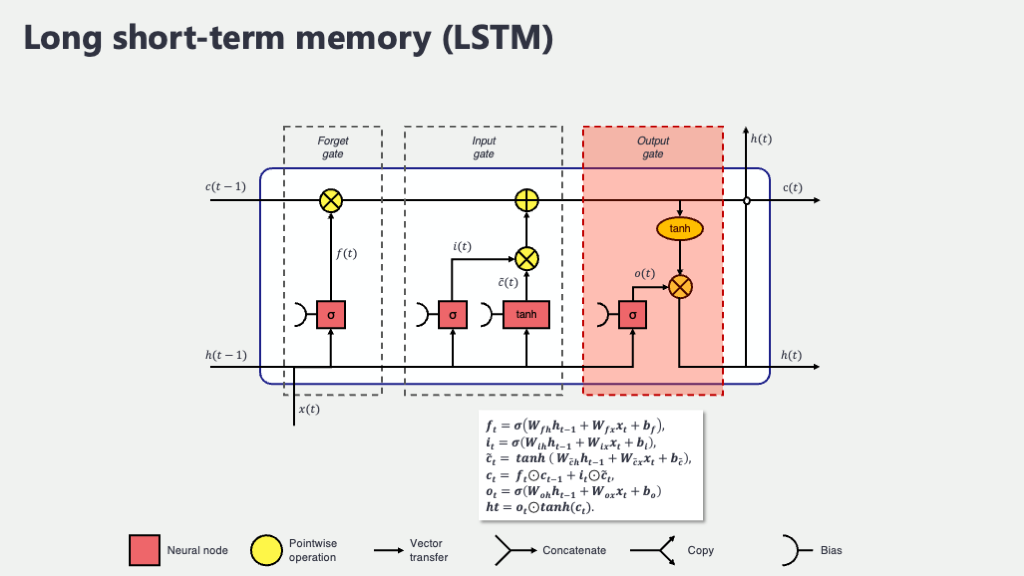
- 出力ゲート (Output Gate), \(o_t\): 「何を出力するか」を決める門番
長期記憶であるセル状態 \(C_t\) が無事に更新されました。しかし、この長期記憶の中から、現在の時刻 \(t\) で「実際に何を出力として使うか」あるいは「次の層にどんな情報を渡すか」を決めなければなりません。いくら素晴らしい情報がセル状態に蓄えられていても、その時々で適切な情報を取り出して使えなければ意味がないですよね。その役割を担うのが、出力ゲート \(o_t\) です。
出力ゲート \(o_t\) も、忘却ゲートや入力ゲートと同様に、前の隠れ状態 \(h_{t-1}\) と現在の入力 \(x_t\) を材料にして、どの情報をどの程度出力するかの「許可度合い」をシグモイド関数 \(\sigma\) で計算します。 \[ o_t = \sigma(W_o [h_{t-1}, x_t] + b_o) \] ここで、\(W_o\) と \(b_o\) は出力ゲート用の重み行列とバイアス項です。
そして、この出力ゲート \(o_t\) の値と、現在のセル状態 \(C_t\) を \(\tanh\) 関数で処理したもの(値を-1から1の範囲に押し込めて、使いやすい形に整えるイメージです)を要素ごとに掛け合わせることで、最終的な現在の時刻の隠れ状態 \(h_t\) が決まります。この \(h_t\) が、単純なRNNで言うところの「短期的な記憶」であり、また、モデルの最終出力や、もしLSTM層が積み重なっている場合は次のLSTM層への入力となります。 \[ h_t = o_t \odot \tanh(C_t) \] セル状態 \(C_t\) の情報をそのまま出すのではなく、一度 \(\tanh\) で値を整え、さらに出力ゲート \(o_t\) で「どの情報を表に出すか」をフィルタリングする、という一手間を加えているのがポイントです。これにより、長期記憶の中から、現在の文脈において本当に必要な情報だけを選択的に取り出すことができるようになるわけですね。
ふぅ…ちょっと数式がたくさん出てきて、頭がパンクしそう…なんてことはないでしょうか? 大丈夫です、全部を一度に完璧に暗記する必要はありません。大切なのは、「セル状態」という長期記憶の幹線道路があって、そこに「忘却」「入力」「出力」という3つの賢い「ゲート」が関わって、情報の流れをきめ細かくコントロールしているんだな、という大きなイメージを掴むことです。これらのゲートは、それぞれシグモイド関数(0~1の値で開閉を調整)やハイパボリックタンジェント関数(-1~1の値で情報をスケーリング)といった活性化関数と、学習によって賢くなる重み \(W\) やバイアス \(b\) を持った、小さなニューラルネットワークのようなものだと考えると良いかもしれませんね。
ここまでのまとめ
各ゲートは、このようなステップ(入力の準備 → 重み付けとバイアス加算 → 活性化関数)を経て、それぞれの役割を果たす値(ゲートの開閉度や記憶の候補)を出力します。そして、これらの値が絶妙に組み合わさることで、セル状態 \(C_t\)(長期記憶)と隠れ状態 \(h_t\)(短期記憶・出力)が賢く更新されていくわけです。この仕組みを初めて知った時、「なんてエレガントで、よく考えられた構造なんだろう!」と、個人的にはとても感動したのを覚えています。
この一見すると複雑に見えるかもしれないゲート機構こそが、LSTMが単純なRNNの限界を打ち破り、時系列データの中に潜む「長期的な依存関係」を効果的に学習できるようになった秘密なのです。医療データのように、数日前、あるいは数週間前の出来事が、今日の患者さんの状態にじわじわと、しかし確実に影響を与えているようなケースでは、このLSTMの「長期記憶力」と「情報の取捨選択能力」が、非常に頼りになる強力な武器となることが期待できる、というわけなんですね。
どうでしょう?LSTMがなぜ登場し、どんな ingenious(独創的)なアイデアで長期記憶の問題に立ち向かっているのか、そしてその内部がどんな部品で、どんな数式で動いているのか、少し具体的なイメージが湧いてきましたでしょうか? もし「まだちょっとモヤモヤする…」という方も、大丈夫です。次のセクションでは、このLSTMの仕組みを、今度はPyTorchというプログラミングの道具を使って、実際にコードとして「触れる」形で見ていきます。実際に手を動かしてみることで、理論だけでは見えなかった側面が、きっとクリアになってくるはずですから!
2. PyTorchによるLSTMの実装
2. PyTorchによるLSTMの実装
さて、前のセクションではLSTMがどんな仕組みで、なぜRNNの弱点を克服できるのか、その理論的な背景を一緒に見てきましたね。頭の中で「なるほど、ゲートってそういう働きをするのか!」とイメージが膨らんできた頃ではないでしょうか!?
ここからは、いよいよそのLSTMを、私たちの手で実際にプログラムとして形にしていく番です! そのための強力な助っ人が、PyTorch という深層学習フレームワークです。PyTorchは、研究者から現場のエンジニアまで幅広く愛用されていて、その柔軟性の高さと使いやすさから、近年ますます人気が高まっているんですよ。まるで、高性能な工具セットと分かりやすい説明書が一緒になったようなもの、とでも言えるかもしれません。これを使えば、複雑に見えるニューラルネットワークのモデル構築も、比較的スムーズに進めることができます。
それでは、PyTorchを使ってLSTMモデルを組み立てていく手順を、一つひとつ見ていきましょう!
2.1 まずは準備体操:必要なライブラリのインポート
何事も準備が大切ですよね。Pythonでプログラミングをするとき、私たちは様々な「ライブラリ」という便利な道具箱を使います。これらは、複雑な計算や処理を簡単に行うための関数やクラスがたくさん詰まっているものです。まずは、今回のLSTMモデル構築とデータ処理、そして結果の可視化に必要となる基本的なライブラリたちを、プログラムの冒頭で「インポート(import)」して呼び出しておきましょう。
# === PyTorch関連 ===
# PyTorchの本体です。テンソル計算など、基本的な機能が詰まっています。
import torch
# ニューラルネットワークを構築するための部品箱(レイヤー、活性化関数など)です。
import torch.nn as nn
# モデルの学習を助ける最適化アルゴリズム(例: Adam)が入っています。
import torch.optim as optim
# データセットの準備や、学習時にデータを効率よく供給するための道具箱です。
from torch.utils.data import DataLoader, TensorDataset
# === その他、便利なライブラリ ===
# 数値計算、特に配列や行列の操作が得意なライブラリです。データの前処理などで活躍します。
import numpy as np
# グラフを描くための定番ライブラリ。学習の進み具合や予測結果を視覚化するのに使います。
import matplotlib.pyplot as plt
# Matplotlibで日本語のラベルやタイトルが文字化けしないようにするためのお助けライブラリです。
# もしインストールしていなければ、ターミナルやコマンドプロンプトで
# pip install japanize-matplotlib
# と入力してインストールしてくださいね。
import japanize_matplotlib
それぞれのライブラリがどんな役割を持っているか、少し補足しますね。
torch: これがPyTorchの心臓部です。ニューラルネットワークで頻繁に行われる「テンソル」という多次元配列の計算や、GPUを使った高速計算などをサポートしてくれます。torch.nn: ニューラルネットワークを構成する様々な「層(レイヤー)」、例えば今回使うLSTM層や、前回少し触れた全結合層(nn.Linear)、さらには活性化関数などがこのモジュール(部品箱)にまとめられています。nn.Moduleという、自分でモデルを設計する際の設計図のテンプレートのようなものもここに入っています。torch.optim: モデルが学習データから学んで賢くなっていく(パラメータを調整していく)過程で、どのような方針でパラメータを更新するかを決める「最適化アルゴリズム」が収められています。今回はAdamという人気のアルゴリズムを使ってみる予定です。torch.utils.data: 大量のデータを効率的にモデルに供給するための仕組み、例えばデータセット全体を小さな塊(ミニバッチ)に分けて扱ったり、データをシャッフルしたりする機能を提供してくれます。numpy: Pythonで科学技術計算を行う際の定番ライブラリですね。PyTorchのテンソルとNumPyの配列は相性が良く、相互に変換も簡単なので、データの前処理や加工で非常によく使われます。matplotlib.pyplot: 学習がうまくいっているか(損失がちゃんと下がっているか)を確認したり、モデルがどんな予測をしたのかをグラフにして見たりするのに欠かせない、可視化の道具です。japanize_matplotlib: Matplotlibは標準だと日本語の表示がうまくいかないことがあるのですが、このライブラリをインポートしておくだけで、グラフのタイトルやラベルに日本語を使っても文字化けしにくくなる、という縁の下の力持ちです。使っている環境によってはフォントの設定が必要なこともありますが、まずはこれを入れておくと安心だと思います。
これらの道具を揃えれば、いよいよLSTMの実装に入る準備が整います!
2.2 PyTorchのLSTMモジュール:nn.LSTMを使いこなそう
PyTorchには、LSTM層を簡単にモデルに組み込めるように、nn.LSTM という便利なクラスが用意されています。これを活用すれば、先ほど理論のセクションで見た複雑なゲートの計算などを自分で一から書く必要はなく、いくつかのパラメータを指定するだけでLSTM層を利用できるんです。本当にありがたいですよね。
では、この nn.LSTM を使う際に押さえておきたい主なパラメータを見ていきましょう。これらは、LSTMの「性格」や「能力」を決める重要な設定値になります。
| パラメータ名 | 説明 | 具体例・補足 |
|---|---|---|
input_size | 入力される特徴量の数(次元数)。各時刻 \(t\) でモデルが受け取る情報の種類や数です。 | 例えば、1日の血糖値だけを追うなら1。もし血糖値とインスリン投与量の2つを同時に見るなら2になります。 |
hidden_size | LSTMの隠れ状態 \(h_t\) およびセル状態 \(C_t\) の次元数。LSTMユニット内部の「作業机の広さ」や「記憶容量」のようなもので、モデルの表現力を左右します。 | 大きな値にするほど複雑なパターンを捉えられる可能性がありますが、計算コストが増えたり、データが少ないと過学習(訓練データにだけ適合しすぎて未知のデータには弱くなる現象)しやすくなったりもします。最初は50や100くらいから試してみることが多いかもしれません。 |
num_layers | LSTM層を何層重ねるか。デフォルトは1です。 | 層を深くする(例えば2層や3層にする)と、より複雑で階層的な特徴を学習できることがあります。ただ、層を増やしすぎると学習が不安定になったり、計算時間が非常にかかったりすることもあるので、バランスが大切です。 |
batch_first | 入力および出力テンソルの次元の順番を指定するブール値(TrueかFalseか)。 | Trueに設定すると、テンソルの形状が (バッチサイズ, シーケンス長, 特徴量数) となります。False (デフォルト) だと (シーケンス長, バッチサイズ, 特徴量数) です。多くのデータ処理ではバッチサイズを最初の次元で扱うことが多いので、一般的にはTrueにしておくと、他の処理との整合性が取りやすく、コードも直感的に書けることが多いと思います。今回はTrueで進めます。 |
dropout | 0より大きく1未満の値を指定すると、最後の層を除く各LSTM層の出力にドロップアウトを適用します。過学習を防ぐための一種の「おまじない」です。 | 例えば0.2を指定すると、訓練中にランダムに20%のニューロン(あるいは接続)を一時的に無効化します。これにより、モデルが特定の特徴に頼りすぎるのを防ぎ、より頑健な学習を促す効果が期待できます。 |
bidirectional | Trueに設定すると、双方向LSTM (BiLSTM) になります。デフォルトはFalseです。 | 双方向LSTMは、過去の情報だけでなく未来の情報も考慮して現在の状態を判断するため、特に自然言語処理などで性能向上に繋がることがあります。今回はまず単純な単方向LSTMから始めますが、こんなオプションもあるんだな、と頭の片隅に置いておくと良いでしょう。 |
これらのパラメータを nn.LSTM に渡すことで、私たちが望む特性を持ったLSTM層が作られます。
次に、nn.LSTM がどのようなデータを受け取り(入力)、どのようなデータを吐き出す(出力)のか、そのデータの「形(形状、shape)」について見ていきましょう。これはテンソルという多次元配列でやり取りされるのですが、その次元の順番や意味をしっかり理解しておくことが、後々モデルを正しく使う上で非常に重要になります。
入力テンソルの形状 (batch_first=True の場合):
入力は、主にシーケンスデータそのものである input と、オプションで初期の隠れ状態 h_0 およびセル状態 c_0 です。
input: 形状は(バッチサイズ, シーケンス長, input_size)となります。バッチサイズ (batch_size): 一度に処理するシーケンスデータの数です。例えば、32人の患者さんのデータをまとめて処理するなら32。シーケンス長 (seq_len): 1つのシーケンスデータの時間の長さです。例えば、10日間の連続した血糖値データなら10。input_size: 各時刻における特徴量の数。先ほどのパラメータ説明と同じですね。
ちょっと図でイメージしてみましょうか。
入力テンソル (input) の形状 (batch_first=True の場合):
+--------------------------------------------------+
| バッチ (batch_size個のシーケンスデータのかたまり) |
| |
| +----------------------------------------------+ --- シーケンス 1 (例: 患者Aのデータ)
| | シーケンス長 (seq_len個の時点のデータが並ぶ) |
| | |
| | [t=1] [t=2] ... [t=seq_len] |
| | データ データ データ |
| | (size D) (size D) (size D) | D = input_size
| +----------------------------------------------+
| |
| +----------------------------------------------+ --- シーケンス 2 (例: 患者Bのデータ)
| | シーケンス長 (seq_len個の時点のデータが並ぶ) |
| | ... |
| +----------------------------------------------+
| |
| ... (バッチサイズ分繰り返す) ... |
| |
+--------------------------------------------------+
h_0(オプション): 初期隠れ状態。形状は(層の数 * 方向数, バッチサイズ, hidden_size)。c_0(オプション): 初期セル状態。形状は(層の数 * 方向数, バッチサイズ, hidden_size)。層の数 (num_layers):nn.LSTMのnum_layersパラメータで指定した値。方向数 (num_directions): 単方向なら1, 双方向 (bidirectional=True) なら2。
出力テンソルの形状:nn.LSTM は主に3つのものを返します。
output: LSTM層の各時刻からの出力(隠れ状態 \(h_t\))をまとめたもの。
形状は(バッチサイズ, シーケンス長, hidden_size * 方向数)。
これは、シーケンスの全ての時刻におけるLSTMの「考え」や「要約」のようなものだと捉えられます。h_n: シーケンスの最後の時刻における隠れ状態。
形状は(層の数 * 方向数, バッチサイズ, hidden_size)。
シーケンス全体の情報を集約した最終的な「記憶」とも言えますね。c_n: シーケンスの最後の時刻におけるセル状態。
形状は(層の数 * 方向数, バッチサイズ, hidden_size)。
これはLSTM内部の長期記憶の最終状態です。
DeepDive! 出力テンソルの形状
(作成中)
多くの場合、時系列予測や分類タスクでは、この output の最後の時刻の隠れ状態や、h_n を次の層(例えば全結合層)への入力として使います。
この入力と出力のデータの形を意識しながら、次のステップで実際にモデルを設計していきましょう。
2.3 設計図を書こう:簡単なLSTMモデルの構築
さて、いよいよPyTorchを使って、私たちがこれから訓練していくLSTMモデルの「設計図」を具体的に描いていく番です!料理で言えば、レシピ作りといったところでしょうか。ここでは、比較的シンプルな構成として、まず入力された時系列データの特徴を捉えるための「LSTM層」を置き、そのLSTM層が処理した情報を受け取って、最終的な予測値を計算するための「全結合層(nn.Linear)」を1つ接続する、というモデルを考えてみます。イメージとしては、LSTM層が時系列データのパターンをじっくり読み解く専門家で、全結合層がその報告を受けて「なるほど、では最終的な予測はこうですね!」と結論を出すマネージャーのような役割分担ですね。
PyTorchでこうしたオリジナルのニューラルネットワークモデルを作る際には、torch.nn.Module という、いわば「モデル設計の基本キット」のようなクラスを「継承」するというお作法があります。この nn.Module を使うことで、モデルの部品(層)を管理したり、学習に必要な計算(例えば誤差逆伝播による勾配計算など)をPyTorchが自動でやってくれたりする、たくさんの便利な機能の恩恵にあずかることができるんです。なんだか、特別な会員証を手に入れて、会員専用の便利な施設を使えるようになるようなイメージですね。
では、早速その設計図となるPythonのクラス定義を見ていきましょう!
# LSTMモデルの「設計図」となるクラスを定義します
class MedicalLSTM(nn.Module):
# この __init__ メソッドは、モデルが作られるときに最初に呼び出される部分です。
# モデルで使う「部品(層など)」をここで準備しておきます。
def __init__(self, input_size, hidden_size, num_layers, output_size):
# まずは、お決まりの呪文として、親クラスである nn.Module の初期化処理を呼び出します。
# これにより、nn.Module が持つ便利な機能を使えるようになります。
super(MedicalLSTM, self).__init__()
# 後で forward メソッドなどで使うLSTMの重要なパラメータを、
# self.変数名 の形でインスタンス変数として保存しておくと便利です。
self.hidden_size = hidden_size # LSTMの隠れ状態の次元数 (記憶ユニットの大きさ)
self.num_layers = num_layers # LSTM層の数
# === ここからモデルの「部品」を定義していきます ===
# 1. LSTM層 (時系列パターンの読解担当)
# nn.LSTM クラスを使って、LSTM層のインスタンスを作ります。
# 各引数の意味は、前のセクションで詳しく見ましたね!
# - input_size: 各時刻で入力されるデータの特徴量の数
# - hidden_size: 隠れ状態の次元数 (LSTMの記憶容量の目安)
# - num_layers: LSTM層の深さ (何層重ねるか)
# - batch_first=True: 入力テンソルの次元の順番を (バッチサイズ, シーケンス長, 特徴量数) にします。
# こうしておくと、データの扱いが直感的になることが多いです。
self.lstm = nn.LSTM(input_size=input_size,
hidden_size=hidden_size,
num_layers=num_layers,
batch_first=True)
# 2. 全結合層 (最終予測の担当)
# nn.Linear クラスを使って、全結合層(線形層とも呼ばれます)のインスタンスを作ります。
# この層は、LSTM層が時系列データから抽出した特徴ベクトル(最後の隠れ状態)を入力として受け取り、
# 最終的に私たちが予測したい値(例えば、次の血糖値など)を出力します。
# - hidden_size: この全結合層への入力特徴量の数。LSTMの隠れ状態の次元数と一致させます。
# - output_size: この全結合層からの出力特徴量の数。予測したい値の数と一致させます。
# (例: 1つの数値を予測するなら output_size=1)
self.fc = nn.Linear(in_features=hidden_size,
out_features=output_size) # fc は "fully connected" (全結合) の略です。
# この forward メソッドは、実際にデータがモデルの中をどのように流れて処理されるか、
# その「計算のレシピ」を記述する部分です。
# モデルに入力データ x が与えられたときに、このメソッドが呼び出されます。
def forward(self, x):
# x は入力される時系列データで、
# (バッチサイズ, シーケンス長, input_size) という形状のテンソルであることを想定しています。
# バッチサイズ: 一度に処理するデータの数
# シーケンス長: 各データの時間的な長さ
# input_size: 各時刻における特徴量の数
# LSTM層に与えるための、初期の隠れ状態 (h_0) とセル状態 (c_0) を準備します。
# 最初は過去の記憶がない状態からスタートするので、通常は全ての要素が0のテンソルで初期化します。
# 形状は (層の数, バッチサイズ, 隠れ層の次元数) です。
# - self.num_layers: __init__で設定したLSTM層の数。
# - x.size(0): 入力データxの0番目の次元、つまりバッチサイズを取得します。
# - self.hidden_size: __init__で設定した隠れ層の次元数。
# .to(x.device) は、このh0やc0を、入力データxが存在するのと同じ計算デバイス
# (CPUまたはGPU) に配置するためのおまじないです。データとモデルが違う場所にいると計算できませんからね。
h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(x.device)
c0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(x.device)
# LSTM層に入力データ x と、初期状態 (h0, c0) をタプルで渡します。
# LSTM層は主に2つのものを返します。
# 1. out: シーケンスの各時刻におけるLSTMの出力 (隠れ状態 h_t) を全て含んだテンソル。
# 形状は (バッチサイズ, シーケンス長, hidden_size) になります (batch_first=True の場合)。
# 2. (hn, cn): タプルで、シーケンスの最後の時刻における隠れ状態 (hn) とセル状態 (cn)。
# hn の形状は (層の数, バッチサイズ, hidden_size)。cnも同様です。
# 今回のモデルでは、out の情報だけを使うので、hn と cn は _ (アンダースコア) で受けて、
# 「この値は今回は使いませんよ」とPythonに教えてあげています。
out, _ = self.lstm(x, (h0, c0))
# LSTMの出力 'out' のうち、シーケンスの「最後の時刻」の出力だけを取り出して使います。
# なぜなら、時系列データ全体をLSTMが読み込んだ結果、最後の時点でどんな状態になっているかが、
# 次の値を予測する上で重要な情報だと考えられるからです (これを「多対一」のタスクと呼びます)。
#
# 'out' の形状は (バッチサイズ, シーケンス長, hidden_size) です。
# PyTorchのスライス機能 out[:, -1, :] を使うと、
# - 全てのバッチ (最初の :) について、
# - シーケンスの最後の要素 (真ん中の -1) の、
# - 全ての隠れ状態特徴量 (最後の :) を取り出すことができます。
# この結果、取り出されたテンソルの形状は (バッチサイズ, hidden_size) になります。
# ちょっと図でイメージしてみましょうか。
# outテンソル (例: batch_size=B, seq_len=S, hidden_size=H)
#
# Batch 1: [ [h_1_1...h_1_H], [h_2_1...h_2_H], ..., [h_S_1...h_S_H] ] <-- シーケンス1
# Batch 2: [ [h_1_1...h_1_H], [h_2_1...h_2_H], ..., [h_S_1...h_S_H] ] <-- シーケンス2
# ...
# Batch B: [ [h_1_1...h_1_H], [h_2_1...h_2_H], ..., [h_S_1...h_S_H] ] <-- シーケンスB
# ↑
# この最後の列 [h_S_1...h_S_H] を
# 全バッチ分取り出すのが out[:, -1, :]
#
last_time_step_output = out[:, -1, :]
# 取り出した「最後の時刻のLSTM出力」(形状: (バッチサイズ, hidden_size)) を、
# __init__ で定義した全結合層 (self.fc) に入力します。
# 全結合層は、入力された hidden_size 次元のベクトルを、
# output_size 次元のベクトル (予測値) に変換します。
predictions = self.fc(last_time_step_output)
# 最終的な予測値 (形状: (バッチサイズ, output_size)) を返します。
return predictions
いかがでしたでしょうか?クラスとしてモデルを定義するというのは、Pythonに慣れていないと最初は少し面食らうかもしれませんが、__init__ でモデルの「部品」を用意し、forward でデータがその部品をどう「流れていくか」のレシピを書く、という2つのパートに分けて考えると、少しずつ整理できてくるのではないかと思います。プラモデルで言えば、__init__でランナーからパーツを切り離して準備し、forwardで説明書通りにパーツを組み上げていく、そんな感じかもしれませんね。
ちょっとだけ補足です:
__init__メソッド(コンストラクタ)の役割:
ここでself.lstm = nn.LSTM(...)やself.fc = nn.Linear(...)のように、層のインスタンスをself.変数名の形で代入しておくことがポイントです。こうすることで、これらの層がこのMedicalLSTMモデルの「管理下にある部品」としてPyTorchに認識され、モデル全体のパラメータ(学習すべき重みやバイアス)をまとめて扱えたり、学習時の勾配計算が自動で行われたりするようになります。super(MedicalLSTM, self).__init__()は、このnn.Moduleの便利な仕組みを正しく有効にするための、いわば「おまじない」のようなものだと考えてください。forwardメソッドの役割:
このメソッドには、入力データxが、__init__で用意した各層(部品)を具体的にどのように通過し、どんな計算を経て、最終的な出力predictionsに変換されるのか、その一連の「データの旅路」を記述します。PyTorchは、このforwardメソッドに書かれた計算の履歴を自動的に記録し、それを使って誤差逆伝播(学習)を行うので、私たちは複雑な微分の計算を自分でする必要がないんです。本当に便利ですよね!- 初期状態 \(h_0\) と \(c_0\) について:
LSTMが時系列データの処理を開始する最初の時点では、当然ながら「それより前の過去の記憶」は存在しません。そのため、初期の隠れ状態 \(h_0\) とセル状態 \(c_0\) は、すべての要素が0のテンソル(ゼロベクトル)で初期化するのが一般的です。これは「何も前提知識がない、まっさらな状態から始めますよ」ということを意味します。 out, _ = self.lstm(x, (h0, c0))の出力について:self.lstmは、処理結果として主に2つのものを返します。一つはoutで、これはシーケンスの各時刻における隠れ状態 \(h_t\) をすべてまとめたものです。もう一つは(hn, cn)というタプルで、これはシーケンスの最後の時刻における隠れ状態 \(h_n\) とセル状態 \(c_n\) です。今回のモデルでは、outの中から最後の時刻の情報を取り出すout[:, -1, :]という方法を使っているため、hnやcnを直接使う必要がありませんでした。そのため、_(アンダースコア) を使って「この返り値は今回は使いませんよ」と明示しています。もちろん、モデルの設計によっては、このhnやcnを活用することも可能です。out[:, -1, :]というスライス操作の心:
これは、PyTorch(やNumPy)でテンソルや配列から特定の部分を効率よく取り出すための非常に便利なテクニックです。「すべてのバッチについて (:)、シーケンスの最後の要素 (-1) の、すべての特徴量 (:) を取ってきてください」という意味になります。時系列データ全体を通しての情報が、最後の隠れ状態に集約されているという期待のもと、この最後の状態を使って予測を行うというのは、時系列処理のタスクでよく見られるアプローチの一つです。例えば、「数日間の患者さんのバイタルサインの推移全体を見て、次の日の状態を予測する」といったシナリオに合致すると言えるでしょう。
こうして、私たちのLSTMモデルの設計図、MedicalLSTM クラスが無事に完成しました!この設計図があれば、あとは実際にこのモデルに魂を吹き込み(インスタンス化し)、データを与えて賢くしていく(学習させる)段階に進むことができます。次のセクションでは、その「学習」のプロセスについて見ていくことにしましょう。楽しみですね!
2.4 モデルの成績表と指導方針:損失関数と最適化アルゴリズム
さて、先ほどのセクションで、私たちの手でLSTMモデルの立派な「設計図」(MedicalLSTMクラス)を描き上げましたね!これで、いつでも同じ設計のモデルをポンと作り出せるようになりました。でも、設計図だけでは、まだモデルは何も知りません。まるで、生まれたばかりの赤んちゃんが、これから世界について学んでいくように、私たちのモデルもデータから何かを学び、賢くなってもらう必要があります。
そのためには、大きく分けて2つの重要なものが必要になります。一つは、モデルの「出来栄え」を評価するための「成績表」、これが「損失関数 (Loss Function)」と呼ばれるものです。そしてもう一つは、その成績をより良くするために、モデルをどう導いていけば良いかという「指導方針」、これが「最適化アルゴリズム (Optimizer)」です。この二つが揃って初めて、モデルは効果的に学習を進めることができるのです。なんだか、子育てや教育にも通じるものがあるかもしれませんね!
損失関数 (Loss Function) とは? 〜モデルの「間違い度合い」を測るモノサシ〜
損失関数というのは、一言でいうと、モデルが出した予測が、実際の「正解」とどれくらい「ズレているか」を数値で表すための関数です。この「ズレ」のことを「損失」とか「誤差」と呼んだりします。当然ながら、この損失の値が小さければ小さいほど、モデルの予測は正解に近い、つまり「うん、よくできているね!」ということになります。逆に、損失が大きいということは、「うーん、ちょっと Insgesamtな予測をしてしまっているね…」というわけです。AIの学習における最大の目標は、この「損失」をできるだけ小さくすること、これに尽きると言っても過言ではありません。
では、具体的にどんな損失関数があるのでしょうか? 今回私たちが取り組んでいるのは、「過去の時系列データから未来の数値を予測する」というタスクですね。例えば、「明日の血糖値を予測する」といった、連続的な数値を当てる問題は「回帰タスク」と呼ばれます。この回帰タスクで、最もポピュラーでよく使われる損失関数の一つに、「平均二乗誤差 (MSE: Mean Squared Error)」というものがあります。
平均二乗誤差(MSE)というのは、その名の通り、各データポイントにおける「モデルの予測値」と「実際の正解値」の差(これを「誤差」と呼びます)を計算し、その誤差をそれぞれ「二乗」し、最後にそれら全てを「平均」したものです。数式で書くと、こんな感じになります。
\[ \text{MSE} = \frac{1}{N} \sum_{i=1}^{N} (y_i – \hat{y}_i)^2 \]
ちょっと数式が出てきてドキッとするかもしれませんが、大丈夫、一つ一つの記号の意味を見ていきましょう。
- \(N\): これは、私たちが評価に使っているデータポイントの総数を表します。例えば、100個のデータで予測のズレを見るなら、\(N=100\) です。
- \(\sum_{i=1}^{N}\) (シグマ記号): これは「\(i\) が1から \(N\) までの間、全部足し合わせるぞ!」という、数学でよく出てくる「合計しますよ」の合図みたいなものです。
- \(y_i\): これは、\(i\) 番目のデータにおける「実際の正解値」です。例えば、\(i\) 番目の日の実際の血糖値ですね。
- \(\hat{y}_i\) (「ワイハットアイ」と読みます): これは、\(i\) 番目のデータに対する「モデルの予測値」です。モデルが「この日の血糖値はこうなるはず!」と予測した値です。
- \((y_i – \hat{y}_i)^2\): これがキモの部分で、「実際の値と予測値の差(誤差)」を計算し、それを「二乗」しています。
- なぜ二乗するのか? 一つには、誤差がプラス(予測が大きすぎた)でもマイナス(予測が小さすぎた)でも、二乗すれば必ずプラスの値になるので、ズレの大きさをシンプルに評価できるという点があります。もう一つ重要なのは、誤差が大きいほど、二乗することでその値がより一層大きくなるため、大きなズレに対してはより大きな「ペナルティ」を与える効果があるんです。つまり、モデルに「大きな間違いは特にダメだよ!」と厳しく教えるわけですね。
- \(\frac{1}{N}\): 最後に、二乗した誤差の合計をデータ総数 \(N\) で割っています。これはつまり「平均」を取っているということで、データ数に関わらず、損失の大きさを同じ基準で比較できるようにするためです。
このMSEが小さければ小さいほど、モデルの予測は全体的によく当たっている、ということになります。PyTorchでは、このMSEを簡単に計算してくれる nn.MSELoss() という便利なクラスが用意されているので、私たちがこの複雑な計算式を自分でプログラムする必要はありません。本当に助かりますよね!
# 損失関数を定義します。今回は「平均二乗誤差 (MSE)」を使います。
# nn.MSELoss() のインスタンス(設計図から作られた実物)を作成するだけで準備OKです。
criterion = nn.MSELoss()
# criterion (クライテリオン) は「基準」や「指標」といった意味の英単語です。
# この変数を使って、後でモデルの予測と正解ラベルから損失を計算します。
ちなみに、回帰タスクで使われる損失関数はMSEだけではありません。例えば、平均絶対誤差(MAE)という、誤差の絶対値の平均を取るものなど、他にも色々な種類があって、タスクの性質やデータの特性によって使い分けられたりします。でも、まずはこのMSEをしっかり押さえておけば大丈夫でしょう。
最適化アルゴリズム (Optimizer) とは? 〜モデルを賢く導く学習戦略〜
さて、損失関数という「成績表」でモデルの出来栄え(予測のズレ具合)が数値で分かるようになりました。でも、成績が悪いときに「ダメだったね」と言うだけでは、モデルは賢くなりませんよね。どうすればもっと良い成績が取れるようになるのか、具体的な「改善方法」を教えてあげなければなりません。その役割を担うのが、「最適化アルゴリズム (Optimizer)」です。
オプティマイザは、損失関数の値をできるだけ小さくするために、モデルの内部にあるたくさんの「学習可能なパラメータ」(私たちのLSTMモデルで言えば、LSTM層や全結合層が持っている重み \(W\) やバイアス \(b\) のことです)を、どの方向に、どれくらいの大きさで調整すれば良いのか、その「更新戦略」を決定します。いわば、モデルを賢くするための「学習ドリルの進め方」や、目標達成へと導く「優秀なコーチ」のような存在だと考えてみてください。
この「パラメータを調整して損失を小さくしていく」という考え方の基本には、「勾配降下法 (Gradient Descent)」というアイデアがあります。ちょっとイメージしにくいかもしれませんが、損失関数の値を「地形」に例えてみましょう。私たちの目標は、この地形で一番低い「谷底」(損失が最小になる場所)を見つけることです。今、モデルのパラメータがある値を取っているとき、私たちはその地形のどこかの一点に立っていると想像してください。勾配降下法では、まず今いる場所の「傾き(勾配)」を調べます。そして、その傾きが最も急になっている下り坂の方向へ、ほんの少しだけ移動するのです。これを繰り返していけば、いつかは谷底にたどり着けるはずだ、という考え方ですね。
損失関数のイメージ(概念図)
損失の値 (Y軸)
^
| /~~~~~~~~~\ <-- パラメータの値が高すぎる/低すぎる (損失大)
| / \
| / 山 \
| / \
| | 現在地(●) |
| | ↓勾配 | <-- 勾配(傾き)が示す最も急な下り方向
| \ パラメータ更新→/
| \ /\ /
| \_____/ \_____/
| 谷底 (損失最小)
+----------------------------> パラメータの値 (X軸)
- ● が現在のモデルのパラメータ状態と、その時の損失の値。
- 「勾配」はその地点での地形の傾き。オプティマイザはこの勾配を頼りに、
損失がより小さくなる方向(谷底方向)へとパラメータを少しずつ動かします。
この「少しだけ移動する」ときの「歩幅の大きさ」を決めるのが「学習率 (Learning Rate)」という非常に重要な設定値です。学習率が大きすぎると、谷底を勢いよく飛び越えてしまって、いつまで経っても安定しなかったり(学習が発散する、と言います)、逆に小さすぎると、ちょこちょこ歩きすぎて谷底にたどり着くまでにものすごく時間がかかってしまったり(収束が遅い、と言います)します。この学習率の調整は、機械学習の職人技の一つとも言える部分なんです。
世の中には、この基本的な勾配降下法をベースに、より賢く、より効率的にパラメータを更新するための様々な最適化アルゴリズムが考案されています。その中でも、近年非常に人気があり、多くの場合で安定して良好な性能を発揮してくれるのが、「Adam (Adaptive Moment Estimation)」というアルゴリズムです。Adamは、これまでの学習の履歴(過去の勾配の大きさや向きなど)をうまく考慮しながら、各パラメータに対して「適応的」に学習率を調整してくれる、かなり賢いコーチだと思ってください。そのため、私たちが細かく学習率をチューニングしなくても、比較的良い感じに学習を進めてくれることが多いんです。PyTorchでは、このAdamも optim.Adam という形で簡単に利用できます。
では、実際にPyTorchで損失関数とオプティマイザを設定してみましょう。そのためには、まず先ほど設計したMedicalLSTMモデルの「実物(インスタンス)」を作る必要がありますね。
# まず、先ほど定義した MedicalLSTM クラスの「実物(インスタンス)」を作ります。
# モデルを作るときには、__init__メソッドで定義した引数を指定します。
# ここでは、例として以下のようなパラメータでモデルを作ってみましょう。
# input_size=1: 各時刻の入力特徴量は1つ (例: 血糖値のみ、など)
# hidden_size=50: LSTMの隠れ状態の次元数 (記憶ユニットの大きさを50に)
# num_layers=2: LSTM層は2層重ねることにします
# output_size=1: 最終的に予測したい値は1つ (例: 次の時点の血糖値、など)
model = MedicalLSTM(input_size=1, hidden_size=50, num_layers=2, output_size=1)
# 次に、最適化アルゴリズム (今回はAdam) を定義します。
# オプティマイザを作るときには、主に2つの情報を渡します。
# 1. どのパラメータを最適化してほしいか? → model.parameters() でモデルが持つ全学習可能パラメータを指定
# 2. 学習率 (lr: learning rate) はどれくらいにするか? → lr=0.001 などと指定
# model.parameters() は、私たちが作った MedicalLSTM モデルが持っている、
# 学習によって調整されていくべき全ての重みやバイアスを、
# オプティマイザに「この子たちを、いい感じに育ててください!」とお願いするイメージです。
# lr=0.001 (0.001が多いですが、0.01や0.0001なども試されます) は学習率の初期値で、
# パラメータを更新する際の「一歩の大きさ」を決めます。この値は結構デリケートで、
# 大きすぎると学習が暴れ、小さすぎると学習がなかなか進まない、ということが起こります。
optimizer = optim.Adam(model.parameters(), lr=0.001)
はい、これで、モデルの「成績表」である損失関数 criterion と、モデルを賢く指導してくれる「コーチ」である最適化アルゴリズム optimizer の準備がバッチリ整いました!
ちょっとだけ補足:ハイパーパラメータという「職人技」の世界
ここで設定した hidden_size (隠れ層の次元数) や num_layers (LSTM層の数)、そしてオプティマイザに渡した lr (学習率) といった値は、「ハイパーパラメータ」と呼ばれます。これらは、モデルが学習を通じて自動的に獲得していくパラメータ(重み \(W\) やバイアス \(b\))とは区別され、私たち人間が「事前に」設定してあげる必要がある値なんです。
どのハイパーパラメータの値が一番良い結果をもたらすかは、残念ながら、扱うデータや解決したいタスクによって変わってきてしまうため、「これさえ設定すればOK!」という魔法のような値は存在しません。実際には、いくつかの異なる値を試してみて、その結果を比較しながら、まるで料理のレシピで塩加減や火加減を調整するように、最適な組み合わせを見つけ出していく、という地道な試行錯誤が必要になることが多いです。このあたりが、機械学習の面白いところでもあり、ちょっぴり根気がいるところでもありますね。最初は、よく使われる定番の値(例えば学習率なら0.001など)から試してみるのが良いスタートかもしれません。
さあ、これでモデルの設計図もできあがり、成績表とコーチも準備万端です。いよいよ次は、実際にデータを使ってモデルを訓練し、育てていくステップに進みます!どんな風にモデルが賢くなっていくのか、楽しみですね!
3. 医療時系列データを用いた実践
3. いよいよ実践!医療時系列データと向き合ってみよう
さて、これまでのセクションでLSTMの基本的な考え方や、PyTorchを使ったモデルの設計図の描き方、そしてモデルを賢くするための成績表(損失関数)と指導方針(最適化アルゴリズム)について学んできました。理論はバッチリ、道具も揃った、という感じでしょうか。
ここからは、いよいよ実際にデータを使って、私たちが作ったLSTMモデルに「学習」という経験をさせて、その成果を見ていくエキサイティングなパートです! とはいえ、実際の医療データは非常に複雑で、個人情報保護の観点からも取り扱いが難しかったり、前処理(データをモデルが食べやすい形に整える作業)に多くの手間がかかったりするものです。
そこで今回は、まずは基本をしっかり掴むために、少し単純化した「擬似(ぎじ)データ」、つまり人工的に作り出したサンプルデータを使って、モデルの学習から評価までの一連の流れを体験してみることにしましょう。これによって、実際の複雑なデータに挑戦する前の、いわば「ウォーミングアップ」ができるというわけです。
3.1 モデルの”ごはん”を用意しよう:サンプルデータの準備
私たちのLSTMモデルに何かを学んでもらうためには、まず学習の元となる「データ」が必要です。ここでは、架空の患者さんの日々の血糖値の変動をイメージして、比較的単純な「サインカーブ」という波形に、ちょっとだけランダムなノイズ(揺らぎ)を加えた時系列データを作ってみます。なぜサインカーブかというと、多くの自然現象や生体情報には周期的な変動が見られることがあり、そこに予測不可能な要素(ノイズ)が加わるというのは、時系列データの基本的な性質を捉えていると言えるからです。このデータを使って、「過去数日間の血糖値の動きから、次の日の血糖値を予測する」というタスクに挑戦してみましょう。
それでは、Pythonのコードを使って、このサンプルデータを作り、モデルが学習できる形に整えていきます。
# --- 必要なライブラリをインポート ---
import numpy as np
import matplotlib.pyplot as plt
# Matplotlibで日本語のタイトルやラベルが文字化けするのを防ぐため、
# japanize_matplotlib をインポートします。
# !!! 注意:事前に `pip install japanize-matplotlib` でインストールが必要です !!!
# Jupyter NotebookやGoogle Colabの場合 `!pip install japanize-matplotlib`
!pip install japanize-matplotlib
import japanize_matplotlib
# --- ステップ1: 時系列データの"素"を作る ---
# まず、NumPyライブラリを使って、元になるデータを作成します。
# 時間軸となる等間隔の数値列を作ります。0から99.9まで、0.1刻みで。
time = np.arange(0, 100, 0.1) # time は [0.0, 0.1, 0.2, ..., 99.9] という配列になります。
# サインカーブを計算します。これが基本的な変動パターン。
# np.sin() はNumPyのサイン関数です。
sin_wave = np.sin(time)
# サインカーブに、ちょっとしたランダムな揺らぎ(ノイズ)を加えます。
# np.random.randn(len(time)) で、timeと同じ数の正規分布に従う乱数を生成します。
# * 0.2 でノイズの大きさを調整しています。この値を大きくすると、よりギザギザしたデータになります。
noise = np.random.randn(len(time)) * 0.2
amplitude = sin_wave + noise # これが私たちの模擬的な血糖値データです。
# ちょっとここで、どんなデータができたか見てみましょうか。
plt.figure(figsize=(12, 4)) # グラフの描画サイズを指定
plt.plot(time[:200], amplitude[:200]) # データの最初200点だけプロットしてみます
plt.title('生成したサンプル時系列データ(最初の200点)') # ← 日本語タイトル
plt.xlabel('時間 (time)') # ← 日本語ラベル
plt.ylabel('値 (amplitude)') # ← 日本語ラベル
plt.grid(True)
plt.show()
(上記のコードを実行すると、サインカーブにノイズが乗ったような時系列データのグラフが表示されるはずです。これにより、私たちがこれから扱うデータのイメージが掴めると思います。)
# --- 【再掲】必要なライブラリをインポート ---
import torch # PyTorchライブラリ
import numpy as np # NumPyライブラリ (数値計算用)
import matplotlib.pyplot as plt # Matplotlibライブラリ (グラフ描画用)
import japanize_matplotlib # Matplotlibでの日本語表示用 (事前に pip install japanize-matplotlib が必要)
# ここから!
# --- ステップ2: PyTorchが扱える形に変換 ---
# NumPyで作ったデータを、PyTorchの「テンソル」という形式に変換します。
# また、多くのニューラルネットワーク処理では、データをfloat32型という浮動小数点数で扱うのが一般的です。
# .astype(np.float32) でデータ型をfloat32に変換。
# .reshape(-1, 1) で、データを (データ数, 1) という2次元の形に整えます。
# 「-1」は「残りの全ての要素」という意味で、ここではデータ数に応じて自動で決まります。
# 「1」は、各時刻の特徴量が1つ(今回は血糖値amplitudeのみ)であることを示します。
data_tensor = torch.from_numpy(amplitude.astype(np.float32)).reshape(-1, 1)
# print(f"data_tensorの形状: {data_tensor.shape}") # torch.Size([1000, 1]) のようになるはずです。
# --- ステップ3: 学習用と評価用にデータを分ける ---
# モデルを訓練するためのデータ(訓練データ)と、学習後のモデルの性能を評価するための
# 未知のデータ(テストデータ)に分割します。これは非常に重要です!
# モデルが訓練データだけを丸暗記してしまって、新しいデータには全く対応できない「過学習」を
# 見抜くためにも、必ず分けて評価します。
# ここでは、全体の80%を訓練用に、残りの20%をテスト用にしてみましょう。
train_data_ratio = 0.8 # 訓練データの割合
train_size = int(len(data_tensor) * train_data_ratio) # 訓練データのサンプル数を計算
# test_size = len(data_tensor) - train_size # テストデータのサンプル数を計算 (今回は直接使わない)
train_data = data_tensor[:train_size] # 訓練データの最初からtrain_size個までを訓練データとする
test_data = data_tensor[train_size:] # train_size個目以降をテストデータとする
# print(f"訓練データの形状: {train_data.shape}, テストデータの形状: {test_data.shape}")
# --- ステップ4: LSTMが学習しやすい形に入力シーケンスとターゲットを作る ---
# LSTMは、過去の連続したデータ(シーケンス)を見て、次の値を予測する、といったタスクが得意です。
# そこで、連続した時系列データを、「入力シーケンス」とその「次の値(ターゲット)」のペアに変換する関数を作ります。
# この処理は、よく「スライディングウィンドウ」という方法で説明されます。
def create_sequences(data, seq_length):
"""
連続した時系列データから、入力シーケンスとターゲットのペアを作成する関数。
Args:
data (torch.Tensor): 元の時系列データ (データ数, 1)。
seq_length (int): 1つの入力シーケンスの長さ(過去何時点を見るか)。
Returns:
Tuple[torch.Tensor, torch.Tensor]: 入力シーケンスのテンソル (サンプル数, seq_length, 1) と
ターゲットのテンソル (サンプル数, 1)。
"""
xs = [] # 入力シーケンスを格納するリスト
ys = [] # 対応するターゲット値を格納するリスト
# データ全体を、seq_lengthずつズラしながら見ていきます。
# 例えば、データが [d1, d2, d3, d4, d5] で seq_length が 3 なら、
# 1回目: x=[d1,d2,d3], y=d4
# 2回目: x=[d2,d3,d4], y=d5 といったペアを作ります。
for i in range(len(data) - seq_length):
# i番目から i+seq_length-1 番目までを入力シーケンスxとする
x = data[i:(i + seq_length)]
# i+seq_length 番目の値をターゲットyとする (次の値を予測)
y = data[i + seq_length]
xs.append(x)
ys.append(y)
# Pythonのリストに格納されたテンソルたちを、PyTorchの torch.stack を使って
# きれいに積み重ねて、1つの大きなテンソルにまとめます。
return torch.stack(xs), torch.stack(ys)
# 入力シーケンスの長さ(過去何日分のデータを使って次を予測するか)を決めます。
# この値も重要なハイパーパラメータの一つで、色々試してみる価値があります。
sequence_length = 10 # 例えば、過去10時点のデータを見ることにしましょう。
# 訓練用とテスト用のシーケンスデータとターゲットを作成します。
X_train, y_train = create_sequences(train_data, sequence_length)
X_test, y_test = create_sequences(test_data, sequence_length)
# print(f"X_trainの形状: {X_train.shape}") # (サンプル数, sequence_length, 1)
# print(f"y_trainの形状: {y_train.shape}") # (サンプル数, 1)
# --- ステップ5: DataLoaderでデータをミニバッチ化する ---
from torch.utils.data import DataLoader, TensorDataset # DataLoaderとTensorDatasetもここでインポートしておくと確実です
# 大量のデータを一度にモデルに渡すと、メモリをたくさん使ってしまったり、
# 学習が不安定になったりすることがあります。
# そこで、データを小さなかたまり(ミニバッチ)に分けて、少しずつモデルに供給するのが一般的です。
# そのための便利な道具が DataLoader です。
# DataLoaderは、元になるデータセット (TensorDataset) と、
# 1回あたりのバッチサイズを指定して作ります。
batch_size = 32 # 1回の学習ステップで、32個のシーケンスデータをまとめて処理します。
# 訓練データ用のDataLoaderを作ります。
# TensorDatasetは、入力テンソル (X_train) とターゲットテンソル (y_train) をペアにしてくれます。
# shuffle=True にすると、エポック(学習の周回)ごとにデータの順番をシャッフルしてくれます。
# これにより、モデルがデータの特定の順番に過度に適合するのを防ぎ、学習の安定化や汎化性能の向上に繋がることが期待できます。
train_dataset = TensorDataset(X_train, y_train)
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True, drop_last=True)
# drop_last=True は、最後のバッチがbatch_sizeに満たない場合に、その不完全なバッチを捨てるオプションです。
# 必須ではありませんが、バッチサイズが揃っている方が処理しやすい場合があります。
# テストデータ用のDataLoaderも同様に作ります。
# ただし、評価の際はデータの順番をシャッフルする必要はないので、shuffle=False のままです。
test_dataset = TensorDataset(X_test, y_test)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False, drop_last=True)
# これで、モデルに与えるためのデータ準備は完了です!
# ちょっと確認で、X_trainとy_trainの形状を出力してみましょう。
# この形状が、先ほど定義したMedicalLSTMモデルの入力と出力の形式に合っているか確認することが大切です。
print(f"最終的な訓練入力データの形状 (X_trainをDataLoaderに通す前): {X_train.shape}")
print(f"最終的な訓練ターゲットデータの形状 (y_trainをDataLoaderに通す前): {y_train.shape}")
# この後に、エラーが出ていた amplitude を使用するコード(ステップ1のデータ生成部分)を続ける
# もし、amplitude がこのコードブロックより前の部分で定義されている場合は、
# その定義部分もこのコードブロックの前に含めるか、
# あるいは、このコードブロックを実行する前に必ず前の部分を実行してください。
# ここでは、amplitude が未定義である可能性も考慮し、サンプルとして再定義しておきます。
if 'amplitude' not in locals() and 'amplitude' not in globals():
print_warning = True
# 時間軸となる等間隔の数値列を作ります。0から99.9まで、0.1刻みで。
time_for_amplitude = np.arange(0, 100, 0.1)
# サインカーブを計算します。
sin_wave_for_amplitude = np.sin(time_for_amplitude)
# サインカーブに、ランダムなノイズを加えます。
noise_for_amplitude = np.random.randn(len(time_for_amplitude)) * 0.2
amplitude = sin_wave_for_amplitude + noise_for_amplitude # amplitude をここで定義
if print_warning:
print("\n[注意] 'amplitude'が未定義だったため、サンプルデータを再生成しました。\n前のステップで'amplitude'が正しく生成されているか確認してください。\n")
# 再度、PyTorchテンソルへの変換(エラー箇所)
# .astype(np.float32) でデータ型をfloat32に変換。
# .reshape(-1, 1) で、データを (データ数, 1) という2次元の形に整えます。
data_tensor = torch.from_numpy(amplitude.astype(np.float32)).reshape(-1, 1)
print(f"data_tensorの形状 (修正後): {data_tensor.shape}")
最終的な訓練入力データの形状 (X_trainをDataLoaderに通す前): torch.Size([790, 10, 1])
最終的な訓練ターゲットデータの形状 (y_trainをDataLoaderに通す前): torch.Size([790, 1])
少し解説です:
- データ生成:
np.arangeで時間軸を作り、np.sinで基本的な波形、np.random.randnでノイズを生成し、それらを足し合わせることで、周期性とランダム性を持つ時系列データを作っています。これは、多くの実際の時系列データが持つ特性を単純化したものです。torch.from_numpyでNumPy配列をPyTorchテンソルに変換し、.astype(np.float32)でデータ型を統一、.reshape(-1, 1)で形状を(データ点数, 1)にしています。この「1」は、各時刻で観測される特徴量が1つ(今回は模擬血糖値のみ)であることを意味します。
- データ分割:
- モデルが学習に使ったデータだけで性能を評価すると、そのデータにだけ特化した「カンニング」のような状態になりかねません。そのため、学習には使わない未知のデータ(テストデータ)を用意して、モデルの真の「実力(汎化性能)」を測るのが一般的です。
create_sequences関数とスライディングウィンドウ:- この関数は、連続した時系列データを、LSTMが学習しやすい「入力シーケンス(過去のデータ)」と「ターゲット(予測したい未来のデータ)」のペアに変換します。 例えば、
seq_length = 3で、データが[10, 20, 30, 40, 50]だとすると、元のデータ: [10, 20, 30, 40, 50] seq_length = 3 の場合: 入力シーケンス(x) ターゲット(y) ----------------- ----------- [10, 20, 30] 40 [20, 30, 40] 50というペアが2つ作られるイメージです。seq_lengthは、過去どれくらいの期間のデータパターンをモデルに見せるかを決める重要なパラメータです。 torch.stack(xs)は、リストに格納された複数のテンソル(この場合は各入力シーケンス)を、新しい次元で積み重ねて一つの大きなテンソルにまとめます。結果として、X_trainの形状は(作成されたシーケンスの数, sequence_length, 1)となります。
- この関数は、連続した時系列データを、LSTMが学習しやすい「入力シーケンス(過去のデータ)」と「ターゲット(予測したい未来のデータ)」のペアに変換します。 例えば、
DataLoaderの役割:TensorDatasetは、入力シーケンスX_trainとそれに対応する正解ラベルy_trainを、インデックスでアクセスできるペアの形で保持してくれます。いわば、データのお弁当箱のようなものです。DataLoaderは、このお弁当箱(TensorDataset)から、指定したbatch_size(例えば32個)ずつデータを取り出して、モデルに供給してくれる給仕係のような役割です。これにより、メモリに優しいミニバッチ学習が可能になります。また、shuffle=True(訓練時)にすることで、エポックごとにデータの供給順をランダムに変え、学習の偏りを防ぎます。
ひとつ、とても大切な補足:データの正規化(Normalization)/ 標準化(Standardization)について
今回のサンプルデータは、もともと値の範囲が-1から1程度に収まっているサインカーブをベースにしているので、特別な処理はしていません。しかし、実際の医療データ(例えば、心拍数が60~100、血圧が80~120、体温が36~38℃など)を扱う場合、それぞれの特徴量の数値のスケール(範囲や単位)が大きく異なることがよくあります。
このようなスケールの異なるデータをそのままニューラルネットワークに入力すると、値が大きい特徴量に学習が引っ張られてしまったり、学習の収束が遅くなったり、不安定になったりすることがあります。そのため、通常は学習を始める前に、すべての特徴量のスケールを一定の範囲に揃える「正規化」や「標準化」という前処理を行います。
- 正規化 (Normalization): 例えば、値を0から1の範囲、あるいは-1から1の範囲に変換します。
sklearn.preprocessing.MinMaxScalerなどがよく使われます。 - 標準化 (Standardization): 値を平均0、標準偏差1となるように変換します。
sklearn.preprocessing.StandardScalerなどがよく使われます。
どちらを使うかはデータやタスクによりますが、多くの場合、これらの処理は学習の安定性や性能向上に大きく貢献するので、実データを扱う際には「ほぼ必須のステップ」と考えておくと良いでしょう。今回はあくまでPyTorchとLSTMの基本的な使い方に焦点を当てるため省略していますが、ぜひ頭の片隅に置いておいてくださいね。
さあ、これでモデルを訓練するための準備が整いました!次はいよいよ、このデータを使ってモデルを学習させていきます。
3.2 モデルを鍛えよう:学習ループの実装
データも準備できたし、モデルの設計図も、成績表(損失関数)も、指導方針(オプティマイザ)も手元にあります。いよいよ、私たちのLSTMモデルに「学習」というトレーニングを積ませて、賢くなってもらう段階です!
ニューラルネットワークの学習は、基本的に「繰り返し」のプロセスです。用意した訓練データセット全体を何度も何度もモデルに見せて(これを「エポック (epoch)」と呼びます)、そのたびにモデルの予測と正解を比較し、間違い(損失)が小さくなるようにモデル内部のパラメータ(重みやバイアス)を少しずつ調整していきます。この一連の繰り返し作業を「学習ループ」と呼びます。
それでは、具体的な学習ループのコードを見ていきましょう。
# --- 【再掲】必要なライブラリをインポート ---
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset # DataLoaderとTensorDatasetも必要
import numpy as np # データ生成や操作にNumPyも必要
import matplotlib.pyplot as plt # グラフ描画にMatplotlibも必要
import japanize_matplotlib # 日本語表示のため (事前に pip install japanize_matplotlib が必要)
# --- 【再掲】モデルの定義 (MedicalLSTMクラス) ---
# このクラス定義は、学習ループの前に一度だけ行えばOKです。
class MedicalLSTM(nn.Module):
def __init__(self, input_size, hidden_size, num_layers, output_size):
super(MedicalLSTM, self).__init__()
self.hidden_size = hidden_size
self.num_layers = num_layers
self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True)
self.fc = nn.Linear(hidden_size, output_size)
def forward(self, x):
h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(x.device)
c0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(x.device)
out, _ = self.lstm(x, (h0, c0))
out = self.fc(out[:, -1, :])
return out
# --- 【再掲】モデルのインスタンス化 ---
# ここで実際にモデルの実体を作成し、'model'という変数に格納します。
# パラメータは、ご自身のタスクに合わせて調整してください。
input_size = 1 # 入力特徴量の数
hidden_size = 50 # LSTMの隠れ状態の次元数
num_layers = 2 # LSTM層の数
output_size = 1 # 出力(予測する値)の数
model = MedicalLSTM(input_size, hidden_size, num_layers, output_size)
# --- 【再掲】損失関数と最適化アルゴリズムの定義 ---
# これらも学習ループの前に定義しておく必要があります。
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
# --- 【再掲】データローダーの準備 (train_loader) ---
# train_loader も学習ループの前に定義されている必要があります。
# 以下はダミーデータとダミーローダーの例です。
# 実際には、前のステップで作成した train_loader を使用してください。
# もし train_loader が未定義の場合は、この部分を実際のデータローダー作成コードに置き換えるか、
# 前のセルの実行を確実に行ってください。
if 'train_loader' not in locals() and 'train_loader' not in globals():
print_warning_loader = True
# ダミーの訓練データとターゲットデータを作成 (形状を合わせるための例)
# 実際には、前のステップで作成した X_train, y_train を使用
dummy_X_train = torch.randn(100, 10, input_size) # (サンプル数, シーケンス長, input_size)
dummy_y_train = torch.randn(100, output_size) # (サンプル数, output_size)
dummy_train_dataset = TensorDataset(dummy_X_train, dummy_y_train)
train_loader = DataLoader(dummy_train_dataset, batch_size=32)
if print_warning_loader:
print("\n[注意] 'train_loader'が未定義だったため、ダミーデータで作成しました。\n実際の'train_loader'が正しく定義・生成されているか確認してください。\n")
# ここから!
# --- 学習の準備 ---
# 何エポック学習させるか (データセット全体を何周するか) を決めます。
num_epochs = 50 # 今回は50周してみましょう。
# モデルを「学習モード」に設定します。
# これは、例えばDropout層やBatchNorm層(今回は使っていませんが)など、
# 学習時と評価時で振る舞いが変わる層がある場合に、適切に動作させるためのお約束です。
model.train() # ここで 'model' が参照されます
# 各エポックでの訓練損失の値を記録しておくためのリストを用意します。
# 後で学習がうまくいったかグラフで確認するのに使います。
train_losses = []
print("学習を開始します...")
# --- 学習ループの開始 ---
# 指定したエポック数だけ、以下の処理を繰り返します。
for epoch in range(num_epochs):
# 各エポックの開始時に、そのエポックでの合計損失をリセットしておきます。
current_epoch_loss = 0.0
# train_loaderから、ミニバッチ単位でデータを取り出して処理します。
# train_loaderは (入力シーケンスのバッチ, 対応するターゲットのバッチ) の形でデータを返します。
for batch_sequences, batch_labels in train_loader:
# sequencesの形状: (batch_size, sequence_length, input_size)
# labelsの形状: (batch_size, output_size)
# 1. 勾配のリセット (毎回のお清め)
# PyTorchでは、勾配は計算されるたびに加算されていく仕様になっています。
# なので、新しいミニバッチで勾配を計算する前に、必ず古い勾配をゼロにリセットします。
# これを忘れると、意図しない学習が進んでしまいます。
optimizer.zero_grad()
# 2. モデルによる予測
# 現在のミニバッチの入力シーケンス (batch_sequences) をモデルに入力し、
# 予測値 (outputs) を得ます。これは forward メソッドが呼び出される処理ですね。
outputs = model(batch_sequences)
# 3. 損失の計算 (モデルの答え合わせ)
# モデルの予測値 (outputs) と、実際の正解ラベル (batch_labels) を使って、
# 損失関数 (criterion、今回はMSE) で損失 (間違いの度合い) を計算します。
loss = criterion(outputs, batch_labels)
# 4. 誤差逆伝播 (間違いの原因究明)
# 計算された損失 (loss) に基づいて、モデルの各パラメータが
# どれだけその損失に「責任」があるか(つまり勾配)を、
# 出力側から入力側へと逆向きに計算していきます。
loss.backward()
# 5. パラメータの更新 (反省と改善)
# 計算された勾配 (各パラメータがどっちにどれだけ動けば損失が減るかの情報) を使って、
# 最適化アルゴリズム (optimizer、今回はAdam) がモデルのパラメータを更新します。
# これでモデルが少しだけ賢くなります。
optimizer.step()
# このバッチでの損失を、エポックの合計損失に加算しておきます。
# lossはテンソルなので、.item() でPythonの数値として取り出します。
current_epoch_loss += loss.item()
# 1エポック分の全てのミニバッチ処理が終わったら、
# そのエポックでの平均損失を計算して記録します。
avg_epoch_loss = current_epoch_loss / len(train_loader)
train_losses.append(avg_epoch_loss)
# 学習の進捗が分かるように、各エポックの最後に損失を表示します。
# (epoch + 1) としているのは、epochが0から始まるため、人間が見やすいように1から表示するためです。
# :.4f は、小数点以下4桁まで表示するという書式指定です。
if (epoch + 1) % 5 == 0: # 5エポックごとに表示
print(f'エポック [{epoch + 1}/{num_epochs}], 平均損失: {avg_epoch_loss:.4f}')
print("学習が完了しました!")
# --- 学習曲線のプロット ---
# 学習がちゃんと進んだか(損失がエポックごとに減少したか)をグラフで見てみましょう。
# これを「学習曲線」と呼びます。
plt.figure(figsize=(10, 5))
plt.plot(train_losses, label='訓練損失 (MSE)')
plt.title('訓練損失の推移')
plt.xlabel('エポック数')
plt.ylabel('平均損失')
plt.legend() # 凡例を表示
plt.grid(True) # グリッド線を表示
plt.show()
学習を開始します...
エポック [5/50], 平均損失: 0.0209
エポック [10/50], 平均損失: 0.0132
エポック [15/50], 平均損失: 0.0106
エポック [20/50], 平均損失: 0.0087
エポック [25/50], 平均損失: 0.0077
エポック [30/50], 平均損失: 0.0068
エポック [35/50], 平均損失: 0.0063
エポック [40/50], 平均損失: 0.0057
エポック [45/50], 平均損失: 0.0052
エポック [50/50], 平均損失: 0.0049
学習が完了しました!

(上記のコードを実行すると、学習の進行状況(各エポックでの損失)が出力され、最後に訓練損失の推移を示す学習曲線グラフが表示されるはずです。損失がエポックを重ねるごとに順調に減少していれば、学習がうまくいっている兆候と言えますね!)
学習ループのポイントをもう一度おさらい:
- エポック (Epoch): 訓練データセット全体を1周すること。このエポック数を重ねることで、モデルは徐々にデータの特徴を学んでいきます。
- ミニバッチ (Mini-batch): 訓練データを小さな塊に分割したもの。
DataLoaderがこれを用意してくれます。 model.train(): モデルを「今から訓練するぞ!」というモードに切り替えます。Dropoutなどの挙動が変わります。optimizer.zero_grad(): 各ミニバッチの最初に、前のバッチで計算された勾配情報をクリアします。これ、忘れがちですが超重要です!outputs = model(sequences): モデルに現在のミニバッチデータを入力し、予測結果を得ます。loss = criterion(outputs, labels): モデルの予測と正解を比較し、損失(間違い具合)を計算します。loss.backward(): 損失を元に、各パラメータがどれだけ損失に影響したか(勾配)を計算します。いわば、モデルの「反省点」を見つけ出すプロセスです。optimizer.step(): 計算された勾配情報を使って、モデルのパラメータを「より良くなる方向」へ少しだけ更新します。これが「学習」そのものです。
この一連の流れを何度も何度も繰り返すことで、モデルは与えられたデータの中からパターンを見つけ出し、より正確な予測ができるように成長していくわけです。なんだか、地道な努力を重ねて成長していくアスリートみたいですよね。
学習曲線を見て、損失がちゃんと下がっていれば一安心ですが、もし損失が下がらなかったり、途中で振動したり、逆に上がってしまったりした場合は、学習率が大きすぎるのかもしれない、モデルの構造が複雑すぎる(または単純すぎる)のかもしれない、など、色々な原因が考えられます。そういった場合は、ハイパーパラメータの調整やモデル構造の見直しなどが必要になってきます。このあたりが、機械学習の試行錯誤の面白さでもあり、難しさでもあるところですね。
3.3 実力診断!モデルの評価と未来予測
さて、私たちのLSTMモデルは、訓練データを使って一生懸命学習してくれました。でも、本当に賢くなったのでしょうか? 訓練データで良い成績を出すのは当然として、モデルが本当に実力があるかどうかは、学習には使っていない「未知のデータ」、つまり「テストデータ」を使って評価してあげる必要があります。これがモデルの「汎化性能」を見るということですね。模擬試験みたいなものです。
それでは、学習済みのモデルを使って、テストデータに対する予測を行い、その精度を評価してみましょう。
# --- 評価の準備 ---
# モデルを「評価モード」に切り替えます。
# これにより、Dropout層などが無効になり、学習時とは異なる挙動になります。
# 評価時には、学習時のランダム性を排除して、一貫した予測結果を得るためです。
model.eval()
# 予測結果 (predictions) と実際の値 (actuals) を保存するためのリストを用意します。
test_predictions = []
actual_values = []
# --- 評価ループ ---
# 評価時には、勾配計算は不要です(パラメータの更新はしないので)。
# torch.no_grad() のコンテキスト内で行うことで、余計な計算を省き、メモリ効率も良くなります。
print("テストデータで評価を開始します...")
with torch.no_grad():
# test_loaderから、ミニバッチ単位でテストデータを取り出します。
for batch_sequences, batch_labels in test_loader:
# モデルにテスト用の入力シーケンス (batch_sequences) を与えて、予測値 (outputs) を得ます。
outputs = model(batch_sequences)
# 予測結果と実際の値を、後でまとめて処理しやすいようにリストに格納していきます。
# .cpu() は、もしデータがGPU上にあればCPUに移動させる処理です(NumPyはCPUで動作するため)。
# .numpy() は、PyTorchテンソルをNumPy配列に変換します。
# .flatten() は、多次元配列を1次元配列に平坦化します (今回は (batch_size, 1) -> (batch_size,) のような変換)。
test_predictions.extend(outputs.cpu().numpy().flatten())
actual_values.extend(batch_labels.cpu().numpy().flatten())
# --- 評価指標の計算 ---
# 予測タスクでよく使われる評価指標の一つに、RMSE (Root Mean Squared Error: 二乗平均平方根誤差) があります。
# これは、MSE (平均二乗誤差) の平方根を取ったもので、誤差の大きさを元のデータと同じ単位で評価できるため、
# 直感的に理解しやすいというメリットがあります。
# RMSE = sqrt( (1/N) * Σ(予測値 - 実際値)^2 )
# まずは、リストに格納した予測値と実際の値をNumPy配列に変換します。
test_predictions_np = np.array(test_predictions)
actual_values_np = np.array(actual_values)
# MSEを計算します。
mse_test = np.mean((test_predictions_np - actual_values_np)**2)
# RMSEを計算します。
rmse_test = np.sqrt(mse_test)
print(f'テストデータでのMSE: {mse_test:.4f}')
print(f'テストデータでのRMSE: {rmse_test:.4f}') # この値が小さいほど、予測精度が高いと言えます。
# --- 予測結果の可視化 ---
# 実際にモデルがどんな予測をしたのか、実際の値と重ねてグラフで見てみましょう。
# これにより、モデルがどの程度うまくパターンを捉えられているか、視覚的に確認できます。
plt.figure(figsize=(12, 6))
plt.plot(actual_values_np, label='実際の値 (テストデータ)', color='blue', marker='.', linestyle='-')
plt.plot(test_predictions_np, label='モデルによる予測値', color='red', marker='.', linestyle='--')
plt.title('医療時系列データの予測結果(テストデータ)')
plt.xlabel('時間ステップ(テストデータ内)')
plt.ylabel('値')
plt.legend()
plt.grid(True)
plt.show()
テストデータで評価を開始します...
テストデータでのMSE: 0.0069
テストデータでのRMSE: 0.0832
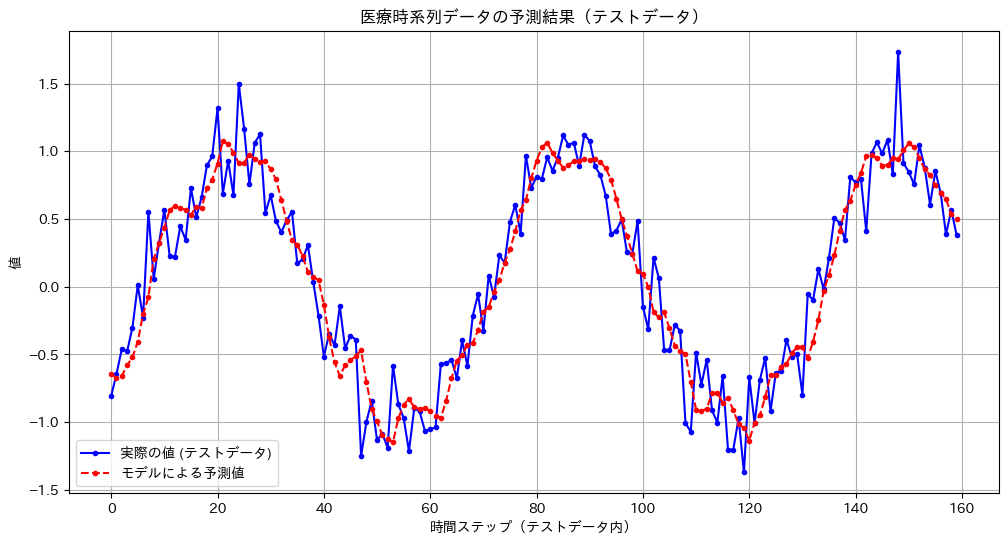
(上記のコードを実行すると、テストデータに対するMSEとRMSEの値が出力され、最後に実際の値とモデルの予測値を比較するグラフが表示されるはずです。赤い破線(予測値)が青い実線(実際の値)にどれだけ近いかで、モデルの性能を直感的に判断できますね。)
評価と予測のポイント:
model.eval(): 評価モードへの切り替えは、学習済みモデルの真の実力を測るためのお約束です。with torch.no_grad():: これで囲むことで、評価時には不要な勾配計算を停止させ、メモリ使用量を抑えつつ計算速度を上げることができます。賢い節約術ですね。- RMSE (Root Mean Squared Error): \( \text{RMSE} = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (y_i – \hat{y}_i)^2} \) という式で計算され、予測誤差の平均的な大きさを元のデータの単位で示してくれます。例えば、血糖値の予測なら、RMSEが5であれば、平均的に5mg/dL程度の誤差で予測できている、というような解釈ができます(あくまで単純化した例ですが)。この値が小さいほど、モデルの予測精度が高いと言えます。
- 結果の可視化: 数値だけではピンとこないモデルの挙動も、グラフにしてみることで「どこが得意で、どこが苦手なのか」「系統的なズレはあるか」といった傾向が見えてくることがあります。これは、モデルをさらに改善していく上での重要なヒントになったりします。
これで、サンプルデータを用いたLSTMモデルの学習から評価、そして予測までの一連の流れを体験することができました!もちろん、今回の擬似データは非常に単純化されたものです。実際の医療現場で得られるデータは、もっと多くの特徴量を含んでいたり、欠損があったり、ノイズが大きかったり、不規則な間隔で記録されていたりと、はるかに複雑です。しかし、今回学んだ「データの準備 → モデルの定義 → 学習 → 評価」という基本的な流れは、そういった複雑なデータに挑む際にも共通する土台となるはずです。
この経験を足がかりに、ぜひ皆さんの興味のある医療データで、AIによる予測や分析に挑戦してみてください。最初はうまくいかないことも多いかもしれませんが、試行錯誤を繰り返す中で、きっと新しい発見や面白い結果が得られると思います!
4. LSTMの医療分野への応用例と可能性
4. LSTMが開く医療の未来:応用例と私たちが考えるべきこと
さて、ここまでLSTMの仕組みから実際のプログラミングまで、一緒に手を動かしながら学んできました。頭の中では、あの複雑なゲートの仕組みや、PyTorchのコードがぐるぐる回っているかもしれませんね。でも、一番大切なのは「で、これを使って何ができるの?私たちの医療現場にどんな良いことがあるの?」という疑問に答えることだと、私は思います。
このセクションでは、LSTMがその「時系列データを読み解く力」を活かして、医療の様々な分野でどのような応用が期待されているのか、具体的な例を挙げながら見ていきたいと思います。そして同時に、この素晴らしい技術を実用化していく上で、私たちが向き合わなければならない課題や、倫理的な側面についても、少し立ち止まって考えてみる時間にしたいと思います。技術の進歩はいつも光と影を伴いますからね。
4.1 LSTM、医療現場での活躍ポテンシャル!具体的な応用例あれこれ
LSTMの「過去の文脈をしっかり記憶し、未来を予測する」という能力は、時間の経過と共に変化する多くの医療データと非常に相性が良いんです。まるで、経験豊富なベテランの医療従事者が、患者さんの細かな変化の積み重ねから何かを察知するような、そんな働きをAIで実現しようという試みとも言えるかもしれません。
具体的にどんな分野で期待されているのか、いくつかピックアップしてご紹介しましょう。
疾患の早期発見・予測:見えないサインを捉える挑戦
病気が本格的に進行する前に、その小さな「芽」を見つけ出すことができれば、治療の選択肢も広がり、患者さんのQOL(生活の質)向上にも大きく貢献できるはずです。LSTMは、そんな「早期発見・予測」の領域で、大きな期待が寄せられています。
- 心臓のささやきを聞き取る:心不全や不整脈の予測
心電図(ECG)のデータは、まさに時間の流れと共に記録される典型的な医療情報ですよね。LSTMは、このECGの波形パターンを学習することで、例えば数時間後、あるいは数日後に起こりうる心不全の急性増悪や、心室細動といった命に関わる危険な不整脈の発生リスクを予測しようという研究が進められています [2, 3]。もし、患者さん自身も気づかないような心電図の微細な変化の積み重ねから、LSTMが「おっと、これは少し注意が必要なサインかもしれませんよ」と警告を発してくれたら、予防的な対応や迅速な治療介入への道が開けるかもしれません。まさに、”未病を治す”という理想に一歩近づけるかもしれない、そんな期待感があります。 - ICUの静かなる危機を見抜く:敗血症の早期アラート
集中治療室(ICU)では、患者さんの心拍数、血圧、呼吸数、体温といったバイタルサインや、様々な検査値が、それこそ秒単位で連続的にモニタリングされています。これらは、まさに「多変量時系列データ」と呼ばれるもので、複数の情報が絡み合いながら時間と共に変化していきます。LSTMは、これらの複雑な情報をまとめて入力として受け取り、例えば敗血症(感染症によって重篤な臓器障害が引き起こされる状態)の発症リスクを、実際に症状が現れる数時間前に予測するシステムの開発が進んでいます [4]。敗血症は時間との戦いですから、この「数時間前」というアドバンテージが、治療成績を大きく左右する可能性があるのです。【多変量時系列データとLSTMのイメージ】 時刻 t-2 時刻 t-1 時刻 t ---------- ---------- ---------- 心拍数: 70 心拍数: 75 心拍数: 85 ----↘ 血圧: 120/80 血圧: 125/82 血圧: 130/88 ----→ LSTM ----→ 敗血症リスク高 (予測) 体温: 36.5 体温: 36.8 体温: 37.5 ----↗ ユニット SpO2: 98% SpO2: 97% SpO2: 95% --↗ ... ... ... (過去の複数のバイタルサインの推移を総合的に判断)この図のように、複数の異なる種類の時系列データ(心拍数、血圧など)を同時にLSTMに入力することで、それぞれのデータの関連性や時間的な変化のパターンを捉え、より高度な予測を目指すわけですね。 - 脳波のパターンから発作を読む:てんかん発作の予測
脳波(EEG)もまた、非常に複雑でダイナミックに変化する時系列信号です。LSTMを使って、てんかん発作が起こる前のEEGデータに潜む特徴的なパターン(発作前兆波形などと呼ばれることもあります)を検出し、発作そのものを事前に予測しようという研究も活発に行われています [5]。もし予測が可能になれば、患者さんが事前に安全な場所に移動したり、場合によっては予防的な薬剤を服用したりする時間を確保できるかもしれません。これは、患者さんの日常生活の安心感に大きく貢献する可能性がありますよね。
治療効果のモニタリングと個別化:一人ひとりに最適な医療を目指して
病気の治療は、画一的なものではなく、患者さん一人ひとりの状態や反応に合わせて調整していくことが理想です。LSTMは、治療経過のモニタリングや、その効果を予測することで、より個別化された医療の実現をサポートする可能性を秘めています。
- 血糖値のジェットコースターを乗りこなす:糖尿病患者さんの血糖値管理
糖尿病の患者さんにとって、日々の血糖コントロールは非常に重要です。最近では、持続血糖モニター(CGM)という、皮下にセンサーを留置して血糖値をリアルタイムで連続的に測定できるデバイスも普及してきました。このCGMから得られる膨大な血糖値の時系列データをLSTMで分析し、例えば数時間後の血糖値を予測する。そんなことができれば、インスリンの投与量をよりきめ細かく調整したり、危険な低血糖や高血糖になる前にアラートを出したりすることに役立てられるかもしれません [6]。患者さん自身が、まるで天気予報を見るように自分の血糖値の未来を予測できたら、日々の自己管理も、もっと主体的に、そして安心して行えるようになるのではないでしょうか。 - 心の波を見守る:精神疾患の症状変動予測
うつ病や双極性障害といった精神疾患では、症状が良くなったり悪くなったり、波のように変動することがあります。最近では、スマートフォンアプリやスマートウォッチのようなウェアラブルデバイスを通じて、日々の活動量、睡眠のパターン、あるいは簡単な気分の記録などを手軽に収集できるようになってきました。これらの日常生活のデジタルな記録(デジタルフェノタイプとも呼ばれます)もまた、一種の時系列データです。LSTMを使ってこれらのデータを分析することで、症状が悪化する兆候や再発のサインを早期に捉え、適切なタイミングで医療者や家族がサポートに入るきっかけを作れるかもしれない、といった研究が進められています [7]。
患者さんの行動パターン理解とリハビリ支援
患者さんの日常の行動や、リハビリテーションの過程も、時系列的な視点から捉えることで新しい知見が得られることがあります。
- リハビリの成果を可視化する:リハビリテーション効果の定量的評価
脳卒中後のリハビリテーションなどでは、患者さんが日々どのような動作をしているか、その改善度はどうか、といった情報が重要になります。ウェアラブルセンサー(加速度センサーやジャイロセンサーなど)を使って、リハビリ中の患者さんの動作データを連続的に収集し、そのデータをLSTMで分析することで、回復の進捗度を客観的かつ定量的に評価したり、あるいは、より効果的なリハビリ計画の個別最適化に繋げたりすることが期待されています。経験豊富な療法士の方の「目」に加えて、データに基づいた客観的な指標が得られれば、リハビリの質向上に貢献できるかもしれませんね。 - 睡眠の質を科学する:睡眠ステージの自動分類
質の良い睡眠は健康の基本ですが、睡眠障害に悩む方も少なくありません。睡眠の状態を詳しく調べるためには、睡眠ポリグラフ検査(PSG)という、脳波(EEG)、眼球運動(EOG)、筋電図(EMG)など、複数の生体信号を一晩中記録する検査が行われます。このPSGデータもまた複雑な多変量時系列データであり、従来は専門家が目で見て睡眠ステージ(レム睡眠、ノンレム睡眠の各段階など)を判定していました。LSTMを用いることで、この睡眠ステージの分類を自動化しようという研究が進んでおり [8]、睡眠障害の診断支援や、より大規模な睡眠研究への応用が期待されています。
ICUにおける包括的な患者モニタリング
先ほどの敗血症予測もそうですが、ICUでは多種多様なバイタルサインや検査値が絶え間なく集積されています。LSTMは、これらの情報を統合的に学習することで、単一の指標だけでは見逃してしまうかもしれない患者さんの状態変化の予兆を捉え、医療スタッフに早期にアラートを発するような、より包括的な患者監視システムの開発にも貢献できると考えられています。
ここに挙げたのは、ほんの一例です。他にも、ゲノム情報と経時的な臨床データを統合した解析や、医療画像の経時変化の追跡など、LSTMの応用範囲はまだまだ広がっていく可能性を秘めていると思います。
4.2 光と影:医療AI導入における課題と私たちが心に留めておくべきこと
さて、ここまでLSTMが医療分野で切り拓くかもしれない、ワクワクするような可能性についてお話ししてきました。まるで夢のような技術に思えるかもしれませんが、どんな強力なツールも、その使い方を誤ったり、準備を怠ったりすると、思わぬ問題を引き起こすことがあります。LSTMを含むAI技術を医療現場に安全かつ有効に導入していくためには、いくつかの重要な「ハードル」や、倫理的に考えなければならない側面があることを、私たちはしっかりと認識しておく必要があるでしょう。
データの「質」と「量」:良い料理は良い材料から
AIモデル、特に深層学習モデルを賢く育てるためには、質の高い、そして十分な量の学習データが不可欠です。「Garbage In, Garbage Out(ゴミを入力すれば、ゴミしか出てこない)」という言葉があるように、不正確だったり、偏っていたりするデータで学習させたモデルは、信頼できる結果を出してくれません。医療データは、残念ながら、しばしば記録が不統一だったり、入力ミスや欠損値(データが抜け落ちていること)が多かったり、あるいは施設ごとにデータの形式がバラバラだったりすることがあります。このような「生の」データを、AIが学習できるような「きれいな」データに整える「前処理」という作業には、実は大変な労力と専門知識が必要とされることが多いのです。これが、医療AI開発の現場でよく聞かれる悩みの一つですね。
また、希少疾患のように、そもそも症例数が少なく、十分な量のデータが集められないケースもあります。データが少ないと、モデルは一般的なパターンを学習することが難しくなり、未知の状況に対応する能力(汎化性能)が低くなってしまう可能性があります。この「データ不足問題」も、医療AIが乗り越えるべき大きな壁の一つと言えるでしょう。
プライバシーとセキュリティ:守るべき大切な情報
言うまでもありませんが、患者さんの医療情報は、極めて機密性の高い個人情報です。氏名や生年月日だけでなく、病歴、検査結果、遺伝情報など、その人の人生そのものに関わるデリケートな情報が詰まっています。これらのデータをAIの学習に利用する際には、患者さんのプライバシーを最大限に尊重し、情報が外部に漏洩したり、不正に利用されたりすることのないよう、厳格なセキュリティ対策と法的・倫理的な枠組みの遵守が絶対条件となります。日本の個人情報保護法、アメリカのHIPAA、ヨーロッパのGDPRといった各国の規制はもちろんのこと、データを匿名化する技術(例えば、k-匿名化や差分プライバシーといった考え方があります)や、データを一箇所に集めずに各医療機関内で分散したまま学習を行う「連合学習(Federated Learning)」のような、プライバシー保護に配慮した新しい技術の活用も進められています。それでもなお、「どこまで匿名化すれば十分なのか」「完全にリスクをゼロにできるのか」といった問いは、常に私たちに突きつけられています。
モデルの「心の声」を聞きたい:解釈可能性と透明性 (Explainable AI – XAI)
特にLSTMのような深層学習モデルは、その内部構造が非常に複雑なため、なぜそのような予測や判断を下したのか、その「理由」や「根拠」を人間が理解することが難しい、いわゆる「ブラックボックス」になりがちです。医療の現場では、医師が最終的な診断や治療方針を決定するわけですから、AIが出してきた結果を鵜呑みにするわけにはいきませんよね。「このAIは、何を根拠にこの患者さんのリスクが高いと判断したのだろう?」という疑問に答えられないと、医師は安心してそのAIの情報を活用することができませんし、ましてや患者さんにその判断を説明することも困難です。そこで重要になってくるのが、「説明可能なAI (Explainable AI – XAI)」という考え方や技術です [9]。モデルが判断に至った根拠を可視化したり、人間が理解できる形で示してくれたりするXAIの技術は、AIと医療従事者が「協調」して、より良い医療を目指すための鍵となると言えるでしょう。ただ、このXAIもまだ発展途上の技術であり、どこまで「本当に説明できた」と言えるのか、その評価も難しいのが現状です。
隠れた偏見が結果を歪める:バイアスと公平性の問題
AIモデルは、学習に使われたデータに含まれるパターンを忠実に学習します。もし、その学習データに、特定の性別、人種、年齢層、あるいは社会経済的背景を持つ人々に関する「偏り(バイアス)」が含まれていたらどうなるでしょうか? 例えば、ある疾患の診断AIを開発する際に、特定の集団のデータばかりで学習させてしまうと、そのAIは、データの少なかった集団に対してはうまく機能せず、結果として診断の精度に差が出てしまうかもしれません。これは、医療アクセスにおける既存の格差を、AIが意図せず助長してしまう危険性をはらんでいます。医療AIは、全ての人々に対して公平で、恩恵をもたらすものでなければなりません。そのためには、学習データの収集段階から多様性に配慮し、モデルの性能評価においても、異なる集団間で公平性が保たれているかを検証する努力が不可欠です。「データは社会の鏡」とも言われますが、その鏡に歪みがあれば、AIも歪んだ結果を映し出してしまうということを、肝に銘じておく必要がありますね。
「もしも」の時、誰の責任?:責任の所在という難問
万が一、AIが誤った予測や診断を下し、それによって患者さんに不利益が生じてしまった場合、その責任は一体誰が負うのでしょうか? AIを開発した企業でしょうか? それとも、AIを導入した医療機関でしょうか? あるいは、最終的にAIの情報を参考に判断を下した医師でしょうか? この「責任の所在」の問題は、非常に難しく、法的な整備も含めて、社会全体で真剣に議論していく必要があります。特に、AIが自律的に学習し進化していくような場合、その判断プロセスがますます複雑になり、責任の所在を特定することが一層困難になる可能性も指摘されています。技術の進歩と並行して、こういった法制度や社会的なルール作りも進めていかなければ、医療現場でのAIの本格的な普及はおぼつかないかもしれません。
期待しすぎは禁物:過度な期待と誤用のリスク
AI、特に深層学習の近年の目覚ましい進歩を見ていると、まるでAIがどんな問題でも解決してくれる「魔法の杖」のように感じてしまうことがあるかもしれません。しかし、現時点でのAIは、決して万能ではありません。得意なこともあれば、苦手なこともありますし、想定外の状況や未知のデータに対しては、時として驚くほど的外れな結果を出してしまうこともあります。AIの能力の限界を正しく理解し、過度な期待を抱かず、あくまで医師の診断や治療方針決定を「支援する高度なツール」として、その特性を活かして適切に利用していく姿勢が大切です。AIの出す結果を鵜呑みにせず、常に批判的な吟味(クリニカルリーズニング)を怠らない、そういった賢明な付き合い方が求められているのだと思います。
これらの課題は、決して簡単なものではありません。しかし、これらの課題から目を背けることなく、技術者、医療従事者、倫理や法律の専門家、そして何よりも患者さん自身を含めた社会全体で知恵を出し合い、一つひとつ丁寧に向き合っていくことで、LSTMを含むAI技術が、真に医療の質の向上と人々の健康に貢献できる未来が拓けるのではないでしょうか。技術の可能性を追求することと、その技術がもたらす影響に責任を持つこと、その両輪で進んでいくことが、これからの私たちには求められているのだと感じています。
5. まとめと次のステップ
5. ゴールと新たな始まり:本章のまとめと次の一歩
いやー、ここまで本当にお疲れ様でした!LSTMという、ちょっぴり複雑だけれども非常に強力なニューラルネットワークの世界を、一緒に探検してきました。理論の理解から始まり、PyTorchを使って実際に手を動かし、そして医療というフィールドでの可能性と課題にまで思いを馳せる…。なかなか濃密な時間だったのではないでしょうか。
本章では、まず「単純なRNNって、どうして長い記憶が苦手だったんだっけ?」という疑問からスタートし、その答えとして登場したLSTMが、あの巧妙な「ゲート」という名の門番たち(忘却ゲート、入力ゲート、出力ゲートですね!)と、「セル状態」という名の記憶のハイウェイを駆使して、どうやって過去の重要な情報をしっかりと未来へ繋いでいくのか、そのカラクリをじっくりと見てきました。頭の中で、情報がゲートを通り抜けたり、セル状態に書き込まれたりするイメージが、少しでも湧いていたら嬉しいです。
そして理論だけでなく、実際にPyTorchという頼れる相棒を使って、LSTMモデルをゼロから(まあ、nn.LSTMという便利な部品がありましたが!)構築し、サインカーブにノイズを加えた、あのちょっと可愛らしい擬似医療時系列データを使って、「未来の値を予測する」というタスクに挑戦しましたね。データを準備し、モデルの設計図を描き、学習のループを回し、そしてドキドキしながらテストデータでその実力を試す…この一連の流れを体験することで、「ああ、機械学習のプロジェクトって、こんなふうに進んでいくんだな」という感覚を掴んでいただけたのではないでしょうか。
さらに、目を転じて医療の現場に目を向ければ、LSTMが心電図の解析から敗血症の早期発見、糖尿病患者さんの血糖値管理支援に至るまで、本当に多岐にわたる分野でその力を発揮し始めている、あるいはその大きな可能性を秘めていることにも触れました。まるでSFのような話が、少しずつ現実のものになろうとしている、そんなワクワク感を感じていただけたなら幸いです。と、同時に、データの質の問題、患者さんのプライバシー、AIの判断根拠の透明性、そして社会的な公平性といった、私たちが真摯に向き合わなければならない課題についても、一緒に考える時間を持てたことは、とても意義深いことだったと思います。
さて、この章で皆さんがどんなことを学び、どんなスキルを身につけたのか、一度ここで整理しておきましょうか。
本章で皆さんが手にした「宝物」(学びの要約)
- LSTMの「賢さ」の秘密、理解しました!
LSTMが、あの巧妙な「ゲート」機構(忘却、入力、出力!)と「セル状態」を駆使して、単純なRNNでは難しかった「あの時あれがあったから、今こうなっているんだ!」というような、時間の壁を越えた情報(長期依存関係)をしっかりと捉えて学習できるようになったこと、その基本的なメカニズムをご理解いただけたと思います。 - PyTorchでLSTMモデル、作れるようになりました!
PyTorchのnn.LSTMモジュールやnn.Linearといった部品を組み合わせることで、時系列データを予測するためのニューラルネットワークモデルを、意外とシンプルに(?)構築できることを体験し、そのコードの書き方もマスターしましたね。 - モデル学習の「レシピ」、手に入れました!
モデルを賢く育てるためには、適切な「成績表」としての損失関数(今回はMSEでしたね)と、「指導方針」としての最適化アルゴリズム(Adamを使いました)を選ぶことがとっても大切で、それらをどうやってPyTorchで設定するのかもバッチリです。 - 時系列データの「下ごしらえ」、できるようになりました!
生の時系列データを、モデルが学習しやすいように入力シーケンスとターゲットのペアに変換したり(あのスライディングウィンドウ、思い出してください!)、訓練用とテスト用に分けたり、そしてDataLoaderで効率的にモデルに供給したりする、といった一連の前処理の流れとその重要性を学びました。 - モデルの「実力診断」、経験しました!
学習が終わったモデルの性能を、学習には使っていない未知のテストデータで評価し、RMSEのような客観的な指標でその精度を測ること、そして予測結果をグラフで可視化して「なるほど、こんな感じで当たってるんだな/外してるんだな」と分析するスキルも身につきました。 - 医療AIの「光と影」、見えてきました!
LSTMが医療の時系列データ分析に革命をもたらすほどの大きな可能性を秘めている一方で、データの質、プライバシー保護、AIの判断の透明性、公平性の確保など、乗り越えるべき倫理的・技術的な課題もたくさんあることを認識しました。
これだけの知識と経験を身につけた皆さんは、もう立派に「医療AIの卵」として、次の一歩を踏み出す準備ができたと言っても過言ではないでしょう!
さあ、冒険は続く!次なるステップへの羅針盤
この章でLSTMの基礎と、医療時系列データへの応用の一端に触れたことで、皆さんの目の前には、より深く、よりエキサイティングなデータ分析の世界への扉が開かれたはずです。「これで終わりじゃない、むしろここからが始まりなんだ!」そんなふうに感じていただけていたら、とても嬉しいです。今後の学習の方向性として、いくつか魅力的な道筋を提案させてください。
- もっとリアルな医療データに挑戦!臨床現場の課題解決へ
今回扱ったのは単純な擬似データでしたが、実際の臨床現場で得られるデータは、もっと手強い相手です。複数のバイタルサインや検査値を同時に扱う「多変量時系列データ」、ところどころ値が抜けている「欠損値を含むデータ」、あるいは記録されるタイミングがバラバラな「不規則サンプリングデータ」など…。これらの現実的なデータと格闘し、意味のある知見を引き出す経験は、皆さんをさらに成長させてくれるはずです。前処理のテクニックや、より頑健なモデル構築法なども学んでいくと良いでしょう。 - LSTMの仲間たち:GRUなど、他のRNN派生モデルも試してみよう
実は、LSTM以外にも、長期依存性を扱えるように改良されたRNNの仲間たちがいます。例えば、「GRU (Gated Recurrent Unit)」というモデルは、LSTMよりも少しシンプルな構造でありながら、同等の性能を発揮することもあると言われています。状況によっては、計算効率が良いGRUの方が適している場面もあるかもしれません。新しい道具を一つ手に入れるように、これらのモデルについても学んで比較検討してみるのは、非常に面白い試みだと思います。 - 「注目」の力で精度アップ?!アテンション機構の導入
人間が長い文章を読むとき、無意識に重要な部分に「注目」していますよね。それと同じような仕組みをニューラルネットワークに持たせたのが「アテンション機構」です。特に長い時系列データや、シーケンスの中で特に重要な情報が散在しているような場合に、このアテンション機構をLSTMと組み合わせることで、モデルが「どこに注目すべきか」を自ら学習し、予測精度を大きく向上させることがあります。これは、現在の深層学習のトレンドの一つでもあり、ぜひ挑戦してほしいテーマです。 - 言葉の海へダイブ!自然言語処理への応用
そして、このコースの次の章(第4章:PyTorchでLSTM:医療自然言語処理編)で詳しく触れますが、LSTMの力は数値の時系列データだけに留まりません。実は、言葉の並びである「テキストデータ」も一種の時系列データと捉えることができ、LSTMは自然言語処理(NLP)の分野でも大活躍しているんです。電子カルテの自由記述欄の解析、医療関連の学術論文の読解支援、患者さんとのコミュニケーションを助けるチャットボットの開発など、医療と「言葉」を結びつけるエキサイティングな領域が待っています。 - AIの「心」を覗き見る:モデルの解釈性向上への挑戦
先ほど「課題」としても挙げましたが、AIの判断根拠が分からない「ブラックボックス問題」は、医療応用における大きな壁です。LIME(ライム)やSHAP(シャップ)といったXAI(説明可能なAI)の手法を学び、モデルが「なぜこのように予測したのか」を可視化したり、人間が理解できる形で説明しようとしたりする試みは、AIへの信頼を高め、より安全な医療応用を実現するために非常に重要です。これは、技術的な面白さと社会的な意義を兼ね備えた、やりがいのあるテーマだと思います。
医療AIの分野は、本当に日進月歩で、新しい論文や技術が次々と生まれています。このコースで学ぶ知識やスキルは、あくまでその広大な世界を探求するための「最初の地図」と「コンパス」のようなものかもしれません。ぜひ、この地図とコンパスを手に、ご自身の興味のある研究テーマや、日々の臨床現場で感じている課題の解決に向けて、AIという強力なツールを活用する道を探求し続けてください。
そして何よりも、プログラミングを通じて、データと対話し、そこから新しい洞察や価値を自分の手で創り出していく、その「創造の喜び」を、これからも大切に持ち続けていただければ、これほど嬉しいことはありません。皆さんのこれからの活躍を、心から応援しています!
6. 参考文献
- Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput. 1997;9(8):1735-1780.
- Faust O, Hagiwara Y, Hong TJ, Lih OS, Acharya UR. Deep learning for healthcare applications based on physiological signals: A review. Comput Methods Programs Biomed. 2018;161:1-13.
- Hannun AY, Rajpurkar P, Haghpanahi M, Tison GH, Bourn C, Turakhia MP, et al. Cardiologist-level arrhythmia detection and classification in ambulatory electrocardiograms using a deep neural network. Nat Med. 2019;25(1):65-69.
- Suresh H, Hunt N, Johnson A, Celi LA, Szolovits P, Ghassemi M. Clinical Intervention Prediction and Understanding using Deep Networks. In: Proceedings of the Machine Learning for Health Care Conference; 2017 Aug 18-19; Boston, MA. PMLR; 2017. p. 26-41. (Proceedings of Machine Learning Research, vol 68).
- Usman SM, Khalid S, Bashir Z. A deep learning framework for robust epileptic seizure detection. IEEE Access. 2020;8:203799-203809.
- Li K, Daniels J, Liu C, Herrero P, Georgiou P. Convolutional recurrent neural networks for glucose prediction. IEEE J Biomed Health Inform. 2020;24(2):603-613.
- Cho CH, Lee T, Kim MG, In HP, Kim L, Lee HJ. Mood prediction of patients with mood disorders by machine learning using passive digital phenotypes based on a smartwatch and smartphone. J Med Internet Res. 2019;21(4):e11029.
- Phan H, Andreotti F, Cooray N, Chén OY, De Vos M. Joint classification and prediction of sleep stages from raw polysomnography data. IEEE Trans Biomed Eng. 2019;66(4):1069-1080.
- Tonekaboni S, Joshi S, McCradden MD, Goldenberg A. An interpretable machine learning model for subtype classification of critically ill patients. Sci Rep. 2019;9(1):15400.
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.





