AIは、予測の間違いを減らすため「最も効率よく間違いが減る方向(勾配)」を計算し、その方向に少しずつパラメータを更新します。この「勾配降下法」という、霧の中で谷底を探すような地道な学習プロセスを視覚的に解説します。
「パラメータを少し変えたら、誤差はどれくらい変わるか?」という瞬間の変化率を計算します。これは坂道の傾きを知るようなものです。
全パラメータの傾きをまとめたもので、損失が最も急激に増える方向を示します。AIが学習で進むべき方向を知るための「コンパス」です。
勾配が示す方向とは「逆」の、最も急な下り坂の方向へ少しずつパラメータを更新する作業を繰り返します。これがAIの学習そのものです。
最近、ニュースや論文で「AIが医療を変える」という話をよく耳にしませんか? 膨大な量の医療画像から病変の兆候を瞬時に見つけ出したり、個々の患者さんに最適な治療法を提案したり。まるで魔法のように思えるその技術ですが、そのAIが一体どうやって「学習」しているのか、中身はまるでブラックボックスのように感じられるかもしれませんね。
実は、AIが賢くなっていくプロセスは、私たち人間が経験から学ぶ姿と、どこか似ているんです。そして、その学習の根幹を支えているのが、一見すると難解に聞こえるかもしれない数学の概念、『微分(びぶん)』と『勾配(こうばい)』なのです。
この章では、このAIの「学習」の心臓部とも言えるメカニズムを、皆さんと一緒に探検していきたいと思います。目指すのは、数式をただ暗記することではありません。医療の現場でAIがどのように役立つのかを具体的にイメージしながら、「なるほど、AIはこんな風に考えているのか!」と、その仕組みを直感的に掴んでいただくことです。
「微分」と聞くと、学生時代の記憶が蘇ってきて、少しだけ身構えてしまう方もいらっしゃるかもしれませんね。ご安心ください。ここでは、複雑な計算問題を解くのが目的ではありません。まずは、AIの学習プロセスにおける各概念の「役割」を、簡単な地図のように整理してみましょう。
このロードマップの解説
上の図は、AIが学習するステップを旅になぞらえたものです。
- 微分は、まず「現在地」を知るための第一歩です。AIが出した答えが、正解とどれくらいズレているか。そして、そのズレを修正するためにAI内部の設定値を少し動かしたとき、ズレがどれくらい改善するのか(あるいは悪化するのか)、その「手応え」や「変化の度合い」を教えてくれます。
- 勾配は、その手応えを全方向について調べ上げて、「こっちに進めば、一番早く麓の目的地(=最も間違いが少ない状態)に着けるよ!」と教えてくれる、信頼できるコンパスのような存在です。AIには無数の設定値がありますが、勾配のおかげで、どの設定値をどう動かせば良いか、という最適な方針が分かります。
- 勾配降下法は、そのコンパスを信じて、実際に一歩を踏み出す「行動」です。この一歩を何回も何回も繰り返すことで、AIはまるで暗闇の中で坂道を転がり落ちるボールのように、最も安定した場所、つまり最も賢い状態へと自動的にたどり着くことができます。
このように、一つ一つの概念が持つ「意味」と「役割」を理解すれば、きっと全体の流れが見えてくるはずです。専門的な数学のバックグラウンドがなくても、一歩一歩進んでいけば、AIの「心」が少しだけ覗けるようになります。さあ、一緒にその不思議でパワフルな仕組みを紐解いていきましょう。
1. 微分とは何か? 直感的な理解
さて、先ほどのロードマップの最初のステップ、『微分』から私たちの旅を始めましょう。
微分と聞くと、高校数学の授業を思い出して「なんだか難しそう…」と、少し身構えてしまう方もいるかもしれませんね。正直なところ、私自身も学生時代は「一体何のためにこんな計算を…?」と感じていた一人ですから、その気持ちはよく分かります。
でも、ご安心ください。深層学習の世界で出会う微分は、テストの点数を取るためのものではありません。AIが賢くなるための「道しるべ」を見つける、とても実践的でパワフルな道具なんです。微分とは、ものすごくシンプルに言えば「ある瞬間の、変化の勢い(傾き)」を教えてくれるもの、だと思ってみてください。
医療現場の例で考えてみよう
この「変化の勢い」という考え方を、身近な医療の例で具体的にイメージしてみましょう。
あなたが、ある薬剤の投与量と、それによる治療効果(例えば、腫瘍の縮小率など)の関係を調べているとします。データを集めて、次のようなグラフが描けました。

このグラフを見ると、投薬量を増やせば効果が上がることが分かりますね。では、ここから一歩踏み込んで、「投薬量が1mgの”まさにその瞬間”において、薬の効き目はどれくらいの勢いで増えているのだろう?」という疑問が湧いたとします。
もし、1mgから2mgに増やしたときの全体の平均的な変化率を知りたいのであれば、A点とB点を直線で結んだ線の傾きを計算すれば良さそうです。
ですが、私たちが知りたいのは、もっとピンポイントな「1mgの瞬間」の勢いです。この「瞬間の勢い」こそが、微分が教えてくれる「傾き」の正体なんです。それは、グラフ上のA点という一点だけに接する、一本の接線の傾きを求めるようなイメージです。
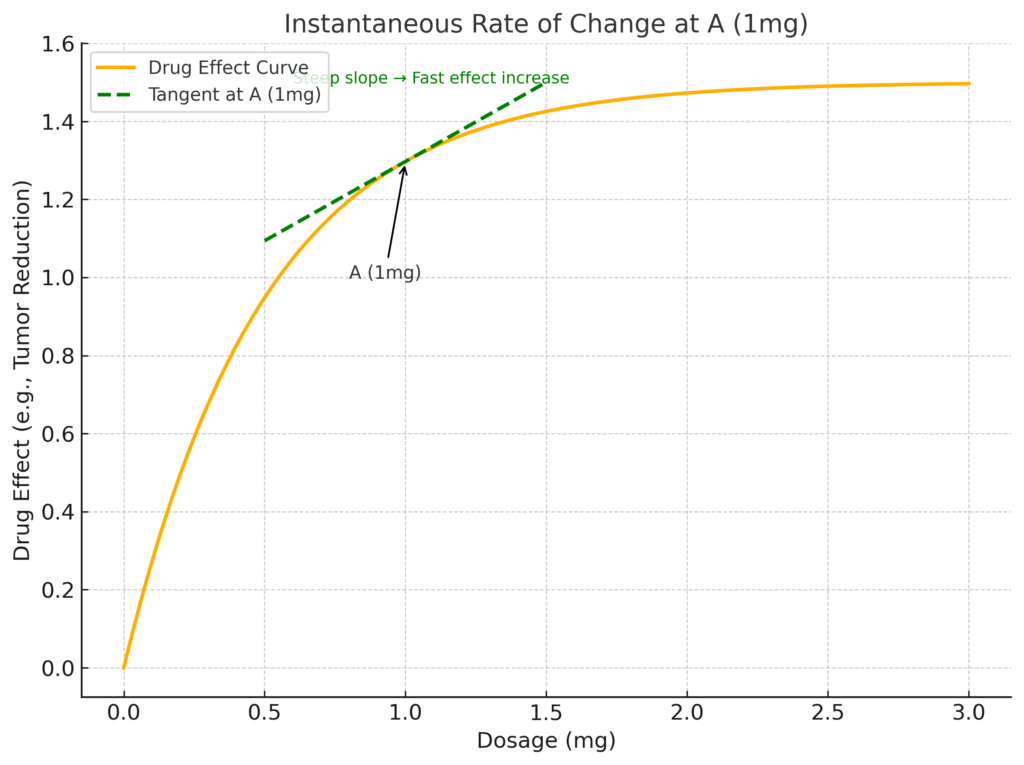
この接線の傾きが急であればあるほど、「その点においては、投薬量を少し増やすだけで、効果がグンと上がる」と言えます。逆に傾きが緩やかであれば、「少し増やしても、効果はそこまで大きくは変わらないな」と判断できます。この微細な変化を捉える感覚、なんとなく掴んでいただけたでしょうか。
微分を数式で覗いてみる
この「瞬間の傾き」の考え方は、数式では次のように表現されます。これが微分の最も基本的な表記です。
\[ \frac{df(x)}{dx} \]
この数式を見ると少し圧倒されてしまうかもしれませんが、一つ一つのパーツの意味が分かれば、決して怖くはありません。分解してみましょう。
| 記号 | 読み方(イメージ) | 意味・役割 |
|---|---|---|
f(x) | エフ・エックス | 原因 x によって決まる「結果」。今回の例では「薬の効果」。 |
x | エックス | 変化させる「原因」。今回の例では「投薬量」。 |
d | ディー | 「ほんの僅かな変化量 (a difference / a delta)」。ギリシャ文字のデルタ(Δ)が由来で、肉眼では見えないくらい、ごくごく僅かな変化を表す記号だと思ってください。 |
df(x) | ディー・エフ・エックス | 結果 f(x) の、ほんの僅かな変化量。 |
dx | ディー・エックス | 原因 x の、ほんの僅かな変化量。 |
df(x)/dx | xで微分する | 全体で「原因xをほんの僅か動かしたとき、結果f(x)がどれくらい変化するか」という変化の割合(=瞬間の傾き)を表します。 |
つまり、\( \frac{df(x)}{dx} \) というのは、「投薬量(\(x\))をほんの少しだけ増やしたときに、薬の効果(\(f(x)\))はどれくらいの割合で変化しますか?」という、先ほどの私たちの疑問を数学の言葉で表現したものに他なりません。
具体的な関数で見てみよう
もう少し具体的な数字で考えてみましょう。仮に、入力 x を2乗するだけのシンプルな関数 \( f(x) = x^2 \) があったとします。この関数を微分すると、その導関数(微分した結果の関数)は \( f'(x) = 2x \) となります。(この計算方法はルールとして決まっており、今は「そうなるんだな」くらいで大丈夫です)。\(f'(x)\) というのは \( \frac{df(x)}{dx} \) を少し省略した書き方で、意味は全く同じです。
この \( f'(x) = 2x \) が教えてくれるのは、「各地点xにおける瞬間の傾き」です。
地点 x の値 | \( f'(x) = 2x \) の値(瞬間の傾き) | この傾きが教えてくれること |
|---|---|---|
| x = 1 | f'(1) = 2 * 1 = 2 | 地点 \(x=1\) では、グラフは上向きに「傾き2」の勢いで変化している。 |
| x = 3 | f'(3) = 2 * 3 = 6 | 地点 \(x=3\) では、グラフはより急な「傾き6」の勢いで変化している。 |
| x = -2 | f'(-2) = 2 * (-2) = -4 | 地点 \(x=-2\) では、グラフは下向きに「傾き4」の勢いで変化している。(マイナスは下向き) |
| x = 0 | f'(0) = 2 * 0 = 0 | 地点 \(x=0\) では、傾きは0。グラフは平坦になっている(谷の底)。 |
このように、x の場所によって変化の勢い(傾き)が全く違うことが分かりますね。これが微分の面白いところです。
それで、これが深層学習とどう繋がるの?
ここまでの話が、いよいよAIの学習と繋がります。
深層学習の目標は「予測の誤差(損失と呼ばれるもの)を、できるだけ小さくすること」でした。AIの内部には、調整可能な無数のダイヤルのようなもの(パラメータと呼ばれます)があります。
AIは、このパラメータを少しずつ調整して、誤差を最小化しようと試みます。そのとき、AIは自問自答するわけです。
「このパラメータAのダイヤルを、ほんの少し右に回したら(=値を増やしたら)、最終的な予測の誤差は、どれくらい増える(あるいは減る)んだろう?」
この問い、どこかで見た形だと思いませんか?
そう、これこそがまさに微分の考え方そのものなんです。
\[ \frac{d(\text{誤差})}{d(\text{パラメータA})} \]
この値を計算することで、AIは「どのダイヤルを、どっちの方向に、どれくらい回せば、最も効率よく誤差を減らせるか」という絶好の手がかりを得ることができます。
- もし計算結果(傾き)が大きなプラスの値なら、「このダイヤルを回すと誤差が急増する!逆方向に回さなきゃ!」と判断します。
- もし計算結果が大きなマイナスの値なら、「素晴らしい!この方向に回せば誤差がどんどん減るぞ!」と判断します。
- もし計算結果が0に近ければ、「このダイヤルは、今はあまり誤差に関係ないみたいだな」と判断します。
このように、微分はAIが学習の進むべき道を探すための、必要不可欠な羅針盤の役割を果たしているのです。
2. 勾配とは何か? 多次元の坂道を下る方向
さて、先ほどの「微分」の話は、いわば一本道での出来事でした。投薬量という一つの原因と、薬の効果という一つの結果の関係性、つまりグラフという線の上での「傾き」を見てきましたね。
ですが、私たちが普段扱う深層学習モデルの内部は、そんなに単純な一本道ではありません。AIの性能を決める調整ダイヤル(パラメータ)は、何百万、ときには何十億という、天文学的な数が存在します。
これを例えるなら、AIの学習とは、たった一つのダイヤルを回す作業ではなく、巨大なオーケストラの指揮者のようなものかもしれません。たった一つの目的「予測誤差(損失)をできるだけ小さくする」ために、無数の楽器(パラメータ)の音量(値)を、一斉に、かつ互いに協調させながら調整していく。そんな壮大なイメージです。
この無数のダイヤルが広がる「多次元空間」という複雑な状況では、先ほどの一本道での傾き(微分)だけを考えても、全体の進むべき方向は見えてきませんよね。そこで登場するのが、今回の主役である『勾配(Gradient)』という概念です。
一つだけ動かしてみる「偏微分」
勾配の正体に迫る前に、まず「偏微分(へんびぶん)」という考え方に触れておきましょう。言葉は少し難しそうですが、やっていることは非常に直感的です。
想像してみてください。あなたは今、無数のダイヤルが並んだ巨大な調整卓の前にいます。ダイヤルAが最終的な結果にどう影響するかを知りたいとき、どうしますか? きっと、他のダイヤルB, C, D…は全て今の位置で固定したまま、ダイヤルAだけをほんの僅かに回してみるはずです。
この、「他のたくさんの原因は一旦無視(固定)して、特定の一つの原因だけを動かしたときの影響を見る」という特別な微分が「偏微分」です。この「特別扱い」を区別するために、数学の世界では、通常の微分で使った d の代わりに、 ∂ という記号(パーシャル、ラウンドディーなどと呼ばれます)を使います。
全員分の「手応え」をまとめたリスト、それが勾配
AIは、この偏微分を全てのパラメータに対して行います。
- 「パラメータ
w₁だけを動かした時の、誤差Lへの手応え(傾き)はどうか?」→ \( \frac{\partial L}{\partial w_1} \) - 「パラメータ
w₂だけを動かした時の、誤差Lへの手応え(傾き)はどうか?」→ \( \frac{\partial L}{\partial w_2} \) - 「パラメータ
w₃だけを動かした時の、誤差Lへの手応え(傾き)はどうか?」→ \( \frac{\partial L}{\partial w_3} \) - … (これを全てのパラメータ分繰り返す)
そして、こうして得られた全員分の手応え(各パラメータ方向の傾き)を、一つのリスト(ベクトル)にまとめたもの。それこそが「勾配」の正体です。
勾配 (Gradient) という名のリスト
∇L = [ w₁方向の傾き, w₂方向の傾き, w₃方向の傾き, ... , wₙ方向の傾き ]
= [ ∂L/∂w₁, ∂L/∂w₂, ∂L/∂w₃, ... , ∂L/∂wₙ ]このリスト、つまり勾配ベクトルが、「どのパラメータを、どの方向に、どれくらいの強さで動かせば、最も効率よく目的を達成できるか」を示す、多次元空間における最強のコンパスの役割を果たしてくれるのです。
勾配の数式表現
この考え方を数式でまとめると、以下のようになります。損失関数を \(L\)、パラメータを \(w_1, w_2, \ldots, w_n\) としたとき、その勾配 \( \nabla L \) は、次のようなベクトルで表されます。
\[ \nabla L = \left( \frac{\partial L}{\partial w_1}, \frac{\partial L}{\partial w_2}, \ldots, \frac{\partial L}{\partial w_n} \right) \]
この式の各要素を、改めて私たちの言葉で翻訳してみましょう。
| 記号 | 読み方(イメージ) | 意味・役割 |
|---|---|---|
| \(L\) | 損失 (Loss) | AIの「予測誤差」。この関数の値を最小にすることが最終目標。 |
| \(w_i\) | パラメータ `i` | AIの性能を決める `i`番目の調整ダイヤル(重み)。 |
| \(\partial\) | パーシャル | 「他のパラメータは全て固定して」という注意書き付きの微分記号。 |
| \( \frac{\partial L}{\partial w_i} \) | 偏微分 | 「`i`番目のダイヤルだけを動かした時の、誤差の変化率(傾き)」。 |
| \(\nabla\) | ナブラ (nabla) | 「これから勾配を計算しますよ」という宣言の記号。ベクトルの概念を含む。 |
| \( \nabla L \) | 勾配ベクトル | 全てのパラメータ方向の傾きをまとめたリスト(ベクトル)。関数\(L\)の値が最も急激に大きくなる方向を指し示す。 |
霧の中の山下り
この勾配が示す「方向」のイメージを掴むために、少し想像の翼を広げてみましょう。
あなたは今、深い霧に覆われた、広大で起伏に富んだ山脈のまっただ中に立っています。視界は数メートルしかなく、地図もコンパスもありません。あなたの目標はただ一つ、山の一番低い谷底(損失が最小の地点)にたどり着くことです。
さて、あなたならどうしますか?
おそらく、あなたにできる唯一のことは、自分の足元、360度全方向の地面の傾斜を、足の裏で慎重に感じ取ることでしょう。そして、その中で「最も急な坂」になっている方向を見つけ出し、そちらへ一歩、また一歩と進んでいく。それが、谷底へたどり着くための最も賢明な方法だと感じるはずです。

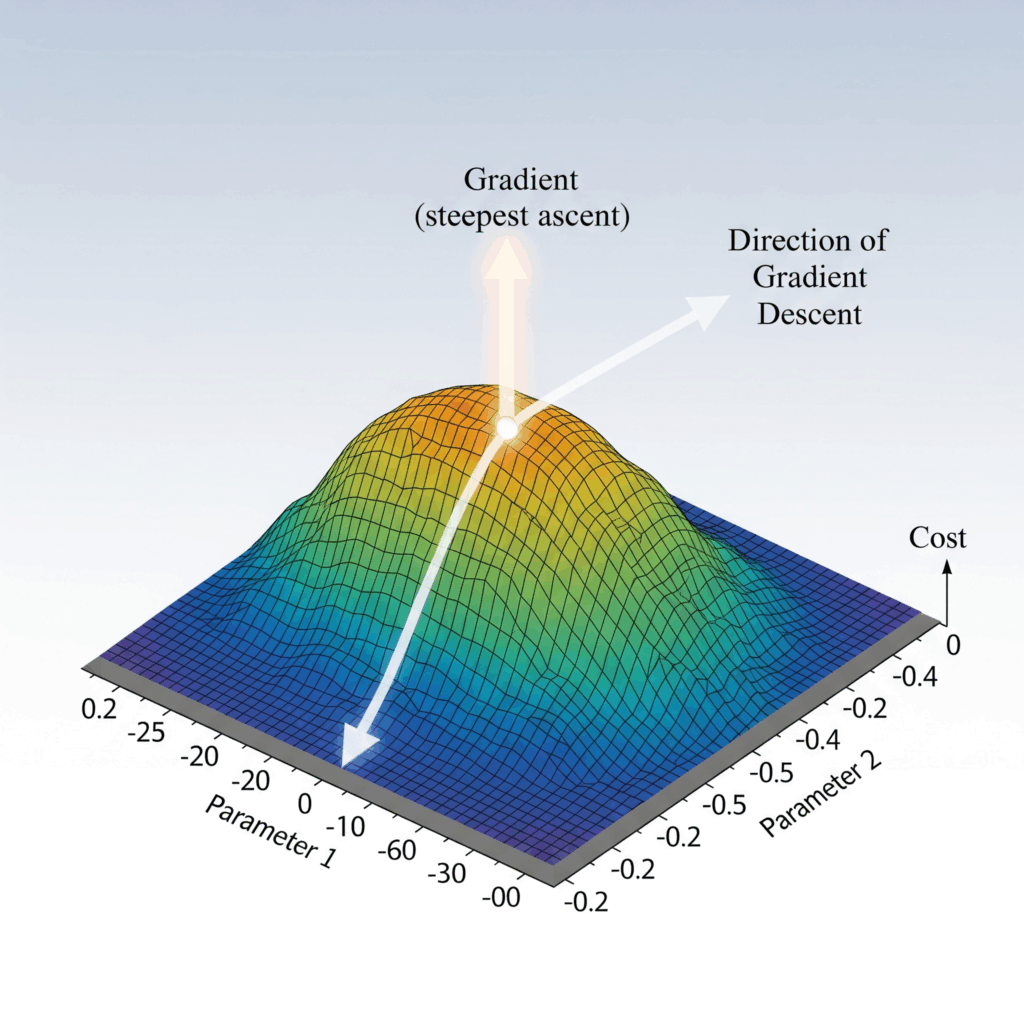
この「最も急な坂の方向」を、何百万次元というパラメータ空間において、数学的にピタリと示してくれるのが、まさに勾配ベクトルなのです。
ここで一つ、とても大切なポイントがあります。勾配 \( \nabla L \) が指し示す方向は、実は「最も急な上り坂」の方向です。関数の値が最も激しく増加する方向を指します。私たちの目標は誤差(損失)を減らすこと、つまり谷底へ下ることなので、AIは勾配が指し示す方向とは真逆の方向へ進んでいきます。これが、AIが賢くなるための学習の基本ステップなのです。
勾配降下法における「勾配(こうばい、Gradient)」とは、多変数関数のある一点において、最も関数値が増加する方向 を示すベクトルのことです。
先ほどの山下りの例えで言うと、あなたが今立っている地点で、「最も急な上り坂の方向」とその「傾きの大きさ」を教えてくれるのが勾配です。
勾配降下法では、関数の最小値を見つけたいので、この「最も増加する方向」とは逆の方向、つまり「最も減少する方向」に進みます。これが「降下」の意味です。
数学的な表現
数学的には、多変数関数 \(f(x_1, x_2, …, x_n)\) の点 \((a_1, a_2, …, a_n)\) における勾配は、それぞれの変数に関する偏微分を成分とするベクトルとして表されます。
\[\nabla f(a_1, a_2, …, a_n) = \left( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, …, \frac{\partial f}{\partial x_n} \right) \Bigg|_{(a_1, a_2, …, a_n)}\]
この数式は、関数 \(f\) の各変数 \(x_i\) に対する偏微分(それぞれの変数が少しだけ動いた時に関数がどれだけ変化するか)を計算し、それらを並べてベクトルにしたものが勾配 \(\nabla f\) であることを示しています。
- ベクトルの方向: 勾配ベクトルの方向は、関数が最も急激に増加する方向を示します。
- ベクトルの大きさ: 勾配ベクトルの大きさは、その方向への傾きの急峻さを示します。傾きが急なほど、ベクトルの大きさは大きくなります。
勾配降下法での役割
勾配降下法では、現在のパラメータの値における勾配を計算し、その逆方向に学習率 \(\eta\) をかけた分だけパラメータを更新します。
\[\mathbf{w}_{t+1} = \mathbf{w}_t – \eta \nabla f(\mathbf{w}_t)\]
この更新式の意味を分解すると、以下のようになります。
- \(\mathbf{w}_{t+1}\): 更新後の新しいパラメータ
- \(\mathbf{w}_t\): 現在のパラメータ
- \(\eta\): 学習率(一歩の大きさ)
- \(\nabla f(\mathbf{w}_t)\): 現在のパラメータにおけるコスト関数の勾配(最も坂が急な上り方向)
つまり、「新しいパラメータ(\(\mathbf{w}_{t+1}\))は、現在のパラメータ(\(\mathbf{w}_t\))から、勾配(\(\nabla f(\mathbf{w}_t)\))とは逆の方向に、学習率(\(\eta\))の分だけ進んだ位置にある」ということを示しています。
このように、勾配は、パラメータをどのように更新すればコスト関数がより小さくなるのか、その道しるべとなる非常に重要な情報を提供してくれるのです。
もしよろしければ、勾配のイメージをさらに具体的にするために、特定の関数の例を使って説明することも可能です。
3. 連鎖率:複雑な計算を紐解く道具
さて、ここまでの話で、ある値が変化したときに別の値がどう変わるか(微分)、そしてその変化の方向を示すリスト(勾配)を知る方法を、私たちは手にしました。
でも、実際の深層学習モデルの中身は、もっと複雑なリレーのような構造をしています。最初の層での計算結果が次の層に渡され、その結果がさらに次の層へ…と、まるでバトンが次々に渡されていくことで、最終的な予測結果というゴールにたどり着くのです。
ここで、一つ大きな疑問が生まれます。それは、「リレーの第一走者(最初の層のパラメータ)のちょっとした変化は、最終的なゴールタイム(予測の誤差)に、一体どれくらい影響を与えたのだろう?」というものです。この問いに答える鍵こそが、『連鎖率(Chain Rule)』と呼ばれる考え方です。
バトンをつなぐ影響力の掛け算
連鎖率を一言で表現するなら、「間接的な影響力を、それぞれの影響力の掛け算で求める」法則です。
ちょっと想像してみてください。シンプルな3人リレーを考えます。
- Aさん(入力)が頑張ると、Bさん(中間結果)のタイムが良くなる。
- Bさんのタイムが良いと、Cさん(最終結果)のタイムも良くなる。
このとき、「Aさんの頑張りが、最終的なCさんのタイムにどれくらい影響したか?」を知るには、
「AがBに与えた影響の度合い」 × 「BがCに与えた影響の度合い」
という計算をすれば、直感的に分かりそうですよね。連鎖率は、この素朴なアイデアを数学的に表現したものです。
具体的な計算の流れで見てみよう
この「影響力の掛け算」を、簡単な計算の繋がりで見てみましょう。全く難しくないので、リラックスして追いかけてみてください。
- まず、入力
xを2倍する計算uがあります。 \( u = 2x \) - 次に、その結果
uを3乗する計算yがあります。 \( y = u^3 \)
この2つの計算は、下のような図で表現できます。x から y への一方通行の計算ですね。これを計算グラフと呼びます。
【計算の流れ】
u = 2x y = u³
┌──────┐ ┌──────┐
[入力 x]───>│ ×2 │───>│ ( )³ │───>[出力 y]
└──────┘ └──────┘
(計算u) (計算y)さて、私たちが知りたいのは「入力xをちょっと動かしたとき、最終的な出力yがどれくらい変化するか?」、つまり \( \frac{dy}{dx} \) です。
連鎖率の考え方を使えば、これを2つのパーツに分解して、それぞれの影響力を掛け合わせることができます。
- 影響力 Part 1:
uがyに与える影響は? → \( \frac{dy}{du} \) を計算します。y = u³をuで微分すると、\( 3u^2 \) になります。(微分の公式より) - 影響力 Part 2:
xがuに与える影響は? → \( \frac{du}{dx} \) を計算します。u = 2xをxで微分すると、\( 2 \) になります。
そして、この2つの影響力を掛け合わせるのです。
\[ \frac{dy}{dx} = \frac{dy}{du} \times \frac{du}{dx} = (3u^2) \times (2) \]
最後に、u を元の 2x に戻してあげると、
\[ \frac{dy}{dx} = 3(2x)^2 \times 2 = 3(4x^2) \times 2 = 24x^2 \]
このように、最終的な影響 \( \frac{dy}{dx} \) は、途中の影響 \( \frac{dy}{du} \) と \( \frac{du}{dx} \) の「鎖(チェーン)」のように繋がった掛け算で求められました。これが連鎖率の力です。
深層学習と誤差逆伝播法への繋がり
この連鎖率が、なぜ深層学習でこれほど重要なのでしょうか。
医療画像AIの例を、先ほどの計算グラフで表現してみましょう。
┌──────┐
[画像]─(w₁)─>[特徴A]─(w₂)─>[特徴B]─(w₃)─>[予測結果]──(損失関数)──>│ 損失L │
└──────┘w₁, w₂, w₃ は、各層が持つパラメータ(重み)です。
AIの学習目標は、最終的な「損失L」を最小にすることでした。そのためには、勾配、つまり「各パラメータ w を動かしたときに、損失 L がどれだけ変化するか(\( \frac{\partial L}{\partial w} \))」を知る必要があります。
例えば、一番最初の層のパラメータ \(w_1\) の勾配 \( \frac{\partial L}{\partial w_1} \) を求めるには、どうすれば良いでしょうか? \(w_1\) と \(L\) の間には、たくさんの計算が挟まっていて、直接的な影響は分かりません。
ここで連鎖率の出番です。AIは、ゴールの「損失L」からスタートして、影響力を逆向きに伝播させていくのです。
【影響力が逆向きに伝わる様子】
∂L/∂w₁ ∂L/∂特徴A ∂L/∂特徴B ∂L/∂予測結果
<────── ◀ <──────── ◀ <──────── ◀ <────────── ◀ ┌──────┐
[画像]─(w₁)─>[特徴A]─(w₂)─>[特徴B]─(w₃)─>[予測結果]──(損失関数)──>│ 損失L │
└──────┘具体的には、\( \frac{\partial L}{\partial w_1} \) を得るために、
\[ \frac{\partial L}{\partial w_1} = \frac{\partial L}{\partial \text{予測結果}} \times \frac{\partial \text{予測結果}}{\partial \text{特徴B}} \times \frac{\partial \text{特徴B}}{\partial \text{特徴A}} \times \frac{\partial \text{特徴A}}{\partial w_1} \]
という、長い長い掛け算の連鎖を解くことになります。
この、最終的な誤差(ゴール)から、まるで伝言ゲームを逆再生するように、一つ前の層、さらにその前の層へと、微分の影響度を次々と掛け合わせながら伝えていく計算手法。これこそが、深層学習の学習アルゴリズムの心臓部である『誤差逆伝播法(Backpropagation)』なのです。

連鎖率は、この誤差逆伝播法を可能にするための、数学的な保証を与えてくれる、縁の下の力持ちと言えるでしょう。この仕組みのおかげで、どんなに深くて複雑なモデルでも、効率的に勾配を計算し、学習を進めることができるのですね。
4. 勾配降下法:AIが賢くなる仕組み
さあ、いよいよ最後のピースが揃います。これまで見てきた『微分』『勾配』そして『連鎖率』。これらの道具をすべて使って、AIが実際にどうやって賢くなっていくのか、その具体的な学習プロセスである『勾配降下法(こうばいこうかほう、Gradient Descent)』の旅に出ましょう。
思い出してみてください、あの「霧の中の山下り」の例え話を。
私たちは、今いる場所で最も急な坂の方向を知るためのコンパス(=勾配)を手に入れました。勾配降下法とは、そのコンパスを信じて、実際に「えいっ」と一歩を踏み出し、山を下っていく行動そのものを指します。

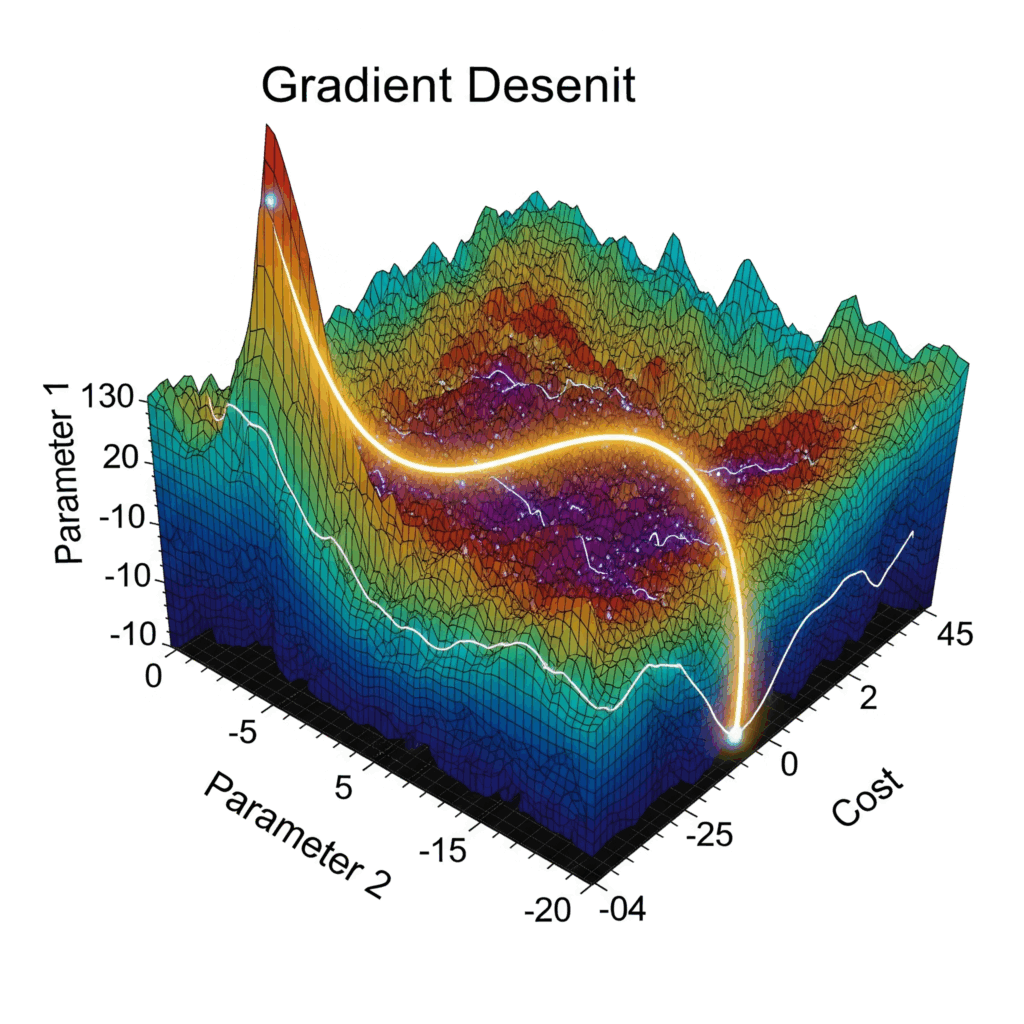
この学習プロセスは、ぐるぐると何度も繰り返される一つのサイクルだとイメージすると分かりやすいかもしれません。
┌──────────────────────────────────┐
│ 【AIの学習サイクル】 │
│ │
┌─▶ 1. とにかく一度やってみる(予測) │
│ │ │
│ └─> 2. 現実と答え合わせ(損失の計算) │
│ │ │
│ └─> 3. 反省と改善点の分析(勾配の計算)│
│ │ │
│ └─> 4. より良くなる方へ一歩進む(更新)│
└──────────────────────────────────┘このサイクルを何千回、何万回と繰り返すことで、AIは少しずつ、しかし着実に賢くなっていくのです。では、各ステップ、特に学習の肝となる「4. 更新」の中身を詳しく見ていきましょう。

それでは勾配降下法について、視覚的に理解しやすいように動的なイラストで解説しましょう。
勾配降下法は、機械学習の最適化において中核となるアルゴリズムです。損失関数の「坂」を下るように、勾配(傾き)の逆方向に少しずつパラメータを更新することで、最適解を見つけ出します。
下の可視化では、二次関数の損失関数上で、学習率や開始位置を変更することで、正常な収束から振動、発散まで、様々な最適化の挙動を体験できます。特に学習率の設定がいかに重要かを実感できるでしょう。
• 学習率α: 0.01-3.0で調整(2.0以上で振動・発散を体験可能)
• 開始位置: -6から6まで設定可能
• 赤い点が勾配に従って最小値(緑点)に向かって移動
• 黄色の軌跡が探索経路を表示
試してみよう:
• α=0.01(遅い収束)、α=0.5(適切)、α=2.5(振動)、α=3.0(発散)
AIが次の一歩を決める更新式
AIがパラメータ(調整ダイヤル)を更新する際のルールは、数式で書くと驚くほどシンプルです。ある一つのパラメータ w を更新する場合、以下の式に従います。
\[w_{\text{new}} = w_{\text{old}} – \eta \times \frac{\partial L}{\partial w}\]
この式が、AIの学習における「魔法の呪文」です。この呪文の解読をしてみましょう。
| 呪文の要素 | 読み方(イメージ) | 意味・役割 |
|---|---|---|
| \(w_{\text{new}}\) | 新しいパラメータ | 更新後の、少しだけ賢くなったパラメータの値。 |
| \(w_{\text{old}}\) | 古いパラメータ | 更新前の、現在のパラメータの値。 |
| \(\frac{\partial L}{\partial w}\) | 勾配の一部 | パラメータwに関する勾配(誤差の坂道の傾き)。この値がプラスなら上り坂、マイナスなら下り坂を示唆。 |
-(マイナス記号) | 逆方向へ | 最重要ポイント。 勾配は「上り坂」の方向を指すため、私たちはその逆の「下り坂」方向へ進みたい。だからマイナスを付けます。 |
| \(\eta\)(イータ) | 学習率 | 坂道を下る際の「歩幅(ステップの大きさ)」。非常に重要な調整役。 |
つまりこの式は、「現在の場所から、コンパス(勾配)が指す方向とは逆向きに、ほんの少し(学習率の分だけ)歩を進める」という、山下りの直感をそのまま数式に翻訳したものなのです。
学習の成否を分ける「学習率」という歩幅
先ほどの式に登場した \(\eta\)(イータ)こと学習率(Learning Rate)は、AIの学習がうまくいくかを左右する、極めて重要な「ハイパーパラメータ」(人間が設定する値)です。
学習率とは、勾配という「進むべき方向」が分かったときに、実際にどれくらいの「歩幅」で進むかを決める値です。この歩幅の調整は、なかなかデリケートで面白いんですよ。
- 歩幅が小さすぎる場合(例: \(\eta = 0.0001\))
チョコチョコとしか進めないので、いつまで経っても谷底(最適解)にたどり着けません。学習が全然進まない、という状況に陥ります。(スタート) ・・・・・・・・・・・・・・・・・・ (ゴール) 解説:一歩が小さすぎて、学習に膨大な時間がかかってしまう。 - 歩幅が大きすぎる場合(例: \(\eta = 1.0\))
一歩の勢いが良すぎて、谷底を飛び越えて反対側の斜面に登ってしまいます。行ったり来たりを繰り返して、いつまでも収束しない(値が安定しない)ことになります。(スタート) * * (ゴールを飛び越えた!) (谷底はここ) * (また飛び越えた!) 解説:歩幅が大きすぎて、最適な地点の周りを行ったり来たりしてしまう。 - ちょうど良い歩幅の場合(例: \(\eta = 0.01\))
効率よく、着実に谷底へ向かって下っていくことができます。これが理想的な状態です。(スタート) * * * (ゴール!) 解説:適切な歩幅で、効率よく最適解にたどり着く。
この学習率をどう決めるか、というのは、実は今でもAI研究者たちの間で活発に議論されているテーマの一つで、まさに職人技の世界。経験と勘がものを言うことも少なくない、奥深い分野なんです。
医師の臨床判断とのアナロジー
この一連の勾配降下法のプロセスは、医師が患者さんの治療計画を立て、改善していくプロセスと非常によく似ています。
| AIの学習(勾配降下法) | 医師の臨床プロセス |
|---|---|
| 損失(Loss) | 治療の「効果の不十分さ」や「副作用の大きさ」。 |
| パラメータ(重み \(w\)) | 薬剤Aの投与量、薬剤Bの投与量、治療間隔など、調整可能な治療介入の要素。 |
| 勾配(Gradient) | 「どの薬剤を増減させれば、最も効果的に状態が改善するか」という、データと経験に基づく医師の臨床的判断。 |
| 学習率(Learning Rate \(\eta\)) | 治療計画を更新する際の「調整の慎重さ」。急に薬を倍増させたりせず、少しずつ様子を見ながら調整する、そのさじ加減。 |
| パラメータの更新 | 診察(効果測定)と判断(勾配)に基づき、実際の投薬量を微調整する行為。 |
| 繰り返し(Iteration) | 定期的な診察を通じて、治療計画を何度も見直し、最適化していくプロセス全体。 |
このように考えると、AIがやっていることは決して魔法ではなく、データに基づいて試行錯誤を繰り返し、最も良い方向へ少しずつ進んでいくという、非常に合理的で、私たちの思考プロセスにも通じるものがあると感じられないでしょうか。
次のセクションでは、この勾配降下法の感動を、実際に動くPythonコードで体験してみましょう。
Pythonによる勾配降下法の直感的な実装
理論はもう十分、と感じている方もいるかもしれませんね。ここからは、これまで学んできた美しい理論たちが、実際のコードの世界でどのように息づいているのか、その生命の躍動を一緒に覗いていくことにしましょう。
ここで挑戦するのは、非常にシンプルな線形モデルを使った勾配降下法の実装です。目的は、与えられたデータ点に最もよくフィットする直線を、AIに自動で見つけてもらうこと。これまで同様、ある薬剤の投与量(入力)と、その効果(出力)の関係を学習するシナリオで進めていきます。このシンプルな例の中に、深層学習の魂が宿っているのを感じていただけたら嬉しいです。
まずは「モデル」と「評価基準」を数式で決めよう
コードに取り掛かる前に、私たちがAIに何をさせたいのか、数学の言葉で整理しておく必要があります。
- モデルの形(仮説)
私たちは、投与量と効果の関係が「直線」で表せるのではないか、と仮説を立てます。直線の式は、中学数学で習った通りですね。 \[ \text{予測される効果} (\hat{y}) = w \times \text{投与量} + b \] 私たちのAIの仕事は、データに最もフィットする直線の傾きw(重み)と切片b(バイアス)を自動で見つけ出すことです。 - 良し悪しの評価基準(損失関数)
「最もフィットする」とは、どういう状態でしょうか? それは「実際の効果と、モデルの予測した効果の間の誤差が、全体として最も小さい」状態です。この誤差を測るためのポピュラーな指標が平均二乗誤差 (Mean Squared Error, MSE) です。 \[ L(w, b) = \frac{1}{N} \sum_{i=1}^{N} (\hat{y}_i – y_i)^2 \] この式がやっていることは、- 各データ点 \(i\) について、予測値 \(\hat{y}_i\) と正解値 \(y_i\) の差(誤差)を計算する。
- その誤差を2乗する(マイナスを消し、大きな誤差をより重視するため)。
- 全データ(\(N\)個)の分を合計し、平均を取る。
勾配計算の裏側(手計算で紐解く)
Pythonコードの中で、いきなり勾配を計算する式が出てきますが、あれは魔法ではありません。先ほど学んだ「連鎖率」を使って、損失関数 \(L\) を各パラメータ \(w\) と \(b\) で偏微分した結果なのです。一度、私たちの手でその計算を追いかけてみましょう。
wの勾配 \( \frac{\partial L}{\partial w} \) を求める
連鎖率を使って分解します: \( \frac{\partial L}{\partial w} = \frac{\partial L}{\partial \hat{y}} \times \frac{\partial \hat{y}}{\partial w} \)- まず \( \frac{\partial L}{\partial \hat{y}} \) は、\(L = \frac{1}{N}\sum(\hat{y}-y)^2\) を \(\hat{y}\) で微分するので \( \frac{1}{N}\sum 2(\hat{y}-y) \) となります。
- 次に \( \frac{\partial \hat{y}}{\partial w} \) は、\(\hat{y} = wx+b\) を
wで微分するのでxとなります。 - これらを掛け合わせると、\( \frac{\partial L}{\partial w} = \frac{1}{N} \sum_{i=1}^{N} 2( \hat{y}_i – y_i ) x_i \) となります。コードの中の
np.mean(2 * (y_pred - y) * X)は、まさにこの計算をしています。
bの勾配 \( \frac{\partial L}{\partial b} \) を求める
同様に分解します: \( \frac{\partial L}{\partial b} = \frac{\partial L}{\partial \hat{y}} \times \frac{\partial \hat{y}}{\partial b} \)- \( \frac{\partial \hat{y}}{\partial b} \) は、\(\hat{y} = wx+b\) を
bで微分するので1となります。 - 掛け合わせると、\( \frac{\partial L}{\partial b} = \frac{1}{N} \sum_{i=1}^{N} 2( \hat{y}_i – y_i ) \) となります。コードの
np.mean(2 * (y_pred - y))がこれですね。
- \( \frac{\partial \hat{y}}{\partial b} \) は、\(\hat{y} = wx+b\) を
スッキリしましたね!(え!?ムズカシイ?飛ばして大丈夫です笑)これで、心置きなくコードの世界に飛び込めます。
Pythonコードで勾配降下法を動かす
# === ライブラリの準備 ===
import numpy as np # Pythonで数値計算、特に配列や行列の計算を高速に行うための定番ライブラリです
# === 1. サンプルデータの準備 ===
# これが私たちの持っている「カルテ」情報だと考えてください。
# 投薬量 X と、それに対応する実際の効果 y が記録されています。
X = np.array([1.0, 2.0, 3.0, 4.0, 5.0]) # 薬剤の投与量 (入力データ)
y = np.array([2.1, 3.9, 6.2, 8.0, 9.8]) # 薬剤の効果 (正解データ)
# === 2. モデルのパラメータ初期化 ===
# AIに、まず「適当な直線を一本引いてみて」とお願いするフェーズです。
# w(重み)とb(バイアス)を、ランダムな値で初期化します。ここが学習のスタート地点。
w = np.random.rand() # 傾きwを0~1のランダムな値で設定
b = np.random.rand() # 切片bを0~1のランダムな値で設定
print(f"学習スタート地点 → 初期重み(w): {w:.4f}, 初期バイアス(b): {b:.4f}")
# === 3. ハイパーパラメータ(人間が決める設定値)の準備 ===
learning_rate = 0.01 # 学習率η: 坂道を下る「歩幅」。大きすぎても小さすぎてもダメな、重要な値。
epochs = 1000 # エポック数: 学習サイクルを繰り返す回数。「何歩、坂道を下るか」の回数。
print(f"学習の進め方 → 学習率: {learning_rate}, エポック数: {epochs}\n")
# === 4. 勾配降下法による学習サイクル ===
# 指定されたエポック数だけ、坂道を下るループを開始します。
for epoch in range(epochs):
# --- 4-1. 順伝播:現在のモデルで予測値を計算 ---
# 今持っている w と b で、AIが「予測される効果」を計算します。
# y_pred = w * X + b は、ベクトル計算です。
# (スカラー) * (ベクトル) + (スカラー) -> (ベクトル) という計算が一括で行われます。
y_pred = w * X + b
# --- 4-2. 損失の計算:予測がどれくらいズレているか評価 ---
# 「予測」と「正解」のズレを、平均二乗誤差(MSE)で評価します。
# この loss の値を小さくすることが、私たちの旅の目的です。
loss = np.mean((y_pred - y)**2)
# --- 4-3. 勾配の計算:どちらに進めば良いかコンパスで確認 ---
# 先ほど手計算で導いた、あの式をそのまま使います。
# これで「wを動かすべき方向」と「bを動かすべき方向」が分かります。
w_grad = np.mean(2 * (y_pred - y) * X) # wに対する損失の勾配
b_grad = np.mean(2 * (y_pred - y)) # bに対する損失の勾配
# --- 4-4. パラメータの更新:実際に一歩進む ---
# 「w_new = w_old - η * w_grad」の更新式を実装します。
# 勾配(坂を上る方向)とは逆向きに、学習率(歩幅)の分だけ進みます。
w -= learning_rate * w_grad # 重みwを更新
b -= learning_rate * b_grad # バイアスbを更新
# --- 4-5. 進捗の表示(おまけ) ---
# 100回に一回、現在の状況を報告してもらいます。
# 損失(loss)がどんどん小さくなっていく様子は、見ていて感動的ですよ。
if (epoch + 1) % 100 == 0:
print(f"エポック {epoch + 1}/{epochs}, 損失: {loss:.4f}, w: {w:.4f}, b: {b:.4f}")
# === 5. 学習完了! ===
print("\n--- 学習完了 ---")
print(f"AIが見つけた最適解 → 最終的な重み(w): {w:.4f}, 最終的なバイアス(b): {b:.4f}")
# === 学習済みモデルで新しい予測をしてみる ===
new_X = 6.0
predicted_y = w * new_X + b
print(f"\n例えば、新しい投与量 {new_X} に対する効果の予測値は: {predicted_y:.4f} です。")
学習スタート地点 → 初期重み(w): 0.9501, 初期バイアス(b): 0.7320
学習の進め方 → 学習率: 0.01, エポック数: 1000
エポック 100/1000, 損失: 0.1245, w: 1.6341, b: 0.8117
エポック 200/1000, 損失: 0.0827, w: 1.7225, b: 0.6124
エポック 300/1000, 損失: 0.0614, w: 1.7766, b: 0.4902
エポック 400/1000, 損失: 0.0494, w: 1.8109, b: 0.4137
エポック 500/1000, 損失: 0.0425, w: 1.8331, b: 0.3662
エポック 600/1000, 損失: 0.0385, w: 1.8479, b: 0.3370
エポック 700/1000, 損失: 0.0361, w: 1.8580, b: 0.3190
エпоック 800/1000, 損失: 0.0347, w: 1.8650, b: 0.3078
エポック 900/1000, 損失: 0.0338, w: 1.8700, b: 0.3009
エポック 1000/1000, 損失: 0.0333, w: 1.8737, b: 0.2968
--- 学習完了 ---
AIが見つけた最適解 → 最終的な重み(w): 1.8737, 最終的なバイアス(b): 0.2968
例えば、新しい投与量 6.0 に対する効果の予測値は: 11.5389 です。このコードを実行すると、上記のような、最初はデタラメだった w と b が、学習を重ねるごとにデータにフィットした値(おそらくw ≈ 1.9, b ≈ 0.3 付近)に近づいていき、損失が劇的に減少していく様子が観察できるはずです。
私たちは、AIに「直線を引きなさい」と教えたわけではありません。「予測と正解の誤差を、勾配を頼りにひたすら小さくしなさい」と命じただけです。それだけで、AIは自動的にデータに最もフィットする直線、つまり「投与量が増えれば効果も増す」という本質的な関係性を見つけ出してくれました。
実際の医療AIはもっと複雑なモデルを使いますが、その根底に流れている「勾配降下法で最適なパラメータを探す」という原理は、ここで体験したものと全く同じなのです。
医療分野での応用と、その先にあるもの
先ほどのPythonコードでは、AIが自動でデータにフィットする直線を見つけてくれましたね。投与量と効果という、たった2つのパラメータの関係性を解き明かす小さな一歩でしたが、実は今、医療の世界で起きている革命の、まさに縮図なんです。
私たちが手探りで見つけた直線の傾きwと切片b。これを、何百万、何十億という次元に拡張し、同じように「勾配降下法」という名の、ひたむきな坂下りをさせることで、AIは人間には到底不可能なレベルで、データに潜む複雑なパターンを学び取っていきます。
その応用範囲は、もはやSFの世界ではありません。微分と勾配、そして勾配降下法というエンジンが、具体的に医療現場でどのように活躍しているのか、その代表的な例を「AIが何を問題とし、何を学習しているのか」という視点で整理してみましょう。
| 応用分野 | AIが解くべき問題(例) | 最小化したい「損失」の例 | AIが学習・調整する「パラメータ」の例 |
|---|---|---|---|
| 疾患診断支援 (画像診断など) | 「この胸部X線写真には、肺がんの疑いがあるか?」 | AIの予測(疑いあり/なし)と、熟練の放射線科医による正解診断との「食い違い」。 | 画像のどの模様・形状・濃度が「がんらしさ」に繋がるかを判断するための、数百万個の画像フィルタの数値。 |
| 個別化医療 (治療法選択) | 「この遺伝子情報を持つ患者さんには、治療薬AとBのどちらがより効果的か?」 | AIが予測した治療効果と、臨床試験や実臨床で得られた実際の治療効果との「ズレ」。 | どの遺伝子変異や生活習慣が、どの薬の効果にどれくらい影響を与えるかを示す、何十万もの「重み」の値。 |
| 新薬開発 (創薬) | 「この新しい化学構造を持つ化合物は、標的となるタンパク質に結合し、薬効を発揮するか?」 | AIが予測した化合物の活性度や毒性と、実験室での測定結果との「誤差」。 | 分子の形や原子の繋がり方を数値化したベクトルと、それが生物学的活性にどう変換されるかのルール(関数の形)。 |
| 予後予測・異常検知 (時系列データ) | 「ICU患者のバイタルサイン(心拍数・血圧など)の推移から、6時間以内に敗血症ショックを発症するリスクは?」 | AIが予測した発症リスクと、実際に患者がその状態に陥ったかどうかの「結果」。 | 時々刻々と変化するデータの中の、「危険な兆候」を示す特定の波形やパターンの数値表現。 |
この表を眺めていると、気づくことがあるかもしれません。それは、応用される場面やデータの種類は違えど、その根底にあるロジックは驚くほど一貫している、ということです。
- 解決したい課題を定義する。
- その課題における「失敗の度合い(損失)」を数式で定義する。
- あとは、AIがその「損失」を最小化するような「パラメータ」を、勾配降下法というひたむきな努力によって、自ら見つけ出していく。
私たちが行った、たった2つのパラメータ w と b を求める旅路が、そのまま何億次元の空間にスケールアップした世界が、ここには広がっています。
もちろん、AIは万能の魔法ではありません。学習データの質や量に大きく依存しますし、AIが出した答えの解釈には、常に深い医学的知見と倫理観が求められます。AIは、医師の経験や患者さんとの対話に取って代わるものではなく、むしろ、人間の医師がより本質的な診断や治療に集中するための、過去にないほど強力な「思考の補助輪」なのだと、私は考えています。
まとめ
今回の内容をまとめると、以下のようになります。
- 微分: ある関数がどれくらいの速さで変化するか(傾き)を示す。
- 勾配: 多次元空間において、最も急な下り坂の方向を示すベクトル。
- 連鎖率: 複雑な関数(複数の層を持つニューラルネットワーク)の微分を効率的に計算するための法則。
- 勾配降下法: 勾配を利用して、モデルのパラメータを少しずつ更新し、予測誤差(損失)を最小化する学習アルゴリズム。
これらの概念を理解することは、深層学習モデルがどのように学習し、どのようにして医療分野の複雑な問題に対処する能力を獲得するのかを深く理解する第一歩となります。次回は、この微分と勾配の概念をさらに深掘りし、「計算グラフ」という視覚的なツールを使って誤差逆伝播をより直感的に理解することを目指します。
この一連のコースを通して、AIの「心臓部」がどのように動いているのか、その息遣いを少しでも感じていただけたなら幸いです。そして、この知識が、皆さまが今後AIという新しい道具と向き合う上で、確かな足場となることを心から願っています。
参考文献
- Esteva A, Topol EJ, Dean H, et al. A guide to deep learning in healthcare. Nature Medicine. 2019;25(1):24-29.
- Mamoshina P, Bunch H, Putin E, et al. Applications of deep learning in precision medicine. NPJ Digital Medicine. 2020;3(1):1-10.
- Mak KK, Pichika MR. Artificial intelligence in drug discovery: current trends and future perspectives. Journal of Pharmaceutical Analysis. 2021;11(1):1-12.
- Rajkomar A, Dean J, Kohane IS. Machine Learning in Medicine. New England Journal of Medicine. 2019;380(14):1347-1358.
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






