AIは医療データなどの情報を「テンソル」という統一された言葉で表現します。そして「行列積」で情報を変換・集約し、「要素ごとの積」で取捨選択するという計算プロセスを経て、新しい知見を生み出します。この一連の流れが、AIの思考の基本です。
AIはあらゆるデータを「テンソル」という統一形式で扱います。これはスカラー(点)、ベクトル(線)、行列(面)といった階層構造を持ち、患者データや医療画像などを数学的に整理するための基本的な「言葉」となります。
AIの計算の核心は2つの積です。
①行列積: 情報を混ぜ合わせ新しい特徴(リスクスコア等)を「変換・集約」します。
②要素ごとの積: 必要な情報だけを「選択・強調」するフィルターの役割を担います。
複雑な計算を支える名脇役がいます。計算の形を整える「転置」や、サイズの違うデータ間の計算を賢く自動化する「ブロードキャスティング」が、AIのプログラミングを効率的かつエレガントにしています。
はじめに:AIの「言葉」と「思考回路」を覗いてみませんか?
みなさんが「AI」や「ディープラーニング」という言葉を耳にするとき、まず、どのようなイメージが頭に浮かぶでしょうか。未来的な診断支援システム、難解な数式が並ぶ論文、あるいは、少し取っつきにくい「魔法」のような技術、といった感じかもしれませんね。
実は、私自身もAIを学び始めた頃、「その動作原理の根底には線形代数があります」と聞いて、「また数学か…」と、正直なところ少しだけ気が重くなった記憶があります。日々の臨床や研究で忙しい中、なぜ今、ベクトルや行列の世界に足を踏み入れなければならないのか、と。
ですが、もし、その「魔法」の正体が、実は非常に合理的で、私たちの臨床現場での思考と驚くほど深く結びついているとしたら、少し興味が湧いてきませんか?
これからお話しする線形代数は、決して無味乾燥な数式暗記ではありません。AIが膨大な医療データを理解し、思考するための、いわば「言葉」や「文法」のようなものなんです。
例えば、みなさんが多くの症例を経験される中で、いくつかの検査値の微妙な組み合わせから「これは、あの疾患の典型的なパターンに近いな」という、一種の「匂い」のようなものを感じ取ることがあると思います。実は、AIがやっていることも、これと本質的に同じなのです。膨大な患者データを「ベクトル」や「行列」という言葉で整理し、その言葉の繋がりの中から「疾患のパターン」という名の匂いを、数学という文法を使って嗅ぎ分けている。そのための強力な道具が、今回学ぶ線形代数というわけです。
今回の講座では、AIが使う基本的な語彙である「ベクトル」「行列」から、それらを包括する「テンソル」という最重要概念まで、一気に解像度を上げていきます。AIが患者さん一人ひとりのデータをどのように「個」として認識し(ベクトル)、患者さんの集団をどうやって「群」として把握し(行列)、そして、それらのデータからどのようにして「関係性」を見つけ出すのか(内積などの計算)。その一連の思考プロセスを、ステップ・バイ・ステップで追体験していきましょう。
この講座が終わる頃には、AIが決してブラックボックスな魔法の箱などではなく、非常に合理的で、ある意味で美しいルールに基づいて動いていることを、きっと実感していただけるはずです。それでは、AIという新しい同僚と効果的に対話するための第一歩を、一緒に踏み出ましょう。
1. AIの視点:世界を「テンソル」で見るということ
さて、いよいよAIの思考回路の探検に出発です。その最初のステップとして、AIが私たちの世界、特に医療データをどのように「見て」いるのか、その「視点」をインストールしてみましょう。
私たち人間が物事を「点・線・面・立体」として自然に認識するように、AIもまた、すべてのデータをある決まった「形」で認識しています。このAIの基本的な世界観を理解することが、AIと対話するための、何よりも重要な第一歩になります。
1-1. データという名のレゴブロック:テンソルの階層
AIの世界では、驚くほど多くのものが、これから紹介するいくつかの「形」の組み合わせで表現されています。なんだか、レゴブロックで世界を組み立てるみたいで、ちょっとワクワクしませんか?
その最も基本的な単位から、順番に見ていきましょう。
- 点からはじまる物語:スカラー (Scalar)
すべての基本は、ただ一つの数値、「点」です。これをスカラーと呼びます。例えば、「ある患者さんの体温が36.5℃である」という情報は、36.5という一つのスカラーです。AIモデルが最終的に出力する「この画像が悪性である確率:0.92」といった、一つの確信度スコアもスカラーですね。 - 点が連なり、線となる:ベクトル (Vector)
このスカラーがいくつか順序をもって並ぶと、「線」になります。これがベクトルです。患者さん一人の検査値データ(体重, 血圧, 血糖値)などが、まさにこれにあたります。心電図の波形のように、時間の経過とともに変化する一連のデータも、一本の長いベクトルとして捉えることができます。 - 線が束になり、面が生まれる:行列 (Matrix)
次に、そのベクトルが何本か束になると、「面」、つまり長方形の表が出来上がります。これが行列(マトリックス)です。みなさんが論文やカルテでよく目にする、縦に患者ID、横に検査項目が並んだ一覧表。あれこそが、行列そのものです。一枚のモノクロCT画像も、ピクセルの明るさを数値として並べた巨大な行列と考えることができます。 - そして、すべてを包み込む言葉:テンソル (Tensor)
さて、ここで最も大切な言葉が登場します。AIの世界では、これまで見てきたスカラー(点)、ベクトル(線)、行列(面)、さらには3次元以上の立体構造(例えば、複数枚のCTスライスを重ねたボリュームデータなど)も、すべて「テンソル」という一つの言葉で統一的に扱います。
この階層構造を、視覚的に確認してみましょう。
【図1:テンソルの階層構造と「次元」】
[ 5 ]
└ スカラー (0階テンソル): 点
- AIの世界での「次元の数 (number of dimensions)」は 0 です (NumPyでは ndim=0)。
- このように、データを並べるための「軸」を一つも持たない、単一の数値を指します。
[ 5, 8, 3 ]
└ ベクトル (1階テンソル): 線
- 「次元の数」は 1 です (ndim=1)。
- データを一列に並べるための「軸」が1つだけ存在します。
- よく「このベクトルは3次元だ」と言ったりしますが、これは「ベクトルの要素数が3つ」という意味で、
AIプログラミングで言うところの「テンソルの次元数(=軸の数)」とは意味が異なる場合があり、
少し紛らわしいので注意が必要です。重要なのは「軸が1つ」という点です。
[[ 5, 8, 3 ],
[ 1, 7, 2 ]]
└ 行列 (2階テンソル): 面
- 「次元の数」は 2 です (ndim=2)。
- お馴染みの「行」と「列」という、2つの軸を持っています。
- NumPyでこの行列の形(shape)を見ると (2, 3) のように表示されます。
これは「1つ目の軸には要素が2つ、2つ目の軸には要素が3つある」という意味です。
[[[ 5, 8, 3 ],
[ 1, 7, 2 ]],
[[ 9, 4, 6 ],
[ 3, 0, 5 ]]]
└ 3階テンソル: 立体
- 「次元の数」は 3 です (ndim=3)。
- 例えば「奥行き」「行」「列」のように、データを配置するための軸が3つあります。
- 医療現場では、複数枚のCTスライスを重ねたボリュームデータ (枚数, 高さ, 幅) や、
カラーの病理画像 (高さ, 幅, 色チャンネル) などが、この3階テンソルとして扱われます。
...これらすべてを包括する概念が「テンソル」です。
AIプログラミング、特にモデルを自作する際には、このテンソルの「次元の数(ndim)」と、
それぞれの次元が持つ「要素の数(shape)」を常に意識することが、
エラーなく、意図通りに計算を進めるための最も重要な鍵となります。
解説:まるでレゴブロックのように、低次元の部品が組み合わさって高次元の構造物が出来上がっていくイメージですね。AI、特にPyTorchやTensorFlowといったライブラリは、どんなに複雑なデータも、この「テンソル」という統一されたブロックとして扱うことで、効率的な計算を実現しているのです。
1-2. 私たちの医療データは、どんな「形」をしている?
さて、この便利な「テンソル」という言葉を手に入れたところで、私たちの身近な医療データが、具体的にどのようにベクトルや行列という「形」に収まっていくのか、もう少しじっくり見ていきましょう。
ベクトル:個々の情報を宿す「矢印」
ベクトルとは、先ほど「線」と表現しましたが、より正確には「大きさと向き」を持った量のことです。AIの世界では、患者さん一人ひとりの状態や、一枚の心電図の波形といった、個別の情報を表現する主役となります。
ここに、ある患者Aさんのデータがあります。
- 体重: 70 kg
- 最高血圧: 130 mmHg
- 血糖値: 95 mg/dL
この3つの情報を (70, 130, 95) という一組のリストにすると、これがAIが扱う「ベクトル」の正体です。私が初めてこれを多次元空間の「矢印」として捉えられたとき、バラバラだった患者さんのデータが、まるで夜空の星座のように意味のある配置に見えてきて、少し感動したのを覚えています。
^ 血圧 (130)
|
| ↗
| ↗ (患者Aのベクトル)
| ↗
+------------------> 体重 (70)
/
/
↙
血糖値 (95)
【図2:患者状態ベクトルのイメージ】
解説:これは3次元空間における患者Aさんの状態を概念的に示したものです。
各軸が検査項目に対応し、その値に向かって原点から伸びる矢印が「ベクトル」です。
この矢印の「向き」と「長さ」自体が、患者さんの総合的な健康状態をユニークに示しています。
別の患者さん、例えば(65, 140, 110)というデータなら、この矢印とは少し違う方向、違う長さになりますよね。
この考え方ができると、「患者AさんとBさんの状態は似ているか?」という臨床的な問いを、「2本のベクトルの矢印は、空間の中でどれくらい近くにあるか?」という、数学的な距離や角度の問題に置き換えられるようになります。これこそ、AIによるデータ解析のすべての始まりです。
行列:データの集合体を扱う「整理棚」
行列は、ベクトルを何本か束ねて立てかけたもので、まずは複数のデータをまとめて格納する「整理棚」としての役割を理解するのが一番分かりやすいと思います。
| 患者 | 体重 (kg) | 最高血圧 (mmHg) | 血糖値 (mg/dL) |
|---|---|---|---|
| 患者A | 70 | 130 | 95 |
| 患者B | 65 | 140 | 110 |
| 患者C | 85 | 150 | 130 |
この見慣れた表が、まさに行列そのものです。臨床研究で扱う大規模なコホートデータは、AIにとっては巨大な行列に他なりません(1)。そして、ここだけの話、この単なるデータの表が、次のセクションではAIの「思考エンジン」へと変貌を遂げます。その話は、また後ほどのお楽しみ、ということにしておきましょう。
1-3. Pythonでテンソルに「命」を吹き込む
さて、理論はこれくらいにして、実際にこのテンソルというものを私たちの手で触ってみましょう。AIプログラミングの世界では、Pythonという言語と、NumPyという数値計算ライブラリを使うのがデファクトスタンダード(事実上の標準)になっています。
NumPyを使うと、これまで話してきたスカラー、ベクトル、行列といった概念に、コンピュータ上で「命」を吹き込み、実際に計算できるオブジェクトに変換することができます。
# coding: utf-8
# NumPyライブラリは、科学計算の分野では必須のツールです。
# 慣例として「np」というニックネームでインポートします。
import numpy as np
# --- ベクトル (1階テンソル) の作成 ---
# まずはPythonのただの数字のリストとして、患者さんのデータを準備します。
patient_a_data = [70, 130, 95] # [体重(kg), 最高血圧(mmHg), 血糖値(mg/dL)]
# np.array()という関数が、ただのリストに命を吹き込み、
# 数学的な計算が可能なNumPy配列(ベクトル)に変換します。
patient_a_vector = np.array(patient_a_data)
print("--- ベクトル (1階テンソル) ---")
print("患者Aのベクトル:", patient_a_vector)
# .shapeは、そのテンソルの「形」を教えてくれます。AI開発では頻繁に使います。
print("形状 (shape):", patient_a_vector.shape) # (3,) は、要素が3つある1次元配列(ベクトル)を意味します。
# type()で、このオブジェクトの正体がnumpy.ndarrayであることを確認します。
print("データ型:", type(patient_a_vector))
# --- 行列 (2階テンソル) の作成 ---
# 今度は、リストの中にリストを入れる形で、複数人分のデータを用意します。
all_patients_data = [
[70, 130, 95], # 患者Aの行
[65, 140, 110], # 患者Bの行
[85, 150, 130] # 患者Cの行
]
# 同じようにnp.array()で、データの集合体を行列に変換します。
patient_matrix = np.array(all_patients_data)
print("\n--- 行列 (2階テンソル) ---")
print("患者データベース行列:\n", patient_matrix)
# 行列の形を見てみましょう。
print("形状 (shape):", patient_matrix.shape) # (3, 3)は、3行3列の2次元配列(行列)を意味します。
--- ベクトル (1階テンソル) ---
患者Aのベクトル: [ 70 130 95]
形状 (shape): (3,)
データ型: <class 'numpy.ndarray'>
--- 行列 (2階テンソル) ---
患者データベース行列:
[[ 70 130 95]
[ 65 140 110]
[ 85 150 130]]
形状 (shape): (3, 3)これから先、AIモデルを扱う際には、入力データやモデルの重みがどのような「形(shape)」をしているかを常に意識することが、エラーを防ぎ、実装をスムーズに進める一番の近道かもしれません。この shape の感覚、ぜひ今のうちに掴んでおいてくださいね。
2. AIの計算の心臓部:性格が違う2つの「掛け算」
さて、前のセクションで、私たちの医療データが「テンソル」という統一された形でAIに認識される、という話をしました。ここからは、いよいよAIの「思考」の核心部分、つまり、入力されたデータをどのように処理していくのかを見ていきます。
AIはテンソルに対して様々な計算を行いますが、その中でも特に重要なのが「積」、つまり掛け算です。面白いことに、AIの思考プロセスには、まるで性格の違う2人の計算担当者がいて、それぞれ全く異なる目的で「掛け算」を使い分けているんです。一人は、様々な情報を混ぜ合わせて新しい知見を生み出す「シェフ」。もう一人は、必要な情報だけを選り分ける「門番」。
この2人の役割の違いを理解することが、AIの振る舞いを理解する鍵となります。
その1:行列積 (Dot Product) – 情報を「変換・集約」するシェフ
まず登場するのは、ニューラルネットワークの主役とも言える計算、行列積です。情報を混ぜ合わせて新しい価値を生み出す「シェフ」の仕事、と考えるとイメージが湧きやすい、という話をしましたね。
でも、そもそもなぜ、情報を「混ぜ合わせる」必要があるのでしょうか?
それは、臨床現場で行っている診断プロセスを思い浮かべると、非常にしっくりくると思います。例えば、糖尿病を診断する際、血糖値だけを見るのではなく、HbA1c、体重、血圧、家族歴といった複数の情報を総合的に判断しますよね。生の検査データそのものよりも、それらを巧みに組み合わせた「複合的な指標」の方が、診断にはずっと有用なはずです。
行列積は、まさにその「複合指標」をデータから自動で作り出すための、極めて強力な手法なんです。
AIの思考法:診断基準リストとしての「重み行列」
この行列積のプロセスを、AIの世界で最も重要な式の一つであるアフィン変換で見てみましょう。
\[y = Wx + b\]
一見するとただの数式ですが、一つ一つの文字に、医療現場での思考に対応する役割があります。
| 数式の要素 | 役割 | 医療現場でのイメージ |
|---|---|---|
| \(x\) | 入力ベクトル | ある患者さんの検査値データ([体重, 血圧, 血糖値]など)です。 |
| \(W\) | 重み行列 | AIの知識や経験そのもの。行列の各行が、一つの診断基準に対応します。例えば、1行目は「心疾患リスク」、2行目は「腎機能リスク」の診断基準、といった具合です。中の各数値は「どの検査値が、その診断にどれだけ重要か」を示す“さじ加減”を表します。 |
| \(b\) | バイアスベクトル | 診断基準の「甘辛調整」役です。計算結果全体を少し底上げしたり(ゲタを履かせる)、引き下げたりします。例えば、ある診断基準が厳しすぎる場合に、バイアスがプラスの値を持つことで、全体的にスコアを少し甘くする、といった微調整を行います。 |
| \(y\) | 出力ベクトル | 入力データが診断基準リストで評価された結果、新しく生成された「リスクスコア」のベクトルです。 |
この「重み行列 \(W\)」と「バイアスベクトル \(b\)」こそが、AIが学習を通じてデータから獲得する「パラメータ」です。つまり、AIの学習とは、この診断リストの“さじ加減”や“甘辛調整”を、おびただしい数のデータに基づいて最適化していくプロセスに他なりません。
計算の核心は「内積」による類似度スコア
では、この計算の内部では、具体的に何が起きているのでしょうか。下のブロック図をもう一度、じっくり見てみましょう。
[重み行列 W] [入力ベクトル x] [出力ベクトル y]
(2行 3列の行列) × (3行 1列のベクトル) = (2行 1列のベクトル)
+-----------------+ +---+ +---+
| w11, w12, w13 | | x1| | y1|
| (診断基準1) | (dot) | x2| -----> | |
| w21, w22, w23 | | x3| | y2|
| (診断基準2) | +---+ +---+
+-----------------+ (3x1) (2x1)
(2x3)
【図3:行列積の計算イメージ】
解説:この計算ができるためには、左の行列の「列数」(3)と、右のベクトルの「行数」(3)が
一致している必要があります。これは絶対的なルールです。注目すべきは、出力 \(y_1\) (心疾患リスクスコア)がどうやって計算されるか、です。
\[y_1 = w_{11}x_1 + w_{12}x_2 + w_{13}x_3\]
この式、どこかで見たことありませんか? そう、これこそが、\(W\)の1行目(診断基準1のベクトル)と、入力ベクトル\(x\)の「内積」そのものなんです。
ここで少し寄り道して、計算の根幹をなす内積について、その意味をしっかりと感じてみましょう。内積は、2つのベクトルがどれだけ「息が合っているか」「同じ方向を向いているか」を測る、類似度(親密さ)の指標です。
幾何学的な意味合いで言うと、2つのベクトル \(\vec{a}\) と \(\vec{b}\) の内積は、
\[\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos\theta\]
と書けます。\(|\vec{a}|\), \(|\vec{b}|\)はそれぞれのベクトルの長さ、\(\theta\)は2つのベクトルがなす角度です。三角関数を思い出すと、\(\cos\theta\) は角度 \(\theta\) が0°のときに1(最大)になりましたよね。つまり、2つのベクトルの向きが完全に一致しているとき、内積の値は最大になります。
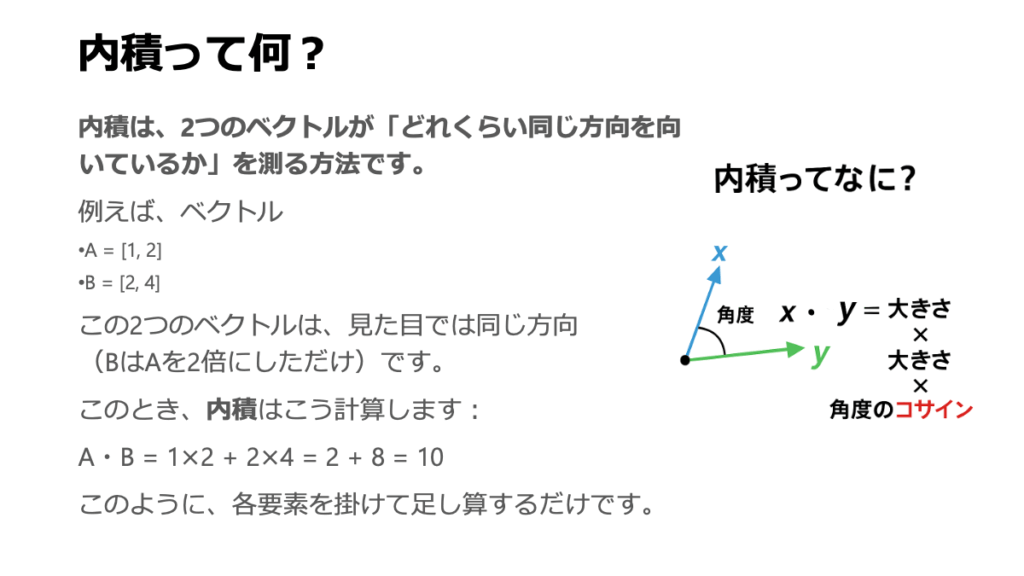
このことから何が言えるでしょうか。
行列積における各スコアの計算とは、「患者さんのデータパターン」のベクトルが、「AIの持つ診断基準」のベクトルと、どれだけ似ているか(同じ方向を向いているか)を評価している、ということに他なりません。非常に直感的だと思いませんか?
Pythonで実践:患者さんのリスクスコアを計算してみる
理屈は分かったところで、この「診断基準との類似度スコア」という考え方が、実際にどのように機能するのか、手を動かして体感してみましょう。
# coding: utf-8
import numpy as np
# 比較のために2人の患者ベクトルを定義します。
patient_a_vector = np.array([70, 130, 95]) # 標準的なAさん
patient_c_vector = np.array([85, 150, 130]) # 全体的に数値が高いCさん
# 「生活習慣病リスクが高い人」の典型的な特徴を表す、架空のプロファイルベクトルを定義します。
# これは、AIが学習の末に獲得するかもしれない「重みベクトル(Wの1行分)」の一つの例だと考えてみてください。
risk_profile_vector = np.array([0.5, 1.0, 1.0]) # [体重の重み, 血圧の重み, 血糖値の重み]
# @ 演算子(内積/行列積)を使って、各患者とリスクプロファイルとの「親密度」を計算します。
score_a = patient_a_vector @ risk_profile_vector
# 計算の内訳: (70 * 0.5) + (130 * 1.0) + (95 * 1.0) = 260.0
print(f"患者Aのリスクスコア(内積): {score_a}")
score_c = patient_c_vector @ risk_profile_vector
# 計算の内訳: (85 * 0.5) + (150 * 1.0) + (130 * 1.0) = 322.5
print(f"患者Cのリスクスコア(内積): {score_c}")
# スコアの大小関係を比較します。
if score_c > score_a:
print("\n計算結果から、患者Cさんの状態ベクトルの方が、リスクプロファイルベクトルと『同じ方向を向いている』度合いが高いと解釈できます。")
患者Aのリスクスコア(内積): 260.0
患者Cのリスクスコア(内積): 322.5
計算結果から、患者Cさんの状態ベクトルの方が、リスクプロファイルベクトルと『同じ方向を向いている』度合いが高いと解釈できます。ここで重要なのは、スコアの絶対値(260.0や322.5)そのものよりも、「患者Cの方が患者Aよりもスコアが高い」という大小関係です。このスコアを使えば、患者さんをリスクに応じて順序付けしたり、一定のしきい値を超えたらアラートを出す、といった応用が可能になるわけです。まさに、情報を変換・集約することで、新たな価値が生まれましたね。
その2:要素ごとの積 (アダマール積) – 情報を「取捨選択」する門番
さて、もう一人の計算担当者の登場です。彼の名前は要素ごとの積(またはアダマール積)。行列積が情報を「混ぜ合わせる」シェフだったのに対し、こちらは、情報を混ぜずに、その場で必要なものだけを通し、不要なものを遮断する「門番」や「ふるい」のような役割を担います。
役割と計算イメージ
計算方法は非常に直感的です。同じ形状を持つ2つのテンソル間で、対応する位置にある要素同士を単純に掛け合わせるだけ。行列の形は変わりません。
【図4:要素ごとの積の計算イメージ】
[元データ A] [マスク B] [フィルタリング後の結果 C]
+----------------+ +----------------+ +----------------+
| 10, 20, 30 | | 1, 0, 1 | | 10, 0, 30 |
| 40, 50, 60 | * | 1, 1, 0 | = | 40, 50, 0 |
+----------------+ +----------------+ +----------------+
解説:とてもシンプルですよね。Aの(1,2)要素である20は、Bの(1,2)要素である0と掛け合わされ、
結果は0になります。一方、Bの要素が1の部分は、Aの元の値がそのまま残ります。
このように、特定の位置の情報を強めたり(1より大きい数を掛ける)、弱めたり(0と1の間の数を掛ける)、
あるいは完全に消したり(0を掛ける)する操作です。
AIの世界での活躍場所
このシンプルな計算が、実は最新のAI技術の根幹を支えています。
- マスキング: 上の図のように、
0と1からなるマスクを掛けることで、不要な情報を完全に遮断します。例えば、言語モデルが文章を生成する際に、未来の単語を「カンニング」してしまわないように、未来の部分に0を掛けて見えなくする、といった使い方をします。 - アテンション (Attention): 近年のAIのブレークスルーである「アテンション機構」の核心部でもあります。「画像の中の、特にこの部分に注目せよ」「文章の中の、この単語が重要だ」といった情報の重要度マップを作成し、元のデータに要素ごとに掛け合わせることで、AIに「注意」を向けさせるのです。
まとめ:2つの「積」の違いを体感しよう
最後に、性格の違う2人の計算担当者、「行列積」と「要素ごとの積」の違いを、実際のコードで体感して、その違いを脳に刻み込みましょう。
| 比較項目 | 行列積 (Dot Product) | 要素ごとの積 (Element-wise Product) |
|---|---|---|
| 目的 | 情報の変換・集約 (特徴量を混ぜ合わせて新しい特徴を作る) | 情報のフィルタリング・マスキング (特徴量を個別に調整) |
| 計算方法 | 行と列の内積を計算 | 対応する要素同士を掛ける |
| 形状の変化 | 変わることが多い(m,n) @ (n,k) -> (m,k) | 変わらない(m,n) * (m,n) -> (m,n) |
| NumPy演算子 | np.dot() または @ | * |
# coding: utf-8
import numpy as np
# --- 2つの積の違いを体感する ---
# 2x3の行列Aを定義
matrix_a = np.array([[1, 2, 3],
[4, 5, 6]])
# 3x2の行列Bを定義
matrix_b = np.array([[10, 20],
[30, 40],
[50, 60]])
# 1. 行列積(@): 情報を変換・集約します
# (2, 3) @ (3, 2) -> (2, 2) の行列が生成されます。形が変わるのがポイント!
dot_product_result = matrix_a @ matrix_b
print("--- 行列積 (シェフの仕事) ---")
print(f"入力Aの形状: {matrix_a.shape}, 入力Bの形状: {matrix_b.shape}")
print(f"出力の形状: {dot_product_result.shape}\n結果:\n{dot_product_result}\n")
# 2. 要素ごとの積(*): 情報をフィルタリングします
# 同じ形状の行列が必要です。matrix_aと同じ形の行列C(マスクのイメージ)を定義します。
matrix_c = np.array([[1, 0, 1], # 2列目の情報を遮断するマスク
[1, 1, 0]]) # 3列目の情報を遮断するマスク
# (2, 3) * (2, 3) -> (2, 3) の行列が生成されます。形は変わりません!
element_wise_result = matrix_a * matrix_c
print("--- 要素ごとの積 (門番の仕事) ---")
print(f"入力Aの形状: {matrix_a.shape}, 入力Cの形状: {matrix_c.shape}")
print(f"出力の形状: {element_wise_result.shape}\n結果:\n{element_wise_result}")
--- 行列積 (シェフの仕事) ---
入力Aの形状: (2, 3), 入力Bの形状: (3, 2)
出力の形状: (2, 2)
結果:
[[220 280]
[490 640]]
--- 要素ごとの積 (門番の仕事) ---
入力Aの形状: (2, 3), 入力Cの形状: (2, 3)
出力の形状: (2, 3)
結果:
[[1 0 3]
[4 5 0]]このコードを実行すれば、2つの「積」が、計算結果も、そして何よりその「役割」も全く異なることが、はっきりとご理解いただけたのではないでしょうか。この違いを区別できることが、AIのモデルの構造を読み解く上で非常に重要になります。
3. AIの計算を支える名脇役:転置とブロードキャスティング
さて、ここまでは行列積のような、AIの計算における「主役」たちを見てきました。ですが、映画に名脇役が欠かせないように、AIの計算も、主役たちを陰で支える素晴らしいテクニックがあって初めて、スムーズかつエレガントに機能します。
ここでは、そんな「名脇役」とも言える2つの重要なテクニック、「転置」と「ブロードキャスティング」をご紹介します。これらを知っていると、AIのライブラリ(NumPyやPyTorch)のコードがなぜあんなにスッキリと、魔法のように書けるのか、その秘密がきっと解けてくるはずです。
転置 (Transpose) – 行列の「視点」を変える準備運動
まず一人目の名脇役は「転置」です。これは一言で言うと、行列の行と列を、パタンと入れ替える操作です。
なぜ、わざわざ入れ替える必要があるの?
一番の理由は、前のセクションで見た行列積の「形」を合わせるためです。行列積では、掛け合わせる2つの行列の内側の次元数が一致している必要がありましたよね。手元のデータの形が、そのままでは計算に合わない…そんな場面は日常茶飯事です。そんなとき、転置を使って片方の行列の形をクイっと変えてあげることで、計算の準備が整うのです。まるで、パズルを解くためにピースの向きを変えるような、地味ながら不可欠な操作ですね。
図とコードで見る転置
行列 A の転置は、数学の世界では右上に T をつけて \(A^T\) と表記します。具体的に見てみましょう。
【図5:転置のイメージ】
[元の行列 A (2x3)] [転置行列 A^T (3x2)]
+-----------------+ (転置) +-------------+
| 1, 2, 3 | -----> | 1, 4 |
| | | |
| 4, 5, 6 | | 2, 5 |
+-----------------+ | |
| 3, 6 |
+-------------+
解説:元の行列の1行目だった [1, 2, 3] が、転置後には1列目になっているのが分かりますね。
ちょうど、左上から右下への対角線を軸にして、行列をパタンと折り返したようなイメージです。この操作は、NumPyでは驚くほど簡単にできます。
# coding: utf-8
import numpy as np
# 2行3列の行列を定義
matrix_a = np.array([[1, 2, 3],
[4, 5, 6]])
print("--- 転置前 ---")
print("形状:", matrix_a.shape)
print("行列:\n", matrix_a)
# .T という属性にアクセスするだけで、転置された行列が手に入ります。
transposed_matrix = matrix_a.T
print("\n--- 転置後 ---")
print("形状:", transposed_matrix.shape) # 形状が (2, 3) から (3, 2) に変わった!
print("行列:\n", transposed_matrix)
--- 転置前 ---
形状: (2, 3)
行列:
[[1 2 3]
[4 5 6]]
--- 転置後 ---
形状: (3, 2)
行列:
[[1 4]
[2 5]
[3 6]]転置は、単に形を合わせるだけでなく、データの「視点」を変えるという意味合いも持っています。例えば、統計解析で相関行列を計算する際など、少し高度な場面でも活躍する、非常にエレガントな手法です。
ブロードキャスティング – 「空気の読める」賢い自動拡張機能
二人目の名脇役は、AIプログラミングを劇的に楽にしてくれる、まさに「魔法」のような機能、ブロードキャスティングです。
これは、NumPyやPyTorchが持つ、形の違うテンソル同士の計算を、ルールに基づいて「よしなに」実行してくれる仕組みです。ループ処理を一行も書かずに、異なるサイズのデータを足したり引いたりできるのは、すべてこの賢い機能のおかげなんです。
「空気を読む」とは、どういうこと?
一言でいえば、「小さい方のテンソルが、大きい方の形に合わせて、自分自身を仮想的にコピー&ペーストしてサイズを揃えてくれる」イメージです。
前のセクションで出てきた \(y = Wx + b\) の、行列積の結果(ベクトル)にバイアスベクトル b を足す計算。あれこそが、ブロードキャスティングの典型的な活躍シーンです。
【図6:ブロードキャスティングのイメージ】
行列 (3x2) + ベクトル (1x2)
+-------------+ +-------+
| 10, 20 | | 100, 1|
| 30, 40 | + +-------+
| 50, 60 |
+-------------+
↓ (ベクトルが空気読んで、自分を下にコピー!)
+-------------+ +-------------+ +-------------+
| 10, 20 | | 100, 1 | | 110, 21 |
| 30, 40 | + | 100, 1 | = | 130, 41 |
| 50, 60 | | 100, 1 | | 150, 61 |
+-------------+ +-------------+ +-------------+
解説:(3,2)の行列と(1,2)のベクトルは、本来は形が違うので足せません。
しかし、ブロードキャスト機能が働き、ベクトルが自分自身を3行に複製したかのように振る舞い、
要素ごとの足し算が行われます。
すごいのは、この「複製」をメモリ上で実際に行うのではなく、あくまで「仮想的」に計算してくれる点です。だから、巨大なデータでもメモリを無駄遣いすることなく、極めて高速に計算できる。まさに魔法のようですが、ちゃんと賢いルールに基づいています。
医療データ処理での活躍
この機能は、データの前処理で特に輝きます。例えば、多数の患者さんのデータ行列に対して、各検査項目の標準化(全患者の平均値を引き、標準偏差で割る)を行う、といった場面。このとき、全患者データ(行列)から平均値(ベクトル)を引き算する、という操作は、ブロードキャスティングがなければ非常に面倒なループ処理が必要です。NumPyなら、それをたった一行で、しかも高速に実行してくれます。
では、この魔法を、実際にコードで体験してみましょう。
# coding: utf-8
import numpy as np
# 3人の患者の検査値行列 (3x2)
# 各行が患者、列が[血糖値, 中性脂肪]とします
patient_data = np.array([[150, 180],
[100, 140],
[180, 220]])
# 全患者に適用したい補正値ベクトル (1x2)
# 例えば、目標値との差を計算するようなイメージです
correction_values = np.array([-120, -150])
print("--- ブロードキャスティングによる計算 ---")
print("元のデータ (3x2):\n", patient_data)
print("補正値 (1x2):", correction_values)
# 形が違うのに、普通に引き算ができてしまう!
# (3,2)の行列の各行から、(1,2)のベクトルがそれぞれ引かれます。
corrected_data = patient_data + correction_values # 足し算でも引き算でもOK
print("\n補正後のデータ (3x2):\n", corrected_data)
--- ブロードキャスティングによる計算 ---
元のデータ (3x2):
[[150 180]
[100 140]
[180 220]]
補正値 (1x2): [-120 -150]
補正後のデータ (3x2):
[[ 30 30]
[-20 -10]
[ 60 70]]転置とブロードキャスティング。これらは主役ではありませんが、AIのプログラミングを驚くほどシンプルで、かつパワフルにしてくれる、まさに「縁の下の力持ち」です。この2つの存在を知っているだけで、これからAIのコードを読むときの解像度が格段に上がるはずですよ。
4. まとめ:AIの思考は「テンソルの流れ」と「計算の組み合わせ」
お疲れ様でした。今回は、AIの思考回路の深部まで、かなり詳しく踏み込んでみました。最後に、今日学んだ知識を一つのストーリーとしてまとめてみましょう。
- まず、患者データ、画像、テキストといったあらゆる情報は、AIの世界ではテンソルという統一された形式に変換されます。
- このテンソルは、ニューラルネットワークの層を次々と流れていきます。
- 各層では、主に行列積 (
@) によって、情報はより抽象的な特徴へと変換・集約されます。このとき、AIの知識である「重み行列」が使われ、その計算の基礎にはベクトル間の類似度を測る内積の考え方があります。 - 時には、要素ごとの積 (
*) によって、特定の情報が強調されたり、不要な情報が除去されたり(フィルタリング)します。 - これらの計算をスムーズに行うため、裏では転置による形の整形や、ブロードキャスティングによる柔軟なサイズ調整が、賢く行われています。
AIの「思考」とは、このように、テンソルというデータが、様々な種類の計算ブロックを通過していく一連の「流れ」として捉えることができます。
これで、AIが話す言葉の単語と、かなり複雑な文法まで手に入れたことになります。次回のテーマは「微分」です。これは、AIが「学習」する、つまり間違いから学んで賢くなっていくための仕組み、言わば「言葉をどう変化させて上達していくか」という動的なプロセスを理解する上で、絶対に欠かせない概念です。今回の線形代数の知識が、その理解をきっと助けてくれるはずです。
参考文献
- Rajkomar A, Dean J, Kohane I. Machine learning in medicine. N Engl J Med. 2019;380(14):1347-1358. doi:10.1056/NEJMra1814259
- Lundervold AS, Lundervold A. An overview of deep learning in medical imaging. Med Image Anal. 2019;54:1-18. doi:10.1016/j.media.2019.03.004
- Wang F, Zhang W, Wang J, et al. The rise of artificial intelligence in healthcare applications. In: Artificial Intelligence in Healthcare. Elsevier; 2021:3-22.
- LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521(7553):436-444. doi:10.1038/nature14539
- Goodfellow I, Bengio Y, Courville A. Deep Learning. Cambridge, MA: MIT Press; 2016. (Chapter 2: Linear Algebra)
- Strang G. Introduction to Linear Algebra. 5th ed. Wellesley, MA: Wellesley-Cambridge Press; 2016.
- Numpy Development Team. NumPy documentation. Available at: https://numpy.org/doc/stable/. Accessed May 27, 2025.
- Paszke A, Gross S, Massa F, et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In: Advances in Neural Information Processing Systems 32. Curran Associates, Inc.; 2019:8024-8035.
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






