はじめに:膨大な「医学の海」で、たった一滴のしずくを見つける技術
想像してみてください。あなたの目の前に、過去10年分の電子カルテ、数百万件の最新医学論文、そして院内の全看護記録や退院サマリが、天井に届くほど山積みになっています。この膨大な情報の山の中から、「特定の希少疾患を持つ患者において、ある薬剤が引き起こした可能性のある副作用の記述」を、わずか0.1秒で見つけ出さなければなりません。
これは、現代の医療AI開発、特にRAG(検索拡張生成)システムの構築において、私たちが直面している課題そのものです。
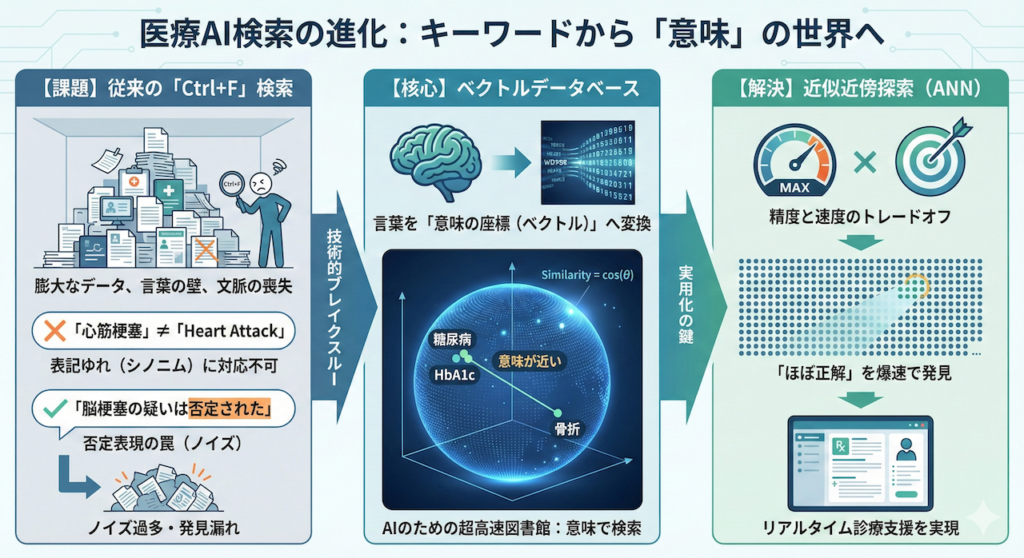
「Ctrl+F」の限界:言葉の壁と文脈の喪失
従来のキーワード検索(いわゆる「Ctrl+F」の世界)では、このミッションは不可能です。なぜなら、医療現場における「言葉」は、あまりにも多様で文脈依存的だからです。
- 表記のゆれ(シノニム): 「心筋梗塞」を検索しても、「AMI (Acute Myocardial Infarction)」や「急性心筋梗塞」、「Heart Attack」と記載されたカルテはヒットしない可能性があります。これらは医学的に同じ意味であるにもかかわらず、コンピュータにとっては「別の文字列」でしかないからです。
- 否定表現の罠: 「脳梗塞の疑い」と検索した場合、「脳梗塞の疑いは否定された」という記述までヒットしてしまいます。キーワード検索は、その単語が存在するかどうかしか見ず、「否定されている」という重要な文脈を理解できません。
このように、従来の検索技術では、本当に必要な医学的知見(エビデンス)を漏らしたり、逆に無関係なノイズを大量に拾い上げたりしてしまい、臨床現場での実用には耐えられませんでした。
ベクトルデータベース:言葉を「意味の座標」へ変換する
ここで救世主として登場するのが、RAGの心臓部となる「ベクトルデータベース」です。これは、言葉を単なる文字の並びとしてではなく、「意味」として管理する、いわばAIのための超高速な図書館です。
具体的には、大規模言語モデル(LLM)のEmbedding(埋め込み)技術を使って、あらゆる単語や文章を数百〜数千次元の数値の列(ベクトル)に変換します。
例えば、ある高次元空間(意味の地図)を想像してください。
- 「糖尿病」という言葉のベクトル \( \mathbf{v}_{\text{diabetes}} \)
- 「HbA1c」という言葉のベクトル \( \mathbf{v}_{\text{hba1c}} \)
- 「骨折」という言葉のベクトル \( \mathbf{v}_{\text{fracture}} \)
この空間内では、「糖尿病」と「HbA1c」は医学的に関連が深いため、座標上の距離が非常に近くなります。一方で、「骨折」はこれらとは遠い場所に配置されます。ベクトル検索では、この「ベクトル間の距離(または角度)」を計算することで、類似度を判定します。
\[ \text{Similarity} = \cos(\theta) = \frac{\mathbf{A} \cdot \mathbf{B}}{\|\mathbf{A}\| \|\mathbf{B}\|} \]
ベクトルデータベースは、ユーザーが入力した質問文の意味(ベクトル)と、データベース内の膨大な医療知識のベクトルとの類似度を一瞬で計算し、「単語は違っても、意味が最も近い情報」を提示します。これにより、「心不全」という検索クエリで、「EF低下」や「BNP上昇」といった関連記述を即座に見つけ出すことが可能になるのです。
近似近傍探索(ANN):精度と速度のトレードオフに挑む
しかし、数億件規模のデータを扱う医療ビッグデータにおいて、すべてのデータとの距離を正確に計算(全探索)していては、応答に何秒、何分もかかってしまいます。救急医療や診療支援において、この遅延は許されません。
そこで重要となるのが、近似近傍探索(ANN: Approximate Nearest Neighbor)です。
「厳密に100%正確な順位でなくてもよいから、ほぼ間違いなく正解に近い上位の情報を、爆速で返す」
この割り切りこそが、現代のリアルタイム医療AIを支えています。本稿では、このANNを実現するアルゴリズム(HNSW等)と、実務における実装戦略について解説していきます。
1. 言葉を「座標」に変える:高次元空間の地図
私たちが普段カルテに記載する「言葉」を、そのままの形ではコンピュータは理解できません。コンピュータにとって、「糖尿病」という文字は単なる「0と1のデータ配列」に過ぎず、そこに医学的な意味を見出すことはできないのです。
そこで、LLM(BERTやGPTなど)の登場です。これらのモデルは、テキストを数百から数千個の数値の列(ベクトル)に変換する能力を持っています。この処理をEmbedding(埋め込み)と呼びます。
少し想像力を働かせてみましょう。私たちの住む世界は「縦・横・高さ」の3次元ですが、AIが見ている世界は、例えば768次元や1536次元といった超高次元の空間です。
この広大な空間の中に、あらゆる医学用語が「座標(点)」としてマッピングされています。
- 点A [糖尿病]: (0.12, -0.59, 0.88, …, 0.05)
- 点B [HbA1c]: (0.15, -0.55, 0.90, …, 0.02)
- 点C [骨折]: (-0.89, 0.22, -0.11, …, -0.78)
この空間における「距離」は、言葉の「意味的な近さ」を表します。点A(糖尿病)と点B(HbA1c)は、医学的に密接に関連しているため、この高次元空間内でも非常に近い位置に配置されます。一方で、点C(骨折)は、内科的な代謝疾患とは文脈が異なるため、遥か遠くに配置されます。
ベクトルデータベースとは、まさにこの「意味の地図」を管理し、ある地点から最も近い情報を瞬時に探し出すナビゲーションシステムのことなのです。
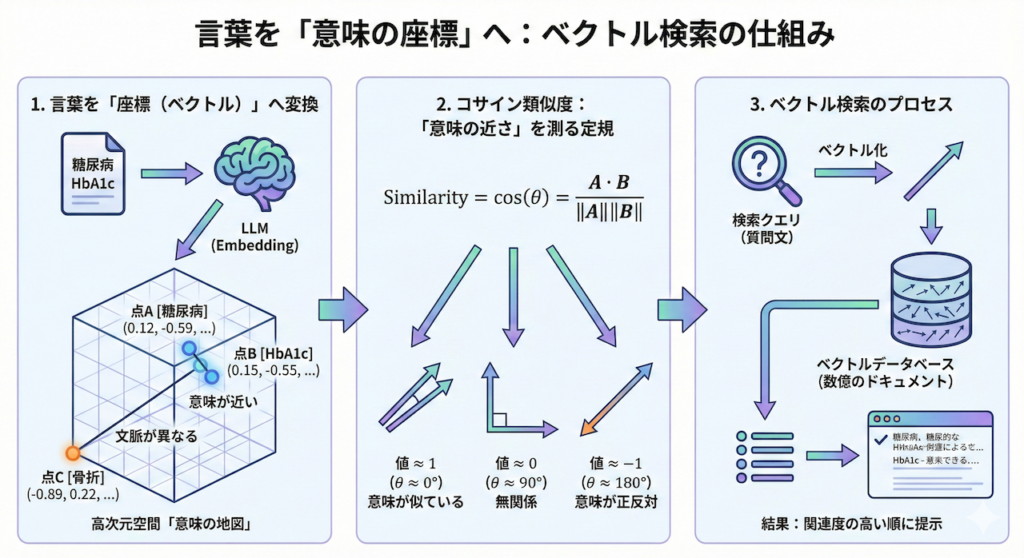
コサイン類似度:意味の近さを測る「定規」
では、この高次元空間で、2つの文章が「どれくらい似ているか」を数学的にどうやって測るのでしょうか? 最も一般的に使われる指標が、コサイン類似度(Cosine Similarity)です。
これは、2つのベクトル(矢印)が向いている「方向」の一致度を測るものです。ベクトル \( \mathbf{A} \)(質問文)とベクトル \( \mathbf{B} \)(ドキュメント)のなす角を \( \theta \) とすると、その余弦(cosine)は以下のように計算されます。
\[ \text{Similarity} = \cos(\theta) = \dfrac{\mathbf{A} \cdot \mathbf{B}}{\|\mathbf{A}\| \|\mathbf{B}\|} = \dfrac{\sum_{i=1}^{n} A_i B_i}{\sqrt{\sum_{i=1}^{n} A_i^2} \sqrt{\sum_{i=1}^{n} B_i^2}} \]
この数式が意味していることは、実はシンプルです。
- 値が \( 1 \) に近い(\( \theta \approx 0^\circ \)): 2つの矢印がほぼ同じ方向を向いている = 「意味が非常に似ている」
- 値が \( 0 \) に近い(\( \theta \approx 90^\circ \)): 2つの矢印が直交している = 「全く無関係である」
- 値が \( -1 \) に近い(\( \theta \approx 180^\circ \)): 2つの矢印が反対を向いている = 「意味が正反対である」
ベクトル検索エンジンは、あなたが入力した質問文(クエリ)を瞬時にベクトル化し、データベース内の数億個のドキュメントベクトルとのコサイン類似度を計算します。そして、その値が「1」に近いものから順に、関連度の高いエビデンスとして提示するのです。
2. なぜ「近似」なのか?:全探索(KNN)から近似探索(ANN)へ
ここで、一つの重大な技術的課題が生じます。それは「計算量の爆発」です。
もし、あなたのデータベースにあるカルテが数千件程度であれば、AIはすべてのカルテとの距離を一つずつ計算し、正確に並び替えることができます。これをKNN(K-Nearest Neighbors:K近傍法)、あるいは「全探索」と呼びます。しかし、データが数百万、数億件という規模になると話は別です。
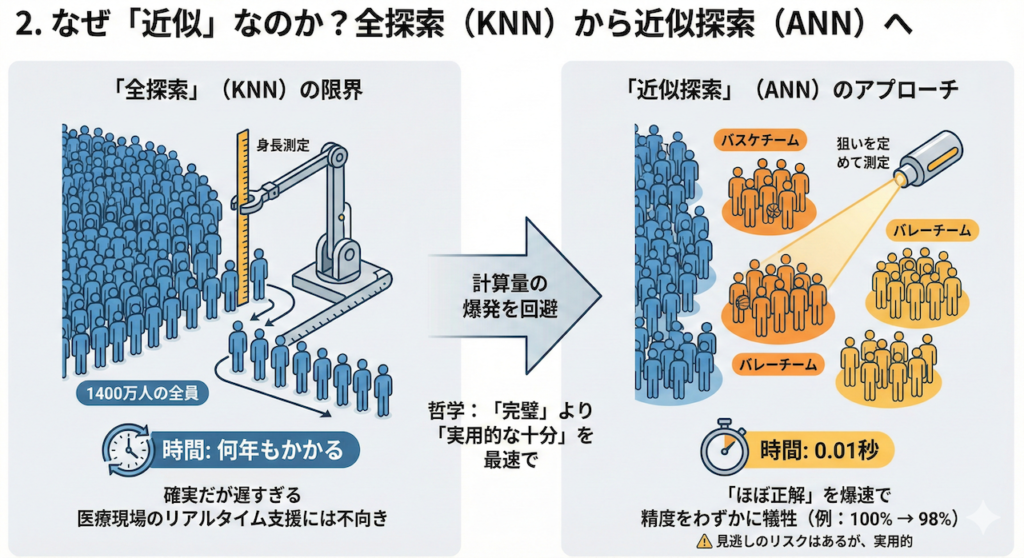
「全探索」の限界:1400万人の身長測定
全探索の非効率さを、直感的な例で考えてみましょう。
「東京都に住む1400万人の中で、最も身長が高い人を見つけたい」とします。
- KNN(全探索)のアプローチ: 1400万人全員を一列に並ばせ、一人ひとり順番に身長を測っていきます。これなら確実に「1番高い人」が見つかりますが、測定が終わる頃には何年も経っているでしょう。
医療現場において、医師が「この症状に似た過去の症例は?」と問いかけたとき、AIが回答するまでに10分もかかっていては、そのシステムは使い物になりません。リアルタイム支援には、ミリ秒単位の応答速度が求められます。
近似近傍探索(ANN):精度と速度のトレードオフに挑む
全探索(KNN)が「1400万人全員の身長を一人ずつ測る」ことだとすれば、数億件のデータを扱う医療AIにおいては、より賢いアプローチが必要です。そこで登場するのが、ANN(Approximate Nearest Neighbor:近似近傍探索)です。
これは、膨大なデータ空間に対して「空間をあらかじめ大まかに区切っておく(インデックス化)」ことで、検索範囲を劇的に絞り込む技術です。
なお一口に「近似近傍探索(ANN)」といっても、その実装アプローチには大きく2つの系統があります。
1つは、データ点同士をグラフ構造で結び、グラフ上を辿りながら近傍を探索するグラフ型(代表例:HNSW)。
もう1つは、ベクトル空間をあらかじめ複数のクラスタ(代表点・重心)に分割し、検索時には有望なクラスタにのみ探索範囲を絞るクラスタリング型(代表例:IVF)です。
以下では、まず直感的に理解しやすいクラスタリング型ANN(IVF系)を例に、なぜ「近似」によって劇的な高速化が可能になるのかを説明します。その後の節で、実運用において広く使われているグラフ型ANN(HNSW)の仕組みと実装上の要点を解説します。
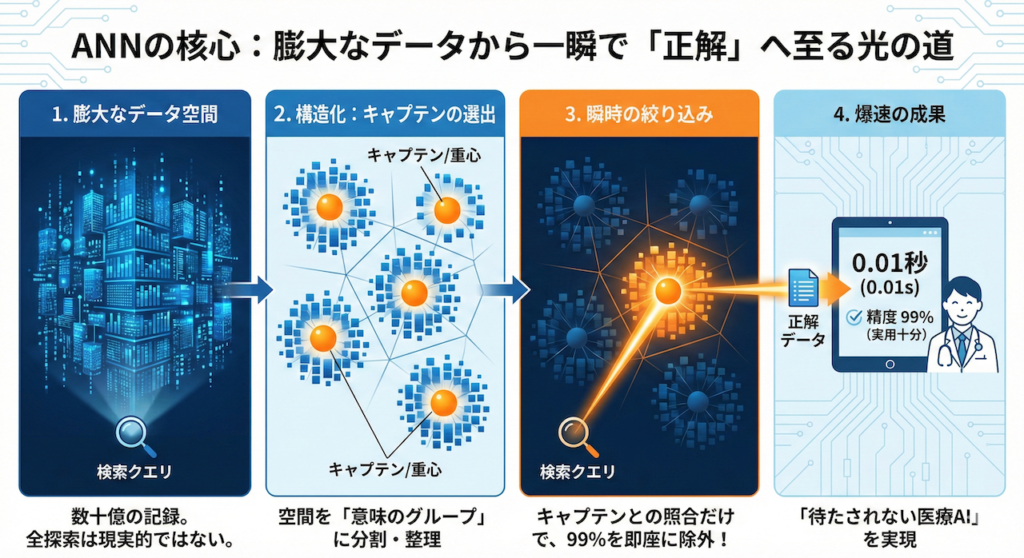
「有望なグループ」に狙いを定めるアプローチ
ANNの基本的な考え方は、全員を測るのではなく、「バスケットボールチーム」や「バレーボールチーム」など、背の高い人がいそうなグループに目星をつけておき、そのグループ内だけを詳細に測定するというものです。
しかし、ここで一つの疑問が浮かびます。「コンピュータは、どうやって『背の高い人がいそうなグループ』を事前に見つけるのか?」ということです。コンピュータには「バスケ=背が高い」という常識はありません。
その答えは、「重心(Centroid)」と「ボロノイ分割(Voronoi Tessellation)」という数学的な仕組みにあります。
グループ化のメカニズム:空間を支配する「チームキャプテン」
コンピュータがデータ空間に「意味のあるグループ」を作るプロセスは、学校の校庭に生徒(データ)を集める避難訓練に似ています。
- キャプテン(重心)の選出:
まず、データ空間全体を見渡し、バランスよく配置されるように数人の「リーダー(代表点)」を選びます。これを専門用語で「セントロイド(Centroid:重心)」と呼びます。K-means法などのアルゴリズムを使い、例えば100人のキャプテンを空間内に配置します。 - ボロノイ分割(縄張りの決定):
次に、全データに対して号令をかけます。「自分から見て、一番近くにいるキャプテンのところに集まりなさい!」
すると、空間全体がキャプテンを中心にきれいに分割されます。こうしてできた「キャプテンと、その周りに集まったデータの集合(ボロノイ領域)」が、私たちが探していた「探索すべきグループ(クラスタ)」になります。
検索時の動き:「1400万人」ではなく「100人の代表」と比べる
準備ができたら、いよいよ検索です。「身長が高い人(クエリ)」がやってきました。ここでコンピュータが行っているのは、魔法ではなく「圧倒的な省略」です。
- キャプテン会議(Coarse Quantizer):
いきなり数億個のデータ全員を見ることはしません。まず、事前に選んでおいた100人のキャプテン(重心ベクトル)だけを見ます。
ここで、「あなたの質問ベクトル」と「各キャプテンのベクトル」の距離を計算します。1400万回ではなく、たった100回の計算で済みます。 - 有望なチームの特定:
計算の結果、「第7キャプテンのベクトルが、あなたの質問に一番近い」と判明します。この瞬間、コンピュータは他の99チーム(数百万件のデータ)をすべて無視することを決定します。 - 詳細探索(Fine Search):
ターゲットは第7チームだけに絞られました。ここで初めて、そのチームに所属しているメンバー(例えば1000件)だけに対して、詳細な距離計算を行い、最終的な回答候補を選び出します。
この仕組みにより、計算量は「1400万回」から「1100回(100+1000)」へと劇的に減り、超高速な応答が可能になるのです。
「境界線」の問題と解決策(nprobe)
ただし、この方法にはリスクがあります。もし、探している「隠れた高身長の人(正解データ)」が、たまたまグループの境界線ギリギリ(隣のチーム)に立っていた場合、その人を見逃してしまうリスク(再現率の低下)があるのです。
そこで、実務では「nprobe(エヌ・プローブ)」というパラメータを使います。
「一番近いチームだけじゃなくて、念のため隣のチームも(上位n個)探しておこう」
nprobe=3 と設定すれば、最も近い上位3つのグループを探索対象にします。これにより、「隣のクラスにいた正解」を見逃すリスクを防ぎつつ、全探索より遥かに高速な検索を実現します。
医療AIにおける「実用的な十分(Good Enough)」の哲学
ANNの哲学は、まさに「完璧(Perfect)を目指して遅れるより、実用的な十分(Good Enough)を最速で提供する」という点にあります。
「厳密に数学的なNo.1でなくてもいい。実質的にほぼ同じ意味を持つ上位の情報を、0.01秒で返してほしい」
この工学的な割り切りこそが、現代の高速なAI検索を支えています。例えば救急外来(ER)で、過去の類似症例を検索する際、精度100%の結果が出るのに10分かかるシステムよりも、精度98%の結果が0.1秒で出るシステムの方が、臨床的価値は圧倒的に高いのです。
私たちは精度をわずかに犠牲にする代わりに、「待たされない快適さ」と「実用的な検索能力」を手に入れたのです。
3. HNSW:ベクトル検索のデファクトスタンダード
現在、ベクトル検索の世界で「デファクトスタンダード(事実上の標準)」として君臨し、OpenAIやMeta(Facebook)、そして多くの医療系AIスタートアップが採用しているアルゴリズム。それが、HNSW(Hierarchical Navigable Small World)です。
名前は少し難解で威圧的ですが、その仕組みは私たちの日常生活にある交通システム、「急行列車と各駅停車」の関係に例えると、驚くほど直感的に理解できます。
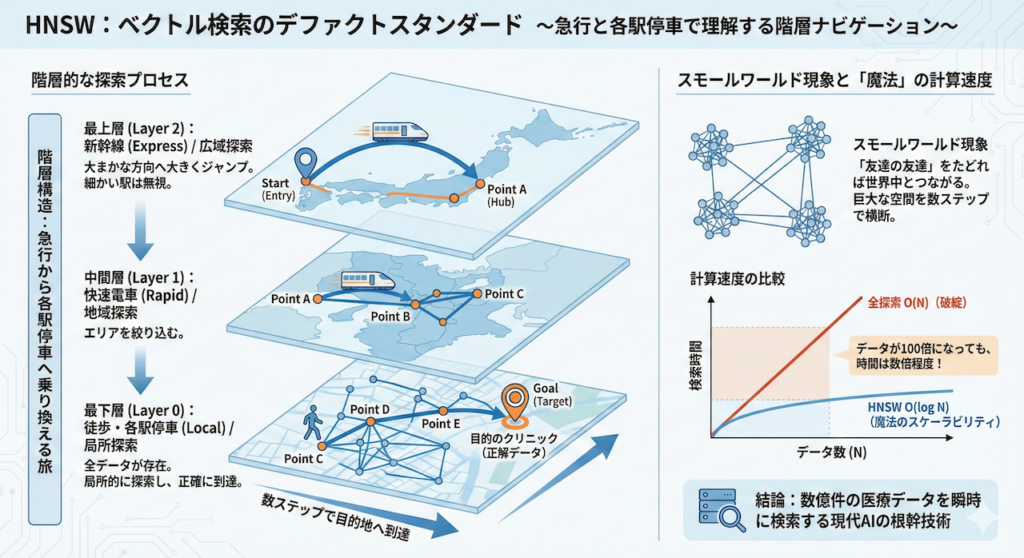
階層構造:急行から各駅停車へ乗り換える旅
HNSWは、データポイント(単語や文章のベクトル)を、「階層構造(Hierarchy)」を持つグラフ(ネットワーク)として管理します。これは、目的地(探したいデータ)にたどり着くまでの「ナビゲーションマップ」のようなものです。
想像してみてください。あなたが「東京」から「大阪の特定の小さなクリニック」へ移動し、そこで診察を受けている患者を探すとします。
- 最上層(Layer 2):新幹線(Express)
まず、東京から大阪まで一気に移動します。途中の静岡や名古屋といった細かい駅(データ)は無視して、大まかな方向へ大きくジャンプします。 - 中間層(Layer 1):快速電車(Rapid)
大阪駅に着いたら、目的の区(エリア)まで快速電車で移動します。少し範囲が絞られます。 - 最下層(Layer 0):徒歩・各駅停車(Local)
最後に、すべてのデータ(建物)がつながっている最下層で、局所的な探索を行い、目的のクリニック(正解データ)へ正確に到達します。
HNSWは、このプロセスをベクトル空間内で行います。
スモールワールド現象と「魔法」の計算速度
このアルゴリズムの背景には、社会学の有名な理論である「スモールワールド現象(Six Degrees of Separation)」があります。「友達の友達」を6回たどれば、世界中の誰とでもつながれるという理論です。
HNSWは、データ同士を「近くの友達(密な結合)」と「遠くの知り合い(長距離リンク)」で巧みに繋ぐことで、巨大なデータ空間を数ステップで横断することを可能にしています。
この構造により、計算量はデータ数 \( N \) に対して \( O(\log N) \) となります。
\[ \text{Time Complexity} \approx O(\log N) \]
これが何を意味するかというと、例えばデータが100万件から1億件(100倍)に増えたとしても、検索にかかる時間は数倍程度しか増えないということです。
医療ビッグデータは日々指数関数的に増加しますが、\( O(N) \) の全探索ではデータ量に比例して時間がかかり破綻します。対して、\( O(\log N) \) のHNSWは、データが増えても速度がほとんど落ちません。この「魔法のようなスケーラビリティ」こそが、数億件の論文やカルテを瞬時に検索する現代の医療AIシステムを支える根幹技術なのです。
アルゴリズムの内部動作:貪欲探索(Greedy Search)
では、実際にHNSWは各レイヤーの中でどのような計算を行い、次の移動先(駅)を決めているのでしょうか?ここで使われているのが、「貪欲探索(Greedy Search)」と呼ばれるアルゴリズムです。名前は少し難しそうですが、仕組みは驚くほどシンプルです。
「今」より「ゴール」に近いなら進む、そうでなければ降りる
ナビゲーションのルールはたった一つ、「現在の場所よりも、もっと目的地(クエリ)に近い友達(隣接ノード)がいるか?」。これだけを、もうこれ以上近づけないという限界まで繰り返し計算します。
このロジックを、実際に動作するPythonコードで見てみましょう。計算の単純さがより明確に分かります。
import numpy as np
def hnsw_greedy_search(query_vector, entry_point, layer_graph, data_vectors):
"""
HNSWの各レイヤーで行われる「貪欲探索」のPython実装
Args:
query_vector (np.array): 探したいデータのベクトル(目的地)
entry_point (int): 探索の開始地点となるノードID
layer_graph (dict): そのレイヤーにおける接続関係 {node_id: [neighbor_ids...]}
data_vectors (dict): 全ノードのベクトルデータ {node_id: np.array}
Returns:
best_node (int): このレイヤーで最も目的地に近いノードID
"""
# 1. 現在地を「暫定ベスト」としてセットします
current_node = entry_point
best_node = entry_point
# 現在地から目的地までの「直線距離」を測ります
min_dist = np.linalg.norm(query_vector - data_vectors[entry_point])
while True:
improved = False # 改善(より近くへ移動)できたかどうかのフラグ
# 2. 現在地の「友達(隣接ノード)」リストをチェックします
neighbors = layer_graph.get(current_node, [])
for neighbor_id in neighbors:
# 各友達から目的地までの距離を計算します
dist = np.linalg.norm(query_vector - data_vectors[neighbor_id])
# 3. 【判定】もし、今いる場所より「友達」の方がゴールに近ければ...
if dist < min_dist:
min_dist = dist # その距離を新しい「最小記録」に更新
best_node = neighbor_id # その友達を新しい「暫定ベスト」にします
improved = True # 「もっと近い場所が見つかった!」というフラグを立てます
# 4. もし、より近い友達が見つかったなら、その人の場所へ移動して探索を続けます
if improved:
current_node = best_node
else:
# どの友達も現在地よりゴールに近くない場合、この層での探索は終了です
# エスカレーターを降りるように、次の下のレイヤーへ移動します
break
return best_node
距離計算の正体:ユークリッド距離
上記のコードにある np.linalg.norm という関数が、実際に「多次元空間での定規」として機能しています。一般的に使われるのは、中学数学で習う「三平方の定理」を多次元に拡張したユークリッド距離(\( L^2 \)ノルム)です。
\[ d(\mathbf{q}, \mathbf{x}) = \sqrt{\sum_{i=1}^{n} (q_i – x_i)^2} \]
HNSWが「魔法」のように速い理由は、この計算をデータ全員に対して行うのではなく、「今いる場所の友達(少数のノード)」に対してのみ行うからです。もし周囲に自分より近いノードが見つからなければ(improved == False)、そこがそのレイヤーにおける「最寄り駅」となります。
こうして各階層で「最寄り」を乗り継ぎ、最終的にデータが最も密に繋がっている最下層(Layer 0)に到達したとき、AIは数億件のデータの中から、あなたの質問に最もふさわしい「真の正解」を正確にキャッチできるのです。
グラフの構築:どうやって「急行」を決めるのか?
HNSW(Hierarchical Navigable Small World)の驚異的な検索スピードを支えるのは、多層的なネットワーク構造です。しかし、そもそもどのデータが「新幹線(最上層)」に選ばれ、どのデータが「各駅停車(最下層)」に留まるのか、その選別基準はどうなっているのでしょうか?
実は、このエリート選別には複雑な審査などは一切なく、「純粋な確率(ランダム)」によって決定されています。これこそが、HNSWが自己組織的であり、メンテナンスフリーで動作する最大の理由です。
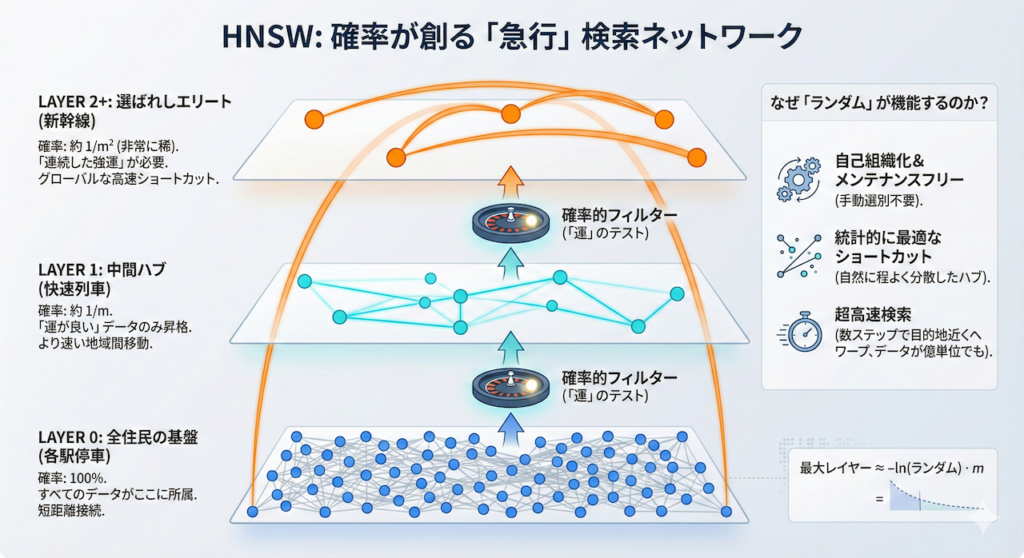
「運」だけで決まるエリート:確率的昇格スキップリスト
新しいデータ(ベクトル)をデータベースに挿入する際、システムは「このデータをどの階層まで配置するか」をその場で決定します。イメージとしては、カジノのルーレットや、何度も挑戦できるコイン投げのようなものです。
- Layer 0(最下層):確率は 100%
すべてのデータは、必ずこの階層に所属します。ここは「全住民」が住む各駅停車の世界です。 - Layer 1(中間層):確率は \( 1/m \)
コインを投げて「表」が出たデータだけが、一つ上の階層へ昇格します(\( m \) は設計パラメータ)。これが「快速列車」の役割を果たします。 - Layer 2(最上層):確率は \( 1/m^2 \)
さらにその中から、もう一度連続で「表」を出した強運なデータだけが、最上層へと昇格します。ここが「新幹線」です。
このように、「運よく高い階層に残ったデータ」が、広大なベクトル空間を飛び越えるための「ハブ(拠点)」となります。一見、ランダムでいい加減に思えるかもしれませんが、この無作為さが空間全体に「程よく散らばったショートカット」を生み出すのです。
なぜ「ランダム」が「高速」につながるのか?
もし、特定の重要なデータ(例えば頻出する医学用語など)を手動で上位レイヤーに選ぼうとすると、データの分布が変わるたびにインデックスを再構築しなければなりません。しかし、ランダムにハブを選ぶHNSWなら、どんなデータが来ても統計的に最適な「急行網」が自然に形成されます。
\[ \text{Max Layer for a node} = \lfloor -\ln(uniform\_random) \cdot m_L \rfloor \]
※内部的には、上記のような対数関数を用いた数式で、どのレイヤーまで積み上げるかを一瞬で計算しています。
この「適度なハブの分散」によって、検索者はどこからスタートしても、まずは上位レイヤーのハブを数ステップ辿るだけで、目的地のすぐ近くまでワープできるようになります。データが1億件に増えても、この「運による階層構造」が維持される限り、検索速度が劇的に落ちることはありません。
このシンプルで数学的な美しさこそが、HNSWが医療AIを含む現代のあらゆる大規模検索エンジンの裏側で、デファクトスタンダードとして採用されている秘密なのです。
4. 実装戦略:FAISS vs Pinecone ― 「自作」か「お任せ」か
さて、理論は分かりました。では、実際に医療現場でシステムを構築する際、どのツールを選ぶべきでしょうか?
医療分野におけるツール選定で最も重要なのは、「データの機密性(プライバシー)」と「運用コスト」のバランスです。選択肢は大きく分けて、オープンソースを自分で運用する「職人コース」と、クラウドサービスを利用する「お任せコース」の2つがあります。
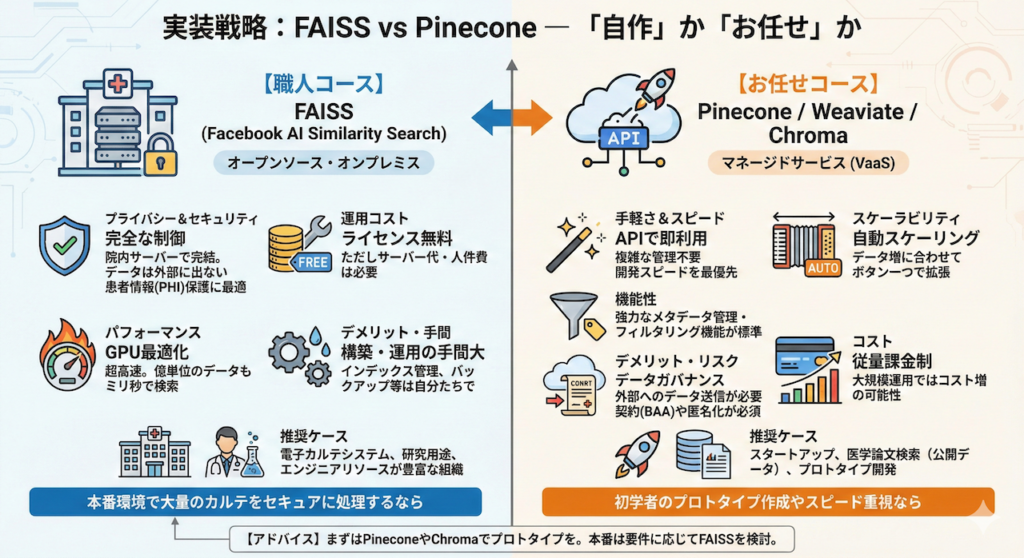
(1) FAISS (Facebook AI Similarity Search) – 職人向け
Meta(旧Facebook)が開発した、世界で最も有名なオープンソースライブラリです。
- メリット:
- 完全なプライバシー制御: 院内のローカルサーバー(オンプレミス)で動作するため、患者の個人情報(PHI)を外部クラウドに一切送信せずにシステムを構築できます。これは大学病院や厳格なセキュリティポリシーを持つ組織にとって最大の強みです。
- コスト: ライセンス料は無料です(サーバー代はかかります)。
- 超高速: GPUを活用した並列計算に最適化されており、億単位のデータでもミリ秒で検索可能です。
- デメリット:
- 構築・運用の手間: サーバーのセットアップ、インデックスの保存・更新、バックアップなど、すべてを自分たちで管理する必要があります。「データベース」というよりは「検索エンジン」のライブラリであるため、データの永続化などは別途実装が必要です。
- 推奨ケース: 電子カルテデータを扱う院内システム、研究用途、エンジニアリソースが豊富な組織。
(2) Pinecone / Weaviate / Chroma – マネージドサービス
これらは「Vector Database as a Service (VaaS)」と呼ばれる、クラウド上で提供される専門サービスです。
- メリット:
- 圧倒的な手軽さ: 複雑なインデックス管理やサーバー構築は不要。APIを呼び出すだけで使えます。
- 自動スケーリング: データが増えても、ボタン一つ(あるいは自動)でサーバーを拡張できます。
- メタデータ管理: 後述する「フィルタリング機能」が標準で強力にサポートされています。
- デメリット:
- データガバナンス: データをクラウド事業者のサーバーに送信する必要があります。契約(BAA:Business Associate Agreement等)や匿名化処理(De-identification)が必須となります。
- コスト: データ量や検索数に応じた従量課金となることが多く、大規模運用ではコストが嵩む可能性があります。
- 推奨ケース: スタートアップ、医学論文の検索システム(公開データ)、開発スピードを最優先する場合。
【アドバイス】 正直なところ、初学者がRAGのプロトタイプを作るなら、まずはPineconeや、ローカルでも手軽に動くChromaから始めるのが挫折しないコツです。しかし、本番環境で大量のカルテをセキュアに処理するなら、FAISSの挙動を理解しておくことは必須スキルと言えるでしょう。
5. 医療RAGの要:メタデータフィルタリング
医療分野でのベクトル検索において、決して避けて通れない最重要テクニックが「メタデータフィルタリング」です。
ベクトル検索は「意味の類似性」を見つけることには長けていますが、「厳密な条件一致」は苦手です。しかし、医療現場ではこの「厳密さ」が求められる場面が多々あります。
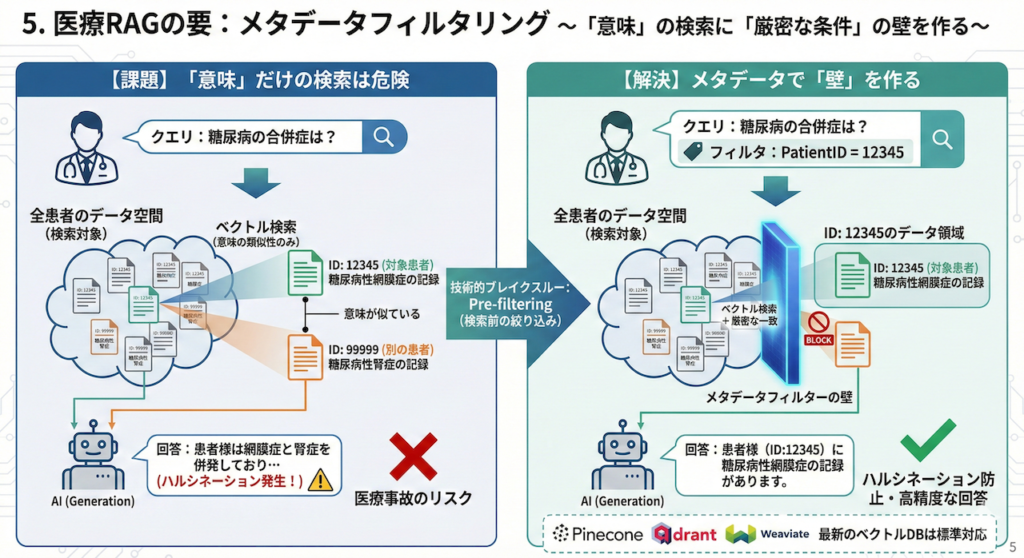
ベクトル検索の落とし穴:「似ている」は「正しい」ではない
例えば、医師が「糖尿病の合併症について」検索したいとします。しかし、検索対象は「全患者」ではなく、「特定の患者(ID: 12345)の過去のカルテのみ」であるべきケースがほとんどです。
- リスク: 単なるベクトル検索(意味の類似度のみ)を行ってしまうと、システムは「別の患者(ID: 99999)の糖尿病の記録」まで、意味が似ているという理由で拾ってきてしまいます。
- 結果: これを回答生成(Generation)に使えば、AIは「患者Aさんには存在しないはずの病歴」をあたかも事実のように語り出すという、医療事故につながりかねない致命的なハルシネーション(幻覚)を引き起こします。
また、研究用途でも同様です。「2024年以降の論文の中から最新の治療法を探す」というタスクで、2010年の古い論文を「内容が似ているから」という理由で提示されては困ります。
Pre-filtering(検索前の絞り込み):検索空間に壁を作る
ここで重要となるのが、Pre-filtering(検索前の絞り込み)という技術です。
これは、ベクトル検索を行う「前(あるいは最中)」に、メタデータ(属性情報)を使って検索対象をフィルタリングする処理です。
\[ \text{Results} = \text{ANN}(\text{Query Vector}, \text{Metadata Filter} = \{ \text{PatientID}: 12345 \}) \]
具体的には、HNSWのグラフを探索する際、「患者IDが12345ではないデータ(ノード)」は、たとえ意味がどれほど似ていても「無視(アクセス禁止)」して進むように制御します。
PineconeやQdrant、Weaviateなどの最新のベクトルデータベースは、この機能を標準で備えています。これにより、「意味的な検索」と「厳密な条件フィルタリング」を両立させ、「正しい患者の、正しい期間のデータに基づいた、正しい回答」を生成することが可能になるのです。
まとめ
ベクトルデータベースは、LLMに「記憶」と「検索能力」を与えるための、いわば「外付けの海馬」です。
- 意味の近さを測るコサイン類似度
- 膨大なデータから一瞬で答えを見つけるHNSWアルゴリズム
- そして、医療の安全性を担保するメタデータフィルタリング
これらを適切に組み合わせることで、これまで病院の地下サーバーで眠っていた膨大なテキストデータは、初めて「臨床で活用可能な生きた知識」へと変わります。
さて、データを「探す」準備は整いました。しかし、その前段階として、そもそも長いカルテや論文を「どのように分割して」データベースに入れるべきでしょうか?
次回は、RAGの精度を左右する隠れた芸術、「L32:医療文書のチャンキング戦略」について解説します。文脈を分断せずに、どこでハサミを入れるべきか? その職人芸に迫ります。
参考文献
- Singhal, A. (2001) ‘Modern Information Retrieval: A Brief Overview’, Bulletin of the IEEE Computer Society Technical Committee on Data Engineering, 24(4), pp. 35–43.
- Li, W. et al. (2020) ‘Approximate Nearest Neighbor Search on High Dimensional Data: Experiments, Analyses, and Improvement’, IEEE Transactions on Knowledge and Data Engineering, 32(8), pp. 1475–1488.
- Malkov, Y.A. and Yashunin, D.A. (2018) ‘Efficient and Robust Approximate Nearest Neighbor Search Using Hierarchical Navigable Small World Graphs’, IEEE Transactions on Pattern Analysis and Machine Intelligence, 42(4), pp. 824–836.
- Johnson, J., Douze, M. and Jégou, H. (2019) ‘Billion-scale similarity search with GPUs’, IEEE Transactions on Big Data, 7(3), pp. 535–547.
- Wang, Y. et al. (2024) ‘A Survey on Vector Database: Storage and Retrieval of Deep Feature Vectors’, ACM Computing Surveys, 56(8), pp. 1–38.
- Lewis, P. et al. (2020) ‘Retrieval-Augmented Generation for Knowledge-Intensive NLP Tasks’, Advances in Neural Information Processing Systems, 33, pp. 9459–9474.
※本記事は情報提供を目的としたものであり、特定の治療法や製品を推奨するものではありません。実装に関する技術的な判断は、各プロジェクトの要件に基づき専門家の助言を仰いでください。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






