「AがBの原因か?」という因果関係を知ることは、医療現場や政策決定で不可欠です。最強のRCTが使えない時、私たちは「準実験的デザイン」という賢い道具を使います。これらは、実世界のデータから「もしも」の比較対象を作り出す手法ですが、それぞれが依拠する「仮定」を理解することが鍵となります。
最強の因果推論であるRCT(ランダム化比較試験)は、倫理・コスト・物理的な問題で実施できないことが多い。単純比較では「交絡(背景の違い)」が結果を歪めてしまいます。
介入群と対照群の「介入前後の変化量」を比較。「もし介入がなくてもトレンドは平行だった」という仮定(平行トレンド仮定)のもと、介入群の「上乗せ効果」を抽出します。
明確な閾値(カットオフ)に着目。カットオフ直前と直後の人々は「ほぼ偶然」割り振られたとみなし、結果の「ジャンプ(不連続)」を介入効果(局所効果)として推定します。
観測できない交絡(U)がある場合、Uとは無関係で処置(X)にのみ影響する「偶然の揺さぶり(Z)」を利用。Zが結果(Y)に与えた影響から、X→Yの真の効果を逆算します。
臨床現場や医療政策の場で、私たちは常に「この治療は、本当に効果があるのか?」「この新しいガイドラインは、患者の予後を改善したのか?」という問いに直面します。
この「AがBの原因か?」という因果関係の問いに答えるのは、実は非常に難しい問題です。なぜなら、私たちの周りには無数の「交絡因子」が潜んでいるからです。例えば、「新しい薬を飲んだ群」と「飲まなかった群」を単純に比較しても、そもそも薬を飲む群は重症だったかもしれませんし、あるいは健康意識が高かったかもしれません。その「背景の違い」が結果に影響してしまうと、薬そのものの真の効果は見えなくなってしまいます。
こうした因果関係の「答え」を知るための最も強力な方法は、ご存知の通りランダム化比較試験(RCT)です (Hernán and Robins, 2020)。参加者をランダム(無作為)に介入群と対照群に分けることで、私たちが知っている要因(年齢、性別など)はもちろん、観測すらできていない未知の要因(例:遺伝的素因、生活習慣の微妙な違い)も含めて、両群の背景を(平均的に)ほぼ同じ状態に揃えることができます。これによって、観測された結果の差を「介入による効果」とみなしやすくなるわけです。まさに「ゴールドスタンダード」と呼ばれる所以ですね。
しかし、このRCTも万能ではありません。
- 倫理的な壁: 例えば、「喫煙が健康に与える影響」を知るために、人をランダムに「喫煙群」と「非喫煙群」に割り当てることは倫理的に許されません。
- 物理的な不可能: 「新しい法律(例:診療報酬改定)が病院の経営に与えた影響」を調べるために、ランダムに法律を適用する地域としない地域を作ることは不可能です。
- コストと時間: 大規模なRCTは、莫大な費用と長い追跡期間を必要とします。
- 一般化の問題: 厳格な基準で選ばれた患者(例:合併症が少ない)でのRCTの結果が、実臨床の多様な患者(RWD: Real World Data)にそのまま当てはまるとは限りません。
では、RCTが使えないとき、私たちは因果推論を諦めるしかないのでしょうか?
いいえ、そんなことはありません。ここで登場するのが、「自然実験(Natural Experiment)」と「準実験的デザイン(Quasi-Experimental Designs)」という、非常に賢いアプローチです。
- 自然実験とは、社会制度の変更や自然災害など、あたかも「誰かがランダムに介入を割り当てたかのような状況」が自然に(あるいは偶然に)発生した状況を指します。
- 準実験的デザインとは、この自然実験のような状況を「利用」したり、あるいはデータの中に「RCTに近い状況」を見つけ出したりすることで、交絡の影響を取り除き、因果関係に迫ろうとする分析手法の総称です (Angrist and Pischke, 2008)。
これらは、実世界で「たまたま起きた」ルールや境界線を巧みに利用して、「比較可能なグループ」をデータから見つけ出す技術とも言えます。
今回は、この準実験的デザインの中でも特に強力で、医療AI研究や臨床疫学研究、医療経済・政策評価の分野で頻繁に使われる「3つの道具」について、その仕組みと使い方を詳しく見ていきましょう。
道具箱①:差分の差分法 (DID) 〜「変化の差」で効果を測る〜
最初の道具は「差分の差分法(Difference-in-Differences: DID)」です。名前は少し難しそうですが、やっていることは「引き算の引き算」という、非常に直感的な方法です。
例えば、ある地域(A地域)だけで2020年から新しい糖尿病の治療ガイドラインが導入されたとします。私たちはこのガイドラインの効果(例:住民の平均血糖コントロールの改善)を知りたいとしましょう。
さて、どうやって比較すれば効果がわかるでしょうか?
- ダメな比較①:導入後のA地域だけを見る(例:2021年のA地域のデータを見る)
これでは、仮に血糖値が改善していても、それがガイドラインのおかげか、あるいは「同時期にたまたま普及した新しい血糖測定アプリ」のおかげか、区別がつきません。このように、介入とは無関係に時間と共にあらわれる変化を「時間トレンド」と呼びます。 - ダメな比較②:導入後に、A地域と、導入されなかったB地域を比較する(例:2021年のA vs B)
これでは、A地域とB地域で「もともと」持っている背景の違いが結果に影響してしまいます。例えば、A地域は大学病院が多く重症患者が集まりやすい地域で、B地域は軽症クリニックが中心の地域だとしたら?その「地域の固定的な差」のせいで、単純比較はできません。
そこでDIDの出番です。DIDは、この「時間トレンド」の問題と「地域の固定差」の問題を、両方同時に解決しようとする賢いアイデアです。
DIDのロジック:「差」の「差」を取る
DIDは、その名の通り「2つの差」を使います。
- 1つ目の差(時間変化の差):
まず、介入群(A地域)と対照群(B地域)それぞれで、介入「前」(例:2019年)と「後」(例:2021年)の血糖コントロールの「変化量」を計算します。 - 2つ目の差(群間差):
次に、介入群の「変化量」(A地域の改善幅)から、対照群の「変化量」(B地域の改善幅)を、さらに差し引きます。
これを、体重測定の例で考えてみましょう。
【比喩:2人の体重測定】
- Aさん(介入群): 新しいダイエットプログラム(介入)を開始。
- Bさん(対照群): プログラムは開始しない。
1. 1つ目の差(時間変化):
- Aさんの体重変化(介入前 → 介入後): 80kg → 75kg で、「-5kg」
- Bさんの体重変化(同じ期間): 60kg → 59kg で、「-1kg」
2. 2つ目の差(DID):
- Aさんの変化 (-5kg) – Bさんの変化 (-1kg) = 「-4kg」
解釈: Bさん(対照群)も、プログラムとは関係なく(例えば季節的な要因で)1kg痩せています。これが「時間トレンド」です。Aさんが痩せた5kgのうち、この1kg分は「プログラムがなくても起きた変化」だと考えられます。
したがって、Bさんの変化分(時間トレンド)を差し引いた、残りの「4kg」こそが、ダイエットプログラムの真の効果(DID推定値)だと考えるわけです。
糖尿病ガイドラインの例に戻れば、「対照群(B地域)で自然に起きたであろう改善(時間トレンド)」を基準にして、「介入群(A地域)でそれを超えて(上乗せして)起きた改善」だけを抽出する。これがDIDの核心的なアイデアです。
最重要ルール:「平行トレンド仮定」
このDIDがうまく機能するためには、絶対に満たさなければならない、非常に重要な仮定があります。それが「平行トレンド仮定(Parallel Trends Assumption)」です。
これは、「もし介入がなかったとしたら(=反実仮想)、介入群(A地域)と対照群(B地域)のアウトカム(血糖値)は、同じように(平行に)推移していただろう」という仮定です。
先ほどの体重の例で言えば、「もしAさんがダイエットプログラムをしていなかったとしても、Bさんと同じ1kgだけ痩せていたはずだ」と仮定する、ということです。
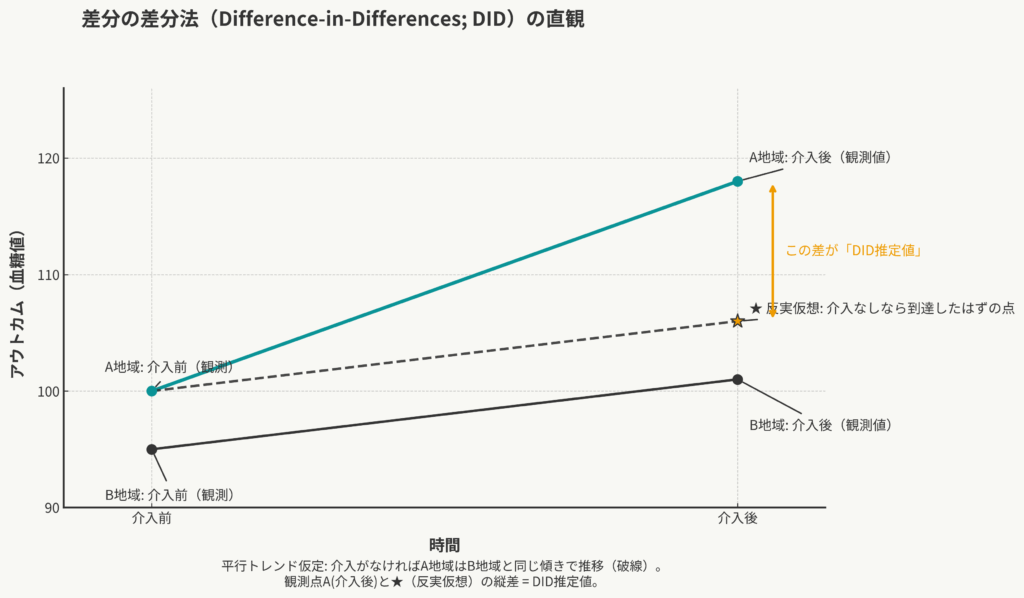
この仮定がもし崩れていたら、どうなるでしょう?
例えば、介入前からA地域だけが(ガイドラインとは無関係に)急激に血糖値が改善するトレンド(例:なぜかA地域だけで運動ブームが起きていた)にあったとします。その場合、B地域のトレンド(傾き)を差し引いても、残った差には「運動ブームの効果」が混じってしまい、ガイドラインの効果を過大評価してしまいます。
だからこそ、研究者は「介入が実施される*前*の期間」のデータをできるだけ長く集め、両群のトレンドが(少なくとも介入前は)本当に平行であったかを可視化して確認することが強く推奨されます (Angrist and Pischke, 2008)。これは仮定が成り立つことを100%証明するものではありませんが、「この仮定は妥当そうだ」と主張するための重要な状況証拠になります。
数式での表現
このロジックを数式で表現すると、非常にスッキリします。
\[ \hat{\delta}_{DID} = (Y_{A, t=1} – Y_{A, t=0}) – (Y_{B, t=1} – Y_{B, t=0}) \]
- \( \hat{\delta}_{DID} \): 私たちが知りたいDID推定値(介入効果)です。
- \( Y_{A, t=1} \): A地域(介入群)の、介入後(t=1)の平均血糖値。
- \( Y_{A, t=0} \): A地域(介入群)の、介入前(t=0)の平均血糖値。
- \( (Y_{A, t=1} – Y_{A, t=0}) \): A地域の「時間変化」。
- \( (Y_{B, t=1} – Y_{B, t=0}) \): B地域の「時間変化」。これを「時間トレンド」の代理とみなします。
この計算は、B地域で起きた時間トレンドを、A地域の変化から差し引いていることに他なりません。
DIDの発展:Staggered DID
この「2群×2期間」のDIDは基本ですが、現実のデータはもっと複雑です。例えば、ガイドライン導入のタイミングが地域ごとにバラバラな場合(A地域は2020年、B地域は2021年、C地域は未導入)などです。これをStaggered DIDと呼びます。
この場合、単純なDIDのモデルを使うと、「先に介入した群(A地域)」が、後から介入する群(B地域)にとっての「対照群」として扱われてしまう期間が生じるなど、複雑な問題が起こり、効果を誤って推定する可能性があることが近年指摘されています (Goodman-Bacon, 2021)。
そのため、Callaway and Sant’Anna (2021) らの研究に代表されるように、「どの群が、いつの時点で、どの群と比較されるべきか」をより厳密に定義する新しい推定方法が活発に開発されています。
道具箱②:回帰不連続デザイン (RDD) 〜「境界線」に隠された局所効果〜
2つ目の道具は「回帰不連続デザイン(Regression Discontinuity Design: RDD)」です。これは、私たちが実験をしなくても、実世界のデータの中に「まるでランダム化比較試験(RCT)が行われたかのような瞬間」を見つけ出す、非常に賢いデザインです。
どういうことでしょうか?
医療現場や公衆衛生の場面では、ある「数値」が「特定の閾値(カットオフ)」を超えたかどうかで、治療や介入の方針が不連続に(ガラッと)変わることがよくあります。
- 例1(治療): LDLコレステロール値が 140 mg/dL を超えたら、スタチン(脂質低下薬)の投薬を「推奨」する。
- 例2(紹介): eGFR(推算糸球体濾過量)が 30 mL/min/1.73m² を下回ったら、腎臓専門医への紹介を「強く推奨」する。
- 例3(公衆衛生): 年齢が 65歳 に達したら、公費によるワクチン接種(例:肺炎球菌ワクチン)の「対象」となる。
RDDは、まさにこの「カットオフ値の“すぐそば”」という、ごく狭い範囲に注目します。
RDDのロジック:「局所的なランダム化」
スタチンの例(カットオフ = 140 mg/dL)で考えてみましょう。
ここに、LDL値が「139 mg/dLの人」と「141 mg/dLの人」がいると想像してください。この2人、LDL値こそわずかに異なりますが、それ以外の点(年齢、性別、生活習慣、合併症のリスク、健康意識など)において、何か系統的な違いがあるでしょうか?
おそらく、ほとんど違いはないはずです。「139」と「141」は、臨床的にはほぼ同じ健康状態であり、この境界線のどちら側に落ちるかは「ほぼ偶然」と言ってもよいのではないでしょうか。
もしそうだとすれば、このカットオフの「すぐ下(139の人たち)」と「すぐ上(141の人たち)」を比較することは、「投薬」以外の条件が(ほぼ)ランダムに揃えられた「局所的なRCT」とみなせる可能性があります。
この状況で、もしカットオフの前後でアウトカム(例:その後の心筋梗塞の発症率)に「ジャンプ(不連続な変化)」が観測されれば、そのジャンプは、唯一不連続に変化したもの、すなわち「カットオフによって誘発された投薬」の効果であると、強く推定できるわけです (Lee and Lemieux, 2010)。
キーコンセプトと最重要の仮定
RDDを正しく理解するには、3つの重要な言葉と、1つの仮定を知る必要があります。
- ランニング変数 (Running Variable): カットオフを決めるための連続的な変数です(例:LDL値、年齢、eGFR)。
- カットオフ (Cutoff): 処置が決まる閾値(例:140 mg/dL)。
- 連続性の仮定 (Continuity Assumption): これが最重要の仮定です。これは、「もし投薬という介入が存在しなかった(あるいは何の効果もなかった)としたら、アウトカム(心筋梗塞の発症率)は、ランニング変数(LDL値)の増加に伴って、カットオフ値(140)の前後でも滑らかに(連続的に)変化したはずだ」という仮定です。
なぜこの仮定が重要なのでしょうか?
もしLDL値が139から141に増えるだけで、薬とは無関係に心筋梗塞のリスクが「ジャンプ」するなら、RDDは使えません。しかし、そんなことは生物学的に考えにくいですよね。リスクは滑らかに増えていくはずです。
この「滑らかだったはず」という仮定があるからこそ、「実際に観測されたジャンプ」を「介入による効果」として切り出すことができるのです。
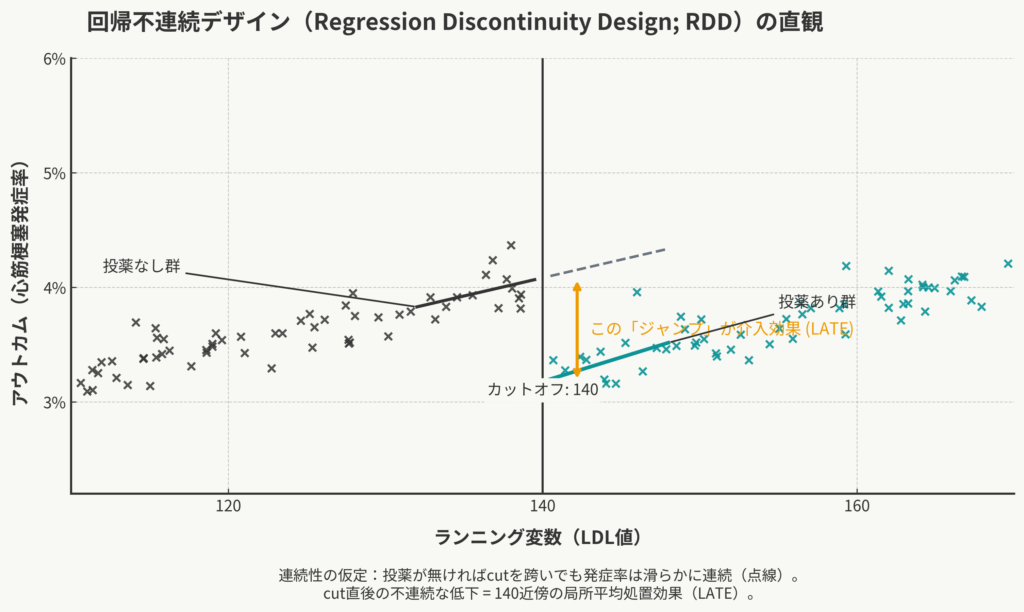
ちなみに、この「連続性の仮定」が妥当かどうかを間接的にチェックする方法があります。それは、介入の影響を受けないはずの他の変数(例:年齢、性別、BMIなど)が、カットオフ値でジャンプしていないかを確認することです。もし年齢までジャンプしていたら、そのカットオフは「局所的なRCT」とは言えず、何か別のバイアスが働いていることになります (Bor et al., 2014)。
Sharp RDD vs. Fuzzy RDD:現実の壁
RDDには、現実の運用に合わせて2つのタイプがあります。
- Sharp RDD(鋭的RDD):
カットオフで介入確率が0%から100%にジャンプする場合です。ルールが絶対的で、例外を認めません(例:「65歳になったら、例外なく全員が公費対象になる」制度)。 - Fuzzy RDD(曖昧RDD):
カットオフで介入確率が「ジャンプ」はするものの、0%から100%にはならない場合です。医療現場では、ほとんどがこちらです。
なぜ医療ではFuzzyになるのでしょうか?
「LDL 140以上で投薬推奨」というルールがあっても、実際は…
- LDLが139でも、他のリスク(喫煙、高血圧)を考慮して医師が投薬する(=カットオフ未満なのに処置)。
- LDLが141でも、患者が服薬を拒否したり、非常に健康的な生活をしているため医師が「様子見」とする(=カットオフ以上なのに非処置)。
このように、カットオフ(140)を超えると投薬される「確率」はジャンプしますが(例:30% → 70%)、100%にはなりません。Fuzzy RDDは、この「カットオフによって高まった投薬確率」を利用して、より複雑な統計手法(操作変数法に近い考え方)を用いて効果を推定します。
RDDは、その仮定が明確で、その仮定の一部をデータで検証もしやすいため、準実験的デザインの中では比較的信頼性が高い(内的妥当性が高い)手法の一つと考えられています。
道具箱③:操作変数法 (IV) 〜「交絡」を断ち切る第三の変数〜
最後の道具は「操作変数法(Instrumental Variable: IV)」です。これは、うまく使えばRCTが不可能な状況でも因果関係に迫れる非常に強力な手法ですが、同時に、その前提条件の厳しさから「最も扱うのが難しい手法」の一つとも言われています。
IV法は、どのような「やっかいな問題」を解決するために必要になるのでしょうか?
最大の敵:「内生性」とは?
IV法が必要になるのは、「内生性(Endogeneity)」という深刻な問題があるときです。これは、私たちが知りたい「処置(原因)」の選択自体が、私たちが観測できない要因によって「結果」と裏でつながってしまっている状態を指します。
言葉だと難しいので、医療の例で考えてみましょう。
問い:「ある新しい薬(処置X)を飲むと、死亡率(結果Y)は下がるか?」
この問いに答えるため、実世界の病院データを集めて、単純に「薬を飲んだ群」と「飲まなかった群」の死亡率を比較したとします。すると、驚くべきことに「薬を飲んだ群の方が、死亡率が高い」という結果が出てしまいました。
これは薬が有害だったからでしょうか? 必ずしもそうとは言えません。現実の臨床現場を想像してみてください。
「医師は、重症で死のリスクが(観測上・非観測上ともに)高い患者ほど、最後の望みをかけてその新しい薬(X)を処方しやすい」
という状況があり得ます。この「観測できない重症度」を(U)としましょう。このUは:
- 薬の処方(X)に影響します(重症だから処方される)。
- 死亡率(Y)にも影響します(重症だから死亡しやすい)。
このUは、処置Xと結果Yの両方に影響を与える「交絡因子」です。このUのせいで、薬(X)の選択自体が「内側で(Endo-)」死亡リスクと関連してしまっている。これが「内生性」です (Hernán and Robins, 2020)。
この状況で単純比較すると、薬の効果ではなく、「重症である」という背景の差を(誤って)薬の効果として推定してしまうのです。
IVのロジック:「偶然」の力を借りる
この強力な交絡(U)を断ち切るため、IV法は「第三の変数(Z)」を探してきます。このZを操作変数(IV)と呼びます。
IVのアイデアは、「処置(X)を直接いじるのではなく、処置(X)を選ぶ『確率』だけを、交絡(U)とは無関係に動かすような、外部からの『偶然の揺さぶり』を見つけ出す」というものです。
サイコロを振って、「1の目が出た人(Z=1)は薬(X)を飲む確率が上がり、それ以外(Z=0)は変わらない」というルールを想像してみてください。サイコロの目(Z)は、患者の重症度(U)とは無関係であり、死亡率(Y)に直接影響するはずもありません。Zはただ、Xを「押す」だけです。
IV法は、この「Zによる偶然の揺さぶり」が、結果(Y)にどれだけの影響を与えたかを測定し、そこから逆算して「XがYに与える本当の効果」をあぶり出そうとします。
操作変数の「3つの厳しい条件」
ある変数Zが「都合の良いサイコロ」すなわち操作変数として認められるには、以下の3つの(非常に厳しい)条件を満たす必要があります (Baiocchi et al., 2014)。
- 関連性 (Relevance):
Zは、処置Xと強く関連している必要があります。(Zが動けば、Xも動く)。
(サイコロの目が、薬を飲む確率にちゃんと影響を与えていないと意味がありません。この関連性が弱いと「弱い操作変数(Weak IV)」の問題が起き、結果が不安定になります。これは統計的に検定可能です。) - 除外制約 (Exclusion Restriction):
これがIVの「アキレス腱」です。Zは、処置Xを経由するルート以外で、結果Yに影響を与えてはいけません。
(サイコロの目(Z)が、薬(X)とは別のルートで、死亡率(Y)に直接影響してはいけません。また、サイコロの目(Z)が患者の重症度(U)と関連があってもいけません。この仮定は統計的に証明不可能であり、臨床的・理論的な知識に基づいて「そう信じるしかない」という非常に強い仮定です。) - 単調性 (Monotonicity):
Zが変化したとき(例:サイコロの目が1になった時)、全ての人が同じ方向(処置を受ける方向、または受けない方向)に動く必要があります。
(「サイコロが1だから薬を飲もう」と思う人はいても、「サイコロが1だから薬を飲むのをやめよう」という「あまのじゃく」な人が混在してはいけない、という仮定です。)
医療におけるIVの古典的な例
このIV法を使った医療経済学の有名な研究に、McClellanら (1994) による心筋梗塞治療の研究があります。
- 問い(X→Y): 集中治療(例:心臓カテーテル治療)(X)は、高齢者の死亡率(Y)を下げるか?
- 内生性の問題(U): 重症な患者(U)ほど集中治療(X)を受けやすい傾向があり、単純比較できない。
- 見つけたIV(Z): 患者の自宅から「カテーテル治療ができる病院」までの『差次的距離』。(=カテーテル病院への近さ ー 最寄り病院への近さ)
彼らのロジックはこうです:
- 関連性: (たまたま)カテーテル病院の近くに住んでいる人(Z)は、遠くに住んでいる人より、カテーテル治療(X)を受ける確率が高いはずだ。(→ データで確認OK)
- 除外制約: 「病院までの距離(Z)」自体が、「カテーテル治療を受ける」という経路(X)を経由せずに、死亡率(Y)に直接影響するだろうか?
(例:近い病院に行くと、カテーテル治療とは無関係な「何か別の要因」で死亡率が下がる? → 考えにくい)。また、病院からの距離(Z)と患者の重症度(U)が関連している?(→ おそらく関連ないだろう)。この仮定が、この研究の核心です。
このロジックに基づき、彼らは「病院への近さ」という「偶然の揺さぶり」を使って、カテーテル治療の真の効果を推定しようと試みました。
LATE: IVが推定する「局所的」な効果
最後に、IV法を解釈する上で非常に重要な注意点があります。IV法が推定する効果は、集団全体の平均的な効果(ATE: Average Treatment Effect)ではありません。
IV法が推定するのは、「操作変数(Z)によってのみ処置(X)の選択が変わった人たち」(この人たちを Compliers と呼びます)に対する効果、すなわち局所的平均処置効果(Local Average Treatment Effect: LATE)です (Angrist et al., 1996)。
先の病院の例で言えば、患者は以下の4タイプに分かれます:
- Compliers(従う人): 「近いから」カテーテル治療を受け、「遠かったら」受けなかった人。
- Always-takers(常時受ける人): 病院が遠くても、必ずカテーテル治療を受ける人。(例:意識が高い、重症)
- Never-takers(絶対受けない人): 病院が目の前にあっても、絶対にカテーテル治療を受けない人。(例:治療を拒否)
- Defiers(あまのじゃく): 遠いから受け、近いから受けない人。(単調性仮定は、この人がいないことを仮定)
IV法(LATE)が推定しているのは、このうち「Compliers」つまり「病院が近いという『偶然』によって背中を押された人たち」だけの治療効果です。「Always-takers」や「Never-takers」の効果は、推定結果に含まれません。
このように、IV法は強力なツールである一方、その仮定の厳しさと、推定される効果の解釈(LATE)の特殊性を理解した上で、慎重に使う必要があるのです。
医療AIへの応用と「動的な世界」の課題
さて、ここまで学んできた準実験的デザイン(DID, RDD, IV)は、医療AIのアルゴリズムやデジタルヘルス介入の「真の効果」を評価する上でも、非常に強力なツールとなります。なぜなら、AIによる診断支援や治療推奨は、それ自体が「介入」に他ならないからです。
「このAIアラートは、本当に患者の予後を改善したのか?」
この問いに答えることは、RCTを実施するのが難しい実臨床環境では、まさに準実験的デザインの得意分野のように見えます。しかし、AIが関与すると、従来の医療介入とは異なる、特有のやっかいな課題が(再び)生じます。
課題①:AIの推奨は「内生性」の塊
私たちがIV法で克服しようとした「内生性」や「交絡」を思い出してください。「重症な患者(U)ほど、治療(X)を受けやすい」という問題でした。
では、AI(特に予測モデル)は何をしているでしょうか?
まさに、データから「高リスク患者(U)」を見つけ出し、「介入すべき(X)」と推奨(アラート)するように設計されています。つまり、AIの推奨(X)は、その設計自体が「観測できない重症度(U)」と強く関連している(=内生性を内包している)のです。
例えば、AIが「介入Aを推奨」した群と「しなかった群」を単純比較したとします。これは、AIが「高リスク(U)と予測した群」と「低リスク(U)と予測しなかった群」を比較しているのに等しく、介入(A)の効果なのか、元のリスク(U)の差なのか、全く区別できません (Hernán and Robins, 2020)。これは古典的な「交絡バイアス(Confounding by indication)」そのものです。
課題②:AIは「学習」し、前提条件を壊してしまう
さらに深刻なのは、多くのAIモデルが「静的」ではなく「動的」に学習し、時間と共に賢くなっていく点です。これが、私たちが頼りにしてきた準実験的デザインの「仮定」を根底から覆す可能性があります。
- DID(平行トレンド仮定)の崩壊:
例えば、AIを導入したA病院と、導入しなかったB病院をDIDで比較したとします。「もしA病院がAIを導入しなくても、B病院と平行なトレンドで改善したはずだ」というのが平行トレンド仮定でした。しかし、AIはA病院のデータから「学習」し、時間と共にもっと賢く(例:アラートの精度が上がる)なります。この「学習による改善」は、B病院では起こり得ない「A病院固有のトレンド」を生み出します。この時点で、もはや平行トレンドは成立しなくなります。 - IV(除外制約)の崩壊:
例えば、「AIサーバーのランダムな停止(Z)」を操作変数として、「AIの使用(X)」が「死亡率(Y)」に与える影響を推定しようとしたとします。除外制約は「サーバー停止(Z)は、AI使用(X)の経路以外で、死亡率(Y)に影響しない」ことでした。しかし、AIが動的学習モデルだった場合、サーバー停止(Z)がAIの「学習プロセス(U)」をリセットしたり、偏らせたりするかもしれません。この「学習の偏り(U)」が、後にAIが再開したときの「死亡率(Y)」に影響を与えるとしたら… Z → U → Y というバイパス経路が開いてしまい、除外制約は崩壊します。
私たちに求められること:データ生成プロセスの理解
このように、AIという「動的な介入」を評価するには、従来の統計手法をそのまま適用するだけでは不十分です。AIの介入効果を正しく評価するには、「AIがいつ、誰に、なぜ(どのロジックで)介入を推奨したか」そして「そのロジック自体がいつ更新されたか」という、データが生成されるプロセス全体を深く理解することが不可欠です。
その上で、因果グラフ(DAG: Directed Acyclic Graph)などを用いて、「何が交絡で、何が介入で、何が結果か」を明示的にモデル化し (Pearl, 2009)、私たちが使おうとしている準実験的手法(DID, RDD, IV)の仮定が、この複雑なシステムの中で本当に成立し得るのかを、一つひとつ慎重に吟味することが求められます。
まとめ:強力だが「仮定」を問うツール
今回ご紹介した、差分の差分法(DID)、回帰不連続デザイン(RDD)、そして操作変数法(IV)は、いずれも非常に強力な分析ツールです。「ゴールドスタンダード」であるRCTが実施困難な実世界のデータ(RWD)や医療の現場で、交絡という大きな壁を乗り越え、因果関係に迫るための、素晴らしい「道具箱」を提供してくれます。
しかし、ここで非常に重要なことをお伝えしなければなりません。これらは「どんなデータでも魔法のように因果関係を教えてくれるツール」ではない、ということです。
これらの手法の信頼性は、すべて、分析者が置く「仮定(Assumption)」の妥当性にかかっています。
私たちが観測できるのは、いつだって「介入が起きた世界の現実」だけです。これらの手法はすべて、「もし、介入がなかったとしたら」という、私たちが観測することのできない「反実仮想(Counterfactual)」の世界が、どうであったかを仮定すること(言い換えれば、適切な「もしも」の比較対象をデータから作り出すこと)に依存しています。
- DIDは、「もし介入がなくても、トレンドは平行だったはずだ」(平行トレンド仮定)
- RDDは、「もし介入がなくても、アウトカムはカットオフで滑らかだったはずだ」(連続性の仮定)
- IVは、「もし操作変数が介入以外のルートで結果に影響せず、交絡とも無関係だったら」(除外制約)
これらはすべて、分析者がデータに対して「そうであったはずだ」と信じている、非常に強力な論理的基盤なのです。
幸いなことに、これらの仮定のいくつかは、データを使ってその「妥当性」をある程度チェックすることができます。例えば、DIDであれば介入前のトレンドを可視化してみる、RDDであればカットオフ付近で他の共変量(年齢や性別など)が不連続にジャンプしていないかを確認する、IVであれば操作変数の関連性が統計的に十分強いか(弱い操作変数でないか)を検定する、といった作業です (Angrist and Pischke, 2008; Hernán and Robins, 2020)。
実際の研究では、これらの仮定がデータでおおむね支持されているかを検証し、その限界(「この仮定は100%証明できるものではない」という限界も含めて)を論文やレポートで明示することが、科学的な誠実さとして極めて重要になります。
私たち分析者、あるいはこれらの結果を利用する医療従事者に求められるのは、手法をただ実行することではありません。その仮定が、目の前のデータが生成されたプロセスや、臨床的な文脈において、本当に妥当だと言えるのかを、常に厳しく問い続ける姿勢です。
これらの道具を正しく理解し、その強みと限界を認識した上で使いこなすこと。それこそが、医療AIとデータサイエンスが、単なる「相関」を超えた「真に意味のあるエビデンス」を生み出すための鍵となるでしょう。
免責事項
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
参考文献
- Angrist, J.D., Imbens, G.W. & Rubin, D.B. (1996). Identification of causal effects using instrumental variables. Journal of the American Statistical Association, 91(434), 444–455.
- McClellan, M., McNeil, B.J. & Newhouse, J.P. (1994). Does more intensive treatment of acute myocardial infarction in the elderly reduce mortality? Analysis using instrumental variables. JAMA, 272(11), 859–866.
- Lee, D.S. & Lemieux, T. (2010). Regression discontinuity designs in economics. Journal of Economic Literature, 48(2), 281–355.
- Hernán, M.A. & Robins, J.M. (2020). Causal Inference: What If. Boca Raton: Chapman & Hall/CRC.
- Angrist, J.D. & Pischke, J.S. (2008). Mostly Harmless Econometrics: An Empiricist’s Companion. Princeton: Princeton University Press.
- Pearl, J. (2009). Causality: Models, Reasoning and Inference (2nd ed.). Cambridge: Cambridge University Press.
- Baiocchi, M., Cheng, J. & Small, D.S. (2014). Instrumental variable methods for causal inference. Statistics in Medicine, 33(13), 2297–2340.
- Bor, J., Moscoe, E., Mutevedzi, P., Newell, M.L. & Bärnighausen, T. (2014). Regression discontinuity designs in epidemiology: A systematic review of applications and methodological aspects. Epidemiology, 25(5), 729–737.
- Callaway, B. & Sant’Anna, P.H. (2021). Difference-in-differences with multiple time periods. Journal of Econometrics, 225(2), 200–230.
- Goodman-Bacon, A. (2021). Difference-in-differences with variation in treatment timing. Journal of Econometrics, 225(2), 254–277.
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






