強化学習は、AIが医師のように「ある状況でどの行動が将来の最善の結果に繋がるか」を試行錯誤から自ら学ぶ技術です。その思考の根幹をなす「マルコフ決定過程」から、状況の良し悪しを測る「価値関数」、そしてAIの叡智の核心「ベルマン方程式」まで、その仕組みを紐解きます。
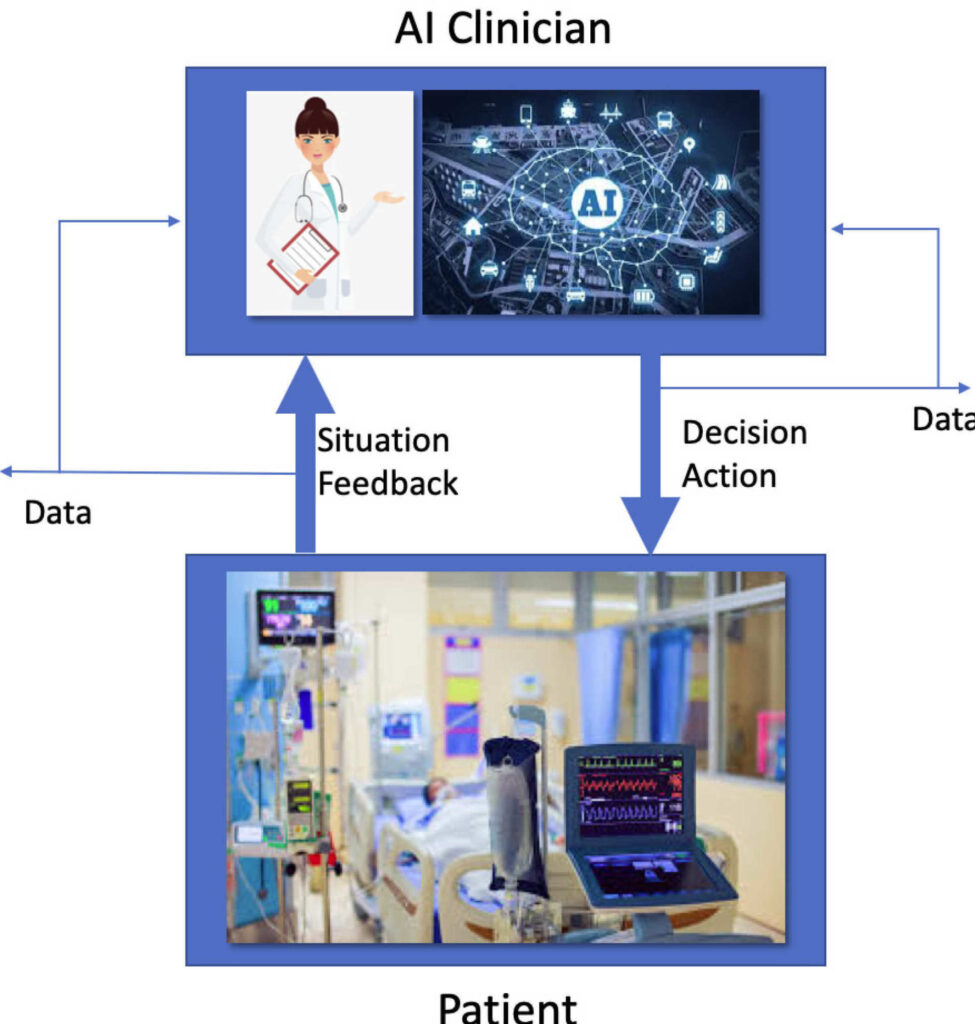
AI(エージェント)が患者(環境)を観察し、治療(行動)を選択。その結果、患者の状態が変化し、フィードバック(報酬)を得ます。この対話を繰り返して最適な治療戦略(方策)を学習します。
AIは「価値関数」を使い、ある状況(状態価値)や特定の行動(行動価値)が長期的にどれだけ良いかを数値化します。これにより、目先の報酬だけでなく、未来を見据えた判断が可能になります。
「現在の価値」は「直後の報酬+割引された未来の価値」で決まるという美しい関係式。これを頼りに、AIは経験から価値観を更新(TD学習)し、究極の治療マニュアル(最適方策)を目指します。
もしあなたが、刻一刻と状態が変化する敗血症の患者さんを前に、次々と最善の治療判断を下し続けなければならないとしたら。血圧、心拍数、尿量、血液ガスデータ…無数の指標が複雑に絡み合い、一つの選択が数時間後の未来を大きく左右する。それはまるで、先の読めないチェスの盤面で、勝利というゴールを目指して駒を進める名プレイヤーのようです。
この「連続する意思決定」の最適化という、医療の核心に迫る課題に、数学的な羅針盤を与えてくれるのが強化学習(Reinforcement Learning: RL)です。単に静的なデータから疾患を予測する(教師あり学習)のとは一線を画し、強化学習はAI自身が仮想的な臨床経験を積みながら、「ある状況で、どのような行動をとれば、将来にわたる患者さんのアウトカムを最大化できるか」という最適な治療戦略(方策)を自ら学習していきます。
例えるなら、経験豊富なベテラン医師の思考プロセスを、数学という言語で再現しようとする壮大な試みとも言えるかもしれません。
では、AIはどのようにして「最善手」を見つけ出すのでしょうか?その思考の根幹を支えるのが、今回私たちが一緒に冒険する、美しくもパワフルな数学の世界です。この記事では、強化学習の物語のルールブックである「マルコフ決定過程」から、状況の良し悪しを判断する「価値関数」、そしてAIの叡智の核心である「ベルマン方程式」まで、その仕組みを一つひとつ丁寧に解き明かしていきます。
一見すると難解に思える数式が、臨床現場の直感や判断プロセスと驚くほど深く結びついている。その発見の瞬間に、きっとあなたもAIの新たな可能性を感じるはずです。さあ、AIの思考回路を覗く冒険を始めましょう。
強化学習の世界観:医師(AI)と患者(環境)の対話
強化学習の物語を理解するために、まずはその世界を構成する登場人物とルールを詳しく見ていきましょう。この物語は、AI医師である「エージェント」と、その治療対象である「環境(患者さん)」との間の、連続的な対話で進んでいきます。これは単なる比喩ではなく、強化学習の数学的な枠組みそのものを表しています。
登場人物の紹介
エージェント (Agent): 私たちの主人公、学習するAI医師
AIと言っても、最初からすべてを知っているわけではありません。むしろ、経験の浅い研修医のような存在です。膨大なデータから学習し、試行錯誤を通じて一人前の専門医へと成長していく、この物語の主人公です。エージェントの唯一の目的は、これから紹介する「報酬」を、長期間にわたって最大化すること。そのために、現在の状況を観察し、「次の一手」としての行動を決定します。
環境 (Environment): AIが働きかける対象、つまり患者さんの身体や病状
環境は、エージェントの行動を受け取り、それに応じて状態を変化させる世界のすべてを指します。医療の文脈では、患者さんの身体そのものです。生命活動は極めて複雑で、同じ治療(行動)をしても、その反応は患者さんごと、あるいは同じ患者さんでも時間によって異なります。環境は、エージェントの行動に対して「状態の変化」と「報酬」という形でフィードバックを返します。
状態 (State, \(s\)): ある特定の時点での患者さんの容態
状態とは、ある一瞬を切り取った環境の姿、つまり「スナップショット」です。臨床現場で言えば、ある時刻 \(t\) における患者さんのバイタルサイン(血圧、心拍数、呼吸数)、血液検査データ(白血球数、CRP、乳酸値)、意識レベル(GCS)、使用している薬剤の量など、判断に必要な情報の集合体です。数学的には、これらの指標をまとめたベクトルとして表現されます。
\[ s_t = [\text{血圧}_t, \text{心拍数}_t, \text{乳酸値}_t, \dots] \]
この「状態」をいかに正確かつ網羅的に定義するかが、強化学習モデルの性能を左右する重要な鍵となります。
行動 (Action, \(a\)): エージェント(AI医師)が状態に対して行う治療介入
エージェントが、観測した状態 \(s\) に基づいて選択する具体的な操作です。例えば、「昇圧剤を \(0.05 \mu g/kg/min\) 増量する」「抗菌薬Aを投与する」「輸液を \(500\text{ml}\) 負荷する」といった医療行為がこれにあたります。行動には、選択肢が限られている離散的行動(薬Aか薬Bか)と、連続的な値をとる連続的行動(薬の投与量調整)があります。
報酬 (Reward, \(r\)): 行動の結果として環境から得られるフィードバック
報酬は、エージェントの行動が「良かったか」「悪かったか」を伝える、即時的な数値フィードバックです。これは強化学習における学習の原動力であり、最も設計が難しい部分でもあります。例えば、敗血症の治療であれば、以下のように設定することが考えられます。
- 乳酸値が改善すればプラスの報酬(例: +1)
- 血圧が安定すればプラスの報酬(例: +0.5)
- 患者さんが死亡してしまえば大きなマイナスの報酬(例: -100)
- 生命維持に繋がらない変化は報酬ゼロ
重要なのは、報酬は短期的な評価であるという点です。エージェントは、この短期的な報酬を手がかりに、長期的に最も良い結果を目指す必要があります。
AIと患者のインタラクション・ループ
これらの登場人物が、時間の流れの中でどのように相互作用するのかを見ていきましょう。強化学習は、以下のステップが連続的に繰り返されるループとしてモデル化されます。
- 観測 (Observe): 時刻 \(t\) で、エージェントは環境の現在の状態 \(s_t\) を観測します。(例:血圧が低く、乳酸値が高い状態を認識)
- 選択 (Act): 観測した状態 \(s_t\) に基づき、エージェントは自身の戦略(方策)に従って行動 \(a_t\) を選択します。(例:「昇圧剤の投与を開始する」と決定)
- 遷移とフィードバック (Transition & Feedback): エージェントの行動 \(a_t\) を受け、環境(患者の身体)が変化します。その結果、時刻 \(t+1\) で、環境は新しい状態 \(s_{t+1}\) へと遷移し、同時にその行動がどれだけ良かったかを示す即時報酬 \(r_{t+1}\) をエージェントに返します。(例:血圧は少し上昇したが、乳酸値はまだ高い。報酬は+0.2)
- 学習 (Learn): エージェントは、この一連の経験(\((s_t, a_t, r_{t+1}, s_{t+1})\))をもとに、自身の戦略を少しだけ賢く更新します。「この状況でこの行動をしたら、こういう結果になった」という経験を蓄積し、次に似た状況に陥ったとき、より良い行動を選択できるように学習するのです。
このループを何度も何度も(時には何百万回も)シミュレーションや過去のデータ上で繰り返すことで、エージェントは徐々に「どの状態でどの行動を取れば、最終的によい結果に繋がるか」という知恵を身につけていきます。
真の目標:累積報酬の最大化
ここで極めて重要なのは、AIの目標が目先の報酬だけを最大化することではない、という点です。
例えば、呼吸が苦しい患者さんに対し、高用量の鎮静剤を投与(行動)すれば、一時的に呼吸は穏やかになり、バイタルも安定するかもしれません(高い即時報酬)。しかし、その結果、自発呼吸が抑制され、人工呼吸器からの離脱が遅れ、最終的には予後が悪化する(将来の報酬が大きくマイナスになる)可能性があります。
そこで強化学習では、将来にわたる報酬の合計(累積報酬)を最大化することを目標とします。これを数学的に収益 (Return) \(G_t\) と呼び、以下のように定義します。
\[ G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \dots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \]
この式を分解してみましょう。
- \(R_{t+k+1}\): 時刻 \(t+1\) から数えて \(k\) ステップ後の未来で得られる報酬。
- \(\gamma\) (ガンマ): 割引率と呼ばれる \(0 \le \gamma \le 1\) の値。
この割引率 \(\gamma\) がミソです。これは、未来の報酬を現在の価値に割り引いて計算するための係数です。「明日の1万円」は「今日の1万円」よりも少し価値が低い、という経済学的な考え方に似ています。
- もし \(\gamma = 0\) なら、AIは未来の報酬を一切考慮せず、目先の報酬 \(R_{t+1}\) のみ最大化しようとする「近視眼的な」エージェントになります。
- もし \(\gamma\) が1に近い値なら、AIは遠い未来の報酬まで見据えて行動を決定する「長期的な視点を持つ」エージェントになります。
この割引率の存在により、AIは単にその場しのぎの良い手を選ぶのではなく、「この一手は、将来どのような素晴らしい展開に繋がるか」までを計算に入れた、真に賢い意思決定を学習することができるのです。これこそが、強化学習が「連続的な意思決定」問題を解くための数学的な核心です。
物語のルールブック:マルコフ決定過程 (MDP)
この「AI医師と患者の対話」という物語を、曖昧さのない数学の言葉で厳密に記述するためのフレームワークが、マルコフ決定過程(Markov Decision Process: MDP)です。これは、強化学習のあらゆる議論の出発点となる、いわば「世界を記述するための文法」です。この文法を理解することで、私たちは複雑な現実の問題を、解くことのできる数学の問題へと変換できるのです。
数学的には、MDPは以下の5つの要素の組(タプル)\(\mathcal{M}\)として定義されます。
\[ \mathcal{M} = (\mathcal{S}, \mathcal{A}, P, R, \gamma) \]
マルコフ性:未来は「今」が決める
MDPを理解する上で最も重要な心臓部が、マルコフ性(Markov Property)という考え方です。これは、「未来の状態は、過去の歴史すべてではなく、現在の状態と行動のみに依存して決まる」という性質を指します。
この考え方を、少しだけ数学の言葉で覗いてみましょう。ある時刻\(t\)の状態を\(S_t\)、行動を\(A_t\)としたとき、次の状態が\(S_{t+1}\)になる確率について、マルコフ性は以下の等式が成り立つことを意味します。
\[ \Pr(S_{t+1}=s’ \mid S_t=s, A_t=a) = \Pr(S_{t+1}=s’ \mid S_0, A_0, \dots, S_t, A_t) \]
この式が意味するのは、「現在の状態 \(S_t\) と行動 \(A_t\) だけが分かっているときに、次の状態が \(s’\) になる確率」(左辺)と、「現在までのすべての歴史(状態と行動の全記録)が分かっているときに、次の状態が \(s’\) になる確率」(右辺)が等しい、ということです。つまり、未来を予測するための「必要十分な情報」が、すべて現在の状態 \(S_t\) に含まれている、という大胆かつ強力な仮定を置くのです。
この仮定は、臨床現場の感覚と驚くほどよく似ています。
例えば、ICUで敗血症性ショックの患者さんを診ているとします。翌朝の治療方針を立てる上で最も重要なのは、何でしょうか?おそらく、今この瞬間のバイタルサイン、最新の血液検査データ、そして現在の人工呼吸器の設定や投与中の薬剤リストですよね。
もちろん、経験豊富な臨床家であれば、「3日前に抗菌薬を変更した影響がどう出ているか」とか「昨日の腎機能の悪化が今日どうなっているか」といった過去の経緯も頭に入っているはずです。しかし、マルコフ性の考え方では、そうした過去の出来事の影響は、すべて巡り巡って「現在の状態(今日の血液データやバイタルサイン)」に織り込まれ、反映されていると考えるのです。つまり、現在の状態という「サマリー」さえ見れば、過去の膨大なカルテをすべて読み返さなくても、未来を予測するための十分な情報が得られる、という割り切りを行います。
この「割り切り」が、AIにとっては生命線とも言えます。もしマルコフ性を仮定しなければ、AIは患者さんの出生からの全医療記録という、時間とともに増え続ける膨大な情報を毎回参照して次の一手を考えなければならず、計算が事実上不可能になってしまいます。マルコフ性という強力な仮定のおかげで、AIは「今この瞬間のスナップショット」に集中でき、複雑な問題を解くことが可能なレベルにまで単純化できるのです。
このMDPの強力な枠組みは、単なる理論にとどまりません。例えば、Komorowskiら (2018) が科学誌『Nature Medicine』で発表した研究では、ICUの実際の患者データを用いて、敗血症に対する最適な治療戦略を強化学習で探索する試みが行われました。この研究でも、患者の状態遷移をモデル化する上で、このマルコフ決定過程が基礎的なフレームワークとして用いられています。
MDPを構成する5つの要素
マルコフ決定過程は、以下の5つの要素の組(タプル)として数学的に定義されます。これら5つをきちんと定義できれば、どんな複雑な意思決定問題もMDPの枠組みで記述できます。
\[ (S, A, P, R, \gamma) \]
| 要素 | 記号 | 説明 | 医療現場での例え |
|---|---|---|---|
| 状態空間 | \(S\) | 起こりうる全ての状態の集合。 | 敗血症患者がとりうる全てのバイタルサインと検査値の組み合わせ。 |
| 行動空間 | \(A\) | エージェントがとりうる全ての行動の集合。 | 昇圧剤の投与、輸液、抗菌薬の変更など、治療選択肢の全リスト。 |
| 遷移確率関数 | \(P\) | ある状態で行動したとき、次にどの状態になるかの確率。 | 患者の状態sで輸液という行動aをしたら、90%の確率で血圧が改善(s’)し、10%の確率で変化なし(s”)になる、という体の反応モデル。 |
| 報酬関数 | \(R\) | ある状態遷移から得られる即時的なフィードバック。 | 血圧が改善したら+1、悪化したら-1、死亡したら-100というスコア。 |
| 割引率 | \(\gamma\) | 未来の報酬を現在の価値にどれだけ割り引くかの係数。 | 明日の小さな改善よりも、今この瞬間の救命を優先する度合い。 |
それぞれの要素をもう少し掘り下げてみましょう。
状態空間 \(\mathcal{S}\) と 行動空間 \(\mathcal{A}\)
これらは、物語の舞台設定そのものです。どのような状況がありえるのか(状態空間 \(\mathcal{S}\))、そしてどのような選択肢があるのか(行動空間 \(\mathcal{A}\))を定義します。
遷移確率関数 (P)
これは、世界のルール、あるいは患者さんの体の「理(ことわり)」を司る関数です。
\[ p(s’ \mid s, a) = \Pr(S_{t+1}=s’ \mid S_t=s, A_t=a) \]
この式は、「エージェントが状態 \(s\) で行動 \(a\) をとったとき、次の状態が \(s’\) になる確率」を意味します。現実の医療では、同じ治療をしても体の反応には個人差や不確実性が伴います。この遷移確率関数は、その確率的なダイナミクスをモデル化します。例えば、この関数が分かっていれば、「この患者さんにこの薬を投与すると、70%の確率で容態が安定し、30%の確率で悪化する」といった予測が可能になります。
報酬関数 (R)
これは、エージェントの行動を導くための「道しるべ」です。ある状態\(s\)で行動\(a\)をとり、次の状態\(s’\)に遷移した際に期待される報酬を定義します。
\[ r(s, a, s’) = \mathbb{E}[R_{t+1} \mid S_t=s, A_t=a, S_{t+1}=s’] \]
この式は、「状態 \(s\) で行動 \(a\) をとり、結果として状態が \(s’\) になったときに受け取る即時報酬の期待値 \(r\)\(_{t+1}\)」を定義します。この報酬設計こそが、AIに「何を達成してほしいか」という目的を教え込むプロセスであり、強化学習の応用において最も人間が知恵を絞る部分です。良い治療戦略を学習させるには、臨床的な目標(例:生存率の向上、合併症の減少)を適切に反映した報酬関数を設計する必要があります。
割引率 (\(\gamma\))
前章でも触れましたが、これはエージェントの「時間感覚」を決めます。\(0 \le \gamma \le 1\) の値を取り、未来の報酬を現在の価値に割り引きます。これは数学的な安定性を確保する役割もありますが、それ以上に「不確実な未来より、確実な現在を重視する」という現実的なポリシーをAIに与える重要なパラメータです。
以上の5つの要素を定義することで、私たちは「医師が患者を治療する」という複雑なプロセスを、完全に数学的な問題として定式化できるのです。このMDPという共通言語があるからこそ、私たちはAIに「最適な戦略とは何か」を教え、それを学習させるアルゴリズムを開発することができるわけです。
AI医師の思考回路:方策と価値関数
さて、MDPというルールブック(世界の理)を手に入れたAI医師は、どうやって無数にある治療の選択肢の中から「最善の行動」を学んでいくのでしょうか。ここからが、AIの頭脳の内部、その思考回路の核心に迫る部分です。その中核を担うのが「方策(Policy)」と「価値関数(Value Function)」という、強化学習における二大巨頭です。
方策 (Policy, \(\pi\)):AIの治療マニュアル
方策とは、一言でいえばAIの「行動指針」あるいは「治療マニュアル」です。ある状態 (\(s\)) に置かれたときに、どの行動 (\(a\)) を選択するかのルールを定めたものです。これは、私たちが臨床現場で用いる治療ガイドラインやプロトコルに非常に似ています。「血圧がこの値以下で、乳酸値がこの値以上なら、この昇圧剤をこの量で開始する」といった具体的なルールブックそのものが方策だとイメージしてください。
方策は、AIの「知識」と「行動」を結びつける、いわば思考から実践への架け橋です。このマニュアルの質が、AI医師の臨床能力を直接的に決定します。方策は、数学的には状態 (\(s\)) を入力とし、行動 (\(a\)) を出力とする関数として表現されますが、その振る舞い方によって大きく2つのタイプに分けられます。
決定的方策 (Deterministic Policy)
「何であるか」: ある状態 (\(s\)) に対して、とるべき行動 (\(a\)) が常に一つに決まっている方策です。「この状況なら、必ずこの治療!」という、迷いのないマニュアルです。数式では \(a = \pi(s)\) とシンプルに表現されます。
「なぜそれを行うのか」: その単純さと予測可能性から、方策の評価や比較が容易になります。学習が完了した後のAIを実際の臨床現場で動かす際には、その行動が明確で一貫していることが求められるため、決定的方策が好まれる場合があります。
「なんの役に立つのか」: 集中治療室(ICU)における血糖管理プロトコルを想像してみてください。「血糖値が180mg/dLを超えたら、インスリンを2単位/時で開始する」といったルールは、決定的方策の典型例です。誰が実行しても、同じ状況であれば同じ行動が選択されるため、安全性が高く、結果のばらつきを抑えることができます。
確率的方策 (Stochastic Policy)
「何であるか」: ある状態 (\(s\)) に対して、行動の選択肢に確率を割り振る方策です。「この状況なら、70%の確率で治療Aを、30%の確率で治療Bを行う」というように、柔軟性を持ったマニュアルです。数式では、条件付き確率 \(\pi(a|s) = P(A_t=a \mid S_t=s)\) を用いて表現されます。
「なぜそれを行うのか」: なぜAIは、わざわざ確率的に行動を選ぶのでしょうか?その最も重要な理由は、学習のためです。もしAIが常に「現時点で最善」と信じている行動だけを取り続ける(決定的方策に従う)と、それ以外の行動が実はもっと良い結果をもたらす可能性があったとしても、それを発見する機会を永遠に失ってしまいます。これを強化学習の文脈で「活用の罠(Exploitation Trap)」と呼びます。確率的に異なる行動を試すことで、AIは未知のより良い戦略を「探索(Exploration)」することができるのです。これは、後のセクションで詳しく学ぶ「探索と活用のトレードオフ」という、強化学習の根源的なジレンマに直接関わっています。
「なんの役に立つのか」: 例えば、ある種の感染症に対して、エビデンスレベルが同等の抗菌薬AとBが存在するとします(臨床的均衡、clinical equipoise)。決定的方策のAIは、過去のデータでわずかにでも成績が良かったAを常に選び続けるかもしれません。しかし、確率的方策のAIは、時にはBも試すことで、「実は特定の遺伝的背景を持つ患者群にはBの方が劇的に効く」といった、これまで知られていなかった新たな知見を発見できる可能性があります。
結局のところ、強化学習の最終的な目標は、この無数に考えられる方策の中から、将来にわたる累積報酬を最大化する「最も優れた方策(最適方策, \(\pi_*\))」を見つけ出すことです。しかし、「優れた方策」とは一体何でしょうか?その良し悪しを判断するための「物差し」がなければ、最適方策を探しようがありません。その物差しこそが、次にお話しする「価値関数」なのです。
価値関数 (Value Function):未来を見通す羅針盤
では、「優れた方策」とは具体的にどのようなものでしょうか?それは、将来にわたって多くの報酬が期待できる方策です。この「将来にわたる報酬の期待値」、つまり「その状況や行動が、長期的にどれだけ良いか」を具体的な数値で表すのが価値関数です。
価値関数は、いわば未来を見通すための羅針盤です。これがあるおかげで、AIは目先の利益(即時報酬)に惑わされず、長期的な視点に立った最適な判断を下すことができるようになります。価値関数にも、評価する対象によって2つの重要な種類があります。
1. 状態価値関数 (\(V^\pi(s)\)):ある「状況」そのものの良さを測る指標
「何であるか」: 状態価値関数 (\(V^\pi(s)\)) は、「ある方策 (\(\pi\)) に従い続けるという前提のもとで、現在状態 (\(s\)) にいることが、将来的にどれだけ有望か」を示す指標です。これは、特定の「戦局」がいかに有利か、あるいは不利かを示す評価値と言えます。
数学的には、以前に定義した収益 (\(G_t\)) の期待値として、以下のように定義されます。
\[ V^\pi(s) = \mathbb{E}_\pi [G_t \mid S_t = s] = \mathbb{E}_\pi \left[ \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \mid S_t = s \right] \]
この数式の意味を、もう一度丁寧に分解してみましょう。
- \(S_t = s\): 「もし今、自分が状態 (\(s\)) にいたら…」という仮定の出発点です。
- \(\mathbb{E}_\pi [\dots]\): 「これからずっと方策 (\(\pi\)) というマニュアルに従って行動していくと、平均的にどれくらいの良いことがあるか」を計算する記号です。なぜ「平均(期待値)」を考えるのかというと、患者さんの体の反応(遷移確率)や、方策自身が確率的である場合があるため、未来は一本道ではなく、無数の可能性に分岐するからです。その無数の未来全体をならして評価するのが期待値の役割です。
- \(\sum_{k=0}^{\infty} \gamma^k R_{t+k+1}\): これは、直後にもらえる報酬 (\(R_{t+1}\)) から、遠い未来にもらえる報酬までを、割引率 (\(\gamma\)) を考慮して合計したものです。将来の価値の総和、すなわち収益 (\(G_t\)) です。
「なぜそれを行うのか」: 状態価値関数を計算することで、AIは異なる状況の「有望さ」を客観的に比較できるようになります。例えば、敗血症において「臓器障害がなくバイタルが安定している状態」の価値は高く、「多臓器不全を伴うショック状態」の価値は極めて低くなるはずです。この価値の勾配を認識することが、より良い状態を目指して行動する上での第一歩となります。
「なんの役に立つのか」: 面白いのは、この価値は絶対的なものではなく、方策 (\(\pi\)) に依存するという点です。同じ「敗血症性ショック」という状態 (\(s\)) でも、
- 優れた方策(ベテラン医師の戦略)を知っているAIにとっては、\(V(s)\) は低いながらもまだ希望のある値を持つかもしれません(「これは厳しいが、次の一手を正しく打てば立て直せる」)。
- 未熟な方策(研修医の戦略)しか知らないAIにとっては、\(V(s)\) は絶望的に低い値になるでしょう(「どうすればいいか分からず、この先は暗い未来しか見えない」)。
このように、状態価値関数は、ある戦略家(方策)から見た、特定の戦局(状態)の評価値なのです。しかし、これだけでは「次の一手」を決めるには不十分です。「状況が悪い」と分かっても、「だから具体的に何をすべきか?」は教えてくれないからです。
2. 行動価値関数 (\(Q^\pi(s, a)\)):ある「行動」そのものの良さを測る指標
「何であるか」: 状態価値関数 (\(V^\pi(s)\)) の限界を乗り越えるのが、強化学習のアルゴリズムで中心的な役割を果たす行動価値関数 (\(Q^\pi(s, a)\))(通称:Q関数、Q値)です。これは、「ある方策 (\(\pi\)) に従う前提のもとで、現在状態 (\(s\)) にいるときに、あえて行動 (\(a\)) をとり、その後はずっと方策 (\(\pi\)) に従って行動し続けた場合に、将来的にどれだけの報酬が期待できるか」を具体的に数値化したものです。
\[ Q^\pi(s, a) = \mathbb{E}_\pi [G_t \mid S_t = s, A_t = a] = \mathbb{E}_\pi \left[ \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \mid S_t = s, A_t = a \right] \]
\(V^\pi(s)\) の式と非常によく似ていますが、条件の部分に \(A_t=a\) が加わっているのが決定的な違いです。これは、「状況」だけでなく「状況と行動のペア」の価値を評価していることを意味します。\(Q^\pi(s, a)\) の値が高いということは、その状況 (\(s\)) でその行動 (\(a\)) をとることが、長期的に見て「良い手」であることを示唆します。
「なぜそれを行うのか(なぜこれが強力なのか)」: もし、ある状態 (\(s\)) において、考えられる全ての行動(\(a_1, a_2, a_3, \dots\))に対するQ値が全て分かっていると想像してみてください。
例えば、敗血症性ショックの状態 (\(s_{\text{shock}}\)) で、AIが取りうる行動と、それに対応するQ値が以下のようになっているとします。
- \(Q(s_{\text{shock}}, a_{\text{輸液負荷}}) = +45.2\)
- \(Q(s_{\text{shock}}, a_{\text{昇圧剤増量}}) = +21.8\)
- \(Q(s_{\text{shock}}, a_{\text{抗菌薬変更}}) = -5.3\)
- \(Q(s_{\text{shock}}, a_{\text{経過観察}}) = -88.0\)
この表があれば、AIは次に何をすべきかを合理的に判断できます。つまり、現在の価値観(\(Q^\pi\)値)が最も高い行動を選択することで、今の方策を改善できる可能性があるのです。この例では、「輸液負荷」が現在の方策\(\pi\)の価値観における最善手となります。このプロセスを方策改善と呼びます。
\[ \pi'(s) = \arg\max_{a} Q^\pi(s, a) \]
(\(\arg\max_{a}\) は、Q値を最大化するような行動\(a\)を見つけ、それを新しい方策\(\pi’\)とする、という意味です)
重要なのは、これが必ずしも「究極の最適行動」ではないという点です。真の最適行動は、あらゆる方策の中で最も優れた最適行動価値関数 \(Q_*(s,a)\) を使って \(\pi_*(s) = \arg\max_{a} Q_*(s, a)\) と定義されます。方策改善は、この究極の目標に一歩近づくための重要なステップなのです。
「なんの役に立つのか」: このQ関数を推定し、最適な治療戦略を見つけ出すアプローチは、すでに実際の臨床研究で成果を上げています。インペリアル・カレッジ・ロンドンのKomorowskiら (2018) が医学誌『Nature Medicine』で発表した有名な研究「AI Clinician」では、ICUの膨大な電子カルテデータを用いて、敗血症患者に対する輸液と昇圧剤の最適な投与戦略を学習させました。この研究の核心は、まさにこのQ関数をデータから推定することにあります。その結果、AIが導き出した治療戦略は、人間の医師の戦略と比較して、院内死亡率を低下させる可能性が示唆されました。
つまり、最適なQ関数(\(Q_*\))を見つけ出すことさえできれば、それはすなわち最適な治療マニュアル(\(\pi_*\))を手に入れたこととほぼ同義なのです。このため、多くの強化学習アルゴリズム(例えば有名なQ学習)は、このQ関数をデータから推定することに全力を注ぎます。
🤿 Deep Dive! 状態価値 (V) と行動価値 (Q) は何が違うのか? 見ている視点の違い
「状態価値 \(V^\pi(s)\) の定義には、結局のところ方策 \(\pi\) に従って『行動』することが含まれている。それなら、特定の『行動』の価値を評価する行動価値 \(Q^\pi(s, a)\) と本質的に同じではないか?」
これは、強化学習の理論を深く学ぼうとすると誰もが一度は抱く、非常に的を射た疑問です。結論から言うと、この2つの価値関数は評価の視点と粒度が明確に異なります。その違いを理解するために、カンファレンスでの症例検討をイメージしてみましょう。
状況の「総合評価」と、治療選択肢の「個別評価」
目の前に、中等症の敗血症の患者さん(状態 \(s\))がいるとします。あなたのチームの標準的な治療プロトコル(方策 \(\pi\))では、「まず輸液を試み、反応が鈍ければ昇圧剤を検討する」といった手順が定められています。
- 状態価値 \(V^\pi(s)\) の視点 (総合評価)
指導医が患者さんのカルテを見て、こう言います。「この患者さんの状態は中等症だね。我々の標準プロトコル(方策 \(\pi\))に従って治療を進めれば、総合的に見て、これくらいの予後が期待できるだろう」。
これが状態価値 \(V^\pi(s)\) の考え方です。特定の「次の一手」に踏み込む前の、その状況全体に対するポテンシャルの評価です。この評価には、プロトコルに従ってこれから行われるであろう複数の行動(輸液や昇圧剤など)の可能性が、全て確率的に平均化されて含まれています。つまり、「今の状況は、私たちのチームの実力(方策)をもってすれば、平均していくらくらいの価値があるか」という、状況そのものへのスコアリングなのです。 - 行動価値 \(Q^\pi(s, a)\) の視点 (個別評価)
次に、研修医が具体的な治療選択肢について質問します。「先生、この状況で、もし我々が最初の選択肢として『A: 積極的な輸液負荷』を選んだ場合、その後の展開はどうなるでしょうか? もし、『B: 早めの昇圧剤導入』を選んだ場合はどうでしょうか?」
これが行動価値 \(Q^\pi(s, a)\) の考え方です。状況 \(s\) は同じでも、「もし、あえてこの行動 \(a\) をとったら」という仮定のもとで、その特定の行動がどれだけ有望かを個別に評価します。これは、治療選択肢一つひとつへのスコアリングです。
数式で見るVとQの美しい関係
この「総合評価」と「個別評価」の関係は、数式で非常に美しく表現できます。ある状態 \(s\) の総合的な価値 \(V^\pi(s)\) は、その状態で取りうる全ての行動 \(a\) の個別評価 \(Q^\pi(s, a)\) を、その行動が選択される確率 \(\pi(a|s)\) で重み付けして足し合わせたもの(期待値)に等しくなります。
\[ V^\pi(s) = \sum_{a \in A} \pi(a|s) Q^\pi(s, a) \]
この式を分解してみましょう。
- \(\pi(a|s)\): 状態 \(s\) のときに、方策 \(\pi\) が行動 \(a\) を選ぶ確率。(例:「60%の確率で輸液」)
- \(Q^\pi(s, a)\): 状態 \(s\) で行動 \(a\) をとった場合の価値。(例:「輸液した場合の価値は46.4点」)
- \(\sum_{a \in A}\): 考えられる全ての行動について、上の掛け算を計算して、全部足し合わせる。
例えば、AIの方策が「60%の確率で輸液、40%の確率で昇圧剤」であり、それぞれのQ値が \(Q(s, a_{\text{輸液}}) = 46.4\) 点、\(Q(s, a_{\text{昇圧剤}}) = 55.0\) 点だったとします。この場合、状態価値 \(V^\pi(s)\) は、
\[ V^\pi(s) = (0.6 \times 46.4) + (0.4 \times 55.0) = 27.84 + 22.0 = 49.84 \text{点} \]
となり、まさに「総合評価(V)」が「個別評価(Q)の加重平均」で計算されていることがわかります。
なぜ両方が必要なのか?
- 価値関数 V は「方策の評価」に使う: 状態価値 \(V\) は、現在の戦略(方策\(\pi\))が全体としてどれくらい優れているかを評価するのに役立ちます。新しい方策を試した結果、全体的にV値が向上すれば、その方策は以前より優れていると判断できます。
- 行動価値 Q は「方策の改善」に使う: 一方で、行動価値 \(Q\) は、次の一手を決めるため、そして方策をより良く改善していくために不可欠です。Q値のリストを比較することで、「今のマニュアルでは輸液を選ぶ確率が高いが、Q値を見ると昇圧剤の方が有望だ。ならば、昇圧剤を選ぶ確率をもう少し上げるようにマニュアルを改訂しよう」という具体的な改善アクションに繋げることができるのです。
このように、VとQは密接に関わりながらも、それぞれが異なる役割を担っています。Vが「今の戦略での総合的な戦況判断」なら、Qは「次の一手を決めるための具体的な作戦評価」と言えるでしょう。この2つの視点を持つことで、AIは自身の戦略を客観的に評価し、かつ具体的な改善策を見つけ出すことができるのです。
方策(マニュアル)と価値関数(羅針盤)は、AIが未知の環境で賢く振る舞うための両輪です。次のセクションでは、この価値関数同士を結びつけ、AIの学習メカニズムの核心に迫る「ベルマン方程式」という美しい関係式を見ていくことにしましょう。
叡智の方程式:ベルマン方程式
さて、私たちはAIの思考の道具として「方策(治療マニュアル)」と「価値関数(未来を見通す羅針盤)」を手に入れました。しかし、ここで一つの巨大な壁に突き当たります。その「価値」という羅針盤は、一体どうすれば手に入るのでしょうか?
臨床現場で考えてみましょう。目の前に敗血症性ショックの患者さんがいます。選択肢は「輸液を追加する」か、「昇圧剤を増量するか」。どちらの行動が、長期的により「価値」が高いのでしょうか?その価値を、どうやって具体的な「-50.3」や「+120.4」といった数字にすれば良いのでしょう?
この、果てしない未来の価値を計算するという難問に、驚くほどエレガントな数学的構造を与えてくれるのが、ベルマン方程式(Bellman Equation)です。
これは、応用数学の巨人、リチャード・ベルマンが1950年代に発見した「今日の価値は、直後の報酬と、次に訪れる状況の価値によって決まる」という、時間を通じた価値の普遍的な関係を示したものです。
この関係を、ベルマン方程式の最もシンプルな形で表現すると、以下のようになります。
\[V(s) = R_{t+1} + \gamma V(S_{t+1})\]
この式が意味するのは、以下の通りです。
- \(V(s)\): 今日の状況(状態 \(s\))が持つ長期的な価値。
- \(R_{t+1}\): 今日の行動の結果、直後にもらえる短期的な成果(報酬)。
- \(V(S_{t+1})\): その結果たどり着いた明日の状況(状態 \(S_{t+1}\))が持つ、そこから先の長期的な価値。
- \(\gamma\): 割引率。「未来の価値は、少しだけ不確実なので割り引いて考えよう」という現実的な視点を表す係数です。
つまりこの式は、「今日の価値 = 直後の成果 + (割引された)明日の価値」という直感的な関係を数学の言葉で表しているに過ぎません。
なぜこの式が「叡智」なのか?:「無限の連鎖」の圧縮
この方程式が「叡智」と呼ぶにふさわしい理由は、その再帰的(Recursive)な構造、つまり価値の「入れ子構造」を見抜いたことにあります。
「今日の治療の価値」とは何か?
それは、「今日の治療で患者さんが少し楽になる(直後の報酬)」ことと、「その結果として期待される、明日の状態の良さ」の合計ですよね。
では、その「明日の状態の良さ」とは何か?
ベルマン方程式によれば、それは「明日の治療でさらに改善する(明日の報酬)」ことと、「その結果として期待される、明後日の状態の良さ」の合計です。
では、その「明後日の状態の良さ」とは…
このように、患者さんの予後というものは、遥か未来まで続く判断の連鎖によって決まります。本来であれば、この果てしなく続く未来の報酬 (\(R_{t+1} + R_{t+2} + R_{t+3} + \dots\)) を、全て足し合わせなければ本当の価値は計算できません。
しかし、ベルマン方程式は、この無限の連鎖を「今の価値」と「次の瞬間の価値」という、たった一つのステップの関係式に圧縮してしまいます。
この構造のおかげで、私たちは複雑で扱いようのなかった「長期的な未来の価値」というものを、コンピュータで計算可能な、解くことのできる問題へと変換できるのです。これこそが、ベルマン方程式が強化学習の理論の根幹をなし、「叡智の方程式」と呼ぶべき所以なのです。
では、この美しい関係式は、具体的にどう役立つのでしょうか?
AIはまだ学習の途上にあり、完璧な価値観を持っているわけではありません。持っているのは、ある未熟な治療マニュアル(方策\(\pi\))と、それに基づいた不正確な価値の予測値(価値関数\(V^\pi(s)\))だけです。
ここでベルマン方程式が、「AIの現在の価値観が、自己矛盾していないか?」をチェックするための強力な検証ツールとして登場します。次のセクションでは、この方程式を使って、特定の治療マニュアル(方策\(\pi\))の「真の実力」を測る方法、すなわちベルマン期待方程式を見ていきましょう。
ベルマン期待方程式:ある方策\(\pi\)の「実力」を測る
ベルマン期待方程式を一言で言うなら、「ある治療マニュアル(方策\(\pi\))の自己評価シート」です。AIが持っている価値観(V値)が、「そのマニュアルに従った場合に起こる未来」と照らし合わせて、矛盾なく一貫しているか(自己無撞着か)をチェックするための関係式です。
状態価値関数\(V^\pi(s)\)が満たすべき一般式は、期待値\(\mathbb{E}\)を用いて以下のように書かれます。
\[ V^\pi(s) = \mathbb{E}_\pi [R_{t+1} + \gamma V^\pi(S_{t+1}) \mid S_t=s] \]
この式は、「状態\(s\)の価値は、現在の方策\(\pi\)に従って行動したときに得られる『直後の報酬』と『割引された次の状態の価値』の期待値に等しい」ことを意味します。この「期待値」という言葉が重要で、方策が確率的に行動を選ぶ可能性や、行動の結果が確率的に変動する可能性をすべて考慮して平均をとる、というニュアンスが含まれています。
この期待計算をより具体的に分解すると、以下のようになります。この式を理解するために、具体的な臨床シナリオを想像しながら、3つのステップに分解していきましょう。
【シナリオ設定】
- 患者さんの状態 (\(s\)): 中等症の敗血症。血圧はやや低めだが、臓器障害はまだない。
- AIの治療マニュアル (\(\pi\)): この状態の患者さんには、「60%の確率で輸液を500ml投与し、40%の確率で昇圧剤を微量開始する」という確率的方策を持っているとします。
- AIの価値観: AIは、現時点でのこの患者さんの状態の価値を \(V^\pi(s) = +50\) 点くらいだと見積もっているとします。
状態価値関数 \(V^\pi(s)\) の場合
このAIの価値観「+50点」が本当に妥当なのかを、ベルマン期待方程式で検証していきます。
\[ V^\pi(s) = \sum_{a \in A} \pi(a|s) \left( \sum_{s’, r} p(s’, r|s, a) \left[ r + \gamma V^\pi(s’) \right] \right) \]
この式は、右側から左側へ、つまり未来から現在へと遡るように読んでいくと、驚くほど直感的に理解できます。
【ステップ1:カッコの最も内側】たった一つの未来の価値を計算する
\[ r + \gamma V^\pi(s’) \]
これがベルマン方程式の心臓部です。これは、ある行動をとった結果として起こりうる、無数の未来の中のたった一つのシナリオの価値を計算しています。
- \(r\) (Reward): 直後にもらえる「ご褒美」です。
- \(\gamma V^\pi(s’)\) (Discounted Future Value): そのシナリオの先に待っている未来全体の価値(\(V^\pi(s’)\))を、割引率\(\gamma\)(ガンマ)で少しだけ割り引いたものです。「未来は不確実だから、今の価値に換算すると少し目減りするよね」という現実的な感覚を表します。
臨床例で見てみましょう
AIが「輸液を500ml投与」という行動をとり、その結果、患者さんの状態が「血圧が少し改善(\(s’\))」したとします。
- この時、血圧が改善したので、即時報酬として \(r = +5\) 点がもらえました。
- そして、遷移した先の「血圧が少し改善」という状態\(s’\)は、AIの価値観によれば \(V^\pi(s’) = +60\) 点の価値があるとします。
- 割引率\(\gamma\)が0.9(未来を10%割り引く)だとすると、このたった一つの未来のシナリオの総合価値は、
\(5 + 0.9 \times 60 = 5 + 54 = 59\) 点となります。
つまり、ステップ1は「直後のご褒美 + その先の未来の価値」を計算しているだけで、これは私たちの臨床感覚と完全に一致します。
【ステップ2:内側の期待値計算】一つの「行動」の平均的な価値を計算する
\[ \sum_{s’, r} p(s’, r|s, a) \left[ r + \gamma V^\pi(s’) \right] \]
ステップ1では、たった一つの未来の価値を計算しました。しかし、医療は不確実です。「輸液を500ml投与」という同じ行動をとっても、患者さんの反応は一つではありません。複数の未来が確率的に起こりえます。
そこで、ステップ2では、考えられる全ての反応(未来のシナリオ)の価値を、それが起こる確率 \(p(s’, r|s, a)\) で重み付けして平均します。これが期待値の計算であり、これによって一つの行動の「本当の平均的な価値」、つまり行動価値関数 \(Q^\pi(s, a)\) が求まるのです。
臨床例で見てみましょう
「輸液を500ml投与(\(a_{\text{輸液}}\))」という行動に対して、体の反応は2パターンあるとします。
- 70%の確率で: 血圧が改善(\(s’_1\))。このシナリオの価値は、ステップ1で計算した 59点。
- 30%の確率で: 肺に水が溜まり呼吸状態が少し悪化(\(s’_2\))。このシナリオは悪い結果なので、報酬は\(r=-10\)点、遷移先の価値は\(V^\pi(s’_2)=+30\)点だとします。すると、このシナリオの総合価値は \(-10 + 0.9 \times 30 = 17\) 点。
この場合、「輸液を500ml投与」という行動の平均的な価値 \(Q^\pi(s, a_{\text{輸液}})\) は、
\(Q^\pi(s, a_{\text{輸液}}) = (0.7 \times 59 \text{点}) + (0.3 \times 17 \text{点}) = 41.3 + 5.1 = 46.4\) 点
となります。これが、「輸液」という選択肢の、平均的な実力です。
【ステップ3:外側の期待値計算】ある「状態」そのものの平均的な価値を計算する
\[ V^\pi(s) = \sum_{a \in A} \pi(a|s) Q^\pi(s, a) \]
ステップ2で、考えられる各行動の平均的な価値(Q値)がわかりました。いよいよ最終ステップです。
AIの治療マニュアル(方策\(\pi\))は、「60%の確率で輸液、40%の確率で昇圧剤」という確率的なルールでした。そこで、ステップ3では、AIがとりうる全ての行動の価値(Q値)を、AIがその行動を選択する確率 \(\pi(a|s)\) で重み付けして平均します。
臨床例で見てみましょう
AIの方策に従った場合の、現在の状態\(s\)の本当の価値 \(V^\pi(s)\) を計算します。
- 行動1「輸液」:
- 選択される確率: \(\pi(a_{\text{輸液}}|s) = 0.6\)
- この行動の価値: \(Q^\pi(s, a_{\text{輸液}}) = 46.4\) 点(ステップ2で計算)
- 行動2「昇圧剤」:
- 選択される確率: \(\pi(a_{\text{昇圧剤}}|s) = 0.4\)
- この行動の価値: (同様にステップ2で計算したら)例えば \(Q^\pi(s, a_{\text{昇圧剤}}) = 55.0\) 点だったとします。
この場合、現在の状態\(s\)の総合的な価値 \(V^\pi(s)\) は、
\(V^\pi(s) = (0.6 \times 46.4 \text{点}) + (0.4 \times 55.0 \text{点}) = 27.84 + 22.0 = 49.84\) 点
となります。
【結論】
ベルマン期待方程式で計算した結果、現在の状態の価値は「49.84点」となりました。AIが当初見積もっていた「+50点」とほぼ同じですね。これは、AIの価値観が、自身の治療マニュアルと照らし合わせて、ほぼ矛盾なく一貫していることを意味します。もし計算結果が「30点」だったら、「君の価値観は楽観的すぎるよ」と修正する必要がある、ということです。
このように、ベルマン期待方程式は、複雑に見える数式の奥で、「未来の可能性を、確率で重み付けして、丁寧に平均をとっている」だけなのです。この美しい構造があるからこそ、AIは自身の戦略の「真の実力」を客観的に評価し、改善していくことができるのです。
ベルマン最適方程式:究極の価値を求める
ベルマン期待方程式は、あくまで特定の治療マニュアル(方策\(\pi\))の「自己評価」に過ぎませんでした。AIは「今のマニュアルだと、この状態の価値は49.84点だな」と知ることはできても、それがベストなのか、もっと良いやり方はないのか、までは分かりません。
私たちの真の目標は、研修医のマニュアルを評価することではなく、世界で最も優れたゴッドハンドを持つ外科医の「究極のマニュアル(最適方策 \(\pi_*\))」を見つけ出すことです。
この「究極のマニュアル」に従い続けた場合に得られる、これ以上ない最高の価値を最適価値関数(\(V_*(s)\), \(Q_*(s, a)\))と呼びます。そして、この究極の価値が満たすべき関係式こそが、ベルマン最適方程式です。これは、いわば強化学習における「北極星」であり、全ての学習アルゴリズムが目指す最終ゴール地点を示しています。
最適状態価値関数 \(V_*(s)\) の場合
「何であるか」: ある状態\(s\)が持つ、潜在的な「最高のポテンシャル」を定義します。
\[ V_*(s) = \max_{a} \sum_{s’, r} p(s’, r|s, a) \left[ r + \gamma V_*(s’) \right] \]
ベルマン期待方程式と並べてみると、違いは一目瞭然です。
- 期待方程式: \(\sum_{a} \pi(a|s) \dots\) → 自分のマニュアルに従って、確率的に行動を選んだ場合の平均点。
- 最適方程式: \(\max_{a} \dots\) → マニュアルは一旦無視。考えうる全ての行動の中から、最も良い結果につながるものを常に選び取った場合の最高得点。
max(マックス)記号は、複数の選択肢の中から最大値を選ぶ操作です。つまりこの式は、「状態\(s\)における究極の価値とは、次に選択可能な全ての行動(輸液、昇圧剤、経過観察…)を頭の中でシミュレーションし、その後の展開が最も良くなるような『神の一手』を常に選び続けた場合の価値である」と宣言しているのです。
臨床例で考えてみましょう
先ほどの敗血症のシナリオを思い出してください。
- 行動「輸液」の平均的な価値 \(Q(s, a_{\text{輸液}})\) は 46.4点でした。
- 行動「昇圧剤」の平均的な価値 \(Q(s, a_{\text{昇圧剤}})\) は 55.0点でした。
ベルマン期待方程式では、AIは自身の方策(60%輸液、40%昇圧剤)に従ったので、状態の価値はこれらの平均である49.84点になりました。
しかし、最適方程式では違います。AIは「もし自分が完璧な存在だったら…」と考えます。目の前にある「46.4点」と「55.0点」という選択肢を見て、迷わずmax、つまり55.0点の方を選びます。したがって、この状態の最適価値\(V_*(s)\)は、55.0点となるのです。これは、現在の未熟な方策が叩き出す価値(49.84点)と、理想的な方策が叩き出せる価値(55.0点)との間にある「伸びしろ」を示唆しています。
最適行動価値関数 \(Q_*(s, a)\) の場合
こちらが、実際の学習アルゴリズムでより中心的な役割を果たす、最も重要な方程式です。
「何であるか」: ある状態\(s\)で特定の行動\(a\)をとることの「究極の価値」を定義します。
\[ Q_*(s, a) = \sum_{s’, r} p(s’, r|s, a) \left[ r + \gamma \max_{a’} Q_*(s’, a’) \right] \]
これもまた、期待方程式との対比で理解するのが一番です。
- 期待方程式: \(r + \gamma \sum_{a’} \pi(a’|s’) Q^\pi(s’, a’)\) → 次のステップでは、自分のマニュアルに従って平均的な手を打つ。
- 最適方程式: \(r + \gamma \max_{a’} Q_*(s’, a’)\) → 次のステップでも、そこで考えうる最高の手(神の一手)を打つ。
この式の意味を翻訳すると、こうなります。
「状態\(s\)で行動\(a\)をとった場合の究極の価値とは? それは、その時にもらえる直後の報酬と、遷移した先の状態\(s’\)に立った時に、そこからまた考えうる『次の一手』の中から常に最善手を選び続けた場合の価値(\(\max_{a’} Q_*(s’, a’)\))の合計の期待値である」
つまり、「常に最善を尽くし続けることを前提とした場合の、今この一手の価値」を計算しているのです。
なぜこれが「ゴール」なのか?
このベルマン最適方程式は、強化学習における「ゴールテープ」そのものです。もし何らかの方法でこの方程式を解き、全ての状態\(s\)と行動\(a\)の組み合わせに対する究極のQ値、\(Q_*(s, a)\)を完全に知ることができれば、問題は解決したも同然です。
なぜなら、究極のQ値のマップさえ手に入れば、最適な治療マニュアル(\(\pi_*\))は驚くほどシンプルになるからです。
\[ \pi_*(s) = \arg\max_{a} Q_*(s, a) \]
この \(\arg\max_{a}\) というのは、「\(Q_*(s, a)\)の値を最大にするような行動\(a\)を見つけてください」という意味の数学記号です。つまり、どんな状態\(s\)に遭遇しても、単純にQ値のリストを眺めて、一番高い数値を持つ行動を選びさえすれば、それが最適方策になるのです。もう確率的に悩む必要はありません。
現実には、状態空間も行動空間も広大で、この方程式を数学のテストのように解析的に解くことはほとんど不可能です。しかし、心配はいりません。この方程式は、AIが目指すべき「価値のあるべき姿」、つまり学習の目標(ターゲット)を示してくれています。
後の章で学ぶ多くの学習アルゴリズム(Q学習など)は、このベルマン最適方程式を、いわば「答え合わせの解答」として利用します。試行錯誤で得られたデータ(経験)を使って、現在の価値関数の推定値を、この方程式が示す「あるべき姿」に少しずつ近づけていく。その地道な反復こそが、強化学習における「学習」の正体なのです。
🤿 Deep Dive! 解けない「宝の地図」は、なぜAIの「北極星」なのか?
ベルマン方程式、特にベルマン最適方程式は、AIが目指すべき「究極の価値」を定義しています。しかし、その方程式はあまりにも壮大で、現実の複雑な問題では直接解くことができません。それなら、一体何の意味があるのでしょうか?
これは、強化学習の本質を理解する上で非常に重要な問いです。結論から言うと、ベルマン方程式の役割は、数学の問題のように「解く」ことではなく、航海の羅針盤が指す「北極星」のように、AIが進むべき正しい方向を指し示すことにあります。
発想の転換:「方程式」から「誤差(エラー)」へ
ベルマン方程式の本当の価値は、その式を少し変形することで見えてきます。
\[ Q_*(s, a) – \left( \mathbb{E} \left[ R_{t+1} + \gamma \max_{a’} Q_*(s’, a’) \right] \right) = 0 \]
この式が意味するのは、「もしAIの持つQ値が本当に究極(最適)ならば、現在のQ値(左側)と、一歩先の未来から計算したQ値(右側)は完全に一致し、その差はゼロになるはずだ」ということです。
ここで、AI研究者たちは画期的な発想の転換をしました。
「この方程式を直接解くのは無理だ。しかし、この『差』を計算することはできる。ならば、この『差(エラー)』がゼロに近づくように、AIのQ値を少しずつ更新していけば、いつかは究極のQ値にたどり着けるのではないか?」と。
この「理想と現実の差」、すなわちベルマン誤差こそが、AIが何を学ぶべきかを示す具体的な「学習信号」となります。次の章で学ぶTD学習やQ学習といったアルゴリズムは、まさにこのベルマン誤差を最小化しようとする、現実的で反復的な手法なのです。
歴史的背景:動的計画法からTD学習へ
ベルマン方程式は、1950年代にリチャード・ベルマンが提唱した動的計画法(Dynamic Programming)という考え方から生まれました。これは、「大きな問題を、より小さな部分問題に分割して解く」という強力な問題解決アプローチです。ベルマン方程式は、この考え方を「将来にわたる価値の計算」という問題に適用したもので、「現在の価値は、直後の報酬と、次の状態の価値で決まる」という再帰的な構造で問題を単純化したのです。
ただし、オリジナルの動的計画法は、遷移確率\(P\)など、環境の全てのルール(世界の理)を完全に知っていることを前提としていました。これは、ルールが明確なチェスのようなゲームには適用できても、患者さんの体の反応のように不確実で未知な部分が多い現実世界には適用できません。
そこで、リチャード・サットンらが発展させたのが、TD学習のような「世界の理を知らなくても、実際の経験からベルマン誤差を計算し、学習できる」手法です (Sutton and Barto, 2018)。これにより、AIは未知の環境を探検しながら、ベルマン方程式という北極星だけを頼りに、自力で宝の地図を完成させることができるようになったのです。
つまり、ベルマン方程式はAIにとって「解くべき問題」ではなく、自身の学習が正しい方向に向かっているかを確認するための「検証ツール」であり、進むべき道を示す「コンパス」なのです。この美しい理論的支柱があるからこそ、AIは闇雲な試行錯誤から脱し、効率的に賢くなることができるわけです。
AIが賢くなる仕組み:学習アルゴリズム
ベルマン方程式は、AIが目指すべき理想の価値、いわば宝の地図を示してくれました。そこには、全ての状態における究極の価値という「宝」のありかが描かれています。しかし、ここで私たちは、理論と現実の間に横たわる、巨大な溝に直面します。
現実の医療のように、患者さんの状態(バイタルサイン、検査値、意識レベル…)や治療の選択肢(薬剤の組み合わせ、投与量の微調整…)の組み合わせが天文学的な数にのぼる複雑な世界では、ベルマン方程式の厳密解を求めることは現実的ではありません。これは「次元の呪い」として知られる現象で、状態空間の次元が増えるにつれて、必要な計算資源が指数関数的に増大してしまうためです。
そこでAIは、動的計画法のように厳密解を求めるアプローチではなく、経験(データ)から近似的に学ぶという、より実践的なアプローチに切り替えます。
これは、医師が成長していくプロセスと全く同じだと思います。
新人研修医は、分厚い医学の教科書(ベルマン方程式の理論)をすべて暗記して臨床現場に出るわけではありません。むしろ、教科書の知識は道標としつつ、一人ひとりの患者さんを受け持ち(エピソード)、指導医の監督のもとで治療方針を立て(行動)、その結果患者さんの容態がどう変化したかを見守り(報酬と次の状態)、そしてカンファレンスで指導医から「あの時の判断は良かった」「次はこう考えた方がいい」とフィードバックをもらう(学習)。この繰り返しを通じて、徐々に自分の中に「臨床の勘」や「優れた治療戦略(方策)」を築き上げていきます。
AIも、シミュレーションや過去の膨大な臨床データの中で、この仮想的な研修医として働きます。一つ一つの症例を経験し、自身の判断がどのような結果をもたらしたかを丹念に記録し、その経験に基づいて、自身の価値観(価値関数)や行動指針(方策)をほんの少しだけ、地道に更新していくのです。
この「経験からの学習」アプローチには、大きく分けて3つの戦略があります。これらのアルゴリズムが、この地図のどこに位置するのかを意識すると、理解が格段に深まるはずです。
| アプローチ | 学習対象 | 何を評価するか? | 例えるなら | 主な役割・特徴 | 代表的なアルゴリズム |
|---|---|---|---|---|---|
| 価値ベース (Value-Based) | 価値関数 | 状況そのものの良さ 🧭 (状態価値 V) | 「この戦局は有利か不利か」という盤面の評価。 | 方策評価に直結。将来の報酬の期待値を近似する土台。 | 基本的なTD学習 (TD(0)) |
| ある状況での行動の良さ 🎯 (行動価値 Q) | 「この盤面での次の一手は良い手か悪い手か」という指し手の評価。 | 制御(最適行動の選択)に直結。Q学習はオフポリシー、SARSAはオンポリシー。 | Q学習, SARSA, DQN | ||
| 方策ベース (Policy-Based) | 方策 | 行動指針そのもの 📖 | ナビマップを作らず、良い結果に繋がった行動を直接強化する運転技術の習得。 | 連続行動を自然に扱えるが、学習の分散が大きくなりやすい。 | REINFORCE, PPO, TRPO |
| Actor-Critic | 価値関数+方策 | 行動指針と行動の良さの両方 🤝 | 運転手(Actor)が運転し、ナビ(Critic)がその運転を評価・フィードバックする二人三脚。 | 両者の利点を享受し、安定かつ高効率。現代手法の主流。 | A2C/A3C, DDPG, TD3, SAC |
*注: TD学習は、Q学習やActor-Criticなど、多くのアルゴリズムで価値を更新するための基礎的な概念としても利用されます。
価値ベースの手法:詳細なナビマップを作る戦略
このアプローチは、まず世界に関する詳細なナビマップ、すなわち「価値」を学習することに専念します。これには2つの粒度があります。
- 状態価値 (V値) の学習: 「この戦局は有利か?」のように、状況そのものの良さを評価します。これは特定の方策がどれだけ良いかを評価する(方策評価)ための土台となりますが、これだけでは「具体的に次に何をすべきか」は直接わかりません。この学習の最も基本的な手法が TD(0) 学習です。
- 行動価値 (Q値) の学習: 「この局面での次の一手は良い手か?」のように、ある状況での特定の行動の良さを評価します。全ての治療選択肢の良し悪しを点数化するため、AIは最も点数が高い行動を選ぶだけで最適な制御(行動選択)が可能になります。Q学習やSARSA、そして関数近似で安定化させたDQNがこの代表です。
方策ベースの手法:コンパスを直接磨く戦略
こちらは、もっと直接的です。価値という中間目標を置かず、「この状況なら、この治療法をこれくらいの確率で選ぶべき」という方策(行動指針)そのものを直接学習します。良い結果(高い報酬)に繋がった行動の選択確率を直接上げるため、薬剤投与量のような連続的な行動を自然に扱えるのが最大の強みです。ただし、学習のばらつき(分散)が大きくなりやすいという課題があり、ベースラインやアドバンテージといった工夫で安定化を図ります。
Actor-Critic法:ナビとコンパスを両方使う戦略
そして、現代の強化学習の最前線で主流となっているのが、この2つを融合させたアプローチです。これは、方策に従って行動を決定する「役者(Actor)」と、その行動がどれだけ良かったかを価値ベースで評価する「評論家(Critic)」の2人が協力するような仕組みです。Actorがコンパスを見て道を選び、Criticがナビでその選択を評価して、より良い道筋をアドバイスする。この二人三脚により、学習はより安定し、効率的になります。
補足として、これらとは別に「モデルベース強化学習」というアプローチも存在します。これは、経験から環境のルール(遷移モデル)そのものを学習し、その内部モデルを使ってシミュレーション(計画)を行うことで、データ効率を高める手法です。
それでは、これらの学習戦略の基礎となる、最も根源的なアイデア「時間差(TD)学習」から、私たちの冒険を始めましょう。
時間差学習 (Temporal Difference, TD学習):経験から学ぶ知恵の核心
AIの学習法の代表格が、時間差学習(Temporal Difference, TD学習)です。これは強化学習の多くのアルゴリズムの根幹をなす、非常にエレガントで強力なアイデアです。
TD学習は価値を評価するための汎用的な枠組みですが、このセクションではまず、ある「状況(状態)」そのものの良さ、すなわち「状態価値」を学習・更新していく方法として解説します。
もしベルマン方程式が「理想の宝の地図」だとしたら、TD学習は「その地図を頼りに、実際に一歩ずつ歩きながら、手元の不完全な地図を書き換えていく現実的な冒険術」と言えるでしょう。
TD学習の核心は、「実際に行動してみて得られた結果(現実)と、事前に行っていた予測とのズレ」を使って、予測の方を現実に近づけるように修正していく、という点にあります。この「予測と現実のズレ」こそが学習の原動力であり、TD誤差(TD Error)と呼ばれます。
これは、私たち人間が経験から学ぶプロセスそのものだと思います。
例えば、ある研修医が、発熱と咳を訴える患者さんを「典型的な市中肺炎」と診断したとします(状態\(S_t\))。彼は教科書知識から「この抗菌薬を投与すれば、明日には解熱してCRPも半減するだろう」と予測します(高い状態価値\(V(S_t)\)を予測)。
しかし翌日、実際に患者さんを診てみると、熱は微熱程度にしか下がっておらず(即時報酬\(R_{t+1}\)が予測より低い)、CRPもほとんど変わっていませんでした(次の状態\(S_{t+1}\)が思ったより良くない)。
この瞬間、研修医の頭の中では何が起こるでしょうか?
「あれ、思ったより手強いぞ。当初の『明日には良くなる』という予測は楽観的すぎたな」と感じるはずです。この「当初の予測」と「一歩進んでみて分かった現実」との間のギャップこそがTD誤差です。そして、彼はこの経験を通じて、「次に似たような肺炎の患者さんを診たら、もう少し慎重に予後を予測しよう」と、頭の中の価値観を少しだけ修正します。
TD学習は、この経験からの学習プロセスを、見事に数学の言葉で定式化したものなのです。
「時間差」とは何か?研修医の思考を覗いてみる
この学習プロセスの名前にもなっている「時間差(Temporal Difference)」という言葉の意味を、先ほどの研修医の思考プロセスに沿って、もう少し深く掘り下げてみましょう。
- 昨日の予測(Time `t`) 🌃
昨日の夜、研修医は患者さんを診て、頭の中で予後を予測します。「この状態なら、教科書通りにいけば予後はかなり良いはずだ。将来的な健康状態の価値を点数化するなら、80点くらいだろう」と。これが最初の予測、いわば『昨日の時点での未来予測』です。 - 今日の現実(Time `t+1`) ☀️
そして一日が経ちました。研修医が抗菌薬を投与(行動)した結果、患者さんの状態は少し変化しました。ここで、研修医は2つの新しい情報を手に入れます。- ① 直後の報酬: 「熱が少し下がったな。これはプラスだ。+5点のご褒美だ」
- ② 新しい未来予測: 「ただ、CRPはまだ高いままだ…。今日のこの状態から改めて未来を予測すると、昨日の時点ほど楽観はできないな。ここから先の未来の価値は70点くらいだろう」
- 「少しマシな」答え合わせ(TDターゲット) 🧠
ここで、研修医は思考を巡らせます。最終的な結果(退院)はまだ分かりません。しかし、昨日よりは少しだけ多くの情報を持っています。彼は、この新しい情報を使って、「昨日の予測」の答え合わせを試みます。
「実際にもらえた+5点と、ここから見える未来の70点を合わせると、昨日の時点での状況は、本当は75点くらいの価値だったんじゃないか?」と。
この「一歩進んでみて分かった、より現実的な価値の見積もり」(この例では75点)こそが、TDターゲットです。 - 予測の”ズレ”(TD誤差)の発見 💡
そして、最も重要な瞬間が訪れます。研修医は、自分の2つの予測を比較します。
「昨日は80点だと思っていたのに、今日になって計算し直したら75点だった。つまり、私の予測は5点分、楽観的すぎたんだ」と気づきます。
この、時間差で生じた2つの予測(昨日の予測 vs 今日の更新版予測)の差こそが、時間差分、すなわちTD(Temporal Difference)誤差なのです。
結局のところ、TD学習とは、「最終的な結果を待たずに、一歩進むごとに行う『答え合わせ』と『反省』のプロセス」と言えるでしょう。最終的な退院日を待つことなく、日々の小さな変化から学び、自分の予測を少しずつ、しかし着実に現実に近づけていく。この地道で賢明な学習スタイルこそが、TD学習が強化学習の世界でこれほどまでに広く使われている理由なのです。
TD学習の更新プロセス
では、この「予測と修正」のプロセスを、AIがどのように実行するのか具体的に見ていきましょう。AIは、ある状態\(S_t\)の価値を\(V(S_t)\)と推定(予測)しているとします。
- 行動 (Act): まず、状態\(S_t\)で何らかの行動\(A_t\)をとります。(例:抗菌薬Aを投与する)
- 観測 (Observe): 行動の結果、世界(患者さん)が反応します。AIは、直後にもらえた報酬\(R_{t+1}\)(例:症状が少し改善したので+1点)と、遷移した先の新しい状態\(S_{t+1}\)(例:翌日のバイタルサインと検査データ)を観測します。
- TDターゲットの計算 (Calculate TD Target):
この時点で、AIは一歩先の未来を実際に「体験」しました。この新しい情報を使って、当初の予測よりも「マシな」目標値を計算します。これをTDターゲットと呼びます。
\[ \text{TDターゲット} = R_{t+1} + \gamma V(S_{t+1}) \] この式の意味は、「実際にもらえた直後の報酬(\(R_{t+1}\))」と、「一歩進んだ先から見える、新しい未来予測(\(\gamma V(S_{t+1})\))」の合計です。
重要なのは、遷移先の価値\(V(S_{t+1})\)もまだ不完全な「予測」であるという点です。しかし、全く情報がなかった最初の予測\(V(S_t)\)に比べれば、\(R_{t+1}\)という一つの確定した現実を経た後の予測なので、少しだけ信頼性が増しています。TD学習は、この「少しマシな予測」を仮の「正解」とみなして学習を進めます。これは、最終結果を待たずに途中の経過から学習する、非常に効率的な方法で、専門的にはブートストラップ法と呼ばれます。 - TD誤差の計算 (Calculate TD Error):
次に、ステップ3で計算した「少しマシな現実(TDターゲット)」と、「当初の甘い予測(\(V(S_t)\))」の差を計算します。これが学習信号となるTD誤差(\(\delta_t\))です。
\[ \text{TD誤差} (\delta_t) = \underbrace{(R_{t+1} + \gamma V(S_{t+1}))}_{\text{一歩進んでみて分かった現実}} – \underbrace{V(S_t)}_{\text{当初の予測}} \]- もしTD誤差がプラスなら、「思ったより良かった!」ということ。当初の予測は悲観的すぎたので、少し上方に修正すべきです。
- もしTD誤差がマイナスなら、「思ったより悪かった…」ということ。当初の予測は楽観的すぎたので、少し下方に修正すべきです。
- 価値の更新 (Update Value):
最後に、計算したTD誤差を使って、元の予測値を修正します。
\[ V(S_t) \leftarrow V(S_t) + \alpha \cdot \delta_t \] これを展開すると、よく教科書で見る以下の式になります。 \[ V(S_t) \leftarrow V(S_t) + \alpha \left[ (R_{t+1} + \gamma V(S_{t+1})) – V(S_t) \right] \] ここで新しく登場した\(\alpha\)(アルファ)は学習率と呼ばれる0から1の間の小さな定数です。これは、一度の経験(TD誤差)で価値観をどれだけ大きく変えるかを決める「素直さ」や「頑固さ」のパラメータです。- もし\(\alpha\)が1に近ければ、AIは非常に素直で、たった一度の経験で「私の以前の考えは完全に間違っていました!」と価値観を大きく変えます。これは、稀な出来事に過剰反応してしまい、学習が不安定になるリスクがあります。
- もし\(\alpha\)が0に近ければ、AIは非常に頑固で、「今回の結果はただの例外だろう」と、価値観をほんの少ししか変えません。これでは、学習が進むのに膨大な時間がかかってしまいます。
この地道な更新を、何千、何万という経験を通じて何度も何度も繰り返すことで、AIの価値観(V値のテーブル)は、徐々に、しかし確実に真の価値(ベルマン方程式を満たす理想の値)へと収束していきます。
🤿 Deep Dive! AIの知性の設計図と建築術:ベルマン方程式とTD学習の密な関係
強化学習を学ぶと、誰もが一度は「ベルマン方程式とTD学習の式は、とてもよく似ている。一体何が違うのだろう?」という疑問に突き当たります。その答えは、両者の役割が「理想の家の設計図」と「日々の建築作業」ほどに違う、というアナロジーで驚くほどクリアになります。
ベルマン方程式:知性の「あるべき姿」を描いた設計図 🗺️
ベルマン方程式は、「理想の価値とは、こうなっているべきだ」という完成形を示した、静的な関係式(ゴール)です。
\[V^\pi(s) \boldsymbol{=} \mathbb{E}_\pi [R_{t+1} + \gamma V^\pi(S_{t+1}) \mid S_t=s]\]
これは数学における「等式 (=)」であり、「もしAIの価値観が完璧ならば、左辺(今日の価値)と右辺(直後の報酬と明日の価値の期待値)は等しくなっているはずだ」という、完成した状態の性質を記述しています。
例えるなら、「理想の家の壁は、この座標に寸分違わず建っているべきだ」と記した設計図そのものです。それは「正解」の姿を示してはくれますが、どうやってそこにレンガを積み、壁を建てていくかという具体的な手順までは教えてくれません。
なぜ設計図(ベルマン方程式)を直接解けないのか? 🧩
ここで当然の疑問が湧きます。「設計図があるなら、それを解いて一気に家を完成させられないのか?」と。
その通りで、もし可能ならそれが最も速い方法です。しかし、現実のほとんどの問題、特に医療のような複雑な世界では、それが事実上不可能なのです。理由は大きく2つあります。
- 世界のルールブックが手元にない: ベルマン方程式を数学的に解くには、「ある状態でこの行動をしたら、次にどの状態になる確率が何%か」という遷移確率 \(p(s’, r | s, a)\) の全てを知っている必要があります。しかし、臨床現場で「この患者にこの薬を投与したら、73.5%の確率で血圧が安定し、26.5%の確率で悪化する」といった世界の完全なルールブックは誰にもわかりません。
- 計算量が天文学的になる: たとえ奇跡的にルールブックが手に入ったとしても、患者さんの状態の組み合わせは天文学的な数にのぼります。何十億もの未知数(各状態の価値\(V(s)\))を含む、何十億もの連立方程式を解くことは、現代のスーパーコンピュータをもってしても不可能です。
つまり、私たちは「不完全な情報」と「限られた計算能力」という制約の中で、どうにかして設計図に描かれた理想の家に近づかなければならないのです。
TD学習:設計図を頼りに家を建てる日々の建築作業 🛠️
そこで登場するのが、TD学習です。こちらは、「設計図に近づけるために、今日の作業で何をすべきか」を示した、動的な更新式(プロセス)です。
\[V(S_t) \boldsymbol{\leftarrow} V(S_t) + \alpha \bigl[ (R_{t+1} + \gamma V(S_{t+1})) – V(S_t) \bigr]\]
こちらは「更新式 (←)」です。「左辺の古い価値(今の壁の位置)を、右辺の計算結果という新しい価値(修正後の壁の位置)に更新しなさい」という、具体的な命令・手順を表しています。
例えるなら、これは建築家の日々の作業です。「今日の作業でレンガを一つ積んでみたら(経験)、壁が設計図の方向に1cm近づいたな。よし、そのズレ(TD誤差)を元に、明日はもう少し設計図に近づくように作業しよう」という、試行錯誤のプロセスそのものです。
なぜ式は似ているのか?:建築家は設計図を見ながら作業する
では、なぜこの2つの式はこれほど似ているのでしょうか?
注目すべきは、TD学習の更新式の中核をなすTDターゲット \((R_{t+1} + \gamma V(S_{t+1}))\) の部分です。この形は、ベルマン方程式の右辺 \(\mathbb{E}[R_{t+1} + \gamma V(S_{t+1})]\) とそっくりです。
これは、建築家(TD学習)が、設計図(ベルマン方程式)を常に参照しながら作業を進めていることを意味します。TD学習は、
- 設計図を確認する: ベルマン方程式が示す理想の関係 \(R + \gamma V’\) を、実際の経験 (\(R_{t+1}, S_{t+1}\)) を使って「今日のお手本(TDターゲット)」として具体化する。
- 現状との差を確認する: 「お手本」と「現在の自分の予測値 \(V(S_t)\)」とのズレ(TD誤差)を測る。
- 修正作業を行う: そのズレを埋める方向に、現在の予測値を少しだけ修正する。
という作業を行っているのです。
つまり、式が似ているのは偶然ではありません。TD学習が、ベルマン方程式という「解くことのできない壮大な設計図」を、現実世界で手に入る経験というレンガを使って、一歩ずつ着実に実現していくための、極めて合理的で実践的なアルゴリズムだからなのです。
ベルマン方程式が価値関数が目指すべき最終的なゴールを定義し、TD学習がそのゴールに向かって一歩ずつ進むための具体的な学習プロセスを提供する。この美しい関係性こそが、AIが経験から賢くなっていく仕組みの根幹を成しているのです。
Q学習 と SARSA:行動価値を学ぶ二大巨頭
前回学んだTD学習は、ある「状況(状態)」の良さ、つまり状態価値\(V(s)\)を更新していく方法でした。しかし、AIが次の一手を決めるためには、より直接的な「この状況で、この行動をとったらどれだけ良いか?」という行動価値\(Q(s, a)\)を知る必要があります。
TD学習のエレガントなアイデアは、この行動価値関数の学習に直接応用できます。その代表的なアルゴリズムが、強化学習の世界における二大巨頭、Q学習(Q-Learning)とSARSAです。どちらもTD学習をベースにしていますが、TDターゲット、つまり「学習のお手本」の計算方法に決定的な違いがあります。そして、この違いがAIに「楽観的で大胆」か、「現実的で堅実」か、という全く異なる「性格」を与えることになるのです。
Q学習 (Q-Learning):理想を追い求める楽観主義者(オフポリシー)
「何であるか」:常に「理想の次の一手」を想定して価値を更新する
Q学習は、「もしこの次の一手で、現時点で考えうる最善の行動をとったら、トータルでどれくらいのリターンが期待できるだろう?」という、常に理想的な未来をシミュレーションして、現在の行動の価値(Q値)を更新していくアルゴリズムです。
この学習プロセスは、以下の更新式として数学的に表現されます。
\[Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \bigl[ \underbrace{R_{t+1} + \gamma \max_{a’} Q(S_{t+1}, a’)}_{\text{学習目標 (TDターゲット)}} – Q(S_t, A_t) \bigr]\]
この式の核心は、AIは「究極の正解である最高のQ値」を知っているわけではない、ということです。AIが参照しているのは、あくまで学習の途中段階である「現時点での不完全な知識(Qテーブル)の中で、最も高いと予測されているQ値」に過ぎません。これは、いわばAIの「現在のベストな仮説」です。
このプロセスを、敗血症治療を学ぶ研修医の思考に例えてみましょう。この研修医は、まだ情報が不完全な自作の「治療プロトコル(=不完全なQテーブル)」を必死に更新しながら学んでいる最中です。
- 行動 (Action): 患者さんの状態 \(S_t\)(血圧低下、頻脈)を見て、研修医は自分のプロトコルに従い、行動 \(A_t\)(初期輸液 20ml/kg)を選択し、実施しました。
- 結果 (Reward & New State): 処置後、報酬 \(R_{t+1}\)(血圧が少し改善したので+5点)が得られ、患者さんは新しい状態 \(S_{t+1}\)(血圧は持ち直したが、呼吸数が少し増加)に変化しました。
- 頭の中でのシミュレーション (\(\max Q\) の部分): ここで研修医は、自分の最初の判断(初期輸液)が正しかったかを評価するために、頭の中で思考実験を始めます。
「さて、患者さんは新しい状態 \(S_{t+1}\) になった。僕の(まだ未熟な)プロトコルによれば、ここから考えられる次の一手のうち、最善の選択肢はなんだろう?」
彼はプロトコルの該当ページを開き、次の選択肢の評価(Q値)を見比べます。- 選択肢a’: 昇圧剤を開始(現在の評価: +50)
- 選択肢b’: 抗菌薬の変更を検討(現在の評価: +20)
- 選択肢c’: 追加の輸液(現在の評価: -30)
- 学習(プロトコルの更新): 研修医は、この思考実験の結果を使って、最初の判断の価値を計算し直します。
- TDターゲット(目標となるべき価値)の計算:
「実際の報酬」+「もし次に最善手を打ったと仮定した場合の未来の価値」
数式では、\(R_{t+1} + \gamma \max_{a’} Q(S_{t+1}, a’)\) となります。今回の例では、「+5点」+ \(\gamma\) ×「+50点」が、学習の目標値となります。 - TD誤差(目標と現在の差)の計算:
上記の「TDターゲット」と、元のプロトコルにあった「初期輸液」の古い評価との差を計算します。 - 更新: 最後に、更新式全体を実行します。この誤差を学習率 \(\alpha\) の分だけ埋めるように、プロトコルの「初期輸液」のページの評価を修正(更新)するのです。
- TDターゲット(目標となるべき価値)の計算:
このように「実際の結果」と「頭の中での理想的な次の手」を組み合わせることで、AIは一歩ずつ、より正確な価値観(Qテーブル)を学習していくのです。
「なぜそれを行うのか(なぜオフポリシーなのか)」:あらゆる経験から最大限に学ぶため
Q学習の最大の特徴であり、強力な点は、AIが学習のために実際に次にとった行動とは無関係に、「もし最善手を打っていたら」という理想に基づいて学習が進むことです。
例えば、先ほどの研修医が次の手として、勉強のためにあえて評価の低い「追加の輸液」(これは探索と呼ばれます)を選んでしまい、結果的に患者さんの状態が悪化(報酬 -40点)したとします。
それでもQ学習の考え方では、最初の「初期輸液」の評価を更新する際に、この失敗した次の行動は完全に無視します。「君が次に失敗したことは、今は置いておこう。もしあの場面で理論上最善の『昇圧剤投与』を選んでいたら、これくらいの価値があったはずだ」と、理想の未来に基づいて評価を更新するのです。
このように、データを集めるための実際の方針(時にランダムな行動もとる方針)と、学習対象となる理想の方針(常に最善手をとる方針)が異なっていても学習できる性質をオフポリシー(Off-policy)と呼びます。
この性質のおかげで、過去に様々な医師が記録した多様な治療のログデータ(成功例も失敗例も、最適なものもそうでないものも含む、いわゆるオフラインデータ)から、効率的に最適な治療戦略を学ぶ理論的な道が拓けるのです。これは医療AI開発において非常に重要な意味を持ちます。
「なんの役に立つのか」:常に理想を目指す、効率的な教育方針
Q学習の振る舞いは、優秀で厳しい指導医との症例検討会によく似ています。
研修医: 「患者さんの状態 \(S_t\) を見て、私は治療 \(A_t\) を行いました。その結果、報酬 \(R_{t+1}\) が得られ、状態は \(S_{t+1}\) になりました」
指導医 (Q学習): 「なるほど。だが、君が次に何をしようと考えていたかは一旦忘れよう。この状態 \(S_{t+1}\) になった時点で、我々のチームが持つ現在の知識に基づけば、理論上の最善手は \(a’_{\text{best}}\) だったはずだ。君の最初の判断 \(A_t\) は、この『理想的な未来』に繋がる価値があったのだと学びなさい」
たとえ研修医が次に何をすべきか分からず戸惑っていたとしても(探索)、指導医は常に「現時点での理論上の最善手」を基準にフィードバックを与えます。この教育方針により、研修医は自身の未熟な経験(時に犯す間違い)に過度に引きずられることなく、常に高い目標(最適方策)に向かって、ある意味で最短距離で成長していくことができるのです。
SARSA:現実の経験に学ぶ堅実家(オンポリシー)
「何であるか」:実際に歩んだ「一連の道のり」から、ありのままに学ぶ
Q学習が「もし次に最善手を打っていたら…」という理想の未来をシミュレーションして学ぶ楽観主義者だったのに対し、SARSAは「AIが実際に体験した一連の出来事」そのものから、ありのままに学ぶ現実的なアルゴリズムです。
その名前は、学習に使う一連の経験データが \( (S_t, A_t, R_{t+1}, S_{t+1}, A_{t+1}) \) 、つまり State(状態)、Action(行動)、Reward(報酬)、next State(次の状態)、next Action(次の行動)の頭文字をつないだものであることに由来します。これは、AIが経験した「見て、行動し、報酬を得て、次の状態になり、そして次に行動した」という、一つの完結したエピソードそのものです。
更新式はQ学習と驚くほどよく似ていますが、学習のお手本となる価値(TDターゲット)の作り方が決定的に異なります。
\[ Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left[ \underbrace{R_{t+1} + \gamma Q(S_{t+1}, \boldsymbol{A_{t+1}})}_{\text{TDターゲット}} – Q(S_t, A_t) \right] \]
Q学習との違いは、以下の部分、ただ一点です。
- Q学習のTDターゲット: \( R_{t+1} + \gamma \max_{a’} Q(S_{t+1}, a’) \)
(未来の価値は、次の状態で取りうる理論上の最善手の価値) - SARSAのTDターゲット: \( R_{t+1} + \gamma Q(S_{t+1}, \boldsymbol{A_{t+1}}) \)
(未来の価値は、次の状態で実際に取った次の一手の価値)
SARSAは、Q学習のように「もし次に最善手を打っていたら…」という思考実験(max計算)を行いません。その代わりに、次の状態 \( S_{t+1} \) になった後で、AIが実際に選択した次の行動 \( A_{t+1} \) のQ値をそのまま使います。「次にこの手をとったのだから、その現実を元に評価しようじゃないか」と考える、非常に実直なアルゴリズムなのです。
「なぜそれを行うのか(なぜオンポリシーなのか)」:自分の行動方針に責任を持つ学習
SARSAは、AIが現在実行している方策(治療マニュアル)の価値を、良い点も悪い点も含めて、ありのままに評価・学習します。この性質を理解するために、再び研修医が「探索」として普段と違う行動をとった場面を考えてみましょう。
- 状況: 敗血症の患者さん(状態 \( S_t \))。研修医の(まだ未熟な)マニュアルでは、昇圧剤の投与が最善手だと書かれています。
- 行動 ( \( A_t \) ): しかし、研修医は勉強のため、あえてマニュアルとは違う「大量輸液」(Q値が低い行動)を試してみました(これは探索です)。
- 結果 ( \( R_{t+1}, S_{t+1} \) ): その結果、患者さんの呼吸状態が悪化(肺水腫)してしまいました(新しい状態 \( S_{t+1} \))。
- 次の行動 ( \( A_{t+1} \) ): 慌てた研修医は、次の手として「利尿薬の投与」を行いました。
この時、SARSAは最初の判断「大量輸液」をどう評価するでしょうか?
SARSAは、実際に起きた出来事の連なりをそのまま評価します。つまり、「大量輸液(\(A_t\))」→「呼吸悪化(\(S_{t+1}\))」→「利尿薬投与(\(A_{t+1}\))」という一連の現実を元に、「なるほど、あの場面で大量輸液という判断をすると、結局は呼吸を悪化させて、利尿薬を投与する羽目になる、という未来に繋がるんだな」と学習します。\(A_{t+1}\)である「利尿薬投与」のQ値が低ければ、最初の判断\(A_t\)「大量輸液」の評価もそれに引きずられて下がることになります。
もしQ学習の指導医であれば、「君が次に慌てて利尿薬を使ったのは君の勝手だ。もしそこで冷静に最善手(例えば人工呼吸器の調整)をとっていたら、最初の大量輸液の評価はもっとマシだったはずだ」と理想論で評価したでしょう。
しかしSARSAは、データを集めるための方策(時に探索も行う実際の方策)と、評価・改善しようとしている方策が常に一致します。自分がとった行動の結果から直接学ぶため、オンポリシー(On-policy)と呼ばれます。AIは自身の行動の結果から逃げずに学ぶため、より安全で、現実的なリスクを考慮した方策を学習する傾向があると言われています。
「なんの役に立つのか」:経験を正直に記録し、現実的なリスクを学ぶ
SARSAの学習プロセスは、日々の臨床経験を詳細な日誌に記録し、そこから学ぶ内省的な研修医に例えることができます。
研修医 (SARSA)の日誌:
「昨日の夜、患者さんの状態が \( S_t \) だった。私は治療 \( A_t \) を行い、その結果、報酬 \( R_{t+1} \) で状態は \( S_{t+1} \) になった。そして、その次の手として私は、治療 \( A_{t+1} \) を選択した。
なるほど、私の判断 \( A_t \) は、この一連の『現実の』経験に繋がったわけか。理想論は置いておいて、実際に起きたこの結果を元に、最初の判断の価値を評価し直そう」
この研修医は、指導医の厳しい理想論(max Q)を聞くのではなく、「自分自身が実際に行った次の一手」の結果から直接学びます。
この性質は、特に安全性への配慮が求められる医療AIにおいて極めて重要です。なぜなら、楽観的なQ学習は、時に危険な方策を「最適」と誤解してしまう可能性があるからです。
まとめ:Q学習とSARSAの比較
| Q学習 (オフポリシー) | SARSA (オンポリシー) | |
|---|---|---|
| 思考法 | 楽観主義 | 現実主義 |
| 未来の評価 | 次に理論上の最善手をとると仮定 (max Q) | 次に実際にとった行動を元に評価 |
| 結果 | 高リスク・高リターンの最適ルートを学習しやすい | 自身の行動方針(ミスをする可能性)を含んだ安全なルートを学習しやすい |
このように、SARSAはAI自身の「性格」や「癖」(つまり、現在の方策)を反映した現実的な価値を学ぶため、AIが学習中に現実世界で実際に行動する場合(例えば、ロボット手術の学習や治療薬の自動投与など)に、予期せぬ危険な行動のリスクをより正確に評価し、安全な方策を獲得するのに役立つと考えられています。
深層強化学習へ:Deep Q-Network (DQN)
これまでのQ学習やSARSAで、AIが経験から行動の価値(Q値)を学んでいく仕組みが見えてきました。これらの手法は、理論的に非常に美しく、強化学習の礎となるものです。しかし、現実の複雑な問題、特に医療データのような高次元の情報を扱おうとすると、途端に巨大な壁にぶつかります。その壁を打ち破り、強化学習を現代AIの主役へと押し上げたブレークスルーこそが、Deep Q-Network(DQN)です。
イントロダクション:Qテーブルを襲う「次元の呪い」
「何であるか」
これまでのQ学習では、考えうる全ての「状態」と「行動」の組み合わせに対して、一つ一つQ値を計算し、それを表に記録していくという方法を暗黙の前提としていました。この巨大な対応表を「Qテーブル」と呼びます。
| 状態 (State) | 行動A (輸液) | 行動B (昇圧剤) | … |
|---|---|---|---|
| 状態1 (血圧100, 心拍数80, …) | 45.2 | 21.8 | … |
| 状態2 (血圧90, 心拍数110, …) | -10.5 | 33.4 | … |
| … | … | … | … |
シンプルな迷路ゲームのような問題であれば、状態の数が限られているため、このQテーブル戦略は非常にうまく機能します。
「なぜそれを行うのか(なぜ限界が来るのか)」
では、このQテーブルを臨床現場に持ち込むとどうなるでしょうか。想像してみてください。患者さんの「状態」を定義するのは、血圧や心拍数だけではありません。呼吸数、体温、意識レベル、そして何十項目にも及ぶ血液検査データ…。仮に、それぞれの指標が取りうる値を10段階に絞ったとしても、指標が10個あるだけで状態の組み合わせは \(10^{10}\)(100億通り)に達します。現実の医療データでは、指標はもっと多く、値も連続的です。考えられる状態の数は、文字通り天文学的、いや、宇宙に存在する原子の数をも軽く超えてしまうでしょう。
これが、高次元のデータを扱う際に必ず直面する「次元の呪い(Curse of Dimensionality)」と呼ばれる現象です。宇宙サイズのQテーブルをコンピュータのメモリに保存することなど不可能ですし、仮にできたとしても、その表の全てのマスを経験で埋めるには、無限に近い時間が必要になってしまいます。
さらに、もう一つ深刻な問題があります。それは「未知との遭遇」です。Qテーブルは、過去に経験した状態にしか対応できません。もし、これまでのデータに一度も現れたことのない、全く新しい組み合わせの検査値を持つ患者さんが現れたら、AIはQテーブルに対応する行を見つけられず、完全に思考停止に陥ってしまうのです。これでは、個々の患者さんに対応する医療には到底使えません。
発想の転換:Qテーブルを「賢い関数」で置き換える
この絶望的な壁を乗り越えるために、研究者たちは驚くほど大胆な発想の転換をしました。
「何であるか」
「そもそも、巨大な表を丸暗記しようとするから無理がある。専門医のように、複雑な患者データから本質的なパターンを読み取り、その状況における各治療の価値を『予測』するような、賢い関数があればいいのではないか?」
この「賢い関数」の役目を、本シリーズのC12で学んだ深層ニューラルネットワーク(DNN)に担わせる。これこそが、Deep Q-Network (DQN) の核心的なアイデアです。
DQNは、Qテーブルの代わりに、ニューラルネットワークを用いて行動価値関数 \(Q(s, a)\) を近似します。この近似された関数を \(Q(s, a; \theta)\) と書きます。ここでの \(\theta\)(シータ)は、ニューラルネットワークの調整可能なパラメータ(重みやバイアス)の集合体です。
「なんの役に立つのか」
このアプローチは、先ほどの問題を一挙に解決する可能性を秘めています。
- 次元の呪いの克服: 巨大なQテーブルを保存する必要はなくなり、代わりに比較的小さなサイズのニューラルネットワークのパラメータ \(\theta\) を保存するだけでよくなります。
- 未知への対応(汎化能力): ニューラルネットワークは、学習データからパターンを抽出する能力に長けています。そのため、過去に一度も見たことのない状態(データ)が入力されても、既存の知識とパターンを組み合わせて、「おそらくこの状況のQ値はこうだろう」と妥当な値を予測(汎化)することができます。
これはまさに、研修医が分厚いマニュアル(Qテーブル)の該当ページを探して右往左往するのに対し、経験豊富な専門医が、膨大な臨床経験から培われた「臨床的直観」という名の高度な関数(近似されたQ関数)を用いて、初めて見る症例でも瞬時に治療方針の良し悪しを判断するプロセスと似ています。
DQNの学習メカニズム
では、このニューラルネットワークは、どのようにして「賢いQ関数」へと成長していくのでしょうか。そのプロセスは、「予測と現実のズレ(TD誤差)」を最小化するというQ学習の考え方が基本ですが、DQNは学習を安定させるための巧妙な工夫が凝らされています。
これを「研修医が、少し前の冷静な自分の講義ノートを参考に、日々の経験を復習して知識を更新していくサイクル」と考えると、非常に分かりやすくなります。
- 予測 (Predict) 🧠 「現在の脳 (θ) で、この患者さんの未来を予測してみる」 まず、研修医(AI)は、患者さんの状態 \(S_t\) を診察します。そして、現在の脳(メインネットワーク、パラメータ \(\theta\))を使い、「もし治療Aを行ったら価値は…」「治療Bなら…」と、各行動のQ値を予測します。 \[ \text{現在の予測値} = Q(S_t, a; \theta) \]
- 学習目標の計算 (Calculate Target) 🎯 「少し前の講義ノート (θ⁻) を使って、『よりマシな答え』を作る」 AIは実際に行動 \(A_t\) をとり、報酬 \(R_{t+1}\) と次の状態 \(S_{t+1}\) を観測します。 ここからがDQNの重要な工夫です。学習目標(TDターゲット)を計算する際、常に変化している現在の脳(\(\theta\))ではなく、一定期間更新を止めている、少し前のバージョンの脳(ターゲットネットワーク、パラメータ \(\theta⁻\))を使います。 \[ \text{学習目標 (TDターゲット)} = R_{t+1} + \gamma \max_{a’} Q(S_{t+1}, a’; \boldsymbol{\theta⁻}) \] これは、常に考えが変わる不安定な自分を基準にするのではなく、「昨日の講義でまとめた、冷静で安定したノート(\(\theta⁻\))」を頼りに答え合わせをするようなものです。これにより、学習目標がコロコロ変わってしまうのを防ぎ、学習全体が劇的に安定します。
🤿 Deep Dive!: このmax操作は、時に価値を過大評価してしまう「楽観的すぎる」性質が知られています。これを抑制するため、Double DQNという手法では、「どの行動が最善か」は最新の脳(\(\theta\))で判断し(argmax)、その行動の「価値」は古い脳(\(\theta⁻\))で評価する、というより洗練された方法をとります。 - 損失の計算 (Compute Loss) 💡 「現在の予測と、『よりマシな答え』はどれだけズレていたか?」 次に、AIは「現在の予測値」と、ターゲットネットワークが算出した「学習目標」を比較し、そのズレの大きさ(TD誤差)を損失(Loss)として計算します。 \[ \text{Loss}(\theta) = \left( \text{学習目標} – \text{現在の予測値} \right)^2 \] この損失こそが、現在の脳(\(\theta\))がどれだけ修正されるべきかを示す学習信号となります。
- 更新 (Update) ✍️ 「ズレを元に、現在の脳(θ)だけをほんの少し修正する」 この損失が最小になるように、勾配降下法を使って現在の脳(メインネットワークのパラメータ \(\theta\))だけをほんの少し更新します。 そして、一定の学習サイクル(例えば1万回)が回るたびに、現在の脳の知識をターゲットネットワークに丸ごとコピー(\(\theta⁻ \leftarrow \theta\))します。これにより、「講義ノート」が定期的に最新版にアップデートされ、学習が安定したまま進行していくのです。
【実践編】「膨大な経験」はどこから来て、どう使うのか?
この学習サイクルを「何度も繰り返す」方法は、AIが置かれている状況によって大きく2つに分かれます。
- 標準的なDQN:「オンライン学習」 オリジナルのDQNは、AI自身がゲームの世界などで実際に行動し(例:ε-greedy法で探索)、リアルタイムに経験を収集します。この自分で集めた経験 (\(S_t, A_t, R_{t+1}, S_{t+1}\)) をリプレイバッファに蓄積し、そこからランダムにミニバッチを抽出して学習します。これをオンライン学習と呼びます。
- 医療AI研究の現実:「オフライン強化学習」 一方、医療AIの研究では、AIをいきなり実際の患者さんに使って試行錯誤させることはできません。そのため、電子カルテ(EHR)などに記録された、過去の医師たちが行った膨大な治療記録(ログデータ)を使います。このように、あらかじめ固定されたデータセットだけで学習する手法をオフライン強化学習(バッチ強化学習)と呼びます。 しかし、このアプローチには特有の難しさと注意点があります。 カバレッジの限界 過去のデータに存在しない治療法(例えば、最新の承認薬)の価値は、原理的に学習できません。AIがデータにない行動を推奨するのは非常に危険です。 分布シフト AIが学習するデータ(過去の医師の治療傾向)と、AI自身が最適だと考える治療方針の分布がズレてしまう問題です。これにより、AIが未知の領域で誤った高いQ値を予測し、危険な判断を下すリスクがあります。 このため、医療データで強化学習を行う場合、標準的なDQNをそのまま使うのではなく、BCQ, CQL, IQLといったオフライン強化学習に特化した専用のアルゴリズムを用いることが推奨されます。これらは、AIがデータに存在する安全な範囲内で判断を下すように制約をかけるなどの工夫がされています。
DQNを天才にした2つの工夫
この一連のプロセスを、膨大な経験データを使って何度も何度も繰り返すことで、ニューラルネットワークは徐々にTD誤差の少ない、つまり精度の高いQ値を予測できる「賢い関数」へと成長していくのです。
実は、単純にQ学習とニューラルネットワークを組み合わせただけでは、学習が非常に不安定になり、うまく収束しないことが知られていました。Google DeepMindの研究チームが2015年に科学誌『Nature』で発表した論文 (Mnih et al., 2015) でDQNを提案した際、彼らはこの不安定性を克服する2つの独創的なテクニックを導入しました。これこそが、DQNを成功に導いた「秘伝のタレ」とも言えるものです。
1. 経験再生 (Experience Replay)
- 何であるか: AIが経験した出来事
(状態 S_t, 行動 A_t, 報酬 R_{t+1}, 次の状態 S_{t+1})の組を、すぐには学習に使わず、一度リプレイバッファと呼ばれる巨大なデータセット(記憶の倉庫)に保存しておきます。そして、ネットワークを更新する際には、時系列を無視して、この倉庫からランダムにいくつかの経験をサンプリングしてきて、それらをひとまとめ(ミニバッチ)にして学習させます。 - なぜそれを行うのか: 強化学習のデータは、時系列に沿っているため、隣り合うデータ同士の相関が非常に高いという特徴があります。例えば、ICUで患者を診ていれば、数時間にわたって似たような状態が続くでしょう。このような相関の強いデータを連続で学習させると、ネットワークが直近の経験に過剰に適合してしまい、過去に学んだことを忘れてしまうなど、学習が不安定になります。経験再生は、経験をシャッフルすることでこの時系列的な相関を断ち切り、学習データを統計的に安定させる効果があります。
- なんの役に立つのか: これは、研修医が一日の終わりに、その日経験した様々な症例(朝の敗血症、昼の心不全、夕方の喘息…)を順不同に思い出しながら復習するのに似ています。特定の症例に思考が偏るのを防ぎ、より汎用的で頑健な知識体系を築くことができます。また、一度経験したデータを何度も学習に再利用するため、データ効率が飛躍的に向上します。
2. ターゲットネットワークの固定 (Fixed Target Network)
- 何であるか: 学習の際に、「現在の予測値」を計算するネットワーク(メインネットワーク)と、「学習目標(TDターゲット)」を計算するネットワークを分離する、というアイデアです。TDターゲットを計算するためのネットワークはターゲットネットワークと呼ばれ、そのパラメータは一定期間、古い状態のまま固定されます。そして、数千回学習ステップが進むごとに、メインネットワークの最新のパラメータがターゲットネットワークにコピー(同期)されます。
- なぜそれを行うのか: もしネットワークが一つしかないと、学習のたびにパラメータ \(\theta\) が更新されるため、学習目標であるTDターゲット自身も毎回コロコロと変わってしまいます。これは、常に動き続ける的を追いかけて矢を射るようなもので、学習が発散しやすくなる原因となります。ターゲットネットワークを一時的に固定することで、学習目標が安定し、AIは「静止した的」を狙って着実に学習を進めることができます。
- なんの役に立つのか: これは、学習プロセスにおける「自己参照の罠」を回避する巧妙な仕組みです。学習中のメインネットワークが「自分はこう思う(予測)」と言い、同時に「自分はこうあるべきだ(目標)」と決めてしまうと、どんどん誤った方向に思い込みを強めてしまう危険があります。そこで、「少し前の冷静だった自分(ターゲットネットワーク)」を「あるべき姿(目標)」として参照することで、学習プロセスに安定のアンカーを打ち込むのです。
DQNが拓いた可能性と臨床応用への道
これら2つの工夫を搭載したDQNは、Atariのビデオゲームを学習するタスクにおいて、人間のプロゲーマーに匹敵スコアを叩き出し、世界に衝撃を与えました (Mnih et al., 2015)。これは、これまで人間が暗黙的に行っていた「画面を見て、状況を判断し、コントローラーを操作する」という複雑な意思決定プロセスを、AIがピクセルデータから直接学習できることを証明した歴史的な成果です。
このブレークスルーは、医療AIの分野にも大きな可能性をもたらしました。DQNやその派生技術を用いることで、電子カルテに含まれるような複雑で高次元の時系列データから、直接、最適な治療戦略を学習しようという試みが世界中で行われています。
もちろん、DQNを実際の臨床現場に導入するには、モデルの解釈性の問題や、未知の状況に対する安全性確保など、乗り越えるべき課題はまだ多く残されています。しかし、この「Qテーブルの呪い」からの解放は、強化学習が理論の世界から現実の複雑な問題へと踏み出すための、決定的かつ重要な一歩となったのです。
方策ベースの手法:直接、行動指針を学ぶ
これまで見てきた価値ベースの手法(Q学習など)は、まず行動の「価値」という名の詳細なナビマップを必死に作成し、その完成したマップ上で最も標高が高い地点(Q値が最大となる行動)を探す、というアプローチでした。
しかし、もしナビマップを作らずに、コンパスだけを頼りに、ひたすら山頂(最も良い結果)を目指して登っていく方法があるとしたらどうでしょう?
これこそが、方策ベース(Policy-Based)の手法の核心的な考え方です。価値関数という中間目標を置かずに、方策(行動指針)そのものを直接最適化しようという、全く異なるアプローチです。
方策勾配法:「良い行動」の確率を直接上げる山登り
そのアイデアは、驚くほど直感的で、私たちの経験則とも一致します。
「ある行動をとった結果、すごく良いこと(高い収益)が起きたなら、次からその状況では、その行動をもっと積極的にとるようにしよう。逆に、ひどい結果になったなら、もうその手は使わないようにしよう。」
このシンプルな試行錯誤のルールを、数学的に洗練させたものが方策勾配法(Policy Gradient Method)です。
AIの治療マニュアル(方策)を、ニューラルネットワークで表現します。このネットワークには、調整可能な多数のネジ(パラメータ \(\theta\) (シータ))が付いていると想像してください。このネジ \(\theta\) を回すことで、マニュアルの中身、つまり「ある状態でどの行動をとりやすいか」という確率 \(\pi_\theta(a|s)\) が変化します。
AIは、一連の治療(エピソード)を終えた後、その結果(得られた累積報酬の期待値 \(J(\theta)\))を振り返ります。そして、「この結果をより良くするためには、どのネジをどちらの方向に回せば良いか?」を考えます。この「ネジを回すべき最適な方向と量」を教えてくれるのが、勾配(Gradient)です。
これは、本シリーズのC12で学んだ勾配降下法とは逆に、累積報酬という「山の標高」が最も急になる方向(勾配)を見つけ、その方向にパラメータ \(\theta\) を少しずつ更新していく勾配上昇法です。この山登りを繰り返すことで、AIの方策は徐々に最適なものへと洗練されていきます。
方策勾配法の進化:REINFORCEからPPOへ
この「山登り」を具体的にどう行うかについては、いくつかのアルゴリズムが考案されてきました。その進化の過程を見てみましょう。
REINFORCE:最も純粋な方策勾配法
- 何であるか: REINFORCEは、方策勾配法の最も基本的なアルゴリズムです。Williams (1992) によって提案されたこの手法は、一つのエピソード(例えば、一人の患者の入院から退院まで)が完了した後に、そのエピソード全体で得られた最終的な収益 \(G_t\) を使って方策を更新します。
- なぜそれを行うのか: 「最終的に良い結果(高い \(G_t\))が出たのなら、そのエピソード中に行った行動は全て『良かった』のだろう」と考え、それらの行動が選ばれる確率をまとめて少し上げます。逆に結果が悪ければ、全ての行動の確率を下げます。
- なんの役に立つのか(と、その課題): このアプローチは非常にシンプルで理解しやすいのが利点です。しかし、大きな課題を抱えています。それは学習のばらつき(高い分散)です。
例えば、ある患者さんが無事退院(高い収益)した場合でも、入院中の治療の全てが完璧だったわけではないはずです。中には最適とは言えない判断もあったかもしれません。しかしREINFORCEは、それらも全て「良い行動」として学習してしまいます。逆に、残念な結果に終わった場合でも、その中で行われた最善の救命措置まで「悪い行動」として確率を下げてしまうのです。この「0か100か」の評価が、学習を不安定にする大きな原因でした。
TRPOとPPO:安定した学習を求めて
このREINFORCEの不安定さを克服するために、「方策を一度に更新しすぎないようにする」というアイデアが生まれました。学習の歩幅が大きすぎると、山登りの途中で足を滑らせ、谷底に落ちてしまう(性能が急激に悪化する)危険があるからです。
- TRPO (Trust Region Policy Optimization): Schulmanら (2015) によって提案されたTRPOは、「信頼領域(Trust Region)」という数学的に厳密な”安全地帯”を設定します。そして、「この安全地帯の中で、最も性能が向上する方向」を見つけて方策を更新します。これは非常に堅実で信頼性の高い方法ですが、計算コストが非常に高いという欠点がありました。例えるなら、一歩進むごとに詳細な安全計算を行う、慎重すぎる登山家です。
- PPO (Proximal Policy Optimization): TRPOの堅実さを、よりシンプルな計算で実現しようとしたのが、Schulmanら (2017) が提案したPPOです。PPOは、方策の更新幅が大きくなりすぎないように、「クリッピング」という単純な仕組みでブレーキをかけます。これにより、TRPOに匹敵する性能と安定性を、はるかに低い計算コストで実現しました。その実装の容易さと性能の高さから、PPOは現在の深層強化学習における標準的なアルゴリズムの一つとして広く利用されています。
詳細は、この「[Series C] Clinical AI Coding 100」の第80-89回の「第VIII部:AIが”試行錯誤”で学ぶ、最強の意思決定術」で触れていく予定です!
方策ベース手法の真価:なぜこのアプローチが必要なのか?
では、なぜわざわざこのような直接的なアプローチが必要なのでしょうか。それは、価値ベースの手法が苦手とする特定のシナリオで絶大な威力を発揮するからです。
1. 連続的な行動空間を持つ問題: 投与量の微調整
- 何であるか: 医療現場での判断は、「抗菌薬AかBか」といったON/OFFの選択だけではありません。「昇圧剤の投与量を時速0.05μg/kg/minにするか、0.06μg/kg/minにするか」といった連続的な値の中から最適なものを選ぶ必要があります。
- なぜ価値ベースでは難しいのか: Q学習のような価値ベースの手法は、全ての行動の選択肢に対してQ値を計算し、最大値を探す(\(\max_a Q(s,a)\))必要があります。しかし、投与量のような連続値では、選択肢は無限に存在します。無限個のQ値を計算して比較することは不可能です。
- なんの役に立つのか: 方策勾配法は、この問題をエレガントに解決します。方策(ニューラルネットワーク)に状態(患者データ)を入力すると、直接「最適な投与量の平均値とばらつき(正規分布など)」を出力するように設計できます。そして、実際の投与量が良い結果をもたらしたなら、「あの状況では、もっと投与量の平均値を上げる方向にネットワークのネジ(\(\theta\))を調整しよう」という「勾配」を直接計算できるのです。「投与量を増やす」という方向性を直接学べるため、無限の選択肢に悩む必要がありません。これは、人工呼吸器の最適な送気圧設定や、インスリンの精密な投与量調整など、多くの臨床場面で不可欠な機能です。
2. 確率的な方策が最適な問題: じゃんけんのような状況
- 何であるか: 常に「最善手」が一つに決まるとは限りません。例えば、じゃんけんで相手が次に何を出すか分からない場合、常にグーを出し続ける(決定的方策)のは良い戦略ではありません。グー・チョキ・パーをそれぞれ1/3の確率で出す(確率的方策)のが最適です。
- なぜ価値ベースでは難しいのか: Q学習は、本質的に最もQ値が高い一つの行動を見つけようとするため、このような確率的な振る舞いを学ぶのが苦手な場合があります。
- なんの役に立つのか: 臨床でも似た状況はありえます。例えば、薬剤耐性菌の出現を防ぐために、複数の抗菌薬を意図的にローテーションさせる戦略(確率的方策)が、常に最強の抗菌薬を使い続ける戦略(決定的方策)よりも長期的には優れているかもしれません。方策勾配法は、このような最適な確率分布そのものを自然に学習することができます。AIは、ある状況で「治療Aを70%、治療Bを30%の確率で使うのが、長期的には最も良い結果を生む」という洗練された戦略を発見できる可能性があるのです。
次のステップへ:Actor-Criticという融合
価値ベースの手法と方策ベースの手法は、それぞれに長所と短所がありました。
- 価値ベース: 学習が比較的安定しているが、連続的な行動が苦手。
- 方策ベース: 連続的な行動を扱えるが、学習が不安定になりやすい(分散が大きい)。
ここで、「方策ベースの不安定さを、価値ベースの安定した評価能力で補うことはできないか?」というアイデアが生まれます。REINFORCEの課題であった「エピソード全体の漠然とした評価」の代わりに、TD学習のような「一歩ごとの的確な評価」を使えば、方策の更新(山登り)はもっとスムーズになるはずです。
この発想こそが、次のセクションで学ぶActor-Critic法の根幹をなすものです。それは、方策(Actor)が行動を決定し、価値関数(Critic)がその行動の結果を的確に評価してフィードバックを与える、という役割分担をする、両者の強みを融合させた洗練された手法なのです。
両者の融合:Actor-Critic法
これまで私たちは、AIの学習戦略として2つの異なるアプローチを探求してきました。
- 価値ベースの手法 (Q学習, DQNなど): まず、全ての「状況」と「行動」の価値を評価する、詳細なナビマップ(QテーブルやQ関数)を作成することに全力を注ぎました。AIは、その完成したマップ上で最も標高が高い地点を探すように、次の一手を決定します。
- 方策ベースの手法 (方策勾配法): 一方で、ナビマップの作成という回り道をせず、いきなりコンパス(方策)だけを頼りに、最も良い結果(高い報酬)が得られた方向にひたすら進んでいく、より直接的なアプローチも学びました。
この2つの戦略は、それぞれに強力な武器を持っています。価値ベースの手法は学習が比較的安定しやすい一方、方策ベースの手法は投与量の微調整のような連続的な行動を自然に扱えます。ここで、誰もがこう考えるのではないでしょうか。「この2つの良いとこ取りはできないだろうか?」と。
その問いに対する、強化学習の世界が出した一つの美しい答えがActor-Critic(アクター・クリティック)法です。
「役者」と「評論家」の二人三脚
「何であるか」
Actor-Critic法は、その名の通り、2人の専門家が協力して学習を進める仕組みです。
- Actor (役者): 現在の状況を見て、次にとるべき行動を決定する役割を担います。これは「方策」そのものであり、方策ベースのアプローチ(方策勾配法など)に基づいています。
- Critic (評論家): Actorがとった行動の結果を評価し、「その行動は、思ったより良かったか、悪かったか?」というフィードバックを返す役割を担います。これは「価値」を評価する役割であり、価値ベースのアプローチ(TD学習など)に基づいています。
この「役者(Actor)」と「評論家(Critic)」は、それぞれが独立したニューラルネットワークで実装されることが多く、互いにフィードバックを交換しながら、二人三脚で賢くなっていくのです。
「なぜそれを行うのか」
なぜ、わざわざ2つのネットワークを用意して、このような複雑な仕組みを作るのでしょうか。それは、方策勾配法が抱えていた大きな課題を解決するためです。
方策勾配法では、「良い結果が出たら、その時とった行動の確率を上げる」という単純なルールでした。しかし、この「結果」は、一連の治療(エピソード)が全て終わってからでないと分かりません。ICUでの治療のように、一つのエピソードが何日にもわたる場合、最終的な結果(生存 or 死亡)に、一体どの時点のどの行動がどれだけ貢献したのかを正確に見積もるのは非常に困難です。これを信用分配問題と呼びます。また、報酬のばらつき(分散)が大きくなり、学習が不安定になりやすいという弱点も抱えていました。
Actor-Critic法は、この問題をCritic(評論家)を導入することで見事に解決します。Criticは、TD学習の要領で1ステップごとに「その行動は、直後の結果を見る限り、当初の予測よりどれだけ良かったか(TD誤差)」を計算します。Actorは、エピソード終了という遠い未来の結果を待つ必要がなく、この即時的で質の高いフィードバックを使って、自身の行動指針(方策)を微調整できるのです。
これにより、学習はより安定し、効率的に進むようになります。
「なんの役に立つのか」
このActor-Criticの枠組みは、現代の強化学習アルゴリズムの基礎となっており、特に複雑な医療問題への応用で大きな期待が寄せられています。
- 動的治療計画 (Dynamic Treatment Regimes) への応用: 糖尿病やHIV、精神疾患のような慢性疾患の管理では、患者の状態に応じて長期的に治療法を調整し続ける必要があります。このようなシナリオで、Actor-Criticモデルは非常に有効です。
- Actorは、現在の患者の状態(血糖値、HbA1c、合併症の有無など)に基づき、次のインスリン投与量や薬剤の変更といった具体的な行動を提案します。
- Criticは、その行動がもたらす短期的な変化(血糖値の安定化など)と、長期的な健康状態(合併症リスクの低下など)の予測を統合し、その行動の価値を評価します。
- より洗練されたアルゴリズムへ: Actor-Criticの基本的な考え方をさらに発展させた、A2C (Advantage Actor-Critic) や、Google DeepMindが開発したA3C (Asynchronous Advantage Actor-Critic) といったアルゴリズムは、TD誤差をさらに洗練させた「アドバンテージ(Advantage)」という指標を使うことで、学習の安定性と効率を劇的に向上させました。
価値ベースの「安定した評価能力」と、方策ベースの「柔軟な行動決定能力」。Actor-Critic法は、この2つの強みを融合させることで、強化学習の可能性を大きく広げた、エレガントかつ強力なフレームワークなのです。
究極のジレンマ:探索(Exploration)と活用(Exploitation)
最後に、強化学習が直面する、本質的かつ臨床的にも非常に共感できるジレンマを紹介しましょう。それは、AIが賢くなるために絶対に避けては通れない「探索と活用のトレードオフ(Exploration-Exploitation Trade-off)」です。
これは、長期的な利益を最大化するために、「現在の最善手」と「未来のための情報収集」のどちらを優先すべきか、という根源的な問いです。AIは常に、この二つの行動の間で悩ましい選択を迫られます。
2つの選択肢
- 活用 (Exploitation):
- 「何であるか」: これまでの経験で最も良い結果をもたらした行動(現時点で最適だと信じている治療法)を選択すること。これは、既知の知識を最大限に利用して、現在の報酬を確実に得ようとする行為です。
- 「臨床での例え」: ある感染症に対し、長年の経験とデータから抗菌薬Aが最も効果的だと知っているベテラン医師が、目の前の患者にも迷わず抗菌薬Aを投与する判断。これは「活用」の典型です。
- 探索 (Exploration):
- 「何であるか」: 「もっと良い行動があるかもしれない」と考え、あえてこれまで試したことのない、あるいはあまり試していない未知の行動(新しい治療法や、効果が不確かだがポテンシャルを秘めた治療法)を試してみること。これは、短期的な報酬を犠牲にする可能性をいとわず、未来のより良い判断のための情報を集める行為です。
- 「臨床での例え」: 同じ感染症に対し、「最近発表された新しい抗菌薬Bは、特定の患者群にはAより効果的かもしれない」と考え、標準治療から外れるリスクを承知の上で、患者に十分な説明と同意を得て抗菌薬Bを試してみる判断。これが「探索」です。
臨床現場との驚くべき類似性
このジレンマ、日々の臨床判断そのものではないでしょうか。ガイドラインで推奨される確立された標準治療(活用)に固執すれば、安全で予測可能な結果が得られますが、あなたの目の前の特定の患者にとってはより効果的な新治療法(探索)を見逃すかもしれません。しかし、未知の治療法ばかりを試していては(過度な探索)、エビデンスのない医療行為で患者さんを危険に晒すことになりかねません。
AIも全く同じジレンマを抱えています。最高の戦略(最適方策)を見つけ出すためには、時には現在の最善手ではないかもしれない行動を大胆に試す「探索」が必要です。もしAIが最初の成功体験に固執し、「活用」ばかりを繰り返していたら、それ以上に良い治療法を発見する機会を永遠に失ってしまいます。しかし、「活用」をおろそかにして手元の報酬を取りこぼしていては、累積報酬は最大化できません。
ε-greedy法:最もシンプルな解決策
この絶妙なバランスをどう取るかが、賢いAIを育てる上での鍵となります。そのための戦略は数多く研究されていますが、最もシンプルで有名なものがε-greedy(イプシロン・グリーディ)法です。
そのルールは非常に単純です。
ここで ε(イプシロン)は、0から1の間の小さな値(例えば0.1)で、「どれくらいの頻度で冒険(探索)に出るか」を決める確率です。
- 確率 \(1-\epsilon\) で、AIは貪欲に(Greedy)、現在の経験から学んだQ値が最も高い行動を選択します(活用)。
- 残りの小さな確率 \(\epsilon\) で、AIはQ値を無視して、行動の選択肢の中から完全にランダムに一つを選びます(探索)。
さらに賢いAIは、この\(\epsilon\)の値を学習の進捗に応じて変化させます(アニーリング)。学習の初期は、まだ何も知らないので\(\epsilon\)の値を大きく設定し(例: 1.0)、積極的にランダムな行動をとって世界について学びます(たくさん探索する)。そして、経験を積んで知識が増えるにつれて、\(\epsilon\)の値を徐々に小さくしていき(例: 0.01)、学習した最善の行動を「活用」する割合を増やしていくのです。
このジレンマの存在は、強化学習が単なる静的な最適化問題ではなく、不確実性の中でリアルタイムに情報を収集しながら意思決定を行う、より現実に近い、動的で複雑な問題に取り組んでいることを示しています。このトレードオフをどう管理するかは、Sutton and Barto (2018) の教科書でも中心的なテーマとして扱われており、強化学習の理論と実践における永遠の課題なのです。
まとめ:未来を最適化する数学のコンパス
今回は、AIが「次の一手」を決めるための数学的な思考回路、強化学習の根幹を探る冒険をしてきました。最後に、その美しい理論の構造を振り返ってみましょう。
世界観の定義 (MDP)
まず私たちは、複雑な現実世界をマルコフ決定過程(MDP)という数学の言葉で記述しました。状態、行動、遷移確率、報酬という要素で世界を定義し、マルコフ性という仮定によって問題を扱いやすくしました。これは、AIが行動する舞台のルールブックを定める作業でした。
目標の数値化 (価値関数)
次に、AIの目標である「長期的な利益」を価値関数(状態価値\(V^\pi(s)\)と行動価値\(Q^\pi(s, a)\))として数値化しました。これは、目先の報酬に惑わされず、未来を見通すための羅針盤をAIに与えることに相当します。そして、AIの具体的な行動指針である方策\(\pi\)の良し悪しが、この価値関数によって測られることを見ました。
理想の関係式 (ベルマン方程式)
そして、現在の価値とその一歩先の未来の価値を結びつける、ベルマン方程式という叡智の核心に触れました。この方程式は、価値関数が満たすべき理想的な関係を示しており、AIが目指すべき「宝の地図」そのものです。
現実的な学習法 (TD学習)
最後に、理想の地図を頼りに、実際の経験から学ぶための具体的なアルゴリズム、時間差(TD)学習を学びました。Q学習やSARSAといった手法は、ベルマン方程式を更新式として利用し、「予測」と「現実」のズレ(TD誤差)を修正していくことで、一歩一歩、理想の価値へと近づいていく地道な学習プロセスでした。
強化学習の数学は、単なる数式の遊びではありません。それは、不確実な未来の中で、経験を通じて自律的に学習し、最善の戦略を練り上げるという、高度な知的活動のプロセスを記述するための、強力かつエレガントな言語なのです。
この言語を理解することは、AIの思考の深淵を覗くだけでなく、私たちが日常的に行っている「意思決定」という行為そのものへの洞察をも与えてくれる、知的な冒険と言えるでしょう。
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
参考文献
- Bellman, R. (1957) Dynamic Programming. Princeton: Princeton University Press.
- Esteva, A. et al. (2021) ‘Deep learning-enabled medical computer vision’, npj Digital Medicine, 4(1), p. 5. doi: 10.1038/s41746-020-00376-2.
- Gottesman, O. et al. (2019) ‘Guidelines for reinforcement learning in healthcare’, Nature Medicine, 25(1), pp. 16–18.
- Komorowski, M., Celi, L.A., Badawi, O., Gordon, A.C. and Faisal, A.A. (2018) ‘The Artificial Intelligence Clinician learns optimal treatment strategies for sepsis in intensive care’, Nature Medicine, 24(11), pp. 1716–1720. doi: 10.1038/s41591-018-0213-5.
- Lillicrap, T.P. et al. (2015) ‘Continuous control with deep reinforcement learning’, arXiv preprint arXiv:1509.02971.
- Mnih, V. et al. (2013) ‘Playing Atari with deep reinforcement learning’, arXiv preprint arXiv:1312.5602.
- Mnih, V. et al. (2015) ‘Human-level control through deep reinforcement learning’, Nature, 518(7540), pp. 529–533. doi: 10.1038/nature14236.
- Mnih, V. et al. (2016) ‘Asynchronous methods for deep reinforcement learning’, in Proceedings of the 33rd International Conference on Machine Learning. PMLR, pp. 1928–1937. Available at: http://proceedings.mlr.press/v48/mniha16.html.
- Raghu, A., Komorowski, M., Celi, L.A., Szolovits, P. and Ghassemi, M. (2017) ‘Continuous state-space models for optimal sepsis treatment: a deep reinforcement learning approach’, arXiv preprint arXiv:1705.08422. Available at: https://arxiv.org/abs/1705.08422.
- Rummery, G.A. and Niranjan, M. (1994) ‘On-line Q-learning using connectionist systems’, Technical Report CUED/F-INFENG/TR 166. Cambridge: Cambridge University Engineering Department.
- Sutton, R.S. and Barto, A.G. (2018) Reinforcement Learning: An Introduction. 2nd edn. Cambridge, MA: MIT Press.
- Tesauro, G. (1995) ‘Temporal difference learning and TD-Gammon’, Communications of the ACM, 38(3), pp. 58–68. doi: 10.1145/203330.203343.
- Watkins, C.J.C.H. (1989) Learning from Delayed Rewards. PhD thesis. Cambridge: University of Cambridge.
- Williams, R.J. (1992) ‘Simple statistical gradient-following algorithms for connectionist reinforcement learning’, Machine Learning, 8(3–4), pp. 229–256. doi: 10.1007/BF00992696.
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






