AIの賢い推論は、統計学の「尤度(ゆうど)」と「推定」に基づいています。これは医師が症状から病気を探る思考プロセスとそっくりです。データから最も「らしい」原因を探す2つの代表的なアプローチを見ていきましょう。
「結果」から「原因」を推測する考え方。確率とは視点が逆です。「38℃の発熱」という結果を見て、「インフルエンザらしいか?」と考える、医師の鑑別診断の思考プロセスそのものです。AIの推論の土台となります。
手元のデータだけを頼りに、尤度が最大になる一点(最も「らしい」原因)を探し出す手法。客観的で分かりやすいですが、データが少ないと不安定になることがあります。大規模な臨床試験などで強力です。
既存の医学知識(事前情報)を、新しいデータ(尤度)で更新し、最終的な結論(事後確率)を得ます。希少疾患などデータが少ない場面でも頑健で、結論の不確実性も評価できるのが強みです。
AIが胸部X線写真から肺炎の影を指摘したり、電子カルテのデータから患者さんの1年後の再発リスクを予測したりするとき、その頭脳の中では一体どのような思考が巡らされているのでしょうか。AIが出す答えは時として驚くほど正確ですが、その判断根拠がブラックボックスに見えて、「本当に信じていいの?」と不安に感じることもあるかもしれません。
実は、AIの思考プロセスは、私たちが臨床現場で行っている診断推論と非常に似ています。手元にある情報(データ)を一つひとつ吟味し、数ある可能性の中から最も医学的に「もっともらしい」結論を導き出す、というあのプロセスです。この論理的な思考の土台をがっちりと支えているのが、尤度(ゆうど)と推定という、統計学のパワフルな概念なのです。
「尤度?推定?なんだか数式ばかりで難しそう…」と感じた方も、どうかご安心ください。一見とっつきにくい言葉ですが、その本質は、私たちが日々の診療で無意識に行っている鑑別診断のプロセスを、数学の言葉で表現したものに他なりません。この章では、AIがどのようにしてデータから「確信」を得るのか、その思考の源泉である尤度と推定のセオリーを、臨床の具体例を交えながら一緒に探っていきます。読み終える頃には、AIの判断の裏側にあるロジックが、きっと腑に落ちるはずです。
尤度(ゆうど)とは?~臨床的「らしさ」の指標~
さて、AIの思考法を理解する上で、避けては通れない最重要コンセプトが「尤度(ゆうど)」です。この言葉、初めて聞く方もいらっしゃるかもしれませんが、実は私たちは毎日の臨床で、この尤度という考え方を無意識に使っています。これは「確率」という言葉とよく混同されがちですが、両者は似て非なるもので、視点が180度異なります。この違いを理解することが、AIの思考を理解する第一歩です。
「確率」と「尤度」の決定的な違い
この二つの概念の違いを、インフルエンザの診断という身近なシナリオで考えてみましょう。これが分かると、一気に視界が開けるはずです。
確率の視点:「原因」から「結果」を予測する(教科書的な知識)
まず「確率」です。これは、ある原因がはっきりしている時に、そこからどんな結果が生まれそうかを予測する考え方です。例えば、内科学の教科書に「インフルエンザに罹患した患者が38度以上の発熱を呈する確率は80%である」と書かれていたとします。これは、原因(インフルエンザという診断)が確定しているという前提のもとで、結果(38度以上の発熱という症状)がどれくらいの割合で起こるかを示しています。まさに、知識として知っている原因から、起こりうる結果を予測する視点ですね。
尤度の視点:「結果」から「原因」を推測する(ベッドサイドの推論)
一方、「尤度」はその逆です。こちらは、目の前の事実、つまり観察された結果から、その背後にある原因を推測する考え方です。救急外来に「38度の発熱」を呈する患者さんが歩いて来たとしましょう。この結果(38度の発熱というデータ)を目の当たりにして、私たちは頭の中で鑑別診断リストを思い浮かべます。「この高熱は、インフルエンザが原因“らしい”か? それとも普通の風邪が原因“らしい”か? はたまた他の疾患か?」と。この時、「38度という高熱が出ているのだから、微熱で済むことが多い普通の風邪よりは、インフルエンザの“らしさ”の方が高いな」と考えると思います。この、観察されたデータを最も上手く説明できる「もっともらしさ」の度合いこそが、尤度なのです。
要するに、確率と尤度はコインの裏表のような関係にあります。
\[ \text{確率} \quad P(D \mid \theta) : \text{ある原因(モデル \(\theta\))を仮定したときに、この結果(データ \(D\))が起こる確率} \]
\[ \text{尤度} \quad L(\theta \mid D) : \text{ある結果(データ \(D\))が得られたときに、どの原因(モデル \(\theta\))が最も「らしい」かという度合い} \]
少し数式を解説しますね。ここでの \(D\) はData(観察されたデータ)、\(\theta\)(シータ)はモデルのパラメータ(考えられる原因)を表します。縦棒「\(\mid\)」は「という条件のもとで」という意味です。 数式の形自体は \( P(D \mid \theta) \) で同じですが、その意味合いが全く異なります。
- 確率を考えるとき、私たちは原因である \(\theta\) を固定し(例:インフルエンザと確定)、これからどんなデータ \(D\) が出てくるか(例:熱は何度になるか?)を考えます。このとき変数は \(D\) です。
- 尤度を考えるとき、私たちは観察データ \(D\) を固定し(例:38度の発熱を確認)、その原因となった \(\theta\) は何だったのか(例:インフルエンザか、風邪か?)を考えます。このとき変数は \(\theta\) なのです。
この視点の転換が、非常に重要です。
この尤度という考え方、まさに私たちが日々ベッドサイドで行っている鑑別診断の思考プロセスそのものだと思いませんか? 目の前に38.5℃の発熱と咳を訴える患者さんがいるとき、私たちの頭の中では瞬時に「ウイルス性上気道炎だろうか? いや、細菌性肺炎の可能性は? もしかしたらインフルエンザかもしれない…」といった鑑別リストが浮かびますよね。そして、聴診所見や迅速検査の結果といった新しい情報(データ)が得られるたびに、「この所見があるなら、肺炎の“らしさ”がぐっと上がるな」とか、「迅速検査が陽性なら、インフルエンザが原因である“もっともらしさ”が極めて高い」というように、頭の中のリストの順位を更新していきます。
AIが行っているのも、本質的にはこれと同じことです。AIは、この「もっともらしさ」を尤度関数という、いわば「可能性の山」を描くグラフとして表現します。この山の横軸には、考えられるすべての原因(例えば、インフルエンザ、肺炎、ただの風邪…といった診断名の候補や、「新薬Aの奏効率は10%か、20%か…80%か」といったパラメータの候補)がずらりと並んでいます。そして縦軸が、それぞれの原因を仮定したときの「もっともらしさ」、つまり尤度の高さを示しているのです。
そしてAIの仕事は、この「可能性の山」を眺めて、その最も高い頂上がどこにあるかを探し出すことです。この頂点こそが、「手元にある全ての臨床データを最も矛盾なく、うまく説明できる原因はこれだ」というAIの結論になります。診断名であったり、治療効果を予測する最も確からしいパラメータの値であったりします。私たち臨床医が経験と知識を総動員して最も妥当な診断を探し当てるように、AIは尤度関数という山を数学的な手法で一気に駆け上がり、その頂点を見つけ出すことで、驚くほど的確な答えを導き出しているのです。この「山の頂上を探す」という考え方が、次のテーマである「最尤推定法」へと繋がっていきます。
最尤推定法(さいゆうすいていほう)~最も「らしい」結論を選ぶ~
さて、目の前の臨床データに対する様々な原因の「らしさ」、つまり尤度を測れるようになりました。次の一手は何でしょうか? もしあなたが鑑別診断リストを片手に悩んでいるとしたら、当然、その中で最も「らしさ」の高い、つまり尤度が最大となる診断を第一に考えますよね。この、尤度が最大になる一点を探し出すという極めて直感的なアプローチこそが、最尤推定法(Maximum Likelihood Estimation, MLE)です。
これは、私たちが日常的に行っている臨床推論そのものです。患者さんの訴え、身体所見、血液検査の結果、画像所見といった全ての観察データ(Data)を総合的に評価し、「これら全ての情報を最も矛盾なく、うまく説明できる診断(原因)はこれに違いない」と一つの結論に至るプロセス。これこそが最尤推定法の心です。AIは、このプロセスを数学的に、そして極めて厳密に行っているに過ぎません。
この考え方を、先ほどの尤度関数を使って視覚的に捉えてみましょう。
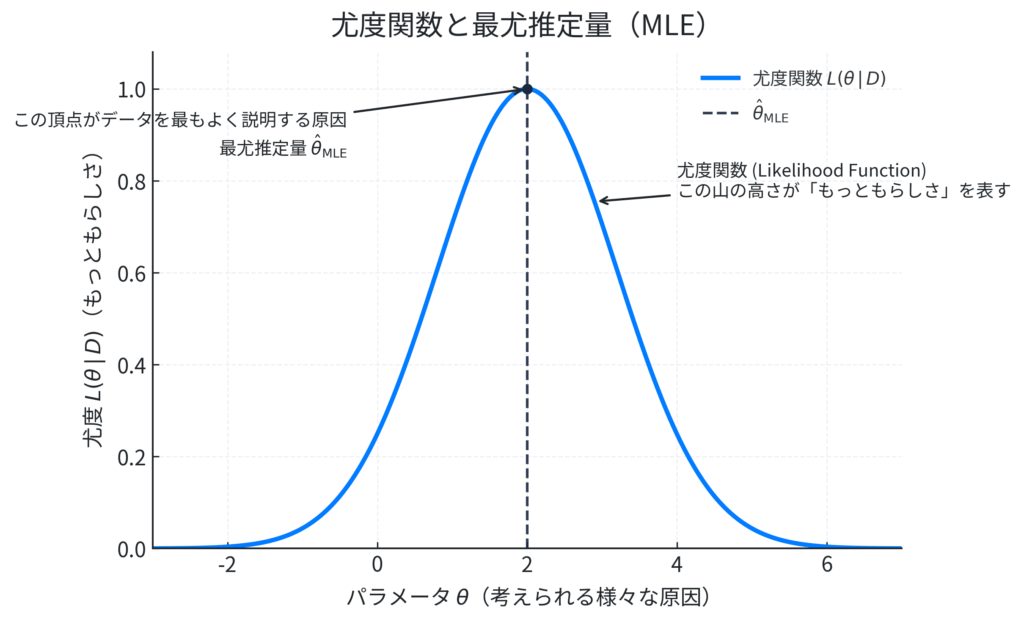
図の解説:
この図は、いわば「もっともらしさの山」です。横軸(\(\theta\))には、考えられるすべての原因が並んでいます。例えば、「新薬Aの真の奏効率」が0%から100%までのどの値か、といった候補たちです。縦軸(\(L(\theta \mid D)\))は、それぞれの原因を仮定したときの「もっともらしさ」、つまり尤度を表します。そして、この山の頂上、つまり尤度が最も高くなる地点。そのときの横軸の値(この例では\(\hat{\theta}_{\text{MLE}}\))こそが、「手元のデータから判断するに、最も確からしい原因はこの値だろう」という結論、すなわち最尤推定量なのです。
最尤推定を数式で見てみる
この「山の頂上を探す」という操作を、数学の言葉で表現すると以下のようになります。
\[ \hat{\theta}_{\text{MLE}} = \underset{\theta}{\mathrm{argmax}} \, L(\theta \mid D) \]
なんだか難しそうに見えますが、分解すれば簡単です。
- \(\hat{\theta}_{\text{MLE}}\) : 「ハット」は推定された値であることを示す記号です。MLEはMaximum Likelihood Estimateの略。つまり、「最尤推定によって求められたパラメータ\(\theta\)」という意味です。
- \(\underset{\theta}{\mathrm{argmax}}\) : これは「argmax(アーグマックス)」と読み、「…を最大にする引数(この場合は\(\theta\))を探しなさい」という命令です。山の頂上の「高さ(最大値)」ではなく、その頂上を与えてくれる「横軸の位置(パラメータ\(\theta\))」を求める操作です。
- \(L(\theta \mid D)\) : 先ほどから見ている通り、「観察データDが与えられた条件のもとでの、パラメータ\(\theta\)の尤度」です。
つまりこの式全体で、「手元のデータDを前提としたときに、尤度関数 \(L(\theta \mid D)\) が最大値をとるようなパラメータ\(\theta\)の値を見つけ出し、それを\(\hat{\theta}_{\text{MLE}}\)と名付けなさい」という意味になります。まさに、山の頂上の位置を探す操作を数式で表現したものですね。
ちなみに、実際の計算では、尤度そのものではなく、尤度を対数変換した対数尤度(Log-Likelihood)を最大化することが一般的です。なぜなら、多くの確率の掛け算は非常に小さな値になり、コンピュータでは扱いにくくなる(アンダーフローという問題が起きます)のですが、対数をとることで掛け算を足し算に変換でき、計算がずっと簡単かつ安定するからです。関数の頂点の位置は、対数をとっても変わらないので、これは非常に賢い工夫と言えます。
この最尤推定法は、その直感的なわかりやすさとパワフルさから、統計学や機械学習の世界で最も基本的かつ重要なパラメータ推定手法の一つとして、広く使われています。疫学研究でオッズ比やリスク比を求めたり、AIモデルが学習データから最適な重みを見つけ出したりする場面の裏では、この最尤推定が活躍しているのです (Myung, 2003)。
ベイズ推定~既存の医学知識で推論を更新する思考法~
最尤推定法が「目の前のデータという客観的な証拠」だけを頼りに、最も合理的な結論を導き出すアプローチだったのに対し、これからお話しするベイズ推定は、もう一歩踏み込んだ、より経験豊かな臨床医の思考に近いアプローチです。
熟練した臨床医は、目の前の患者さんの所見だけでなく、これまでの経験則や、教科書・論文で得た医学的知識(これを「事前情報」と呼びます)といった、いわば「頭の中のデータベース」を無意識に参照しています。そして、新しい検査結果という証拠に触れるたびに、頭の中の鑑別リストの順位を柔軟に更新していきますよね。この、「既存の知識」を「新しいデータ」で更新していくという、極めて知的でダイナミックな思考プロセスを、数学の言葉で見事に体系化したのがベイズ推定なのです。
ベイズ推定の三つの要素:「事前」「尤度」「事後」
ベイズ推定の核心は、私たちの知識や信念が、新しいデータ(証拠)によってどのように更新(アップデート)されるかをモデル化する点にあります。このプロセスを理解するために、3つの重要なキーワードが登場します。これらは、私たちの診断推論のステップそのものです。
1. 事前分布 (Prior Distribution): 「最初のあたり」をつける
これは、目の前の患者さんのデータを見る前に、私たちが持っている知識や信念のことです。言ってみれば、その疾患に対する「初期の疑いの強さ」や「pre-test probability(検査前確率)」に相当します。例えば、「この地域ではAという感染症の有病率は0.1%と非常に低い」という疫学的な知識や、「この患者さんの年齢や背景を考えると、Bという疾患の可能性は高いだろう」といった経験則がこれにあたります。ベイズ推定では、この「あたり」を確率分布という形で表現します。
2. 尤度 (Likelihood): 「新しい証拠」を吟味する
これは先ほどの最尤推定で学んだものと全く同じ、非常に重要なコンセプトです。ベイズ推定における「尤度」とは、私たちの推論を更新するための「新しい客観的な証拠」が持つ重みを評価するプロセスそのものです。目の前の患者さんから得られた新しいデータ(例えば、ある検査で陽性反応が出た、特定の画像所見が見つかったなど)が、私たちが考えているそれぞれの仮説を前提としたときに、どれくらい「ありえそうな」結果なのか、その「もっともらしさ」を測る物差しと言えます。
もっと本質的な部分に焦点を当てるために、話を単純化してみましょう。臨床現場で最も基本的な問い、「ある疾患にかかっているか、いないか」という状況で考えてみます。
ある患者さんについて「特定の疾患D」を疑い、その診断のために特異度が99%と非常に高い「検査X」を実施した、という場面を想像してください。そして、検査結果は「陽性」でした。
この「検査Xが陽性だった」という新しいデータ (\(D\)) を使って、尤度を吟味していきます。この時点で私たちの頭の中には、対立する2つの仮説 (\(\theta\)) があります。
- 仮説1 (\(\theta_1\)): 患者は疾患Dにかかっている
- 仮説2 (\(\theta_2\)): 患者は疾患Dにかかっていない
この「陽性」という一つの事実を、それぞれの仮説のレンズを通して眺めてみましょう。
- 仮説1(疾患あり)のもとでの尤度: もし患者が本当に疾患Dにかかっているとしたら、この「陽性」という結果はどのくらい「もっともらしい」でしょうか? これは検査の感度 (sensitivity) に相当します。仮にこの検査の感度が90%だとすれば、疾患Dの患者さんが陽性となるのはごく自然なことであり、このデータが観察されるもっともらしさ(尤度)は0.9となります。
- 仮説2(疾患なし)のもとでの尤度: では、もし患者が疾患Dにかかっていないとしたら、この「陽性」という結果はどのくらい「もっともらしい」でしょうか? これは検査の偽陽性率 (false positive rate) にあたります。特異度が99%ということは、疾患にかかっていない人が誤って陽性と判定される確率は \(100\% – 99\% = 1\%\) です。つまり、「疾患なし」という仮説のもとでこのデータが観察されるもっともらしさ(尤度)は、わずか0.01ということになります。
いかがでしょうか。同じ「陽性」という一つの事実でも、「疾患がある」という仮説に立てばきわめて順当な結果(もっともらしさ 0.9)に見えるのに対し、「疾患がない」という仮説に立つと、それは極めて稀な、考えにくい結果(もっともらしさ 0.01)に見えるのです。
この「データが、それぞれの仮説をどれだけ強く支持しているか」という度合いこそが、尤度です。この場合、「陽性」というデータは、「疾患なし」という仮説よりも「疾患あり」という仮説の方を \(0.9 / 0.01 = 90\) 倍も強く支持していることになります。特異度の高い検査で陽性という結果が出た場合、尤度は「疾患あり」の仮説に大きく傾きます。なぜなら、その疾患以外の状態では「めったに起こらないはずの結果」が実際に起こったからです。それは、疾患の存在を強く示唆する、非常に重みのある証拠となるわけです。
このように、尤度はそれぞれの仮説に対して、新しい証拠がどれだけフィットするかを点数化する役割を担っています。そして、この尤度という「新しい証拠の重み」を、元々持っていた知識である「事前確率」に掛け合わせることで、私たちの診断推論はより確かなものへと更新されていくのです。
3. 事後分布 (Posterior Distribution): 「最終的な結論」を更新する
これがベイズ推定のゴールです。事前情報(最初のあたり)と、新しい証拠であるデータ(尤度)を数学的に組み合わせた結果、更新された最終的な結論です。これが「post-test probability(検査後確率)」に相当します。例えば、事前情報では「可能性は極めて低いだろう」と思っていた稀な疾患も、その疾患に特異的な所見(高い尤度を持つデータ)が得られれば、「この患者さんに限っては、強く疑うべきだ」と、私たちの確信度は大きく更新されるわけです。
この「知識の更新プロセス」は、18世紀にトーマス・ベイズによって定式化された、有名なベイズの定理によって表されます。
\[ P(\theta \mid D) = \dfrac{P(D \mid \theta) P(\theta)}{P(D)} \]
この式がベイズ推定の心臓部です。一つずつ見ていきましょう。
- \( P(\theta \mid D) \) (事後確率): これが求めたい答えです。「データDという新しい証拠を見た後での、原因\(\theta\)の確からしさ」を表します。
- \( P(D \mid \theta) \) (尤度): 「もし原因が\(\theta\)だと仮定した場合に、データDが観察されるもっともらしさ」です。
- \( P(\theta) \) (事前確率): 「データDを見る前の段階で私たちが持っていた、原因\(\theta\)に関する知識や信念」です。
- \( P(D) \) (分母): これは「周辺尤度」や「エビデンス」と呼ばれ、事後確率の合計がちゃんと1(100%)になるように調整するための、いわば「規格化定数」です。今は「そういう調整役がいるんだな」くらいに思っておけば大丈夫です。
本当に重要なのは、分母を無視した以下の比例関係です。
\[ \text{事後確率} \propto \text{尤度} \times \text{事前確率} \]
この式が語っているのは、「新しい証拠(尤度)によって更新された私たちの最終的な信念(事後確率)は、元々持っていた信念(事前確率)と、新しい証拠のもっともらしさ(尤度)の掛け算で決まる」ということです。私たちの頭の中で行われている、経験と証拠の統合プロセスを、見事に数式で表現していると思いませんか。
なぜ医療でベイズ推定が重要なのか?
では、なぜこのベイズ推定が、現代の医療やAIにとってこれほど重要なのでしょうか。その理由は、医療現場が持つ特有の課題と、ベイズ推定の強みが完璧にマッチするからです。
例えば、非常に稀な疾患の診断を考えてみましょう。ある疾患の有病率(事前確率)が1万人に1人だとします。ここに、感度99%、特異度99%という、かなり高性能な検査があるとします。ある患者さんがこの検査を受けて陽性(高い尤度を持つデータ)になったとき、その患者さんが本当にその疾患である確率はどのくらいでしょうか?
直感的には「99%くらいだろう」と思いがちですが、ベイズの定理で計算すると、実は約9%にしかなりません。これは、そもそも疾患母集団が極めて小さい(事前確率が極端に低い)ため、検査の偽陽性が、真の陽性者の数を上回ってしまうからです。最尤推定のようにデータ(検査陽性)だけを見ると判断を誤る可能性がありますが、ベイズ推定は疫学的な知識(事前確率)を組み込むことで、私たちをこうした「ベースレートの誤謬」から守ってくれます。これは臨床医が日常的に行っている思考プロセスであり、ベイズ統計学の重要性を示す好例です (Ashby, 2006)。
さらに、ベイズ推定はデータが少ない場合でも頑健な推論が可能なため、患者数が少ない希少疾患の臨床試験や、個々の患者に最適化された治療法を探る個別化医療の分野で、その力を発揮します。既存の生物学的な知見や、類似薬のデータを事前情報として組み込むことで、限られたデータからでもより信頼性の高い結論を導き出すことができるのです。
このように、私たちの臨床知を自然な形で数理モデルに統合できるベイズ推定は、データと知識の両輪で駆動する未来の医療AIにとって、無くてはならない思考法だと言えるでしょう。
最尤推定 vs ベイズ推定、どちらのアプローチを選ぶべきか?
さて、データから「もっともらしさ」を追求する二つの強力なアプローチ、最尤推定(MLE)とベイズ推定を見てきました。片方は目の前のデータに徹する客観主義者、もう片方は過去の知見も重んじる経験豊富な専門家、といったところでしょうか。では、医療AIを開発したり、臨床研究の結果を解釈したりする上で、私たちはどちらの思考法を用いるべきなのでしょうか?
これは「どちらが優れているか」という単純な二元論ではありません。むしろ、「どのような問いに、どのようなデータで答えようとしているのか?」によって使い分けるべき、いわば思想の異なる二つの道具箱のようなものです。それぞれの長所と短所を深く理解し、状況に応じて最適な道具を選ぶことが、質の高い医学研究やAI開発には不可欠です。
ここで、両者の違いをより解像度高く理解するために、いくつかの重要な側面から比較してみましょう。
思想とアプローチの違い:客観的な事実 vs 更新される信念
最尤推定とベイズ推定、この二つのアプローチの根底には、統計学における二大潮流ともいえる「頻度論」と「ベイズ主義」の哲学的な対立があります。どちらが良いという話ではなく、世界をどう見るか、という思想の違いが、アプローチの違いに直結しているのです。
- 最尤推定法 (MLE):「データは、それ自体が雄弁に真実を語る」
最尤推定法の背後にあるのは、頻度論 (Frequentism) という思想です。これは、私たちが知りたい真の値(例えば、新薬の真の奏効率)は、天動説の時代の星々のように、どこかに一つだけ固定で存在している、という考え方に基づきます。私たちの仕事は、手元にあるデータという望遠鏡だけを頼りに、その真の値がどこにあるかを当てることです。研究者の個人的な経験や「たぶんこの辺りだろう」といった主観(事前知識)が入り込むことを徹底的に排除し、あくまでデータという客観的な証拠のみから、最も「ありえそうな」一点を指し示す。このストイックなまでの客観性こそが、頻度論の真骨頂です。
大規模なランダム化比較試験(RCT)や数万人規模の疫学研究を想像してみてください。これだけ大量のデータがあれば、事前知識に頼らずとも、データそのものが真実を浮かび上がらせてくれます。このような場面で、「このデータセットが示す限り、最も可能性の高いリスク比は2.3です」と明快な結論を示す上で、最尤推定法は絶大な信頼性と説得力を発揮します。 - ベイズ推定:「私たちの知識は、新しい証拠によって常に更新されていく」
一方、ベイズ推定 (Bayesian Estimation) は、全く異なる世界観に立脚します。こちらでは、真の値は固定された一点ではなく、私たちの知識や信念の度合いを反映した確率分布として捉えられます。つまり、「真の奏効率は70%だ」と断定するのではなく、「おそらく60%から80%の間にありそうで、70%あたりが一番可能性が高いだろう」というように、不確実性を含んだ形で考えます。
このアプローチは、経験豊富な臨床医が診断を下すプロセスと驚くほど似ています。私たちは、患者さんを診る前に、教科書的な知識や過去の診療経験から、「この年代のこの症状なら、あの疾患の可能性が高いだろう」という初期仮説(事前情報)を持っています。そこに、診察所見や検査結果という新しいデータ(尤度)が加わることで、「やはり思った通りだ」とか、「いや、これは意外な所見だから、当初考えていた診断の可能性は下げて、別の疾患を考えよう」というように、頭の中の確信度(事後確率)を柔軟に更新していきますよね。
ベイズ推定は、まさにこの「知識の動的な更新プロセス」を数学的に体系化したものです。過去の研究データや生物学的な妥当性といった既存の医学的知見を「事前分布」という形で数式に組み込み、限られたデータからでも、より現実に即した、頑健な結論を導き出すことを得意とします。
得られる「答え」の形:一点の値 vs 幅を持つ分布
これは、最尤推定とベイズ推定を分ける最も決定的で、かつ実用上も非常に重要な違いです。最終的に得られる「答え」の形が全く異なるため、それが臨床的な意思決定に与える影響も大きく変わってきます。
- 最尤推定法 (MLE) が提供する答え:シャープな「点推定値」
最尤推定が最終的に導き出す答えは、パラメータの「点推定値 (Point Estimate)」です。これは、尤度関数という「もっともらしさの山」の、まさに頂点そのものです。例えば、「この治療法による腫瘍縮小効果のオッズ比は2.5です」というように、最も尤もらしいとされる単一の値を、非常にシャープに提示します。
もちろん、その推定値がどの程度確かなのか、その不確実性を示すために「95%信頼区間 (Confidence Interval)」が併記されるのが一般的です。しかし、この信頼区間の解釈は少し注意が必要です。頻度論の考え方では、「もし同じ実験を100回繰り返したとしたら、そのうち95回で得られる信頼区間が、どこかにあるはずの『真のオッズ比』を含むだろう」という意味であり、「この区間内に真の値が95%の確率で存在する」と直接的に言えるわけではないのです。シンプルで分かりやすい反面、私たちが直感的に知りたい「この値がどれくらいの確信度で言えるのか」という情報が、少し失われてしまう側面もあります。 - ベイズ推定が提供する答え:柔軟な「事後分布」
一方で、ベイズ推定の答えは、単一の値ではありません。パラメータがとりうる全ての値の可能性を、一つの連続的な「事後分布 (Posterior Distribution)」という確率分布そのものとして提供します。
これは、いわば「可能性の地形図」のようなものです。最も高い山の頂上(事後分布の最頻値)が、最も可能性の高い値(例えばオッズ比2.5)を示しますが、それだけでなく、その周りに広がる丘や裾野の形から、「どの範囲の値が、どの程度の確率でありえそうか」という情報を全て含んでいます。
この分布から、私たちは「95%信用区間 (Credible Interval)」を計算できます。これは、「オッズ比の真の値が、95%の確率で2.0から3.0の間に存在する」という、非常に直感的で分かりやすい解釈が可能です。この「不確実性の可視化」は、臨床現場での意思決定において極めて重要です。例えば、ある治療法の効果を示すオッズ比の事後分布が非常に広く、効果がないことを示す「1」をまたいでいる場合、「平均的には効果がありそうに見えても、実際には効果がない、あるいはごく僅かである可能性も十分に考えられる」と判断できます。こうした繊細なリスクとベネフィットの評価は、特に患者さん一人ひとりへの治療方針を考える個別化医療において、非常に重要な示唆を与えてくれるのです。
医療現場での具体的な使い分け
これまでの議論で、最尤推定とベイズ推定の思想や特性の違いが見えてきました。では、実際の臨床研究や医療AIの開発現場では、この二つの道具をどのように使い分けているのでしょうか。これは、どちらが絶対的に優れているという話ではなく、解決したい課題の性質と、手元にあるデータの量によって最適なアプローチが決まります。
例えば、大規模コホート研究で数万人のデータを解析し、高血圧が心筋梗塞に与える影響(ハザード比)を推定する場面を考えてみましょう。これだけ潤沢なデータがあれば、事前知識に頼らずとも、データ自身が雄弁に真実を語ってくれます。このような場面では、計算が高速で、結果の解釈が世界中の研究者や規制当局の間で標準化されている最尤推定法が、今なお第一選択となることが多いでしょう。客観性と再現性が何よりも重視されるからです。
しかし、場面が変わり、希少疾患に対する新薬の臨床試験ではどうでしょうか。被験者を集めること自体が非常に困難で、数十人程度のデータしか得られないことも少なくありません。このようなデータが限られた状況で最尤推定を行うと、偶然得られた一人か二人の極端な結果に推定値が大きく引っ張られてしまい、非常に不安定になる危険性があります。ここでベイズ推定がその真価を発揮します。過去の類似薬の有効性に関するデータや、その疾患の生物学的なメカニズムに関する専門家の知見を「事前分布」としてモデルに組み込むことで、限られたデータからでも、より安定した、信頼性の高い治療効果の推定が可能になります。事実、米国食品医薬品局(FDA)は、特に医療機器や希少疾患の臨床試験において、このような外部の証拠(Real-World Evidenceなど)を事前情報として活用するベイズ的アプローチを積極的に推奨するガイダンスを発表しており、その有用性は広く認められています (FDA, 2010)。
Deep Dive! なぜ規制当局はベイズ統計学の活用を推し進めるのか?
「米国食品医薬品局(FDA)が、ベイズ統計学の利用を推奨している」—この事実は、単に新しい統計手法の導入を意味するだけではありません。これは、医療製品開発の哲学そのものが、21世紀のデータ環境に合わせて歴史的な転換点を迎えていることを示す、極めて重要なサインです。特に、従来の臨床試験が設計困難だった希少疾患や、技術革新のスピードが速い医療機器の分野で、この動きは大きな希望となっています。一体なぜFDAを始めとする規制当局は、伝統的な統計学の牙城ともいえる臨床試験の世界に、ベイズという新しい風を吹き込もうとしているのでしょうか。
その背景には、20世紀を通じて臨床試験のゴールドスタンダードとして君臨してきたランダム化比較試験(RCT)が、その厳格さゆえに抱えるジレンマがあります。数千人規模の患者を集め、プラセボ群と比較して有効性を証明する—この頻度論に基づくアプローチは、多くの医薬品開発で絶大な成功を収めてきました。しかし、この手法は「データが潤沢にある」という大前提に立脚しています。
では、患者数が極端に少ない希少疾患ではどうでしょう?あるいは、迅速な改良が繰り返されるペースメーカーのような医療機器で、承認を得るたびに大規模なRCTを繰り返すのは現実的でしょうか?また、倫理的な観点から、有効性が期待される治療があるにもかかわらず、多くの患者をプラセボ群に割り当てることは常に許容されるのでしょうか?
こうした課題意識の高まりを受け、FDAはより柔軟で効率的なアプローチを模索し始めました。その答えの一つが、ベイズ的アプローチの活用です。2010年にFDAが発表したガイダンス「Guidance for the Use of Bayesian Statistics in Medical Device Clinical Trials」は、その象徴的な一歩でした(FDA, 2010)。このガイダンスは、主に医療機器を対象としていましたが、その核心にある「利用可能な全ての情報を統合して、より合理的な意思決定を行うべきである」というメッセージは、医薬品開発にも応用可能な概念として大きな注目を集めました。
ここでいう「利用可能な全ての情報」の代表格が、近年その重要性を増しているリアルワールドエビデンス(Real-World Evidence, RWE)です。これは、電子カルテ、レセプト(診療報酬明細書)データ、疾患レジストリなど、日常診療の中で得られる膨大なデータから創出されるエビデンスを指します。ベイズ統計学は、こうした過去の臨床データや類似製品のデータ(RWE)、あるいは生物学的な作用機序に関する専門家の知見といった「事前情報」を、新しく行う臨床試験のデータと数学的に統合することを可能にします。この考え方は、FDAが2018年に発表した「Framework for FDA’s Real-World Evidence Program」とも完全に整合するものです(FDA, 2018)。
これは、臨床試験をゼロから始めるのではなく、人類がこれまでに築き上げてきた医学知識の肩の上に立って、新しい知見を積み重ねていくという思想です。例えば、ある希少がんに対する新薬の試験で、過去の類似薬のデータから「このタイプの薬剤であれば、少なくとも20%程度の奏効率は期待できるだろう」という事前情報があれば、それを事前分布として組み込むことができます。これにより、従来のアプローチよりも少ない被験者数で、統計的に有意な結論を導き出せる可能性が生まれるのです。これは試験期間の短縮と開発コストの削減に直結し、何よりも治療法を待ち望む患者へ一日でも早く新しい選択肢を届けることにつながります。
さらにFDAは、アダプティブデザイン(Adaptive Design)と呼ばれる、試験の進行状況に応じて計画を柔軟に変更していく臨床試験デザインを推奨しており、このアダプティブデザインとベイズ統計学は非常に親和性が高いことが知られています。著名なレビュー論文でもその有用性が詳説されているように(Pallmann et al., 2018)、試験の中間解析の結果、新薬の有効性が予想以上に高ければ、倫理的観点から試験を早期に終了させたり、より多くの患者を新薬群に割り当てたりといった判断が、統計的な妥当性を保ちながら可能になるのです。
2010年のガイダンス以降も、この流れは加速しています。医薬品・生物製剤の分野では、ベイズ統計のみを主題とした包括的な最終ガイダンスはまだ存在しませんが、「Adaptive Designs for Clinical Trials of Drugs and Biologics (FDA, 2019)」や「Interacting with the FDA on Complex Innovative Trial Designs (FDA, 2020)」といったガイダンスの中で、ベイズ的手法を含むモデリングやシミュレーションの活用が想定されており、その利用可能性は制度的枠組みに組み込まれつつあります。さらにFDAは、将来的に医薬品分野のベイズ統計に関するガイダンス草案を出す意向を示しており、2024年には実務応用を促進する「Bayesian Statistical Analysis (BSA) Demonstration Project」を開始するなど、その活用に向けた動きは活発化しています。
もちろん、このアプローチは万能薬ではありません。質の低いリアルワールドデータを事前情報として用いれば、誤った結論を導くリスクもあります(バイアスの問題)。そのためFDAは、事前分布を設定する際の透明性や、異なる事前分布を用いた場合に結果がどう変わるかを確認する「感度解析」の実施を強く求めています(FDA, 2010)。しかし、FDAが示した方向性は明確です。それは、厳格な科学的規律を維持しつつも、利用可能なあらゆるデータを賢く活用することで、より効率的で、倫理的で、患者中心の医療開発を実現しようとする、力強い意志の表れなのです。
これらの違いを、以下の表に整理しました。
| 特徴 | 最尤推定法 (MLE) | ベイズ推定 (Bayesian Estimation) |
|---|---|---|
| 思想 | データという客観的事実のみを信頼し、尤度を最大化する一点の真実を探す(頻度論) | 既存の知識(事前情報)は、新しいデータ(尤度)によって常に更新されるべきという信念(ベイズ主義) |
| 答えの形式 | パラメータの「点推定値」と、その信頼区間(例:オッズ比は2.5 [95%CI: 2.1-2.9]) | パラメータがとりうる値の「確率分布」(事後分布)と、その信用区間(例:オッズ比が2.0~3.0の間にある確率は95%) |
| 強み | ・計算が比較的シンプルで速い ・客観性が高く、手法が広く標準化されている ・データ量が潤沢な場合に非常に強力 | ・既存の医学知識や外部データを有効活用できる ・データが少ない場合でも頑健な推定が可能 ・結果の「不確実性」を直感的に評価できる |
| 課題 | ・データが少ないと結果が不安定になりがち ・事前知識を数式に組み込むことができない | ・事前分布をどう設定するかに客観的な合意形成が難しい場合がある(主観性の問題) ・モデルが複雑になると計算コストが高い |
| 輝く場面 | 大規模コホート研究、標準的なRCT、疫学調査におけるリスク因子の評価など | 希少疾患の臨床試験、個別化医療、診断支援AI、複雑な因果関係のモデリングなど |
結論として、手元に大規模なデータセットがあり、客観的で標準化された推定値が求められる場面では、最尤推定が依然として強力なツールです。一方で、過去の知見を有効活用したい、データが限られている、あるいは結論の「確信度」や「ばらつき」まで含めて、より繊細な臨床判断を下したいという場面では、ベイズ推定がその真価を発揮します。近年、コンピュータの計算能力が飛躍的に向上したことで、これまで計算が困難だった複雑な医療AIモデルにおいても、ベイズ的なアプローチを採用する例は着実に増加しています。スタンフォード大学のEtzらの研究(2018)でも指摘されているように、両者の特性を深く理解し、適切に使い分ける能力は、これからの医療データサイエンスにおいてますます重要になっていくでしょう。
まとめ:データから「医学的確信」を紡ぎ出す二つの思考法
今回は、AIが臨床データという限られた情報から、いかにして「医学的確信」とも呼べる結論を導き出すのか、その思考の根幹にある二つのアプローチ、最尤推定とベイズ推定の世界を探求してきました。最後に、今回の学びの核心を振り返ってみましょう。
まず、すべての土台となるのが尤度という考え方でした。これは、目の前のデータが、考えられる様々な原因のどれを支持しているのか、その「もっともらしさ」を測る、臨床推論のコンパスのような指標でしたね。
そのコンパスだけを頼りに、データが指し示す最も「らしい」一点を目指すのが最尤推定です。これは、客観的なデータに徹底的に向き合う、いわばデータ駆動型の実直な思考法です。
一方、そこに経験豊富な医師の知識や直感を加えるのがベイズ推定でした。過去の医学知識(事前情報)という地図を片手に、新しいデータ(尤度)というコンパスの示す方角を吟味し、最終的な目的地(事後確率)を柔軟に更新していく、知識統合型の洗練された思考法と言えるでしょう。
一見すると難解な数式に見えたかもしれませんが、その本質は、私たちが日々ベッドサイドで行っている思考プロセスと驚くほど似ています。AIが行う診断支援や予後予測、あるいは新しい治療法の効果を推定するアルゴリズムの裏側では、必ずこれらの推定理論が静かに、しかし力強く動いています。
AIが出した答えを鵜呑みにするのではなく、その思考の背景にあるロジック、つまり「なぜAIはこの結論に自信を持っているのか」を理解すること。それこそが、これからの時代にAIを単なる道具として使うのではなく、信頼できるパートナーとして臨床現場で賢く、そして効果的に活用していくための鍵となるはずです。今回の学びが、その第一歩となれば幸いです。
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
参考文献
- Ashby, D. (2006). Bayesian statistics in medicine: a 25 year review. Statistics in Medicine, 25(21), pp.3589-3631. Available at: https://doi.org/10.1002/sim.2672.
- Bishop, C.M. (2006). Pattern Recognition and Machine Learning. Springer.
- Etz, A. and Vandekerckhove, J. (2018). Introduction to Bayesian inference for psychology. Psychonomic Bulletin & Review, 25(1), pp.5-34. Available at: https://doi.org/10.3758/s13423-017-1262-3.
- Hastie, T., Tibshirani, R. and Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Second Edition. Springer.
- Myung, I.J. (2003). Tutorial on maximum likelihood estimation. Journal of Mathematical Psychology, 47(1), pp.90-100. Available at: https://doi.org/10.1016/S0022-2496(02)00028-7.
- Pallmann, P., Bedding, A.W., Choodari-Oskooei, B., Dimairo, M., Flight, L., Hampson, L.V., Holmes, J., Maughan, T.S., Morris, T.P., Pirrie, S.J., Rudd, A.G., Sydes, M.R., Tudur Smith, C., Villar, S.S., Wason, J., Whitehead, J., Williamson, P.R., Woolfall, K. and Jaki, T. (2018). Adaptive designs in clinical trials: why use them, and how to run and report them. BMC Medicine, 16(1), p.29. Available at: https://doi.org/10.1186/s12916-018-1017-7.
- U.S. Food and Drug Administration (2010). Guidance for the Use of Bayesian Statistics in Medical Device Clinical Trials. [Online] Available at: https://www.fda.gov/regulatory-information/search-fda-guidance-documents/guidance-use-bayesian-statistics-medical-device-clinical-trials (Accessed: 12 October 2025).
- U.S. Food and Drug Administration (2018). Framework for FDA’s Real-World Evidence Program. [Online] Available at: https://www.fda.gov/media/120060/download (Accessed: 12 October 2025).
- U.S. Food and Drug Administration (2019). Adaptive Designs for Clinical Trials of Drugs and Biologics Guidance for Industry. [Online] Available at: https://www.fda.gov/media/78495/download (Accessed: 12 October 2025).
- U.S. Food and Drug Administration (2020). Interacting with the FDA on Complex Innovative Trial Designs for Drugs and Biological Products Guidance for Industry. [Online] Available at: https://www.fda.gov/media/139920/download (Accessed: 12 October 2025).
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






