臨床現場にあふれる「たぶん」という不確かさ。それに名前を与え、形を描き、中心と広がりを測り、新しい情報で考えを更新する。データに基づいた意思決定能力を飛躍させる、確率・統計の基本ツールを学びます。
不確かな事象を「確率変数」(離散/連続)という箱に入れ、その値の出やすさを一覧にした「確率分布」という設計図で全体像を把握します。
「期待値」で最も確からしい中心点を、「標準偏差」で結果のばらつき(リスク)を数値化し、データの特性を要約します。
ある情報(例: 検査陽性)が得られた時、考えるべき世界が絞り込まれ、確率が更新される仕組みを理解します。これがベイズの定理への入口です。
事前の確率(有病率など)と新しい証拠(検査結果)を組み合わせ、より確からしい「事後確率」へと合理的に信念を更新する強力な思考法です。
「この検査、陽性だったけど、本当に病気なのかな…?」
「新しい治療法、どれくらいの効果が『期待』できるんだろう?」
臨床現場は、「たぶん」「おそらく」「〜かもしれない」といった”不確かさ”との連続した戦いです。この漠然とした不確かさに、私たちの経験や直感だけで立ち向かうのには、どうしても限界があります。
もし、この「たぶん」の度合いを客観的な言葉で表現し、科学の力で乗りこなすことができたなら、医療の質は劇的に変わると思いませんか?
それを実現する最強の武器が、確率論と統計学です。なんだか難しそうですが、心配はいりません。その本質は、驚くほどシンプルで、「不確かさを科学の土俵に乗せるための、信頼できるルールブック」のようなもの。このルールブックを手にすることは、日々の臨床判断の精度を高めるだけでなく、医療AIがどのように「思考」しているのか、その頭脳の中を覗くための「鍵」を手に入れることにも繋がります。
この章では、まず確率分布という「不確かさの全体像を描く設計図」を学び、期待値という「最も確からしい未来を予測する道具」を手にします。そして最後には、ベイズの定理という「新しい情報から学び、考えを更新していくための知恵」を身につけていきます。
さあ、不確かさを味方につけ、データに基づいた意思決定能力を飛躍させる冒険へ、一緒に出発しましょう!
確率変数:「何が起こるかわからない」を扱うための魔法の箱 📦
最初は「確率変数(Random Variable)」の登場です。統計学やAIの世界を探検する上で、この相棒なしでは一歩も前に進めません。
この概念を理解するために、最も古典的で分かりやすい「サイコロを振る」という行為をイメージしてみましょう。🎲
サイコロを手に持っているとき、振った後にどの目が出るかはまだ「確定」していません。しかし、出る可能性があるのは {1, 2, 3, 4, 5, 6} のどれかである、ということは決まっていますよね。
この「サイコロを振ったときに出る、”何か”の目」という、結果が決まる前の不確かな事象そのものが確率変数です。数学というと難しく聞こえますが、やっていることはシンプルで、この不確かな現象に「X」や「Y」といった名前(ラベル)を付けて、数学の土俵で扱えるようにしているだけなんです。まさに、「何が起こるかわからない」というモヤモヤした現象を一時的に入れておくための”魔法の箱”だと考えてみてください。
この魔法の箱には、中に入れるものによって大きく2つのタイプがあります。
1. 離散確率変数:カチッと決まる、とびとびの値
これは、サイコロの目のように、とりうる値が1, 2, 3…と数えられる(とびとびの)ものです。1.5のような途中の値は存在しません。まさに、先ほどのサイコロの例がこのタイプにあたります。
- 医療の例:
- ある病棟で1日に発生するインシデントの件数(0件, 1件, 2件…)
- 5人の患者のうち、新薬が奏効した人数(0人, 1人, 2人, 3人, 4人, 5人)
- ある患者が1週間に経験する喘息発作の回数
2. 連続確率変数:滑らかにつながる、無限の値
こちらは、身長や体重のように、値が滑らかにつながっているものです。2つの値の間には、必ず別の値が存在します。アナログの時計の秒針や、昔ながらの水銀体温計をイメージすると分かりやすいかもしれません。針は特定の数字の上だけでなく、目盛りの間のどこにでも止まることができますよね。
- 医療の例:
- 患者さんの収縮期血圧(120.1 mmHgや120.15 mmHgなど、理論上は無限に細かい値をとれる)
- 空腹時血糖値
- 腫瘍の直径
臨床研究やAIモデルが扱っているデータのほとんどは、これら確率変数の集まりです。例えば、AIがある患者の「1年後の心筋梗塞発症リスク(確率変数Y)」を予測する場合、そのAIは「現在の血圧(確率変数X1)」「年齢(確率変数X2)」「コレステロール値(確率変数X3)」といった、他のたくさんの確率変数の関係性を学習しているのです。
まずは目の前にある不確かな数値を、「これは離散確率変数だな」「これは連続確率変数だな」と意識すること。それが、データと科学的に対話するための、非常に重要な第一歩となります。
確率分布:不確かさの「全体設計図」を手に入れる
さて、魔法の箱である「確率変数」を手に入れました。しかし、箱だけあっても冒険は始まりません。本当に知りたいのは「箱の中に何が、どんな割合で入っているか?」ですよね。その謎を解き明かすのが、今回のテーマ「確率分布(Probability Distribution)」です。
これは、先ほどのサイコロの例で言えば、「それぞれの目が、どれくらいの確率で出るか」を完全にリストアップした”サイコロの取扱説明書”に相当します。つまり、確率変数がとりうる全ての値と、それぞれの値をとる確率の対応関係をすべて記述した「不確かさの全体設計図」なんです。
この設計図があれば、不確かさの全体像、つまりどんな結果が起こりやすく、どんな結果が起こりにくいのかが一目瞭然になります。
離散確率分布:棒グラフで見る「取扱説明書」
確率変数がサイコロの目のようにとびとびの値をとる場合(離散確率変数)、その分布を示すのは比較的シンプルです。先ほどのサイコロの例を見てみましょう。
大事なポイントは、すべての確率を足し合わせると、必ず1(100%)になることです。「これらのうちのどれかは絶対に起こる」というわけですね。このように、個々の確率が”質量”のようにカチッと決まる関数を確率質量関数と呼びます。
連続確率分布:曲線で見る「地形図」
一方で、確率変数が血圧のように滑らかな値をとる場合(連続確率変数)、話は少しだけ複雑になります。なぜなら、120.0 mmHgピッタリになる確率、というのは天文学的に低く、実質ゼロだからです。
そこで登場するのが確率密度関数(Probability Density Function, PDF)という考え方です。これは、特定の点の確率そのものではなく、その値の周辺がどれだけ「起こりやすいか」という密度(混み具合)を示します。
山の地形図をイメージしてみてください。🗻
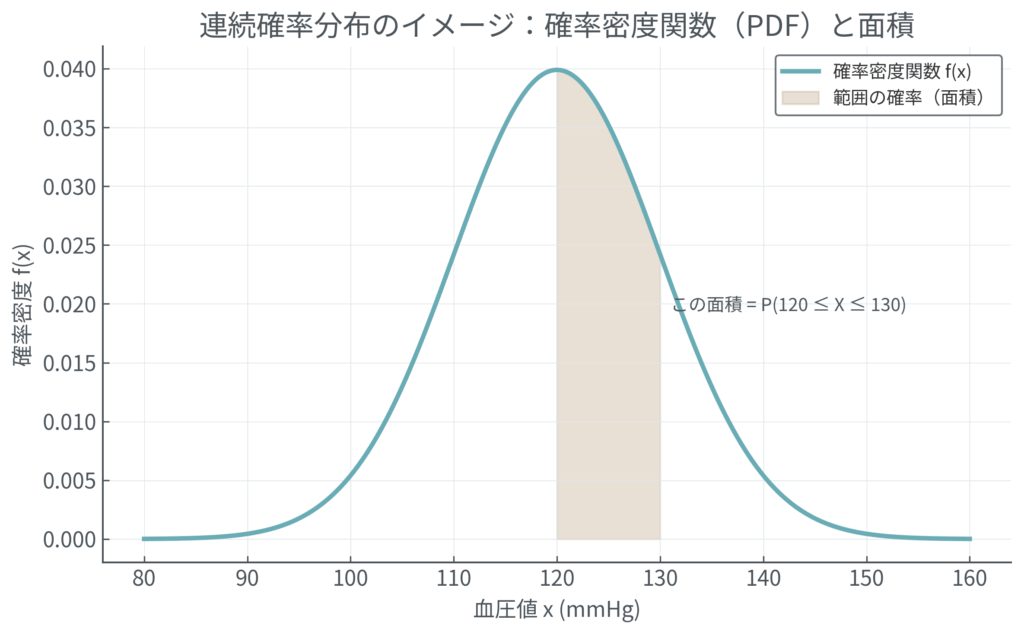
標高が高い場所ほど等高線が混み合っていますよね。あれと同じで、確率密度関数のグラフで山が高くなっている部分ほど、そのあたりの値が発生しやすい(密度が高い)ことを意味します。そして、ある範囲(例えば血圧が120〜130 mmHgの間)の確率は、グラフのその区間の面積として計算されます。ここでも、グラフ全体の面積を合計すると、必ず1になります。
医療現場でおなじみの「確率分布」たち
臨床現場や研究で出会うデータは、特定のパターンの分布に従うことがよくあります。これらの有名な分布の形を知っておくと、データをより深く理解する助けになります。
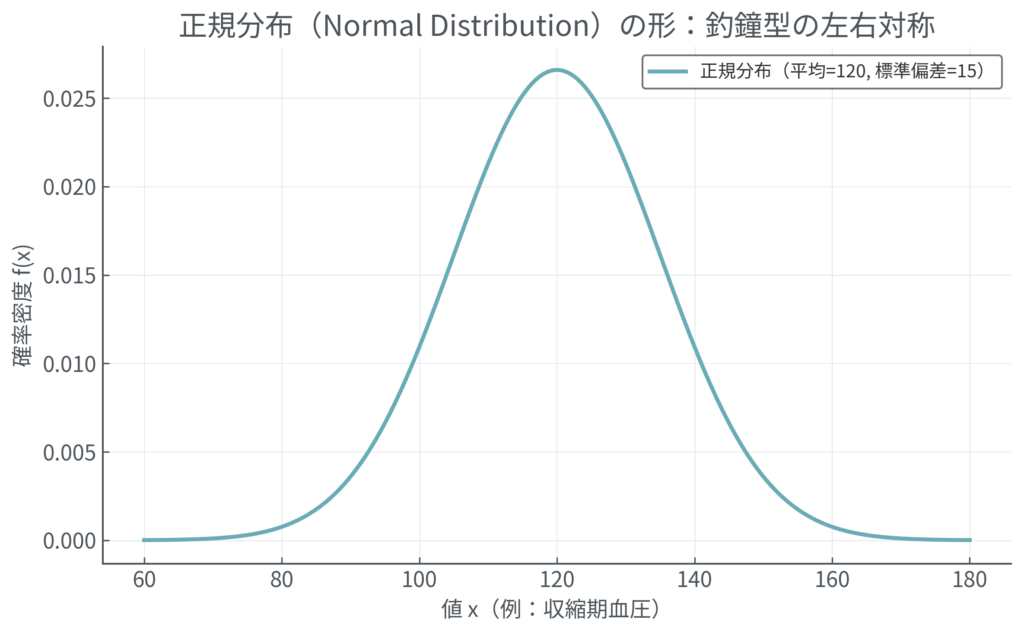
- 正規分布 (Normal Distribution):
- 健康な人の検査値など、多くの自然現象に見られる左右対称の美しい釣鐘型の分布。平均値の周りが最も密度が高く、離れるほど少なくなります。「ガウス分布」とも呼ばれます。
- 例: 成人男性の身長、健康な人の収縮期血圧など。
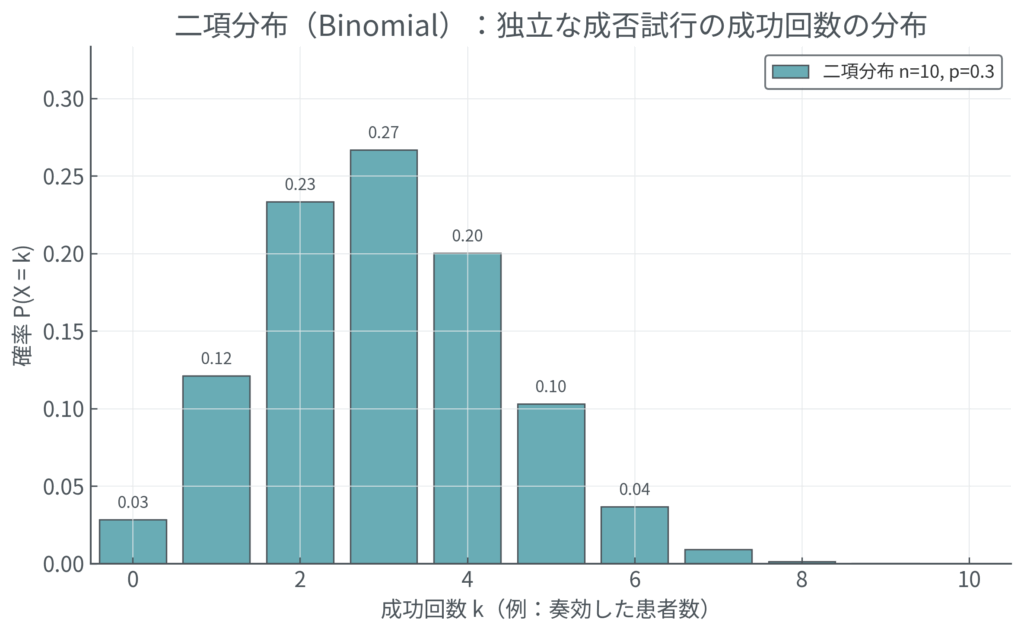
- 二項分布 (Binomial Distribution):
- 「成功か失敗か」のように結果が2つしかない試行を繰り返したときの、成功回数の分布です。
- 例: 10人の患者に新薬を投与したとき、奏効する人数の分布。
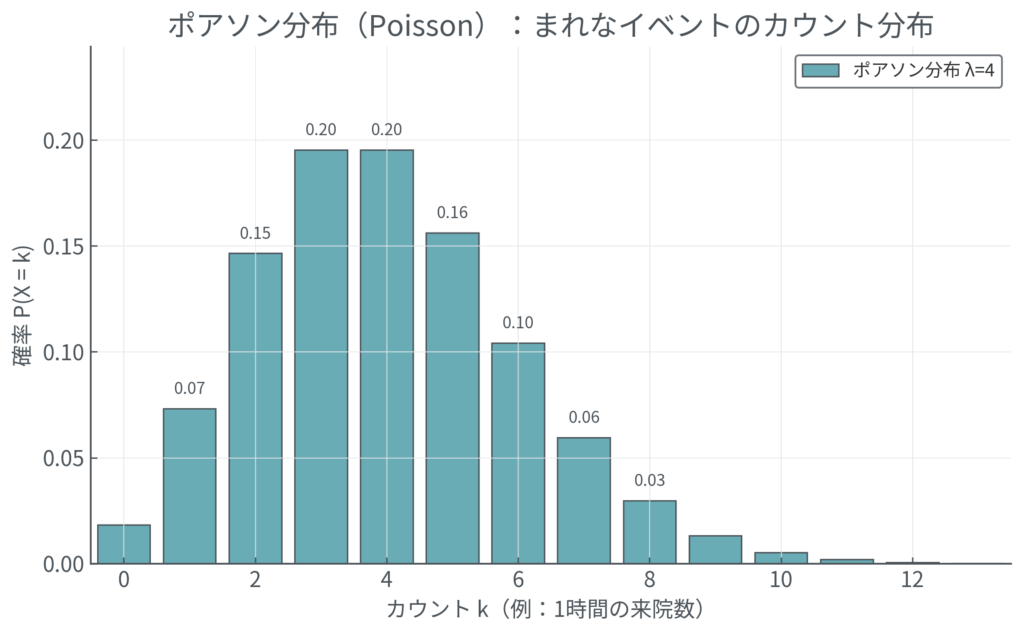
- ポアソン分布 (Poisson Distribution):
- ある一定の期間や範囲で、まれなイベントが平均して何回起こるか、という回数の分布。
- 例: ある病院の救急外来における、1時間あたりの心筋梗塞患者の到着数の分布。
この「分布の形」を特定することこそ、統計的仮説検定やAIモデル構築の出発点となります。目の前のデータがどの設計図に従っているのかを見抜くことが、データを理解し、未来を予測する鍵となるのです。
期待値:不確かさの中心を見抜く「重心」
不確かさの全体設計図(確率分布)を手に入れた私たちが次に知りたいのは、おそらくこういうことでしょう。「で、結局のところ、一番『ありえそう』な結果は何なのか?」あるいは「長い目で見たら、どんな結果に落ち着きそうなのか?」ということです。
この、分布全体の”ど真ん中”を指し示す代表値、それが「期待値(Expected Value)」です。物理学の言葉を借りれば、分布全体の「重心」と考えると、とてもイメージが湧きやすいと思います。
期待値は、私たちがよく使う単純な平均(例:3人のテストの点を足して3で割る)とは少し違います。一番の違いは、起こりやすさ(確率)の”重み”を考慮する点です。起こりやすい結果はより重視し、起こりにくい結果は軽めに扱うことで、より現実に即した「平均像」を計算するのです。
宝くじで「期待値」を体感する
身近な例として、簡単な宝くじを考えてみましょう。100本の中に、以下の当たりくじが入っているとします。
- 1等: 10,000円 (1本) → 確率は 1/100
- 2等: 1,000円 (10本) → 確率は 10/100
- ハズレ: 0円 (89本) → 確率は 89/100
このくじを1枚引いたとき、「期待できる」賞金額はいくらでしょう?単純に平均すると (10000 + 1000 + 0) / 3 = 3667円 になりそうですが、これは間違いです。なぜなら、1万円が当たる確率はハズレの確率よりずっと低いからです。
そこで、賞金額にそれぞれの確率という”重み”を掛けて足し合わせます。これこそが期待値の計算です。
\[ \begin{aligned} E[X] &= (10000 \text{円} \times \dfrac{1}{100}) + (1000 \text{円} \times \dfrac{10}{100}) + (0 \text{円} \times \dfrac{89}{100}) \\ &= 100\text{円} + 100\text{円} + 0\text{円} \\ &= 200\text{円} \end{aligned} \]
計算の結果、期待値は200円となりました。これは、このくじを何度も何度も(例えば100万回)引き続けた場合、1枚あたりの平均賞金額が200円に近づいていく、ということを意味します。もしこのくじが1枚300円で売られていたら、長期的には損をしそうだな、という判断ができますよね。
数式の中身を覗いてみよう
この計算を一般的に書いたのが、以下の数式です。
\[ E[X] = \sum_{i} x_i P(X=x_i) \]
なんだか難しそうに見えますが、やっていることは宝くじの計算と全く同じです。
- \( x_i \): i番目の結果(例: 10,000円、サイコロの目なら「1」)
- \( P(X=x_i) \): その結果が起こる確率(例: 1/100、サイコロなら「1/6」)
- \( \sum_{i} \): すべての結果について(iを動かして)、「結果 × 確率」を計算し、最後に全部足し合わせる記号。
臨床現場での期待値
この考え方は、臨床現場での意思決定に極めて重要です。例えば、新しい抗がん剤Aの効果を評価する臨床試験を考えてみましょう。患者さんの生存期間は様々です。3ヶ月で亡くなる方もいれば、5年以上生存する方もいるかもしれません。
この「生存期間」という確率変数の期待値を計算することで、「この治療を受けた患者集団は、平均して何ヶ月の生存が期待できるか」という中心的な指標を得ることができます。もちろん、ある一人の患者さんが期待値ぴったりの生存期間になるとは限りません。しかし、治療法を評価し、他の治療法と比較するための客観的なモノサシとして、期待値は不可欠な役割を果たしているのです。
分散と標準偏差:結果の「ばらつき」を測るモノサシ
さて、分布の重心である「期待値」がわかりました。しかし、物語はまだ半分です。期待値だけを見て物事を判断すると、時として大きなリスクを見落としてしまうかもしれません。
ここで、2つの新しい降圧薬、薬剤Aと薬剤Bを比較するシナリオを考えてみましょう。どちらも臨床試験の結果、「期待値」として平均10mmHg血圧を下げることが示されました。これだけ聞くと、どちらも同じくらい優秀な薬に見えますよね?
しかし、個々の患者さんのデータを見てみると、様相は一変します。
- 薬剤A: ほとんどの患者さんで、血圧が安定して8〜12mmHg下がった。
- 薬剤B: ある患者では30mmHgも下がったが、逆に5mmHg上がってしまった患者もいた。
期待値(平均の効果)は同じでも、薬剤Aの方が効果が安定しており、臨床的にはずっと「予測可能で安全」だと感じるはずです。この「結果のばらつき具合(散らばり具合)」を客観的な数値で表現するのが、分散(Variance)の役割です。
データの「広がり」を可視化する
言葉だけだと分かりにくいので、5人の患者さんの血圧変化を数直線でプロットしてみましょう。
どうでしょう。同じ平均値でも、データの広がり方が全く違うことが一目瞭然ですよね。分散は、この「広がり」の大きさを定量的に測るための指標なのです。
分散の計算方法:「ズレの2乗」の平均
分散は、直感的には「各データが、期待値(平均)からどれくらいズレているかの平均」を計算します。ただし、一つ工夫が必要です。単にズレ(結果 - 期待値)を平均すると、プラスのズレとマイナスのズレが互いに打ち消し合って、ばらつきがゼロに見えてしまうことがあります。
そこで、それぞれのズレを2乗します。こうすれば、すべてのズレが正の値になり、打ち消し合うことがなくなります。この「ズレの2乗」の期待値(平均値)こそが、分散の正体です。
\[ \text{Var}(X) = E\left[ (X – E[X])^2 \right] \]
この式は、以下の3ステップで計算していることを示しています。
- ズレを求める: 各データが期待値 \( E[X] \) からどれだけ離れているか \( (X – E[X]) \) を計算する。
- ズレを2乗する: それぞれのズレを2乗 \( (X – E[X])^2 \) して、すべて正の値にする。
- 平均を求める: 2乗したズレの期待値 \( E[…] \) をとる。
標準偏差:もっと直感的なモノサシ
分散はばらつきを測る優れた指標ですが、一つだけ扱いにくい点があります。それは、値を2乗しているため、元のデータの単位まで2乗されてしまうことです(例: mmHg → mmHg²)。「血圧のばらつきは25 mmHg²です」と言われても、臨床的にピンときませんよね。
この問題を解決してくれるのが標準偏差(Standard Deviation, SD)です。計算はとても簡単で、分散の正の平方根をとるだけ。
\[ \text{SD}(X) = \sigma = \sqrt{\text{Var}(X)} \]
こうすることで、単位が元の単位(mmHg)に戻り、非常に直感的に理解できるようになります。「この薬の効果は、平均-10mmHgで、標準偏差は2mmHgです」と言われれば、「だいたい-8mmHgから-12mmHgの間に収まることが多いんだな」と、効果の範囲を具体的にイメージできます。
期待値が分布の「位置」を示す中心的な指標であるのに対し、分散や標準偏差は分布の「広がり」を示す指標です。この両方を見ることで、私たちは初めて不確かさの全体像を正確に捉えることができるのです。
条件付き確率:新たな情報が「世界」を書き換える
これまでの話は、いわば静的な「設計図」を眺めているようなものでした。しかし、実際の臨床現場はもっとダイナミックです。目の前の患者さんから「昨日から熱があって…」と聞かされた瞬間、私たちの頭の中にある病気の可能性リスト(確率分布)はガラリと書き換わりますよね。
このように、ある新しい情報(出来事B)が手に入ったことで、関心のある出来事(A)の確率がどう変化するのかを記述するための強力なツールが、「条件付き確率(Conditional Probability)」です。
図書館で「確率の世界」を体感する
巨大な図書館にいると想像してみてください。この図書館の蔵書10,000冊の中から、 ランダムに一冊の本を取り出すとします。その本が「医学書」である確率は、医学書が100冊あるなら 100/10000 = 1% です。これが、何も情報がないときの事前確率です。
ここで、友人が「僕が選んだ本、表紙が赤色だったよ」という新しい情報をくれました。この瞬間、私たちの考えるべき「世界」は、10,000冊の蔵書全体から、「赤色の表紙の本(仮に500冊)」だけにギュッと絞り込まれます。
もし、この赤色の本500冊の中に、医学書が20冊含まれていたとしたらどうでしょう?友人が選んだ本が医学書である確率は、20/500 = 4% に上昇します。
これが条件付き確率の本質です。新しい情報(B: 表紙が赤色)によって、考えるべき母集団(分母)が変化し、それに応じて確率も更新されるのです。これを \( P(A \mid B) \) という記号で書き、「Bという条件のもとでAが起こる確率」と表現します。
数式で「世界の絞り込み」を表現する
このプロセスを数式で表現したものが、以下になります。
\[ P(A \mid B) = \dfrac{P(A \cap B)}{P(B)} \]
少し難しく見えますが、図書館の例で考えれば簡単です。
- \( P(A \mid B) \): 「表紙が赤い」という条件で「医学書」である確率 (←求めたいもの)
- \( P(A \cap B) \): 「医学書」であり、かつ「表紙が赤い」確率。\( (20/10000) \)
- \( P(B) \): (元の世界で)「表紙が赤い」確率。\( (500/10000) \)
計算すると、\( (20/10000) \div (500/10000) = 20/500 = 4% \) となり、先ほどの直感的な計算と一致しますね。要するに、「新しい世界(B)の中で、Aが占める割合」 を計算しているに過ぎないのです。
臨床診断における条件付き確率
この考え方は、臨床診断の根幹をなします。ある疾患Dの有病率(事前確率)が1%だとします。ここに、「ある検査Tで陽性だった」という新しい情報が加わったとき、私たちが本当に知りたいのは「検査陽性という条件下で、本当にその疾患である確率」、つまり \( P(D \mid T_{\text{陽性}}) \) です。
この確率は、検査の性能だけでなく、元の有病率にも大きく左右されます。この「確率を更新する」という考え方が、次にお話しするベイズの定理へと直接つながる、極めて重要な架け橋となるのです。
ベイズの定理:「経験」から学ぶための知性のエンジン
いよいよ本日の主役、「ベイズの定理(Bayes’ Theorem)」の登場です。これは単なる数式ではありません。私たちが新しい証拠(データ)に基づいて、自身の信念(確率)を合理的に更新していくための、いわば「知性のOS」とも呼べる、深遠なルールです。
このルールは、私たち医療者が日々行っている診断推論のプロセスそのものであり、同時に、AIがデータから「学習」するプロセスの根幹でもあります。
直感のワナ:検査陽性=病気?
ここで、具体的な臨床シナリオで考えてみましょう。ある珍しい疾患Dがあり、その有病率(事前確率)は1%だとします。この疾患を発見するために、感度99%、特異度95%という、かなり高性能なスクリーニング検査があるとします。
- 感度 99%: もし本当に疾患Dを持っているなら、99%の確率で検査は陽性になる。
- 特異度 95%: もし疾患Dを持っていなければ、95%の確率で検査は陰性になる。
さて、ある患者さんがこの検査を受けて「陽性」と出ました。このとき、この患者さんが本当に疾患Dを持っている確率は、何%くらいだと思いますか?
多くの人が「感度が99%だから、99%くらいだろう」と考えてしまいがちです。しかし、これが「直感のワナ」なのです。ベイズの定理を使えば、このワナを回避し、客観的な確率を導き出すことができます。
10,000人の村で考える「確率の地図」
数式に入る前に、10,000人が住む村を想像して、この問題を可視化してみましょう。これが一番わかりやすい方法です。
- 病気の人と、そうでない人を分ける
有病率は1%なので、村には100人の患者がいて、残りの9,900人は健康です。 - 患者グループ(100人)に検査する
感度は99%なので、100人のうち99人は正しく「陽性」(真陽性)と判定されます。
残りの1人は、残念ながら「陰性」(偽陰性)と判定されます。 - 健康なグループ(9,900人)に検査する
特異度は95%なので、9,900人のうち95%にあたる9,405人は正しく「陰性」(真陰性)と判定されます。
しかし、残りの5%にあたる495人は、健康なのに間違って「陽性」(偽陽性)と判定されてしまいます。
この結果を、表にまとめてみましょう。
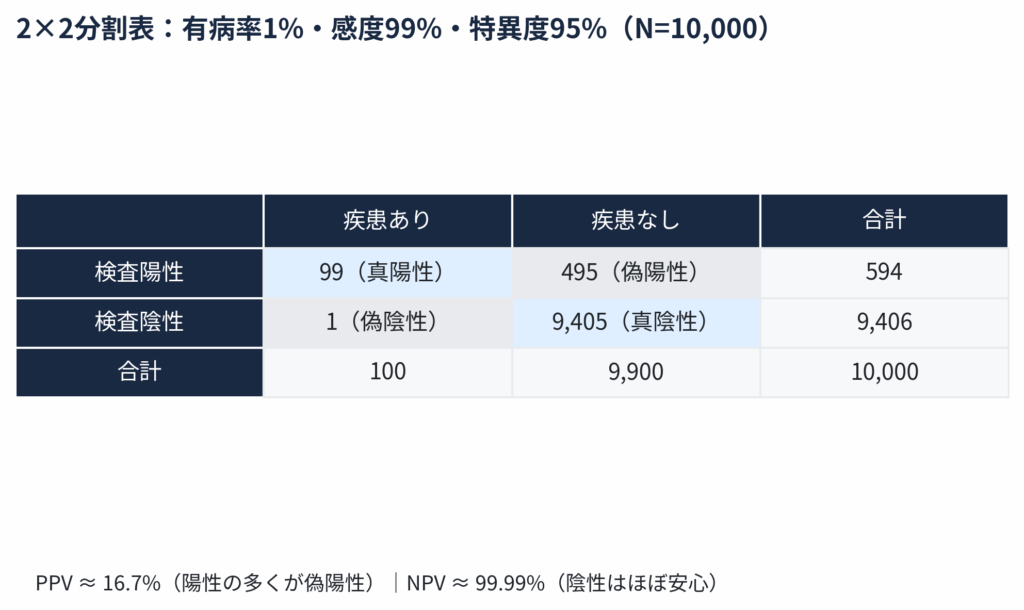
さあ、最初の問いに戻りましょう。「検査が陽性だったとき、本当に病気である確率」は?
この表を見れば一目瞭然です。検査で陽性になった人は全部で 594人(99 + 495)。このうち、本当に病気だったのは 99人です。したがって、求める確率は…
\[ \dfrac{99}{594} \approx 0.167 \quad \to \quad \textbf{約16.7%} \]
どうでしょう?「99%くらい」という直感とは、かけ離れた結果になりました。これが、有病率という「事前確率」の低さを考慮に入れた、客観的な事後確率なのです。
ベイズの定理とのつながり
この直感的な計算プロセスを、エレガントな数式で表現したのがベイズの定理です。
\[ P(A \mid B) = \dfrac{P(B \mid A) P(A)}{P(B)} \]
今回の例に当てはめてみましょう。
- \( P(A \mid B) \): 求めたい事後確率 \( P(\text{疾患あり} \mid \text{陽性}) \)
- \( P(B \mid A) \): 尤度(感度) = 0.99
- \( P(A) \): 事前確率(有病率) = 0.01
- \( P(B) \): 証拠(検査が陽性になる全体の確率) = 594 / 10000 = 0.0594
これを計算すると、\( (0.99 \times 0.01) \div 0.0594 \approx 0.167 \) となり、先ほどの村の例と完全に一致します。
この定理が教えてくれるのは、「検査後に本当に病気である確率は、検査の性能だけでなく、検査前の確率にも強く依存する」という、臨床上極めて重要な事実です (Casscells, Schoenberger, & Graboys, 1978)。
特に、今回の例のように有病率が極めて低い疾患を対象とする場合、この事前確率の影響は顕著に現れます。なぜなら、集団の大多数を占める「疾患を持たない人々」の中から、たとえわずかな割合であっても、誤って陽性と判定される「偽陽性」の絶対数が、もともと数が少ない「疾患を持つ人々」の中から正しく判定される「真陽性」の絶対数を、簡単に上回ってしまうからです。今回の例でも、疾患を持つ100人から出た真陽性(99人)に対し、疾患を持たない9,900人から出た偽陽性は495人にも上りました。この偽陽性の多さが、検査陽性という結果が出ても、本当に疾患である確率(陽性的中率)を直感よりはるかに低くしてしまう根本的な原因なのです。
AI、特に機械学習モデルは、まさにこのベイジアン的な枠組みを使い、データという「証拠」を取り込みながら、予測の精度(事後確率)を絶えず更新していきます。私たちが経験を通して確率的な判断を洗練させていくように、AIもデータという「証拠」に基づいて学習を続けています。その学習の原理は、ベイズの定理に通じる「確率の更新」の考え方です。
より詳しく知りたい方はこちら👇


まとめ:不確かさを「科学」する冒険の始まり
今回は、「たぶん」という不確かさを科学の言葉で語るための、基本的な道具一式を学びました。
冒険は、まず不確かな現象に確率変数という名前を与えるところから始まりました。次に、その全体像を確率分布という設計図で描き出し、期待値でその中心(重心)を、分散や標準偏差でそのばらつき具合を測りました。
そして最後には、条件付き確率という考え方を使って「新しい情報」を取り込み、ベイズの定理という知性のエンジンを回して、私たちの信念(確率)を合理的に更新する方法を手にしました。
これらのコンセプトは、一見すると抽象的で、日々の臨床とは縁遠いように感じるかもしれません。しかし、実はその逆です。これらは、診断推論、治療法の選択、エビデンスの吟味といった、私たち医療者が毎日行っている知的作業の根幹を支える思考のフレームワークそのものです。
そして、このフレームワークは、これから私たちが探検していく医療AIの世界を理解するための、絶対に欠かせない「OS(オペレーティングシステム)」となります。AIがどのようにデータから「学習」し、賢くなっていくのか、その秘密の核心部分を、私たちは今日学んだのです。
今回の知識をコンパスに、次回からはさらに具体的なデータ解析の世界へと足を踏み入れていきましょう。
参考文献
- Gigerenzer, G. (2002). Calculated Risks: How to Know When Numbers Deceive You. Simon & Schuster.
- Sox, H. C., Higgins, M. C., & Owens, D. K. (2013). Medical Decision Making (2nd ed.). Wiley-Blackwell. (DOI: 10.1002/9781118341579)
- Goodman, S. N. (1999). Toward Evidence-Based Medical Statistics. 1: The P Value Fallacy. Annals of Internal Medicine, 130(12), 995-1004. (DOI: 10.7326/0003-4819-130-12-199906150-00008)
- Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2013). Bayesian Data Analysis, Third Edition. Chapman and Hall/CRC. (DOI: 10.1201/b16018)
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






