AIの驚異的な学習能力は、実は「微分」という強力な数学の原理に支えられています。ここでは、AIが間違いを減らし賢くなるための「谷底を目指す旅」の核心を解説します。
AIの学習とは、予測の「間違い(損失)」を最小化する旅です。霧深い山中で、地形の最も低い「谷底(最適解)」を手探りで目指すプロセスに例えられます。
微分は、現在地の「瞬間の傾き」を計算する道具です。これにより、最も効率的に間違いを減らせる「最急な下り坂」の方向を正確に見つけ出すことができます。
勾配降下法は、①勾配(傾き)を計算し、②その逆方向へ少し進み、③これを繰り返すアルゴリズムです。この地道な繰り返しで、AIは自ら賢くなっていきます。
AIが医療画像を解析して病変を指摘する、あるいは膨大な医学論文を読み解いて新たな治療法のヒントを見つけ出す。こうした技術はもはやSFの世界の話ではありません。
では、AIは一体どうやって、これほどまでに高度な「判断能力」を身につけるのでしょうか?
その驚くべき学習能力の根幹には、実は、私たちが高校時代に出会ったかもしれない、非常にシンプルでありながら、この上なく強力な数学の原理が隠されています。それが「微分」です。
「うわ、数学か…」と、少し身構えてしまった方もいらっしゃるかもしれませんね。ご安心ください。この記事の目的は、複雑な数式を暗記することではありません。数式が苦手な方でも、まるで面白い物語のページをめくるように、微分の「本質」を直感的に理解できるよう、その考え方の核心をじっくりと解き明かしていくことです。
AIが、単なるプログラムから「賢い」存在へと飛躍するための秘密の鍵、それを一緒に探求しにいきましょう。
AIの学習とは「手探りで谷底を目指す旅」である
それでは、AIがどうやって学習するのか、その直感的なイメージを掴むために、一つ壮大な旅の例え話をさせてください。
AIにとっての学習とは、「間違い(=損失)を可能な限りゼロに近づける、『正解』という名の谷底」を探す、果てしない旅のようなものです。
少し想像してみてください。あなたは今、深い霧に包まれた広大な山脈に、たった一人で立っています。与えられたミッションは、この山脈の中で最も低い「谷底」にたどり着くこと。しかし、濃い霧のせいで視界は足元数メートルしかなく、全体の地図も持っていません。
この例え話に出てくる山脈の複雑な地形こそ、AIが解き明かそうとしている現実の課題そのものです。例えば、「ある患者さんの臨床データから、30日以内の心不全再入院リスクを予測する」という課題があったとします。この場合、地形は予測モデルの性能を表します。
山の標高の高さ ⛰️
これは「間違いの大きさ」を意味します。AIの世界では、この間違いの度合いを数値化したものを損失関数(Loss Function)と呼びます。標高が高い、つまり山の上にいるほど、AIの予測が実際の結果から大きく外れている(間違いが大きい)状態です。
あなたの現在地 📍
これは「AIの現在の性能」、つまり、現時点での予測モデルが持っているパラメータ(設定値)の状態を示します。
最も低い谷底 ✨
これこそが、私たちの目指すゴール。「最も間違いが少なく、理想的とされる状態」です。この地点にたどり着ければ、AIの予測精度は最大化されます。
さて、この絶望的にも思える状況で、あなたならどう行動するでしょうか?
おそらく、やみくもに歩き回ることはしないはずです。きっと、まず足元の地面を慎重に調べ、「どちらの方向が下り坂になっているか?」とその傾斜を確認するでしょう。そして、最も急だと感じられる下り坂の方向へ、まずは一歩、踏み出してみる。そしてまた、その新しい地点で同じように足元の傾きを調べる…
実は、AIが学習の過程で行っていることも、これと全く同じことなのです。そして、この「足元の傾きを調べる」という、旅に不可欠な魔法の道具こそが、これからお話しする「微分」なのです。
微分:AIに「進むべき方向」を教えるコンパス
さて、霧の立ち込める山で「足元の傾き」を調べて、下り坂を見つけるという方針が決まりました。この、きわめて重要な操作を数学的に実現してくれる道具が微分(Differentiation)です。
一言でいうと、微分とは「ある一点における、ごくわずかな変化の度合い(=瞬間の傾き)」を求める計算のことです。
山の例えで言えば、「あなたが今いるその地点で、一歩足を踏み出すと標高がどれくらい変化するか?」を、あらゆる方向について正確に教えてくれます。もし計算結果が「急なマイナス」なら、そちらは急な下り坂。「ほぼゼロ」なら、そこは平坦な場所か、あるいは谷底(または山の頂上)かもしれない、という具合です。
数式の裏にある「極限までズームする」という考え方
ここで少しだけ、数式にも触れてみましょう。中学校で習った「変化の割合」、つまり「(yの増加量)÷(xの増加量)」という直線の傾きの計算を覚えていますでしょうか?微分は、あの考え方を極限まで突き詰めたものです。
ある関数を \(y=f(x)\) としたとき、その微分(専門的には導関数と言います)は \(\frac{dy}{dx}\) という記号で表されます。
\[ \frac{dy}{dx} = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} \]
この数式を見て、「難しそうだ」と感じる必要は全くありません。この式が表現しているのは、とてもシンプルなアイデアです。
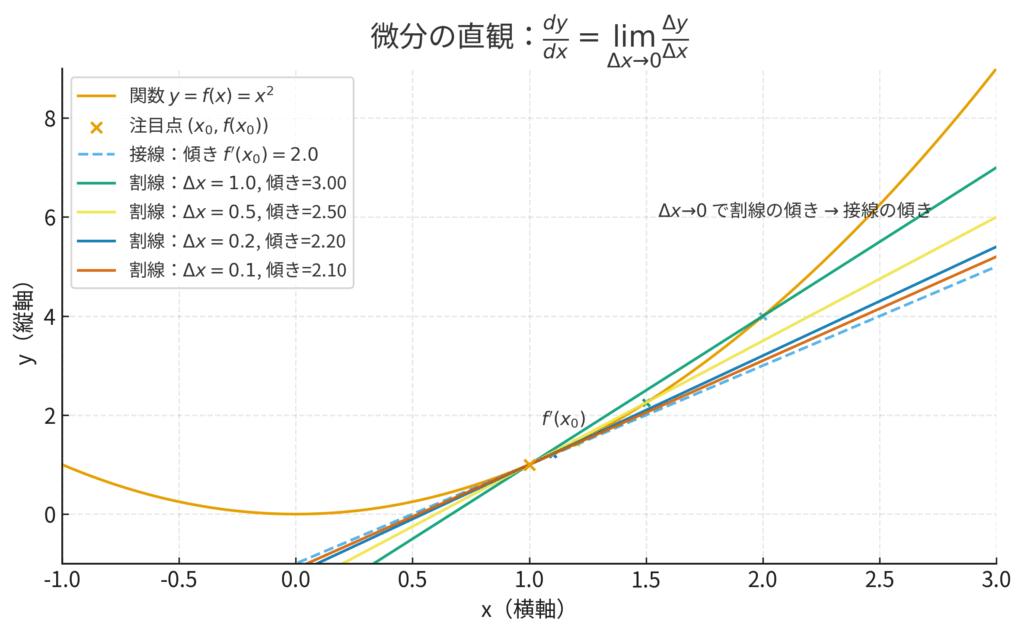
「xの変化量である \(\Delta x\) を、ゼロに限りなく近づけるほど小さくしたとき、yの変化量 \(\Delta y\) との比率はどうなりますか?」
ということです。地形のようにぐにゃぐにゃと曲がった関数のグラフも、どこか一点を顕微鏡で見るように極限まで拡大していくと、その部分はほとんど直線に見えますよね。微分とは、その「ほとんど直線に見える部分」の傾きを計算しているに過ぎません。要は、「ごくごくミクロな世界の傾き」を調べているのです。
医療現場での微分:心電図の「瞬間速度」を読む
この考え方は、医療現場でも極めて重要です。
例えば、心電図(ECG)の波形を考えてみましょう。
P波やQRS波、T波といった全体の形から心臓の状態を読み取るのはもちろんですが、微分的な視点を持つと、さらに深い情報が得られます。例えば、心室の興奮を表すQRS波が立ち上がる、そのまさに一瞬の傾きはどうなっているでしょうか?
この「瞬間の傾き」、つまり \( \frac{d(\text{電圧})}{d(\text{時間})} \) は、心室の伝導速度の鋭敏な指標となります。もし、この立ち上がりが平常時よりなだらかであれば、心筋の伝導系に何らかの異常(例えば、虚血や線維化による伝導遅延)が存在する可能性を示唆します (Goldberger et al., 2000)。
このように、単に波形の高さ(電圧)を見るだけでなく、その「変化の勢い(瞬間の速度)」を捉えることで、より詳細な病態生理に迫ることができるのです。微分は、AIが学習の方向性を見定めるだけでなく、私たちが生命現象をより深く理解するための強力なレンズでもあるのです。
勾配と偏微分:無数の選択肢から「最善の一手」を見つける
さて、これまでの話は、いわば地図上の東西南北、つまり2次元の世界を前提としていました。しかし、AIが挑む現実の医療課題は、はるかに複雑で、比較にならないほど多くの次元を持っています。
AIが心不全の30日以内再入院を予測するモデルを学習するケースを、もう一度考えてみましょう。この予測に影響を与える可能性のある因子(AIの専門用語でパラメータや特徴量と呼びます)は、一体いくつあるでしょうか?
年齢、性別、収縮期血圧、心拍数、左室駆出率(LVEF)、BNP値、クレアチニン値、併存疾患の有無、服用中の薬剤リスト、過去の入院歴…。これらを合わせると、優に数十、場合によっては数百の要素(次元)に及びます。これはもはや、私たちが想像できる3次元の山脈ではありません。数百の軸が絡み合った、人間の感覚では捉えられない「超多次元空間」を旅するようなものなのです。
こんな途方もない空間で、どうすれば「最も急な下り坂」という、ただ一つの最適な方向を見つけ出せるのでしょうか?
ここで登場するのが、偏微分(Partial Differentiation)と勾配(Gradient)という、二つの強力な数学的コンセプトです。
偏微分:一つの要素だけに、そっと焦点を当てる
超多次元空間と聞くと圧倒されてしまいますが、ここでの戦略は驚くほどシンプルです。それは、古くから科学者が行ってきた信頼性の高いアプローチ、すなわち「一つの変数だけを動かし、他の変数はすべて固定して影響を見る」という方法です。
これを数学的に行うのが偏微分です。
例えば、AIは現在のパラメータ設定で、ある患者さんの再入院リスクを「50%」と予測したとします。しかし、実際のところ、この患者さんは再入院しませんでした(正解は0%)。この「50%の間違い」を減らすために、AIは次のような自問自答を、すべてのパラメータに対して行います。
「もし、他の全データが今のままだったとして、収縮期血圧(SBP)の値だけが少し高かったとしたら、予測リスクはどう変化しただろうか?」
「もし、他の全データが今のままだったとして、左室駆出率(LVEF)の値だけが少し低かったとしたら、予測リスクはどう変化しただろうか?」
このように、たった一つの要素だけにごくわずかな変化を与え、その時の「間違いの大きさ(損失関数)」の変化率を計算する。これが偏微分の本質です。
関数を \(f\)、変数を \(x_1, x_2, \dots, x_n\) とすると、変数 \(x_1\) に関する偏微分は \( \frac{\partial f}{\partial x_1} \) のように、通常の微分\(d\)とは少し違う\(\partial\)という記号を使って書きます。これは「たくさんの変数がある中で、今は \(x_1\) だけに注目していますよ」という合図だと思ってください。
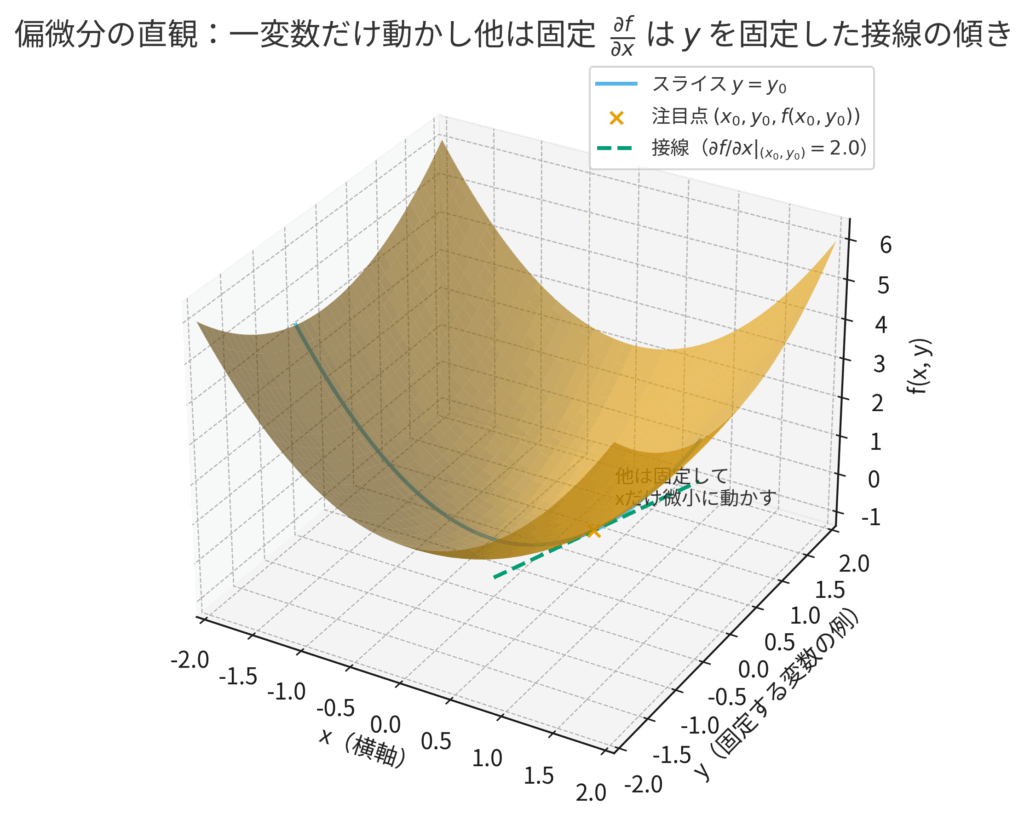
勾配:すべての傾きを束ねた「最強のコンパス」
さて、AIは偏微分を使って、すべてのパラメータ(血圧、LVEF、年齢…)が「間違い」に与える影響度を一つひとつ計算しました。ここからが本番です。
これらの、いわば「各方向ごとの傾きの情報」を、すべて集めて一つのセットにしたもの。それが勾配(Gradient)です。勾配は、数学的にはベクトル(方向と大きさを持つ量)として表現されます。
言葉だけだと少しイメージしづらいので、図解してみましょう。
この勾配ベクトルこそ、私たちの旅における「最強のコンパス」です。なぜなら、このベクトルが指し示す方向は、その地点において「最も標高が急になる上り坂の方向(=最も間違いが大きくなる方向)」と、数学的に一致することが証明されているからです。
旅の目的は、谷底へ向かうことでした。最も急な「上り坂」の方向がわかったのなら、「下り坂」へ向かうのは簡単ですね。
そうです。勾配が指し示す方向と、まったく逆の方向へ進めば良いのです。
この勾配というコンパスを手に入れることで、AIはたとえ何百、何百万次元の複雑な空間であっても、決して迷うことなく、最も効率的に間違いを減らせる「最短の下り坂」へと、着実に一歩を進めることができるのです。
連鎖律:巨大なAIの「末端のネジ」の貢献度を測る
現代のAI、特に深層学習(ディープラーニング)のモデルは、単一の計算式というよりは、むしろ巨大で複雑な「工場の組立ライン」に似ています。
患者さんのCT画像のような生データがベルトコンベアの始点(入力層)に乗せられると、いくつもの処理ステーション(中間層または隠れ層)を通過していきます。各ステーションでは、データが少しずつ加工・変換され、最終的に「この肺結節が悪性である確率は85%」といった製品(出力層)となってラインの終点から出てきます。
ここで、一つ大きな問題が持ち上がります。
もし、このAIの予測が「間違い」だった場合、どうすればよいでしょうか? 例えば、病理検査の結果、その結節は良性(正解は0%)だったとします。この時、AIは組立ラインのどこかを修正して、次回からもっとうまくやらなければなりません。しかし、この巨大な工場には、調整可能なネジやダイヤル(パラメータ)が何百万個も存在します。最終製品の欠陥に対して、組立ラインの一番最初の工程にある、たった一つの小さなネジは、一体どれくらいの「責任」を負うべきなのでしょうか?
この、原因と結果が直接結びついていない、間接的な影響の連鎖を正確に計算するための道具が、微分の世界における連鎖律(Chain Rule)です。日本語のことわざで言うところの「風が吹けば桶屋が儲かる」的な、波及効果を数学的に解き明かすルールです。

影響度を掛け算で伝播させる
連鎖律の数式そのものは、非常にエレガントです。
\[ \frac{dz}{dx} = \frac{dz}{dy} \cdot \frac{dy}{dx} \]
この式が示しているのは、「\(x\) が \(y\) に影響を与え、その \(y\) が \(z\) に影響を与える」という関係があるとき、 \(x\) が最終的に \(z\) に与えるトータルの影響度 \( \frac{dz}{dx} \) は、個々の影響度 \( \frac{dy}{dx} \) と \( \frac{dz}{dy} \) の単純な掛け算で計算できる、ということです。
この考え方を、医療の現場に当てはめてみましょう。
ある降圧薬の「投与量 (\(x\))」が、最終的に患者さんの「脳卒中リスク (\(z\))」にどう影響するかを知りたいとします。この影響は直接的ではなく、「血圧の変化 (\(y\))」を介して起こります。
- ステップ1 (\(\frac{dy}{dx}\)): まず、薬物動態学から「投与量(\(x\))が血圧(\(y\))に与える影響」を調べます。例えば、「投与量を1mg増やすと、血圧が平均で2mmHg下がる」という関係があったとします。ここでの影響度は「-2」です。
- ステップ2 (\(\frac{dz}{dy}\)): 次に、大規模臨床試験から「血圧(\(y\))が脳卒中リスク(\(z\))に与える影響」を調べます。例えば、「血圧が1mmHg下がると、脳卒中リスクが相対的に0.5%低下する」という関係があったとします。ここでの影響度は「-0.5」です。
連鎖律によれば、投与量が脳卒中リスクに与える総合的な影響 \( \frac{dz}{dx} \) は、これらを掛け合わせるだけで求まります。
\[ \frac{dz}{dx} = \frac{dz}{dy} \cdot \frac{dy}{dx} = (-0.5) \times (-2) = 1 \]
これはつまり、「投与量を1mg増やすと、脳卒中リスクが1%低下する」という最終的な関係を導き出せることを意味します。
バックプロパゲーション:間違いを逆流させる学習プロセス
AIの学習、特にバックプロパゲーション(誤差逆伝播法)と呼ばれる手法は、この連鎖律を工場の組立ラインで、しかも逆方向に適用するようなものです。
最終出力で生じた「間違い」という情報を、連鎖律を使いながら出力側から入力側へと次々に逆流させていくのです。そして、その過程で「君のネジの設定が、最終的な間違いにこれだけ貢献してしまった。だから、設定をこちらの方向に少し変えなさい」と、何百万個あるすべてのネジを個別に、かつ同時に微調整していきます。
この地道なプロセスの繰り返しこそが、巨大なAIモデルが自らの間違いから学ぶための、極めて重要な学習のメカニズムなのです。
勾配降下法:AIの学習アルゴリズムの王様
さあ、これまでの旅で、私たちの道具箱はすっかり充実しました。
一点の傾きを測る「微分」、多次元空間での最短の下り坂を指し示す「勾配」、そして巨大なAI内部での責任の所在を明らかにする「連鎖律」。
いよいよ、これらの道具をすべて使って、AIが実際に学習していくプロセス、勾配降下法(Gradient Descent)を見ていきましょう。これは、何を隠そう、私たちが最初に描いた「霧のかかった山で谷底を探す旅」のシナリオそのものです。

この旅のステップは、驚くほどシンプルです。
- 現在地の傾きを調べる(勾配を計算)
まず、AIは現在の地点(現時点でのパラメータ設定)に立ち、これまで見てきた方法で勾配を計算します。これにより、「最も急な上り坂」の方向が正確にわかります。 - 傾きと真逆の方向に、ほんの少しだけ進む
次に、計算した勾配とは180度逆の方向、つまり「最も効率的な下り坂」の方向へと、一歩だけ進みます。この時に進む「歩幅」の大きさは、AIの学習において極めて重要な学習率(Learning Rate)と呼ばれる設定値です。 - 新しい地点で、1.に戻る
一歩進んだ先は、また新しい景色(と傾き)が広がっています。そこで再び勾配を計算し、また逆方向へ一歩進む。AIは、このプロセスを何万回、何百万回と、ひたすら繰り返します。
この単純なプロセスの繰り返しこそが、勾配降下法のすべてです。
学習の成否を分ける「歩幅(学習率)」
この旅がうまくいくかどうかは、「歩幅」である学習率の調整にかかっていると言っても過言ではありません。
歩幅が大きすぎる場合 (学習率 > 大):
谷底に向かって勢いよく駆け下りた結果、谷底を飛び越えて反対側の斜面に駆け上がってしまうかもしれません。これを繰り返すと、永遠に谷底にたどり着けず、むしろどんどん頂上へ向かってしまうことさえあります。AIの世界では、これを「学習が発散する」と呼びます。
歩幅が小さすぎる場合 (学習率 < 小):
一歩一歩が慎重すぎて、谷底にたどり着くまでに途方もない時間がかかってしまいます。限られた時間と計算資源の中では、事実上、学習が「停滞している」のと同じことになってしまいます。
この最適な歩幅を見つけるチューニングは、AI開発における一種の「職人技」でした。しかし、近年では、この歩幅を状況に応じて自動的に調整してくれる、より洗練されたアルゴリズムが主流となっています。AdamやRMSpropといった手法がその代表例で、現代のほとんどのAIモデルの学習は、これらの勾配降下法の派生アルゴリズムによって支えられています。
勾配降下法は、そのシンプルさにもかかわらず、AIという複雑なモデルに「自ら学ぶ力」を与える、まさに王様と呼ぶにふさわしいアルゴリズムなのです。
まとめ:微分は、AIが自ら学ぶための「知性」の源
今回は、AIが学習する仕組みのまさに心臓部である「微分」の世界を探検してきました。霧深い山頂から、一歩ずつ谷底へと下りていく旅も、これで終わりです。最後に、私たちの旅の軌跡を振り返ってみましょう。
- AIの学習とは、予測の「間違い(損失)」を最小化するための、壮大な「谷探し」の旅であること。
- 微分とは、その旅に不可欠な、現在地の「瞬間の傾き」を教えてくれる魔法の道具であること。
- 勾配とは、たとえ何百万次元の複雑な空間であっても、「最も効率的な下り坂」を指し示してくれる、究極のコンパスであること。
- 連鎖律とは、巨大なAI工場の最終的な失敗に対し、組立ラインの末端にあるネジ一本一本の「責任」までをも解明する、見事な伝達メカニズムであること。
- そして勾配降下法とは、これらの道具一式を手に、一歩、また一歩と、着実に谷底へと向かうための具体的な旅の進め方そのものであること。
次にあなたが、AIがX線写真から微細な病変を見つけ出したり、ゲノムデータから疾患リスクを予測したりするニュースを目にしたとき、その裏側で、この地道で健気な「谷探し」が何百万回と繰り返されていることを、少しだけ思い出していただけたら嬉しいです。
それは決して魔法ではありません。微分という、驚くほどシンプルで美しい数学的な概念が、AIに「間違いから学ぶ能力」という、知性の根源にも似た力を与えているのです。このシンプルな原理の積み重ねが、医療の未来を大きく、そして確実によい方向へと変えていく原動力となっているのです。
参考文献
- Goldberger, A.L., Amaral, L.A.N., Glass, L., Hausdorff, J.M., Ivanov, P.C., Mark, R.G., Mietus, J.E., Moody, G.B., Peng, C.-K. and Stanley, H.E. (2000). PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologi1c Signals. Circulation, 101(23), pp.e215–e220. doi:10.1161/01.cir.101.23.e215.
- Goodfellow, I., Bengio, Y. and Courville, A. (2016). Deep Learning. MIT Press. Available at: https://www.deeplearningbook.org/
- Kingma, D.P. and Ba, J. (2014). Adam: A Method for Stochastic Optimization. arXiv:1412.6980 [cs]. Available at: http://arxiv.org/abs/1412.6980
- LeCun, Y., Bengio, Y. and Hinton, G. (2015). Deep learning. Nature, 521(7553), pp.436–444. doi:10.1038/nature14539.
- Rajpurkar, P., Irvin, J., Zhu, K., Yang, B., Mehta, H., Duan, T., Ding, D., Bagul, A., Langlotz, C., Shpanskaya, K., Lungren, M.P. and Ng, A.Y. (2017). CheXNet: Radiologist-Level Pneumonia Detection on Chest X-Rays with Deep Learning. arXiv:1711.05225 [cs, stat]. Available at: http://arxiv.org/abs/1711.05225
- Ruder, S. (2016). An overview of gradient descent optimization algorithms. arXiv:1609.04747 [cs.LG]. Available at: https://arxiv.org/abs/1609.04747
- Rumelhart, D.E., Hinton, G.E. and Williams, R.J. (1986). Learning representations by back-propagating errors. Nature, 323(6088), pp.533–536. doi:10.1038/323533a0.
- Shickel, B., Tighe, P.J., Bihorac, A. and Rashidi, P. (2018). Deep EHR: A Survey of Recent Advances in Deep Learning Techniques for Electronic Health Record (EHR) Analysis. IEEE Journal of Biomedical and Health Informatics, 22(5), pp.1589–1604. doi:10.1109/jbhi.2017.2767063.
- Esteva, A., Kuprel, B., Novoa, R.A., Ko, J., Swetter, S.M., Blau, H.M. and Thrun, S. (2017). Dermatologist-level classification of skin cancer with deep neural networks. Nature, 542(7639), pp.115–118. doi:10.1038/nature21056.
- Topol, E.J. (2019). High-performance medicine: the convergence of human and artificial intelligence. Nature Medicine, 25(1), pp.44–56. doi:10.1038/s41591-018-0300-7.
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






