[The Medical AI : A13] 【統計学】そのグラフ、嘘をついていないか？データの「声なき声」を聴く作法

「AIが自動でデータを解析し、最適な治療法を提示してくれる」——そんな未来がすぐそこまで来ています。Pythonを学び、最新のアルゴリズムを動かす術を身につければ、私たちは「データの万能感」を手に入れたような気持ちになります。

しかし、ここで一つの冷酷な真実を直視しなければなりません。どれほど高度なAIモデルを使っても、扱う人間側に「統計的な直感」が欠けていれば、そのアウトプットは患者さんを救うどころか、判断を狂わせる毒にすらなり得るということです。

データサイエンスの世界には、”Garbage In, Garbage Out（ゴミを入れれば、ゴミが出てくる）”という有名な言葉があります。しかし、医療においてはさらに一歩進んで、“True Data In, Misinterpretation Out（正しいデータを入れても、解釈を間違えれば誤診が出る）”というリスクを常に孕んでいます。

本記事では、私たちが無意識に信じ込んでいる「平均値」や「p値」といった数字がいかにして私たちを欺くのか、そしてPythonという武器を使って、どうすればその「嘘」を見破れるのかを解説します。コードが書けるだけの『エンジニア』ではなく、データを正しく読み解き、患者の未来を予測できる『データサイエンティストとしての医師』への第一歩を、ここから踏み出しましょう。

---

平均値という「嘘つき」に騙されないために：データの真の姿を見る作法

私たち医師は、日々の診療や研究において「平均」という言葉を無意識に、そして頻繁に使っています。「この疾患の平均在院日数は？」「この患者群の平均HbA1cは？」「この治療法による平均生存期間は？」

確かに、平均値（Mean）はデータを要約する上で非常に便利な指標です。しかし、データサイエンスの視点から見ると、「データの分布（全体像）を確認せずに、平均値（要約）だけを信じて判断すること」は、患者さんのレントゲン画像を見ずに、カルテの要約文だけを読んで手術に臨むようなものです。これは極めて危険な行為と言わざるを得ません。

なぜ平均値だけでは不十分なのでしょうか？ それは、平均値が計算された瞬間に、個々のデータが持っていた「ばらつき」や「偏り」といった重要な情報が削ぎ落とされてしまうからです。

もしも、ビル・ゲイツがあなたのクリニックに来たら？（外れ値の衝撃）

平均値がいかに「外れ値（Outlier）」に弱いか、極端な例で考えてみましょう。

「平均年収」のトリック

ある小さなクリニックの待合室に、年収300万円の患者さんが10人座っています。この集団の「平均年収」はもちろん300万円です。

\[ \frac{300 \times 10}{10} = 300 \text{（万円）} \]

そこに突然、資産家のビル・ゲイツ（年収を仮に数千億円としましょう）が検診に現れ、待合室に入ってきました。

するとどうでしょう？ 待合室にいる11人全員の「平均年収」は、一瞬にして数百億円に跳ね上がります。

しかし、元からいた10人の患者さんはお金持ちになったでしょうか？ なっていません。彼らの生活水準は何も変わっていないのです。

これが「平均値の罠」です。たった一人の極端な外れ値（ビル・ゲイツ）の影響をまともに受けてしまい、平均値は「集団の代表値」としての機能を失ってしまいます。実態とかけ離れた数字が、さも真実かのように一人歩きしてしまうのです。

🏥 医療現場でのリアル：生存期間と治療効果の二極化

「年収の話は医療に関係ない」と思われるかもしれません。しかし、これと同じ現象は医療データでも頻繁に起こります。

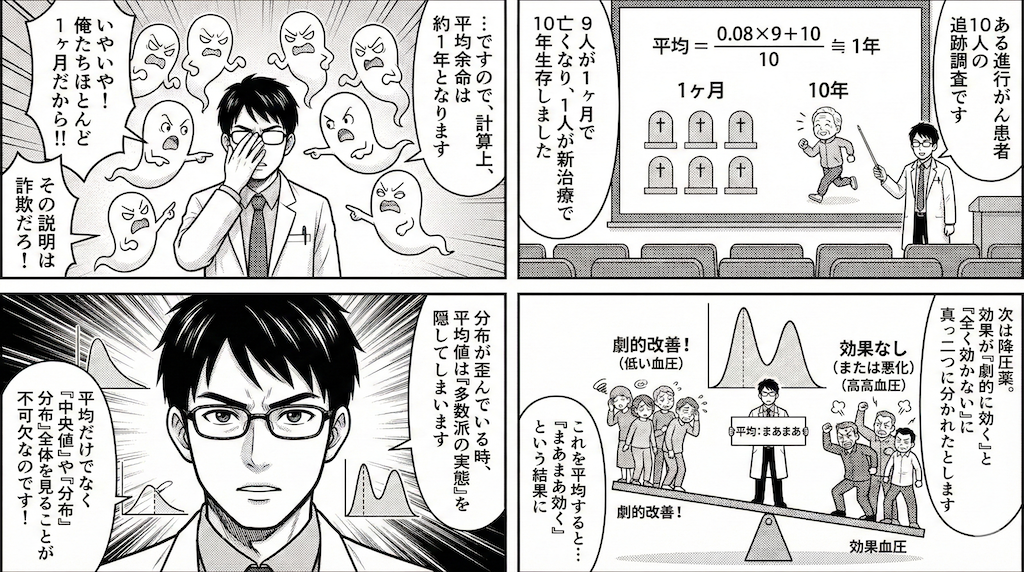
ケース1：平均生存期間のミスリーディング

ある進行がんの患者さん10人の生存期間を追跡したとします。

• 9人は病状が厳しく、残念ながら1ヶ月（0.08年）でお亡くなりになりました。
• しかし、残りの1人は新しい治療が劇的に効いて、10年間生存しました。

このとき、平均生存期間を計算してみましょう。

\[ \text{平均} = \frac{(0.08 \times 9) + 10}{10} = \frac{0.72 + 10}{10} = 1.072 \text{（年）} \]

計算上は「平均約1年生きられる」という結果になります。しかし、これをこれから治療を受ける患者さんに「この病気の平均余命は1年です」と伝えて良いでしょうか？
大半の人（90%）にとっての実態は「1ヶ月」です。平均値は、一部の長期生存者に引きずられ、大多数の実感とは異なる楽観的な数字を示してしまっています。

このように分布が歪んでいる場合（右裾が長い分布など）、実態をより適切に表しているのは平均値ではなく「中央値（Median）」です。上記の場合、中央値は「1ヶ月」となり、こちらの方が多数派の現実に即しています。

ケース2：治療効果の二極化（二峰性分布）

ある降圧薬を投与したとき、「劇的に効いて血圧が下がる群」と「全く効かない（むしろ上がるかもしれない）群」に真っ二つに分かれたとします。これらを混ぜて平均をとると、「まあまあ血圧が下がる」という結果になりかねません。
「平均的には効く」と言われて処方された薬が、自分には全く効かないか、あるいは効きすぎて低血圧になるリスクがあるとしたら？ 平均値だけを見ていては、このリスク（反応の二極化）に気づくことができません。

【Python実践】ヒストグラムで「分布」を可視化せよ

言葉だけで説明しても実感が湧きにくいかもしれません。Pythonを使って、「要約統計量（平均やSD）は全く同じなのに、中身（分布）が全く違うデータ」を作り出し、可視化してみましょう。

ここでは以下の2つのパターンを生成します：

1. パターンA（正規分布）：平均値の周りにデータが集まっている、教科書通りの「普通の山型」。
2. パターンB（二峰性分布）：データが「低い値」と「高い値」の2つの山に分かれているが、平均すると真ん中になるパターン。

このコードを実行して、数字のトリックをその目で確認してください。

# Google Colabなどで実行する場合は、事前に以下のコマンドでインストールしてください
# !pip install japanize-matplotlib

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib  # ←★これを追加するだけで日本語が表示されます

# 乱数のシードを固定（毎回同じ結果が出るようにする）
np.random.seed(42)

# ---------------------------------------------------------
# 1. パターンA：正規分布（普通の山型）のデータ生成
# ---------------------------------------------------------
# 平均=50, 標準偏差=10, サンプルサイズ=1000
data_normal = np.random.normal(loc=50, scale=10, size=1000)

# ---------------------------------------------------------
# 2. パターンB：二峰性分布（山が2つある）のデータ生成
# ---------------------------------------------------------
# 平均30の集団(500人)と、平均70の集団(500人)を混ぜ合わせる
# 全体としての平均は(30+70)/2 = 50 くらいになるはず
data_bimodal = np.concatenate([
    np.random.normal(loc=30, scale=5, size=500),
    np.random.normal(loc=70, scale=5, size=500)
])

# ---------------------------------------------------------
# データの可視化（ヒストグラムの描画）
# ---------------------------------------------------------
# グラフの描画設定（横に2つ並べる）
fig, axes = plt.subplots(1, 2, figsize=(14, 6))

# --- 左側：正規分布の描画 ---
sns.histplot(data_normal, kde=True, ax=axes[0], color='blue', alpha=0.3)
axes[0].set_title(f'パターンA：正規分布\n平均: {np.mean(data_normal):.1f}, SD: {np.std(data_normal):.1f}')
# 平均値の場所に赤い点線を引く
axes[0].axvline(np.mean(data_normal), color='red', linestyle='--', linewidth=2, label='平均値')
axes[0].legend()

# --- 右側：二峰性分布の描画 ---
sns.histplot(data_bimodal, kde=True, ax=axes[1], color='orange', alpha=0.3)
axes[1].set_title(f'パターンB：二峰性（山が2つ）\n平均: {np.mean(data_bimodal):.1f}, SD: {np.std(data_bimodal):.1f}')
# 平均値の場所に赤い点線を引く
axes[1].axvline(np.mean(data_bimodal), color='red', linestyle='--', linewidth=2, label='平均値')
axes[1].legend()

plt.tight_layout()
plt.show()

👀 実行結果の注目ポイント

生成されたグラフを見比べてみてください。

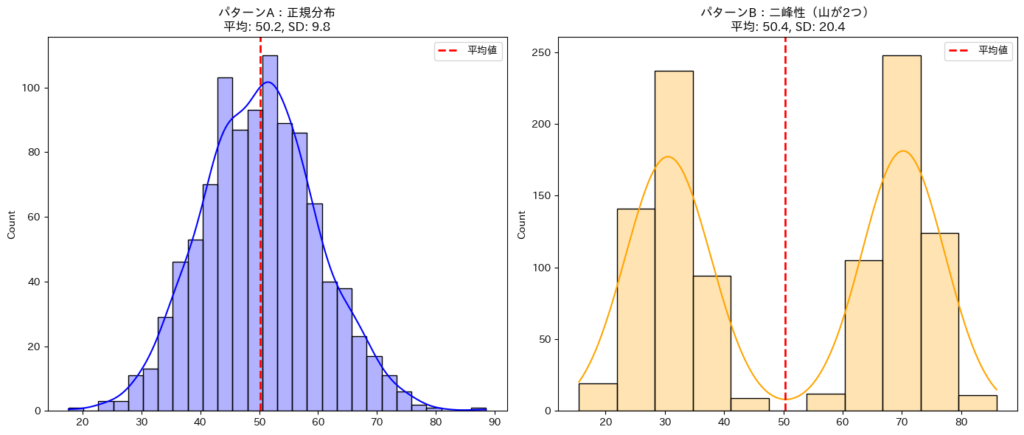
• 左のグラフ（青）： 平均値（赤い点線）の周辺に、最も多くのデータが集まっています。平均値は集団をよく代表しています。
• 右のグラフ（オレンジ）： 平均値（50付近）は、2つの山の間の「谷」に位置しています。つまり、平均値ちょうどの値を持つデータ（患者さん）は、実際にはほとんど存在しません。

もしこれが「ある治療薬の効果スコア」だったとしたらどうでしょう？
パターンBの場合、「平均スコア50だから、中くらいの効果がある」と判断するのは大間違いです。実際には「あまり効かない群（左の山）」と「すごく効く群（右の山）」にはっきりと分かれているのです。

このように、平均値と標準偏差（SD）という要約された数字だけを見ていると、データの真の姿を見誤るリスクがあります。Pythonによる可視化（ヒストグラムや箱ひげ図の作成）は、こうしたデータの「声なき声」を聴くための聴診器のような役割を果たします。まずはデータをグラフにしてみる。この習慣が、データ分析の第一歩です。

---

p値（ピー・バリュー）という名の「お守り」を捨てる

論文を読むとき、思考停止して 「\( p < 0.05 \)」 という記号を探していませんか？
もしあなたが「\( p < 0.05 \) だから、この薬は95%の確率で効果がある！」と思っているなら、それは致命的な誤解です。

p値は「無実の人から、こんな証拠が出る確率」だと思え

統計的仮説検定の考え方は、非常にひねくれています。「この薬には効果がある！」といきなり証明するのではなく、「裁判（推定無罪）」と全く同じ手順を踏んで、外堀から埋めていくのです。

統計学法廷のドラマ

ここに「新薬」という名の容疑者がいます。

• 検察官（あなた）：「こいつは『効果がある』という罪を犯しました！ 有罪判決を求めます！」
• 弁護人（統計学）：「異議あり。疑わしきは罰せず（推定無罪）です。証拠（データ）がない限り、この薬は『無実（効果ゼロ）』として扱われるべきです」

ここで、まず「新薬は全く効かない（＝無実）」という仮定を置きます。これを専門用語で「帰無仮説（\( H_0 \)）」と呼びます。

そして、現場検証（臨床試験）を行い、証拠（データ）を集めます。
もし、そこから出てきた証拠が、以下のようなものだったらどうでしょう？

「全く効かない薬（無実の人）のポケットから、血の付いたナイフと、犯行時刻のアリバイ崩れと、自白の録音テープ（＝劇的な治療効果データ）が出てきた」

裁判長（私たち）はこう考えます。
「もしこいつが無実だとしたら、こんな証拠が全部たまたま揃う確率は、確率的にありえない！」

「無実である」という前提に無理がある。
だから、「無実（帰無仮説）」を棄却し、「有罪（効果あり）」という判決を下す。
これが統計的仮説検定のロジックであり、この「無実だとしたら、こんな証拠が出てきてしまう確率」こそが p値 なのです。

p値の正体

ここで計算される \( p = 0.03 \)（3%） とは、以下の確率を指します。

p値の翻訳

「もし新薬が全くの偽物（小麦粉）だとしたら、こんな凄いデータが出る確率は、たった3%しかありません」

これを聞いて、裁判長（私たち）はこうツッコミを入れます。

「たった3%！？
小麦粉だったとしたら、3%しかないはずの『超レアな奇跡』が、たまたま起きたって言うのか？
いや、そんな偶然はありえない。
そもそも『この薬は偽物だ（無実）』という最初の前提が間違っていたんだ。
だから、この薬は本物だ（有罪）！」

これが「有意差あり（帰無仮説を棄却する）」の正体です。
決して「97%の確率で正しい」という意味ではありません。「まぐれだとすれば、あまりにも確率が低すぎる（ありえない）」と判断して、その可能性を捨てた、という意味なのです。

「コイン投げ」で体感するp値

もっとシンプルに、イカサマコインを見抜くゲームで考えましょう。

• あなた： 「このコイン、表が出やすいイカサマコインだろ！」
• 相手： 「いや、普通のコインだよ（帰無仮説）。」

実際に投げてみます。

1. 1回目：表 → 「まあ、普通だね（p = 0.5）」
2. 2回目：表 → 「まだ偶然ありえるね（p = 0.25）」
3. 3回目：表 → 「うん…（p = 0.125）」
4. 4回目：表 → 「ちょっと怪しいけど…（p = 0.0625）」
5. 5回目：表 → 「おい待て！普通のコインで5回連続表が出る確率は3%（p = 0.03125）だぞ！さすがに『普通のコイン』ってのは無理があるだろ！」

この 「おい待て！さすがに偶然じゃ説明がつかないぞ！」 とツッコミを入れたくなる境界線。それが一般的に使われる \( p < 0.05 \)（5%水準） です。

結論：明日から使える「p値の脳内翻訳」

明日から、論文や学会で 「\( p = 0.03 \)」 という数字を見かけたら、頭の中でこう「翻訳」してツッコミを入れてください。

p値 = 0.03 に対する裁判官（あなた）の思考

「小麦粉だったとしたら、3%しかないはずの『超レアな奇跡』が、たまたま起きたって言うのか？」

「いや、そんな偶然はありえない。」

「そもそも『この薬は偽物だ（無実）』という最初の前提が間違っていたんだ。」

「だから、この薬は本物だ（有罪）！」

これが「有意差あり」と判断する瞬間の頭の中身です。
p値とは、「『全部まぐれでした』という言い訳が、どれくらい苦しいか（＝3%という無理がある確率か）」を表す数字なのです。

【Python実践】t検定をシミュレーションする

言葉だけでは抽象的なので、Pythonを使って実験してみましょう。
2つのグループ（投薬群とプラセボ群）の血圧データを乱数で作成し、実際にp値を計算します。

実験のポイント： コード内の n = 30（サンプルサイズ：人数）を変えると、p値はどう変化するでしょうか？

import numpy as np
from scipy import stats

# ---------------------------------------------------------
# 実験設定：サンプルサイズ（N数）
# ここを「30」から「1000」に変えるとどうなるか想像してみてください。
# ---------------------------------------------------------
n = 30  

# 乱数のシードを固定（再現性のため）
np.random.seed(42)

# データの生成
# A群（プラセボ）：平均130, SD10 の正規分布
group_A = np.random.normal(loc=130, scale=10, size=n)

# B群（新薬）：平均125, SD10 の正規分布
# ※ 設定上、A群より「5」だけ低い（効果がある）データを作っています。
group_B = np.random.normal(loc=125, scale=10, size=n)

# t検定の実行（2群の平均値に統計的な差があるか？）
t_stat, p_val = stats.ttest_ind(group_A, group_B)

# 結果の表示
print(f"サンプル数(N): {n}")
print(f"A群平均: {np.mean(group_A):.1f}")
print(f"B群平均: {np.mean(group_B):.1f}")
print(f"p値: {p_val:.5f}")

# 判定（有意水準 5%）
if p_val < 0.05:
    print("判定：有意差あり (p < 0.05) ★")
else:
    print("判定：有意差なし")

サンプル数(N): 30
A群平均: 128.1
B群平均: 123.8
p値: 0.07217
判定：有意差なし

⚠️ p値のハック：サンプルサイズの魔法と罠

上記のコードで、n = 1000 に書き換えて実行してみてください。
平均値の差（効果の大きさ）が全く同じ設定でも、p値は劇的に小さくなり、確実に「有意差あり」になります。

サンプル数(N): 1000
A群平均: 130.2
B群平均: 125.7
p値: 0.00000
判定：有意差あり (p < 0.05) ★

これは統計学の性質上、必然です。サンプルサイズ（N数）を増やせば増やすほど、どんなに微小な差でも「統計的有意差」として検出できるようになるからです。

しかし、ここに落とし穴があります。
例えば、降圧薬で血圧が「0.1 mmHg」しか下がらなかったとしましょう。1万人のデータを集めれば、p値は0.05を下回り「有意差あり」となるでしょう。

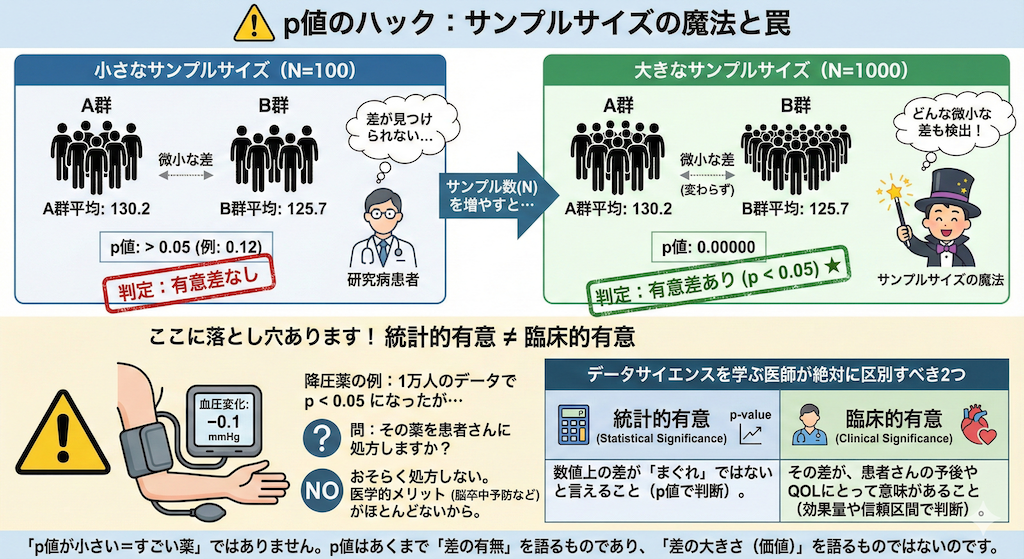
問：その薬を患者さんに処方しますか？

おそらく処方しないでしょう。0.1 mmHg の低下には、医学的なメリット（脳卒中予防など）がほとんどないからです。
データサイエンスを学ぶ医師が絶対に区別しなければならないのが、この2つです。

• 統計的有意（Statistical Significance）： 数値上の差が「まぐれ」ではないと言えること（p値で判断）。
• 臨床的有意（Clinical Significance）： その差が、患者さんの予後やQOLにとって意味があること（効果量や信頼区間で判断）。

「p値が小さい＝すごい薬」ではありません。p値はあくまで「差の有無」を語るものであり、「差の大きさ（価値）」を語るものではないのです。

---

相関関係の罠：アイスクリームで溺死者は増えるのか？

AIや統計分析に慣れていない人が、最も陥りやすく、かつ最も恥ずかしいミス。それが「相関関係（一緒に動いている）」を「因果関係（片方が原因で片方が結果）」と勘違いすることです。

有名なパラドックス：アイスと水難事故

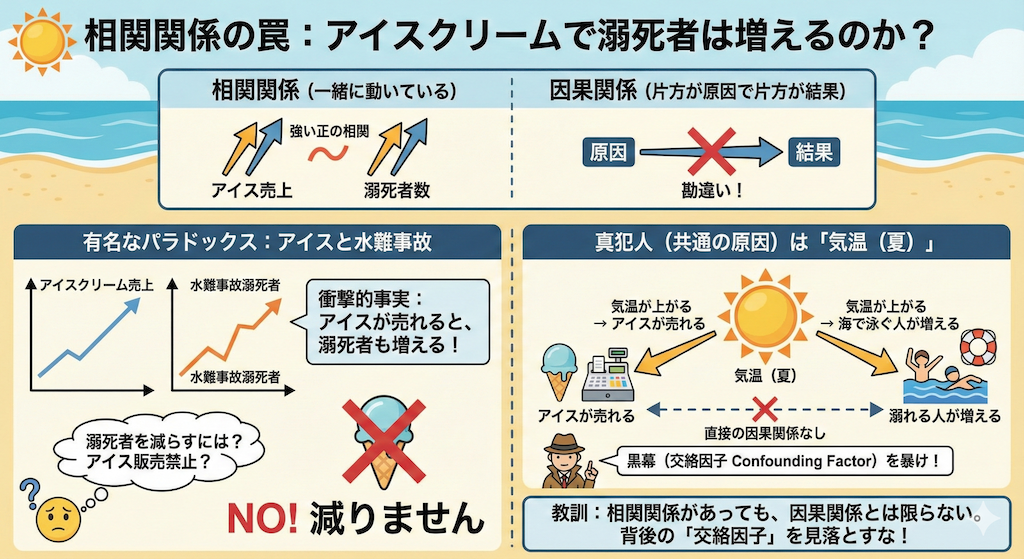
ある海岸のデータを分析したところ、衝撃的な事実が判明しました。
「アイスクリームの売上が増える日には、水難事故による溺死者も増えている」（強い正の相関）

さて、溺死者を減らすために、我々はどうすべきでしょうか？
「アイスクリームの販売を法律で禁止する」……これで溺死者は減りますか？

減りませんよね。なぜなら、アイスクリームが人を溺れさせたわけではないからです。
真犯人（共通の原因）は「気温（夏）」です。

• 気温が上がる → アイスが売れる
• 気温が上がる → 海で泳ぐ人が増える → 溺れる人が増える

アイスと溺死者の間に直接の関係はありません。この「気温」のような、背後に隠れて両方の数値に影響を与える黒幕を「交絡因子（Confounding Factor）」と呼びます。

【Python実践】見せかけの相関を作ってみる

「そんな子供騙しな……」と思われるかもしれません。しかし医学研究の歴史は、この交絡との戦いでした。かつて「コーヒーを飲むと膵臓がんになる」という論文が出たことがありますが、これも後に「コーヒーを飲む人は喫煙率が高かった（タバコが真犯人）」という交絡が指摘されました。

Pythonでこの「見せかけの相関（偽相関）」を再現してみましょう。プログラムの中で「アイス」と「溺死者」は一切関係を持たせていません。共通の親である「気温」に依存させているだけです。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# 乱数シードの固定
np.random.seed(42)

# ---------------------------------------------------------
# 交絡因子のシミュレーション
# ---------------------------------------------------------
n_samples = 100

# 1. 真犯人：気温（平均30度, SD5度）
temperature = np.random.normal(30, 5, n_samples)

# 2. アイスの売上：気温が高いほど売れる（気温に依存）
# ※溺死者数とは無関係に決まる
ice_cream = 50 * temperature + np.random.normal(0, 50, n_samples)

# 3. 溺死者数：気温が高いほど増える（気温に依存）
# ※アイスの売上とは無関係に決まる
drowning = 2 * temperature + np.random.normal(0, 5, n_samples)

# ---------------------------------------------------------
# 可視化：アイスと溺死者の関係
# ---------------------------------------------------------
plt.figure(figsize=(8, 6))
sns.scatterplot(x=ice_cream, y=drowning)

# 相関係数の計算
corr = np.corrcoef(ice_cream, drowning)[0,1]

plt.title(f"アイス売上 vs 溺死者数\n相関係数: {corr:.2f} (強い相関あり！)", fontsize=14)
plt.xlabel("アイスクリーム売上 (円)")
plt.ylabel("溺死者数 (人)")
plt.grid(True, alpha=0.3)
plt.show()

👀 実行結果の注目ポイント

グラフを描くと、見事に右肩上がりになります（相関係数は0.8以上になることが多いです）。
「アイスが売れれば売れるほど、人が死んでいる」ように見えます。

しかし、ここに因果関係はありません。アイスの販売を禁止しても、気温が高い限り、人々は海に行き、事故は減らないでしょう。

この「交絡」を統計的に処理し、見せかけの相関を取り除いて、真の因果効果（薬の効果など）を取り出す技術こそが「因果推論（Causal Inference）」です。

重要なのは、「ただデータをAIに食わせるだけでは、AIはこの交絡を見抜けない」ということです。AIは「アイスと溺死者には相関がある」としか言いません。「気温が原因だ」という因果の構造（地図）を描くのは、医学知識を持った人間の仕事なのです。

👉 さらに深く学びたい方は：
交絡の正体と、それを解決する「層別化」「多変量解析」「傾向スコア」といった手法は、[Series S] 第I部（S10〜S19）および第IV部（S40〜）で扱います。ここは現代のデータサイエンスで最も熱い分野です。

---

Series S への招待状：AIを使う側から、データを支配する側へ

このA13の記事では、Pythonを使って統計の基礎的な概念（分布、検定、相関）を「体験」しました。
しかし、これは広大な「医療データサイエンス」の入り口に立ったに過ぎません。

AI（機械学習）は強力な計算機ですが、「そのデータ、そもそも偏ってない？」「交絡因子は調整した？」「そのパターン、ただのノイズじゃない？」という本質的な問いには答えてくれません。
それを見抜き、計算結果を正しい医学的結論へと導く力こそが「統計学・疫学・因果推論」です。

次なるステップ、[Series S] 📊 Medical Data Science 100 : 医療AI時代のデータサイエンス大全：統計・疫学・因果推論・データサイエンス100講では、あなたの疑問に答えるための「武器」を網羅的に揃えています。

あなたの「知りたい」は、Series Sのどこにある？

目的別インデックス（処方箋）

• 「p値や信頼区間、実はよくわかってない…」
  👉 S0〜S9（基礎統計）：まずはここから。t検定の意味から、直感的に理解し直しましょう。
• 「自分のクリニックのデータを解析して学会発表したい」
  👉 S20〜S29（疫学・研究デザイン）：バイアスを避け、質の高い臨床研究を設計する作法を学びます。
• 「ロジスティック回帰や生存時間分析（Cox）をPythonでやりたい」
  👉 S30〜S39（モデリング）：医学論文で最も使われる多変量解析を、自分の手で実装します。
• 「観察データから『薬の効果』を証明したい（RCTは無理）」
  👉 S40〜S49（因果推論）：傾向スコアや操作変数法など、現代データサイエンスの必須スキルです。
• 「AIや深層学習を、もっと医学的に正しく使いたい」
  👉 S50〜（AI×因果推論）：ブラックボックスを開け、因果関係を理解する「次世代AI」へ。

「コードが書ける」だけでなく、「そのコードが出した結果が科学的に正しいか」を判断できる医師へ。
さあ、[Series S] の扉を開けましょう。

👉 [Series S] 第0回：ようこそ統計学の世界へ

参考文献

• Altman, D.G. (1991) Practical Statistics for Medical Research. London: Chapman and Hall.
• Spiegelhalter, D. (2019) The Art of Statistics: Learning from Data. Pelican Books.
• Huff, D. (1954) How to Lie with Statistics. W. W. Norton & Company.

※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。

---

ご利用規約（免責事項）

当サイト（以下「本サイト」といいます）をご利用になる前に、本ご利用規約（以下「本規約」といいます）をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。

第1条（目的と情報の性質）

1. 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
2. 本サイトで提供されるすべてのコンテンツ（文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません）は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為（以下「医行為等」といいます）を提供するものではありません。
3. 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
4. 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。

第2条（法令等の遵守）
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律（薬機法）、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。

第3条（医療行為における責任）

1. 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
2. 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家（医師、歯科医師等）が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
3. 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。

第4条（情報の正確性・完全性・有用性）

1. 本サイトは、掲載する情報（数値、事例、ソースコード、ライブラリのバージョン等）の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
2. 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。

第5条（AI生成コンテンツに関する注意事項）
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション（事実に基づかない情報の生成）やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。

第6条（知的財産権）

1. 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
2. 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。

第7条（プライバシー・倫理）
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。

第8条（利用環境）
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境（OS、ハードウェア、依存パッケージ等）を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。

第9条（免責事項）

1. 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害（直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません）について、その原因の如何を問わず、一切の法的責任を負わないものとします。
2. 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
3. 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
4. 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。

第10条（規約の変更）
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。

第11条（準拠法および合意管轄）
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。

---

For J³, may joy follow you.