データの「真ん中」を示す平均値だけでは、集団の本当の姿は見えません。データの「ばらつき」を理解することで、その個性を深く読み解くことができます。
分散は「各データと平均値の差(偏差)の2乗」の平均値で、ばらつきの大きさを示します。 しかし単位が2乗(例: cm²)され直感的ではありません。
標準偏差は分散の平方根をとったもので、単位が元に戻ります。 「データが平均からどのくらい離れているか」を直感的に示します。
データの分布を視覚化した「レントゲン写真」です。 中央値、データの中心50%が収まる範囲(箱)、全体の広がり(ひげ)、外れ値などを一目で把握できます。 複数のグループのばらつきを比較するのに非常に便利です。
平均値という「点」の情報に、標準偏差や箱ひげ図で示される「広がり」の情報を加えることで、データの姿を立体的に捉えることができます。
前回の冒険では、データの集団を代表する「真ん中」のキャプテン、平均値と中央値について学びましたね。これで、データの大まかな中心点がどこにあるのか、バシッと掴めるようになったはずです。でも、本当にそれだけで十分でしょうか?
想像してみてください。ここに、新薬Aを投与したグループと、新薬Bを投与したグループがいます。どちらのグループも、治療後の血圧の「平均値」はぴったり同じ120mmHgでした。これだけ見ると、「なんだ、どっちの薬も効果は同じくらいか」と思ってしまいそうですよね。
ところが、データをよーく見ると、グループAの患者さんは全員が115〜125mmHgの間に収まっているのに、グループBの患者さんは80mmHgの人もいれば160mmHgの人もいる…。もしそうなら、話は全く違ってきます。グループBの薬は、人によって劇的に効いたり、逆に全く効かなかったりする「クセの強い薬」なのかもしれません。
そう、データの「真ん中」だけを見ていては、その集団が持つ本当の「個性」や「性格」を見逃してしまうんです。この個性こそが、データの「ばらつき(散布度)」。今回は、この散らかり具合を解き明かすための最強の探偵ツール、「分散」と「標準偏差」の物語です!
なぜ「ばらつき」が重要?平均点が同じ、でも中身が違う2つのクラス
データのばらつきの重要性を、もっと身近な例で考えてみましょう。ここに、AクラスとBクラスという2つのクラスがあります。どちらもテストの平均点は70点でした。
- Aクラス: ほとんどの生徒が65点から75点の間にいて、みんなの実力が拮抗しているクラス。
- Bクラス: 90点以上の優秀な生徒と、40点以下の苦手な生徒に二極化しているクラス。
平均点だけ見れば同じでも、この2つのクラスに必要な指導が全く違うことは、誰の目にも明らかですよね。Aクラスは全体のレベルを少し上げる指導、Bクラスは個々のレベルに合わせた手厚いフォローが必要になりそうです。
これは医療現場でも全く同じ。同じ平均値を持つ2つの治療グループでも、効果のばらつきが大きければ、「なぜ一部の患者には効きにくいのか?」という新しい問いが生まれます。もしかしたら、そこに特定の遺伝子型や生活習慣が関係しているのかもしれません。このように、ばらつきは、私たちに次なる研究へのヒントを与えてくれる宝の山なんです。
ばらつきを数値化せよ!「分散」という名のアイデア
「ばらつきが大きい/小さい」と言うのは簡単ですが、それを客観的な「数字」で表すにはどうすれば良いでしょう?
一番シンプルなアイデアは、「各データが、平均値からどれくらい離れているか」を測ることですよね。この、平均値からの距離を「偏差」と呼びます。
でも、ここに一つ問題が。偏差にはプラス(平均より大きい値)とマイナス(平均より小さい値)があります。もし、全ての偏差を単純に足し合わせると、プラスとマイナスが打ち消し合って、合計が必ずゼロになってしまうんです。これでは、ばらつきの大きさを測れません。
そこで、ある賢い数学者がひらめきました。「そうだ!全部2乗してしまえば、マイナスが消えて全部プラスになるじゃないか!」
この素晴らしいアイデアから生まれたのが「分散 (Variance)」です。分散の計算は、以下のステップで行われます。
- 各データの「偏差(平均値との差)」を求める。
- それぞれの偏差を「2乗」する。
- 2乗した値を全部足し合わせて、最後にデータの個数(あるいは個数-1)で割る。
要するに、分散とは「偏差の2乗の平均値」なんです。式で書くとこうなります。
\[ s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i – \bar{x})^2 \]
一つずつ見ていきましょう。
- \(s^2\): 分散を表す記号です(sの2乗)。
- \((x_i – \bar{x})\): これが偏差。i番目のデータから平均値 \(\bar{x}\) を引いています。
- \((x_i – \bar{x})^2\): 偏差を2乗して、マイナスを消しています。
- \(\sum\): 全てのデータについて、計算した値を合計する記号でしたね。
- \(\frac{1}{n-1}\): 最後に合計値を割っています。
ここで「あれ?なんで \(n\) じゃなくて \(n-1\) で割るの?」と疑問に思った方は、とても鋭い! 私たちが扱うデータは、ほとんどの場合、もっと大きな集団(母集団)から取ってきた一部(サンプル)ですよね。そのサンプルから母集団全体のばらつきを推定しようとすると、実は少しだけズレが生じてしまうんです。そのズレを数学的に補正するために、\(n-1\) で割る、と今はふんわり理解しておけば大丈夫です。これを「不偏分散」と呼び、統計学ではこちらが主役です。
ただ、分散には一つだけ分かりにくい点が。値を2乗しているので、単位も2乗されてしまうんです。例えば、身長(cm)のデータの分散は、単位が \(cm^2\) (平方センチメートル) になってしまい、直感的にピンときませんよね。
最強の相棒「標準偏差」!元の世界にカムバック
分散の「単位が2乗されちゃって分かりにくい問題」を解決するために登場したのが、今回の真のヒーロー、「標準偏差 (Standard Deviation, SD)」です。
作り方は驚くほど簡単。分散に平方根(ルート \(\sqrt{\quad}\))をかぶせるだけ。
\[ s = \sqrt{s^2} = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (x_i – \bar{x})^2} \]
たったこれだけで、単位が元のデータと同じ(\(cm^2\) が \(cm\) に)戻ってきます。これにより、標準偏差は「データがおおよそ平均値からどれくらい離れて散らばっているか」を示す、とても直感的な指標になるんです。
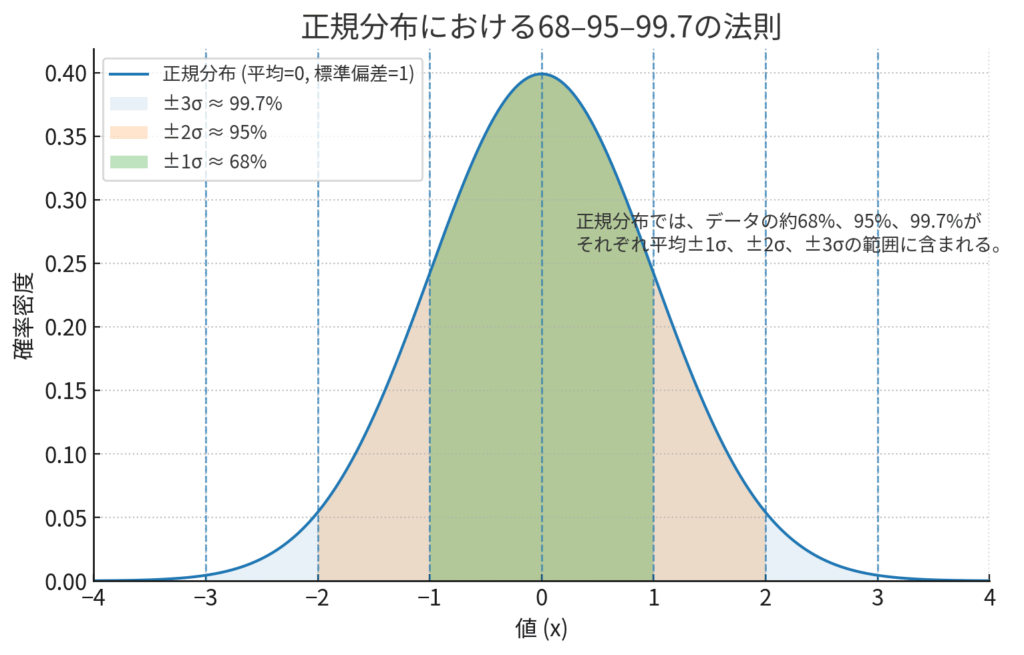
標準偏差がなぜこれほどまでに愛されているかというと、特にデータが正規分布(きれいな左右対称の釣鐘型の分布)に近い場合、次のような美しい関係があるからです(68-95-99.7ルール)。
- 「平均値 ± 1 × 標準偏差」の範囲に、約68%のデータが含まれる。
- 「平均値 ± 2 × 標準偏差」の範囲に、約95%のデータが含まれる。
- 「平均値 ± 3 × 標準偏差」の範囲に、約99.7%のデータが含まれる。
論文のグラフでよく見る、平均値の棒グラフに生えているヒゲ(エラーバー)。あれが、この標準偏差(や、それを応用した標準誤差、信頼区間)を表していることが多いんです。つまり標準偏差は、データのばらつきを評価し、群間で比較するための世界共通言語とも言えるんですね。
データのレントゲン写真!「箱ひげ図」で一目瞭然
分散や標準偏差は、ばらつきを一つの数字にまとめてくれるパワフルなツールです。でも、時には「数字だけじゃなくて、もっと全体像をパッと見たい!」と思うこともありますよね。
そんな時に役立つのが、データの分布を視覚化する「箱ひげ図 (Box Plot)」です。これは、データの散らばり具合を「箱」と「ひげ」で表現したグラフで、まさにデータのレントゲン写真のようなもの。
箱ひげ図は、データを小さい順に並べ、それを4等分するポイントを使って描かれます。
この図から、こんなにも多くの情報を読み取れるんです。
- 箱の長さ(四分位範囲, IQR): 箱の部分は、データ全体の真ん中50%が収まる範囲を示します。この箱が長ければ長いほど、データのばらつきが大きいことを意味します。
- 箱の中の線(中央値): データ全体のど真ん中です。これが箱の中心からどちらかにズレていれば、データの分布が左右非対称に「歪んでいる」ことが分かります。
- ひげの長さ: 上下(左右)に伸びる線は、データ全体のおおよその広がりを示します。
- 外れ値(点): 箱やひげから大きく外れた場所にプロットされる点で、極端な値の存在を教えてくれます。
臨床研究で2つの治療群を比較する際、それぞれの結果を箱ひげ図で隣り合わせに並べてみてください。平均値や中央値の高さの違いだけでなく、箱の長さ(ばらつき)や分布の歪み、外れ値の有無まで、一目で比較することができます。統計学者ジョン・テューキーが考案したこの図は、探索的データ解析において非常に強力な武器となります (Tukey, 1977)。
まとめ:ばらつきを知れば、データはもっと饒舌になる
いかがでしたか?今回は、データの「真ん中」だけでなく、その「散らかり具合」に焦点を当ててきました。
- データの「真ん中」が同じでも、「ばらつき」が違えば、集団の性質は全く異なる。
- 分散と標準偏差は、そのばらつきを客観的な「数値」で示してくれる強力なツール。
- 箱ひげ図は、データの分布、歪み、外れ値までを「視覚的」に教えてくれるレントゲン写真。
平均値や中央値という「点」の情報に、標準偏差や箱ひげ図という「広がり」の情報を加えることで、私たちはデータの姿をより立体的(3D)に捉えることができるようになります。CONSORT声明のような臨床試験の報告ガイドラインでも、結果を要約する際には、ばらつきの指標(標準偏差など)を併記することが強く推奨されています (Schulz et al., 2010)。
データは、私たちが正しく問いかけさえすれば、本当に多くの物語を語ってくれます。次回は、今回少しだけ顔を出した「グラフ」に焦点を当て、データをさらに魅力的に、そして直感的に表現するための可視化の魔法について探求していきましょう!
参考文献
- Altman, D. G. (1990). Practical statistics for medical research. CRC Press.
- Altman, D. G., Bland, J. M. (1996). Statistics notes: Standard deviations and standard errors. BMJ, 313(7048), 903.
- Bland, M. (2015). An introduction to medical statistics (4th ed.). Oxford University Press.
- Bland, J. M., & Altman, D. G. (1996). Statistics notes: Transforming data. BMJ, 312(7033), 770.
- Campbell, M. J., Machin, D., Walters, S. J. (2007). Medical statistics: A textbook for the health sciences (4th ed.). Wiley.
- Kirkwood, B. R., & Sterne, J. A. C. (2003). Essential medical statistics (2nd ed.). Blackwell Science.
- Norman, G., & Streiner, D. (2014). Biostatistics: The bare essentials (4th ed.). PMPH-USA.
- Schulz, K. F., Altman, D. G., & Moher, D. (2010). CONSORT 2010 statement: updated guidelines for reporting parallel group randomised trials. BMJ, 340, c332.
- Swinscow, T. D. V., & Campbell, M. J. (2002). Statistics at square one (10th ed.). BMJ Books.
- Tukey, J. W. (1977). Exploratory data analysis. Addison-Wesley.
- Vittinghoff, E., Glidden, D. V., Shiboski, S. C., & McCulloch, C. E. (2012). Regression methods in biostatistics: Linear, logistic, survival, and repeated measures models (2nd ed.). Springer.
- Sheskin, D. J. (2020). Handbook of parametric and nonparametric statistical procedures (6th ed.). CRC Press.
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






