高性能なAIを育てるには、モデルに「個性」と「規律」を与えることが重要です。「活性化関数」で柔軟な表現力を与え、「正則化」で訓練データの丸暗記(過学習)を防ぎ、未知のデータにも強い、信頼性の高いモデルを構築します。
線形変換に非線形性を加え、モデルの表現力を高めます。ReLUは入力が負なら0、正ならそのまま出力するシンプルかつ強力な関数で、学習の安定化にも貢献します。
学習中にランダムにニューロンを休ませ、特定の特徴への過度な依存を防ぎます。これによりモデルの「丸暗記」(過学習)を抑制し、未知のデータへの対応力を高めます。
モデルの重みが大きくなりすぎることにペナルティを課し、過度に複雑でギザギザなモデルになるのを防ぎます。より滑らかで、汎用性の高いモデルの学習を促します。
私たちは、ニューラルネットワークというAIモデルの基本的な骨格を組み立て、損失関数でモデルの「間違い」を測り、そして最適化アルゴリズムを使ってその間違いを少しずつ減らしていく、という一連のプロセスを一緒に体験してきましたね。
私たちがここまで作ってきたニューラルネットワークは、いわば生まれたばかりのAIの赤ちゃんのようなものかもしれません。基本的な構造(骨格)はあり、間違いを指摘されれば(損失関数)、改善しようと素直に努力する(最適化)。とても良い子ですよね。
しかし、この「素直」なままでは、現実世界の複雑な問題を解決するには、まだ少し力が足りないのです。なぜなら、これまでのモデルは、物事を直線的にしか捉えられないため、もっと複雑なパターンを見抜く「柔軟な思考」ができません。
そしてもう一つ、もしこのAIの赤ちゃんが勉強熱心すぎると、訓練データという教科書に書かれていることを一字一句「丸暗記」してしまい、いざ本番のテスト(未知のデータ)に臨んだときに全く応用が利かない、「ガリ勉タイプ」になってしまう危険性も潜んでいます。
そこで今回は、このAIの赤ちゃんを、より賢く、そして社会で通用する大人へと成長させるための、二つの大切な「教育方針」について学んでいきたいと思います。
- 一つは、物事を多角的に捉えるための『柔軟な思考力(個性)』を育む活性化関数 (Activation Function)。
- もう一つは、知識をただ詰め込むだけでなく、本質を理解し応用する力を養うための『学びの規律』を教える正則化 (Regularization)です。
この講義では、そのための具体的な道具として、現代のディープラーニングの世界で活躍している、いわば「三種の神器」とも言える手法に焦点を当てていきます。
- ReLU: シンプルだけど、脳の働きにも似た賢いスイッチとなる活性化関数
- Dropout: あえて仲間をサボらせて、チーム全体を強くするユニークな戦略
- L2正則化: モデルが自信過剰(過学習)にならないよう、そっと見守るブレーキ役となる正則化
これらの概念を自分のものにすることは、皆さんがこれから医療の現場で本当に役立つ、高性能で信頼性の高いAIモデルを育て上げていく上で、間違いなく決定的な一歩となるでしょう。さあ、一緒にAIの「教育」を始めていきましょう!
1. 活性化関数 (Activation Function) – ニューロンに「個性」を与える非線形の魔法
さて、まずは活性化関数そのものについて、そもそも「なぜ、そんなものが必要なの?」という、一番根本的なところからお話しさせてください。これが分かると、AIモデルがなぜあんなに複雑なことができるのか、その秘密の一端が見えてくるはずです。
1.1 なぜ活性化関数が必要なのか? 〜透明なガラスから、魔法のレンズへ〜
これまでの私たちのモデルは、入力に重みを掛けてバイアスを足す、という線形変換の組み合わせでしたね。
\[ \text{出力} = \text{重み} \times \text{入力} + \text{バイアス} \]

これは、例えるなら「どこまでも透明なガラス板」を何枚も何枚も重ねているようなものなんです。10枚重ねても100枚重ねても、結局は向こう側が透けて見えるだけで、景色が面白く変化したりはしません。つまり、どんなに層を深くしても、モデル全体でできることは、結局たった1層の線形変換と変わらない、ということになってしまいます。
これでは、世の中の複雑な現象、例えば医療データでよく見られる「ある検査値が低すぎても高すぎてもリスクが高い」といった、直線では到底表現できないような関係性を、AIが学習することはできません。
そこで登場するのが、この重ねたガラス板の間に、光を屈折させるプリズムや、色を付けるセロハンを挟むような役割を果たす、活性化関数なんです。この「非線形」というひと工夫を各層の計算の後に挟んであげることで、層を重ねるごとに表現できる関数の複雑さが爆発的に増え、私たちのAIモデルは、まるで粘土に自在に形を与えるように、どんな複雑なデータにもフィットしていく能力(表現力)を獲得するのです。まさに、AIに豊かな「個性」と「表現の幅」を与える、魔法のスパイスと言えるかもしれませんね。
1.2 ReLU (Rectified Linear Unit) – シンプルイズベストな標準選手
では、その魔法のスパイスにはどんな種類があるのでしょうか。歴史的にはシグモイド関数やtanh関数といったものが使われてきました。

現在のディープラーニングの世界、特に画像認識などの分野では、ある活性化関数が圧倒的な人気を誇り、いわば「迷ったら、まずこれを使え」と言われるほどの標準的な選択肢となっています。それが、今回主役となるReLU(レルー、Rectified Linear Unit)です。
ReLUの考え方は、その人気とは裏腹に、驚くほどシンプルで、拍子抜けするほどです。
入力された信号がプラスなら、そのまま通してあげる。でも、マイナスだったら、そこでバッサリと信号を止めて、0にしてしまう。
たったこれだけなんです。まるで、ポジティブな情報だけを通す、超効率的な関所のようなものですね。数式で書くと次のようになります。
\[ f(x) = \max(0, x) \]
これは、入力 \(x\) と \(0\) を比べて、大きい方を出力する、という意味です。
ReLU関数のグラフイメージ
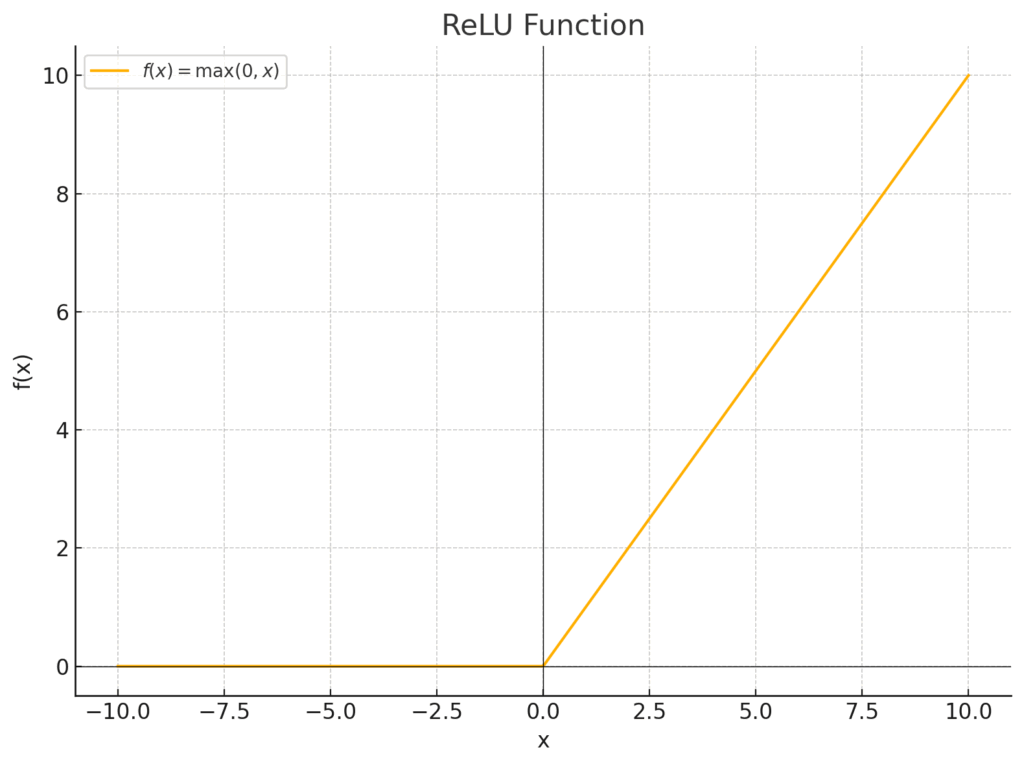
なぜReLUはこんなに人気なのでしょうか? その理由は、主に3つの大きな利点にあります。
- 勾配消失問題の緩和: これはReLUの最大の功績の一つかもしれません。以前の活性化関数(シグモイド関数など)では、層を深くすると、学習信号である勾配が過去に遡るにつれてどんどん小さくなり、やがて消えてしまう「勾配消失問題」が深刻でした。これは、関数のどの部分でも微分値(グラフの傾き)が1より小さいため、掛け算を繰り返すうちに0に収束してしまうのが原因でした。しかし、ReLUを見てください。入力が正の領域では、グラフの傾きは常に「1」ですよね。これは微分値が1だということです。つまり、勾配が過去の層に伝わる際に、その大きさを減衰させることなく、そのままの勢いで伝えてあげることができるんです。これにより、深いネットワークでも学習が効率的に進むようになりました。
- 計算効率の良さ: これも大きな魅力です。コンピュータにとって、
max(0, x)という計算は、入力値が0より大きいかどうかをチェックするだけの、非常に単純で軽い処理です。これが、複雑な指数関数などを使う他の活性化関数と比べて、計算速度を大幅に向上させ、学習全体の時間を短縮することに貢献しています。 - スパースな表現の獲得: これは少し専門的な話になりますが、面白い性質です。入力が負のニューロンの出力は強制的に0になるため、結果としてネットワーク内の全てのニューロンが常に活動するのではなく、入力に応じて一部のニューロンだけが発火(活性化)する、という状態が生まれます。これをネットワークの「スパース性」と呼びます。実は、私たちの脳も、全てのニューロンが常にフル稼働しているわけではなく、必要な部分だけが活動していると考えられています。このスパースな活性化が、より効率的で、ノイズに強い学習に繋がるのではないか、と考えられているんですね。
医療分野での示唆:
例えば、患者さんのデータの中で、「血圧がある一定値を超えた場合にのみ、他の因子との関連性が重要になる」といったシナリオを考えてみてください。ReLUのこの「閾値0でオンになる」というスイッチのような性質は、そうした条件付きの非線形な関係性をモデルが捉える上で、非常に直感的で強力なメカニズムとして機能する可能性があります。
Pythonコード例:PyTorchでReLUを体験する
では、このシンプルでパワフルなReLUの動きを、PyTorchのコードで実際にその目で確かめてみましょう。入力した数値がどう変わるか、注目してみてくださいね。
# 必要なライブラリをインポートします
import torch
import torch.nn as nn
# --- 1. サンプルデータを作成 ---
# ReLUの動作を確認するために、正の値、0、負の値を含む簡単なテンソルを用意します。
# 5つの数値を持つ、1次元のテンソルです。
input_tensor = torch.tensor([-3.0, -0.5, 0.0, 1.0, 2.5])
print("--- ReLU適用前 ---")
print("入力テンソル:", input_tensor)
# --- 2. ReLUのインスタンスを作成 ---
# PyTorchのニューラルネットワーク部品(nn)の中から、ReLUを呼び出して準備します。
# これで、ReLUという「機能」を持つオブジェクトが作成されます。
relu_activation = nn.ReLU()
# --- 3. ReLUを適用 ---
# 作成したReLUを、入力テンソルに適用します。
# これにより、テンソルの各要素に対して、関数 f(x) = max(0, x) が適用されます。
output_tensor = relu_activation(input_tensor)
print("\n--- ReLU適用後 ---")
print("出力テンソル:", output_tensor)
# === ここから下が上記のprint文による実際の出力 ===
# --- ReLU適用前 ---
# 入力テンソル: tensor([-3.0000, -0.5000, 0.0000, 1.0000, 2.5000])
#
# --- ReLU適用後 ---
# 出力テンソル: tensor([0.0000, 0.0000, 0.0000, 1.0000, 2.5000])
ご覧の通り、本当にシンプルですよね。負の値は容赦なく0に、正の値はそのままに。この単純明快なルールが、現代のディープラーニングを支える大きな柱の一つになっているというのは、なんだかとても興味深いことだと思います。
2. 正則化 (Regularization) – モデルに「規律」を教え込む賢いブレーキ
さて、活性化関数という魔法のスパイスを手に入れた私たちのAIモデルは、理論上はどんなに複雑なパターンでも捉えられる豊かな表現力(個性)を持つようになりました。でも、強力な力には、時として大きな副作用が伴うものです。その代表例が、多くのAI開発者が頭を悩ませる過学習(Overfitting)という現象なんです。
2.1 過学習とは? 〜訓練には強いが、本番に弱い「ガリ勉」モデル〜
過学習とは、AIモデルが訓練データをあまりにも熱心に学習しすぎた結果、そのデータに含まれる細かなノイズや、たまたまそうなっていただけの偶然のパターンまで「一字一句すべて丸暗記」してしまい、いざ本番のテスト、つまり未知の新しいデータに直面したときには、全く力を発揮できなくなってしまう状態を指します。
例えるなら、「模擬試験の問題と解答のペアを完璧に暗記して模試では満点を取るけれど、問題の本質的な解き方を学んでいないため、少し問題の形式が変わる本番の試験では全然歯が立たない学生」のような状態です。この学生の「本番の試験での実力」にあたるのが、AIモデルの般化性能(Generalization Performance)です。私たちが本当に作りたいのは、訓練データで良い点を取ることだけが目的のモデルではなく、般化性能の高い、つまり未知のデータにも強い「地力のある」モデルですよね。
過学習の概念図(学習曲線)
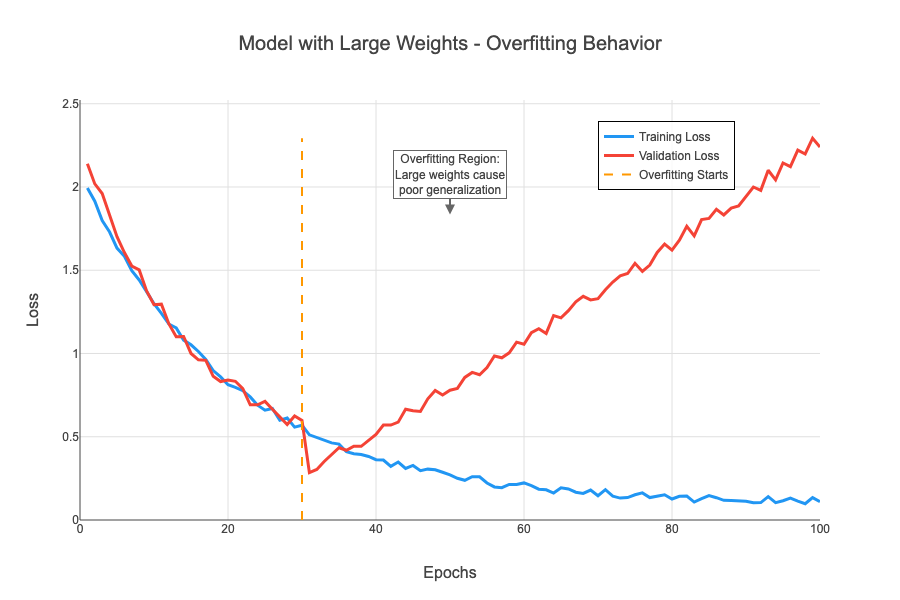
解説:
- 訓練データに対する損失(訓練損失)は、学習を進めるほど順調に下がり続けます。
- 一方、訓練に使っていない未知のデータ(検証データ)に対する損失(検証損失)は、
学習の初期では一緒に下がっていきますが、ある時点から逆に上昇し始めます。
- この「訓練損失は下がり続けるのに、検証損失が上がり始める」ポイントが、
モデルが訓練データを丸暗記し始め、般化性能を失っている(過学習している)サインです。
医療分野での深刻さ:
これが医療AIの世界で起こると、本当に深刻な問題になります。例えば、A病院の患者さんのデータだけで訓練したAIモデルが、A病院のデータでは99%という驚異的な精度を叩き出したとします。でも、いざB病院の、少し傾向の違う患者さんのデータで試してみたら、精度が50%までガクッと落ちてしまった…。これでは、臨床の現場で安心して使えるとは到底言えませんよね(1)。私たちが目指すのは、特定の訓練データだけに特化した「実験室のAI」ではなく、どんな病院の、どんな患者さんのデータに対しても、安定して高い性能を発揮できる、頑健で信頼性の高いAIなのです。
この、モデルが訓練データに媚びすぎてしまう「過学習」という暴走を防ぎ、未知のデータに対する真の実力(般化性能)を高めるために、モデルに適切な「規律」を教え込むためのテクニック。その総称が、正則化です。いわば、AIの学習における賢い「ブレーキ役」のようなものですね。
2.2 Dropout – ニューロンをランダムに休ませるチームワーク向上策
数ある正則化手法の中でも、非常に独創的で、今なお広く使われているのがDropout (ドロップアウト) です(2)。Dropoutの考え方は、人間社会のアナロジーで考えると非常に分かりやすいので、少し想像してみてください。
ある専門家チームで複雑な問題に取り組んでいるとします。もし、チームの中に一人だけ、とてつもなく優秀な天才がいたら、他のメンバーはその天才に頼りきりになってしまい、チーム全体の力は育ちませんよね。そこで、会議のたびに、ランダムに何人かのメンバーに「今日は休んでください」と強制的に休ませます。そうすると、残ったメンバーは、いつもの天才がいない状況でも何とか問題を解決しようと、各自がより能力を高め、協力し合うようになります。結果として、個々のメンバーが成長し、チーム全体としてより頑健で、誰か一人が欠けても機能する、強い組織になります。
Dropoutは、まさにこの「強制的なチームワーク向上策」をニューラルネットワークの世界で実現する、非常に独創的でパワフルな手法なんです。学習の過程で、各ニューロンを一定の確率 \(p\) でランダムに「無効化」(つまり、そのニューロンからの信号を一時的にゼロにする)のです。これにより、ネットワークは特定のニューロンに過度に依存することをやめ、より多くのニューロンが協調して特徴を学習するようになり、結果として過学習が抑制され、般化性能が向上します。
Dropoutの概念図
【通常のネットワーク】 【Dropout適用中のネットワーク】
入力層 隠れ層 出力層 入力層 隠れ層 出力層
( ● ) ---- ( ● ) ---- ( ● ) ( ● ) ---- ( ● ) ---- ( ● )
| \ / | | | \ | |
| \ / | | | \ | |
( ● ) -- ( ● ) ---- ( ● ) ( ● ) -- ( X ) -- ( ● )
| / \ | | | / \ | |
| / \ | | | / \ | |
( ● ) ---- ( ● ) ---- ( ● ) ( ● ) ---- ( ● ) ---- ( ● )
(X) は確率pでDropoutされた
(活動停止した)ニューロン
見方を変えると、Dropoutは学習のたびに異なるニューロンの組み合わせを持つ、膨大な数の「小さなサブネットワーク」を同時に学習させている、と解釈することもできます。そして、最終的な推論時には、それらたくさんのサブネットワークの意見を平均化(アンサンブル)するような効果が生まれます。色々な専門家の意見を聞くと、より堅実で偏りのない結論にたどり着きやすいのと似ていますね。これが、Dropoutが強力な般化性能をもたらす理由の一つだと考えられています。
重要な注意点:
ここで一つ、とても大切なポイントがあります。この「ニューロンを休ませる」という操作は、モデルが学習している訓練時(model.train()モード)にだけ行われます。モデルの性能を評価したり、実際に未知のデータに対して推論したりする際(model.eval()モード)には、全てのニューロンが総出で活動状態に戻ります。PyTorchの nn.Dropout レイヤーは、この train() と eval()のモード切り替えを検知して、自動で振る舞いを変えてくれるので、私たちは安心して使うことができるんですね。
Pythonコード例:PyTorchでDropoutを体験する
# 必要なライブラリをインポートします
import torch
import torch.nn as nn
# --- 1. Dropoutレイヤーを作成 ---
# nn.Dropout() でDropout層を作ります。
# p=0.5 は、各要素が50%の確率で0になる(ドロップアウトする)ことを意味します。
dropout_layer = nn.Dropout(p=0.5)
# --- 2. サンプルデータを作成 ---
# 全ての要素が1.0である、分かりやすいテンソルを用意します。
# 形状は (1, 10) で、1つのバッチに10個の要素があるデータです。
input_tensor = torch.ones(1, 10)
print("--- Dropout適用前 ---")
print("入力テンソル:", input_tensor)
# --- 3. 訓練モード (model.train()) でDropoutを適用 ---
# モデルを「訓練モード」に設定します。これによってDropoutが有効になります。
dropout_layer.train()
# この状態でデータを入力すると、Dropoutが適用されます。
output_train_mode = dropout_layer(input_tensor)
print("\n--- 訓練モード (train) での出力 ---")
print("出力テンソル:", output_train_mode)
print("# いくつかの要素が確率的に0になり、残りの要素は2倍にスケールされている点に注目!")
# --- 4. 評価モード (model.eval()) でDropoutを適用 ---
# 今度はモデルを「評価モード」に設定します。これによってDropoutが無効になります。
dropout_layer.eval()
# この状態で同じデータを入力します。
output_eval_mode = dropout_layer(input_tensor)
print("\n--- 評価モード (eval) での出力 ---")
print("出力テンソル:", output_eval_mode)
print("# 全ての要素が元の値 (1.0) のまま。Dropoutは適用されません。")
# === ここから下が上記のprint文による実際の出力の例(乱数なので結果は毎回変わります) ===
# --- Dropout適用前 ---
# 入力テンソル: tensor([[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]])
#
# --- 訓練モード (train) での出力 ---
# 出力テンソル: tensor([[2., 0., 2., 2., 0., 0., 2., 0., 2., 0.]])
# # いくつかの要素が確率的に0になり、残りの要素は2倍にスケールされている点に注目!
# (注: PyTorchのDropoutは、0にならなかった要素を 1/(1-p) 倍します。p=0.5なので、1/(1-0.5) = 2倍になります。
# これは、評価時に何もしなくて済むようにするための実装上の工夫です。)
#
# --- 評価モード (eval) での出力 ---
# 出力テンソル: tensor([[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]])
# # 全ての要素が元の値 (1.0) のまま。Dropoutは適用されません。
訓練モードと評価モードで、見事に振る舞いが変わるのが面白いですよね。PyTorchのnn.Dropoutレイヤーとtrain()/eval()メソッドが、この面倒な切り替えを裏で全部やってくれるので、私たちは安心して使うことができるわけです。
2.3 L2正則化 (Weight Decay) – モデルの「行き過ぎ」にブレーキをかける
さて、もう一つの代表的な正則化手法が、L2正則化です。その仕組みから、しばしばWeight Decay(重み減衰)とも呼ばれます。先ほどのDropoutが、いわばチームのメンバーを入れ替えることで組織の柔軟性を高める「構造改革」アプローチだったのに対し、こちらはモデルが目指すべき「目標(損失関数)」そのものに、新たな価値観を付け加えるアプローチです。一体どういうことでしょうか?
L2正則化の考え方 〜レシピに加わる「調味料は控えめに」の教え〜
「味を良くするために(元の損失を小さくする)、色々な調味料(重み)を使うのは良いけれど、一つの調味料をドバドバ使いすぎる(重みが大きくなる)のはやめようね。全体のバランスを考えて、色々な調味料を少しずつ使った方が、上品で深みのある味になるよ」
L2正則化は、まさにこのような「レシピの注意書き」を、AIモデルの学習ルールに加えるようなイメージです。
具体的には、モデルが最小化を目指す損失関数に、ある種の「ペナルティ項」を追加します。
\[ L_{\text{total}} = L_{\text{original}} + \lambda \sum_{i} w_i^2 \]
この式、なんだか難しそうに見えるかもしれませんが、一つ一つの意味はとてもシンプルです。
- \( L_{\text{original}} \) は、これまで私たちが扱ってきた「元の損失」です。モデルの予測と正解データとの間の誤差(例えばMSEや交差エントロピー誤差)のことで、モデルはこれを小さくしようと必死に頑張ります。
- \(\sum_{i} w_i^2\) の部分は、ネットワーク内に存在する全ての重み \(w_i\) を、それぞれ2乗して、全部足し合わせたものです。モデルの重みの絶対値が大きくなればなるほど、この項の値も大きくなります。これが「ペナルティ項」です。
- そして \(\lambda\) (ラムダ) は、私たちが設定するハイパーパラメータで、「どれだけ重みの大きさを気にするか」という、ペナルティの「厳しさ」をコントロールする係数です。この値が大きいほど、AIは重みを小さく保つことを強く意識するようになります。
AIモデルは、「新しい全体の損失」である \(L_{\text{total}}\) を最小化するように学習します。これはつまり、「予測を正解に近づけたい!(\(L_{\text{original}}\)を小さくしたい)」という気持ちと、「でも、そのためだけに派手な調味料(大きな重み)を使いすぎてペナルティを受けるのは避けたい!(\(\lambda \sum w_i^2\)も小さくしたい)」という気持ちの、いわば二つの力の綱引きをしながら、その絶妙なバランス点を探して学習を進めることを意味するのです。
なぜ重みが小さいと良いのか? 〜なだらかなモデルを目指して〜
では、なぜ重みを小さく保つと、過学習を防ぐ助けになるのでしょうか?
直感的には、個々の重みの値が大きいモデルというのは、入力がほんの少し変わるだけで、出力がジェットコースターのように激しく変動する、とても過敏で「ギザギザ」な関数になりがちです。このようなモデルは、訓練データに含まれる小さなノイズの一つ一つにまで過剰に反応してしまい、結果として過学習に陥りやすくなります。
L2正則化は、このギザギザの原因となる大きな重みにペナルティを課すことで、モデルをより「なだらか」で、未知のデータに対しても安定した性能を発揮する、素直な関数になるよう導いてくれるのです。
モデルの複雑さと汎化性能のイメージ
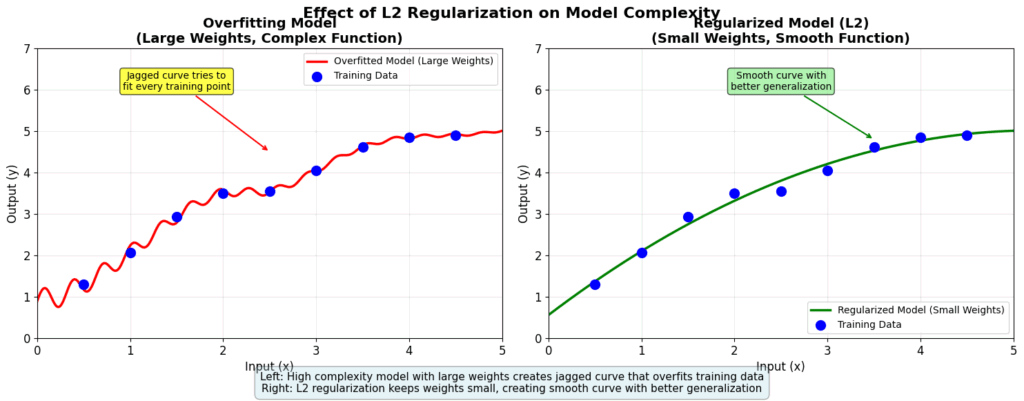
解説:
- 左のモデルは、訓練データの全ての点(●)を無理やり通ろうとするため、
重みが大きくなり、関数がギザギザになります。未知のデータが来たときに、
大きな誤差を生みやすい状態です。
- L2正則化は、右のモデルのように、重みを小さく保つことで関数をなだらかにし、
訓練データに過剰にフィットしすぎるのを防ぎます。
なぜ「Weight Decay (重み減衰)」と呼ばれるの?
ところで、L2正則化がなぜ「Weight Decay(重み減衰)」と呼ばれるのか、不思議に思いませんか?これは、勾配降下法における重みの更新式を見ると、その理由がよく分かります。
L2正則化がない場合の、ある重み \(w\) の更新式は、概念的には以下のようになります。
\[ w_{\text{new}} = w_{\text{old}} – (\text{学習率}) \times \frac{\partial L_{\text{original}}}{\partial w_{\text{old}}} \]
ここにL2正則化項が加わると、\(\frac{\partial L_{\text{total}}}{\partial w} = \frac{\partial L_{\text{original}}}{\partial w} + 2 \lambda w\) となるため、更新式は次のようになります。
\[ w_{\text{new}} = w_{\text{old}} – (\text{学習率}) \times \left( \frac{\partial L_{\text{original}}}{\partial w_{\text{old}}} + 2 \lambda w_{\text{old}} \right) \]
この式を少し変形してみましょう。
\[ w_{\text{new}} = (1 – 2\lambda \cdot \text{学習率}) w_{\text{old}} – (\text{学習率}) \times \frac{\partial L_{\text{original}}}{\partial w_{\text{old}}} \]
この式をよく見てください。元の更新ステップに加えて、毎回、古い重み \(w_{\text{old}}\) に \((1 – 2\lambda \cdot \text{学習率})\) という1より少し小さい係数が掛けられていますよね。つまり、重みを更新するたびに、元の重み自体が少しだけ『減衰(Decay)』していくんです。これが、Weight Decayと呼ばれる所以です。面白い仕組みだと思いませんか?
PyTorchでの使い方 〜オプティマイザに一行加えるだけ〜
では、このエレガントな仕組みを、PyTorchではどうやって使うのでしょうか?驚くほど簡単なんですよ。Dropoutのように層としてモデルに組み込むのではなく、オプティマイザ(最適化アルゴリズム)のパラメータとして設定するのが一般的です。例えば、torch.optim.Adam や torch.optim.SGD を作成する際に、weight_decay という引数に、先ほどの \(\lambda\) に相当する値を設定します。
# 例: AdamオプティマイザにL2正則化(weight_decay)を設定する場合
# model.parameters()は、モデルが持つ全ての学習可能な重みを指します。
# lr は学習率です。
# weight_decay に設定した値が、L2正則化の係数λになります。
# 1e-4 は 0.0001 のことで、比較的一般的な設定値です。
optimizer = torch.optim.Adam(model.parameters(), lr=0.001, weight_decay=1e-4)
たったこれだけです。オプティマイザを定義するときにこの一行を追加するだけで、学習の各ステップで自動的にL2正則化が適用されるようになり、モデルが過学習に陥るのを防ぐ助けとなります。
3. まとめと次のステップ
今回は、AIモデルの性能と信頼性を大きく左右する、活性化関数と正則化という二つの重要な概念について学びました。
- 活性化関数(特にReLU)は、ニューラルネットワークに非線形性を導入し、複雑なデータを表現するための「個性」や「表現力」を与えてくれます。
- 正則化(DropoutやL2正則化)は、モデルが訓練データを丸暗記してしまう「過学習」を防ぎ、未知のデータにも対応できる般化性能、すなわち「規律」や「堅牢性」を高めてくれます。
これらのテクニックは、現代のディープラーニングモデルを構築する上で、いわば「常識」とも言える基本的な部品です。私たちが目指す医療AIのような、非常に高い信頼性が求められる分野では、これらの概念を正しく理解し、適切に使いこなすことが不可欠と言えるでしょう。
さて、モデルに豊かな表現力と規律を与える方法を学んだことで、私たちはより洗練されたニューラルネットワークを構築する準備が整いました。次の第11回では、大量のデータを効率的に、そして安定してモデルに供給するための「ミニバッチ学習とDataLoader」について詳しく見ていきます。実際の医療データは非常に大規模なことが多いですから、このデータハンドリングの技術もまた、実践的なAI開発には欠かせないスキルとなります。
一歩一歩、着実に実践的なモデル構築のスキルを身につけていきましょう!
参考文献
- Zhao Y, Wang T, Zhang W, et al. A review of the application of deep learning in medical image processing. J Healthc Eng. 2021;2021:6653818.
- Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: a simple way to prevent neural networks from overfitting. J Mach Learn Res. 2014;15(1):1929-1958.
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






