再帰型ニューラルネットワーク(RNN)は、過去の情報を記憶し、心電図やテキストなどの順序データから未来を予測するAI技術です。本要約では、RNNの基本構造からPyTorchによる実装、医療応用まで、その核心を分かりやすく解説します。
RNNは、ネットワーク内に「ループ構造」を持つことで過去の情報を「隠れ状態」として記憶します。これにより、心電図やテキストなど、順序が重要なデータの時間的文脈を理解し、次の値を予測したり内容を分類したりできます。
PyTorchを使い、①データ準備(シーケンス化)、②RNNモデル定義、③損失関数・最適化設定、④学習ループ、⑤評価というステップで実装します。柔軟なライブラリにより、時系列予測モデルを直感的に構築できます。
心疾患の予測や電子カルテ解析など医療応用が期待されます。一方で、長期記憶の難しさ(→LSTM/GRU)や、モデルの解釈性、データバイアスといった課題の克服も重要です。
はじめに
医療分野における人工知能(AI)の活用は、診断支援、治療法の最適化、創薬、患者ケアの質の向上など、多岐にわたる革新をもたらす可能性を秘めています。特に、人間の言語や音声、心電図や脳波といった時系列データなど、順番に意味を持つシーケンシャルな情報を扱うAI技術は、医療現場の様々な課題解決に貢献すると期待されています。
本記事は、「Medical AI with Python」シリーズの第15章として、そのようなシーケンシャルデータの扱いに長けたニューラルネットワークの一種である再帰型ニューラルネットワーク(Recurrent Neural Network: RNN)について、Pythonの代表的な深層学習ライブラリであるPyTorchを用いて実装する方法を解説します。
RNNの基本的な仕組みを理解し、PyTorchを使った実装スキルを習得することで、医療データの新たな可能性を探求する第一歩を踏み出しましょう。
1. 再帰型ニューラルネットワーク (RNN) とは?
1.1. RNNの基本的な概念
再帰型ニューラルネットワーク(RNN)とは、時系列データやテキストのようなシーケンシャルデータ(順序に意味があるデータ)を扱うことに特化したニューラルネットワークの一種です [1]。
従来の基本的なニューラルネットワーク(例:全結合型ニューラルネットワーク)は、入力されたデータに対して一度だけ計算を行い結果を出力します。このタイプのネットワークは、入力データ間の順序や時間の経過に伴う変化を捉えることが苦手でした。例えば、ある瞬間の患者さんのバイタルサインだけを見ても、それが平常時なのか、急変の兆候なのかを判断するのは難しい場合があります。前後の脈絡、つまり時間の経過と共にどのように変化してきたかという情報が重要になります。
RNNは、この「時間の流れ」や「順序」を考慮するために、ネットワーク内部に「ループ構造」を持っています(図1)。このループ構造により、過去の情報を記憶し、それを現在の計算に反映させることができます。ちょうど私たちが文章を読むとき、前の単語の意味を記憶しながら次の単語を理解していくのに似ています。
図1: RNNの基本的な概念図
入力(t) -----> [ RNNセル ] ------> 出力(t)
↑ |
|------| 隠れ状態(t-1) から 隠れ状態(t) へ
図1はRNNの基本的な動作を示しています。時刻 \(t\) の入力と、一つ前の時刻 \( (t-1) \) の隠れ状態(情報)を元に、時刻 \(t\) の出力と新しい隠れ状態を生成します。
1.2. RNNはどのようなデータに適しているか?
RNNは、データの順序や時間的な連続性が重要な意味を持つ様々な種類のデータに適用できます。
- 時系列データ:
- 医療分野: 心電図(ECG)、脳波(EEG)、患者のバイタルサイン(体温、血圧、心拍数など)の連続記録、血糖値の推移など。これらのデータから異常を検知したり、将来の状態を予測したりするのに役立ちます [2]。
- その他: 株価、気象データ、音声信号など。
- シーケンシャルデータ:
- 医療分野: 電子カルテの臨床記述、問診記録、論文などのテキストデータ。これらのテキストデータから情報を抽出したり、内容を分類したり、あるいは新たなテキストを生成(例:報告書の下書き作成)したりする応用が考えられます [3]。
- その他: DNA配列、自然言語の文章(機械翻訳、感情分析など)。
1.3. RNNの基本的な構造
RNNの核心部分は、「RNNセル」と呼ばれる計算ユニットです。このセルが、各時刻のデータ(例:ある日の心拍数)を受け取るたびに、情報を更新し、出力を生成する処理を担います。この処理は、大きく分けて以下の2つのステップで行われます。
- 記憶の更新:過去の記憶と現在の情報から、「今日の記憶」を新しく作り出す。
- 出力の生成:その「今日の記憶」を元に、最終的な答えを計算する。
それぞれのステップで登場する重要な要素を見ていきましょう。
ステップ1:記憶の更新(隠れ状態 ht の計算)
まず、RNNは過去から引き継いだ情報と、新しく入ってきた情報を使って、内部の状態を更新します。
- 入力 ( \(x_t\) ): 時刻 \(t\) における「現在の情報」です。例えば、ある瞬間の心拍数や、文章中の一つの単語などがこれにあたります。
- 前の隠れ状態 ( \(h_{t-1}\) ): 時刻 \(t-1\) から引き継いだ「過去の記憶」です。一つ前のステップで計算されたRNNの内部状態を指します。
- 隠れ状態 ( \(h_t\) ): 上記の2つを元に計算される「現在の記憶」です。RNNセルの内部状態であり、過去から現在までの情報を要約したものです。この隠れ状態が、RNNが「記憶」を持つメカニズムの核心です。
ステップ2:出力の生成(最終出力 yt の計算)
次に、ステップ1で更新された「現在の記憶」を使って、具体的な答えを生成します。
- 出力 ( \(y_t\) ): 時刻 \(t\) におけるRNNからの「最終的な答え」です。これは、隠れ状態 \(h_t\) を元に計算されます。タスクによって、各時刻で答え(例:時系列の各点での異常ラベル)を出す場合もあれば、シーケンス全体の情報を要約した最後の隠れ状態から、一度だけ答え(例:文章全体の感情分析結果)を出す場合もあります。
数式で見るRNNの動き
この2段階のプロセスは、数式で表すと以下のように整理できます。
隠れ状態の計算式 (ステップ1: 記憶の更新)
過去の記憶(\(h_{t-1}\))と現在の入力(\(x_t\))から、現在の記憶(\(h_t\))を計算します。
\[ h_t = \tanh(W_{hh}h_{t-1} + W_{xh}x_t + b_h) \]
出力の計算式 (ステップ2: 出力の生成)
現在の記憶(\(h_t\))を元に、最終的な出力(\(y_t\))を計算します。
\[ y_t = W_{hy}h_t + b_y \]
ここで、\(W_{hh}, W_{xh}, W_{hy}\) は重み行列(学習によって最適化されるパラメータ)、\(b_h, b_y\) はバイアス項(同じく学習パラメータ)です。そして、\(\tanh\) は活性化関数と呼ばれるものです。
なぜ活性化関数に tanh が使われるの?
RNNでは、なぜ \(\tanh\) (ハイパボリック・タンジェント) がよく使われるのでしょうか?それは、情報の交通整理をして、学習を安定させるという重要な役割があるからです。
RNNは、同じ計算を何度も繰り返すループ構造を持っています。もし、計算結果が際限なく大きくなったり小さくなったりすると、ループを繰り返すうちに情報が「爆発」したり「消失」したりして、学習がうまくいかなくなってしまいます。
\(\tanh\) は、どんな数値が入力されても、出力を必ず -1から1の範囲に収めてくれる性質があります。これにより、情報が常に一定の範囲内に保たれ、ネットワークが安定して学習を進めることができるのです。-1は「強い否定」、+1は「強い肯定」、0は「中立」といったように、情報の方向性や強さを表現する役割も担っています。
この構造の最も重要なポイントは以下の2点です。
- 情報の時間的な伝播: \(h_t\) を計算する際に、必ず一つ前の隠れ状態である \(h_{t-1}\) が使われています。これにより、過去の情報がシーケンスの最後まで、川の流れのように伝播していきます。
- 要約からの出力: 最終的な出力 \(y_t\) は、入力 \(x_t\) から直接計算されるのではなく、RNNが内部で文脈を要約した「記憶」である隠れ状態 \(h_t\) を経由して計算されます。これにより、RNNは単なる入力だけでなく「過去の流れ」を考慮した判断ができるのです。
1.4. RNNの課題:勾配消失・勾配爆発問題
RNNは強力なモデルですが、特に長いシーケンスを扱う際に勾配消失問題や勾配爆発問題が発生しやすいという課題があります [4]。これは、誤差逆伝播法(ネットワークの重みを更新するためのアルゴリズム)において、勾配(誤差の指標)が過去に遡るにつれて非常に小さく(消失)なったり、逆に非常に大きく(爆発)なったりする現象です。
- 勾配消失問題: 過去の情報がうまく伝わらず、長期的な依存関係(例:数時間前のバイタルサインの異常が現在の状態に影響している、など)を学習するのが難しくなります。
- 勾配爆発問題: 学習が不安定になり、うまく収束しなくなります。
これらの問題を軽減するために、LSTM (Long Short-Term Memory) [5] や GRU (Gated Recurrent Unit) [6] といった、より複雑なゲート機構を持つ改良型のRNNセルが考案されています。これらは、情報の流れをより効果的に制御することで、長期依存性を捉えやすくしています。本記事ではまず基本的なRNNを扱いますが、これらの発展形があることも覚えておくと良いでしょう。
Deep Dive! RNNの行列計算
RNNの心臓部:行列計算の流れとその本質
RNNが「過去の情報を記憶しながら新しい情報を処理する」仕組みは、一見複雑に見えますが、その本質はとてもシンプルです。ここでは、RNNの計算の裏側で「何が起きているのか」を、各要素の役割や本質に迫りながら解き明かしていきます。
料理に例えるなら、「秘伝のソース(過去の記憶)に、新しい食材(今日の情報)を、シェフの長年の経験(重み行列)に基づいて加え、味をなじませ(活性化関数)、今日の新しいソースを作る」という、職人技の工程を覗いてみるイメージです 🍳。
登場人物とその本質
まず、RNNを構成する主要な登場人物たちと、その「本質的な役割」を見ていきましょう。
| 登場人物 | 形(次元) | 本質的な役割・意味 |
|---|---|---|
| \(x_t\) (入力) | [input_size] | 「現在の情報」。時刻 \(t\) に観測された生のデータ点(例:心拍数、株価、文章中の単語)。 |
| \(h_{t-1}\) (前の隠れ状態) | [hidden_size] | 「過去の文脈」。一つ前の時刻までにRNNが読み解いた情報の要約。 |
| \(W_{xh}\), \(W_{hh}\), \(W_{hy}\) (重み行列) | (様々) | 「知識・経験の結晶」。情報の関連性を決める無数の調整ツマミの集まり。行列の各要素は「ある情報が、次の情報にどれだけ強く影響を与えるか」というルールの強さを表します。学習とは、この知識をデータから自動で獲得する作業です。 |
| \(b_h\), \(b_y\) (バイアス) | (様々) | 「基本的な傾向・好み」。入力情報が何もない状態での、ニューロンの基本的な発火のしやすさを示します。いわば、シェフの「基本は少し甘めに」といった味付けのベースです。 |
| \(h_t\) (隠れ状態) | [hidden_size] | 「文脈を凝縮した特徴ベクトル」。過去と現在の情報を統合して作られる、いわばRNNの「現在の状況認識」です。詳細は後述します。 |
| \(y_t\) (最終出力) | [output_size] | 「最終的な結論・答え」。現在の状況認識(\(h_t\))を元に、タスクに合わせて変換された具体的なアウトプットです。 |
本質:隠れ状態 h とは何か? ― 具体例でイメージする「状況分析レポート」
隠れ状態 \(h_t\) は、単なる数字の羅列ではありません。それは、その時点までの情報をすべて考慮した、RNNによる「状況分析レポート」だと考えることができます。このレポートは、hidden_size 個の項目を持つベクトルで表現されます。
例えば、ICU患者のバイタルサインを監視するRNN(仮に hidden_size=4 とします)を考えてみましょう。ある時刻の隠れ状態 \(h_t\) が [0.9, -0.8, 0.1, 0.7] というベクトルだったとします。この各要素は、以下のような(私たちが推測する)意味を持っているかもしれません。
- 第1要素 (0.9):「循環器系の危険度」
+1に近いほど危険。血圧低下や頻脈といったパターンを検知し、「非常に危険な兆候あり」と判断している状態。 - 第2要素 (-0.8):「呼吸器系の安定度」
+1が安定、-1が不安定。-0.8なので、「呼吸状態に注意が必要」と判断している。 - 第3要素 (0.1):「発熱の傾向」
過去数時間の体温データから、「微熱傾向だが、まだ大きな問題ではない」と判断している。 - 第4要素 (0.7):「特定の薬剤Aへの反応」
+1に近いほど良好な反応。「過去に投与された薬剤Aが、効果を発揮している」という文脈を記憶している。
新しいデータ(次の心拍数など)が入力されるたびに、RNNはこの「状況分析レポート」を更新していきます。例えば、血圧がさらに下がれば、第1要素の値はさらに+1に近づくでしょう。
重要な注意点:これらの「意味」は、あくまで私たちが人間にとって分かりやすいように解釈したものです。AIは、このような意味を直接学習するわけではありません。AIは、最終的な予測精度が最も高くなるように、タスクを解く上で「都合の良い中間的な特徴」を自ら発見し、ベクトルの各要素に格納しているのです。
RNNの2段階計算プロセスとその本質
RNNの計算は「①記憶の更新」と「②出力の生成」の2段階で行われます。それぞれのステップの本質に迫りましょう。
ステップ1:記憶の更新(隠れ状態 ht の計算)
このステップでは、過去の文脈(\(h_{t-1}\))と現在の情報(\(x_t\))から、RNNの新しい「状況分析レポート」である隠れ状態(\(h_t\))を生成します。
\[ h_t = \tanh(W_{hh}h_{t-1} + W_{xh}x_t + b_h) \]
この式は、以下の処理を一度に行っています。
- 情報の重み付け: \(W_{hh}h_{t-1}\) と \(W_{xh}x_t\) の計算です。これは、「過去の状況のどの部分」と「現在の情報のどの部分」が、次の状況判断に重要かを判断するプロセスです。重み行列 \(W\) が「この情報とあの情報の関連性は、これくらい重要」という知識として働き、情報にメリハリをつけます。
- 情報の統合: 2つの重み付けされた情報を足し合わせます。
- 情報の取捨選択(活性化): 統合された情報を活性化関数 \(\tanh\) に通します。
本質:なぜ tanh を通すのか? ― 情報の「ゲート」としての役割
これは、\(\tanh\) が記憶に残すべき情報の「重要度」を判断し、取捨選択するゲート(関所)として機能するからです。\(\tanh\) は、入ってきた情報を必ず**-1から1の範囲**に変換し、その出力値が情報の扱い方を決める指令になります。
- 出力が1に近い: 「この情報は非常に重要(正の方向で)なので、強く記憶に残せ」
- 出力が-1に近い: 「この情報は非常に重要(負の方向で)なので、強く記憶に残せ」
- 出力が0に近い: 「この情報はあまり重要ではないので、忘れるか無視しろ」
このように、\(\tanh\) は単に計算を安定させるだけでなく、どの情報を次の記憶に渡し、どの情報を捨てるかという、能動的な情報の取捨選択を行っているのです。
ステップ2:出力の生成(最終出力 yt の計算)
次に、ステップ1で生成された「状況分析レポート」 \(h_t\) を元に、私たちが求める「最終的な答え」 \(y_t\) を計算します。
\[ y_t = W_{hy}h_t + b_y \]
これは、RNNの内部的な状況認識(例:『循環器系の危険度が0.9』)を、人間が理解できる具体的な答え(例:『危険アラートを発する確率85%』)に翻訳するプロセスです。ここでも重み行列 \(W_{hy}\) が「翻訳ルール」として機能します。
RNNはどうやって「賢く」なる? 学習の仕組み
RNNは、この複雑な「知識(重み行列)」を、大量のデータから自動で学習します。そのプロセスが「逆伝播(バックプロパゲーション)」です。
学習の4ステップ
- 予測する (Forward Pass)
データを入力し、ここまでに解説した2段階の計算プロセスを経て「予測値」(\(y_t\))を出力します。 - 答え合わせ (損失計算)
モデルの「予測値」と「正解値」を比べ、どれだけ間違っているか(損失)を計算します。 - 原因を遡って探る (Backward Pass)
「損失」という間違いが、どの「知識(重み)」や「状況認識(隠れ状態)」が原因で生じたのかを、時間を遡って逆向きに分析します。これを時間を通した誤差逆伝播(BPTT)と呼びます。 - 知識を更新する (パラメータ更新)
分析結果に基づき、間違いの原因となった「知識(重み行列の各要素)」を、損失が小さくなる方向にほんの少しだけ修正します。これは、専門家が経験を積んで、知識のネットワークをより洗練させていく作業に似ています。
この「予測 → 答え合わせ → 原因分析 → 知識の更新」のサイクルを何万回と繰り返すことで、RNNはデータに潜む複雑な時間的パターンを捉えるための、膨大で精緻な「知識(重み行列)」を自ら築き上げていくのです。
Deep Dive! 時間を通した誤差逆伝播(BPTT)
RNNの学習、その正体は「失敗から学ぶ」こと
まず大前提として、AIの学習は、人間と同じで「失敗から学ぶ」プロセスそのものです。RNNの学習も、以下の4ステップをひたすら繰り返しています。
| ステップ | シェフの行動に例えると… | やっていること |
|---|---|---|
| 1. 予測 | 「今日のレシピで、とりあえず作ってみる」 | 現在の知識(重み)で、答えを予測してみる(フォワードパス) |
| 2. 答え合わせ | 「試食して、理想の味と比べる」 | 予測した答えと、本当の正解を比べて、間違いの大きさ(損失)を計算する |
| 3. 原因分析 | 「なぜ味が違った?塩か?隠し味か?昨日のソースか?」 | 間違いの原因を、時間を遡って徹底的に分析する(← ここがBPTT!) |
| 4. 知識の更新 | 「原因がわかった。明日はレシピをこう直そう」 | 分析結果をもとに、知識(重み)をほんの少しだけ修正する(パラメータ更新) |
今回フォーカスするのは、この中でも一番のキモであるステップ3、「原因分析」の部分です。RNNは過去の情報を記憶しながら答えを出すので、間違いの原因を探るのも、ただ単純にはいきません。時間を遡る必要があるんですね。
なぜ「時間を遡る」必要があるの? ― 継ぎ足しの秘伝ソース問題
RNNの最大の特徴は、過去の情報を「隠れ状態 \(h\)」という形で、次の瞬間の自分に伝えていくことでした。これは、毎日継ぎ足して作る「秘伝のソース」のようなものだとイメージしてみてください。
今日のディナーに出す一皿(時刻\(t\)の出力)の味がなんだかおかしい…。その原因は、
- 今日加えた食材(時刻\(t\)の入力) のせいかもしれないし、
- 今日の味付けの仕方(出力層の計算) がマズかったのかもしれない。
- でも、それだけじゃなく、今日の味のベースになっている「秘伝のソース(時刻\(t-1\)の隠れ状態)」自体 に問題があったのかもしれないですよね。
そして、そのソースの味は、さらにその前の日、またその前の日から…と、ずっと影響を受け継いでいるわけです。
今日の味 (出力 y_t)
↑
影響
↑
今日のソース (隠れ状態 h_t) <-- 今日の食材 (入力 x_t) の影響も受ける
↑
影響 (前の日のソースがベースになっている)
↑
昨日のソース (隠れ状態 h_{t-1})
↑
影響
↑
一昨日のソース (隠れ状態 h_{t-2})
:つまり、現在の間違いの原因は、過去のすべての判断に少しずつ責任があるかもしれないのです。だから、間違いの原因を正確に突き止めるには、時間を遡って「あの時の、あの判断が、巡り巡って今の間違いにどれだけ影響したんだろう?」と、一つひとつ影響度を調べていく必要があります。
この「時間を遡る原因分析」、それこそが時間を通した誤差逆伝播(BPTT)の正体です。
BPTTの旅:間違いの原因を探る3つのステップ
では、具体的にBPTTがどのように原因を分析していくのか、その旅路を一緒に辿ってみましょう。
ステップ1:旅の始まりは「最後のゴール」から
原因分析の旅は、未来から過去へ、つまりシーケンスの一番最後の出力からスタートします。
まず、最後の出力 \(y_T\) (\(T\)はシーケンスの最後の時刻)と、正解ラベルを比べて、「最後の間違い(損失 \(L_T\))」を計算します。そして、この間違いに対して、直接関係した要素たちがどれだけ「責任」を負うべきかを計算します。
- 犯人候補①:出力層の重み \(W_{hy}\)
隠れ状態 \(h_T\) から最終出力 \(y_T\) を作る際の「翻訳ルール」です。
計算するのは \(\frac{\partial L_T}{\partial W_{hy}}\) 。これは「もし \(W_{hy}\) が少しだけ違っていたら、最後の間違いはどれだけ変わっていたか?」という「\(W_{hy}\)の責任の大きさ」を表します。 - 犯人候補②:最後の隠れ状態 \(h_T\)
最後の「状況分析レポート」です。
計算するのは \(\frac{\partial L_T}{\partial h_T}\) 。これは「もし \(h_T\) の内容が少しだけ違っていたら、最後の間違いはどれだけ変わっていたか?」という「\(h_T\)の責任の大きさ」を表します。
ここが、時間を遡る旅の「最初の発見」になります。
ステップ2:時間を遡る「責任」の伝言ゲーム
さて、ステップ1で「最後の隠れ状態 \(h_T\) の責任の大きさ」がわかりました。でも、\(h_T\) は単独で生まれたわけではありません。一つ前の隠れ状態 \(h_{T-1}\) と、その時の入力 \(x_T\) から作られました。
\[ h_T = \tanh(W_{hh}h_{T-1} + W_{xh}x_T + b_h) \]
ということは、\(h_T\) の責任の一部は、その材料である \(h_{T-1}\) にもあるはずです。この「責任の伝達」を計算するのが、数学で言うところの「連鎖律(Chain Rule)」です。
難しく考えず、「AがBに影響し、BがCに影響するなら、AがCに与える総合的な影響は、個々の影響力を掛け合わせたもの」という、ごく自然な考え方だと思ってもらえれば大丈夫です。
この考え方を使って、「\(h_{T-1}\) の責任」を計算します。
\[ \frac{\partial L_T}{\partial h_{T-1}} = \frac{\partial L_T}{\partial h_T} \times \frac{\partial h_T}{\partial h_{T-1}} \]
この式の意味を、言葉で翻訳してみましょう。
[時刻T-1の隠れ状態の責任] = [時刻Tの隠れ状態の責任] × [T-1からTへの影響度]
この計算で、\(h_{T-1}\) が最後の間違いにどれだけ影響したかがわかります。そしたら、今度はこの \(h_{T-1}\) の責任を、さらにその前の \(h_{T-2}\) に伝えて…と、まるで伝言ゲームのように、どんどん過去へ過去へと責任を伝播させていくのです。
この様子を図にすると、こんなイメージです。
【時間を遡る勾配(責任)の流れ】
時刻 t=1 時刻 t=2 ... 時刻 t=T-1 時刻 t=T
----------- ----------- ----------- -----------
入力 x_1 入力 x_2 入力 x_{T-1} 入力 x_T
↓ ↓ ↓ ↓
[RNNセル] -----> [RNNセル] --...--> [RNNセル] ------> [RNNセル] ----> 出力 y_T --> 損失 L_T
↑ h_0 ↑ h_1 ↑ h_{T-2} ↑ h_{T-1} ↑
| | | | |
| (∂L/∂h_1) | (∂L/∂h_2) | (∂L/∂h_{T-1}) | (∂L/∂h_T) | (∂L/∂y_T)
+---------------|------------------------|-----------------|---------------------+
+------------------------|-----------------|---------------------+
+-----------------|---------------------+
+---------------------+
<---------------------------------------------------------------------------------
誤差(損失)の勾配が時間を遡って伝播していく図の解説:
- まず一番右の「損失 \(L_T\)」が計算されます。
- この損失に対する各要素の「責任(勾配)」が、矢印を逆向きに辿るように計算されていきます。
- \(h_T\) の責任 (\(\partial L / \partial h_T\)) が計算され、それが \(h_{T-1}\) へ、さらに \(h_{T-2}\) へと、時間を遡って伝播していく様子が見て取れると思います。この逆向きの情報の流れが、まさにBPTTの核心です。
ステップ3:全時間から「共通の犯人」への責任を合算する
BPTTの旅で、もう一つとても大事なことがあります。RNNでは、各時刻で使われる「レシピ」、つまり重み行列(\(W_{hh}\) や \(W_{xh}\))は、全ての時間で全く同じものが使い回されています。
シェフが一日中、全く同じレシピで料理を作っているようなものです。
ということは、「今日の料理が全体的にイマイチだった」というフィードバックは、朝の料理にも、昼の料理にも、夜の料理にも、共通のレシピが原因として潜んでいるはずです。
だから、レシピ(重み)の本当の責任を明らかにするには、各時刻で計算された「この重みのせいで、どれだけ間違いが起きたか」という責任(勾配)を、全部足し合わせる必要があります。
\[ \frac{\partial L}{\partial W_{hh}} = \sum_{t=1}^{T} \frac{\partial L_t}{\partial W_{hh}} \]
この式は、「重み \(W_{hh}\) の最終的な責任の総量は、時刻1から最後の時刻Tまでの、各時点における \(W_{hh}\) の責任をすべて合計したものですよ」という意味です。\(W_{xh}\) についても同様です。
こうして全ての時間を旅して、全ての責任を合算することで、ようやくモデルの知識(重み行列)をどちらの方向に、どれくらい修正すれば良いのかがわかるのです。
行列計算の舞台裏を覗いてみよう
最後に、この計算の中心である隠れ状態の更新が、コンピュータの中でどんな形で行われているのか、ブロックのイメージで覗いてみましょう。
\[ h_t = \tanh(W_{hh}h_{t-1} + W_{xh}x_t + b_h) \]
この計算は、以下のようなテンソル(多次元の箱)の変形操作として行われています。
[前の隠れ状態 h_{t-1}]
(hidden_size × 1)
■
■
■
+---------------------------------------------------------------------------------+
| |
| [重み W_hh] × [h_{t-1}] = [変換後の過去情報] |
| (hidden_size × hidden_size) (hidden_size × 1) (hidden_size × 1) |
| ■■■■■ ■ ■ |
| ■■■■■ ■ ■ |
| ■■■■■ ■ ■ |
| |
| + |
| |
| [重み W_xh] × [入力 x_t] = [変換後の現在情報] |
| (hidden_size × input_size) (input_size × 1) (hidden_size × 1) |
| ■■■ □ ■ |
| ■■■ □ ■ |
| ■■■ □ ■ |
| |
+---------------------------------------------------------------------------------+
↓
[統合された情報] + [バイアス b_h]
(hidden_size × 1)
■
■
■
↓
[ tanh() を通す ]
↓
[新しい隠れ状態 h_t]
(hidden_size × 1)
■
■
■図の解説:
- この図は、ベクトル(縦長のブロック)と行列(四角いブロック)の計算を表しています。
- まず、過去の情報(\(h_{t-1}\))と現在の情報(\(x_t\))が、それぞれ対応する「知識の結晶」である重み行列(\(W_{hh}, W_{xh}\))によって、「hidden_size」という共通の次元を持つベクトルに変換されます。これは、異なる種類の情報を、同じ土俵(次元)で比較・統合できるように下ごしらえするイメージです。
- その後、2つの情報が足し合わされ、バイアス(基本的な味付け)が加えられます。
- 最後に、活性化関数 `tanh` という「情報の交通整理係」を通って、不要な情報を削ぎ落とし、重要な情報だけを凝縮した、新しい隠れ状態 \(h_t\) が完成します。
BPTTでは、この計算プロセスを完全に逆再生するようにして、「完成した \(h_t\) の責任」を、その材料である \(h_{t-1}\) や重み \(W_{hh}\) などに分配していくわけですね。
いかがでしたでしょうか。BPTTは、一見すると複雑な数式のオンパレードに見えるかもしれませんが、その本質は「時間を遡って、間違いの原因となった共通のレシピを探し出し、全員の意見を聞いてから修正する」という、とても地道で誠実なプロセスなんだ、と感じていただけたら嬉しいです。
この仕組みを理解すると、なぜRNNが長いシーケンスの学習で「昔のことを忘れてしまう(勾配消失問題)」のか、という次の課題にも自然と繋がっていきます。
Deep Dive! ハイパボリックタンジェント関数 (tanh)
ハイパボリックタンジェント関数(tanh)は、特にリカレントニューラルネットワーク(RNN)において、中間層の活性化関数として広く利用される双曲線関数の一つです。記号 tanh で表されます。
定義
ハイパボリックタンジェント関数 \(\tanh(x)\) は、指数関数 \(e^x\) を用いて以下のように定義されます。
\[ \tanh(x) = \frac{e^x – e^{-x}}{e^x + e^{-x}} \]
また、ハイパボリックサイン関数 \(\sinh(x)\) とハイパボリックコサイン関数 \(\cosh(x)\) を用いて、以下のように表すこともできます。
\[ \tanh(x) = \frac{\sinh(x)}{\cosh(x)} \]
ここで、
\[ \sinh(x) = \frac{e^x – e^{-x}}{2} \]
\[ \cosh(x) = \frac{e^x + e^{-x}}{2} \]
です。
グラフと主な特徴
\(\tanh(x)\) のグラフは以下のようなS字型の曲線を描き、その出力は \((-1, 1)\) の範囲に収まります。これはRNNにおいて、勾配消失問題を緩和するのに役立ちます。
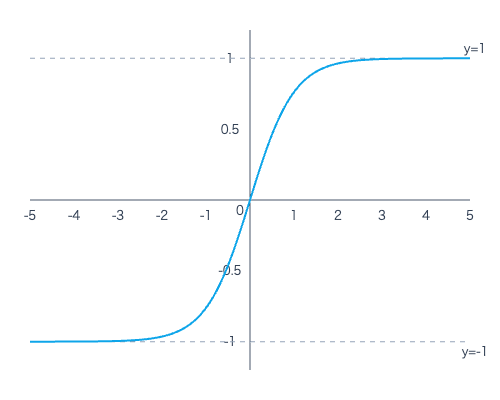
x軸とy軸があり、原点(0,0)を通り、xが負の無限大に近づくとyは-1に漸近し、xが正の無限大に近づくとyは1に漸近するS字型の曲線
主な特徴:
- 定義域: 全ての実数 \((-\infty, \infty)\)
- 値域: \((-1, 1)\) (RNNの出力値をこの範囲に正規化します)
- 漸近線: \(y = 1\) および \(y = -1\)
- \(x=0\) のとき \(\tanh(0) = 0\) となります。(入力が0のとき、出力も0となるため、学習の安定性に寄与することがあります)
- \(x \to \infty\) のとき \(\tanh(x) \to 1\)
- \(x \to -\infty\) のとき \(\tanh(x) \to -1\)
性質 (RNNに関連する点)
- 奇関数: \(\tanh(-x) = -\tanh(x)\) であり、グラフは原点対称です。これにより、データの平均が0に近い場合に学習効率が良いとされることがあります。
- 微分: \[ \frac{d}{dx} \tanh(x) = 1 – \tanh^2(x) \] この微分値は、\(\tanh(x)\) の出力値のみから計算できるため、RNNの誤差逆伝播法(Backpropagation Through Time, BPTT)における勾配計算が効率的に行えます。また、微分値の範囲は \((0, 1]\) となり、シグモイド関数の微分値の範囲 \((0, 0.25]\) よりも広いため、勾配消失が起こりにくいとされています。
RNNにおける用途
- 活性化関数: RNNの中間層(隠れ層)の活性化関数として主に使用されます。各タイムステップにおける隠れ状態の計算結果を \(-1\) から \(1\) の範囲に変換(正規化)します。
- シグモイド関数も活性化関数として用いられますが、tanh関数は出力の中心が0であるため、勾配の消失/爆発問題をある程度緩和し、学習の収束を速める効果が期待できます。
- 特に、長期依存性のある時系列データを扱う際に、勾配情報をより効果的に伝播させるのに役立ちます。
2. PyTorchとは?
PyTorchは、FacebookのAI研究グループ(現Meta AI)によって開発された、Pythonベースのオープンソース機械学習ライブラリです [7]。主に、ニューラルネットワークを用いた深層学習アプリケーションの開発に使用されます。
2.1. PyTorchの特徴
- 柔軟性とPythonicな操作感: PyTorchはPythonの思想に沿って設計されており、Pythonの豊富な機能やライブラリとシームレスに連携できます。直感的で理解しやすいコードを書くことができます。
- Define-by-Run (動的計算グラフ): TensorFlowの初期バージョンなどが採用していたDefine-and-Run(静的計算グラフ)とは異なり、PyTorchは計算グラフをプログラムの実行時に動的に構築します。これにより、デバッグが容易になり、可変長の入力シーケンスなど、より複雑なモデル構造も柔軟に扱うことができます。RNNのように入力の長さが変わることがあるモデルにとっては特に有利です。
- 強力なGPUサポート: 深層学習の計算は非常に負荷が高いため、GPU(Graphics Processing Unit)による並列計算が不可欠です。PyTorchはNVIDIAのCUDAを介してGPUを簡単に利用でき、計算を大幅に高速化できます。
- 活発なコミュニティと豊富なリソース: 研究者や開発者の間で広く採用されており、チュートリアル、フォーラム、事前学習済みモデルなどが豊富に存在します。これにより、学習や問題解決が比較的容易に進められます。
2.2. なぜ医療AI開発でPyTorchが選ばれるのか?
医療AIの研究開発においてPyTorchが好まれる理由としては、以下のような点が挙げられます。
- 研究プロトタイピングの速さ: Define-by-Runの性質により、新しいアイデアを試したり、モデル構造を柔軟に変更したりすることが容易なため、研究開発のサイクルを速く回すことができます。
- 学術界での普及: 特に学術論文ではPyTorchを用いた実装が多く見られ、最新の研究成果を追試したり、自身の研究に取り入れたりする際に便利です。
- Pythonエコシステムとの親和性: 医療データの解析には、Pandas(データ操作)、NumPy(数値計算)、Matplotlib/Seaborn(可視化)、Scikit-learn(機械学習)といったPythonライブラリが広く使われています。PyTorchはこれらとスムーズに連携できます。
PyTorchの基本的なインストールやテンソル操作については、本記事では詳細を割愛しますが、公式ウェブサイト [8] に非常に分かりやすいドキュメントがありますので、初めての方はそちらをご参照ください。
3. PyTorchでRNNを実装してみよう
それでは、実際にPyTorchを使って簡単なRNNモデルを構築し、時系列データを学習させてみましょう。ここでは、ある模擬的な患者のバイタルサイン(例えば、1時間ごとの心拍数)のシーケンスデータから、次の時刻の値を予測するタスクを想定します。
3.1. 準備
まず、必要なライブラリをインポートします。
import torch # PyTorchのメインライブラリ
import torch.nn as nn # ニューラルネットワークのモジュール(RNNセル、全結合層など)を格納
import numpy as np # 数値計算ライブラリ、データ作成に使用
import matplotlib.pyplot as plt # グラフ描画ライブラリ、結果の可視化に使用
import japanize_matplotlib # matplotlibで日本語を表示するためのライブラリ (事前に pip install japanize-matplotlib が必要)
japanize_matplotlib は、グラフのラベルなどに日本語を使用したい場合にインポートしておくと便利です。もしインストールされていない場合は、お使いの環境で pip install japanize-matplotlib を実行してください。
3.2. サンプルデータの準備
今回は、サイン波にノイズを加えた簡単な時系列データを生成し、これを用いてRNNの学習を行います。医療データではありませんが、RNNの動作を理解するための基本的な例として適しています。
# シーケンスデータの生成
np.random.seed(0) # 乱数のシードを固定し、再現性を確保
data_length = 200 # データ全体の長さ
time_steps = np.linspace(0, np.pi * 10, data_length) # 0から10πまでを200等分した時間ステップ
data = np.sin(time_steps) # サイン波を生成
data = data + np.random.normal(scale=0.2, size=data_length) # ノイズを加える
data = data.astype(np.float32) # データをfloat32型に変換(PyTorchのデフォルトに合わせて)
# データを訓練用とテスト用に分割
train_size = int(data_length * 0.8) # データの80%を訓練用とする
train_data = data[:train_size] # 訓練データをスライスして取得
test_data = data[train_size:] # テストデータをスライスして取得
# 訓練データを可視化してみる
plt.figure(figsize=(12, 4)) # グラフのサイズを指定
plt.title("訓練用データ (模擬的なバイタルサイン)") # グラフのタイトルを設定
plt.xlabel("時間ステップ") # x軸のラベルを設定
plt.ylabel("値") # y軸のラベルを設定
plt.plot(train_data, label="訓練データ") # 訓練データをプロットし、ラベルを設定
plt.legend() # 凡例を表示
plt.show() # グラフを表示
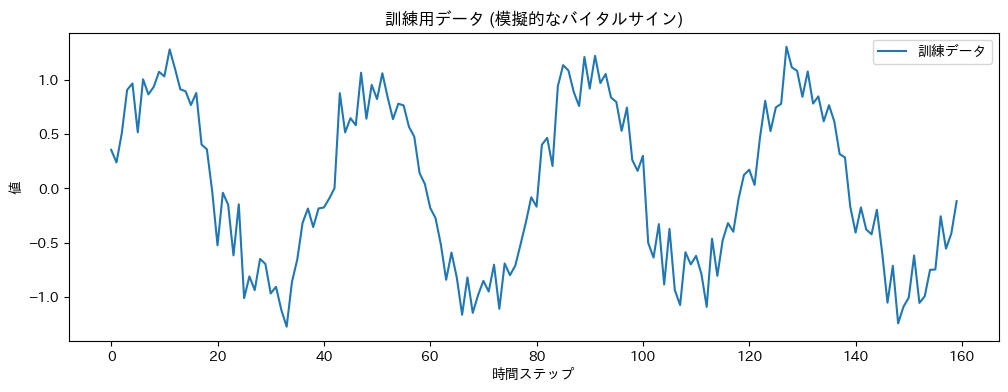
上記のコードでは、まずNumPyを使ってサイン波に基づいた時系列データを生成し、それにランダムなノイズを加えています。これを模擬的なバイタルサインデータと見なします。そして、データ全体を訓練用(モデルの学習に使用)とテスト用(学習済みモデルの評価に使用)に分割しています。
3.3. データセットの作成
RNNは、過去の一定期間のシーケンスを入力として、次の値を予測するように学習させます。そのため、元の時系列データから「入力シーケンス」と「対応する正解ラベル(予測対象の値)」のペアを作成する必要があります。
def create_sequences(input_data, sequence_length):
"""
時系列データから入力シーケンスとターゲットのペアを作成する関数。
Args:
input_data (np.array): 元の時系列データ。
sequence_length (int): 入力シーケンスの長さ。
Returns:
tuple: (入力シーケンスのリスト, ターゲットのリスト)
"""
sequences = [] # 入力シーケンスを格納するリストを初期化
labels = [] # 対応するターゲット(正解ラベル)を格納するリストを初期化
# input_dataの長さからsequence_lengthを引いた回数だけループ
for i in range(len(input_data) - sequence_length):
# iからi+sequence_length-1までのデータをシーケンスとして取り出す
seq = input_data[i:i + sequence_length]
# シーケンスの次の値 (i+sequence_length) をターゲットとして取り出す
label = input_data[i + sequence_length]
sequences.append(seq) # 作成したシーケンスをリストに追加
labels.append(label) # 作成したラベルをリストに追加
# PyTorchのテンソルに変換
# RNNの入力は (シーケンス長, バッチサイズ, 特徴量数) または (バッチサイズ, シーケンス長, 特徴量数)
# 今回は特徴量数が1なので、unsqueeze(-1)で次元を追加して (サンプル数, シーケンス長, 1) の形状にする
# labels も同様に (サンプル数, 1) の形状にする
return torch.tensor(sequences).unsqueeze(-1), torch.tensor(labels).unsqueeze(-1)
# 入力シーケンスの長さを定義
# 例えば、過去10ステップのデータを見て次の1ステップを予測する場合
sequence_length = 10
# 訓練用データとテスト用データからシーケンスとラベルを作成
X_train, y_train = create_sequences(train_data, sequence_length)
X_test, y_test = create_sequences(test_data, sequence_length)
# 作成されたデータの形状を確認
print(f"訓練用入力シーケンスの形状: {X_train.shape}") # (サンプル数, シーケンス長, 特徴量数)
print(f"訓練用ターゲットの形状: {y_train.shape}") # (サンプル数, 特徴量数)
create_sequences関数は、指定された sequence_length の長さでデータをスライスし、入力シーケンスと、そのシーケンスの直後に続く値をターゲット(正解ラベル)としてペアにします。例えば、sequence_length が10の場合、時刻0から9までのデータが最初の入力シーケンスとなり、時刻10のデータがその正解ラベルとなります。次に、時刻1から10までのデータが入力シーケンスとなり、時刻11のデータが正解ラベル…というようにスライドしながらデータセットを作成します。
unsqueeze(-1) は、特徴量の次元を追加しています。今回のデータは1次元(心拍数など単一の値)なので、RNNが期待する入力形式 (バッチサイズ, シーケンス長, 特徴量数) に合わせるために、最後に次元を1つ追加しています。
3.4. RNNモデルの定義
次に、PyTorchの nn.Module を継承してRNNモデルを定義します。
class SimpleRNN(nn.Module): # nn.Moduleを継承して新しいクラスSimpleRNNを定義
def __init__(self, input_size, hidden_size, num_layers, output_size):
"""
RNNモデルの初期化関数。
Args:
input_size (int): 入力特徴量の数(今回は1つのバイタルサインなので1)。
hidden_size (int): RNNの隠れ状態の次元数。モデルの記憶容量に関わる。
num_layers (int): RNN層の数(スタックするRNNの数)。深くすることでより複雑なパターンを学習できる可能性がある。
output_size (int): 出力特徴量の数(今回は次の1ステップの値を予測するので1)。
"""
super(SimpleRNN, self).__init__() # 親クラス nn.Module の初期化メソッドを呼び出すことが必須
self.hidden_size = hidden_size # 隠れ状態の次元数をインスタンス変数として保存
self.num_layers = num_layers # RNN層の数をインスタンス変数として保存
# RNN層を定義
# input_size: 入力の特徴量の次元数 (今回は1)
# hidden_size: 隠れ状態の次元数
# num_layers: RNN層の数
# batch_first=True: 入力テンソルの形状を (バッチサイズ, シーケンス長, 特徴量数) にする指定
self.rnn = nn.RNN(input_size, hidden_size, num_layers, batch_first=True)
# RNNの出力から最終的な予測値を得るための全結合層(線形層)
# 入力は隠れ状態の次元数、出力は予測値の次元数
self.fc = nn.Linear(hidden_size, output_size)
def forward(self, x):
"""
フォワードパス(順伝播)を定義する関数。モデルが入力データを受け取って出力を返す流れを記述。
Args:
x (torch.Tensor): 入力データ。形状は (バッチサイズ, シーケンス長, 特徴量数)。
Returns:
torch.Tensor: モデルの予測出力。
"""
# 初期隠れ状態をゼロで初期化
# 形状は (層の数 * 方向数, バッチサイズ, 隠れ状態の次元数)
# 今回は単方向RNNなので方向数は1
# x.size(0) でバッチサイズを取得
h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(x.device)
# x.device とすることで、入力テンソル x と同じデバイス(CPUまたはGPU)に隠れ状態を配置する
# RNN層にデータを入力
# out: 各時刻ステップのRNNの出力隠れ状態 (バッチサイズ, シーケンス長, 隠れ状態の次元数)
# hn: 最後の時刻ステップの隠れ状態 (層の数 * 方向数, バッチサイズ, 隠れ状態の次元数)
out, _ = self.rnn(x, h0) # hn (最後の隠れ状態) は今回は使わないので _ (アンダースコア) で受ける
# 最後の時刻ステップの出力のみを全結合層に入力する
# out[:, -1, :] は、全バッチ (:) の、シーケンスの最後の要素 (-1) の、全ての隠れ状態特徴量 (:) を選択
out = self.fc(out[:, -1, :])
return out # 最終的な予測値を出力
# モデルのパラメータを設定
input_dim = 1 # 入力特徴量の次元数(今回は1つの値なので1)
hidden_dim = 32 # 隠れ層の次元数。この値を大きくするとモデルの表現力は上がるが、計算量が増え過学習のリスクも高まる
num_rnn_layers = 1 # RNN層の数
output_dim = 1 # 出力次元数(次の1ステップの値を予測するので1)
# モデルのインスタンスを作成
model = SimpleRNN(input_dim, hidden_dim, num_rnn_layers, output_dim)
print(model) # モデルの構造を表示して確認
この SimpleRNN クラスでは、以下の主要な部分から構成されています。
__init__(コンストラクタ):nn.RNN: PyTorchが提供するRNNモジュールです。input_size: 入力データの特徴量の数(今回は1つのバイタルサインなので1)。hidden_size: RNNの隠れ状態の次元数。この値が大きいほど、モデルはより複雑なパターンを記憶・学習できますが、計算コストも増加します。num_layers: RNN層をいくつ重ねるか。層を深くすることで、より高レベルな特徴抽出が期待できますが、学習が難しくなることもあります。batch_first=True: これを指定すると、入力テンソルの形状を(バッチサイズ, シーケンス長, 特徴量数)の順にします。PyTorchでは一般的にこの形式が扱いやしいため、指定することが推奨されます。
nn.Linear: 全結合層です。RNNの最後の隠れ状態を受け取り、最終的な予測値(次の時刻の値)を出力します。
forward(フォワードパス):h0 = torch.zeros(...): 各シーケンスの処理を開始する際に、最初の隠れ状態をゼロベクトルで初期化します。x.deviceを指定することで、入力データがGPU上にあれば隠れ状態もGPU上に作成されます。out, _ = self.rnn(x, h0): RNN層に入力xと初期隠れ状態h0を渡します。self.rnnは2つの出力を返します。out: シーケンスの各時刻におけるRNN層の出力(隠れ状態)。形状は(バッチサイズ, シーケンス長, 隠れ状態の次元数)。_(hn): シーケンスの最後の時刻における隠れ状態。形状は(層の数, バッチサイズ, 隠れ状態の次元数)。今回は使いませんが、タスクによってはこのhnを利用することもあります。
out = self.fc(out[:, -1, :]): RNNの出力outのうち、シーケンスの最後の時刻の出力 (out[:, -1, :]) だけを取り出し、全結合層self.fcに入力して最終的な予測値を得ます。:はその次元の全要素を、-1は最後の要素を意味します。
3.5. 学習の準備 (損失関数と最適化アルゴリズム)
モデルを学習させるためには、以下の2つを定義する必要があります。
- 損失関数 (Loss Function): モデルの予測がどれだけ正解から外れているかを測る指標です。今回は回帰タスク(数値を予測する)なので、平均二乗誤差 (Mean Squared Error: MSE) を使用します。
- 最適化アルゴリズム (Optimizer): 損失関数の値を最小化するように、モデルのパラメータ(重みやバイアス)を更新するアルゴリズムです。今回は広く使われている Adam を使用します。
# 損失関数: 平均二乗誤差 (MSE) をインスタンス化
criterion = nn.MSELoss()
# 最適化アルゴリズム: Adam をインスタンス化
# model.parameters() でモデル内の学習可能な全パラメータをオプティマイザに渡す
# lr は学習率 (learning rate)。パラメータを一度にどれだけ更新するかを決める重要なハイパーパラメータ
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
学習率 lr は、学習の進み具合を調整する重要なパラメータです。大きすぎると学習が不安定になり、小さすぎると学習に時間がかかりすぎたり、局所解に陥ったりする可能性があります。
3.6. 学習ループ
いよいよモデルの学習を行います。学習は通常、以下のステップを繰り返します(エポックごとに)。
- フォワードパス: 訓練データをモデルに入力し、予測値を得る。
- 損失計算: 予測値と正解ラベルを損失関数に渡し、損失を計算する。
- 勾配初期化: 前のイテレーションの勾配が残っていると影響するため、最適化アルゴリズムの勾配をリセットする (
optimizer.zero_grad())。 - バックワードパス (誤差逆伝播): 損失に基づいて、モデルの各パラメータに関する勾配を計算する (
loss.backward())。 - パラメータ更新: 計算された勾配に従って、最適化アルゴリズムがモデルのパラメータを更新する (
optimizer.step())。
# 学習パラメータ
num_epochs = 200 # 学習を行うエポック数。データセット全体を何回繰り返して学習するか。
batch_size = 16 # 一度に処理するデータ(シーケンス)の数。
# DataLoaderの準備 (オプションだが、大規模データセットではメモリ効率が良い)
# 今回はデータが小さいので直接テンソルを使っても良いが、一般的な書き方として紹介
from torch.utils.data import TensorDataset, DataLoader # 必要なモジュールをインポート
train_dataset = TensorDataset(X_train, y_train) # 訓練用の入力シーケンスとターゲットからTensorDatasetを作成
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True) # TensorDatasetからDataLoaderを作成
# shuffle=True にすることで、エポックごとにデータの順序をシャッフルし、学習の偏りを防ぐ
# 学習ループ
losses = [] # 各エポックの損失を記録するための空のリストを初期化
for epoch in range(num_epochs): # 指定されたエポック数だけループ
model.train() # モデルを訓練モードに設定 (Dropout層やBatchNorm層がある場合に挙動が変わるため)
epoch_loss = 0.0 # このエポックの累積損失を初期化
# データローダーからバッチごとにデータを取り出して学習
for sequences, labels in train_loader: # 1バッチ分のシーケンスとラベルを取得
# sequences の形状: (バッチサイズ, シーケンス長, 特徴量数)
# labels の形状: (バッチサイズ, 特徴量数)
# 1. フォワードパス
outputs = model(sequences) # モデルにシーケンスを入力し、予測値を取得
# 2. 損失計算
loss = criterion(outputs, labels) # 予測値と正解ラベルから損失を計算
epoch_loss += loss.item() * sequences.size(0) # バッチの損失を累積 (loss.item()でPythonスカラー値を取得し、バッチサイズを掛ける)
# 3. 勾配初期化
optimizer.zero_grad() # 前のバッチで計算された勾配をリセット
# 4. バックワードパス
loss.backward() # 損失に基づいて勾配を計算 (誤差逆伝播)
# 5. パラメータ更新
optimizer.step() # 計算された勾配に従ってモデルのパラメータを更新
# エポックごとの平均損失を計算して記録
avg_epoch_loss = epoch_loss / len(train_dataset) # 累積損失をデータセットのサイズで割って平均損失を算出
losses.append(avg_epoch_loss) # 計算した平均損失をリストに追加
if (epoch + 1) % 20 == 0: # 20エポックごとに損失を表示
print(f'エポック [{epoch+1}/{num_epochs}], 損失: {avg_epoch_loss:.4f}')
print("学習完了!")
# 学習過程の損失をプロット
plt.figure(figsize=(10, 5)) # グラフのサイズを指定
plt.plot(losses) # 記録した損失のリストをプロット
plt.title("学習中の損失の変化") # グラフのタイトルを設定
plt.xlabel("エポック") # x軸のラベルを設定
plt.ylabel("平均二乗誤差 (MSE)") # y軸のラベルを設定
plt.show() # グラフを表示
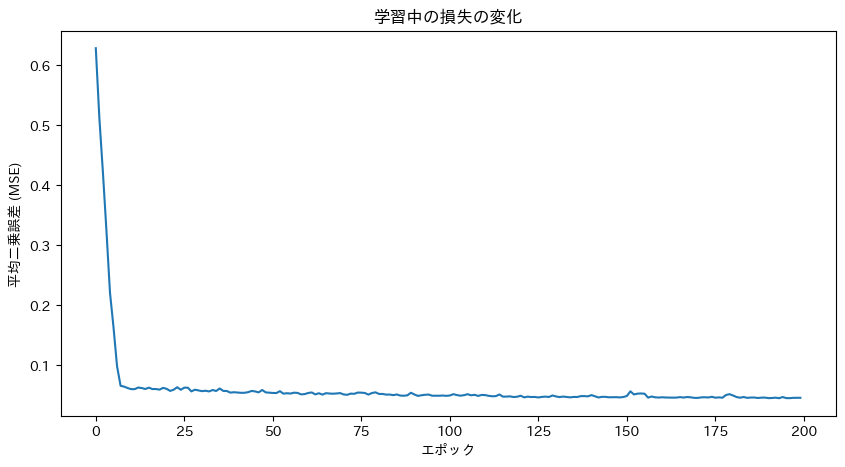
DataLoader を使用すると、大きなデータセットを扱う際に、データを小さなバッチに分割して効率的にメモリにロードし、モデルに供給することができます。shuffle=True は、各エポックの開始時に訓練データをシャッフルすることで、モデルがデータの順序に過度に依存するのを防ぎ、汎化性能を高める効果があります。
model.train() は、モデルを訓練モードに設定します。これは、Dropout層やBatchNorm層など、訓練時と評価時で挙動が異なる層がある場合に重要です(今回のシンプルなRNNモデルでは必須ではありませんが、習慣として記述しておくと良いでしょう)。
学習ループが完了すると、学習中の損失の変化がプロットされます。損失がエポックの進行と共に減少していれば、学習が順調に進んでいることを示します。
3.7. 学習済みモデルによる予測と評価
学習が完了したモデルを使って、未知のデータ(テストデータ)に対する予測性能を評価してみましょう。
# モデルを評価モードに設定
model.eval() # Dropout層やBatchNorm層の挙動を評価用に切り替える (例: Dropoutを無効化)
# テストデータで予測
predicted_outputs = [] # 予測結果を格納するための空のリストを初期化
actual_outputs = [] # 実際の値を格納するための空のリストを初期化
with torch.no_grad(): # 勾配計算を無効にし、メモリ消費を抑え、計算を高速化する (評価時には必須)
for i in range(len(X_test)): # テストデータの各サンプルに対してループ
# テストデータからi番目のシーケンスとラベルを取得
seq = X_test[i].unsqueeze(0) # バッチ次元を追加 (1, シーケンス長, 特徴量数) してモデル入力形式に合わせる
label = y_test[i] # 対応する正解ラベルを取得
# モデルで予測
pred = model(seq) # 学習済みモデルにシーケンスを入力し、予測値を取得
# 結果をリストに追加
predicted_outputs.append(pred.item()) # .item()でテンソルからPythonスカラー値を取得してリストに追加
actual_outputs.append(label.item()) # 同様に正解ラベルもリストに追加
# 予測結果と実際の値を比較してプロット
plt.figure(figsize=(12, 6)) # グラフのサイズを指定
plt.title("テストデータにおける予測結果と実際の値") # グラフのタイトルを設定
plt.xlabel("時間ステップ(テストデータ内)") # x軸のラベルを設定
plt.ylabel("値") # y軸のラベルを設定
plt.plot(actual_outputs, label="実際の値", marker='.') # 実際の値をプロットし、ラベルとマーカーを設定
plt.plot(predicted_outputs, label="予測値", marker='.') # 予測値をプロットし、ラベルとマーカーを設定
plt.legend() # 凡例を表示
plt.show() # グラフを表示
# 簡単な評価指標 (MSE)
# predicted_outputs と actual_outputs はPythonのリストなので、PyTorchのテンソルに変換してMSEを計算
test_loss = nn.MSELoss()(torch.tensor(predicted_outputs), torch.tensor(actual_outputs))
print(f"テストデータに対する平均二乗誤差 (MSE): {test_loss.item():.4f}")
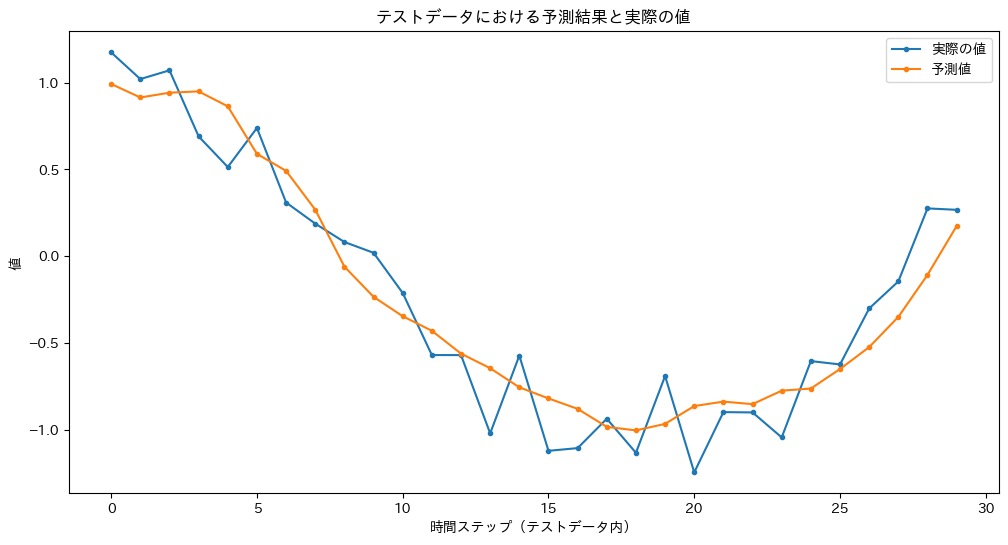
model.eval() は、モデルを評価モードに設定するための重要な一行です。これにより、学習中にだけ機能するDropout(一部のニューロンを無効化して過学習を防ぐ機能)が無効になるなど、モデルが予測に専念するモードに切り替わります。
with torch.no_grad(): ブロック内では、学習時には必須だった勾配の計算がすべて行われなくなります。これにより、余計なメモリ消費を抑え、計算速度を大幅に向上させることができます。予測や評価の際には、この2つをセットで記述するのが定石です。
このコードの核心部分は、forループによる予測プロセスです。ここでは、テストデータX_testをインデックスの0, 1, 2, ...というように最初から最後まで順番に処理していきます。ループの各ステップでは、テスト用の波形から切り出された一つ分のシーケンス(例:10個の連続したデータ点)を入力し、その直後の1点を予測します。これは、あたかも元の波形の上を解析用のウィンドウが1ステップずつスライドしながら、次の値を次々と予測していくような動作です。
このようにして得られた予測値のリスト predicted_outputs は、元のテストデータに対応した一つの連続した波形となります。だからこそ、その結果と実際の値を重ねてプロットすることで、モデルが時系列のパターンをどれだけうまく捉え、未来の値を予測できているかを視覚的に確認できるのです。また、テストデータ全体に対するMSE(平均二乗誤差)を計算することで、モデルの汎化性能を「予測誤差の平均」という形で数値的に評価できます。
このサンプルコードは、RNNの基本的な実装の流れを示したものです。実際の医療データに適用する際は、ノイズの多いデータの扱いや欠損値への対応といった前処理、より長期の依存関係を捉えるためのモデル構造(LSTMやGRU)の調整、そして様々なハイパーパラメータのチューニングが、さらに重要になってきます。
4. 医療分野におけるRNNの応用例と今後の展望
RNNとその発展形であるLSTMやGRUは、その時系列・シーケンシャルデータ処理能力から、医療分野で多岐にわたる応用が研究・開発されています。
4.1. 具体的な応用例
- 生理学的信号の解析と異常検知:
- 心電図 (ECG): 不整脈の検出、心筋梗塞の早期発見など、ECGの波形パターンから心疾患のリスクを予測する研究が進んでいます [9, 10]。RNNは、ECGの複雑な時間的特徴を捉えるのに適しています。
- 脳波 (EEG): てんかん発作の予測、睡眠ステージの分類、脳卒中後の機能回復評価など、EEG信号の時系列パターンから脳の状態を分析します [11]。
- 患者モニタリング: ICU(集中治療室)などで連続的に収集されるバイタルサイン(心拍数、血圧、呼吸数、SpO2など)の時系列データを解析し、患者の状態悪化(敗血症、心停止など)を早期に予測するシステムの開発が期待されています [12]。
- 電子カルテ (EHR) や医療テキストデータの解析:
- 疾患予測・診断支援: 医師の記録や看護記録、検査結果などのテキスト情報を含むEHRデータから、特定の疾患の発症リスクを予測したり、診断の手がかりを抽出したりする研究が行われています [3, 13]。RNNは、テキスト内の単語の順序や文脈を理解するのに役立ちます。
- 医療情報の抽出: 膨大な医学論文や臨床ガイドラインから、特定の治療法や薬剤に関する情報を効率的に抽出する自然言語処理タスクに応用されます。
- 予後予測:
- 患者の過去の治療歴、検査値の推移、生活習慣などの時系列データを用いて、特定の治療に対する反応や生存期間などの予後を予測するモデルの開発が進められています [14]。
- ウェアラブルデバイスからの健康データ分析:
- スマートウォッチやフィットネストラッカーから得られる活動量、睡眠パターン、心拍数などの連続的なデータをRNNで解析し、個人の健康状態のモニタリングや生活習慣病のリスク評価、行動変容の促進などに繋げる試みがあります [15]。
- 医療画像のシーケンシャルな解析:
- 動画内視鏡検査の映像や、連続的なMRIスライス画像など、順序性のある画像シーケンスの解析にもRNNの考え方が応用されることがあります。例えば、動画内の異常部位の検出や追跡などです。
4.2. RNNの限界と発展形
基本的なRNNには前述の通り勾配消失・爆発問題があり、長期的な依存関係の学習が苦手です。このため、医療応用においても、より複雑なパターンや長期依存性を捉える能力が高いLSTM (Long Short-Term Memory) [5] や GRU (Gated Recurrent Unit) [6] が広く用いられています。これらのモデルは、セル内部に「ゲート」と呼ばれる情報選択機構を持つことで、必要な情報を長期間記憶し、不要な情報を忘れることを可能にしています。
近年では、Transformer [16] という、RNNの再帰構造を用いずにアテンション機構(入力シーケンスのどの部分に注目すべきかを学習する仕組み)のみでシーケンスを処理するモデルが、特に自然言語処理の分野で大きな成功を収め、医療テキスト解析などにも応用が拡大しています。Transformerは並列計算に優れており、非常に長いシーケンスに対しても効果的です。
4.3. 倫理的・社会的な考慮事項
医療AI、特にRNNのような複雑なモデルを実臨床に応用する際には、技術的な側面だけでなく、倫理的・社会的な課題も慎重に考慮する必要があります。
- データのプライバシーとセキュリティ: 患者の機微な医療情報を扱うため、データの匿名化、アクセス制御、セキュアなデータ管理体制が不可欠です [17]。
- モデルの解釈性と説明責任 (Explainable AI, XAI): なぜAIがそのような予測や判断を下したのかを人間が理解できるようにすることは、医療現場での信頼を得て、誤診を防ぐ上で非常に重要です [18]。RNNやLSTMは内部状態が複雑なため、判断根拠の解釈が難しい「ブラックボックス」モデルと見なされることがあります。この解釈性を向上させるための研究(XAI)が活発に行われています。
- バイアスの問題: AIモデルは学習データに含まれるバイアス(例:特定の性別や人種に偏ったデータ)を学習し、増幅してしまう可能性があります。これにより、特定の患者群に対して不利益な結果をもたらす恐れがあるため、データの収集段階から公平性に注意し、モデルのバイアスを検証・軽減する取り組みが必要です [19]。
- 規制と承認: 医療AIシステムを実際の診断や治療に使用するためには、薬事承認などの規制当局の審査をクリアする必要があります。安全性と有効性を客観的に示すための厳密な検証が求められます。
4.4. 今後の展望
RNNを含む深層学習技術は、医療分野において今後ますます重要な役割を果たすと予想されます。
- 個別化医療の推進: 個々の患者の遺伝情報、生活習慣、リアルタイムの生理データなどを統合的に解析し、一人ひとりに最適化された予防法や治療法を提供する「個別化医療(プレシジョン・メディシン)」の実現に貢献することが期待されます。
- 予防医療への貢献: ウェアラブルデバイスやEHRからのデータを継続的にモニタリングすることで、疾患の早期兆候を捉え、発症前に介入する「予防医療」の精度向上に繋がる可能性があります。
- 医療リソースの効率化: AIによる診断支援や業務自動化は、医療従事者の負担を軽減し、より専門的な業務に集中できる環境を作ることで、医療システム全体の効率化に貢献する可能性があります。
- 学際的協力の重要性: 医療AIの開発と社会実装を成功させるためには、医学・情報科学・工学・倫理学・法学など、多様な分野の専門家が協力し、技術開発と社会受容性の両面から課題に取り組むことが不可欠です。
5. まとめ
本記事では、医療AIの初学者向けに、PyTorchを用いた再帰型ニューラルネットワーク(RNN)の基本的な概念から実装方法、そして医療分野での応用例と今後の展望について解説しました。
RNNは、心電図や電子カルテのテキストデータといった時系列・シーケンシャルな情報を扱う上で強力なツールであり、その基本的な仕組みを理解し、実際にコードを書いてみることは、医療AIの世界への第一歩となります。
今回紹介したサンプルコードは非常にシンプルなものでしたが、これを足がかりとして、より複雑なモデル(LSTM、GRUなど)や実際の医療データを用いた応用に挑戦していただければ幸いです。医療AIの開発は、プログラミングスキルだけでなく、医療ドメインの知識、そして倫理的な視点も求められる奥深い分野です。この記事が、皆様の研究や臨床における新たな取り組みの一助となることを願っています。
6. 参考文献
- Rumelhart DE, Hinton GE, Williams RJ. Learning representations by back-propagating errors. Nature. 1986;323(6088):533-536.
- Faust O, Hagiwara Y, Hong TJ, Lih OS, Acharya UR. Deep learning for healthcare applications based on physiological signals: A review. Comput Methods Programs Biomed. 2018;161:1-13.
- Rajkomar A, Oren E, Chen K, et al. Scalable and accurate deep learning with electronic health records. NPJ Digit Med. 2018;1:18.
- Bengio Y, Simard P, Frasconi P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans Neural Netw. 1994;5(2):157-166.
- Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput. 1997;9(8):1735-1780.
- Cho K, Van Merriënboer B, Gulcehre C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In: Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP); 2014:1724-1734.
- Paszke A, Gross S, Massa F, et al. PyTorch: An imperative style, high-performance deep learning library. In: Advances in Neural Information Processing Systems 32; 2019:8026-8037.
- PyTorch Documentation. PyTorch.org. Accessed May 23, 2025. https://pytorch.org/docs/stable/index.html
- Hannun AY, Rajpurkar P, Haghpanahi M, et al. Cardiologist-level arrhythmia detection and classification in ambulatory electrocardiograms using a deep neural network. Nat Med. 2019;25(1):65-69.
- Attia ZI, Kapa S, Lopez-Jimenez F, et al. Screening for cardiac contractile dysfunction using an artificial intelligence–enabled electrocardiogram. Nat Med. 2019;25(1):70-74.
- Roy Y, Banville H, Albuquerque I, Gramfort A, Falk TH, Faubert J. Deep learning-based electroencephalography analysis: a systematic review. J Neural Eng. 2019;16(5):051001.
- Shickel B, Loftus TJ, Adhikari L, et al. DeepSOFA: A Continuous Acuity Score for Critically Ill Patients Using Clinically Interpretable Deep Learning. Sci Rep. 2019;9(1):1879.
- Choi E, Bahadori MT, Schuetz A, Stewart WF, Sun J. Doctor AI: Predicting Clinical Events via Recurrent Neural Networks. JMLR Workshop Conf Proc. 2016;56:301-318.
- Esteva A, Robicquet A, Ramsundar B, Kuleshov V, DePristo M, Chou K, Cui C, Fakoor R, Ennis C, Kim S, et al. A guide to deep learning in healthcare. Nat Med. 2019;25(1):24-29.
- Majumder S, Deen MJ. Smartphone Sensors for Health Monitoring and Diagnosis. Sensors (Basel). 2019;19(9):2164.
- Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. In: Advances in Neural Information Processing Systems 30; 2017:5998-6008.
- Price WN 2nd, Cohen IG. Privacy in the age of medical big data. Nat Med. 2019;25(1):37-43.
- Amann J, Blasimme A, Vayena E, Frey D, Madai VI; Precise4Q consortium. Explainability for artificial intelligence in healthcare: a multidisciplinary perspective. BMC Med Inform Decis Mak. 2020;20(1):310.
- Chen IY, Joshi I, Ghassemi M, et al. Treating health disparities with artificial intelligence. Nat Med. 2024;30(4):969-971.
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






