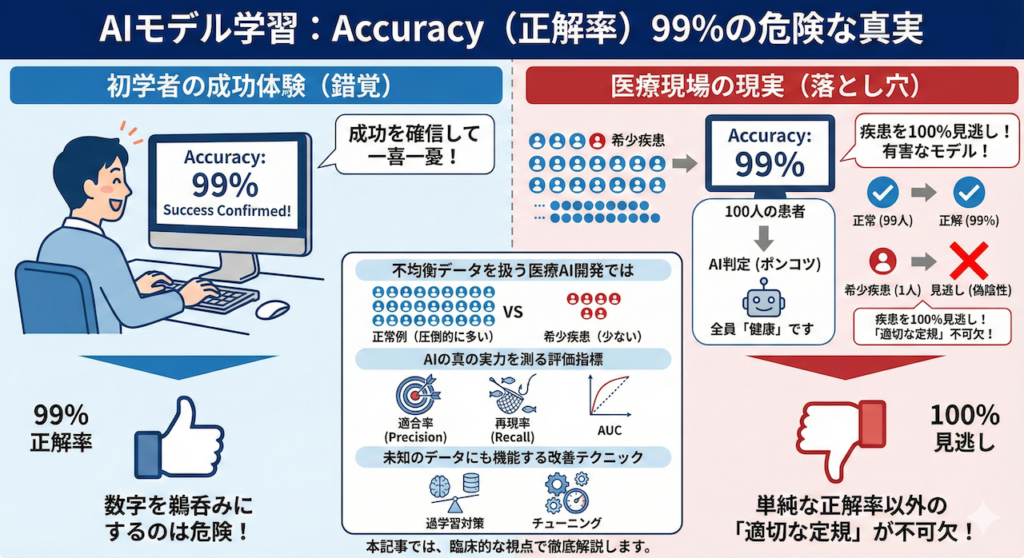
[Clinical AI Coding 100 : C37] あなたのAIを最強にする！モデル評価と改善の必須テクニック

2026年1月4日

AIモデルの学習が終わり、画面に「Accuracy（正解率）：99%」と表示された瞬間、多くの初学者は成功を確信して一喜一憂してしまいます。しかし、命を扱う医療現場において、この数字を鵜呑みにすることは極めて危険です。なぜなら、その99%は「何も診断していない」ことの証かもしれないからです。

想像してみてください。100人に1人しか罹患していない希少疾患の診断モデルを作るとします。仮にAIが、診察する全員に対して何も考えず「あなたは健康です」と答え続けるポンコツなプログラムだったとしても、計算上の正解率は「99%」になってしまいます。しかし、このAIは肝心の疾患を100%見逃しています（偽陰性）。病気の見逃しが許されない臨床現場において、このようなモデルは「役に立たない」どころか「有害」です。

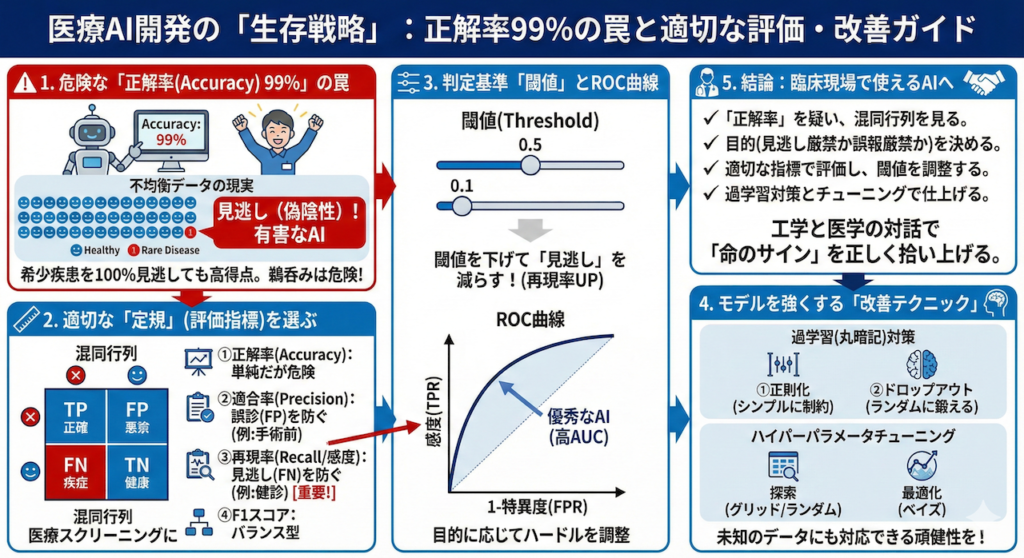
このように、正常例が圧倒的に多い「不均衡データ」を扱う医療AI開発では、単純な正解率以外の「適切な定規」で性能を測ることが不可欠です。本記事では、AIの真の実力を解剖するための評価指標（適合率、再現率、AUCなど）と、学習したAIが未知の患者データに対しても正しく機能するための改善テクニック（過学習対策とチューニング）について、臨床的な視点を交えて徹底解説します。

1. 混同行列（Confusion Matrix）：AIの「成績表」を解剖する

AIの良し悪しを判断するとき、ただ「正解率90点！」と言われても、実は中身がわかりません。そこで登場するのが「混同行列（こんどうぎょうれつ）」です。

名前は難しそうですが、要するに「AIがどうやって正解し、どうやって間違えたか」を4つのパターンに分けた詳しい成績表のことです。

がん検診を例に、「AI先生」が患者さんを診察するシーンを想像してみましょう。AI先生の診断結果は、以下の4つのどれかになります。

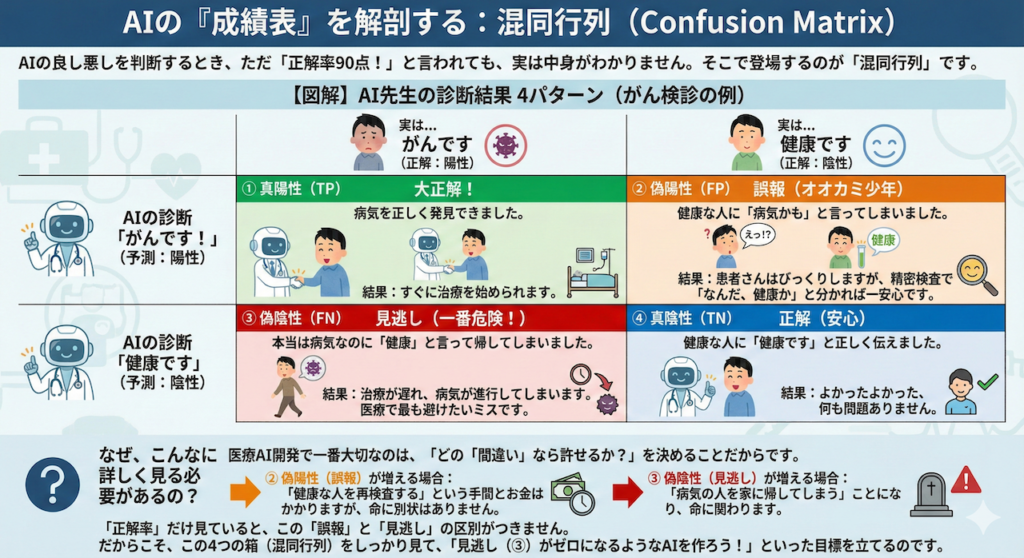
【図解】AI先生の診断結果 4パターン

	実は… がんです（正解：陽性）	実は… 健康です（正解：陰性）
AIの診断「がんです！」（予測：陽性）	① 真陽性 (TP) 大正解！病気を正しく発見できました。結果：すぐに治療を始められます。	② 偽陽性 (FP) 誤報（オオカミ少年）健康な人に「病気かも」と言ってしまいました。結果：患者さんはびっくりしますが、精密検査で「なんだ、健康か」と分かれば一安心です。
AIの診断「健康です」（予測：陰性）	③ 偽陰性 (FN) 見逃し（一番危険！）本当は病気なのに「健康」と言って帰してしまいました。結果：治療が遅れ、病気が進行してしまいます。医療で最も避けたいミスです。	④ 真陰性 (TN) 正解（安心）健康な人に「健康です」と正しく伝えました。結果：よかったよかった、何も問題ありません。

なぜ、こんなに詳しく見る必要があるの？

医療AI開発で一番大切なのは、「どの『間違い』なら許せるか？」を決めることだからです。

② 偽陽性（誤報）が増える場合：
「健康な人を再検査する」という手間とお金はかかりますが、命に別状はありません。
③ 偽陰性（見逃し）が増える場合：
「病気の人を家に帰してしまう」ことになり、命に関わります。

「正解率」だけ見ていると、この「誤報」と「見逃し」の区別がつきません。だからこそ、この4つの箱（混同行列）をしっかり見て、「見逃し（③）がゼロになるようなAIを作ろう！」といった目標を立てるのです。

2. 評価指標：目的に応じた「定規」を選ぶ

混同行列の4つの数字（TP, FP, FN, TN）が出揃ったら、次はそれを使って「AIの賢さ」を通知表のように点数化します。しかし、AIの通知表には「国語・算数・理科…」のように色々な科目（指標）があり、「どの科目を重視するか」は目的によって全く異なります。

ここでは、医療AIで特によく使われる4つの指標を解説します。

① 正解率 (Accuracy)：一番シンプルだけど、一番危険な指標

「テストで何点取れたか？」と同じ、最も直感的な指標です。全体のデータの中で、正解（TPとTN）の割合を計算します。

\[ \text{Accuracy} = \dfrac{TP + TN}{TP + FP + FN + TN} \]

⚠️【注意】「正解率の罠」に気をつけて！

一見良さそうですが、医療データではこの指標は役に立たないことが多いです。
例えば、100人中1人しか病気ではないデータの場合、AIが何も考えずに「全員健康です！」と答えても、99人は正解なので正解率は99%になってしまいます。
これでは、肝心の1人の病気を見逃しているポンコツAIを見抜くことができません（Chicco and Jurman 2020）。

② 適合率 (Precision)：AIの「自信」を疑う指標

「AIが『病気です（陽性）』と診断した人の中で、本当に病気だった人の割合」です。いわば、AIの診断の「確からしさ」や「精密さ」を表します。

\[ \text{Precision} = \dfrac{TP}{TP + FP} \]

この数字が低いと、AIは「あなたも病気、この人も病気」と手当たり次第に診断している（オオカミ少年状態）ことになります。

この指標を重視すべき場面：
- 「確定診断」や「手術」の前：
  AIが「がん」と診断したら、すぐに体にメスを入れる手術をするとします。もしAIが間違っていたら、健康な人の体を傷つけてしまいます。こういう場合は、「AIが陽性と言ったら、それは間違いなく陽性である（偽陽性 FP が少ない）」ことが求められるため、適合率を最重要視します。

③ 再現率 (Recall) / 感度 (Sensitivity)：見逃しを許さない指標

「実際に病気の人の中で、AIがどれだけ見つけ出せた（回収できた）かの割合」です。医療の世界では「感度」とも呼ばれ、非常に重要視されます。

\[ \text{Recall} = \dfrac{TP}{TP + FN} \]

この数字が低いと、病気の人を見逃して家に帰してしまっていることになります。

この指標を重視すべき場面：
- 「健康診断」や「スクリーニング」：
  がん検診の目的は、「怪しい人を一人残らず拾い上げる」ことです。多少健康な人を「要再検査」としてしまっても（適合率が下がっても）、本当の病気の人を絶対に見逃さない（偽陰性 FN をゼロにする）ことが優先されます。そのため、ここでは再現率（感度）が王様となります（Altman and Bland 1994）。

④ F1スコア (F1-Score)：バランス型の優等生

実は、「適合率（慎重さ）」と「再現率（見逃さない力）」はシーソーの関係にあります。慎重になりすぎると見逃しが増え、見逃しを減らそうとすると誤報が増えます。

そこで、この2つの指標をいい感じに統合して、総合的なバランスを見るのがF1スコアです。

\[ F1 = 2 \times \dfrac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} \]

特徴：単純な平均（足して2で割る）ではなく、「調和平均」という計算を使います。これは、「どちらか片方でも成績が悪いと、全体の点数もガクッと下がる」という厳しい採点方式です。そのため、極端な偏りのない優秀なモデルだけが高いスコアを出せます。
使う場面：病気の人と健康な人の数が極端に違うデータ（不均衡データ）で、総合力を評価したいときによく使われます。

3. ROC曲線とAUC：判定の「ハードル」を変えても強いか？

ここまで「正解率」や「感度」の話をしてきましたが、実はこれらは「ある1つの基準」で合否を決めた場合の結果に過ぎません。

AIモデルは通常、「がんです！」といきなり断定するのではなく、「がんである確率は 85% です」というふうに「確率（スコア）」を出力します。

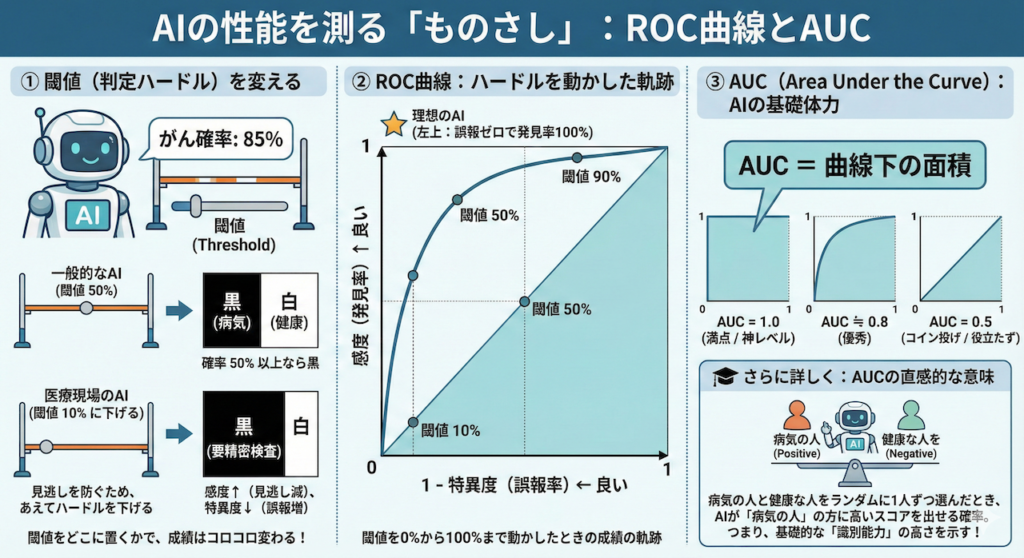
① 「閾値（しきいち）」という名の判定ハードル

この「確率 85%」を、白（健康）か黒（病気）かに決めるには、どこかに境界線を引く必要があります。この境界線を閾値（Threshold）と呼びます。

一般的なAI：
- 「確率 50% 以上なら黒（病気）」とすることが多いです。
医療現場のAI：
- 「がんの見逃しは絶対にダメだ。疑わしい人は全員拾いたい」と考えます。
- そこで、あえてハードルを下げて「確率 10% 以上なら黒（要精密検査）」と設定を変えることがあります。

このように、閾値（ハードル）をどこに置くかで、AIの成績（感度や特異度）はコロコロ変わってしまいます。

② ROC曲線：ハードルを動かしたときの「軌跡」

では、この閾値を「0%（全員病気）」から「100%（全員健康）」まで、少しずつ動かしていったらどうなるでしょうか？

ハードルを動かすたびに変わる成績を、グラフ上にプロットして線でつないだもの。それがROC曲線（Receiver Operating Characteristic Curve）です。

【ROC曲線の見方】

縦軸（Y軸）：感度（病気を発見できる率）
→ 上に行くほど良い（見逃しがない）。
横軸（X軸）：1 – 特異度（誤報率）
→ 左に行くほど良い（健康な人を間違えない）。

つまり、グラフの「左上（誤報ゼロで発見率100%）」に近づくカーブほど
優秀なAIということになります。

③ AUC (Area Under the Curve)：AIの「基礎体力」

ROC曲線は「線」なので、モデル同士を比較しにくい（どっちの線が上か分かりにくい）ことがあります。そこで、「ROC曲線の下側の面積」を計算して、一つの数字で表したのがAUCです。

AUC = 1.0 （満点）：
- どんなにハードルを変えても完璧に診断できる「神レベル」のAI。
AUC = 0.5 （最低ライン）：
- コイン投げで適当に決めるのと同じレベル。「役立たず」です。

一般的に、AUCが 0.8以上 あれば、かなり性能が良いモデルと言えます。

🎓 さらに詳しく：AUCの直感的な意味

AUCの数値には、とても分かりやすい解釈があります。
「病気の人と健康な人をランダムに1人ずつ連れてきたとき、AIが『病気の人』の方に、より高い『病気確率』を出せる確率」です（Hanley and McNeil 1982）。
つまり、AUCが高いということは、閾値をどう設定しようが、「病気の人と健康な人を正しく区別する基礎能力（識別能）が高い」ことを意味します。

4. 過学習（Overfitting）への処方箋：AIの「丸暗記」を防ぐ

AI開発で最も頻繁に起こり、かつ厄介な問題が「過学習（Overfitting）」です。

これは一言で言えば、「練習問題（学習データ）は100点満点なのに、本番の試験（未知のデータ）では赤点」という状態です。AIがデータの本質的な法則（病気の特徴など）を理解せず、たまたまそのデータに含まれていたノイズや些細なクセまで「丸暗記」してしまった結果、応用力がゼロになってしまうのです。

医療データはノイズ（アーアーチファクトや個人差）が多いため、特に過学習が起きやすい分野です。これを防ぐための代表的なテクニックを2つ紹介します。

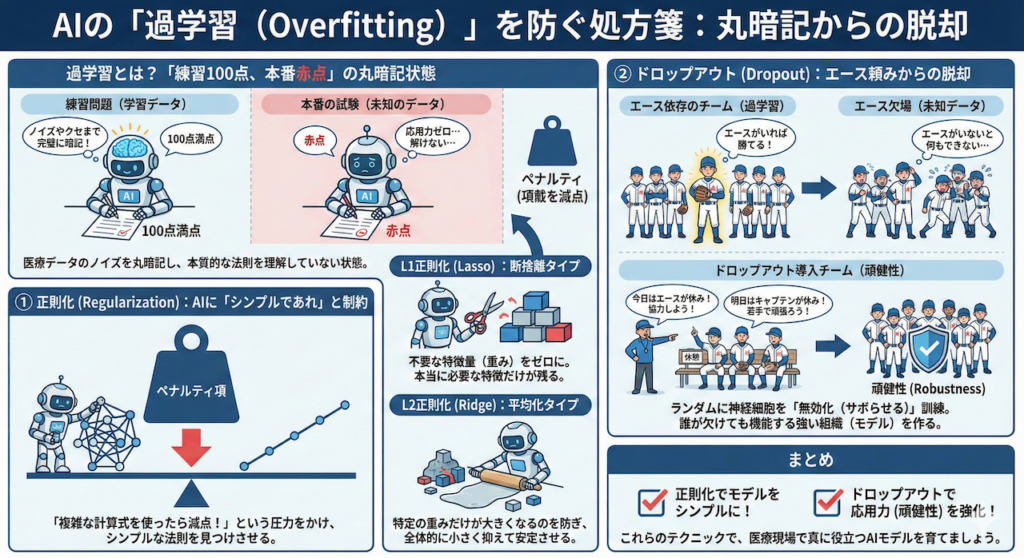
① 正則化 (Regularization)：AIに「シンプルであれ」と制約をかける

AIは放っておくと、正解率を上げるためにどんどん複雑でひねくれた解釈（モデル）を作ろうとします。そこで、AIの学習時の目標（損失関数）に「ペナルティ項」というルールを追加します。

これは「正解するのは大事だけど、複雑な計算式を使ったら減点するぞ」とAIにプレッシャーをかけるようなものです。これにより、AIは「できるだけシンプルな法則」を見つけようとします。

L1正則化 (Lasso)：
- 「断捨離」タイプです。重要でないデータの特徴（重み）をバッサリと「ゼロ」にします。
- 結果として、「本当に必要な特徴量」だけが残るため、どの検査項目が効いているかが分かりやすくなります（特徴量選択の効果）。
L2正則化 (Ridge)：
- 「平均化」タイプです。特定の特徴量だけを極端に重視することを防ぎ、全体的に重みを小さく抑えます（Weight Decay）。
- 特定のデータに振り回されにくく、安定したモデルになります。

② ドロップアウト (Dropout)：エース頼みからの脱却

ニューラルネットワークの学習中に、ネットワーク内のニューロン（神経細胞）をランダムに選んで、一時的に「無効化（サボらせる）」手法です（Srivastava et al. 2014）。

⚾️ 野球チームに例えると…

ある特定のエース選手（特定の特徴量）だけに頼り切りのチームは、その選手が怪我をすると（未知のデータでその特徴がないと）一気に弱くなります。
ドロップアウトは、「練習のたびにランダムに選手を休ませる」ようなものです。

「今日はエースがいないから、残りのメンバーで協力して勝とう」
「明日はキャプテンが休みだから、若手が頑張ろう」

こうして強制的に厳しい環境で訓練することで、「誰が欠けてもチーム全体として機能する（冗長性を持った）」強い組織（モデル）が出来上がるのです。
これを専門用語で「頑健性（Robustness）」と言います。

5. ハイパーパラメータチューニング：AIの「才能」を限界まで引き出す

AIモデルの性能は、単にデータを読み込ませるだけでは決まりません。学習を始める前に、人間が手動で設定しなければならない重要な「設定値」があります。これをハイパーパラメータと呼びます。

🍳 料理に例えると…

「パラメータ（重み）」は、AIが学習中に自力で見つける「塩加減」や「火加減」の微調整です。
一方、「ハイパーパラメータ」は、料理を始める前に人間が決める「オーブンの設定温度」や「煮込む時間」のようなものです。

どんなに良い食材（データ）があっても、オーブンの設定（ハイパーパラメータ）が間違っていたら、料理は黒焦げになったり生焼けになったりします。
この「最高の設定」を探し出す作業をチューニングと呼びます。

代表的な3つの探索方法を紹介します。

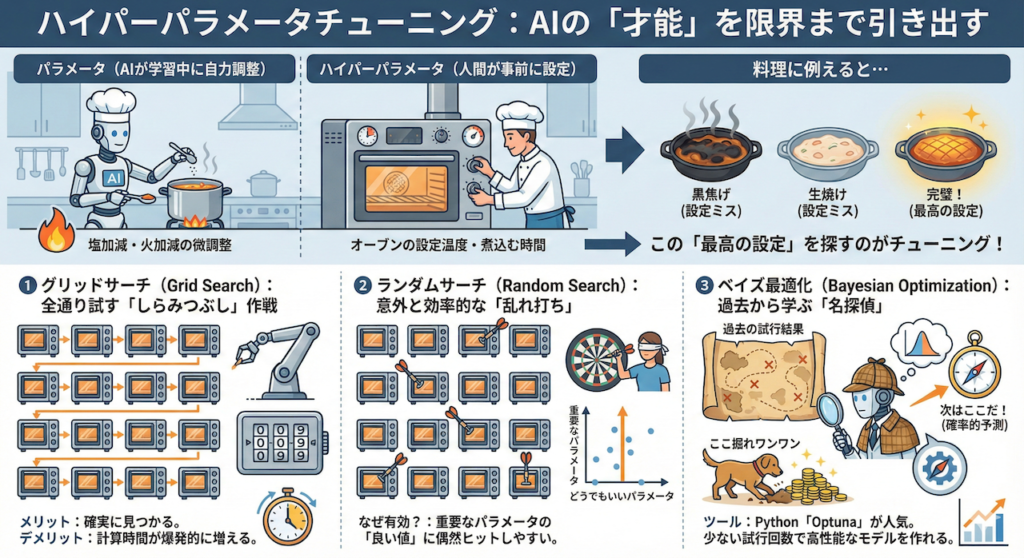
① グリッドサーチ (Grid Search)：全通り試す「しらみつぶし」作戦

あらかじめ設定した候補の組み合わせを、全てのパターンで総当たりして試す方法です。

イメージ：3桁のダイヤル錠を開けるために、「000」から「999」まで全ての番号を順番に試すようなものです。
メリット：指定した範囲内であれば、確実に「一番良い設定」が見つかります。
デメリット：組み合わせが増えると、計算時間が爆発的に増えてしまい、現実的な時間で終わらなくなることがあります。

② ランダムサーチ (Random Search)：意外と効率的な「乱れ打ち」

設定した範囲内から、ランダムに値を選んで試す方法です。

イメージ：ダーツを目隠しして投げるようなものですが、AIの世界ではこれが意外と有効です。
なぜ有効か？：実は、AIの性能には「めちゃくちゃ重要なパラメータ」と「どうでもいいパラメータ」があります。グリッドサーチだと「どうでもいいパラメータ」も細かく調べて時間を浪費しますが、ランダムなら重要なパラメータの「良い値」に偶然ヒットする確率が高くなることが知られています（Bergstra and Bengio 2012）。

③ ベイズ最適化 (Bayesian Optimization)：過去から学ぶ「名探偵」

最も高度で現代的な手法です。これまでの試行結果（過去のデータ）を分析し、「次はどこを探せば良いスコアが出そうか？」を確率的に予測しながら探索します。

イメージ：宝探しです。「ここ掘れワンワン」と適当に掘るのではなく、「さっきあっちで金が出たから、その近くの山脈が怪しいぞ」と推測しながら効率よくポイントを絞ります。
ツール：Pythonでは「Optuna（オプチュナ）」というライブラリがこの手法を使っており、非常に人気があります。少ない試行回数で高性能なモデルを作れるため、現在の主流となっています。

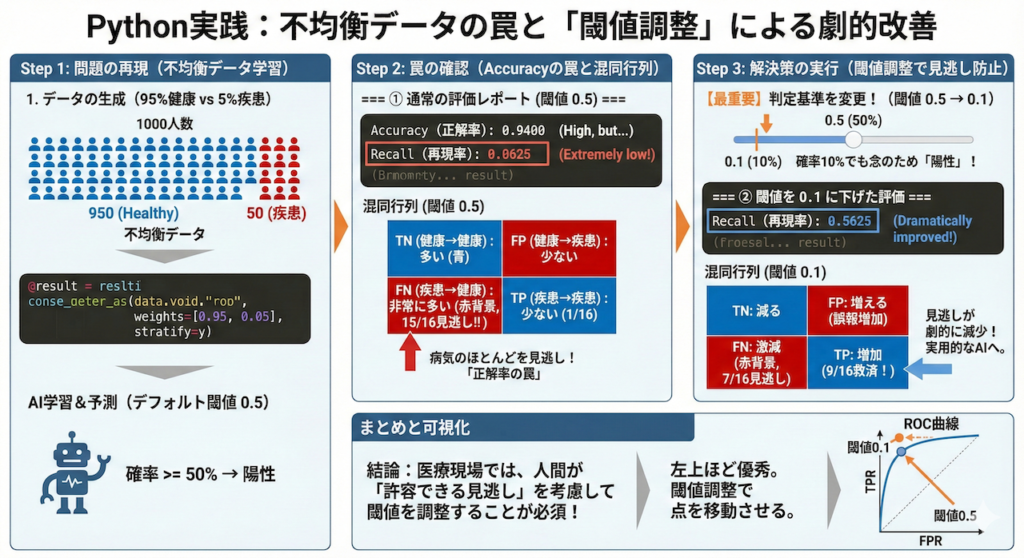
6. Pythonによる実装：不均衡データの罠と「閾値調整」による解決

ここでは、がん診断を模した「陽性（病気）が極端に少ないデータ」を作成し、AIが陥りやすい罠を確認します。
さらに、「判定の基準（閾値）を変えることで、見逃し（偽陰性）を劇的に減らす」という、医療現場で必須のテクニックまで実装します。

🚀 この実習のゴール

「正解率95%」でも、がんを見逃している危険な状態を確認する。
混同行列を使って、AIのミス（見逃し vs 誤報）を可視化する。
【最重要】判定の閾値（しきいち）を調整し、実用的な「見逃さないAI」へ修正する。

【実行前の準備】

以下のコードで日本語のグラフを表示させるには、あらかじめターミナルやコマンドプロンプトでライブラリをインストールしてください。

pip install japanize-matplotlib

【Google Colabの場合：実行前の準備】

以下のコードで日本語のグラフを表示させるには、あらかじめ以下のコードセルを実行してライブラリをインストールしてください。

!pip install japanize-matplotlib

実践コード（全解説付き）

# ==========================================
# 0. ライブラリのインポート
# ==========================================
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib  # グラフの日本語表示用

# データを生成するためのライブラリ
from sklearn.datasets import make_classification
# データを訓練用とテスト用に分けるライブラリ
from sklearn.model_selection import train_test_split
# 基本的な分類モデル（ロジスティック回帰）
from sklearn.linear_model import LogisticRegression
# 評価指標を計算するライブラリ群
from sklearn.metrics import (
    confusion_matrix, accuracy_score, precision_score, 
    recall_score, f1_score, roc_curve, auc
)

# ==========================================
# 1. データの生成（医療現場を模した不均衡データ）
# ==========================================
# 1000人の患者データを生成します。
# 特徴量は20個（検査値などとお考えください）。
X, y = make_classification(
    n_samples=1000,        # 全患者数
    n_features=20,         # 検査項目の数
    n_classes=2,           # 0:陰性(健康), 1:陽性(疾患)
    weights=[0.95, 0.05],  # 【重要】95%が健康、5%だけが疾患（不均衡データ）
    random_state=42        # 実行するたびに同じ結果になるように固定
)

# データを「学習用」と「テスト用（未来の患者さん）」に分割する
# stratify=y は「陽性・陰性の比率」を保ったまま分割する必須オプションです。
# これを忘れると、テストデータに陽性患者が一人もいない！なんてことが起きます。
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42, stratify=y
)

print(f"全データ数: {len(y)}")
print(f"テストデータの陽性数: {sum(y_test)} (全体の約5%)")
print("-" * 30)

# ==========================================
# 2. モデルの学習（ロジスティック回帰）
# ==========================================
# シンプルなモデルを使います。今回はモデルの性能より「評価方法」が主役です。
model = LogisticRegression(random_state=42)
model.fit(X_train, y_train)  # AIに過去のデータを学習させる

# ==========================================
# 3. 予測（通常の方法）
# ==========================================
# AIが出した「0か1か」の診断結果（デフォルトでは確率50%以上を1とする）
y_pred = model.predict(X_test)

# AIが出した「陽性である確率（0.0〜1.0）」
# [:, 1] は「クラス1（陽性）」の確率だけを取り出すという意味です
y_prob = model.predict_proba(X_test)[:, 1]

# ==========================================
# 4. 評価指標の算出（通常の閾値 0.5 の場合）
# ==========================================
print("=== ① 通常の評価レポート (閾値 0.5) ===")
print(f"Accuracy  (正解率): {accuracy_score(y_test, y_pred):.4f}")
print(f"Precision (適合率): {precision_score(y_test, y_pred):.4f}")
print(f"Recall    (再現率): {recall_score(y_test, y_pred):.4f}  <-- ここに注目！")
print(f"F1 Score  (F1):     {f1_score(y_test, y_pred):.4f}")
print("-" * 30)

# ==========================================
# 5. 混同行列の可視化
# ==========================================
# 混同行列（正解と予測の組み合わせ）を計算
cm = confusion_matrix(y_test, y_pred)

plt.figure(figsize=(6, 5))
# ヒートマップで表示（青色が濃いほど数が多い）
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues', annot_kws={"size": 14})
plt.title('混同行列 (閾値 0.5)', fontsize=14)
plt.xlabel('AIの予測', fontsize=12)
plt.ylabel('実際の診断', fontsize=12)
plt.xticks([0.5, 1.5], ['陰性 (健康)', '陽性 (疾患)'])
plt.yticks([0.5, 1.5], ['陰性 (健康)', '陽性 (疾患)'])
plt.show()

# ==========================================
# 6. 【応用】閾値（判定基準）を下げて見逃しを防ぐ
# ==========================================
# 医療現場では「見逃し」が一番怖いため、判定を厳しくします。
# 「確率が 10% (0.1) 以上なら、念のため陽性（要再検査）とする」に変更してみます。
threshold = 0.1
y_pred_adjusted = (y_prob >= threshold).astype(int)

print(f"=== ② 閾値を {threshold} に下げた場合の評価 ===")
print(f"Recall (再現率): {recall_score(y_test, y_pred_adjusted):.4f}  <-- 劇的に改善するはず！")
print(f"混同行列:\n{confusion_matrix(y_test, y_pred_adjusted)}")
print("-" * 30)

# ==========================================
# 7. ROC曲線の描画
# ==========================================
# 閾値をいろいろ変えたときの性能変化をグラフにする
fpr, tpr, thresholds = roc_curve(y_test, y_prob)
roc_auc = auc(fpr, tpr)

plt.figure(figsize=(8, 6))
# ROC曲線を描画
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (AUC = {roc_auc:.2f})')
# ランダム（当てずっぽう）の場合の線を点線で引く
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')

plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate (偽陽性率: 誤報の多さ)')
plt.ylabel('True Positive Rate (真陽性率: 見逃しのなさ)')
plt.title('ROC曲線：左上に行くほど優秀なAI')
plt.legend(loc="lower right")
plt.grid(True)
plt.show()

全データ数: 1000
テストデータの陽性数: 16 (全体の約5%)
------------------------------
=== ① 通常の評価レポート (閾値 0.5) ===
Accuracy  (正解率): 0.9400
Precision (適合率): 0.2500
Recall    (再現率): 0.0625  <-- ここに注目！
F1 Score  (F1):     0.1000
------------------------------

=== ② 閾値を 0.1 に下げた場合の評価 ===
Recall (再現率): 0.5625  <-- 劇的に改善するはず！
混同行列:
[[266  18]
 [  7   9]]
------------------------------

コードと結果の徹底解説

1. データの生成と分割

weights=[0.95, 0.05]：
- これが「不均衡データ」を作る肝です。95%が健康、5%が病気という、実際の検診に近い状況を再現しています。
stratify=y：
- 訓練データとテストデータに分ける際、このオプションがないと「テストデータに病気の人が一人もいない（たまたま全員健康だった）」という事故が起き得ます。stratify は、元のデータの「95:5」の比率を維持したまま分割してくれる、実務では必須のおまじないです。

2. 結果の解釈：Accuracyの罠

実行結果（①）を見ると、おそらくAccuracy（正解率）は高い数値（0.95付近）が出ているはずです。しかし、Recall（再現率）を見てください。低くなっていませんか？

全データ数: 1000
テストデータの陽性数: 16 (全体の約5%)
------------------------------
=== ① 通常の評価レポート (閾値 0.5) ===
Accuracy  (正解率): 0.9400
Precision (適合率): 0.2500
Recall    (再現率): 0.0625  <-- ここに注目！
F1 Score  (F1):     0.1000
------------------------------

これはAIが「どうせほとんど健康なんだから、全員『健康』って言っておけば正解率は稼げるぞ」とサボることを覚えた結果です。
これが「Accuracyの罠」です。医療現場でこのAIを使うと、病気の人の多くが見逃されてしまいます。

3. 解決策：閾値（Threshold）の調整

コードの後半（②）では、判定基準をデフォルトの「50%」から「10%（0.1）」に下げています。

=== ② 閾値を 0.1 に下げた場合の評価 ===
Recall (再現率): 0.5625  <-- 劇的に改善するはず！
混同行列:
[[266  18]
 [  7   9]]
------------------------------

意味：「病気の確率が10%でもあるなら、念のため『陽性（要検査）』と判定しよう」という設定です。
効果：実行結果を見ると、Recall（再現率）が劇的に向上しているはずです。その代わり、Precision（適合率）は下がります（健康な人を誤って再検査に呼ぶ「空振り」が増えるため）。
結論：医療AI開発では、モデルを作って終わりではなく、「どのくらいの見逃しなら許容できるか？」を考えて、人間がこの閾値を調整することが、実用化への最後の鍵となります。

まとめ：医療AI開発の「生存戦略」

本記事では、AIモデルの性能を正しく評価し、臨床現場で真に役立つツールへと昇華させるための重要な概念と技術を解説しました。ここで改めて、重要なポイントを振り返りましょう。

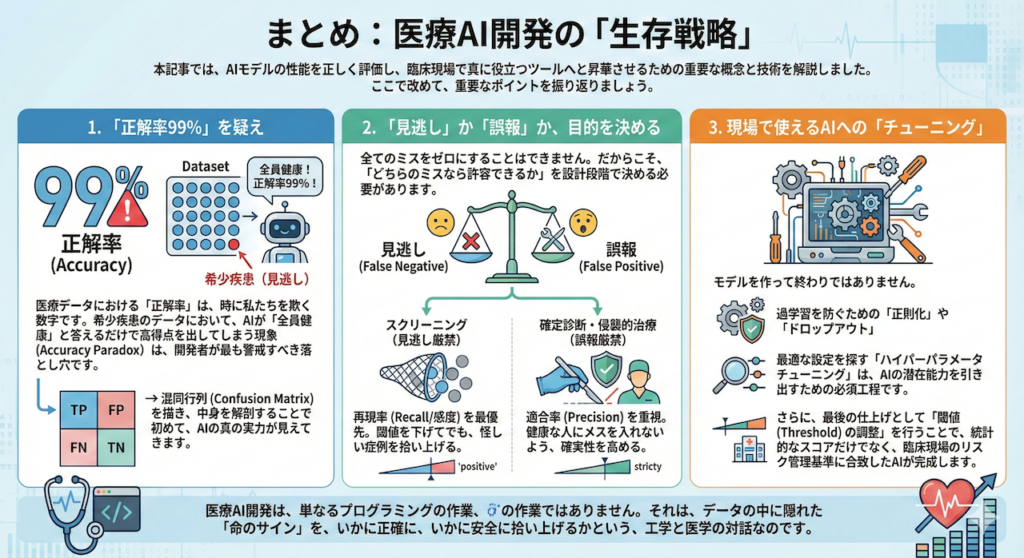
1. 「正解率99%」を疑え

医療データにおける「正解率（Accuracy）」は、時に私たちを欺く数字です。希少疾患のデータにおいて、AIが「全員健康」と答えるだけで高得点を出してしまう現象（Accuracy Paradox）は、開発者が最も警戒すべき落とし穴です。
混同行列（Confusion Matrix）を描き、中身を解剖することで初めて、AIの真の実力が見えてきます。

2. 「見逃し」か「誤報」か、目的を決める

全てのミスをゼロにすることはできません。だからこそ、「どちらのミスなら許容できるか」を設計段階で決める必要があります。

スクリーニング（見逃し厳禁）：再現率（Recall/感度）を最優先。閾値を下げてでも、怪しい症例を拾い上げる。
確定診断・侵襲的治療（誤報厳禁）：適合率（Precision）を重視。健康な人にメスを入れないよう、確実性を高める。

3. 現場で使えるAIへの「チューニング」

モデルを作って終わりではありません。過学習を防ぐための「正則化」や「ドロップアウト」、そして最適な設定を探す「ハイパーパラメータチューニング」は、AIの潜在能力を引き出すための必須工程です。
さらに、最後の仕上げとして「閾値（Threshold）の調整」を行うことで、統計的なスコアだけでなく、臨床現場のリスク管理基準に合致したAIが完成します。

医療AI開発は、単なるプログラミングの作業ではありません。それは、データの中に隠れた「命のサイン」を、いかに正確に、いかに安全に拾い上げるかという、工学と医学の対話なのです。

参考文献

Altman, D.G. and Bland, J.M. (1994). Diagnostic tests. 1: Sensitivity and specificity. BMJ, [online] 308(6943), p.1552. Available at: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2540489/ [Accessed 25 Aug. 2023].
Bergstra, J. and Bengio, Y. (2012). Random Search for Hyper-Parameter Optimization. Journal of Machine Learning Research, [online] 13(10), pp.281–305. Available at: https://www.jmlr.org/papers/v13/bergstra12a.html [Accessed 25 Aug. 2023].
Chicco, D. and Jurman, G. (2020). The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genomics, [online] 21(1). Available at: https://doi.org/10.1186/s12864-020-6413-7.
Hanley, J.A. and McNeil, B.J. (1982). The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology, [online] 143(1), pp.29–36. Available at: https://doi.org/10.1148/radiology.143.1.7063747.
Powers, D.M.W. (2011). Evaluation: from precision, recall and F-measure to ROC, informedness, markedness and correlation. Journal of Machine Learning Technologies, [online] 2(1), pp.37–63. Available at: https://dspace2.flinders.edu.au/xmlui/handle/2328/27165 [Accessed 25 Aug. 2023].
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I. and Salakhutdinov, R. (2014). Dropout: A Simple Way to Prevent Neural Networks from Overfitting. Journal of Machine Learning Research, [online] 15(56), pp.1929–1958. Available at: https://jmlr.org/papers/v15/srivastava14a.html.

※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。

ご利用規約（免責事項）

当サイト（以下「本サイト」といいます）をご利用になる前に、本ご利用規約（以下「本規約」といいます）をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。

第1条（目的と情報の性質）

本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
本サイトで提供されるすべてのコンテンツ（文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません）は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為（以下「医行為等」といいます）を提供するものではありません。
本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。

第2条（法令等の遵守）
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律（薬機法）、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。

第3条（医療行為における責任）

本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家（医師、歯科医師等）が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。

第4条（情報の正確性・完全性・有用性）

本サイトは、掲載する情報（数値、事例、ソースコード、ライブラリのバージョン等）の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。

第5条（AI生成コンテンツに関する注意事項）
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション（事実に基づかない情報の生成）やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。

第6条（知的財産権）

本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。

第7条（プライバシー・倫理）
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。

第8条（利用環境）
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境（OS、ハードウェア、依存パッケージ等）を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。

第9条（免責事項）

本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害（直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません）について、その原因の如何を問わず、一切の法的責任を負わないものとします。
本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。

第10条（規約の変更）
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。

第11条（準拠法および合意管轄）
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。

For J³, may joy follow you.

よかったらシェアしてね！

URLをコピーしました！

URLをコピーしました！

この記事を書いた人

髙﨑洋介（医師・医学博士・MBA） | Prof. TAKASAKI Yohsuke, MD, PhD, ScM, MPA, MBA, FRSM

医師・医学博士・AI研究者・連続起業家
元厚生労働省幹部・ハーバード大学理学修士・ケンブリッジ大学MBA・コロンビア大学行政修士（経済）
岡山大学医学部卒業後、内科・地域医療に従事。厚生労働省で複数室長（医療情報・救急災害・国際展開等）を歴任し、内閣官房・内閣府・文部科学省でも医療政策に携わる。
退官後は、日本大手IT企業や英国VCで新規事業開発・投資を担当し、複数の医療スタートアップを創業。現在は医療AI・デジタル医療機器の開発に取り組むとともに、東京都港区で内科クリニックを開業。
複数大学で教授として教育・研究活動に従事し、医療関係者向け医療AIラボ「Medical AI Nexus」、医療メディア「The Health Choice | 健康の選択」を主宰。
ケンブリッジ大学Associate・社会医学系指導医・専門医・The Royal Society of Medicine Fellow