はじめに:数式アレルギーへの「処方箋」
~AIとの共通言語を手に入れる~
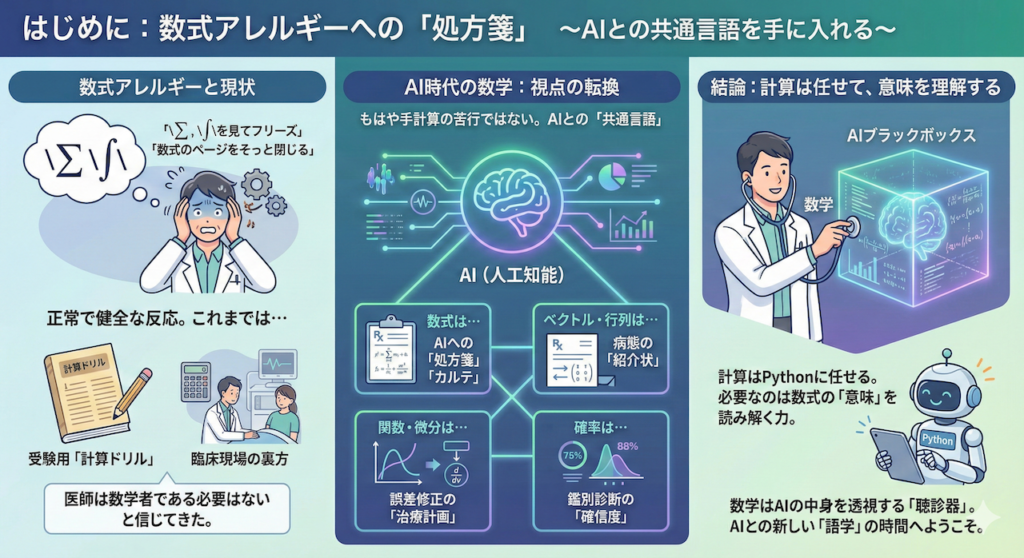
「\(\sum\)(シグマ)や \(\int\)(インテグラル)を見た瞬間、思考がフリーズする」
「数式が出てきたページは、条件反射でそっと閉じてしまう」
正直に申し上げますと、これは極めて正常で、健全な反応です。
私たち医療従事者にとって、数学とは何だったでしょうか? 多くの方にとって、それは遠い昔、受験のために詰め込んだ「計算ドリル」であり、臨床現場に出てからは、電卓や統計ソフト、あるいは検査機器が勝手にやってくれる「裏方の作業」に過ぎなかったはずです。
「医師は文系科目も理系科目もできる必要があるが、数学者である必要はない」
そう信じて、私たちは目の前の患者さんに向き合ってきました。
しかし、AI(人工知能)が医療現場に浸透し始めた今、数学の役割は劇的に変化しています。
もはや数学は、人間が手計算で答えを出すための苦行ではありません。それは、AIという「言葉の通じない超・優秀なパートナー」に、的確な指示を出し、その思考回路を理解するための「共通言語」なのです。
少し視点を変えてみましょう。
もし、目の前にある難解な数式が、単なる「計算問題」ではなく、AIに対する「処方箋(オーダー)」や「カルテ(経過記録)」だとしたらどうでしょうか?
- ベクトルや行列は、患者さんの病態を正確に記述した「紹介状」です。
- 関数や微分は、「誤差を修正して正しい診断に近づけ」というAIへの「治療計画」です。
- 確率は、AIが弾き出した「鑑別診断の確信度」です。
私たちがドイツ語や英語の医学用語を学ぶのは、それが医療現場での共通言語だからです。それと同じように、AI時代の医療現場では、数式の「読み方」を知っていることが、最強の武器になります。
数式の「解き方」を覚える必要はありません。計算はPythonという優秀な助手に任せればいいのです。
必要なのは、数式が語る「意味」を読み解く力。AIが何を見て、どう考え、なぜ間違えたのか。そのブラックボックスの中身を透視する「聴診器」として、数学を捉え直してみませんか?
ここから始まるのは、計算ドリルの時間ではありません。AIという新しい相棒と心を通わせるための、少し不思議で刺激的な「語学」の時間です。
AIの正体:魔法の箱ではなく「3つの臓器」を持つ生命体

AI、特にディープラーニングと聞くと、「何でもできる魔法のブラックボックス」のようなイメージを持っていませんか?
「データを入れれば、中で何か凄いことが起きて、答えが出てくる」。そう思ってしまうと、AIは得体の知れない恐怖の対象になってしまいます。
しかし、その中身を外科医のようにメスで切り開き、分解してみると、そこにあるのは魔法などではありません。実は、非常に精巧に設計された「3つの数学的パーツ」が、まるで臓器のように連携して動いているだけだということが分かります (Deisenroth et al., 2020)。
この3つのパーツを、私たちに馴染み深い医学的なアナロジー(例え)で捉え直すと、その役割が驚くほどスッキリと見えてきます。
1. 線形代数 = データの「解剖学 (Anatomy)」
解剖学が、骨格や筋肉、臓器の配置といった人体の「構造」を学ぶ学問であるように、線形代数(Linear Algebra)は、データの「形」と「空間的な位置関係」を扱う学問です。
- 役割: 目の前の患者さん(膨大な生データ)を、AIが理解・処理できる「行列(Matrix)」や「ベクトル(Vector)」という骨格に整形します。
- イメージ: 私たちがCT画像を見るとき、そこには無数のピクセル(細胞)が整然と配列され、組織を形成していますよね。線形代数は、このピクセルの配列を座標として記述する「地図」のようなものです。これがないと、AIはデータを「見る」ことさえできません。
2. 微分 = 学習の「生理学 (Physiology)」
生理学が、体温調節や血糖値の維持といった「機能」や「恒常性(ホメオスタシス)」のメカニズムを解き明かすように、微分(Calculus)は、AIの「変化」と「修正」を司る機能です。
- 役割: AIが予測を間違えたとき(誤差が生じたとき)、その原因を突き止め、「どのパラメータ(神経結合の強さ)をどう調整すれば改善するか」を計算します。
- イメージ: これはまさに生体のフィードバック機能です。異常な検査値(エラー)を感知し、ホルモンや神経伝達物質を微調整して正常値に戻そうとする「生体システムの最適化プロセス」そのものです。微分こそが、AIに「学習」という動的な生命を吹き込みます。
3. 確率・統計 = 不確実性の「診断学 (Diagnosis)」
そして診断学が、不確実な情報の中から最も確からしい病態を推論するように、確率・統計(Probability & Statistics)は、AIの「判断」と「予測」を担います。
- 役割: データのばらつきやノイズを考慮しながら、「この画像は80%の確率で肺炎であり、20%は肺水腫の可能性がある」といった尤度(もっともらしさ)を弾き出します。
- イメージ: 臨床現場に「100%の正解」はありません。私たちは常に、検査前確率や感度・特異度を考慮しながら、霧の中を進むように鑑別診断を絞り込んでいきます。この「医師の思考プロセス(推論)」を数学的に記述したものが、確率・統計です。
いかがでしょうか。
AIは魔法ではなく、「解剖(データ構造)」を基盤に、「生理(学習機能)」を回し、「診断(確率的予測)」を出力する、極めてロジカルなシステムなのです。
本シリーズでは、これら3つの数学的エンジンが具体的にどう動いているのか、計算機科学の世界的名著『Deep Learning』(Goodfellow et al., 2016) の知見をベースに、数式という名の「聴診器」を使って、その内部を診察(解説)していきます。
【Part 1】線形代数:データの「解剖図」を読む
~世界を「数値の羅列」として捉える~
正直に白状しましょう。「線形代数(せんけいだいすう)」という四字熟語を聞いただけで、蕁麻疹が出そうになりませんか? 私はなります。
しかし、ここでページを閉じないでください。
安心してください。私たち医師がここで学ぶ線形代数は、ややこしい計算問題を解くためのものではありません。AIという「優秀だけど融通の利かない部下」に、的確な指示を出すための「言語」として捉え直せば、恐れるに足りません。
難しい計算は一切抜きです。「ベクトル」や「行列」が、医療現場で具体的に何を表していて、どう役立つのか。その正体を見ていきましょう。
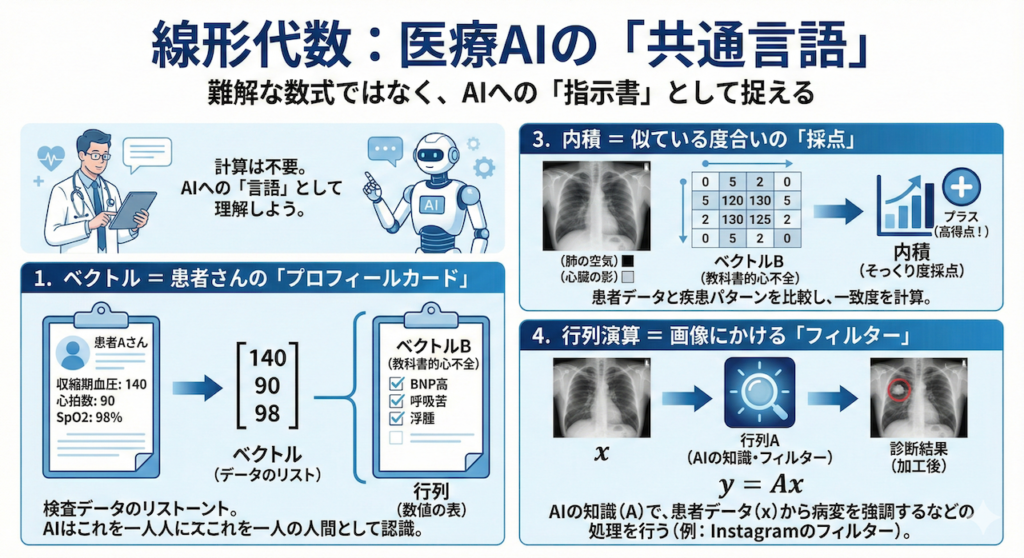
1. 「ベクトル」=「患者さんのプロフィールカード」

数学の教科書で「ベクトル」というと、空間に伸びる「矢印」が出てきますよね。物理学なら「力と方向」を表す矢印ですが、医療データの文脈であの矢印をイメージすると、多くの人が挫折します。
医療AIにおいて、ベクトルをもっと単純に、実務的に捉えましょう。
ベクトルとは、ズバリ「検査データのリスト」です。
例えば、ある患者Aさんが救急搬送されてきたとします。電子カルテやバイタルモニターには、次のような数値が表示されます。
- 収縮期血圧:140 mmHg
- 心拍数:90 bpm
- SpO2:98 %
これらはバラバラの数字ですが、AIにとっては「患者Aさん」という一人の人間を表すセットの情報です。これを縦に並べて、カギ括弧でパッキングしたもの。これがベクトルです。
\[ \mathbf{x} = \begin{bmatrix} 140 \\ 90 \\ 98 \end{bmatrix} \]
ただこれだけのことです。
AIにとって、患者さん一人ひとりは、この「数字のパッケージ(ベクトル)」として認識されています (Strang, 2016)。
私たちが「ベクトル \(\mathbf{x}\) を分析しろ」と命令するのは、プログラマー風に言えば「この患者さんのバイタルサインのリスト(プロフィールカード)を読み込め」と言っているのと全く同じことなのです。
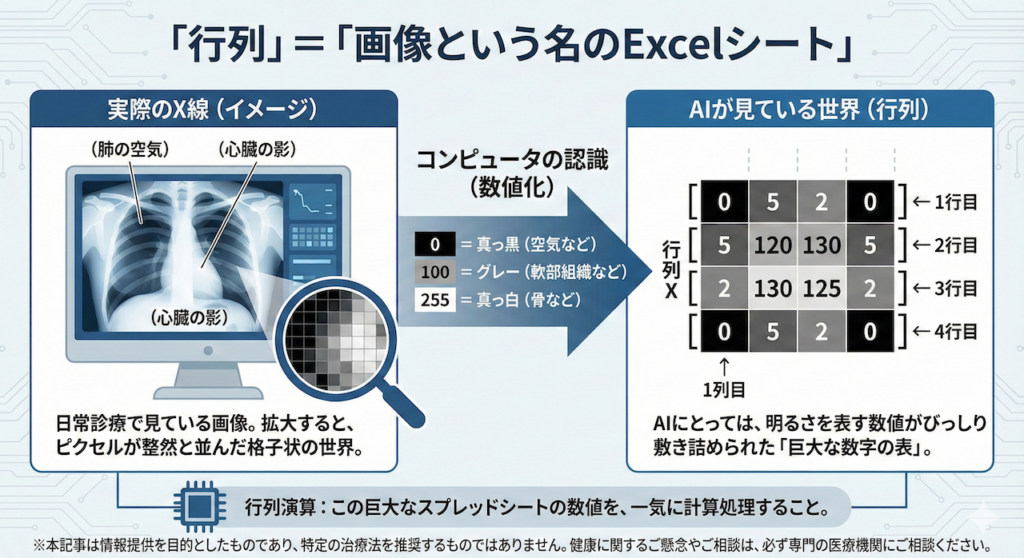
2. 「行列」=「画像という名のExcelシート」
次は「行列(Matrix)」です。映画のタイトルみたいで構えてしまいますが、これも難しく考える必要はありません。
私たちが日常診療で毎日見ている「レントゲン写真」や「CT画像」そのものが、実は行列なのです。
画像を限界まで拡大ズームしていくと、どうなるでしょうか?
小さな正方形の点(ピクセル)が、縦横に整然と並んだ格子状の世界が見えてきます。コンピュータは、その点の一つひとつを「絵」としてではなく、「明るさの度合いを表す数値」として記憶しています。
- 0 = 真っ黒(空気など)
- 255 = 真っ白(骨や造影剤など)
- 100 = グレー(軟部組織など)
つまり、胸部X線画像とは、縦と横に数字がびっしり敷き詰められた「巨大なExcelシート(表)」なのです。
この「数字の表」全体を、数学では大文字のアルファベット(例:\(\mathbf{X}\))で表し、「行列」と呼びます (Goodfellow et al., 2016)。
「行列演算」と聞くと難しそうですが、要するに「この巨大なスプレッドシートの数値を、一気に計算処理すること」に他なりません。
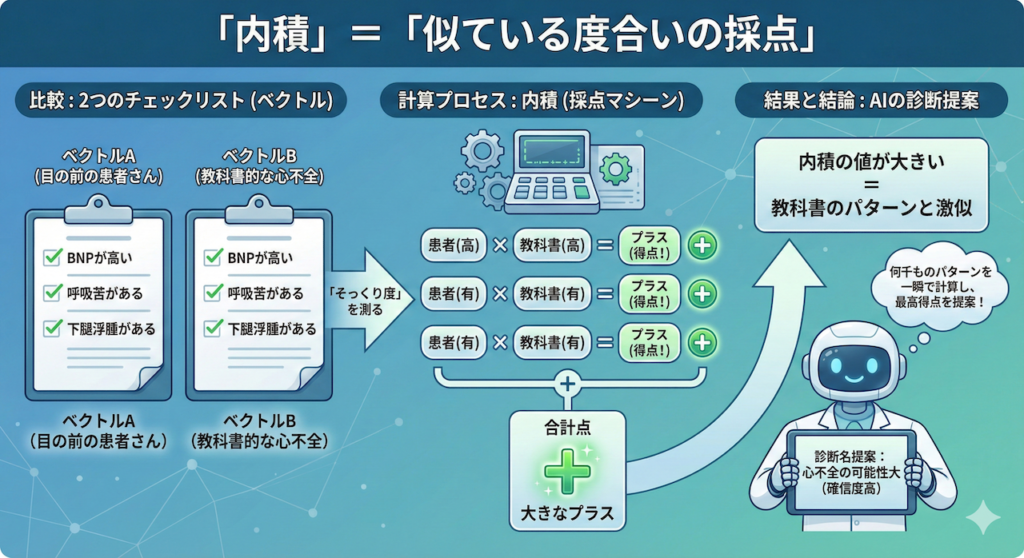
3. 「内積」=「似ている度合いの採点」
さて、ここからがAIの「思考回路」の核心です。
私たち医師は、患者さんを診察した時、「うーん、この症状の揃い方は心不全っぽいな」とか、「これはマイコプラズマ肺炎のパターンだな」と直感的に判断しますよね。
AIはこの「〜っぽい」という感覚を、どうやって計算しているのでしょうか?
ここで使う道具が「内積(ないせき)」です。
数式の定義は忘れてください。これは、2つのベクトルの「そっくり度」を測る採点マシーンです。
想像してみてください。ここに2つのチェックリスト(ベクトル)があります。
- ベクトルA(目の前の患者さん): [BNPが高い, 呼吸苦がある, 下腿浮腫がある]
- ベクトルB(教科書的な心不全): [BNPが高い, 呼吸苦がある, 下腿浮腫がある]
AIは、この2つのリストの項目同士を掛け算して、足し合わせます。
- BNP: 患者(高) × 教科書(高) = プラス(得点!)
- 呼吸苦: 患者(有) × 教科書(有) = プラス(得点!)
- 浮腫: 患者(有) × 教科書(有) = プラス(得点!)
合計点は「大きなプラス」になります。つまり、内積の値が大きいということは、「この患者さんの症状は、教科書的な心不全のパターンと激似である」ということを意味します。
逆に、症状が一致しなければ「プラス × ゼロ = ゼロ」となり、点数は伸びません。AIはこの単純な掛け算と足し算(内積)を何千種類もの病気パターンに対して一瞬で行い、最も点数が高い病気を「診断名」として提案してくるのです。
4. 「行列演算」=「画像にかけるフィルター」
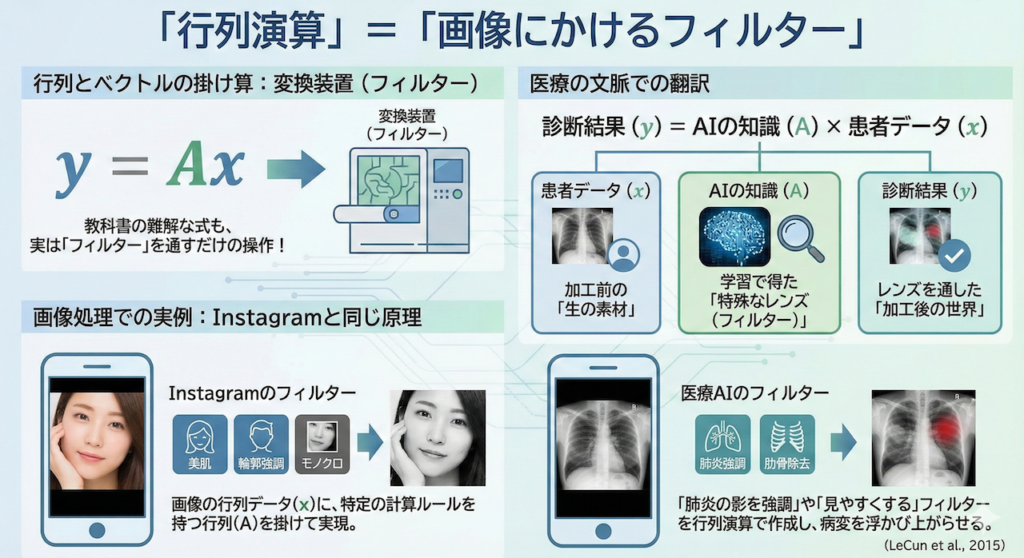
最後に、一番の難所とされる「行列とベクトルの掛け算」です。
教科書に出てくる \(\mathbf{y} = \mathbf{A}\mathbf{x}\) という式。これを見ただけで拒絶反応が出るかもしれませんが、実はこれ、「変換装置(フィルター)」以外の何物でもありません。
これを医療の文脈で翻訳すると、こうなります。
\[ \text{診断結果}(\mathbf{y}) = \text{AIの知識}(\mathbf{A}) \times \text{患者データ}(\mathbf{x}) \]
- \(\mathbf{x}\)(患者データ): 加工前の「生の素材」です。
- \(\mathbf{A}\)(行列): AIが学習によって手に入れた「特殊なレンズ(フィルター)」です。
- \(\mathbf{y}\)(結果): レンズを通して見た、加工後の「世界」です。
画像処理での実例:Instagramと同じ原理
もっと視覚的にイメージしましょう。皆さんがスマホで使っているInstagramや写真加工アプリの「フィルター」と同じです。
- 「美肌フィルター」
- 「輪郭強調フィルター」
- 「モノクロフィルター」
これらは魔法ではなく、画像の行列データ(\(\mathbf{x}\))に対して、特定の計算ルールを持った小さな行列(\(\mathbf{A}\))を掛け算することで実現しています。
医療AIも全く同じです。「肺炎の淡い影だけを強調するフィルター」や「肋骨の影を消して肺野を見やすくするフィルター」を、行列演算によって作り出し、人間には見えにくい病変を浮かび上がらせているのです (LeCun et al., 2015)。
小まとめ:計算は「助手(Python)」に丸投げせよ
ここまで読んで、「理屈は分かった。でも、何万個ものピクセルの数値をいちいち掛け算するなんて、絶対にやりたくない」と思いませんでしたか?
その通りです。人間がやる必要は1ミリもありません。
手術室で例えるなら、執刀医がいちいちメスを消毒したり、ガーゼを数えたりしないのと同じです。それらは専門のスタッフや機械がやるべき仕事です。
数百万回に及ぶこの面倒な単純計算を、文句ひとつ言わずに、しかも0.1秒で終わらせてくれる「超・優秀な助手」。それがプログラミング言語、Python(パイソン)です。
私たち医師の役割は、電卓を叩くことではありません。
「この画像(行列)に、このフィルター(行列)を掛けろ」と、たった1行の指示(コード)を書くだけでいいのです。
これで、AIの「解剖学」である線形代数のイメージは掴めたはずです。
次回からの実践編では、実際にPythonを使って、この「魔法の命令書」を書いていきます。無味乾燥に見えた数学の記号が、目の前で鮮やかな画像処理に変わる瞬間を体験しましょう。
【実践編】助手(Python)への「命令書」を書いてみよう
Pythonの超基礎・入門は、以下👇で学びましたね。

では、実際に私たちの「優秀な助手(Python)」に命令を出してみましょう。
「プログラミング」と身構える必要はありません。やることは、先ほど解説した「ベクトル」と「行列」を定義して、「計算しろ」と一行書くだけです。
ここでは、数値計算の専門家であるライブラリ「NumPy(ナンパイ)」を使用します。
1. 患者データを「ベクトル」にする
まず、救急搬送された患者Aさんのバイタルデータを、AIが読める形(ベクトル)にします。
import numpy as np # 数値計算の専門家「NumPy」を呼び出す
# 患者Aさんのデータ(収縮期血圧140, 心拍数90, SpO2 98)
# これが「ベクトル」です
patient_x = np.array([140, 90, 98])
print("患者ベクトル x:")
print(patient_x)【実行結果】
患者ベクトル x:
[140 90 98]たったこれだけです。数字を [ ] で囲むだけで、Pythonはこれを「ひとまとまりのベクトル」として認識します。
2. 類似度を「内積」で採点する
次に、この患者さんが「教科書的な心不全」とどれくらい似ているか、内積(そっくり度)を計算させてみましょう。
# 教科書的な心不全のパターン(重み付けベクトル)
# 血圧が高いほど、心拍数が高いほど「心不全っぽい」とする単純な例
textbook_pattern = np.array([0.5, 0.3, -0.1])
# 内積を計算せよ(命令)
# np.dot が「掛け合わせて足す」という計算を一瞬でやってくれます
score = np.dot(patient_x, textbook_pattern)
print(f"心不全らしさのスコア(内積値): {score}")【実行結果】
心不全らしさのスコア(内積値): 87.2np.dot という呪文を唱えるだけで、Pythonは面倒な掛け算と足し算を一瞬で終え、「87.2点」というスコアを弾き出しました。
AIはこのスコアを見て、「基準より高いから、アラートを出そう」と判断するわけです。
3. 画像(行列)にフィルターを掛ける
最後に、画像処理です。ここでは簡単にするため、極小の「3×3ピクセル」の画像を想定します。
行列 \(\mathbf{A}\)(フィルター)を行列 \(\mathbf{X}\)(画像)に適用する計算も、Pythonなら一瞬です。
# 3x3の小さな画像(0=黒, 255=白)
image_X = np.array([
[0, 255, 0], # 黒・白・黒
[255, 255, 255],# 白・白・白
[0, 255, 0] # 黒・白・黒
])
# フィルター(強調したい特徴を抽出するレンズ)
filter_A = np.array([
[1, 0, 0],
[0, 1, 0],
[0, 0, 1]
])
# 行列演算を実行せよ(命令)
# @ マークは「行列の掛け算」を表す記号です
processed_image = filter_A @ image_X
print("加工後の画像データ:")
print(processed_image)いかがでしたか?
私たちがやるべきことは、数式を解くことではありません。「データ(患者)」と「道具(数式)」を定義して、Pythonに「実行(Run)」と命令すること。
これが、AI時代の医師に必要な「数学的リテラシー」の正体です。
【Part 2】微分:学習という名の「治療プロセス」
~失敗(誤差)から学び、最適解へ導く~

前回の「Part 1:線形代数」で、AIはデータを「解剖」し、その構造を行列として捉えることができるようになりました。
しかし、解剖図を眺めているだけでは、病気は治せませんし、AIも賢くなりません。死体に命は宿っていないのです。
必要なのは、現状を変化させ、動的なバランスを保ちながら、より良い状態(恒常性)へ導く「機能」です。これこそがAIの「生理学」、すなわち「微分(Calculus)」の役割です。
1. 勾配(Gradient)=「暗闇の山を下る羅針盤」
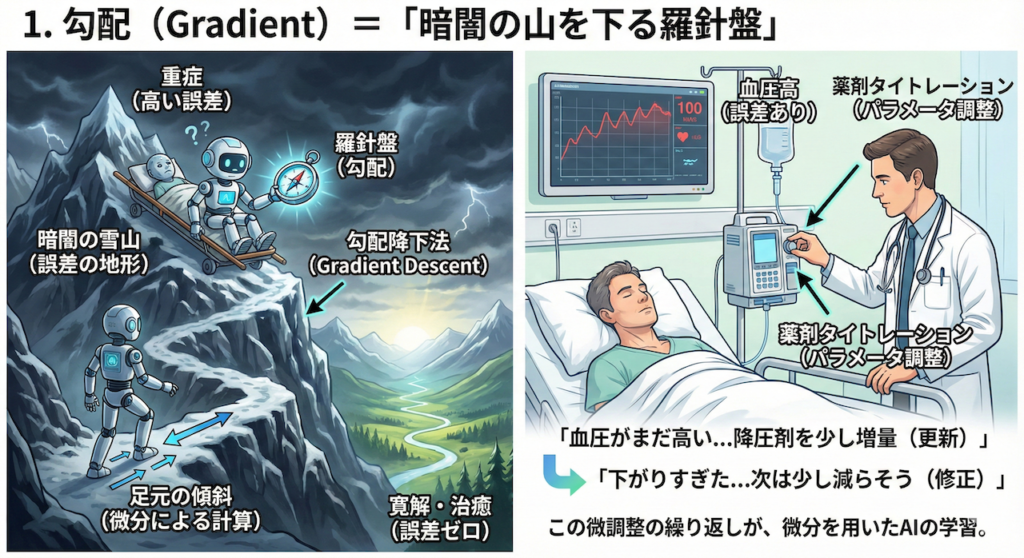
AIの究極の目的はたった一つ。出力結果の「誤差(エラー)」を最小にすることです。診断なら「誤診ゼロ」、予後予測なら「ズレなし」の状態です。
これを医療現場の感覚に例えるなら、「重症(高い誤差)」の状態から、「寛解・治癒(誤差ゼロ)」という谷底を目指して、治療を進めるプロセスだと考えてください。
しかし、AIにとってこの道のりは平坦ではありません。
学習を始めたばかりのAIは、どのパラメータ(重み)をどういじれば正解に近づくのか、全く分かっていません。あたかも、地図を持たずに「真っ暗闇の雪山」に放り出されたようなものです。どこが山頂で、どこが麓なのか、全体像が見えていないのです。
そこで頼りになるのが、自分の「足元の傾斜」です。
「右足側に体重をかけると、少し下っている感覚があるぞ」と分かれば、そちらに慎重に一歩踏み出せますよね。逆に、登っている感覚があれば、そちらに行ってはいけません。
この「足元の傾斜(変化の割合)」を数学的に計算するのが「微分」であり、その傾きと方向を「勾配(Gradient)」と呼びます。
そして、この勾配に従って、少しずつ、慎重にパラメータ(薬の量や処置の強さ)を調整し、誤差を減らしていく手法を「勾配降下法(Gradient Descent)」と言います (Goodfellow et al., 2016)。
これは、私たちが日常的に行っている「薬剤のタイトレーション(用量調整)」と全く同じ思考プロセスです。
- 「血圧がまだ高い(誤差あり)」
→「降圧剤を少し増量してみよう(パラメータ更新)」 - 「下がりすぎた(行き過ぎ)」
→「次は少し減らそう(修正)」
この微調整の繰り返しこそが、微分を用いたAIの学習なのです。
2. 誤差逆伝播(Backpropagation)=「M&Mカンファレンス」
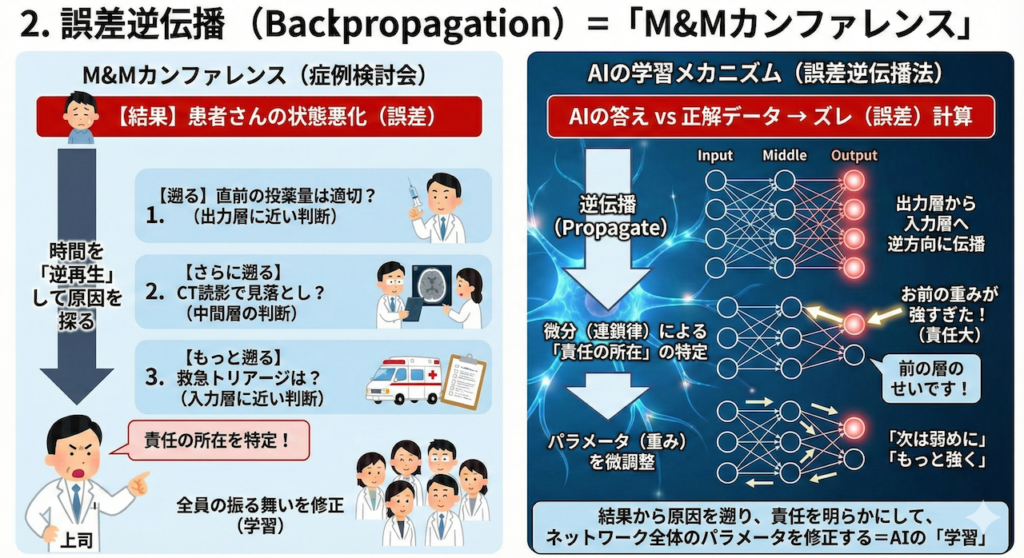
では、AIはどうやって「自分のどこが悪かったのか」を知り、賢くなっていくのでしょうか?
ただ漫然と間違え続けるだけでは、成長はありません。
ここで登場するのが、ディープラーニングの核心技術であり、AIを現在のブームへと押し上げた立役者、「誤差逆伝播法(ごさぎゃくでんぱほう)」、英語でバックプロパゲーション(Backpropagation)です。
名前は恐ろしいほど難しそうですが、やっていることは私たち医療従事者が病院で定期的に行っている「M&Mカンファレンス(Morbidity & Mortality Conference:症例検討会)」そのものです。
時間を「逆再生」して原因を探る
ある症例で、残念ながら望ましくない結果(誤差)が出てしまったとします。
その時、カンファレンスでは何をするでしょうか? 結果から出発して、時間を逆向き(Back)に遡りながら、プロセスのどこに問題があったかを究明しますよね。
- 【結果】 患者さんの状態が悪化した。(ここが出発点)
- 【遡る】 「直前の投薬量は適切だったか?」(出力層に近い判断)
- 【さらに遡る】 「その前の、CT画像の読影で見落としはなかったか?」(中間層の判断)
- 【もっと遡る】 「そもそも、救急搬送時のトリアージや初期情報の聴取は正しかったか?」(入力層に近い判断)
AIも、これと全く同じことを行います。
出力された「AIの答え」と「正解データ」とのズレ(誤差)を計算し、それを出力層から入力層に向かって逆方向に伝播(Propagate)させます。
微分(連鎖律)による「責任の所在」の特定
この時、AI内部では、まるで厳しい上司のような叱責が行われます。
- 「おい、今回ミスったのは、お前(あるニューロン)の重み付けが強すぎたせいだぞ!」
- 「いや、私だけの責任じゃありません。その前の層のアイツが変な信号を送ってきたからです!」
こうして、「誰がどのくらいミスに貢献してしまったか」という「責任の所在(勾配)」を、微分(連鎖律:Chain Rule)という数学テクニックを使って正確に計算します。
そして、「責任の重いニューロン」ほど、そのパラメータ(重み)を大きく修正させられます。「次はもう少し弱めに反応しろよ」「お前はもっと強く主張しろ」と、ネットワーク全体の数億個のパラメータを微調整していくのです。
この「結果から原因を遡り、責任の所在を明らかにして、全員の振る舞いを修正する」というプロセスこそが、AIにおける「学習」の正体です (Rumelhart et al., 1986)。
小まとめ:失敗こそが学習の糧
微分とは、単なる計算テクニックではありません。
それは、「失敗(誤差)を検知し、そこからフィードバックを得て、自己を修正する能力」です。
人間なら数ヶ月に一度のM&Mカンファレンスを、AIは秒間数千回という猛烈なスピードで繰り返します。
この高速な「反省と改善のサイクル」を回し続けることで、AIはやがて熟練医のような直感と精度を獲得していくのです。
次回、最後の【Part 3】では、不確実な医療の世界でAIがどうやって決断を下すのか、「確率・統計(診断学)」のお話で締めくくりましょう。
【実践編】AIに「反省会(学習)」をさせてみよう
ここまで、「微分」や「バックプロパゲーション」といった仰々しい言葉が出てきましたが、実際に私たちがやることはシンプルです。
M&Mカンファレンスの議事録を書くように、AIに対して「反省して、次は直せ」という命令をPythonで送るだけです。
ここでは、現在のAI開発のデファクトスタンダードであるライブラリ「PyTorch(パイトーチ)」を使った書き方を紹介します。
PyTorchには「自動微分(AutoGrad)」という魔法の機能があり、面倒な微分の計算はすべて勝手にやってくれます。
学習の4ステップ=「PDCAサイクル」
AIの学習コードは、基本的に以下の4行の繰り返しで書かれています。これはまさに、医療のPDCAサイクルそのものです。
- 予測(Forward): とりあえず診断してみる。(Do)
- 誤差計算(Loss): 正解とどれくらいズレたか採点する。(Check)
- 逆伝播(Backward): なぜ間違えたか、責任の所在(勾配)を計算する。(Act / M&Mカンファレンス)
- 更新(Optimizer Step): 反省を活かして、脳のシナプス(パラメータ)を修正する。(Action / 改善)
実際のコード(命令書)
では、実際のコードを見てみましょう。英語の命令文ですが、コメントを読めば意味が分かるはずです。
# --- AIの学習サイクル(1回分) ---
# 1. 【予測】 患者データ(x)から、AIが診断(prediction)を出してみる
# 「たぶん、肺炎の確率は30%くらいかな...」
prediction = model(x)
# 2. 【評価】 正解データ(target)と答え合わせをして、誤差(loss)を計算する
# 正解は100%(1.0)なのに、30%(0.3)と答えた → 「大外れだ!(誤差大)」
loss = criterion(prediction, target)
# 3. 【反省】 誤差逆伝播(M&Mカンファレンス)
# 「loss.backward()」という呪文を唱えると、
# PyTorchが自動的に時間を遡り、「誰のせいで間違えたか(勾配)」を計算してくれる
loss.backward()
# 4. 【改善】 パラメータの更新
# 「optimizer.step()」で、特定された責任の重さに応じて、
# 全ニューロンの結合強度を少しだけ修正する(賢くなる)
optimizer.step()いかがでしょうか。loss.backward() と optimizer.step()。
たったこれだけの命令で、AIは「失敗から学び、自己を修正する」という、生物のような振る舞いを行います。
この4行を、1万回もしくはそれ以上はるかに多くループさせる(for文で回す)こと。
それが、私たちが「AIのトレーニング」と呼んでいる作業の全貌です。
【Part 3】確率・統計:不確実性の「診断学」
~「絶対」はない世界で、未来を予測する~
「Part 1:線形代数」で身体(データ構造)を手に入れ、「Part 2:微分」で学習能力(自己修正)を獲得したAI。
さあ、これで完璧な医師になれるでしょうか?
残念ながら、まだ足りません。なぜなら、私たちが戦っている医療の現場は、数学の教科書のような「正解」のある世界ではなく、霧のような「不確実性」に満ちているからです。
「この薬を飲めば100%治る」「この影は絶対に癌である」
臨床現場で、そう言い切れる場面は実はほとんどありませんよね。検査値が正常範囲でも病気のことはあるし、典型的な症状がなくても重症なことはあります。
こうした曖昧な情報の中から、最も確からしい答えを導き出す力。
それがAIにとっての「診断学」、すなわち「確率・統計(Probability & Statistics)」です。

1. 確率分布 = 「正常と異常の境界線」
統計学の基本は、データのばらつきを「分布(Distribution)」として捉えることです。
これは、私たちが毎日見ている健康診断の「基準値範囲」をイメージすれば一発で分かります。
多くの健康な人のデータを集めてヒストグラムを作ると、真ん中が高くて裾が低い、綺麗な山なりのカーブ(正規分布など)ができますよね。
AIも全く同じことをします。学習データから、「正常な肺の画像」や「典型的な心電図」がどのような形の分布をしているのか、その「正常の山」の形を徹底的に学習します (Bishop, 2006)。
そして、新しい患者さんのデータが来たとき、AIはこう考えます。
「この患者さんのデータは、正常の山の『中心に近い(よくある=正常)』か、それとも『裾の端っこにある(めったにない=異常)』か?」
これが、AIによる「外れ値検知」や「異常検知」の基本原理です。
「基準値から外れているから異常だ」と判断する私たちの思考回路と、驚くほど似ていると思いませんか?
2. 尤度(Likelihood)と確信度 = 「鑑別診断の重み付け」
また、AIが「これは肺炎です」と答えるとき、その裏側では「イエスかノーか」の二択で決めているのではありません。常に「確率(%)」を計算しています。
これは、医師が頭の中で行っている「鑑別診断」のプロセスそのものです。
- 「発熱と咳嗽があるな。インフルエンザの可能性が70%、細菌性肺炎が20%、その他が10%くらいかな…」
AIも出力層(Output Layer)で、これと同じ計算を行っています(ソフトマックス関数などを使用)。数式で書くとこうなります。
\[ \text{P}(\text{Pneumonia} \mid \text{X-ray}) = 0.85 \]
これを翻訳すると、「このレントゲン画像(条件)を見たとき、それが肺炎である確率(尤度)は85%である」となります。
このように、確率・統計は、AIに「自信の度合い(Confidence)」を語らせるための言語なのです (Murphy, 2012)。
「100%絶対です」と嘘をつくのではなく、「85%の確率でそうです」と正直に不確実性を伝える。これこそが、医療AIが信頼されるパートナーたり得る理由なのです。
3. 生成AIとサンプリング = 「神様のサイコロ」

最後に、今世界中で話題になっている「生成AI(Generative AI)」についてお話ししましょう。
「Midjourney」で絵を描いたり、「ChatGPT」と対話したり。これらはまるで魔法のように見えますが、実はその正体も、この「確率・統計」の応用に過ぎません。
AIが手に入れた「神様の設計図」
先ほど、AIは正常データの「確率分布(データの山)」を学習すると言いました。
この「確率分布」とは、言ってみれば「データが生まれるための設計図」のようなものです。
- 「人間の肺の画像とは、大体こういう画素の集まりである」
- 「心電図の波形は、通常こういうパターンを取る確率が高い」
AIは学習を通じて、この「神様の設計図(分布)」を自分の中にコピーします。
サイコロを振って「架空の患者」を創る
では、この設計図を使って、どうやって新しいデータを創るのでしょうか?
ここでAIが行うのが「サンプリング(Sampling)」、すなわち「サイコロを振る」という行為です。
AIは、学習した確率分布に従って、ランダムに値を選び出します。
数式で書くと、こうなります。
\[ x_{\text{new}} \sim P_{\text{model}}(x) \]
「モデルが学習した確率分布 \(P\) に従って、新しいデータ \(x\) をランダムに抽出せよ」という命令です。
するとどうなるか?
「年齢は60代、性別は男性、軽度の肺気腫あり…」といった特徴が、サイコロの出目によってランダムに、しかし医学的に矛盾のない組み合わせで決定されます。
その結果、「実在しないけれど、いかにもありそうな架空の患者画像」が生成されるのです。
医療における「創造」の価値
「架空のデータなんて作って何になるんだ?」と思われるかもしれません。しかし、これこそが医療AIのブレイクスルーなのです。
- プライバシーの保護(Synthetic Data): 実在しない患者データなら、個人情報を気にせず研究機関で共有できます。
- 希少疾患のデータ増幅(Data Augmentation): 症例数が少ない病気の画像を、AIに「似たような画像」として大量に生成させ、学習データとして使うことができます。
確率・統計は、単に既存のデータを「分析」するだけでなく、そこから新しい価値を「創造」するためのエンジンにもなるのです。
【まとめ】3つが合体して「AI」になる
~ニューラルネットワークの物語~
ここまで、AIを支える3つの数学的支柱について、医学的なアナロジーを用いて解説してきました。
- 線形代数(解剖学):データの構造と変換
- 微分(生理学):誤差の修正と学習
- 確率・統計(診断学):不確実な予測と判断
最後に、これらが一つに合体したとき、どのような物語が生まれるのかを見てみましょう。これこそが、現代のAIの主役である「ニューラルネットワーク」の動作原理です。
AIが「賢くなる」一連のサイクル
AIの学習プロセスは、私たち医師が臨床経験を積んで成長していく過程と全く同じサイクルを描きます。
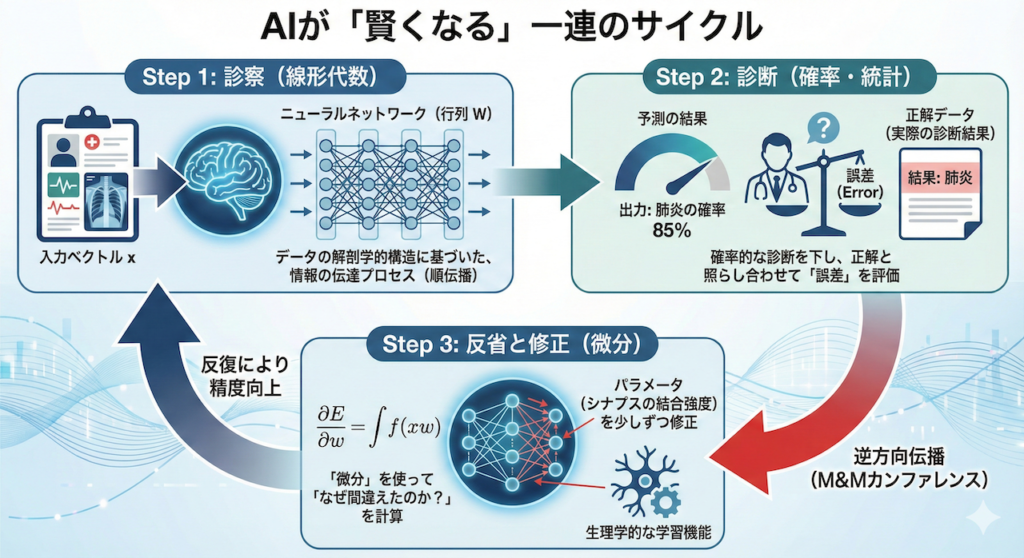
Step 1:診察(線形代数)
まず、目の前の患者データ(入力ベクトル \(\mathbf{x}\))がAIに入力されます。データは、層状に重なったニューロンのネットワーク(行列 \(\mathbf{W}\))を通過しながら、次々と変換されていきます。
「データの解剖学的構造」に基づいた、情報の伝達プロセスです(順伝播)。
Step 2:診断(確率・統計)
ネットワークを通り抜けた情報は、最終的な出力として現れます。「肺炎の確率 85%」といった予測です。
ここでAIは、「確率的な診断」を下します。そして、その結果を正解データ(実際の診断結果)と照らし合わせ、「どれくらい間違っていたか(誤差)」を評価します。
Step 3:反省と修正(微分)
もし誤診してしまったら、ここからが本番です。AIは「微分」を使って、「なぜ間違えたのか?」を計算します。
誤差を逆方向にたどり(M&Mカンファレンス)、ネットワーク内の数億個のパラメータ(シナプスの結合強度)を少しずつ修正します。
これが「生理学的な学習機能」です。
次なる旅へ:理論から実装へ
この Step 1 ~ 3 のサイクルを何万回、何億回と繰り返すこと。それが「ディープラーニング」の正体です。
3つの数学は、バラバラに存在しているのではなく、このサイクルを回すための「歯車」として噛み合っているのです (Goodfellow et al., 2016)。
さて、これで「AIへの命令書」である数式の読み方は分かりました。
しかし、読み書きができるだけでは不十分です。実際にペンを取り、物語を綴らなければなりません。
次のステップはいよいよ「実装」です。
Pythonというペンを使って、この数学的な仕組みを実際のプログラムとして記述し、あなたの手元のコンピュータの中に「知能」を生み出していきましょう。
数式という共通言語を手に入れた今、もはやAIはブラックボックスではありません。あなたの良きパートナーとなる準備は整いました。
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
参考文献
- Bishop, C.M. (2006). Pattern Recognition and Machine Learning. Springer.
- Deisenroth, M.P., Faisal, A.A. and Ong, C.S. (2020). Mathematics for Machine Learning. Cambridge University Press.
- Goodfellow, I., Bengio, Y. and Courville, A. (2016). Deep Learning. MIT Press.
- LeCun, Y., Bengio, Y. and Hinton, G. (2015). Deep learning. Nature, 521(7553), 436–444.
- Murphy, K.P. (2012). Machine Learning: A Probabilistic Perspective. MIT Press.
- Rumelhart, D.E., Hinton, G.E. and Williams, R.J. (1986). Learning representations by back-propagating errors. Nature, 323(6088), 533–536.
- Strang, G. (2016). Introduction to Linear Algebra. 5th ed. Wellesley-Cambridge Press.
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






