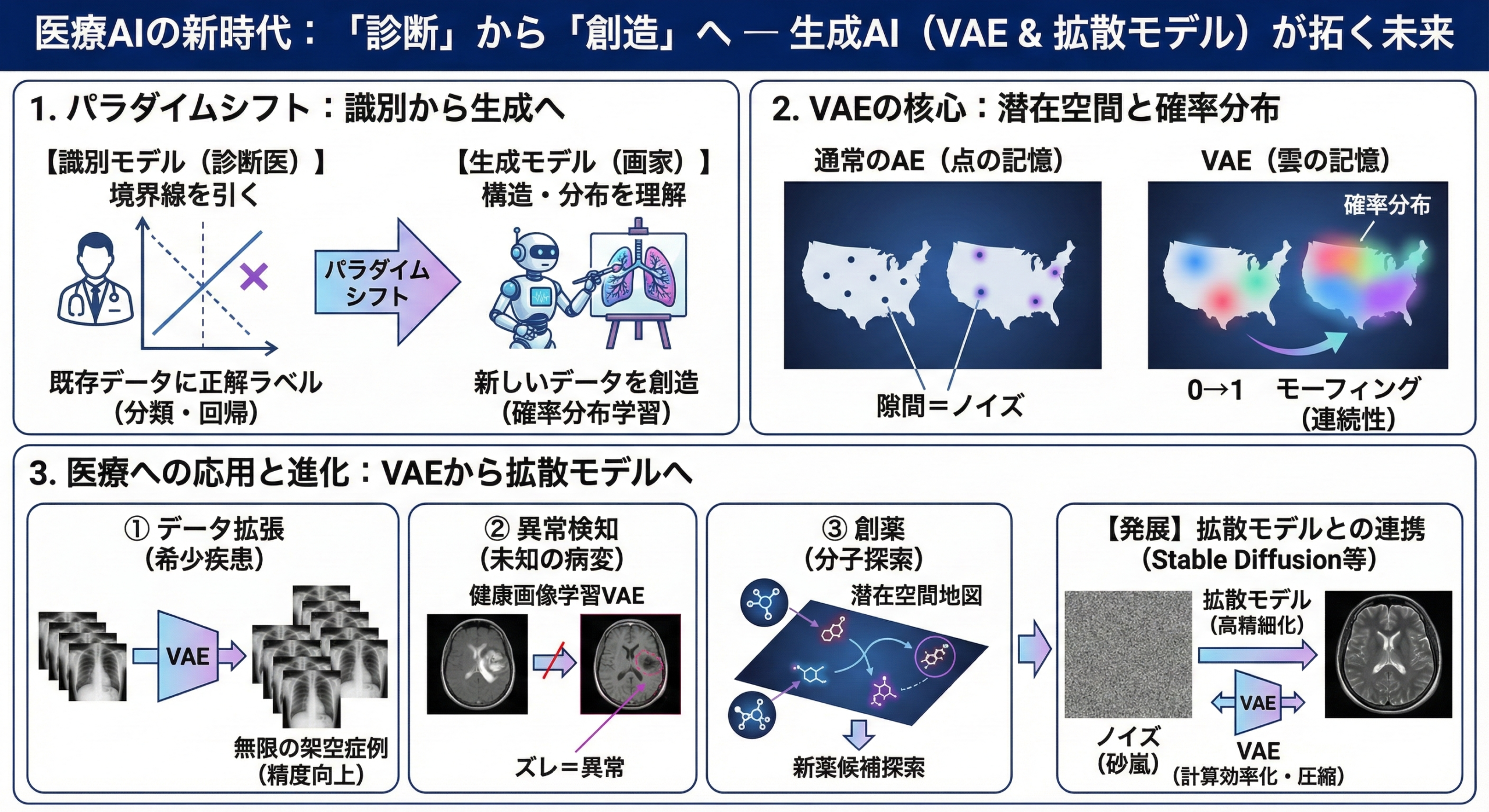
「診断」から「創造」へ:生成AIが拓く医療の新たな地平
ようこそ、生成AIの入り口へ。
これまでの講義では、レントゲン画像から「肺炎か、正常か」を見分けたり(分類)、血液検査の値から「将来の発症リスク」を予測したり(回帰)するAIを扱ってきました。これらは、既存のデータに対して正解のラベルを貼る、いわば「識別(Discriminative)」のタスクであり、医師による「診断」のプロセスに近いものです。
しかし、今日私たちが扱うのは、全く別の次元の技術です。
生成AIの二つの顔:ChatGPT(LLM)と画像生成(VAE)
まず、「生成AI」という言葉を聞いて、真っ先に思い浮かぶのは何でしょうか?
おそらく、日常診療のサマリ作成や論文校正で活躍しているChatGPTやGeminiといった大規模言語モデル(LLM)ではないでしょうか。これらは、私たちが投げかけた質問に対して、まるで人間が書いたような流暢な言葉を「生成」して返してくれます。
「今回は画像の生成? じゃあ、LLMとは関係ない話か……」
もしそう思われたなら、少し立ち止まってください。実は、最先端のLLMも、今回私たちが学ぶVAE(変分オートエンコーダ)も、根底にある「魔法の仕掛け」は驚くほど似ているのです。
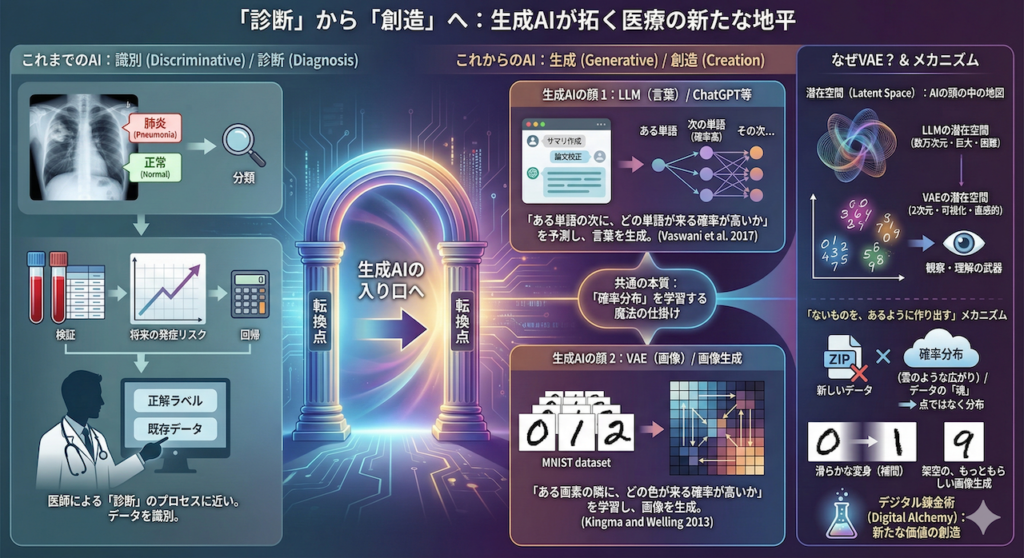
両者の本質は、データの「確率分布」を学習することにあります。
- LLM(言葉): 「ある単語の次に、どの単語が来る確率が高いか」という分布を予測し、次の言葉を選び出します (Vaswani et al. 2017)。
- VAE(画像): 「ある画素の隣に、どの色が来る確率が高いか(どういうパターンが画像として自然か)」という分布を学習し、新しい画像を生成します (Kingma and Welling 2013)。
なぜ今、VAEから学ぶのか?
扱うデータは違いますが、どちらもAIの内部に「潜在空間(Latent Space)」という、データの意味を圧縮した地図を持っています。
LLMの潜在空間は数万次元とあまりに巨大で、人間がイメージするのは困難です。一方、今回扱うVAE(手書き数字)の潜在空間は、わずか「2次元」に設定できます。つまり、「AIが頭の中でどのようにデータを理解し、整理し、新しいものを創造しているのか」を、目に見える地図としてハッキリと観察できるのです。
ここで得られる直感的な理解は、将来的にLLMの仕組みを深く学ぶ際にも、強力な武器となります。
「ないものを、あるように作り出す」メカニズム
ここまでの説明で、VAEを単なる「データ圧縮技術」だと思っているとしたら、それは少しもったいない誤解です。通常のデータ圧縮(ZIPファイルなど)は、解凍すれば元のデータが完璧に戻りますが、そこから「新しいデータ」は生まれません。
一方、VAEが行うのは、データの「魂」とも言える本質的な特徴を抽出し、それを「確率分布(雲のような広がり)」として学習することです (Kingma and Welling 2013)。データの特徴を「点」ではなく「分布」として捉えることで、その分布の中を探索し、自由自在にデータを操作できるようになります。
例えば、手書き数字の「0」から「1」へ滑らかに変身する途中経過を描き出したり、この世に存在しない「架空の、しかしもっともらしい画像」を生み出したりすることができます。これはまさに、データの要素を組み替えて新たな価値を生む「デジタル錬金術」と言えるでしょう。
医療現場における「創造」の意義
「架空の画像を作って、医療の何に役立つのか?」と疑問に思うかもしれません。しかし、この技術はすでに臨床や研究の現場で極めて実用的な応用につながっています。
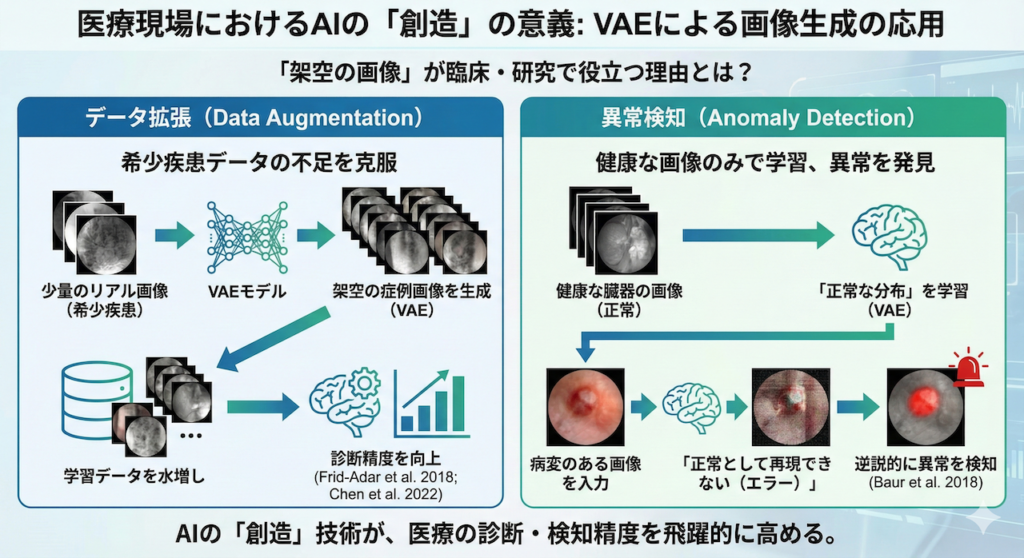
- データ拡張(Data Augmentation):
希少疾患などデータが少ないケースにおいて、VAEで「架空の症例画像」を生成して学習データを水増しし、診断精度を向上させます (Frid-Adar et al. 2018; Chen et al. 2022)。 - 異常検知(Anomaly Detection):
健康な臓器の画像だけをAIに学習させ、「正常な分布」を覚え込ませます。すると、病変のある画像が入力されたときに「正常として再現できない(エラー)」ため、逆説的に異常を検知することができます (Baur et al. 2018)。
さあ、ブラウザ上のコードで、この創造の扉を開けましょう。数式上の「確率分布」が、目に見える「画像」として立ち上がる瞬間を体験してください。
1. 識別モデルと生成モデル:医師と画家の違い
まず、私たちがこれから学ぶAIが、これまで学んできたAIとどう違うのか、その立ち位置を明確にしましょう。キーワードは「境界線」と「全体像」です。
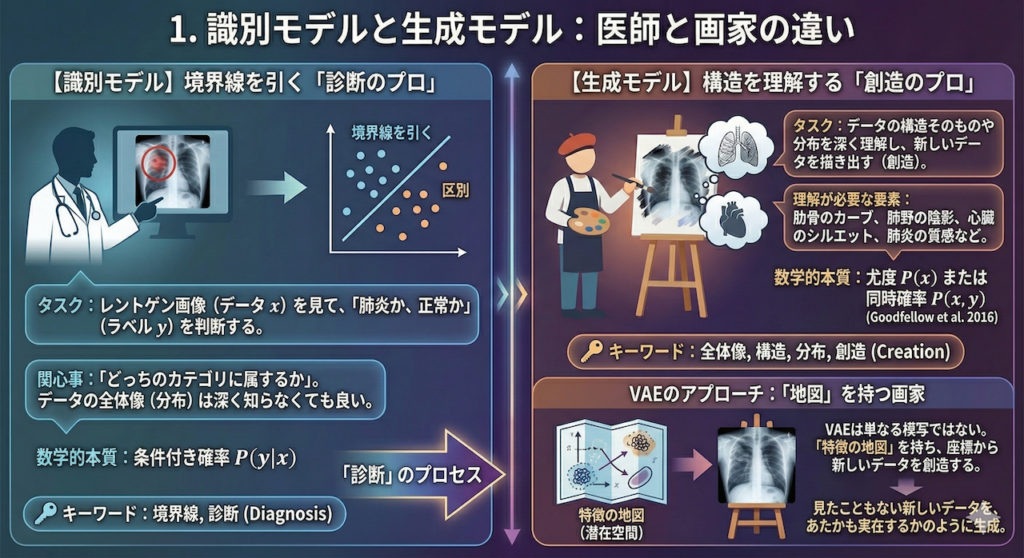
【識別モデル】境界線を引く「診断のプロ」
これまでの講義で扱ってきた分類(Classification)や回帰(Regression)は、専門用語で「識別モデル(Discriminative Model)」と呼ばれます。
これは、医療現場における「診断医」の役割に似ています。
- タスク: レントゲン画像(データ \(x\))を見て、「肺炎か、正常か」(ラベル \(y\))を判断する。
- 数学的本質: データ空間に「境界線」を引くこと。
識別モデルの関心事は、「どっちのカテゴリに属するか」という区別だけです。極端な話、境界線のこちら側が「正常」、あちら側が「肺炎」と分かればよく、そのデータが具体的にどのような画素値の分布をしているか(データの全体像)までを深く知る必要はありません。
数式で言えば、データ \(x\) が与えられたときに、正解 \(y\) になる確率、すなわち条件付き確率 \( P(y|x) \) を求めていることになります。
【生成モデル】構造を理解する「創造のプロ」
一方、今回学ぶ「生成モデル(Generative Model)」は、全く異なるアプローチをとります。これは、キャンバスに向かう「画家」の役割です。
もしあなたが画家に「肺炎のレントゲン写真を描いてください」と依頼したとしましょう。画家は、単に「正常と異常の境界線」を知っているだけでは描けません。
- 肋骨はどのようなカーブを描くか?
- 肺野の陰影はどの程度の濃さか?
- 心臓のシルエットはどう映るか?
- 肺炎の浸潤影はどのような質感か?
これら全て、つまり「データの構造そのもの」や「データの分布」を深く理解していなければ、新しい画像を描き出すことは不可能です (Goodfellow et al. 2016)。
数式で言えば、データ \(x\) そのものがどのくらいの確率で発生するかという尤度 \( P(x) \)、あるいはデータとラベルの同時確率 \( P(x, y) \) をモデル化することに相当します。
VAEのアプローチ:「地図」を持つ画家
生成モデルの中でも、今回学ぶVAE(変分オートエンコーダ)は、単なる「模写(丸暗記)」をする画家ではありません。
VAEは、描こうとする対象(データ)の特徴を整理整頓した「特徴の地図(潜在空間)」を持っています。「この座標あたりの特徴を使えば、こんな画像になるはずだ」という地図を手に入れることで、VAEは見たこともない新しいデータを、あたかも実在するかのように描き出す(生成する)ことができるのです。
2. 潜在空間(Latent Space):データの「住所」を決める
VAEというAIがどのようにして「創造」を行っているのか。その秘密は、AIの頭の中に作られる「潜在空間(Latent Space)」という不思議な地図にあります。
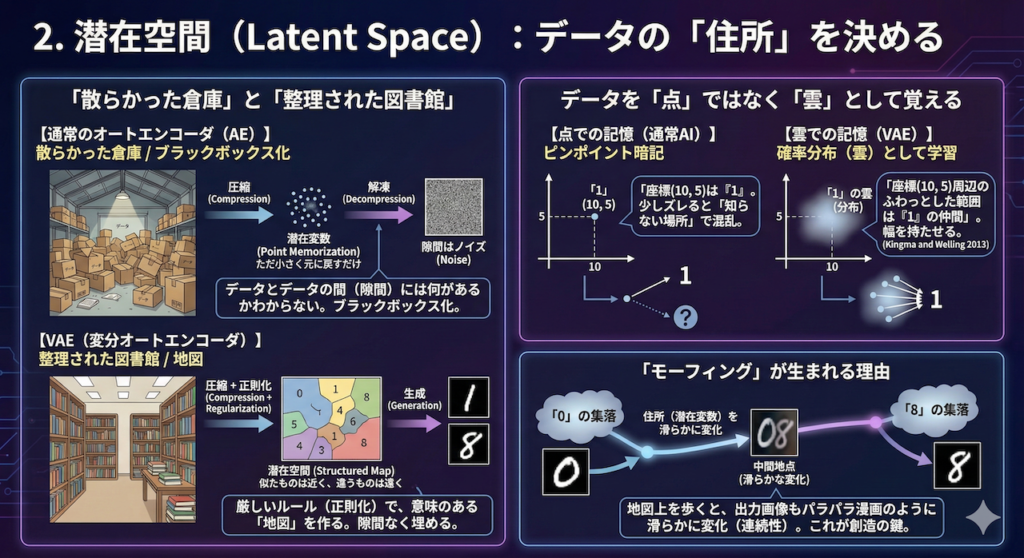
「散らかった倉庫」と「整理された図書館」
まず、比較対象として「通常のオートエンコーダ(AE)」を考えてみましょう。これもデータを圧縮する技術ですが、そのやり方は少し乱暴です。
通常のオートエンコーダは、データを圧縮袋に入れて掃除機で空気を抜くように、とにかく「小さくすること」と「元に戻せること」だけに特化しています。その結果、圧縮されたデータ(潜在変数)が置かれる空間は、いわば「整理整頓されていない、散らかった倉庫」のような状態になりがちです。
倉庫の中にある「学習したデータそのもの」は取り出せますが、データとデータの間にある「隙間」には何があるかわかりません。もしその隙間を指定して画像を生成させようとすれば、意味不明なノイズ(砂嵐のような画像)が出てきてしまうでしょう。これが「ブラックボックス化」の問題点です。
一方、VAEのアプローチは全く異なります。VAEはデータを圧縮する際に、「似ているデータは近くに、違うデータは遠くに配置しなさい」という厳しいルール(正則化)を課します。
これは、膨大な蔵書を分類ごとに棚に並べ、住所(請求記号)を割り振って管理する「整理された図書館」や、区画整理された「地図」を作る作業に似ています。
データを「点」ではなく「雲」として覚える
VAEの最大の発明は、データを「点」として記憶するのではなく、「確率分布(雲のような広がり)」として学習することです (Kingma and Welling 2013)。
- 点での記憶(通常AI): 「座標(10, 5)は数字の『1』である」とピンポイントで暗記します。これでは、少しズレて(10.1, 5)になった瞬間に、AIは「知らない場所だ」と混乱してしまいます。
- 雲での記憶(VAE): 「座標(10, 5)を中心とした、半径1メートルくらいのふわっとした範囲(分布)は、だいたい『1』の仲間である」と学習します。
このように「幅」を持たせて学習することで、潜在空間という地図の上には、数字の「0」の雲、「1」の雲、「8」の雲……といった具合に、それぞれのテリトリー(縄張り)が形成されます。
雲と雲は互いに押し合いへし合いしながら、空間を隙間なく埋め尽くそうとします。その結果、地図上のどこを指しても、必ず何かしらの「意味のあるデータ」が存在するようになるのです。
「モーフィング」が生まれる理由
この「地図」の上を歩いてみることを想像してください。
地図の左下にある「0」の集落から出発し、右上にある「8」の集落に向かって、一直線に歩いていきます。
- 最初は完全に「0」の領域にいます。
- 歩くにつれて、「0」の雲が薄くなり、徐々に隣り合う他の数字の影響が混ざり始めます。
- 中間地点では、「0」とも「8」ともつかない、しかし文字として成立している不思議な形が現れます。
- そして最終的に、「8」の領域に到達します。
このように、住所(潜在変数)を滑らかに変化させると、出力される画像もパラパラ漫画のように滑らかに変化(モーフィング)していきます。この「連続性(Continuity)」こそが、VAEが単なるコピー機ではなく、新しいデータを生み出せる「創造マシン」である理由なのです。
3. 実装:手書き数字を操る錬金術
「論より証拠」です。実際にコードを動かして、VAEが数字の概念を獲得していく様子を目撃しましょう。
今回は、AI学習の「Hello World」とも呼ばれる手書き数字データセット「MNIST」を使用します。フレームワークはPyTorchを使いますが、複雑な処理は極力シンプルに記述しています。
【準備】錬金釜を温める
まず、可視化の際に日本語のグラフを表示できるように準備をします。Google ColabなどのNotebook環境を使用している場合は、以下のコマンドを実行してライブラリをインストールしてください。
# 日本語フォント表示用ライブラリのインストール(Google Colab等で実行する場合)
!pip install japanize-matplotlibGoogle Colabの使い方はこちら👇
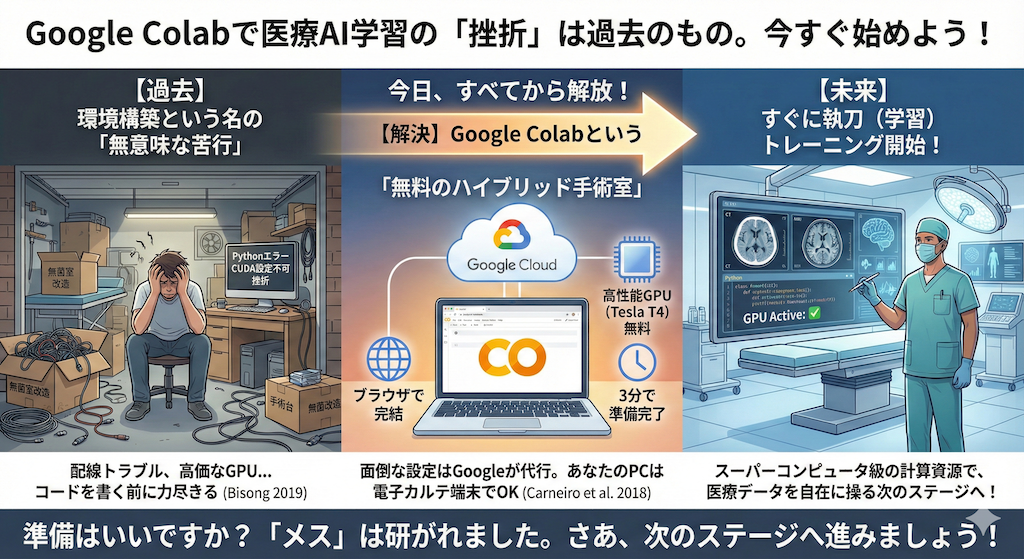
【構造】VAEの設計図
コードを書く前に、AIの中でデータがどのように流れるか、その設計図を確認しておきましょう。VAEは、データを圧縮する「エンコーダ」と、復元する「デコーダ」の2つの部分から成ります。
ポイントは、エンコーダがいきなり「圧縮データ」を出すのではなく、「確率分布のパラメータ(平均と分散)」を出力する点です。ここから「ノイズ」を混ぜてサンプリングすることで、AIは「点」ではなく「分布(広がり)」を学習することになります。
【実装】モデルの構築と学習
では、実装コードです。心臓部となる reparameterize (再パラメータ化)メソッドに注目してください。これが、ランダムなノイズを含みながらも学習(誤差逆伝播)を可能にする、VAE特有の「魔法」です。
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np
# --- 1. 設定と準備 ---
# 再現性確保のため、乱数シードを固定します(誰がやっても同じ結果が出るように)
torch.manual_seed(42)
# GPUが使える場合はGPUを、なければCPUを使用するように自動設定
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# ハイパーパラメータ(AIの学習設定値)
BATCH_SIZE = 128 # 一度に学習する画像の枚数
EPOCHS = 5 # 学習を繰り返す回数(デモ用に短く設定しています)
LATENT_DIM = 2 # 潜在変数の次元数(2次元なら平面地図として描画可能)
# データセットの読み込み(MNIST:手書き数字データ)
# 画像をTensor(0.0〜1.0の数値の行列)に変換する設定
transform = transforms.ToTensor()
# 学習用データをダウンロードして読み込みます
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('./data', train=True, download=True, transform=transform),
batch_size=BATCH_SIZE, shuffle=True
)
# --- 2. VAEモデルの定義 ---
class VAE(nn.Module):
def __init__(self):
super(VAE, self).__init__()
# 【エンコーダ部】:画像を圧縮する役割
# 入力:28x28ピクセル = 784個の数値 → 中間層:400個の数値へ圧縮
self.fc1 = nn.Linear(784, 400)
# 潜在変数の「平均(mu)」と「対数分散(logvar)」を出力する層
# ここがVAEの肝です。データを「点」ではなく「確率分布」として捉えます
self.fc21 = nn.Linear(400, LATENT_DIM) # 平均(分布の中心)
self.fc22 = nn.Linear(400, LATENT_DIM) # 分散(分布の広がり具合)
# 【デコーダ部】:潜在変数から画像を復元する役割
# 入力:潜在変数(2個) → 中間層:400個
self.fc3 = nn.Linear(LATENT_DIM, 400)
# 中間層:400個 → 出力:784個(元の画像サイズ)
self.fc4 = nn.Linear(400, 784)
# エンコード処理:画像から潜在変数のパラメータ(平均と分散)を計算
def encode(self, x):
h1 = F.relu(self.fc1(x)) # 活性化関数ReLUを通す
return self.fc21(h1), self.fc22(h1)
# 【重要】再パラメータ化トリック(Reparameterization Trick)
# 確率分布からランダムに点を取る操作を、学習可能な形にする魔法
# 式: z = mu + sigma * epsilon
def reparameterize(self, mu, logvar):
std = torch.exp(0.5 * logvar) # 対数分散から標準偏差(sigma)を計算
eps = torch.randn_like(std) # 標準正規分布からノイズ(epsilon)を生成
return mu + eps * std # 平均から「ゆらぎ」の分だけずらす
# デコード処理:潜在変数から画像を生成
def decode(self, z):
h3 = F.relu(self.fc3(z)) # 潜在変数を中間層へ拡大
return torch.sigmoid(self.fc4(h3)) # 最終出力を0~1の範囲(画素値)に収める
# 順伝播:データがモデルを通る一連の流れ
def forward(self, x):
# 画像(28x28)を一直線のベクトル(784)に変換(Flatten)
mu, logvar = self.encode(x.view(-1, 784))
# 潜在ベクトルzをサンプリング(分布から点を取る)
z = self.reparameterize(mu, logvar)
# 画像を復元
return self.decode(z), mu, logvar
# モデルの実体を作成し、デバイス(GPU/CPU)に転送
model = VAE().to(device)
# 最適化手法(Adam)を設定:学習率 0.001
optimizer = optim.Adam(model.parameters(), lr=1e-3)
# --- 3. 損失関数の定義 ---
# VAEの損失 = 「復元誤差(似ているか)」 + 「KLダイバージェンス(分布が整っているか)」
def loss_function(recon_x, x, mu, logvar):
# 復元誤差:生成画像と元画像の違い(バイナリクロスエントロピー)
BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784), reduction='sum')
# KLダイバージェンス:潜在分布を標準正規分布(きれいな山)に近づけるための項
# これがないと、データが潜在空間でバラバラに配置されてしまい、モーフィングできなくなります
KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
return BCE + KLD
# --- 4. 学習ループ ---
print(f"学習開始(デバイス: {device})...")
model.train() # 訓練モードに設定
for epoch in range(1, EPOCHS + 1):
train_loss = 0
# データローダーからミニバッチごとにデータを取り出す
for batch_idx, (data, _) in enumerate(train_loader):
data = data.to(device) # データをデバイスへ
optimizer.zero_grad() # 勾配(学習の方向)をリセット
# モデルにデータを通す
recon_batch, mu, logvar = model(data)
# 損失(間違いの大きさ)を計算
loss = loss_function(recon_batch, data, mu, logvar)
# 誤差逆伝播:間違いの原因を遡って特定
loss.backward()
# パラメータの更新:モデルを少し賢くする
train_loss += loss.item()
optimizer.step()
# 1エポックごとの平均損失を表示
print(f'Epoch: {epoch} | Loss: {train_loss / len(train_loader.dataset):.4f}')
print("学習完了!")100%|██████████| 9.91M/9.91M [00:00<00:00, 18.8MB/s]
100%|██████████| 28.9k/28.9k [00:00<00:00, 503kB/s]
100%|██████████| 1.65M/1.65M [00:00<00:00, 4.67MB/s]
100%|██████████| 4.54k/4.54k [00:00<00:00, 10.1MB/s]
学習開始(デバイス: cuda)...
Epoch: 1 | Loss: 191.3612
Epoch: 2 | Loss: 168.4394
Epoch: 3 | Loss: 163.7505
Epoch: 4 | Loss: 161.1259
Epoch: 5 | Loss: 159.3324
学習完了!【実験】潜在空間を旅して「変身」を目撃する
学習が終わりました。ここからが「錬金術」の本番です。
潜在空間(2次元平面)の座標 \( (x, y) \) を、グリッド状に少しずつ変化させながらデコーダに入力してみます。座標が変わるにつれて、生成される数字がどのように変化していくかを見てみましょう。
# --- 5. 潜在空間のグリッド表示 ---
def plot_latent_space(model, n=20, digit_size=28):
# n x n のグリッド(画像全体)を作成するための空のキャンバス
figure = np.zeros((digit_size * n, digit_size * n))
# 座標空間の範囲を設定(正規分布に従うので-3~+3あたりを見る)
grid_x = np.linspace(-3, 3, n)
grid_y = np.linspace(-3, 3, n)[::-1] # 上から下へ座標をとるため反転(画像の座標系に合わせる)
model.eval() # 評価モード(学習ストップ・ノイズ固定)
with torch.no_grad(): # 勾配計算をしない(メモリ節約)
for i, yi in enumerate(grid_y):
for j, xi in enumerate(grid_x):
# 潜在変数 z を指定して作成(ここが創造の起点!)
z_sample = torch.tensor([[xi, yi]]).float().to(device)
# デコーダに通して画像を生成
x_decoded = model.decode(z_sample)
# データの形を画像用(28x28)に整える
digit = x_decoded[0].reshape(digit_size, digit_size).cpu()
# キャンバスの所定の位置に画像を埋め込む
figure[i * digit_size: (i + 1) * digit_size,
j * digit_size: (j + 1) * digit_size] = digit
# グラフの描画設定
plt.figure(figsize=(10, 10))
plt.imshow(figure, cmap='Greys_r') # 白黒反転で表示
plt.title("VAE潜在空間の可視化:数字のモーフィング", fontsize=16)
plt.axis('off') # 軸を消す
plt.show()
# 関数を実行して描画
plot_latent_space(model)
出力された画像を見てください。ある数字から別の数字へ、パッと切り替わるのではなく、徐々に形を変えながら遷移している様子が確認できるはずです。たとえば、「6」のループが閉じて「0」になったり、「1」が傾いて「7」になったりします。
この「連続的な変化」こそが、AIが数字を単なる記号としてではなく、構造的な特徴を持った「分布」として理解している証拠なのです。
4. なぜ「確率」にするのか? 数学的な直感
「なぜ、わざわざややこしい『確率分布(平均と分散)』などを学習させるのか?」
これは多くの初学者が抱く疑問です。普通のオートエンコーダのように、単純に座標(点)だけを学習させたほうが楽なはずです。しかし、そこには決定的な理由があります。それは、冒頭でも触れたように「空白地帯を許さないため」です。
「点」で覚える弱点、「範囲」で覚える強み
通常のオートエンコーダは、画像 \(x\) を潜在空間上の「点」に変換します。例えば「数字の1」を座標 \((10, 10)\) に置くとしましょう。しかし、AIは \((10, 10)\) 以外の場所、例えば \((10.1, 10)\) については何も教わっていません。
その結果、少しでも座標がズレると、AIは何を描いていいかわからず、意味のないノイズを出力してしまいます。これでは、滑らかなモーフィングは不可能です。
一方、VAEは画像 \(x\) を「範囲(確率分布)」として捉えます。「数字の1」は \((10, 10)\) を中心とした「半径1メートルくらいのフワッとした雲」として配置されます。こうすると、中心から多少ズレた場所であっても、そこはまだ「雲の中」なので、AIは「たぶん1っぽい画像」を生成することができます。
損失関数の「綱引き」
この「雲」をうまく配置するために、VAEの学習では2つの相反する命令(損失関数)が与えられます。数式で見ると難解ですが、やっていることは単純な「綱引き」です (Kingma and Welling 2013)。
\[ \mathcal{L} = \underbrace{-\mathbb{E}_{z \sim q_{\phi}(z|x)}[\log p_{\theta}(x|z)]}_{\text{① 復元誤差}} + \underbrace{D_{KL}(q_{\phi}(z|x) \| p(z))}_{\text{② 正則化項(KLダイバージェンス)}} \]
命令①:復元誤差(Reconstruction Error)
「元の画像とそっくりの絵を描け!」という命令です。
この項だけだと、AIはズルをしようとします。「数字の0」と「数字の1」が混ざらないように、それぞれの雲を無限に遠くへ離し、さらに雲のサイズを極限まで小さくして「点」にしようとします。これでは普通のオートエンコーダに戻ってしまい、隙間だらけの空間になります。
命令②:正則化項(KL Divergence)
「地図(潜在空間)を散らかすな! 全員、原点 \((0,0)\) の近くに集まれ!」という命令です。
具体的には、分布を「標準正規分布(平均0、分散1のきれいな山)」に近づけようとする力です。これは、各データの雲を原点に向かって引っ張る「バネ」や「重力」のような役割を果たします。
この2つが戦うとどうなるか?
①の力(似せたいから離れたい)と、②の力(まとまりたいから集まりたい)がバランスを取り合うと、潜在空間はどうなるでしょうか。
- データ同士は、互いに重なりすぎない程度に離れつつ、原点の近くにギュッと密集します。
- 雲(分布)は「点」にならず、ある程度の「広がり」を保ちます。
- その結果、雲と雲が隣り合い、隙間(空白地帯)が埋め尽くされます。
この「隙間なく敷き詰められた状態」こそが、どこを指しても意味のある画像が生成され、滑らかな変身(モーフィング)が可能になる理由なのです。この数学的なバランス感覚こそが、VAEの美しさと言えるでしょう。
5. 医療AIへの応用:VAEは何に役立つのか?
「手書き数字を変身させて、何が楽しいの?」と思われたかもしれません。しかし、この「モーフィング(連続的な変化)」や「生成(分布からのサンプリング)」という機能こそが、現代医療が抱える深刻なデータ課題を解決する鍵となっています。
VAEをはじめとする生成モデルが、実際の医療現場でどのように役立っているのか、代表的な3つの応用例を見てみましょう。
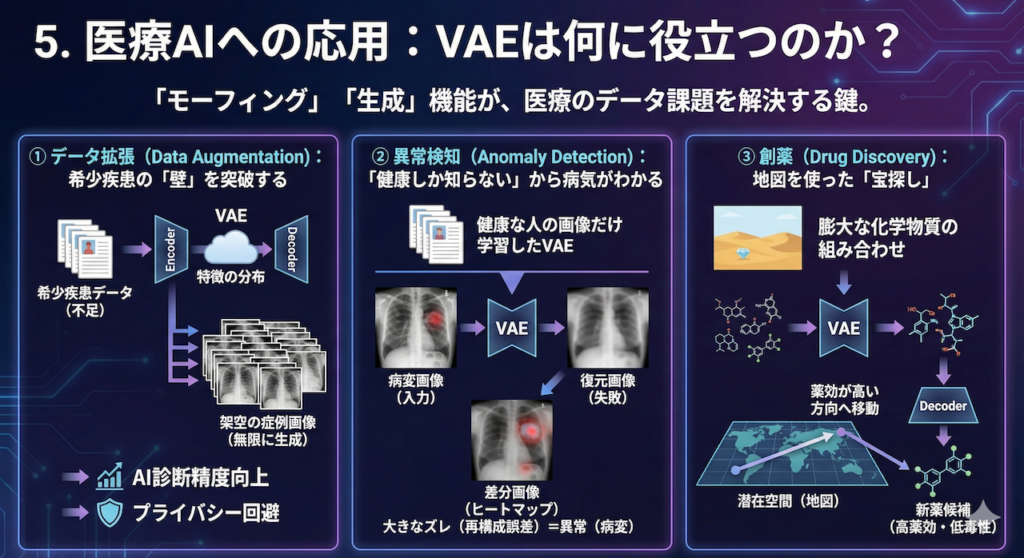
① データ拡張(Data Augmentation):希少疾患の「壁」を突破する
医療AI開発における最大のボトルネックは「データの不足」です。特に希少疾患や、集めるのが難しい特定の病変画像は、AIを学習させるのに十分な数が集まらないことがよくあります。
ここで、VAEをはじめとする生成モデル(Generative Models)の出番です。これらのAIは、少数の既存データからその背後にある「特徴の分布」を学習します。一度分布を覚えてしまえば、そこからランダムにサンプリングすることで、「実在はしないが、医学的に矛盾のない架空の症例画像」を無限に生成(水増し)することができます。
これを学習データに加えることで、AIの診断精度を向上させる研究が進んでいます。著名な例として、GAN(敵対的生成ネットワーク)を用いた研究ではありますが、肝病変の合成画像を学習データに追加することで、分類精度が有意に向上することが実証されています (Frid-Adar et al. 2018)。
また、これらは実在する患者のデータではないため、プライバシー問題を回避しながらデータを共有できる(合成データ化)という大きな利点もあります。

② 異常検知(Anomaly Detection):「健康しか知らない」からこそ病気がわかる
これは「逆転の発想」を用いた応用です。通常、病気を見つけるAIを作るには「病気の画像」が大量に必要ですが、集めるのは大変です。そこで、集めやすい「健康な人の画像だけ」をVAEに学習させます。
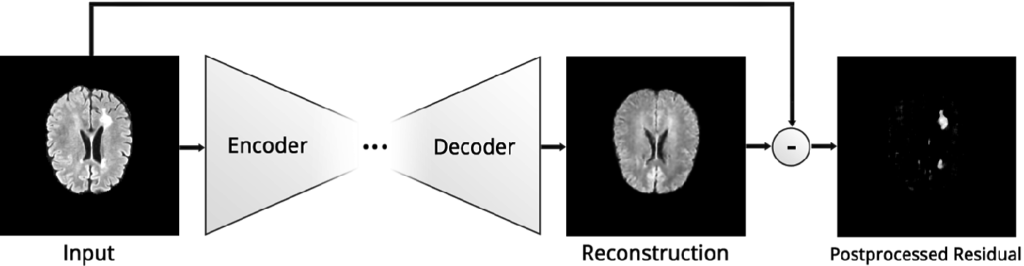
すると、このAIは「健康な画像」なら完璧に復元できる画家に育ちます。そこに、未知の「病変がある画像」を入力するとどうなるでしょうか?
- AIは「健康な臓器」の描き方しか知りません。
- そのため、病変(腫瘍や肺炎の影)の部分をうまく描けず、無理やり「健康な状態」に直そうとして失敗します。
- 結果として、入力画像と復元画像の間に「大きなズレ(再構成誤差)」が生じます。
このズレが大きい部分こそが「異常(病変)」であると判定できるのです。代表的な事例として、健康な脳MRI画像のみを学習させたVAEを用いて、多発性硬化症(MS)の病変や脳腫瘍を、教師データなしで検出することに成功した研究があります (Baur et al. 2018)。これにより、事前の学習データになかった未知の疾患でも検知できる可能性が示されています。
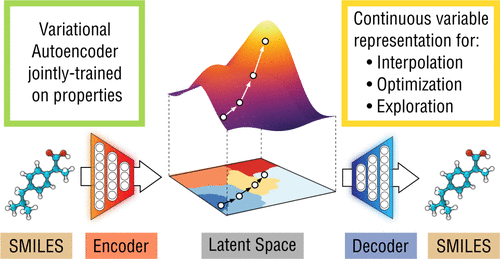
③ 創薬(Drug Discovery):地図を使った「宝探し」
新しい薬を開発するには、膨大な数の化学物質の組み合わせの中から、有効なものを探し出す必要があります。これは「砂漠の中から一粒のダイヤを探す」ような途方もない作業です。
VAEを使うと、離散的で扱いにくい「化学構造(分子の形)」を、滑らかな「潜在空間(地図)」に変換(マッピング)することができます。
一度地図ができれば、あとは数学の力を使えます。「薬効が高い」方向へ地図上の座標を移動させ、その座標をデコード(復元)すれば、「薬効が高く、かつ毒性が低い」という条件を満たす新しい分子構造を逆算して提案できるのです。これは従来のしらみつぶしの探索に比べて、圧倒的に効率的なアプローチです (Gómez-Bombarelli et al. 2018)。
番外編:VAEのその先へ — 「拡散モデル」という革命
ここまでVAEを学んでみて、生成された数字の画像が少し「ぼんやり」していることに気づいたでしょうか?
実は、VAEには「全体像を捉えるのは得意だが、細部のくっきりとした描写(高周波成分)が苦手」という宿命的な弱点があります。その壁を打ち破り、今まさに世界中の画像生成AI(Stable DiffusionやDALL-E 3など)の中核となっている技術。それが「拡散モデル(Diffusion Models)」です。
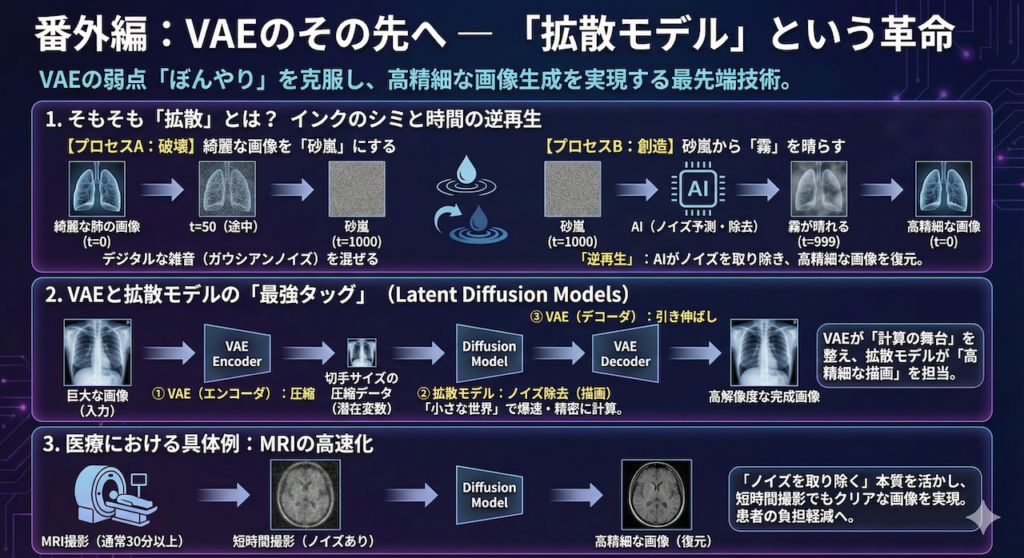
1. そもそも「拡散」とは? インクのシミと時間の逆再生
「拡散」という言葉は、物理の授業で聞いたことがあるかもしれません。コップの水にインクを一滴垂らすと、時間はかかりますが、最終的には水全体に均一に広がり、元のインクの形は跡形もなくなります。これが拡散です。
画像生成における拡散モデルは、この現象を「時間の逆再生」として利用します。
【プロセスA:破壊】綺麗な画像を「砂嵐」にする
まず、AIに「破壊」を教えます。鮮明なレントゲン画像(データ)に、少しずつ少しずつ、デジタルな雑音(ガウシアンノイズ)を混ぜていきます。
- t=0(元画像): 綺麗な肺の画像。
- t=50(途中): ザラザラして見にくいが、まだ肺だとわかる。
- t=1000(完全なノイズ): もはやテレビの砂嵐(完全なランダム)と同じ。元の情報はゼロに見える。
これは誰にでもできる簡単な作業です。
【プロセスB:創造】砂嵐から「霧」を晴らす
ここからがAIの出番です。AIに課されるミッションは、このプロセスの「逆」を行うことです。
「おいAI、この『砂嵐(t=1000)』からノイズを少し取り除いて、『t=999』の状態に戻してみろ」
AIは、大量の画像データを使って学習することで、「砂嵐の中に、うっすらと見える『本来あるべき画像の断片』」を見つけ出す能力(ノイズ予測能力)を身につけます。
これを1000回繰り返すとどうなるでしょうか?
最初はただの砂嵐だった画面から、徐々に霧が晴れるように輪郭が浮かび上がり、最終的には驚くほど高精細な画像が出現します。これが拡散モデルの「創造」です。
2. VAEと拡散モデルの「最強タッグ」
「拡散モデルがそんなに綺麗に描けるなら、もうVAEは要らないのでは?」
そう思うのが自然ですが、実は逆です。拡散モデルには、一つだけ致命的な弱点があります。それは「とにかく計算に時間がかかる(遅い)」ことです。
例えば、スマホで撮ったような高画質な写真(数百万個の画素の集まり)に対して、先ほどの「ノイズ除去」を1000回も繰り返すのは、AIにとってあまりに過酷な重労働です。そのままでは、画像を1枚作るのに何十分も待たされてしまい、実用的ではありません。
そこで開発されたのが、VAEと拡散モデルを合体させるというアイデアです。専門用語では「潜在拡散モデル(Latent Diffusion Models)」と呼ばれます。
現在、ニュースやSNSなどで話題になっている「言葉から一瞬で高画質な絵を描くAI(Stable Diffusionなど)」の多くは、実はこの仕組みで動いています。彼らが数秒で綺麗な絵を出せるのは、裏側でVAEが「作業台を小さく整える」というサポートをしてくれているおかげなのです。
役割分担:圧縮のプロと、描画のプロ
彼らは以下のように完璧な連携プレーを行います。
- ① VAE(エンコーダ)の仕事:
巨大なレントゲン画像を、意味を保ったまま「切手サイズの圧縮データ(潜在変数)」に縮小します。 - ② 拡散モデルの仕事:
その小さな「切手サイズの世界」の中で、ノイズ除去(画像の描画)を行います。データが小さいので、計算は爆速で、しかも精密です。 - ③ VAE(デコーダ)の仕事:
拡散モデルが描き上げた「切手サイズの設計図」を、最後に高解像度の画像へと引き伸ばして完成させます。
つまり、皆さんが今日学んだVAEは、最先端AIの中で「計算の舞台を整える」という極めて重要な役割を担っているのです。
3. 医療における具体例:MRIの高速化
この技術は、すでに医療現場を変えつつあります。
例えばMRI検査は、撮影に30分以上かかることがあり、患者さんにとって苦痛です。撮影時間を短くするためにデータを間引いて取得すると、画像はノイズだらけ(あるいはボケた状態)になりますが、拡散モデルを使えば、その「不完全な短時間画像」から「高精細な画像」を逆算して復元することができます。
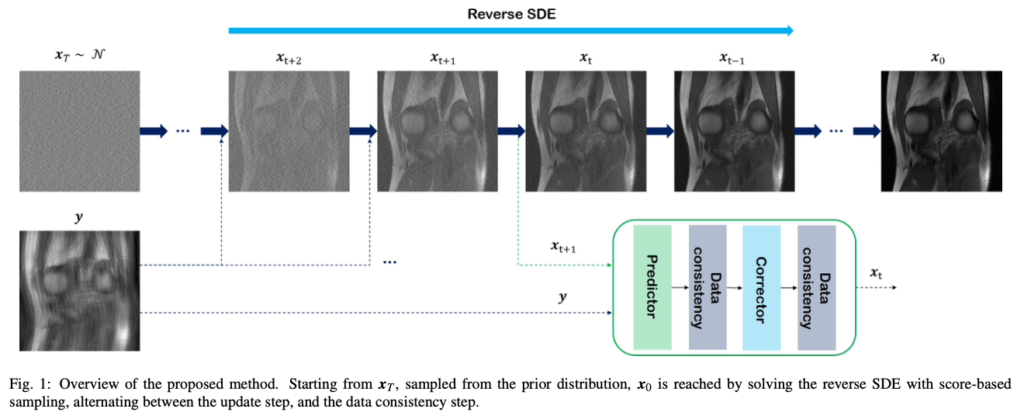
「ノイズを取り除く」という拡散モデルの本質は、医療画像のクリア化と相性が抜群です。実際に、スコアベース拡散モデル(Score-based Diffusion Models)を用いて、大幅にデータを間引いた(高速撮影した)MRIデータからでも、診断に十分な高品質画像を再構成できることが実証されています (Chung et al. 2022)。これは、患者の負担軽減と検査効率の向上に直結する重要な応用です。
まとめ:創造の第一歩
今回、私たちはVAEという技術を通じて、データを「点」として記憶するのではなく、「分布(広がり)」として理解するAIの世界に触れました。
VAEの本質は、単なる画像生成ツールではありません。複雑に見えるデータの中から、その裏にある本質的な「意味(潜在変数)」を抽出し、それを私たちが操作可能な形(地図上の座標)に変換する技術です。
今日、皆さんのブラウザ上で数字が滑らかに変身したあの瞬間。あれこそが、医療画像生成や新薬探索といった、未来の医療を変える高度な応用へと続く「創造の第一歩」なのです。
参考文献
- Baur, C., Wiestler, B., Albarqouni, S. and Navab, N. (2018). Deep autoencoding models for unsupervised anomaly segmentation in brain MR images. arXiv preprint.
- Chen, X., Xu, X., Yang, Y., Wu, J. and Zheng, N. (2022). Deep generative models in medical image computing. Journal of Medical Imaging, 9(5), 051402.
- Chung, H. and Ye, J.C. (2022). Score-based diffusion models for accelerated MRI. Medical Image Analysis, 80, 102479.
- Frid-Adar, M., Diamant, I., Klang, E., Amitai, M., Goldberger, J. and Greenspan, H. (2018). GAN-based synthetic medical image augmentation for increased CNN performance in liver lesion classification. Neurocomputing, 321, 321–331.
- Gómez-Bombarelli, R., Wei, J.N., Duvenaud, D., Hernández-Lobato, J.M., Sánchez-Lengeling, B., Sheberla, D., Aguilera-Iparraguirre, J., Hirzel, T.D., Adams, R.P. and Aspuru-Guzik, A. (2018). Automatic chemical design using a data-driven continuous representation of molecules. ACS Central Science, 4(2), 268–276.
- Goodfellow, I., Bengio, Y. and Courville, A. (2016). Deep Learning. Cambridge, MA: MIT Press.
- Kingma, D.P. and Welling, M. (2013). Auto-encoding variational Bayes. arXiv preprint.
- Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, Ł. and Polosukhin, I. (2017). Attention is all you need. Advances in Neural Information Processing Systems, 30.
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.