研修医が経験を積んで専門医になっていくプロセスに例えて整理しました。
前回までは、PyTorchを使ってAIモデル(ニューラルネットワーク)の「骨組み」を作る方法を一緒に見てきましたね。
しかし、骨組みができただけでは、AIはまだ何もできません。言ってみれば、生まれたばかりの赤ん坊のようなもの。右も左も分からず、診断なんてとてもできません。
そこで今回は、このAIモデルを「一人前の医師」へと賢く育て上げるための『学習サイクル(Training Loop)』についてお話しします。
実は、AIの学習プロセスは、私たちが医学部で学び、研修医として現場で経験を積んでいく過程と驚くほど似ているんです。
「自分の診断がどれくらい間違っていたのかを認識し(損失関数)」、「次はどう考え方を変えれば正解に近づくかを修正し(最適化)」、そして「効率よく大量の症例を経験していく(ミニバッチ学習)」。
この一連の仕組みを理解すれば、難解に見えるコードの向こう側で、AIがどのように成長しているのかが手に取るように分かるようになりますよ。
1. 学習サイクルの全体像:研修医の成長プロセス

AIの学習(Training)とは、専門用語で言えば「パラメータ(重みとバイアス)の最適化」ですが、これだけではイメージが湧きにくいですよね。
そこで、このプロセスを「新米研修医が、何万もの症例を経験して、指導医のような達人になっていく過程」に例えてみましょう。
AIの中にある「ニューラルネットワーク」は、まだ右も左も分からない研修医の脳そのものです。
この研修医(AI)は、以下の4つのステップを高速で繰り返すことで、少しずつ、しかし着実に「医師としての直感(精度)」を磨いていきます。
STEP 1:予測 (Forward Propagation) = 「診断を下す」
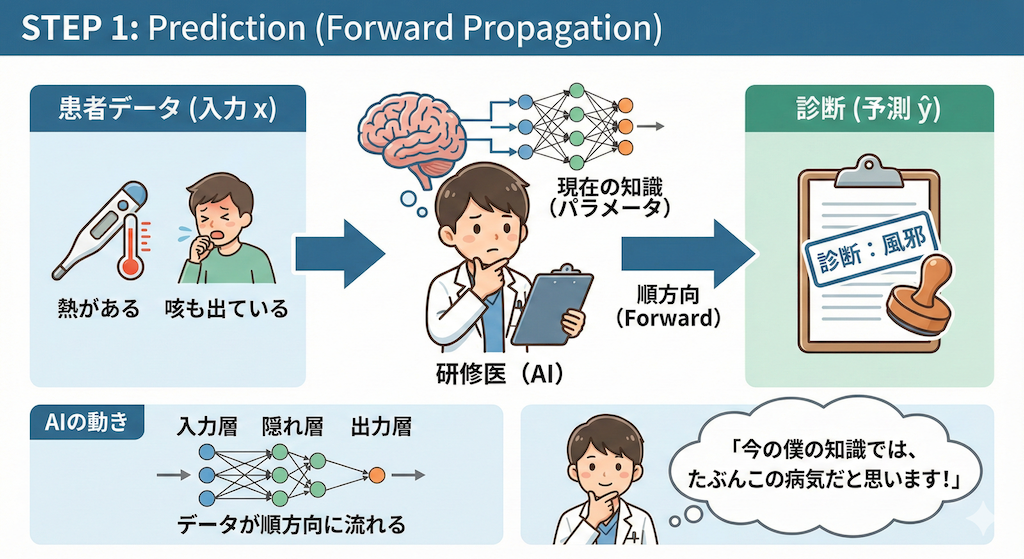
まず、研修医(AI)は患者さんのデータ(入力 \(x\))を見ます。
「熱があるな」「咳も出ている」といった情報を、自分の今の知識(現在のパラメータ)に照らし合わせて、「これは風邪です」と診断(予測 \(\hat{y}\))を下します。
- AIの動き:データが入力層から出力層へと順方向に流れていきます。
- 研修医の心境:「今の僕の知識では、たぶんこの病気だと思います!」
STEP 2:採点 (Loss Calculation) = 「指導医との答え合わせ」

次に、その診断が合っていたかどうか、正解(教師データ \(y\))と照らし合わせます。
ここで登場するのが損失関数(Loss Function)という名の「鬼指導医」です。
指導医は、「正解は肺炎だ。君は風邪と診断したね。その誤差(Loss)はこれくらい大きいぞ!」と、間違いの度合いを厳密な「数値」として突きつけます。
- AIの動き:予測値と正解ラベルのズレを計算します。
- 研修医の心境:「うわっ、全然違った…。こんなに間違えてしまった(Lossが大きい)。」
STEP 3:反省 (Backward Propagation) = 「原因の究明(誤差逆伝播)」

ここが学習のハイライトです。ただ「間違えた」で終わらせず、「なぜ間違えたのか?」を振り返ります。
「肺の音の聞き取りが甘かったのか?」「レントゲンの影を見落としたのか?」
診断のプロセスを出力から入力へと逆順(Backward)に辿り、「どこの判断(パラメータ)が間違いの原因だったのか」を特定します。
- AIの動き:算出された誤差を逆方向に流し、各パラメータの修正量(勾配)を計算します。
- 研修医の心境:「そうか、あの時のレントゲンの解釈が間違っていたんだ。ここを修正しなきゃ。」
STEP 4:修正 (Optimization) = 「思考回路のアップデート」

最後に、特定された原因に基づいて、脳内のシナプス(重みとバイアス)を実際に書き換えます。
これを担当するのがオプティマイザ(最適化アルゴリズム)です。
「次はレントゲンのこのパターンを、もっと重要視するようにしよう」と、思考の重み付けを微調整するのです。
- AIの動き:計算された勾配に従って、パラメータの数値を少しだけ更新します。
- 研修医の心境:「よし、学び取ったぞ。次の患者さん(データ)が来たら、もっとうまく診断できるはずだ!」
この ①予測 → ②採点 → ③反省 → ④修正 のサイクルを、AIは何万回、何十万回と繰り返します。
最初はデタラメな診断しかできなかったAIも、膨大な「反省と修正」の積み重ねによって、やがて人間をも凌駕する診断能力を獲得するのです。
2. 損失関数(Loss Function):AIにとっての「痛み」と「採点表」
AIモデルを育てる上で最も重要なもの、それが「損失関数(Loss Function)」です。
これは、AIの出した答えが正解からどれくらいズレているかを評価する「厳格な採点表」のようなものです。
AIはこの採点結果(Lossという数値)を「痛み」として感じ、この痛みをできるだけ小さくしようと努力することで学習が進みます。
では、具体的にどのような基準で採点されるのでしょうか?医療AIで頻出する2つのパターンを、数式の意味まで掘り下げて見ていきましょう。
① 平均二乗誤差(MSE):回帰タスク(数値を当てる)
これは、「血圧」や「入院日数」など、連続する数値を予測する(回帰)場合に使われる、最もポピュラーな採点基準です。
【数式の意味】
AIの予測値(\(\hat{y}\))と、正解(\(y\))の差(ズレ)を計算し、それを「二乗」します。
\[ L = \dfrac{1}{N} \sum_{i=1}^{N} (y_i – \hat{y}_i)^2 \]
- \( y_i \): 正解(実際の値)
- \( \hat{y}_i \): AIの予測値
- 差(\(y – \hat{y}\))を二乗することで、プラスマイナスの符号を消し、すべて「ズレの大きさ」として扱います。
【なぜ「二乗」するのか?ここに医療的な意義がある!】
単に差を取るのではなく「二乗」することには、大きな意味があります。それは、「大外し」に対して、極端に重いペナルティを与えるためです。
例えば、血圧の予測を考えてみましょう。
- ケースA(惜しい): 正解120mmHgに対して、AIが「122」と予測。
ズレは2です。二乗すると \(2^2 = 4\) のペナルティ(痛み)になります。 - ケースB(大外し): 正解120mmHgに対して、AIが「140」と予測。
ズレは20です。しかし二乗すると \(20^2 = 400\) のペナルティになります。
ズレは「10倍」ですが、ペナルティは「100倍」になっていますね。
医療において、少しの誤差は許容範囲でも、極端な判断ミスは患者さんの命に関わる重大なリスクとなります。
「小さなミスは優しく叱るが、大きなミスは雷を落とす」。MSEは、そんなメリハリのある指導医のような関数なのです。
② 交差エントロピー誤差(Cross-Entropy):分類タスク(AかBか)
こちらは、「病気あり/なし」「悪性/良性」といったカテゴリーを分類するタスクで使われます。
【数式の意味】
これは、「正解のラベルに対する自信のなさ」を罰する計算式です。
\[ L = – \sum_{i} y_i \log(\hat{y}_i) \]
- \( y_i \): 正解ラベル(例:がん=1, 正常=0)
- \( \hat{y}_i \): AIが出した「がんである確率」(0〜1の間)
- \( \log \): 対数関数。ここでは「確率が低いほど、値がマイナス無限大に急降下する」性質を利用します。
【直感的な理解:自信満々の間違いを許さない】
この関数は、「自信満々で間違えた時」に最大のペナルティ(無限大の痛み)を与えます。
例えば、ある画像が「悪性腫瘍(正解=1)」だったとします。
- AI「たぶん悪性です(確率0.9)」
\(- \log(0.9) \approx 0.1\)
→ 痛みは小さい。「よくできたね」と褒められます。 - AI「たぶん悪性です(確率0.6)」
\(- \log(0.6) \approx 0.5\)
→ 痛みは中くらい。「もう少し自信を持って」と指導されます。 - AI「絶対に良性です!悪性の確率は0.01です!」(大間違い)
\(- \log(0.01) \approx 4.6\)
→ 激痛が走ります。
もしAIが「悪性の確率は0(絶対ない)」と言い切って間違えた場合、ペナルティは計算上「無限大」になります。
臨床現場において、見逃し(False Negative)を「異常なし」と断言してしまうことほど恐ろしいことはありません。交差エントロピーは、そのような「根拠のない過信」を徹底的に矯正するように働くのです。
このように、損失関数は単なる数式ではなく、「どのようなAI医師に育ってほしいか」という教育方針そのものと言えます。
タスクの性質(数値を当てたいのか、白黒つけたいのか)に合わせて、適切な「教育方針(損失関数)」を選んであげることが、優れたAIを育てる第一歩なのです。
3. 最適化アルゴリズム(Optimizer):改善への羅針盤
損失関数によって「自分の診断がどれくらい間違っていたか(Loss)」は分かりました。しかし、間違っていると分かっただけでは成長しません。
次は、「じゃあ、どう思考回路(パラメータ)を修正すれば、次は正解できるのか?」を考え、実行する必要があります。
この「修正の実行部隊」としての役割を担うのがオプティマイザ(Optimizer:最適化アルゴリズム)です。
このプロセスは、よく「霧のかかった山を下る」ことに例えられます。
【イメージ:霧の山下り】
- 現在地(山の頂上付近):Lossが高い状態(診断が下手)。
- 目的地(谷底):Lossが0の状態(診断が完璧)。
- 状況:濃い霧で視界ゼロ。谷底がどっちにあるか見えません。
- 頼れるもの:足元の傾斜(勾配:Gradient)のみ。
「谷底は見えないけれど、足元を見ると右側が下り坂になっている。とりあえず右に一歩進もう」
これを何万回も繰り返して、少しずつ谷底(正解)へ近づいていくのです。この手法を勾配降下法(Gradient Descent)と呼びます。
SGD(確率的勾配降下法):基本にして王道
最も基本的で、古典的な手法です。
シンプルに「今の足元の傾斜(勾配)を見て、その反対方向(下る方向)に一歩進む」ということを繰り返します。
数式で見ると難しそうですが、やっていることは単純です。
\[ w_{new} = w_{old} – \eta \cdot \nabla L \]
- \( w \):パラメータ(脳内の重み)。
- \( \nabla L \):損失の勾配。「こっちに行くとLossが増えちゃうよ(上り坂だよ)」という方向。
- \( – \)(マイナス):勾配の「逆方向(下り坂)」に進むため。
- \( \eta \)(イータ):学習率。「一歩の大きさ」を調整する係数。
【SGDの特徴と弱点】
SGDは、目の前のデータ(患者さん1人や少数のグループ)だけを見て判断します。
そのため、ある患者さんには「右に行け」、次の患者さんには「左に行け」と言われるがままに動くため、ジグザグとした動きになりやすく、谷底にたどり着くのに時間がかかることがあります。
Adam(Adaptive Moment Estimation):現代のデファクトスタンダード
現在、ディープラーニングの世界で「とりあえずこれを使っておけば間違いない」と言われる事実上の標準(デファクトスタンダード)が、このAdam(アダム)です (Kingma & Ba, 2014)。
SGDの弱点を克服するために、以下の2つの「賢い機能」が追加されています。
- 慣性(Momentum)の利用:
「さっきまで右に進んでいたから、急に左と言われても、右への勢いを少し保とう」という考え方です。
重いボールが坂を転がるように、多少のデコボコがあっても、慣性でスムーズに谷底へ向かいます。これにより、SGDのようなジグザグした動きが抑えられます。 - 適応的学習率(RMSpropの要素):
パラメータごとに「更新の大きさ」を自動調整します。
「この判断基準はずっと大きくブレているから少し慎重に更新しよう」「こっちは滅多に動かないから、動くときは大胆に変えよう」と、状況に合わせて歩幅を変えてくれる機能です。
【臨床医へのアナロジー:SGD vs Adam】
- SGDは「素直すぎる研修医」:
目の前の症例1例ごとに「次はこうします!」「やっぱりあっちでした!」と、その都度全力で方針を変えてしまい、なかなか定まりません。 - Adamは「経験豊富なベテラン指導医」:
「この症例は例外的なノイズかもしれない。これまでの傾向(慣性)を踏まえると、方針は大きく変えないほうがいい」
「この検査値は稀にしか異常が出ないから、出たときは重視しよう(適応的学習率)」
このように、過去の経験を踏まえつつ、柔軟かつ安定して正解(谷底)へと近づいていけるのです。
実際にコードを書く際は、迷ったらまず optim.Adam を選択するのが現代のセオリーです。
SGD (研修医)
基本にして王道。目の前のデータに全力。
Adam (指導医)
慣性と適応学習率。経験を活かす。
「次へ」を押して、2つのアルゴリズムの動きの違いを観察してください。
4. 学習率(Learning Rate):修正の「さじ加減」を決める最重要パラメータ
最適化アルゴリズム(SGDやAdam)が「どちらに進むか(方向)」を決めるコンパスだとしたら、学習率(Learning Rate, \(\eta\))は「どれくらいの歩幅で進むか(大きさ)」を決めるアクセルです。
これはAIの学習において、最も調整が難しく、かつ結果に直結する重要なハイパーパラメータです。
臨床で言えば、「薬の種類(オプティマイザ)」が決まった後に、「投与量(学習率)」をどうするか、という決断に似ています。
数式では、勾配(\(\nabla L\))に掛かる係数として登場しましたね。
\[ w_{new} = w_{old} – \underbrace{\eta}_{\text{学習率}} \cdot \nabla L \]
この値が不適切だと、AIは永遠に賢くなれません。具体的に何が起こるのか見てみましょう。
ケースA:学習率が「大きすぎる」場合(Over-shooting)
「早く正解にたどり着きたい!」と焦って学習率を大きくしすぎると、谷底(正解)を通り越して対岸の山に登ってしまいます。
最悪の場合、谷の両側を行ったり来たりして振動し続けたり、どこか遠くへ飛んでいってしまったりして、いつまでも収束しません(発散)。
- イメージ:ゴルフで力任せにパターを打ち、カップを何度も通り過ぎて行ったり来たりしている状態。
- 臨床アナロジー:薬の量が多すぎて、副作用(発散)が出てしまい、治療どころではなくなる状態。
ケースB:学習率が「小さすぎる」場合(Slow Convergence)
慎重になりすぎて学習率を小さくしすぎると、谷底に向かうスピードが遅くなりすぎます。
学習が終わるまでに途方もない時間がかかるだけでなく、本当の谷底(大域的最小解)の手前にある「小さな窪み(局所解:Local Minima)」にハマってしまい、「ここがゴールだ」と勘違いして抜け出せなくなるリスクがあります。
- イメージ:アリのような歩幅で富士山を下山しようとしている状態。日が暮れてしまいます。
- 臨床アナロジー:薬の量が少なすぎて、病状が全く改善しない(収束しない)状態。
【図解:学習率の影響】
現場での「相場観」とテクニック
通常、学習率は 0.001 (1e-3) や 0.0001 (1e-4) 程度からスタートするのがセオリーです。
学習の推移(Lossの減り方)グラフを見ながら、「減りが遅いな(小さすぎる?)」や「ギザギザして安定しないな(大きすぎる?)」と判断し、調整していきます。
【応用テクニック:学習率スケジューリング】
熟練の医師が、最初は標準量を投与し、症状が落ち着いてきたら徐々に減薬していくように、AI学習でも「最初は大きめの歩幅で大胆に進み、ゴールが近づいたら歩幅を小さくして慎重に位置合わせをする」という手法(Learning Rate Scheduling)がよく使われます。
これにより、スピードと精度の両立を目指すのです。
5. 効率的な学習のために:Batch, Epoch, DataLoader
さて、学習の仕組みは分かりましたが、実際に「10万人の患者データ」が手元にあるとして、これをAIにどう渡せば効率よく勉強してくれるでしょうか?
「全部まとめてドン!」と渡すべきか、「一人ひとり丁寧に」渡すべきか。ここは計算資源(マシンスペック)と学習効率のバランスが問われる腕の見せ所です。
ここで登場する3つの重要用語「バッチサイズ」「エポック」「データローダー」を、医学部の勉強法に例えて完全にマスターしましょう。
① ミニバッチ学習(Mini-batch Learning):32症例ごとのカンファレンス
10万人のデータをAIに学習させる方法は、大きく3つあります。
- 一括学習(バッチ学習):
10万人全員のデータを一度に見て、全員分の誤差を計算してから、たった1回だけパラメータを更新する方法。
× デメリット:メモリ(脳の容量)がパンクしますし、更新回数が少なすぎて学習が進みません。 - オンライン学習(確率的勾配降下法):
患者さん1人を見るたびに、毎回パラメータを更新する方法。
× デメリット:1人のデータに振り回されすぎます。たまたま例外的な症例に当たると、学習の方向が大きくブレてしまい不安定です。 - ミニバッチ学習(現在の主流!):
「32人」や「64人」といった小グループ(ミニバッチ)に分けて学習する方法。
◎ メリット:「32人の症例を診たら、一度ミニ・カンファレンスを開いて知識を修正する」というサイクルです。計算も速く、学習の方向も安定します。
この「一度に渡すデータの数」をバッチサイズ(Batch Size)と呼びます。通常は \(2^n\) (32, 64, 128…)の数字が選ばれます。
② エポック(Epoch):教科書を何周したか
ミニバッチ学習を繰り返して、手持ちのデータ(10万人分)を「一通りすべて」学習し終えることを、「1エポック(Epoch)」と言います。
私たちも、分厚い医学書を1回読んだだけで完璧に覚えるのは無理ですよね?
AIも同じです。1周目(1エポック目)では全体の傾向をなんとなく掴み、2周目、3周目と繰り返すことで、細かい特徴まで深く理解できるようになります。
- 1 エポック = 全データを1回学習した状態。
- 学習回数 = (データ総数 ÷ バッチサイズ)× エポック数
③ DataLoader:優秀な「配膳係」
では、この「10万個のデータを32個ずつに切り分け、順番にAIに渡す」という面倒な作業を、誰がやるのでしょうか?
手動でやるのは大変すぎますよね。
そこで活躍するのが、PyTorchのDataLoader(データローダー)です。
これは、AI専属の「超優秀な配膳スタッフ」だと思ってください。以下の仕事を全自動でこなしてくれます。
【DataLoaderの仕事】
- 🍰 1. 小分けにする(Batching)
膨大なデータを、指定されたバッチサイズ(例:32)に綺麗に切り分けます。 - 🎲 2. シャッフルする(Shuffling)
これが非常に重要です。「前半は全部がん患者、後半は全部正常」のような偏った順序で学習すると、AIは変な癖がついてしまいます。
DataLoaderはトランプを切るように毎回データを混ぜ合わせ、ランダムな順序で提供してくれます。 - ⚡ 3. 高速に運ぶ(Parallel Loading)
AIが学習している間に、裏で次のデータを準備(ロード)しておき、待ち時間ゼロで次々と「おかわり」を出してくれます。
コード上では、このDataLoaderをforループで回すだけで、あとは勝手にバッチサイズ分のデータを取り出してきてくれます。
私たちがすべきなのは、「配膳係(DataLoader)」を雇って、「32個ずつ持ってきてね」と指示するだけなのです。
まとめ:コードで見る学習サイクル ― AI育成のレシピ
これまで学んできた「モデル」「損失関数」「オプティマイザ」、そして「データローダー」。
これら全てのパーツを組み合わせると、AIを育てるための「学習ループ(Training Loop)」が完成します。
以下のコードは、PyTorchを使った学習の「基本の型(テンプレート)」です。
どんなに複雑な最新AIも、基本的にはこの型に従って動いています。一行ずつ、臨床の現場に置き換えて読み解いてみましょう。
import torch
import torch.nn as nn
import torch.optim as optim
# ==========================================
# 1. 道具の準備(セットアップ)
# ==========================================
# ① 脳を用意する(モデルのインスタンス化)
model = MyMedicalAI()
# ② 採点基準を決める(損失関数)
# ここでは「回帰(数値を当てる)」用のMSE(平均二乗誤差)を選択
criterion = nn.MSELoss()
# ③ 教育係を決める(オプティマイザ)
# 修正担当は「Adam」、学習率(指導の厳しさ)は0.001
optimizer = optim.Adam(model.parameters(), lr=0.001)
# ==========================================
# 2. 学習ループ(研修医の修行)
# ==========================================
# 「教科書(全データ)」を10周する
num_epochs = 10
for epoch in range(num_epochs):
running_loss = 0.0
# データローダーから「ミニバッチ(32症例)」ずつ取り出す
# inputs: 患者データ(レントゲン等), labels: 正解(診断結果)
for inputs, labels in dataloader:
# --------------------------------------
# ステップ①:頭を空っぽにする(勾配の初期化)
# --------------------------------------
# 前回の学習で残った「反省(勾配)」をリセットします。
# これを忘れると、過去の反省が蓄積されて混乱してしまいます。
optimizer.zero_grad()
# --------------------------------------
# ステップ②:診断を下す(Forward: 順伝播)
# --------------------------------------
# 患者データ(inputs)を見て、AIなりの答え(outputs)を出します。
outputs = model(inputs)
# --------------------------------------
# ステップ③:答え合わせ(Loss Calculation)
# --------------------------------------
# AIの答え(outputs)と正解(labels)を比較し、
# 間違いの大きさ(loss)を計算します。
loss = criterion(outputs, labels)
# --------------------------------------
# ステップ④:原因究明(Backward: 誤差逆伝播)
# --------------------------------------
# 「なぜ間違えたのか?」を振り返り、
# 修正すべきパラメータの方向と量(勾配)を計算します。
loss.backward()
# --------------------------------------
# ステップ⑤:思考の修正(Optimization)
# --------------------------------------
# 計算された勾配に基づいて、実際にパラメータを更新(学習)します。
optimizer.step()
# --------------------------------------
# 記録:進捗確認用
# --------------------------------------
running_loss += loss.item()
# 1エポック(教科書1周)終わるごとに、成績を表示
print(f'Epoch {epoch+1}, Total Loss: {running_loss:.4f}')
print("学習完了!一人前のAI医師になりました。")このサイクルの本質
いかがでしたか?
プログラムのコードを見ると難しく感じるかもしれませんが、やっていることは非常に人間的です。
- 予測する(Forward)
- 間違いを認める(Loss)
- 原因を考える(Backward)
- 修正して次に活かす(Optimizer Step)
このサイクルは、私たち人間が新しいスキルを習得するプロセスと全く同じです。
このループがコンピュータの中で高速に(1秒間に何百回も!)回転することで、AIは少しずつ、しかし着実に「医療の目」を養っていくのです。
次回は、いよいよAIに「視覚」を与える技術、画像認識モデル(CNN)の実践に入ります。
レントゲンやCT画像から、病変の特徴を自動で抽出する仕組みに迫りましょう!
参考文献
- Goodfellow, I., Bengio, Y. and Courville, A. (2016). Deep Learning. MIT Press.
- Kingma, D.P. and Ba, J. (2014). Adam: A Method for Stochastic Optimization. International Conference on Learning Representations (ICLR).
- Paszke, A. et al. (2019). PyTorch: An Imperative Style, High-Performance Deep Learning Library. Advances in Neural Information Processing Systems 32 (NeurIPS 2019).
- Topol, E.J. (2019). High-performance medicine: the convergence of human and artificial intelligence. Nature Medicine, 25(1), pp.44–56.
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






