AIは水晶玉で未来を見ているわけではありません。過去のデータという「星空」に、最も合理的な「線(トレンド)」や「境界(区切り)」を描く幾何学的な作業こそが、予測医療の本質です。
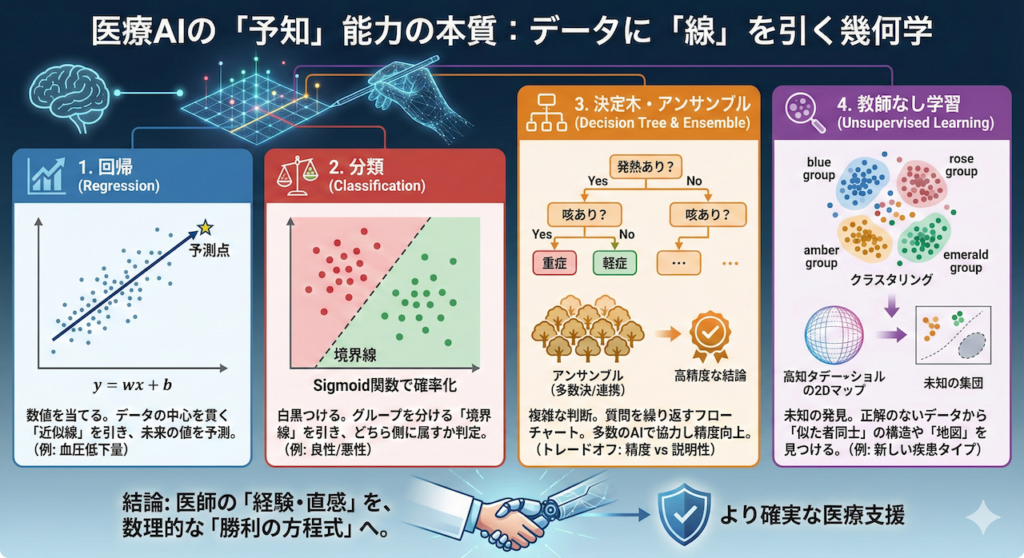
「血圧が何mmHg下がるか?」など、具体的な数値を当てます。データの中心を貫く「近似線」を引き、その延長線上で未来を予測します。
「良性か悪性か?」などの白黒(クラス)を判定します。グループを分ける「境界線」を見つけ、確率はシグモイド関数で計算します。
「熱はある?→Yes」のように質問を繰り返し、フローチャートで判断します。何百人のAIで多数決をとる「アンサンブル」は最強の精度を誇ります。
正解のないデータから「似た者同士」を集めたり(クラスタリング)、複雑な情報を要約して未知の地図を描きます。新種発見の鍵です。
診療の現場において、私たちは常に「未来」と向き合っています。
「この治療を行えば、1ヶ月後の検査値はどう変化するか?」「この患者さんが5年以内に再発する確率はどれくらいか?」。医師の頭の中では、経験とエビデンスに基づいた高度なシミュレーション、すなわち「予測(Prediction)」が絶えず行われています。
近年、医療AIがこの「予測」の精度を飛躍的に向上させていますが、AIは決して水晶玉で未来を見通しているわけではありません。実は、AIが行っていることの正体は、驚くほどシンプルで、かつ泥臭い作業です。
それは、「データという夜空に散らばる星々の間に、一本の最適な『線』を引くこと」。
今回は、機械学習の根幹をなす「回帰(数値を当てる)」と「分類(白黒つける)」、さらに複雑な現実に対応するための「決定木(判断の樹形図)」や「クラスタリング(未知の地図作り)」といった概念を通じて、AIがどのようにして過去のデータから未来の勝利の方程式を導き出しているのか、その幾何学的な思考プロセスを紐解いていきましょう。
1. 未来はグラフの上にある:散布図という「星空」
まず、AIが世界をどのように「見ている」のか、その視点を共有しましょう。
私たち人間は、患者さんの顔色や話し方といった五感からの情報も大切にしますが、AIにとっての現実はすべて「数値」と「座標」の中にあります。
具体的なシナリオで考えてみます。ある降圧薬の「投与量(\(x\) mg)」と、それによって得られる「血圧低下量(\(y\) mmHg)」の関係を知りたいとしましょう。
過去数百人の患者さんの臨床データを集めて、グラフ上にプロットしていくとどうなるでしょうか?
教科書のように綺麗な一直線には決してなりません。点はバラバラに散らばり、まるで夜空の星々のようなカオスな模様を描きます。
なぜなら、人体は工場製品ではないからです。年齢、遺伝的背景、腎機能、塩分摂取量、測定時の緊張感……無数の「ノイズ(個人差や誤差)」が入り込むため、同じ20mgを投与しても、10mmHg下がる人もいれば、30mmHg下がる人もいます。
この点の集まりを統計学では「散布図(Scatter Plot)」と呼びます。
この散布図こそが、AIにとっての「星空」です。
そしてAIに課せられたミッションは、この混沌とした星々の配置を眺め、その中心を貫く隠された法則性(=星座のライン)を見つけ出すことに他なりません。
2. 回帰分析(Regression):数値を当てる「予言の矢」
「もし、この患者さんに投与量を25mgに増量したら、血圧は具体的に何mmHg下がるだろうか?」
このように、「Yes/No」ではなく、具体的な「数値(連続値)」をピンポイントで予測するタスクを、機械学習の世界では「回帰(Regression)」と呼びます。
本来「回帰」という言葉は、フランシス・ゴルトンが「背の高い親の子は、平均的な身長に近づく(平均への回帰)」という現象を発見したことに由来しますが、現代のAIにおいては「入力データから、出力数値を導き出す関数を作ること」を指します(Bishop, 2006)。
直線を引くことの意味
なぜ、散布図に線を引くことが「予測」になるのでしょうか?
それは、「過去のデータの中心を貫く直線こそが、未来のデータが通るであろう『最も確からしい道』である」と仮定するからです。
一度この「道(モデル)」が完成すれば、まだ試していない「未知の投与量(\(x\))」が決まった瞬間に、その線上の点として「予測される効果(\(y\))」が自動的に求まります。
この直線を数式で表すと、中学数学で慣れ親しんだ一次関数の形になります。これが最もシンプルなAIの思考回路です。
\[ y = wx + b \]
- \(y\)(目的変数 / Target):予測したい未来の結果(例:血圧低下量 mmHg)
- \(x\)(説明変数 / Feature):予測の手がかりとなるデータ(例:投与量 mg)
- \(w\)(重み / Weight):直線の「傾き」。そのデータが結果にどれほど強く影響するかを表す係数。
(例:\(w\)が大きければ「この薬は少量でもガツンと効く」ことを意味します) - \(b\)(バイアス / Bias):直線の「切片」。入力がゼロの時のベースライン値。
(例:プラセボ効果や自然変動など、薬以外の要因による変化)
AIの学習=「定規」の微調整
では、AIはどのようにして「最適な線」を見つけるのでしょうか?
最初は、AIも適当な線を引いています。しかし、AIは大量のデータを読み込むたびに、「現実のデータ点」と「自分の引いた線」とのズレ(誤差)を計算し、そのズレが最小になるように、持っている定規の「角度(\(w\))」と「位置(\(b\))」を少しずつ動かしていきます。
この「ズレの二乗の合計」を最小にする数学的手法を、最小二乗法(Least Squares Method)と呼びます。
\[ \text{誤差} E = \sum_{i=1}^{n} (y_i – (wx_i + b))^2 \]
AIが「学習中」と言っている時、その内部では、この誤差 \(E\) をゼロに近づけるために、ひたすら計算と修正(パラメータの更新)を繰り返しているのです(Hastie et al., 2009)。
3. 分類(Classification):白黒つける「境界線」
一方で、医療の現場では「数値」を予測するだけでは不十分な場面が多々あります。最終的に求められるのは、明確な「決断」だからです。
「この腫瘍は良性か、それとも悪性か?」「この患者さんは5年後に生存しているか、否か?」「ICUに入室させるべきか、一般病棟でよいか?」
このように、連続的な数値ではなく、データを特定のカテゴリー(クラス)に分けるタスクを、機械学習では「分類(Classification)」と呼びます。
「分かつ線」を引く
ここでもAIは「線」を引きます。しかし、その線の意味合いは「回帰」とは全く異なります。
- 回帰の線:データの中心を貫く「近似線」(トレンドを表す)。
- 分類の線:データとデータの間を切り分ける「境界線(Decision Boundary)」(エリアを分ける)。
例えば、腫瘍マーカーの値と腫瘍の大きさをグラフにした時、悪性のグループ(●)と良性のグループ(○)を綺麗に分けるような線を見つけることができれば、新しい患者さんのデータ(?)が線のどちら側に落ちるかで、診断を予測できます。
ロジスティック回帰:確率への変換装置
この分類問題において、医学研究で最も頻繁に用いられるアルゴリズムが「ロジスティック回帰分析(Logistic Regression)」です。
名前に「回帰」と付いているため混乱しやすいのですが、これは立派な「分類」のための手法です。では、なぜ「回帰」の手法を使って「分類」ができるのでしょうか? その秘密は、計算結果を通す「変換装置」にあります。
通常の直線の式 \(y = wx + b\) のままでは、計算結果が「マイナス無限大」から「プラス無限大」までいってしまい、「確率(0%〜100%)」として扱うことができません(確率は必ず0から1の間でなければなりません)。
そこで、この直線の出力を「シグモイド関数(Sigmoid Function)」という特殊な関数に通します。すると、どんなに大きな値も小さな値も、魔法のように 0 から 1 の範囲(0% 〜 100%) にギュッと押し込められてしまうのです。
\[ P(y=1 \mid x) = \dfrac{1}{1 + e^{-(wx + b)}} \]
- \(P(y=1 \mid x)\):あるデータ \(x\) が与えられた時、結果が陽性(1)である確率。
- \(e\):ネイピア数(自然対数の底)。
この変換によって、AIは「スコア:1500」といった曖昧な数値ではなく、「悪性である確率:85%」といった具体的なリスク確率を出力できるようになります。
そして、「確率が50%(0.5)以上なら陽性(黒)、未満なら陰性(白)」というルール(閾値)を決めることで、最終的な白黒(クラス分類)をつけるのです。
心血管疾患の10年発症リスクを予測する有名な「Framinghamリスクスコア」も、この多変量ロジスティック回帰モデルの原理を応用して構築されています(Wilson et al., 1998)。
4. 「直線」で引けない現実はどうする?(モデル選択の羅針盤)
ここまで、データを「直線」で切る話をしましたが、臨床の現実はそう単純ではありません。
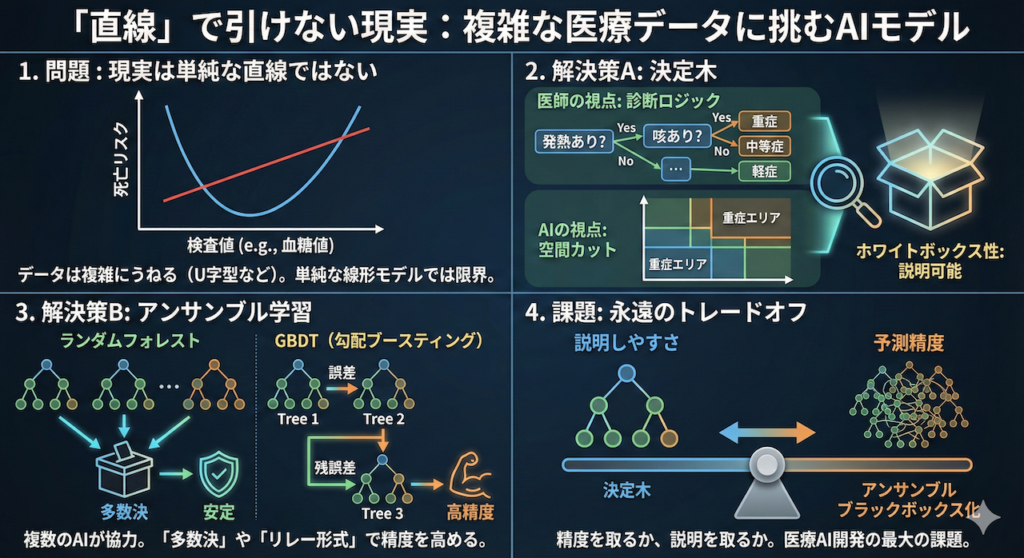
例えば、血糖値やコレステロール値は、高すぎても低すぎても死亡リスクが上がる「U字型(またはJ字型)」のカーブを描くことがよくあります。「薬を増やせば増やすほど効く(直線関係)」とは限らず、ある量を超えると副作用で逆に悪化することもあります。
データが直線ではなく、複雑にうねっていたり、飛び地になっていたりする場合、定規で直線を引くだけの単純なAI(線形モデル)では太刀打ちできません。では、どうすればよいのでしょうか?
決定木(Decision Tree):AIが作るフローチャート
ここで登場するのが、私たち医師にとって非常に馴染み深い「診断アルゴリズム」のような構造を持つモデル、決定木(Decision Tree)です。
これは、データを一度に線で切るのではなく、「質問」を繰り返しながら段階的に絞り込んでいく手法です。「熱はあるか? Yesなら右へ」「咳はあるか? Noなら左へ」……。これは幾何学的には、空間を縦横にカットして「階段状の境界線」を作り、データを四角い領域に囲い込んでいく作業に似ています。
決定木の最大のメリットは、「中身が完全に透けて見える(ホワイトボックス)」であることです。
AIが「この患者さんは重症化リスクが高い」と予測した時、医師はその理由を「発熱があり、かつ酸素飽和度が低かったからだ」とトレース(追跡)することができます。これは、説明責任が問われる医療現場において極めて重要な特性です。
ランダムフォレスト・GBDT:三人寄れば文殊の知恵
しかし、たった一つの決定木だけでは、たまたまそのデータの癖に引きずられて判断を誤る(過学習する)ことがあります。
そこで生まれたのが、「一人でダメなら、何百人ものAIで相談して決めよう」という発想です。これをアンサンブル学習(Ensemble Learning)と呼びます。
- ランダムフォレスト(Random Forest):
データを少しずつ変えて育てた何百本もの決定木に投票させ、「多数決」で結論を出します。「三人寄れば文殊の知恵」を地で行く、非常に安定した手法です。 - GBDT(勾配ブースティング決定木):
XGBoostやLightGBMなどが代表格です。これは多数決というより「リレー形式」です。1人目のAIが間違えた問題を、2人目のAIが重点的に復習して修正し、さらに3人目が……と、弱点を補強しながら精度を高めていきます。
これら(特にGBDT)は、現代の医療データ分析(テーブルデータ)において、しばしばディープラーニングをも凌駕する最強クラスの予測精度を叩き出します。
「精度」か「説明」か? 永遠のトレードオフ
しかし、ここには落とし穴があります。何百本もの木が複雑に絡み合った結果、人間にはもはや「なぜそう判断したのか」が直感的に理解できなくなってしまうのです。これが「ブラックボックス化」の問題です。
「理由はわからないけれど、99%の確率で癌です」というAIを、医師や患者は受け入れられるでしょうか?
「精度(Accuracy)」を取るか、「説明しやすさ(Interpretability)」を取るか。このトレードオフは、医療AI開発における最大の課題の一つとなっており、近年ではブラックボックスの中身を解釈するための技術(SHAP値など)の研究も進んでいます(Lundberg et al., 2017)。
5. 正解のないデータから「患者像」を浮かび上がらせる(教師なし学習)
ここまでの話(回帰、分類、決定木)はすべて、データの中に「正解(診断結果や予後など)」が含まれていることを前提としていました。これを専門用語で「教師あり学習(Supervised Learning)」と呼びます。「入力(問題)」と「出力(模範解答)」のセットを与えて、AIにパターンを暗記させる方法です(Bishop, 2006; Hastie et al., 2009)。
しかし、医学の世界は既知のことばかりではありません。未知のウイルス、原因不明の症候群、複雑に絡み合った慢性疾患……。そもそも「何が正解なのか誰も知らない」場合はどうすればよいのでしょうか?
AIには、正解(教師)を与えられなくても、データそのものの構造を読み解き、勝手にルールを見つけ出す能力があります。これを「教師なし学習(Unsupervised Learning)」と呼びます。
クラスタリング:似たもの同士を集める
その代表的な手法が「クラスタリング(Clustering)」です。
例えば、敗血症のような複雑な病態を持つ何千人もの患者データを、正解(重症度分類など)を教えずにAIに投げ込み、「バイタルサインや検査値が似ている患者さん同士でグループを作って」と指示します(K-Means法など)。
するとAIは、人間が見落としていた微細な特徴の組み合わせを発見し、「実はこの病気、これまで考えられていた3タイプではなく、全く異なる特徴を持つ4つのサブタイプ(表現型)に分かれますよ」と提案してくることがあります。
実際に2019年のJAMA誌に掲載された研究では、AI(機械学習)を用いた解析によって、敗血症患者が従来の重症度分類とは異なる4つの臨床的フェノタイプ(表現型)に分類され、それぞれ治療反応性や予後が大きく異なることが示されました(Seymour et al., 2019)。
次元削減:高次元のデータを「地図」にする
また、遺伝子解析データのように、患者一人につき何万項目もの情報(変数)がある場合、人間にはそれを全体的に把握することは不可能です。私たちは3次元(縦・横・高さ)以上の世界を視覚化できないからです。
そこで使われるのが「次元削減(Dimensionality Reduction)」という技術(PCA, t-SNE, UMAPなど)です。
これは、複雑すぎる多次元データを、情報の意味をなるべく保ったまま、人間が見てわかる2次元や3次元の地図にギュッと圧縮する技術です。
これは、丸い地球(3次元)を、メルカトル図法の地図(2次元)に展開する作業に似ています。AIが描いたこの「地図」を眺めることで、研究者は「あ、ここの集団だけ他と離れている。何か特殊な遺伝子変異があるのかもしれない」といった新たな仮説を立てることができるのです。
教師なし学習は、予測のための「線引き」というより、未知の大陸に足を踏み入れ、「新しい疾患地図(患者層別化)」を描く探索的な作業と言えるでしょう。
6.医師の直感を「勝利の方程式」へ
ここまで見てきたように、AIによる「未来予知」の正体とは、決して魔法の水晶玉などではありませんでした。それは、過去の膨大なデータに基づいて、最も合理的で美しい「数理的な構造(線や境界)」を見つけ出す、極めて論理的なプロセスです。
AIがやっていることを、もう一度シンプルに整理してみましょう。
- 数値を予測したいなら:データの中心を貫く「線」を引く(回帰)。
- 白黒つけたいなら:データの間を区切る「境界線」を引く(分類)。
- 複雑な判断が必要なら:条件分岐の「フローチャート」を作る(決定木・アンサンブル)。
- 正解がないなら:未知の大陸の「地図」を描く(クラスタリング・次元削減)。
これらは実は、熟練の医師が長い臨床経験を通じて無意識のうちに獲得している「直感(クリニカル・パール)」そのものではないでしょうか?
ベテラン医師は、患者さんの僅かな変化から「このカーブは危ない気がする(回帰的直感)」や「この症状の組み合わせはあの病気っぽい(クラスタリング的直感)」を感じ取ります。
AIは、その個人の頭の中にある暗黙知(アート)を、数式という明確な形式知(サイエンス)として記述し、可視化し、そして世界中で共有可能なものにしてくれるのです(Steyerberg, 2019; Moons et al., 2015)。
AIは医師から仕事を奪う敵ではありません。私たちの経験という名の財産を、より確実な「勝利の方程式」へと昇華させてくれる、最強のパートナーなのです。
さて、ここまでは「既にあるデータ」を分析し、線を引く技術について学んできました。
しかし、AIの進化はそこで止まりません。
次回、「A7:生成(Generation)」では、データから線を引くだけでなく、その線(確率分布)に基づいて「この世に存在しない新しいデータ」そのものを生み出す、AIの創造性の源泉に迫ります。
参考文献
- Bishop, C.M. (2006). Pattern Recognition and Machine Learning. New York: Springer.
- Hastie, T., Tibshirani, R. and Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd edn. New York: Springer.
- Lundberg, S.M. and Lee, S.I. (2017). A Unified Approach to Interpreting Model Predictions. Advances in Neural Information Processing Systems, 30.
- Moons, K.G.M., et al. (2015). Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis (TRIPOD): the TRIPOD statement. Annals of Internal Medicine, 162(1), pp.55–63.
- Seymour, C.W., et al. (2019). Derivation, Validation, and Potential Treatment Implications of Novel Clinical Phenotypes for Sepsis. JAMA, 321(20), pp.2003–2017.
- Steyerberg, E.W. (2019). Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating. 2nd edn. Cham: Springer.
- Wilson, P.W., et al. (1998). Prediction of coronary heart disease using risk factor categories. Circulation, 97(18), pp.1837–1847.
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
参考文献
- Bishop, C.M. (2006). Pattern Recognition and Machine Learning. New York: Springer.
- Hastie, T., Tibshirani, R. and Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd edn. New York: Springer.
- Lundberg, S.M. and Lee, S.I. (2017). A Unified Approach to Interpreting Model Predictions. Advances in Neural Information Processing Systems, 30.
- Moons, K.G.M., et al. (2015). Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis (TRIPOD): the TRIPOD statement. Annals of Internal Medicine, 162(1), pp.55–63.
- Steyerberg, E.W. (2019). Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating. 2nd edn. Cham: Springer.
- Wilson, P.W., et al. (1998). Prediction of coronary heart disease using risk factor categories. Circulation, 97(18), pp.1837–1847.
※本記事は情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
ご利用規約(免責事項)
当サイト(以下「本サイト」といいます)をご利用になる前に、本ご利用規約(以下「本規約」といいます)をよくお読みください。本サイトを利用された時点で、利用者は本規約の全ての条項に同意したものとみなします。
第1条(目的と情報の性質)
- 本サイトは、医療分野におけるAI技術に関する一般的な情報提供および技術的な学習機会の提供を唯一の目的とします。
- 本サイトで提供されるすべてのコンテンツ(文章、図表、コード、データセットの紹介等を含みますが、これらに限定されません)は、一般的な学習参考用であり、いかなる場合も医学的な助言、診断、治療、またはこれらに準ずる行為(以下「医行為等」といいます)を提供するものではありません。
- 本サイトのコンテンツは、特定の製品、技術、または治療法の有効性、安全性を保証、推奨、または広告・販売促進するものではありません。紹介する技術には研究開発段階のものが含まれており、その臨床応用には、さらなる研究と国内外の規制当局による正式な承認が別途必要です。
- 本サイトは、情報提供を目的としたものであり、特定の治療法を推奨するものではありません。健康に関するご懸念やご相談は、必ず専門の医療機関にご相談ください。
第2条(法令等の遵守)
利用者は、本サイトの利用にあたり、医師法、医薬品、医療機器等の品質、有効性及び安全性の確保等に関する法律(薬機法)、個人情報の保護に関する法律、医療法、医療広告ガイドライン、その他関連する国内外の全ての法令、条例、規則、および各省庁・学会等が定める最新のガイドライン等を、自らの責任において遵守するものとします。これらの適用判断についても、利用者が自ら関係各所に確認するものとし、本サイトは一切の責任を負いません。
第3条(医療行為における責任)
- 本サイトで紹介するAI技術・手法は、あくまで研究段階の技術的解説であり、実際の臨床現場での診断・治療を代替、補助、または推奨するものでは一切ありません。
- 医行為等に関する最終的な判断、決定、およびそれに伴う一切の責任は、必ず法律上その資格を認められた医療専門家(医師、歯科医師等)が負うものとします。AIによる出力を、資格を有する専門家による独立した検証および判断を経ずに利用することを固く禁じます。
- 本サイトの情報に基づくいかなる行為によって利用者または第三者に損害が生じた場合も、本サイト運営者は一切の責任を負いません。実際の臨床判断に際しては、必ず担当の医療専門家にご相談ください。本サイトの利用によって、利用者と本サイト運営者の間に、医師と患者の関係、またはその他いかなる専門的な関係も成立するものではありません。
第4条(情報の正確性・完全性・有用性)
- 本サイトは、掲載する情報(数値、事例、ソースコード、ライブラリのバージョン等)の正確性、完全性、網羅性、有用性、特定目的への適合性、その他一切の事項について、何ら保証するものではありません。
- 掲載情報は執筆時点のものであり、予告なく変更または削除されることがあります。また、技術の進展、ライブラリの更新等により、情報は古くなる可能性があります。利用者は、必ず自身で公式ドキュメント等の最新情報を確認し、自らの責任で情報を利用するものとします。
第5条(AI生成コンテンツに関する注意事項)
本サイトのコンテンツには、AIによる提案を基に作成された部分が含まれる場合がありますが、公開にあたっては人間による監修・編集を経ています。利用者が生成AI等を用いる際は、ハルシネーション(事実に基づかない情報の生成)やバイアスのリスクが内在することを十分に理解し、その出力を鵜呑みにすることなく、必ず専門家による検証を行うものとします。
第6条(知的財産権)
- 本サイトを構成するすべてのコンテンツに関する著作権、商標権、その他一切の知的財産権は、本サイト運営者または正当な権利を有する第三者に帰属します。
- 本サイトのコンテンツを引用、転載、複製、改変、その他の二次利用を行う場合は、著作権法その他関連法規を遵守し、必ず出典を明記するとともに、権利者の許諾を得るなど、適切な手続きを自らの責任で行うものとします。
第7条(プライバシー・倫理)
本サイトで紹介または言及されるデータセット等を利用する場合、利用者は当該データセットに付随するライセンス条件および研究倫理指針を厳格に遵守し、個人情報の匿名化や同意取得の確認など、適用される法規制に基づき必要とされるすべての措置を、自らの責任において講じるものとします。
第8条(利用環境)
本サイトで紹介するソースコードやライブラリは、執筆時点で特定のバージョンおよび実行環境(OS、ハードウェア、依存パッケージ等)を前提としています。利用者の環境における動作を保証するものではなく、互換性の問題等に起因するいかなる不利益・損害についても、本サイト運営者は責任を負いません。
第9条(免責事項)
- 本サイト運営者は、利用者が本サイトを利用したこと、または利用できなかったことによって生じる一切の損害(直接損害、間接損害、付随的損害、特別損害、懲罰的損害、逸失利益、データの消失、プログラムの毀損等を含みますが、これらに限定されません)について、その原因の如何を問わず、一切の法的責任を負わないものとします。
- 本サイトの利用は、学習および研究目的に限定されるものとし、それ以外の目的での利用はご遠慮ください。
- 本サイトの利用に関連して、利用者と第三者との間で紛争が生じた場合、利用者は自らの費用と責任においてこれを解決するものとし、本サイト運営者に一切の迷惑または損害を与えないものとします。
- 本サイト運営者は、いつでも予告なく本サイトの運営を中断、中止、または内容を変更できるものとし、これによって利用者に生じたいかなる損害についても責任を負いません。
第10条(規約の変更)
本サイト運営者は、必要と判断した場合、利用者の承諾を得ることなく、いつでも本規約を変更することができます。変更後の規約は、本サイト上に掲載された時点で効力を生じるものとし、利用者は変更後の規約に拘束されるものとします。
第11条(準拠法および合意管轄)
本規約の解釈にあたっては、日本法を準拠法とします。本サイトの利用および本規約に関連して生じる一切の紛争については、東京地方裁判所を第一審の専属的合意管轄裁判所とします。
For J³, may joy follow you.






